Реакции опор расчет: Определение реакций опор. Примеры и видео

Содержание

Уточненный расчет валов. Силы в зацеплении. Расчетная схема ведущего вала. Суммарные реакции в опорах. Расчетная схема промежуточного вала

10. Уточненный расчет валов

Рисунок 4.Силы в зацеплении.

Для определения опорных реакций и изгибающих моментов необходимо составить расчетную схему, основанием которой является эскизная компоновка и схема сил в зацеплении. Опорные реакции определяют, составляя уравнение равновесия в каждой из плоскостей действия сил. В цилиндрической прямозубой передаче силу в зацеплении одной пары зубьев раскладывают на две взаимно перпендикулярные составляющие (рисунок 4,а): окружную силу — F_t и радиальную — F_r. В цилиндрической косозубой передаче силу в зацеплении раскладывают на три составляющие (рисунок 4, б): окружную — F_t, радиальную — F_r и осевую — F_a. Окружная сила на шестерне направлена по касательной к делительному диаметру в противоположном направлении вращения, а для колеса направление окружной силы совпадает с направлением вращения.

Радиальные силы направлены по радиусу к центру колес. Радиальная сила в косозубой цилиндрической передаче направлена по радиусу к центру колеса.

Рисунок 5 – Расчетная схема ведущего вала

Определяем реакции опор в вертикальной плоскости ведущего вала.

(10.1)

(10.2)

Проверяем правильность решения в вертикальной плоскости вала:

(10.3)

Реакции опор найдены верно!

Определяем реакции опор в горизонтальной плоскости ведущего вала:

(10. 4)

(10.5)

Проверяем правильность решения в горизонтальной плоскости вала:

(10.6)

Реакции опор найдены верно!

Определяем суммарные реакции в опорах:

(10.7)

(10.8)

Рисунок 6.Расчетная схема промежуточного вала

Определяем реакции опор в вертикальной плоскости промежуточного вала:

(10.9)

(10. 10)

Проверяем правильность решения в вертикальной плоскости вала:

(10.11)

Реакции опор найдены верно!

Определяем реакции опор в горизонтальной плоскости промежуточного вала.

(10.12)

(10.13)

Проверяем правильность решения в горизонтальной плоскости вала:

(10.14)

Реакции опор найдены верно!

Определяем суммарные реакции в опорах по формуле:

(10. 15)

(10.16)

Рисунок 7. Расчетная схема выходного вала

Определяем реакции опор в вертикальной плоскости выходного вала.

(10.17)

(10.18)

Проверяем правильность решения в вертикальной плоскости вала:

(10.19)

Реакции опор найдены верно!

Определяем реакции опор в горизонтальной плоскости выходного вала.

(10.20)

(10.21)

Проверяем правильность решения в горизонтальной плоскости вала:

(10.22)

Реакции опор найдены верно!

Определяем суммарные реакции в опорах:

(10.23)

(10.24)

11. Проверочный расчет подшипников

Определяем эквивалентную нагрузку:

, (11. 1)

где Х – коэффициент радиальной нагрузки, принимаем X=1;

V – коэффициент, учитывающий вращение колец, принимаем V=1,0;

F_r_{_n – радиальная нагрузка
подшипника;}

Y – коэффициент осевой нагрузки;

F_a_{_n – осевая нагрузка;}

- коэффициент безопасности, принимаем = 1,2;

- температурный коэффициент, принимаем = 1,0;

Вал I

Шарикоподшипник № 207

Так как на ведущем валу передача прямозубая, то, следовательно, осевая сила отсутствует.

Принимаем .

Вал II

Шарикоподшипник № 209.

На промежуточном валу передача косозубая, в зацеплении присутствует осевая нагрузка .

В зависимости от отношения , где С₀- статическая грузоподъемность подшипника, определяем коэффициент осевого нагружения по табл. 7.3 [1], где выбираем X и Y.

С₀=17,8 кН.

, данному значению соответствуют коэффициенты x=0,56; y=1,71.

Для дальнейшего расчета определяем отношение , где -реакция в опоре и -сила в зацеплении, и сравнить его с нормативным значением коэффициента е: если данное отношение больше е, то осевую нагрузку F_a учитываем при определении P_экв , если меньше е, то не учитываем.

Данный расчет ведем для наиболее нагруженной опоры.

Принимаем

<-осевую нагрузкуне учитываем.

Принимаем

>-осевую нагрузку учитываем.

Принимаем .

Вал III

Шарикоподшипник № 215

На выходном валу передача косозубая, в зацеплении присутствует осевая нагрузка .

С₀=41,1 кН.

, данному значению соответствуют коэффициенты x=0,56; y=1,99.

a учитываем при определении P_экв , если меньше е, то не учитываем.

Данный расчет ведем для наиболее нагруженной опоры.

Принимаем

<-осевую нагрузкуне учитываем.

Принимаем

>-осевую нагрузку учитываем.

Принимаем .

Определяем расчетную долговечность подшипников по формуле:

(12.1)

(12.2)

где L – долговечность, в млн. об;

L_Н – долговечность, в ч;

С – динамическая грузоподъемность подшипника;

m – коэффициент, равный для шариковых подшипников 3;

n – частота вращения вала;

Вал I

Вал II

Вал III

12. Расчет ведомого вала по переменным напряжениям.

Рисунок 8.Эпюра моментов вычодного вала.

Расчет производим по выходному валу, так как он наиболее нагружен

Расчет реакции в узлах конструкции в программе SCAD Office

Расчет несущей способности здания не ограничивается только подбором основных конструктивных элементов. Немаловажным параметром расчета является расчет узловых соединений, а также предоставление данных об усилиях в узлах. Получить усилия в узле можно, проанализировав эпюры усилий в элементах, или воспользоваться специальным инструментом «Нагрузки от фрагмента схемы». Рассмотрим все возможности работы с этой функцией программного комплекса SCAD Office.

Для начала стоит определиться с группой узлов (в которых необходимо получить реакцию) и группой элементов (с которых будет выполнен сбор усилий). Рассмотрим пример сбора нагрузок в основании колонны.

Исходные данные начинаем вводить с объединения в группы элементов и узлов:

Отметка группы узлов

Отметка группы элементов

В группу узлов попадают те узлы, в которых требуется получить реакцию (для базы колонн – узлы со связями). В группу элементов попадают элементы, усилие с которых требуется проанализировать при получении реакции. Если нет исключений (например, если в узел приходят два элемента, а реакцию надо получить только с одного элемента), то в группу элементов добавляется вся схема. Далее необходимо перейти в дерево процессов и указать, какие именно из множества групп узлов и элементов следует использовать при расчете. После этого жмем «Записать участок».

Анализ результатов происходит в Графическом анализе – постпроцессы. Важно установить текущее направление реакции и загружение (комбинацию). При активации реактивной силы, на схеме будут отображены стрелки направления действия нагрузки на узел. С помощью инструмента «Оцифровка» можно подсветить значение реакции.

Для создания отчетной таблицы реакций по всем опорным узлам (например, для заполнения таблицы КМ в документации) необходимо обратиться в раздел документирования. В графе «Виды результатов выбрать «нагрузки от фрагмента схемы от комбинации загружений», выбрать нужные направления реакций, список узлов (по ранее сформированной группе), и заданную комбинацию.

Результатом может служить таблица в текстовом или табличном редакторе. Выбрав максимальные значения по нескольким комбинациям можно перенести их в таблицу документации раздела КМ.

Пример:

Нагрузки от фрагмента схемы от комбинаций загружений

Единицы измерения:

Силы: Т
Единицы длины для силовых факторов: м

Параметры выборки:

Список узлов/элементов: 1 3 25 27 49 51 73 75 97 99 121 123

Список загружений/комбинаций: 1

Список факторов: R_X, R_Y, R_Z, R_UX, R_UY, R_UZ

Нагрузки от фрагмента схемы от комбинаций загружений
Узел	Комбинация	Значение
		R_X	R_Y	R_Z	R_UX	R_UY	R_UZ
1	1	0. 099	0.015	8.188	-0.036	0.682	-2.601e-004
3	1	-0.099	0.015	8.188	-0.036	-0.682	2.601e-004
25	1	0.181	0.005	15.173	-0.014	1.288	-1.408e-004
27	1	-0.181	0.005	15. 173	-0.014	-1.288	1.408e-004
49	1	0.189	1.059	15.504	0.011	1.314	-7.77e-005
51	1	-0.189	1.061	15.504	0.011	-1.314	7.777e-005
73	1	0.19	-1.059	15.518	-0.011	1. 323	-5.055e-005
75	1	-0.19	-1.061	15.569	-0.011	-1.323	5.048e-005
97	1	0.181	-0.005	15.185	0.015	1.291	1.392e-004
99	1	-0.181	-0.005	15.236	0.015	-1.291	-1. 392e-004
121	1	0.099	-0.015	8.188	0.035	0.682	2.509e-004
123	1	-0.099	-0.015	8.188	0.035	-0.682	-2.509e-004

Следует отметить, что для узла может быть несколько различных сочетаний нагрузок, ориентироваться при этом нужно на максимальный изгибающий момент, поперечную и продольную силу при соответствующем действии остальных нагрузок.

Таким же способом можно получить реакцию в узле, не имеющим связевых закреплений. Для этого создаем новую группу узлов, в которую попадает нужный нам узел, и группу элементов, с которых хотим собрать усилия на этот узел. В примере ниже изображена колонна с консолью, я хочу получить изгибающий момент от действия крановой нагрузки, если я хочу также учесть вес конструкции выше, то выберу верхнюю часть колонны, если этого не нужно, то выделенным оставляем только консоль и добавляем ее в группу элементов.

В нашем случае реакция момента консоли пригодится нам для расчета узла крепления консоли, продольная сила здесь нам не нужна, поэтому в нашем случае в группу элементов попадает только консоль.

Таким образом, можно вычислить реакцию в любом ферменном узле, узле крепления балки к колонне, стыковом узле балок и др. Полученные усилия можно использовать для формирования таблицы рабочей документации и, соответственно, для расчета самого узла, например, в программе КОМЕТА 2.

Механика для людей — Расчет опорных реакций для простой двухопорной балки

Рефераты и письменные задания, выполненные для вас

Получите помощь с любым заданием — от школьного эссе до кандидатской диссертации

Дизайн схема балки представлена на рис. 1

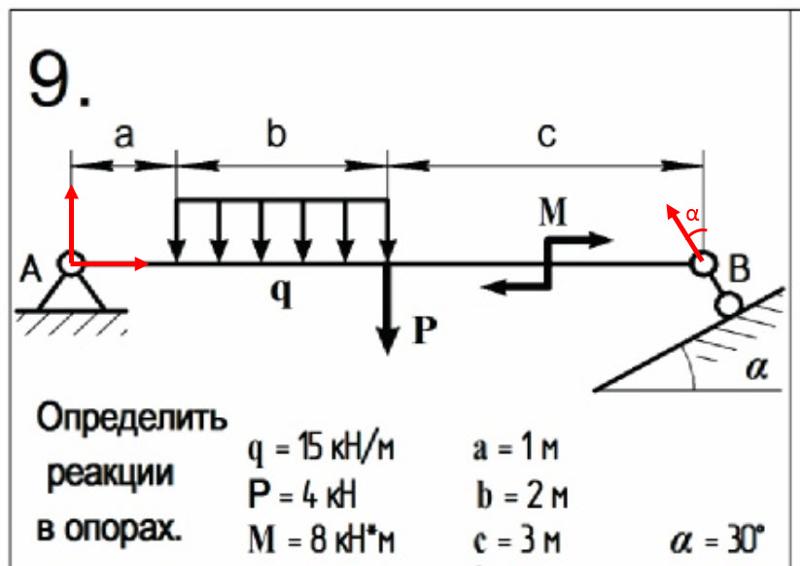
Для заданной двухопорной балки с консольной частью, нагруженной комплексом нагрузки: силой F, моментом m и распределенной нагрузкой q, определить величину и направление опорных реакций.

Рис. 1

Пролет балки 3 м. Длина консольной части 1,5м.

Расчет опорных реакций

Рекомендуем посмотреть наш видеоурок по расчету опорных реакций балки:

Видео по теме (содержит субтитры)

Для решения задачи обозначим характерные точки (сечения) балки (точки А, В, С и D) и определить положение системы координат y-z, выбрав ее начало например в объеме А (рис. 2)

Рис.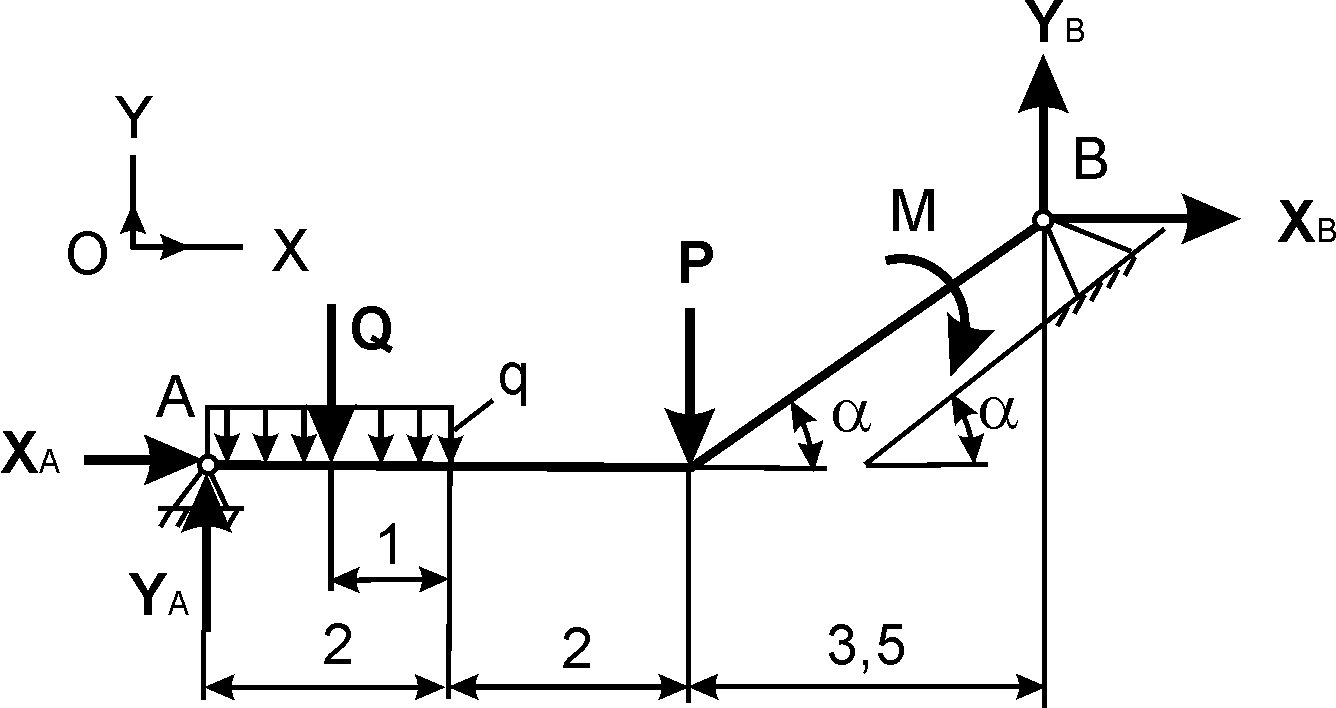 2

Обе балочные опоры шарнирные, поэтому в каждой из них будет возникать только сила, обозначим их соответственно R _A и R _C

Так как все приведенные нагрузки расположены исключительно в вертикальном плоскость (плоскость поперечного изгиба) и не дают проекций на ось z, то и опорные реакции будут только вертикальными.

Вообще говоря, реакции в опорах – это такие силы, которые необходимы для удержания балки с приложенными к ней нагрузками в статическом (неподвижном) состоянии. В данном случае эти силы не позволяют ему вращаться и двигаться в вертикальной плоскости.

Эту балку можно определить статически, поскольку уравнений равновесия достаточно для определения неизвестных сил в опорах балки.

Для составления уравнений статики опорные реакции R _A и R _C предварительно направляют произвольно, например, вверх (рис. 3).

Рис. 3

Для определения двух неизвестных реакций потребуются два уравнения.

Запишем уравнения статики:

Балка не движется вертикально, т.е. сумма проекций всех сил на ось у равна нулю:

Здесь по правилу знаков проекции сил на оси, нагрузки которых совпадают с положительным направлением оси у, записываются положительными и наоборот.

То, что балка не вращается, свидетельствует о том, что сумма моментов относительно любой ее точки также равна нулю, то есть:

В этом уравнении по правилам знаков для моментов сосредоточены силы, моменты и распределенные нагрузки, стремящиеся повернуть балку против часовой стрелки относительно рассматриваемой точки А, записывают положительными и наоборот.

Здесь показано, как записывать момент распределенной нагрузки.

Сила, приложенная в точке, относительно которой считается сумма моментов, в уравнении не участвует, так как плечо момента для нее равно нулю.

Здесь сумму моментов лучше записывать относительно точки, расположенной на опоре (например, А), так как в этом случае соответствующая реакция R _А в уравнении не участвует.

Из выражения (2) определяем R _C :

и подставляя его в выражение (1) находим R _A :

Направление и величина реакций обычно необходимы для дальнейших расчетов балки на прочность и жесткость, поэтому для во избежание возможных ошибок рекомендуется выполнить проверку найденных значений.

- Проверка опорных реакций балки >
- Построение Q- и М-диаграмм балки >

Сочинения и письменные задания, выполненные для вас

Получите помощь с любым заданием — от школьного эссе до докторской диссертации

Типы нагрузок, балки, расчет опоры и реакции опоры 9000 1 Типы расчет нагрузок, балок, опор и опорных реакций

Объявление

1 из 22

Верхняя обрезанная направляющая

Скачать для чтения в автономном режиме

Машиностроение

дать информацию о:- виды нагрузок виды балок виды поддержки расчет реакции поддержки

Объявление

Типы нагрузок, балки, опоры и расчет реакции опор

Типы нагрузок, балки, опоры И поддержка расчета реакции ИМЯ СТУДЕНТА НОМЕР ЗАЧИСЛЕНИЯ ДЖАХАРИЯ СМЕЕТ Р. 180013119023 ХАРИЯ РАЙ Дж. 180013119021 ГАНДИ КАЛП Дж. 180013119018 ЛАД БХАВИК К. 180013119027 МЕХАНИКА ТВЕРДОГО ТЕЛА (2130003)
ВВЕДЕНИЕ Почему мы собираемся обсуждать эту концепцию?? Как инженер-механик и инженер-строитель, мы всегда работаем с машины под структурными нагрузками или мы будем проектировать конструкции с различными типами опор и балок. Этот является базовой концепцией для инженера, который должен знать, чтобы делать все такие вещи. К концу этой концепции мы ожидаем студента сможет идентифицировать все опоры, бобы и нагрузки.
Типы нагрузок • Точечная нагрузка • Равномерно распределенная нагрузка • Равномерно изменяющаяся нагрузка
Точечная нагрузка • Когда нагрузка действует сосредоточенно на определенная точка, то она называется как сосредоточенная нагрузка или точка нагрузка. Мы можем увидеть некоторые лучшие примеры точечной нагрузки в ниже цифры.
РАВНОМЕРНО РАСПРЕДЕЛЕННАЯ НАГРУЗКА • Распределенная нагрузка — это нагрузка растянутый на некоторую длину балки, т. е. причина, по которой она измеряется интенсивностью в единицах Ньютон/метр. • Если интенсивность постоянна вдоль длина, то она называется УДЛ.
РАВНОМЕРНО ИЗМЕНЯЮЩАЯСЯ НАГРУЗКА • Распределенная нагрузка – это нагрузка, распространяется на некоторую длину луча, т.е. Причина, по которой он измеряется в интенсивность в единицах Ньютон/метр. • Если интенсивность постоянна вдоль длина, то он называется UDL.
Типы балок • Фиксированный луч • Консольные балки • Балка с одним шарнирным концом и роликом на другом конце. • Просто поддерживаемые балки • Над подвесными балками • Непрерывный луч
Фиксированная балка • Балка с фиксированными опорами на обоих концах он называется фиксированные лучи, и мы можем видеть некоторые анимированные и реальные примеры этих виды балок и как они ограничивают движение луча.
КОНСОЛЬНАЯ БАЛКА • Балка, имеющая фиксированная опора на конце другой конец свободен, это известно как консольная балка
БАЛКА С ОДНИМ КОНЦЕМ, ПОДВЕСНАЯ И ДРУГОЙ КОНЦЕВОЙ РОЛИК • У этой балки один конец шарнирный, а другой конец поддерживается роликом. •Такие балки способны выдерживать нагрузки в любых направление.
ПРОСТО ПОДДЕРЖИВАЕМАЯ БАЛКА • Балка с простой опорой ровно на двух концах балка тогда называется свободно опертой балкой.
НАД ПОДВЕСНОЙ БАЛКОЙ • ЭТИ БАЛКИ ТАКЖЕ БУДУТ ИМЕТЬ ОПОРЫ, НО ОДИН КОНЕЦ ИЛИ НА ОБЕИХ КОНЦАХ БАЛКИ БУДЕТ НЕКОТОРОЕ РАСШИРЕНИЕ ПОСЛЕ ПОДДЕРЖКИ
НЕПРЕРЫВНАЯ БАЛКА • Это балка, которая несет более двух опор.
ТИПЫ ОПОР • ФИКСИРОВАННАЯ ПОДДЕРЖКА • ПРОСТАЯ ПОДДЕРЖКА • РОЛИКОВАЯ ОПОРА • ШАРНИРНАЯ ОПОРА
ФИКСИРОВАННАЯ ОПОРА •Эта опора фиксирует конец балки, т.е. конец балки устойчив к любому перемещению или изгибу момент.
ПРОСТАЯ ПОДДЕРЖКА • В этом типе поддержки балка может опираться свободно на опоре.
ОПОРА РОЛИКА •Роликовая опора дает возможность перемещения уважаемый луч, соединенный с ним, может быть по нормали направляющих или он также может вращаться вокруг опоры.
ПОДВЕСНАЯ ОПОРА • Шарнирная опора ограничивает движение балки в любом направлении, но это позволит лучу вращаться вокруг опоры только как дверь.