§15. Решение задач

Решение многих задач статики сводится к определению реакций опор, с помощью которых закрепляются балки и мостовые фермы.

В технике обычно встречаются три типа опорных закреплений (кроме рассмотренных в § 2):

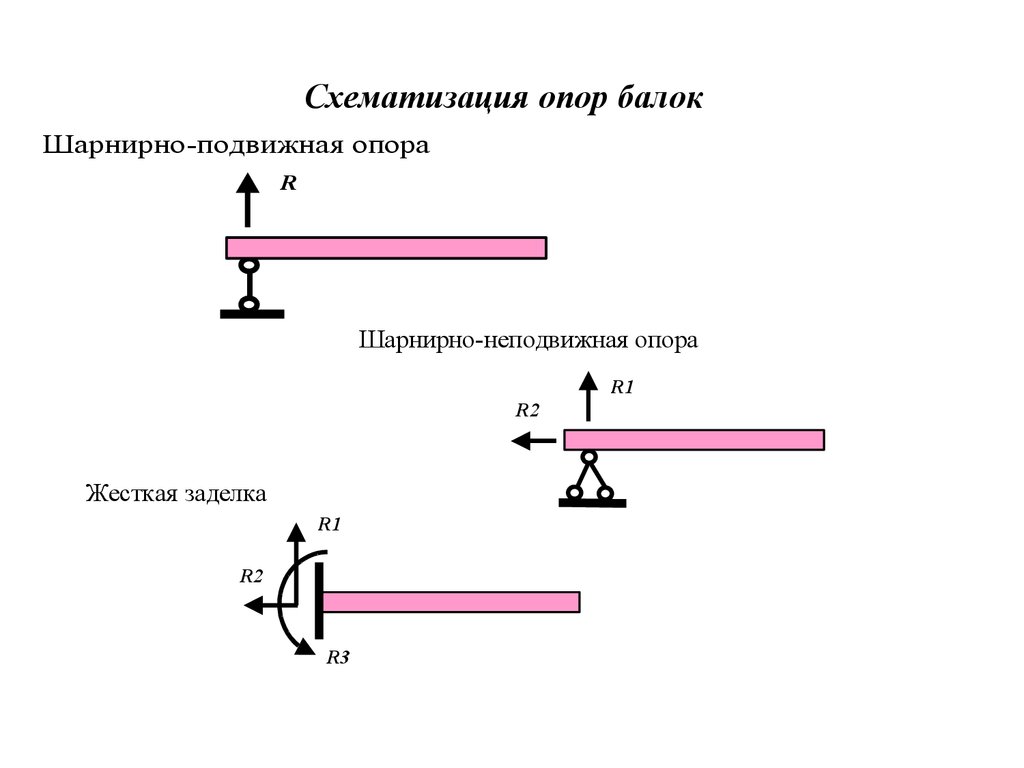
1. Подвижная шарнирная опора (рис. 28, опора А). Реакция такой опоры направлена по нормали к поверхности на которую опираются катки подвижной опоры.

2. Неподвижная шарнирная опора (рис. 28, опора В). Реакция такой опоры проходит через ось шарнира и может иметь любое направление в плоскости чертежа. При решении задач будем реакциюизображать ее составляющимиипо направлениям координатных осей. Модульопределим по формуле .

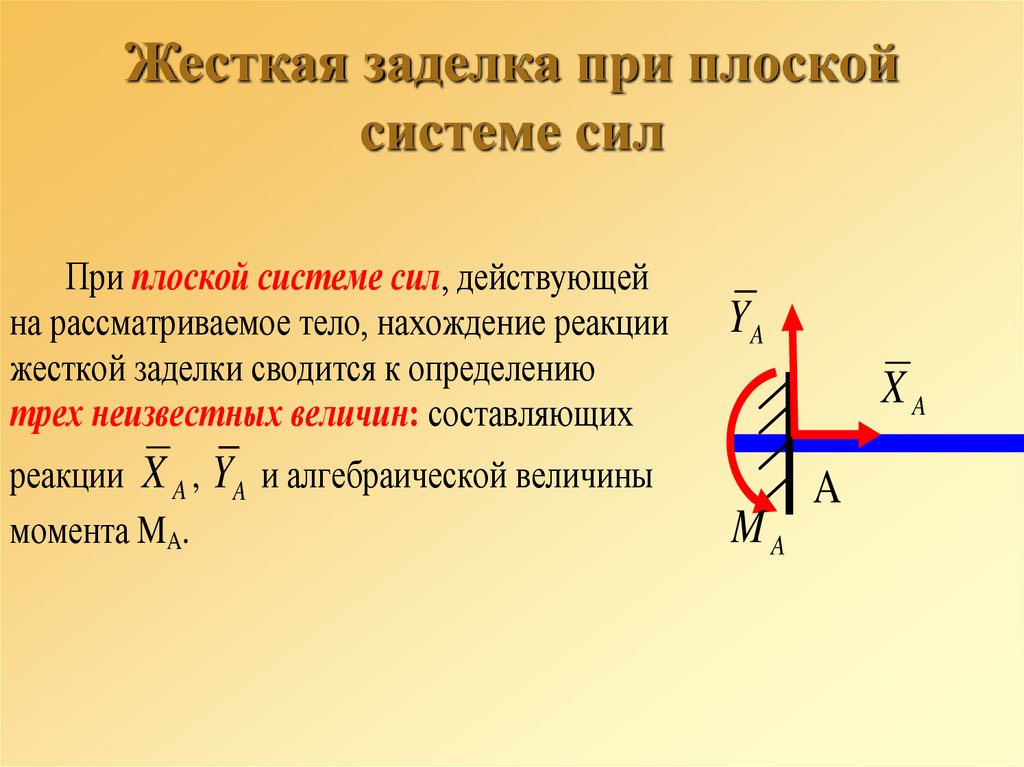
3. Жесткая заделка (рис. 29, а). Рассматривая заделанный конец балки и стену как одно целое, жесткую заделку изображают так, как показано на рис. 29, б. В этом случае на балку в ее поперечном сечении действует со стороны заделанного конца система распределенных сил (реакций).

Считая эти силы приведенными к центру А сечения, можно их заменить одной силой и парой с неизвестным моментомm_A (рис. 29, а). Силу можно изобразить ее составляющими,(рис. 29, б).

Таким образом, для нахождения реакции жесткой заделки надо определить три неизвестные величины X_A, Y_A, m_A.

Рис. 28 Рис. 29

Отметим также, что в инженерных расчетах часто приходится встречаться с нагрузками, распределенными вдоль поверхности по тому или иному закону. Рассмотрим некоторые примеры распределенных сил.

Плоская система распределенных сил характеризуется ее интенсивностью q, т.е. значением силы, приходящейся на единицу длины нагруженного отрезка. Измеряется интенсивность в ньютонах, деленных на метры (Н/м).

а) Силы, равномерно распределенные вдоль отрезка прямой (рис.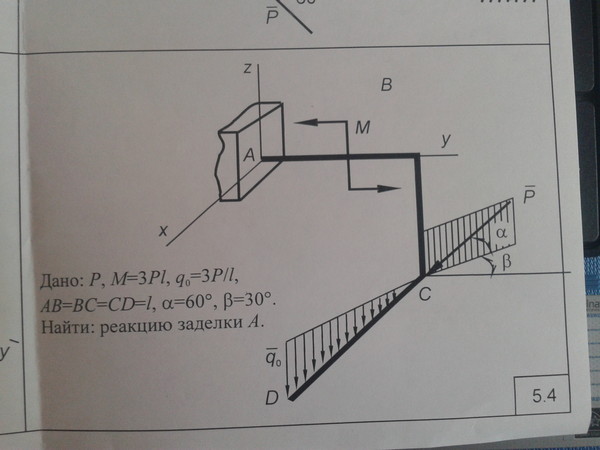  30, а). Для такой системы интенсивность q имеет постоянное значение. При расчетах эту систему сил можно заменить равнодействующей . По модулю

Q = aq . (33)

Приложена сила Q в середине отрезка АВ.

б) Силы, распределенные вдоль отрезка прямой по линейному закону (рис. 30, б). Для этих сил интенсивность q является величиной переменной, растущей от нуля до максимального значения q_m. Модуль равнодействующей в этом случае определяется по формуле

Q = 0,5aq_m . (34)

Приложена сила на расстоянииа/3 от стороны ВС треугольника АВС.

Рис. 30

Задача 3. Определить реакции неподвижной шарнирной опоры А и подвижной опоры В балки (рис.  31), на которую действуют активные силы: одна известная сосредоточенная сила F = 5 кН, приложенная в точке С под углом 60⁰, и одна пара сил с моментом m = 8 кНм.

Рис. 31

Решение. 1) Выбираем объект исследования, т.е. рассматриваем равновесие балки АВС. 2) Изобразим внешние силы, действующие на балку: силу , пару сил с моментомm и реакции связей , , (реакцию неподвижной шарнирной опоры А изображаем двумя ее составляющими). В результате имеем произвольную плоскую систему сил. 3) Проведем координатные оси x, y и составляем условия равновесия (28). Для вычисления момента силы , иногда, удобно разложить ее на составляющие и , модули которых равняются F

1 = F cos60⁰ = 2,5 кН, F₂ = F cos30⁰ = 4,33 кН. Тогда получим:

, ,

.

Решая эту систему уравнений, найдем:

X_A = F₁ = 2,5 кН, Y_B = (m + F₂∙5)/3 = 9,88 кН, Y_A = F₂ – Y_B = – 5,55 кН.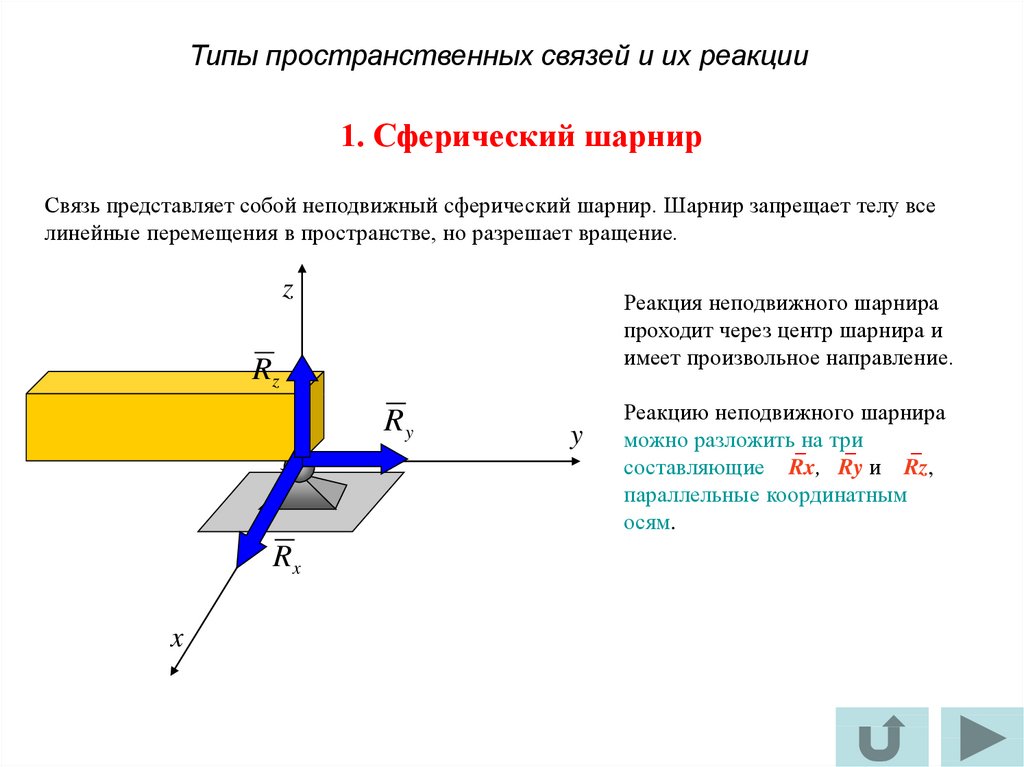

Знак минус реакции Y_A показывает, что эта реакция направлена вертикально вниз.

Для проверки составим уравнение моментов относительно нового центра, например, относительно точки В:

, 5,55∙3 – 8 – 4,33∙2 = – 0,01 ≈ 0.

Задача 4. Определить реакции заделки консольной балки (рис. 32), на которую действуют активные силы: сосредоточенная сила F = 6 кН, приложенная в точке С под углом 45⁰, равномерно распределенная нагрузка интенсивностью q = 2 кН/м и пара сил с моментом m = 3 кНм.

Рис. 32

Решение. 1) Выбираем объект исследования, т.е. рассматриваем равновесие балки АВС. 2) Изобразим внешние силы, действующие на балку: силу , равномерно распределенную нагрузку интенсивностьюq, пару сил с моментом m и реакции заделки, т.е. три неизвестные величины X_A, Y_A, m_A (реакцию жесткой заделки изображаем двумя ее составляющими X_A, Y_A, а пару – неизвестным моментом m_A, как на рис.

 29). Силу разложим на две составляющие и , модули которых равняются F₁ = F₂ = F cos45⁰ = 4,24 кН, а распределенную нагрузку интенсивностью q заменим сосредоточенной силой с модулем равным

Q = 3∙q = 6 кН.

Сила приложена в середине отрезка АВ. В результате имеем произвольную плоскую систему сил. 3) Проведем координатные оси x, y и составляем уравнения равновесия (2):

, ,

.

Решая эти уравнения, найдем:

X_A = F₁ = 4,24 кН, Y_A = Q – F₂ = 1,76 кН, m_A = Q∙1,5 + m – F₂∙5 = – 9,2 кНм.

Для проверки составим уравнение моментов относительно точки С:

, – 9,2 + 21 – 3 – 8,8 = 0.

Задача 5. Определить реакции опор А, В, С и усилие в промежуточном шарнире D составной конструкции (рис.

 33), на которую действуют активные силы: сосредоточенная сила F = 4 кН, приложенная в точке Е под углом 45⁰, равномерно распределенная нагрузка интенсивностью q = 2 кН/м и пара сил с моментом m = 10 кНм.

Рис. 33

Решение. Один из способов решения задач об определении реакции опор составной конструкции состоит в том, что конструкцию расчленяют на отдельные тела и составляют условия равновесия каждого из тел в отдельности. Воспользуемся этим способом и разобьем конструкцию на две части: левую AD и правую DC. В результате приходим к задаче о равновесии двух тел. Силовые схемы задачи показаны на рис. 7,8. Для упрощения вычислений разложим силу на составляющие и , модули которых равны F₁ = F₂

 = F cos45⁰ = 2,83 кН, а распределенную нагрузку интенсивностью q заменим сосредоточенной силой с модулем равнымQ = 10 кН. Сила приложена в середине отрезкаBD.

Рис. 34 Рис. 35

Анализ приведенных силовых схем показывает, что они включают шесть неизвестных величин: X_A, Y_A, Y_B, X_D, Y_D, Y_C.

Так как на рис. 34,35 имеются плоские системы уравновешенных сил, то для них можно записать условия равновесия (28) в виде шести линейных алгебраических уравнений:

Левая часть Правая часть

, ,

, ,

, .

Поскольку составленная система шести уравнений зависит от шести неизвестных X_A, Y_A, Y_B, X_D, Y_D, Y_C, то она является замкнутой.

Решая систему, найдем:

X_A = – 2,83 кН, Y_A = – 0,93 кН, Y_B = 11,76 кН, Y_C = 2 кН, X_D = 0, Y_D = 2 кН.

Для проверки составим уравнение моментов относительно точки D:

= 2,83∙7 – (– 0,93)∙15 – 11,76∙5 + 10∙2,5 – 10 + 2∙5 = – 0,04 ≈ 0.

Как определить реакции опор?

Привет! В этой статье предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции опор, чему учат еще в рамках дисциплины — «теоретическая механика». Но для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.

Так как этот урок для чайников, я многие моменты буду упрощать и рассказывать только самое основное, чтобы написанное здесь, было понятно даже самому неподготовленному студенту — заочнику.

В рамках статьи рассмотрим 4 примера: двухопорная балка, загруженная посередине пролёта сосредоточенной силой, такая же балка, но загруженная распределённой нагрузкой, консольная балка и плоская рама.

Что такое реакция опоры?

Чтобы лучше понять, что такое реакция опоры (опорная реакция), давай рассмотрим следующий пример — балку (стержень) лежащую на опорах:

На балку давит нагрузка – сила, в свою очередь, балка давит на опоры. И чтобы балка лежала на опорах (никуда не проваливалась), опоры выполняют свою основную функцию — удерживают балку. А чтобы удерживать балку, опоры должны компенсировать тот вес, с которым балка давит на них. Соответственно, действие опор можно представить в виде некоторых сил, так называемых — реакций опор.

Для балки, и нагрузка, и реакции опор, будут являться внешними силами, которые нужно обязательно учитывать при расчёте балки. А чтобы учесть опорные реакции, сначала нужно научиться определять их, чем, собственно, и займёмся на этом уроке.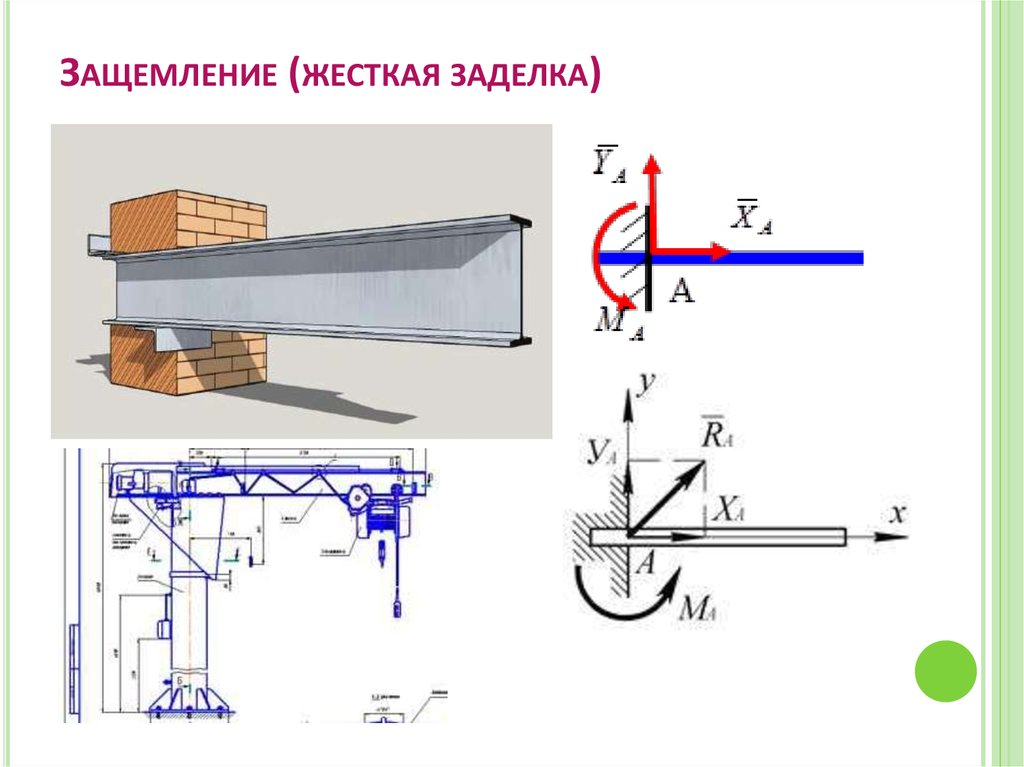

Виды связей и их реакции

Связи – это способы закрепления элементов конструкций. Опоры, которые я уже показывал ранее – это тоже связи.

 В этой статье будем рассматривать три вида связей: жёсткая заделка, шарнирно-подвижная и шарнирно-неподвижная опора.

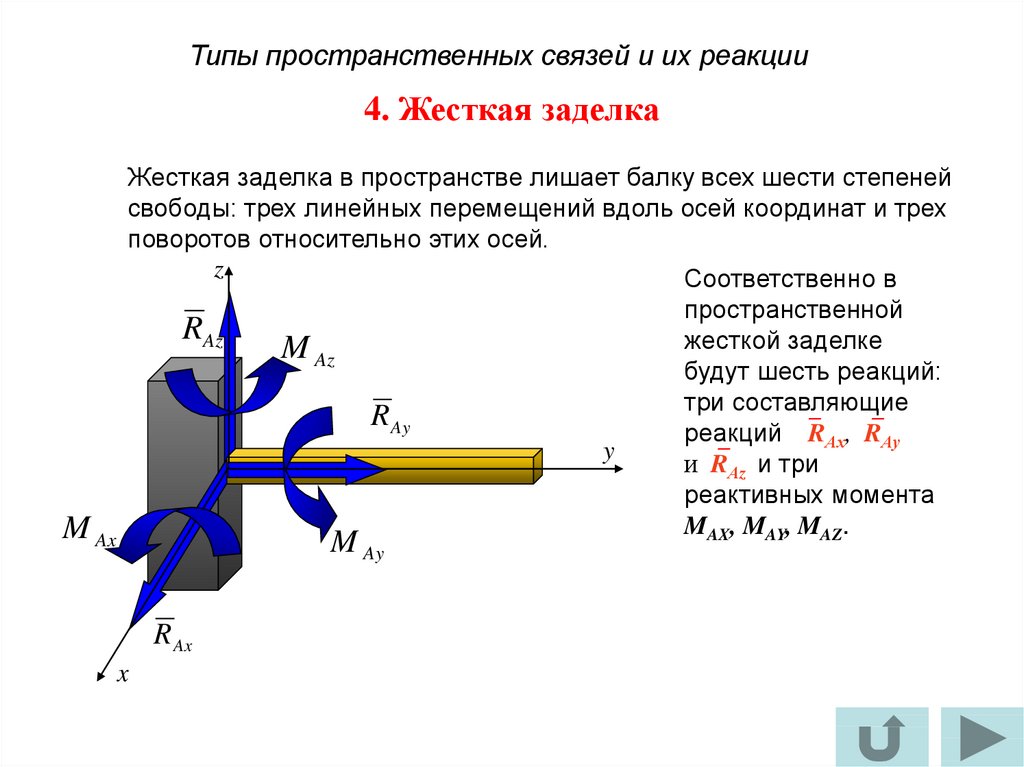
Жёсткая заделка

Жёсткая заделка — это один из вариантов закрепления элементов конструкций. Этот тип связи препятствует любым перемещениям, тем самым для плоской задачи, может возникать три реакции: вертикальная (R_A), горизонтальная (H_A) и момент (M_A).

Шарнирно-подвижная и шарнирно-неподвижная опора

В этой статье будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

В шарнирно-неподвижной опоре возникает две реакции: вертикальная и горизонтальная. Так как опора препятствует перемещению в этих двух направлениях. В шарнирно-подвижной опоре возникает только вертикальная реакция.

Однако, видов связей и их условных обозначений достаточно много, но в рамках этой статьи их все рассматривать не будем. Так как, изученные ранее виды связей, являются основными и практически всегда, при решении задач по сопромату, ты будешь сталкиваться именно с ними.

Что такое момент силы?

Также необходимо разобраться с понятием момент силы.

Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр.

Проиллюстрирую написанное:

На изображении показано, как определить момент силы F, относительно точки O.

Правило знаков для моментов

Также для моментов, нужно задаться каким-то правилом знаков. Я в своих уроках буду придерживаться такого правила:

• если сила относительно точки стремится повернуть ПРОТИВ часовой стрелки, то момент положительный;

• если она стремится повернуть ПО часовой стрелке, то момент отрицательный.

Всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнём с простейшей расчётной схемы балки.

Определение реакций для двухопорной балки

Возьмём балку, загруженную посередине сосредоточенной силой и опирающейся на шарнирно-неподвижную и шарнирно-подвижную опору:

Введём систему координат: направим ось x вдоль балки, а ось y вертикально. Обозначим реакции в опорах как H_A, R_A и R_B:

Для тех, кто пришёл сюда, ещё будучи на этапе изучения теоретической механики, а я знаю, таких будет много, важно отметить, что в сопромате не принято указывать знаки векторов над силами.

В термехе же, в обязательном порядке, преподаватель от тебя настойчиво будет требовать указывать знак вектора над всеми силами, вот так:

Условия равновесия системы

Чтобы найти все реакции, нужно составить и решить три уравнения — уравнения равновесия:

Данные уравнения являются условиями равновесия системы. А так как мы предполагаем, что опоры обеспечивают это состояние равновесия (удерживают балку). То составив и решив уравнения равновесия — найдём значения опорных реакций.

Первое уравнение называется уравнением проекций — суммой проекций всех сил на координатную ось, которая должна быть равна нулю. Два других уравнения называются уравнениями моментов — суммами моментов всех сил относительно точек, которые должны быть равны нулю.

Уравнения равновесия

Как видишь, чтобы научиться находить реакции опор, главное — научиться правильно составлять уравнения равновесия.

Уравнение проекций

Запишем первое уравнение — уравнение проекций для оси x.

В уравнении будут участвовать только те силы, которые параллельны оси x. Такая сила у нас только одна — H_A. Так как H_A направлена против положительного направления оси x, в уравнение её нужно записать с минусом:

Тогда H_A будет равна:

Поздравляю, первая реакция найдена!

Уравнения моментов

А теперь самое интересное…запишем уравнение моментов, относительно точки A, с учётом ранее рассмотренного правила знаков для моментов.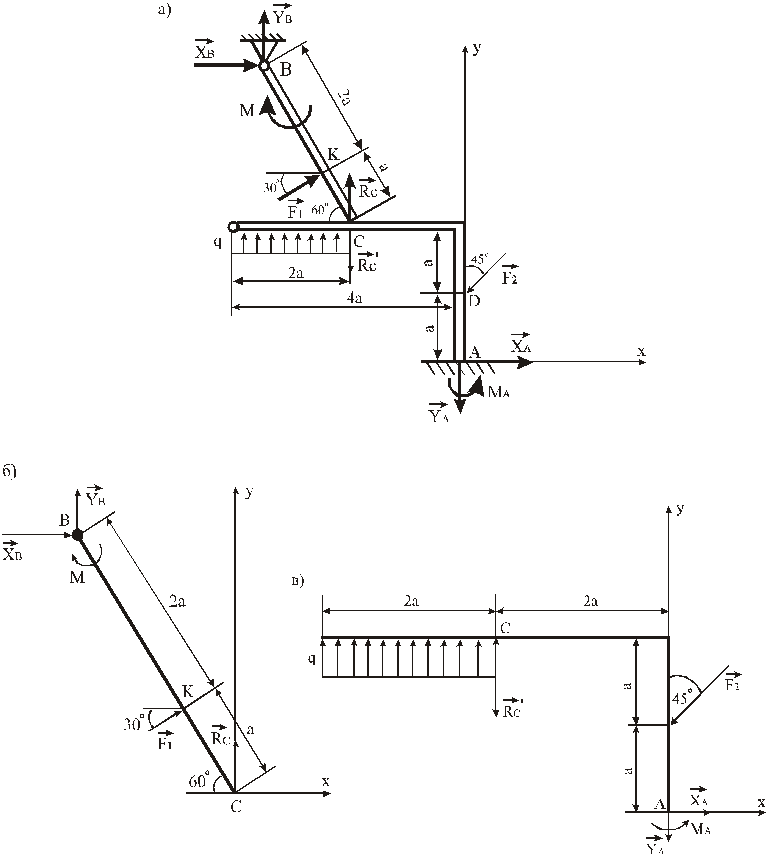

Так как сила F поворачивает ПО часовой стрелке, записываем её со знаком «МИНУС» и умножаем на плечо.

Так как сила R_B поворачивает ПРОТИВ часовой стрелки, пишем её со знаком «ПЛЮС» и умножаем на плечо. И, наконец, всё это приравниваем к нулю:

Из полученного уравнения выражаем реакцию R_B:

Вторая реакция найдена! Третья реакция находится аналогично, но только теперь уравнение моментов записываем относительно другой точки:

Проверка правильности найденных опорных реакций

Чем хороши задачи на определение реакций, так это тем, что правильность расчёта реакций легко проверить. Для этого достаточно составить дополнительное уравнение равновесия, подставить все численные значения и если сумма проекций сил или сумма моментов будет равна нулю, то и реакции, значит, найдены — верно, а если нет, то ищем ошибку.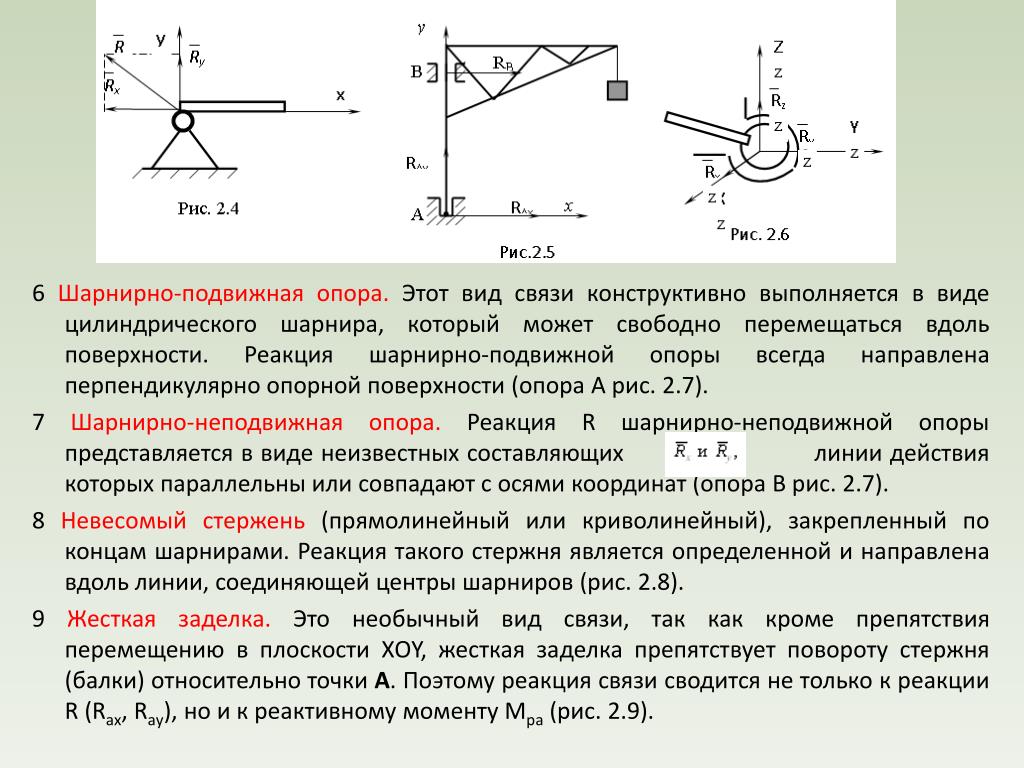

Составим дополнительное уравнение проекций для оси y и подставим все численные значения:

Как видишь, реакции опор найдены правильно.

Определение реакций опор для балки с распределенной нагрузкой

Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно «свернуть» до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:

Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:

Расчёт реакций для консольной балки

Давай рассмотрим теперь пример с жёсткой заделкой – консольную балку. Заодно посмотрим, как учесть силу, приложенную под углом (α = 30^°).

Силу, направленную под определённым углом, нужно разложить на две составляющие – горизонтальную и вертикальную. А их значения найти из силового треугольника:

Покажем реакции в заделке и выполним расчёт:

Для этой задачи выгоднее использовать другую форму условий равновесия:

А выгодна она тем, что из каждого записанного уравнения будем сразу находить реакцию:

Не пугайся отрицательного значения реакции! Это значит, что при указании реакции, мы не угадали с её направлением. Расчёт же показал, что M_A, направлена не по часовой стрелке, а против.

В теоретической механике, когда реакции получают с «минусом» обычно не заморачиваются и не меняют их направление на схеме, так и оставляют в ответе отрицательное значение, оговаривая, что да реакция найдена, но с учётом знака, на самом деле направлена в другую сторону. Потому что найденные реакции в задачах на статику, являются конечной точкой расчёта.

У нас же, в сопромате после нахождения опорных реакций, всё только начинается. Найдя реакции, мы всего лишь находим ВСЕ силы действующие на элемент конструкции, а дальше по сценарию стоит задача определить внутренние усилия, возникающие в этом элементе, расчёты на прочность и т.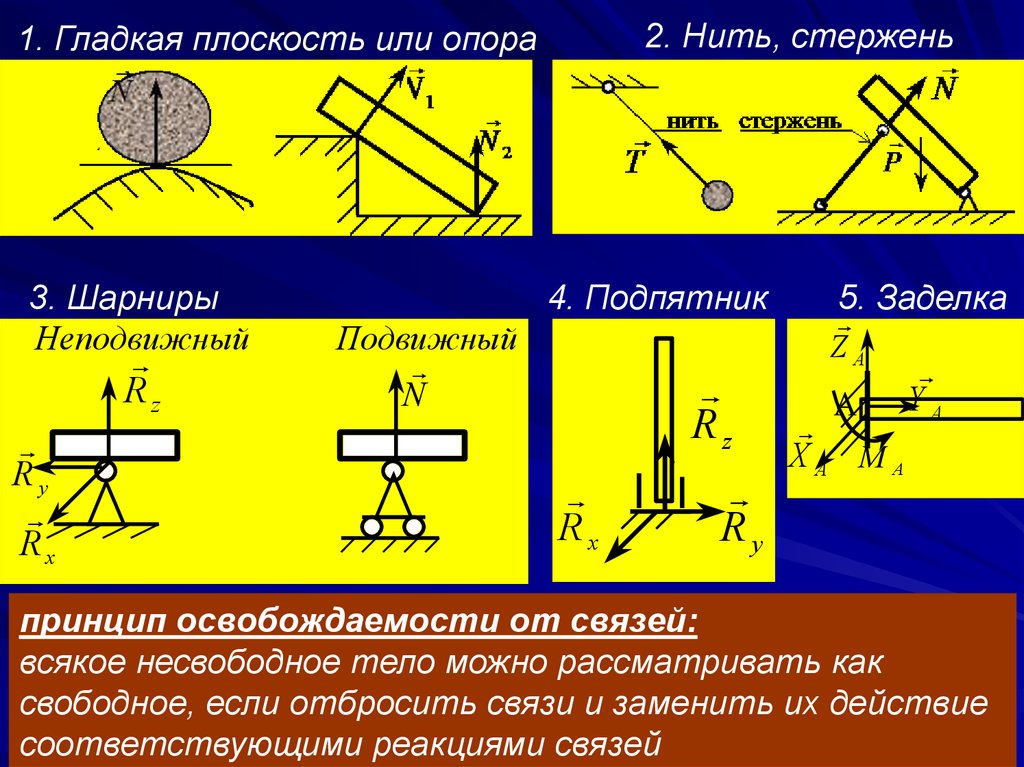 д. Поэтому на схеме, обязательно следует указывать истинное направление реакций. Чтобы потом, когда будут рассчитываться внутренние усилия ничего не напутать со знаками.

Если получили отрицательное значение, нужно отразить это на схеме:

С учётом изменений на схеме реакция будет равна:

Сделаем проверку, составив уравнение равновесие, ещё не использованное – сумму моментов относительно, скажем, точки B, которая, при правильном расчёте, конечно, должна быть равна нулю:

Если не менять направление реакции, то в проверочном уравнении нужно учесть этот «минус»:

Можешь посмотреть еще один пример, с похожей схемой, для закрепления материала, так сказать.

Реакции опор для плоской рамы

Теперь предлагаю выполнить расчёт плоской рамы. Для примера возьмём расчётную схему, загруженную всевозможными видами нагрузок:

Проводим ряд действий с расчетной схемой рамы:

• заменяем опоры на реакции;
• сворачиваем распределенную нагрузку до сосредоточенной силы;
• вводим систему координат x и y.

Выполняем расчёт реакций опор:

Меняем направление реакции R_A:

В итоге получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумма будет равна нулю, то расчет выполнен верно:

Как видим, расчет реакций выполнен правильно!

Инициация, распространение, прекращение – Master Organic Chemistry

Инициирование, распространение и прекращение в свободнорадикальных реакциях

В предыдущем посте о реакциях свободнорадикального замещения мы говорили о том, почему в свободнорадикальных реакциях требуется тепло или свет. В этом посте мы рассмотрим механизм реакции свободно-радикального замещения, которая состоит из трех ключевых типов стадий: инициация, распространение и завершение.

Содержание

1. Механизм свободнорадикального замещения алкана Cl ₂
2. Стадия, на которой происходит чистое увеличение количества свободных радикалов, называется «инициацией»
3. Стадия, на которой нет чистой Прирост или потеря свободных радикалов называется «распространением»
4. Остерегайтесь этой распространенной ошибки при определении механизмов свободнорадикального Свободные радикалы называются «прекращение»
5. Полный механизм свободнорадикального замещения алкана
6. Резюме: реакции свободнорадикального замещения
7. Примечания
8. (Дополнительно) Ссылки и дополнительная литература

---

1.

Механизм свободнорадикального замещения Алкан С Cl ₂

Возможно, вы помните, что видели эту реакцию в предыдущем посте – это свободнорадикальное хлорирование метана с Cl ₂ .

Это замена углерода, потому что связь C-H разрывается и образуется новая связь C-Cl. Побочным продуктом является HCl.

Теперь, когда мы знаем немного больше о том, что такое свободные радикалы и их основные свойства, сегодня мы ответим: « как работает эта реакция? ».

Мы рассмотрим ключевые этапы этой реакции и узнаем, что они состоят из трех ключевых фаз: инициация , завершение и распространение .

2. Этап, на котором происходит чистое увеличение количества свободных радикалов, называется «инициация»

Свободнорадикальные реакции обычно требуют применения тепла или света. Это связано с тем, что любой из этих источников энергии может привести к гомолитическому расщеплению относительно слабых связей, таких как Cl-Cl, с образованием свободных радикалов [т. е. Cl•  ]

Каждая свободнорадикальная реакция начинается со стадии образования свободных радикалов, и по этой причине этот начальный этап называется инициированием.

Вот уравнение для этого начального шага. Два момента, на которые следует обратить внимание:

1. Реакция является равновесной – в любой момент времени присутствует лишь небольшая концентрация присутствующего свободного радикала (но этого будет достаточно, как мы увидим)
2. Обратите внимание, что в этой реакции чистое увеличение количества свободных радикалов . Мы переходим от ноль (в реагентах) к два (в продуктах).

3. Этап, на котором нет чистого прироста или потери свободных радикалов, называется «размножением». Радикалы хлора очень реакционноспособны и могут соединяться с водородом из метана с образованием метильного радикала • CH

₃

Если вы подсчитаете количество свободных радикалов в этом уравнении, вы заметите, что один из них содержится в реагентах, а другой — в продуктах. Таким образом, нет чистого увеличения количества свободных радикалов.

Этот тип шага называется «распространением».

Если вы ведете подсчет, к этому моменту вы должны увидеть, что до завершения нашей реакции остается сформировать только одну связь. Все, что нам нужно сделать, это образовать связь C-Cl.

4. Остерегайтесь этой распространенной ошибки при определении механизмов действия свободных радикалов

Здесь легко допустить небольшую ошибку. Учитывая, что на стадии инициирования образуются два радикала хлора, было бы казаться естественным объединить радикал метила и радикал хлора с образованием CH ₃ –Cl . Верно?????

Нееет!

Обратите внимание, что количество свободных радикалов уменьшилось на здесь, , а не осталось прежним. Это не может быть распространением! (На самом деле это прекращение, о котором мы поговорим через минуту).

5.

В свободно-радикальном замещении есть две стадии распространения

На самом деле, мы можем сделать правильную стадию «размножения» следующим образом: возьмем метильный радикал, и он реагирует с все еще присутствующим Cl ₂ . Это дает нам Ch4Cl и радикал хлора. Обратите внимание, что чистого изменения количества свободных радикалов не произошло, так что это все еще «распространение».

Еще раз обратите внимание, что мы образуем радикал хлора! Что в этом такого важного? Это важно, потому что этот радикал хлора может затем выполнить этап распространения № 1 на новой молекуле нашего субстрата (CH ₄ ), продолжая процесс. Это цепная реакция — после образования радикал хлора становится каталитическим. Вот почему для протекания этой реакции нам нужно лишь небольшое количество радикала хлора. Нет ничего необычного в том, что 10 ⁴ или более из этих циклов продолжаются до того, как произойдет завершение.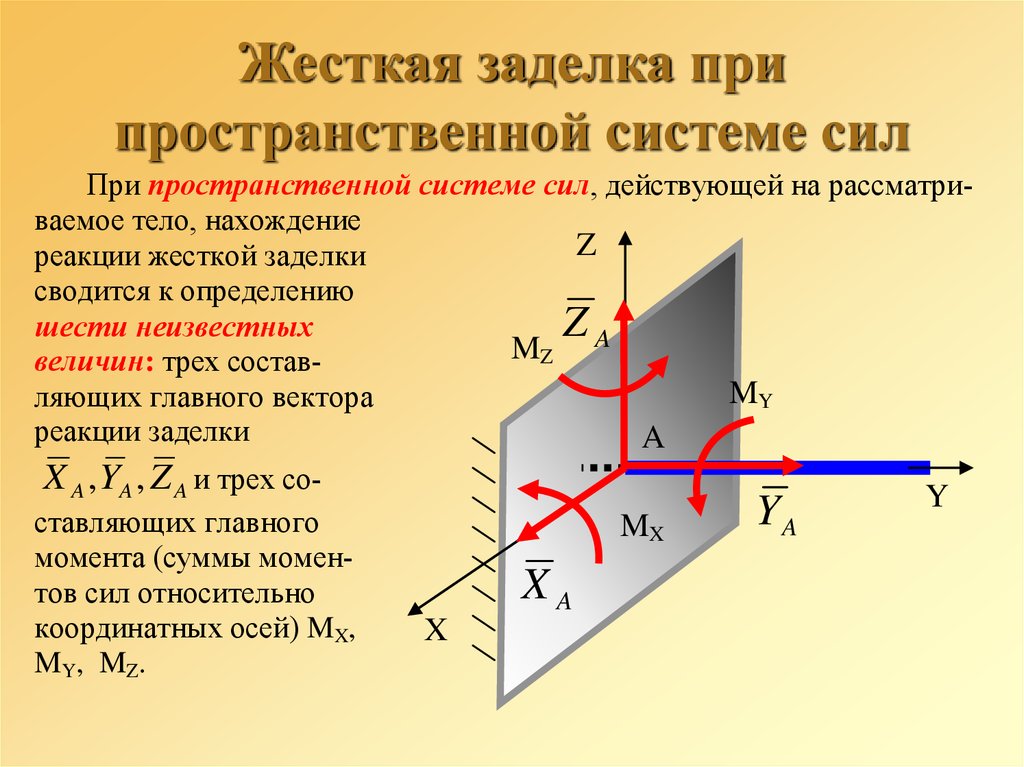 [Ref]

6. Этап, на котором происходит чистое снижение содержания свободных радикалов, называется «прекращением»

Может ли эта цепная реакция продолжаться вечно? №

Рассмотрим два предельных случая. Если концентрация Cl ₂ низка по сравнению с CH ₄ (другими словами, Cl ₂ является нашим лимитирующим реагентом), то скорость этапа распространения № 2 будет замедляться по мере уменьшения его концентрации. Без какого-либо Cl ₂ , с которым можно было бы реагировать, наши радикалы •CH ₃ могут просто соединиться с другим свободным радикалом (таким как •Cl), чтобы получить, например, CH ₃ Cl. Для этой реакции практически нет препятствий. Обратите внимание, что здесь количество свободных радикалов уменьшается с 2 до нуля. Это называется прекращение.

Также возможно объединение двух метильных групп с образованием CH ₃ –CH ₃ ; это тоже прекращение!

7.

Полный механизм свободно-радикального замещения алкана

Давайте объединим все эти этапы, чтобы мы могли четко видеть этапы инициации, распространения и завершения.

 

8. Резюме: реакции свободнорадикального замещения

Эти три типа стадий встречаются в каждой свободнорадикальной реакции.

Суть в том, что путем подсчета количества радикалов, созданных или уничтоженных на каждом этапе, вы можете определить, является ли этот этап инициацией, распространением или завершением.

• Инициация -> чистое образование радикалов
• Распространение -> отсутствие изменений в количестве свободных радикалов
• Прекращение -> чистое разрушение свободных радикалов

Мы оставим два тизера для будущих постов.

Во-первых… обратите внимание, что здесь мы используем канал ₄ , где каждая связь C–H идентична. Что могло бы произойти, если бы мы использовали алкан, в котором все связи C–H не равны… как, например, пропан или пентан?

Во-вторых, эта реакция резко проваливается , когда Br ₂ используется вместо Cl ₂  для реакции CH ₄ .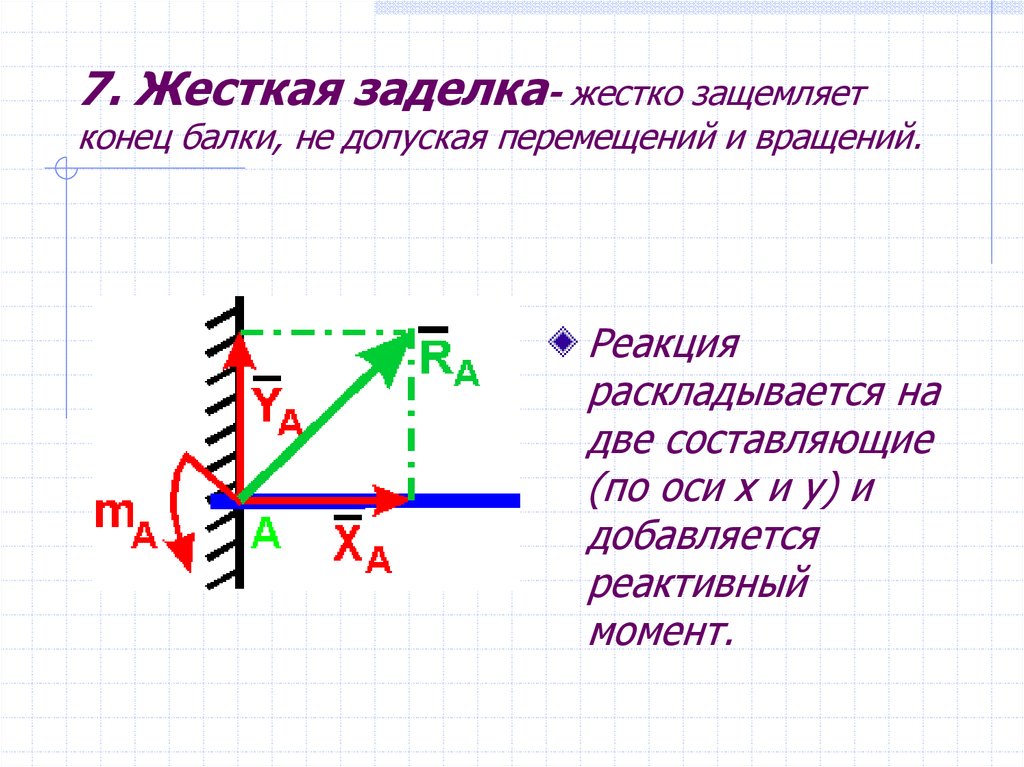 Однако мы увидим, что Br ₂ может работать в некоторых особых случаях.

Скоро еще!

Следующее сообщение: Изомеры из свободнорадикальных реакций

---

Примечания

БОНУСНЫЙ материал.

Мы только что говорили о ситуации, когда используется один эквивалент хлора (Cl ₂ ). Что происходит, когда мы используем несколько эквивалентов или даже чрезмерное их количество?

Задумайтесь на секунду. Представьте, что у нас есть несколько эквивалентов Cl ₂ в присутствии CH ₃ Cl. Как вы думаете, что может произойти?

Атом Cl• может реагировать с CH ₃ Cl с образованием • CH ₂ Cl [и HCl], который затем может реагировать с Cl ₂  отдать CH ₂ Cl ₂  !

Аналогично, если у нас все еще есть избыток Cl ₂ , то мы будем наблюдать преобразование CH ₂ Cl ₂  в CHCl ₃ .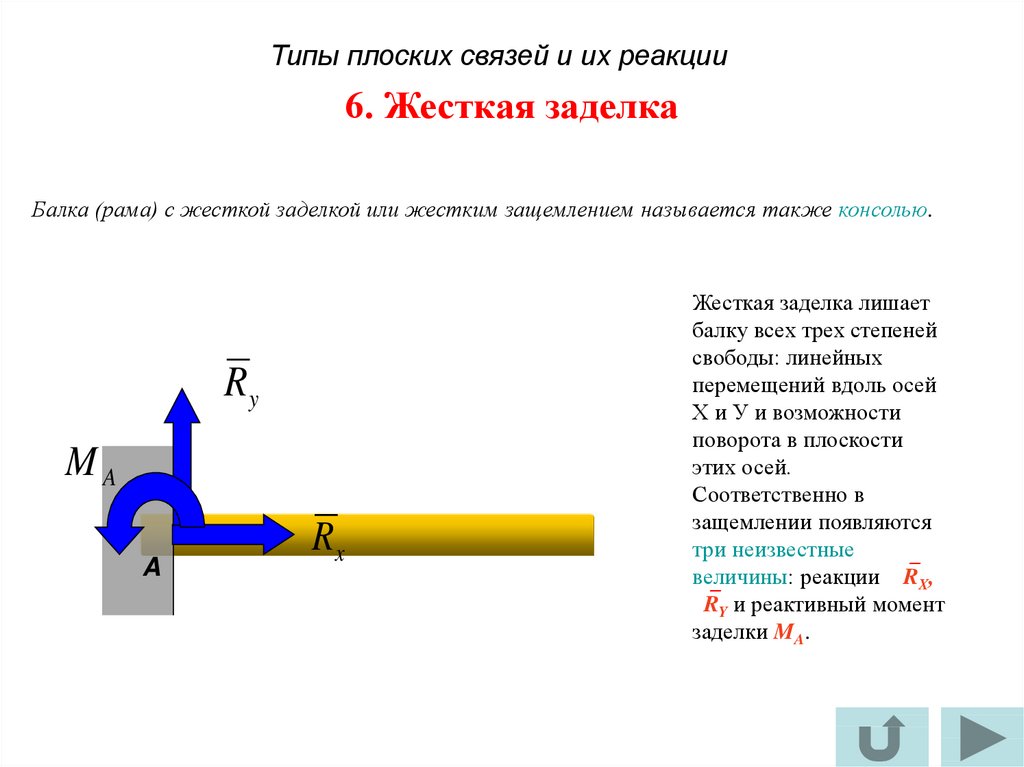

Наконец, при наличии достаточного количества Cl ₂  мы можем представить преобразование CHCl ₃  в CCl ₄ .

В этот момент больше нет связей C-H, чтобы реагировать с радикалом хлора, и, таким образом, наша реакция в конечном итоге прекратится.

Суть здесь в том, что алканы при достаточно большом избытке Cl ₂ в конечном итоге заменят весь водород на хлор.

Этот путь на самом деле представляет собой промышленное производство дихлорметана (CH ₂ Cl ₂  – обычный лабораторный растворитель), хлороформа (CHCl ₃ ) и четыреххлористого углерода (CCl ₄ ). В течение многих десятилетий CCl ₄  производился в мегатоннах для использования в качестве хладагента и растворителя для химической чистки, пока исследования не выявили его и другие ХФУ в разрушении озонового слоя.

---

(Дополнительно) Ссылки и дополнительная литература

1. Walling, C. in Free Radicals In Solution , Wiley and Sons, New York 1957 p. 352
2. Хлорирование метана
   T. McBee, H. B. Hass, C. M. Neher и H. Strickland
   Промышленная и инженерная химия 1942, 34 (3), 296-300
   DOI : 10.102 (3), 296-300
   DOI : 10.102 (3), 296-300
   : : 10.102 (3), 296-300
   : : 10.102 (3). /ie50387a009
   В этой статье показано, что хлорированием метана можно управлять, чтобы получить любой желаемый хлорметан с высоким выходом. Это важно, потому что CH ₃ Cl, CH ₂ Cl ₂ , CHCl ₃ и CCl ₄ являются важным сырьем или растворителем, и именно так они производятся в промышленности.
3. Кинетика термического хлорирования метана
   Роберт Н. Пиз и Джордж Ф. Вальц
   Журнал Американского химического общества 1931, 53 (10), 3728-3737
   (10), 3728-3737
   : : : : : : (10).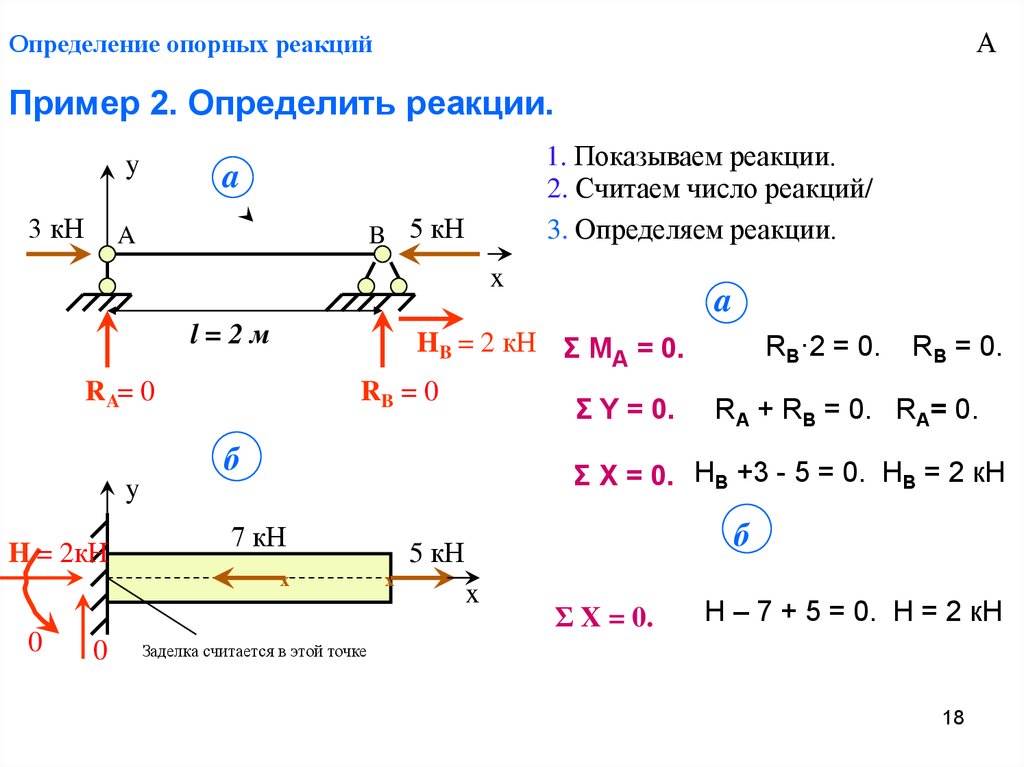 /ja01361a016
   В этой статье представлены кинетические доказательства того, что хлорирование метана 2 9Заказ 0138 и (первый заказ как по метану, так и по Cl ₂ ).
4. Бромирование циклогексана, метилциклогексана и изобутана
   M. S. Kharasch, William Hered и Frank R. Mayo
   Журнал органической химии 1941 06 (6) 1941 06 (6) DO 1941 06 (6) DOISHISTIOST 9 06 (6). : 10.1021/jo01206a005
   Природа механизма свободнорадикальной цепной реакции замещения алканов не была полностью выяснена до 1940-х годов. В этом новаторском 1941, Kharasch предлагает цепной механизм, который мы сейчас читаем в учебниках:
   а) Br2 + hv -> 2 Br• (инициация)
   б) R—H + Br• -> R• + HBr (шаг распространения 1)
   c ) R• + Br2 -> R-Br + Br•  (этап размножения 2)
   Kharasch сообщает, что свободнорадикальное замещение циклогексана на Br2 протекает очень медленно в темноте или в отсутствие кислорода. В низкой концентрации кислород может действовать как инициатор свободных радикалов (образуя радикалы Br• из Br2), но здесь Хараш также отмечает, что кислород в высокой концентрации может ингибировать свободнорадикальные реакции. Отмечается также селективность реакции Br• со связями C-H в порядке третичная > вторичная > первичная.

Initiation Propagation Termination in Radical Reactions

Radical Reactions

Initiation Propagation Termination in Radical Reactions

 

Let’s discuss the chlorination of ethane to illustrate the three important steps of radical halogenation :

 

The reaction starts с гомолизом σ-связи с образованием двух радикалов. Это называется инициированием – началом радикальных цепных реакций. Мы разрываем связь в исходных материалах, поэтому эта стадия требует энергии света или тепла :

Обратите внимание, что в отличие от большинства других реакций в органической химии, таких как нуклеофильное замещение, отщепление или присоединение, радикальные реакции показаны полуконечными стрелками и одна стрелка показывает движение один электрон.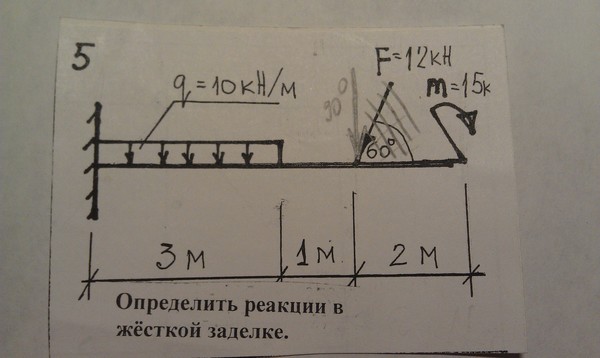

Полукруглые стрелки , также известные как стрелки в виде рыболовных крючков, указывают на то, что σ-связь разрывается гомолитически, т. е. электроны ковалентной связи являются общими для двух атомов.

 

Инициирование при умеренных температурах также может катализироваться пероксидами . Одной из особенностей пероксидов является наличие слабой связи О-О , которая при разрыве образует радикалы.

Вы когда-нибудь задумывались, почему одни лекарства продаются в темных бутылках, а другие в темных?

Ацилпероксиды особенно полезны для этой цели, поскольку образующиеся радикалы стабилизированы резонансом:

 

Простые пероксиды действуют аналогичным образом, образуя алкоксильные радикалы, которые затем используются в радикальных реакциях:

 

Радикалы Cl• , образующиеся на стадии инициирования , очень нестабильны . Это атомы хлора, а из общей химии вы знаете, что галогены существуют в виде двухатомных молекул, а не атомов.

На следующем этапе эти реактивные радикалы быстро реагируют с этаном путем отрыва водорода :

 

 

0004 заключается в том, что создается новый радикал.

Отщепление водорода радикалом галогена является определяющей скоростью стадией радикального галогенирования.

 

Алкильные радикалы также очень реакционноспособны , и они реагируют с газообразным хлором с образованием нового радикала хлора . Таким образом, процесс продолжается снова и снова без необходимости подачи энергии для повторного запуска:

 

 

Вот почему радикальные реакции классифицируются как цепные реакции — для запуска реакции требуется только начальный толчок, и однажды начавшись, процессы продолжаются многократно.

Стоит также отметить, что отщепление водорода отличается от реакций переноса протона , которые следуют ионному механизму. Абстракция водорода — это движение радикала H•, а перенос протона — это движение H ⁺ ion:

 

Шаги инициации и распространения, которые мы рассмотрели до сих пор, представляют собой монохлорирование с образованием хлорэтана (этилхлорида). Однако , если Cl ₂ добавляют в избыточном или равном количестве, наблюдается полихлорирование .

Например, , когда равные количества метана и хлора смешивают и облучают светом соответствующей длины волны, в результате реакции образуется смесь следующих продуктов:

 

 

Причина получения этого смесь моно- и полихлорированного метана — изменение концентраций реагентов и продуктов по мере протекания реакции.

Первоначально присутствуют только хлор и метан, при их реакции образуются хлорметан и хлороводород:

 

Однако в ходе реакции концентрация хлорметана в смеси увеличивается . Кроме того, хлорметан более реакционноспособен, чем метан, и, несмотря на его более низкую концентрацию, он начинает реагировать с хлором с образованием дихлорметан :

 

 

Аналогичным образом, по мере увеличения концентрации дихлорметана образуется трихлорметан , который затем превращается в тетрахлорметан .

При хлорировании этана образуются 1,1-дихлорэтан и 1,2-дихлорэтан, а также смесь более высокохлорированных этанов:

 

Следовательно, для достижения моногалогенирования алкан всегда должен использоваться в избытке . Моногалогенирование важно, так как позволяет проводить селективное галогенирование с использованием брома и в целом более полезно для получения галогеналканов, используемых в органическом синтезе.

 

У вас может возникнуть один хороший вопрос:

  Ответ на этот вопрос: да. На самом деле, , когда встречаются два радикала , они реагируют очень быстро из-за своей нестабильности.