Реакции заделки: жесткая, скользящая, бискользящая и реакции в них

Содержание

Реакция заделки.

Р ассмотрим балку один конец которой АВ заделан в стену. Такое крепление конца балки АВ называется заделкой в точке В. Пусть на балку действует плоская система сил. Определим силы, которые надо приложить к точке В балки, если часть балки АВ отбросить. К сечению балки (В) приложены распределенные силы реакции. Если эти силы заменить элементарными сосредоточенными силами и затем привести их к точке В, то в точке В получим силу (главный вектор сил реакции) и пару сил с моментом М (главный вектор сил реакции относительно точки В) . Момент М называют моментом заделки или рективным моментом. Силу реакции можно заменить двумя составляющими и .

Заделка в отличие от шарнира создает не только неизвестную по величине и направлению реакцию , но еще и пару сил с неизвестным моментом М в заделке.

Рассмотрим равновесие сил, приложенных к системе взаимодействующих между собой тел.

Тела могут быть соединены между собой с помощью шарниров или иным способом.

Силы, действующие на рассматриваемую систему тел, можно разделить на внешние и внутренние.

Внешними называются силы, с которыми на тела рассматриваемой системы действуют тела, не входящие в эту систему сил.

Внутренними называются силы взаимодействия между телами рассматриваемой системы.

Связи, соединяющие части данной конструкции, будем называть внутренними в отличие от внешних связей, скрепляющих конструкцию с телами, в нее не входящими (например, с опорами).

Способ решения подобных задач состоит в том, что конструкцию сразу расчленяют на отдельные тела и составляют условия равновесия каждого из тел в отдельности (см. задачу 24). При этом реакции внутренних связей будут попарно равны по модулю и противоположны по направлению. Для конструкции из п тел, на каждое из которых действует произвольная плоская система сил, получится таким путем Зп уравнений, позволяющих найти Зп неизвестных (при других системах сил число уравнений соответственно изменится).

Если для данной конструкции число всех реакций связей будет больше числа уравнений, в которые эти реакции входят, то конструкция будет статически неопределимой.

Внутренними усилиями в каком-нибудь сечении тела или конструкции (балки, арки и др.) называют силы, с которыми части тела, разделенные этим сечением, действуют друг на друга. Метод определения внутренних усилий аналогичен методу, применяемому при изучении равновесия систем тел. Сначала рассматривают равновесие всего тела (конструкции) в целом и определяют реакции внешних связей. Затем сечением, в котором требуется найти внутренние усилия, разделяют тело на две части и рассматривают равновесие одной из них. При этом, если система действующих на тело внешних сил плоская, то действие отброшенной части заменится в общем случае’ плоской системой распределенных по сечению сил; эти силы, как и в случае жесткой заделки (см. рис. 55), представляют одной приложенной в центре сечения силой с двумя наперед неизвестными, составляющими X, Y и парой с наперед неизвестным моментом m.

Домашнее задание №1

Стр. 1, задача 1, растяжение-сжатие колонны
Данная задача была исключена из домашнего задания в 2016 году из-за сокращения программы курса. Тем не менее задачи на растяжение-сжатие я продолжаю рассматривать и на семинарах, и в данном руководстве, поскольку, во-первых, относительно простая тема позволяет лучше понять суть метода сечений и процедуру построения любых эпюр, а во-вторых, при выполнении и защите домашнего задания №2 строить эпюры для колонн все равно придётся.

Итак, вначале ищем реакцию заделки. Для этого складываем силы, вызывающие растяжение вблизи заделки и направленные, следовательно, вправо. Получается 2F + 3F = 5F. Далее, сила, взывающая сжатие, одна и равна F. Таким образом, «побеждают» растягивающие и создают в заделке силу 5F — F = 4F. Теперь можно идти слева направо, изображая скачки́ на эпюре там, где приложены силы. Причём силы, направленные вправо, создают растяжение (плюс) слева и сжатие (минус) справа, то есть скачок идет от плюса к минусу, то есть вниз.

Придя к правому торцу, мы встречаем силу, направленную влево. Рассуждая аналогично, приходим к выводу, что скачок должен выполняться вверх. Поскольку текущее (на третьем участке) значение нормальной силы равно – F, то мы приходим в нуль, что является проверкой решения.
Можно рассуждать и проще – на конце последнего участка усилие определяется силой, приложенной к торцу. Она равна F и является сжимающей, значит, порождающей отрицательное усилие того же модуля. То есть проверку можно закончить в точке приложения силы 2F.
Наконец, ещё проще не искать реакцию заделки и строить эпюру не слева направо, а в обратном направлении. Правда, тогда мы лишаем себя проверки на левом конце, зато выигрываем время.

Стр. 2, задача 2, изгиб шарнирно опёртой балки
Решение выполнено внизу, эпюры изображены под расчетной схемой. К ним мы вернёмся позже.
Отбрасываем опоры, заменяем их реакциями {1}, {2}. Направления их выбираем, вообще говоря, произвольно, но можно постараться их предугадать – это позволит лучше понять «физику» задачи.

В данном случае обе распределённые нагрузки направлены вниз, то есть, скорее всего, обе реакции (одна-то уж наверняка) направлены вверх. Елизавета Ильинична так и поступила.
Составляем сумму сил на вертикаль {3}. Пока в нём мало проку – одно уравнение содержит две неизвестных.
Теперь выберем точку для составления суммы моментов {4}. Разумеется, она может быть произвольной, но удобно выбирать точку приложения реакции – это позволит исключить её из уравнения. Елизавета Ильинична выбрала точку В. Произвольное правило знаков для моментов {5} не слишком удачно: гораздо удобнее выбирать направление так, чтобы неизвестная величина (в данном случае R_D) вошла с минусом. Это позволит, перенеся её в правую часть, сменить её знак с минуса на желанный плюс и больше никаких знаков не менять.
Далее из {4} находим R_D {6} и, подставляя её в {3}, определяем реакцию R_В {7}. Как и предполагалось, обе реакции оказались положительными.
Альтернативный способ составления уравнений равновесия в подобных задачах заключается в том, что составляют уравнения моментов относительно точек приложения реакций, а сумма на вертикаль не составляют вовсе.

Это позволяет получить не систему второго порядка (в данном случае {3} и {4}), а два независимых уравнения относительно реакций. Недостаток способа – дробные величины плеч реакций. Не берусь безусловно порекомендовать ни тот, ни другой путь. Следует попробовать оба и выбрать понравившийся.
Есть и ещё (по крайней мере) один способ – для истинных гурманов. Особенно эффективен он, когда имеется лишь один участок распределённой нагрузки. Тогда уравнение моментов составляется относительно середины этого участка, тем самым слагаемые, связанные с распределённой нагрузкой, в уравнение не входят. К данной задаче, как видно, способ хоть и применим, но не ведёт к упрощению решения.

Стр. 3, задача 2, продолжение
Изображаем безопорную расчётную схему {1}. На участке АВ выбираем произвольное сечение Е с текущей координатой z_AB {2} и вводим неизвестные внутренние силовые факторы Q_y {3} и M_x {4} c направлениями строго согласно правилам знаков.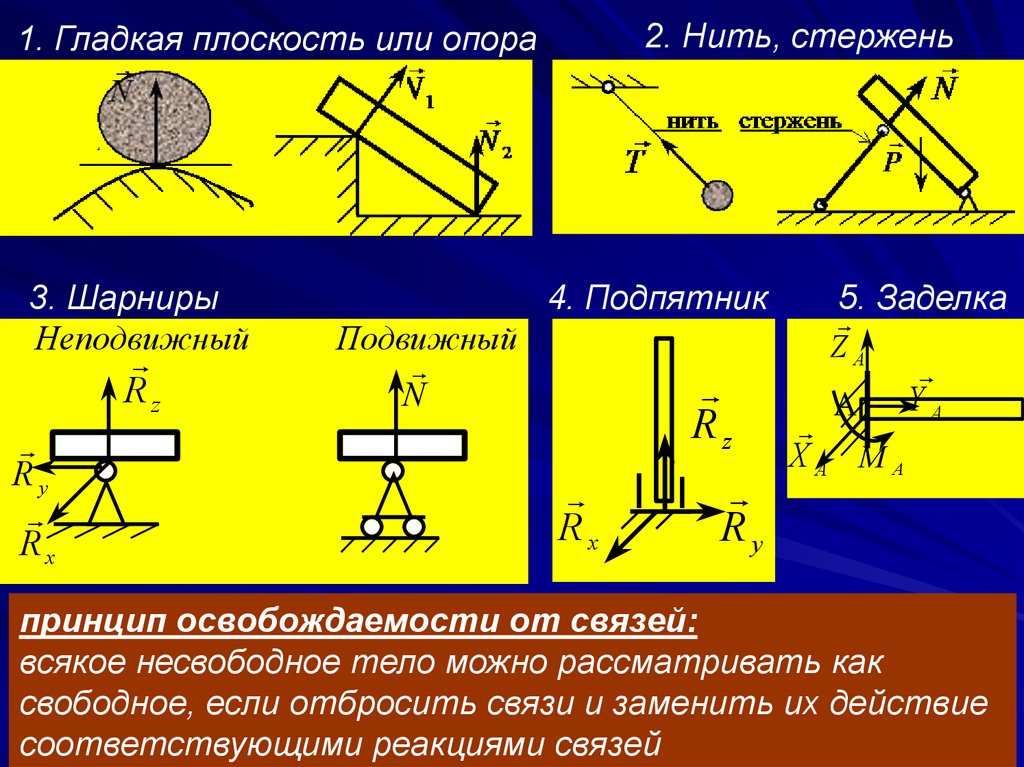 А вот произвольное направление положительного момента {5} на этот раз выбрано удачно, в чём мы убедимся ниже.
Составляем сумму сил на вертикаль {6}, выражаем искомую поперечную силу Q_y и подставляем в него значения координаты в начале {7} и в конце {8} участка. Видно, что сила знак не меняет, значит, экстремума изгибающего момента на этом участке нет. Сумма моментов {9} составляется относительно текущей точки Е, что позволяет исключить из уравнения поперечную силу. С учетом выбранного правила знаков переносим неизвестный момент

M_x в правую часть и без смены знаков получаем функцию момента относительно координаты. Подставляем в него начальное {10} и конечное {11} значения координаты и получаем моменты на краях участка.
При рассмотрении участков от второго и далее удобно делать не одно, а два сечения. Первое из них находится на дифференциально малом расстоянии слева от (раньше, не доходя до) начала текущего участка {12}. Второе – текущее в точке К.

В левое сечение переносим найденные в конце предыдущего участка значения силы и момента: сила получилась отрицательной {8} и, значит, на левом конце расчётной схемы по правилу знаков она направляется вниз {13}. Отрицательный момент {11} по той же причине направляется против часовой стрелки {14}.
На участке CD поперечная сила меняет знак с плюса {15} на минус {16}. Это значит, что момент достигает экстремума. Для его поиска левую часть уравнения для силы {17} приравниваем нулю и находим координату экстремума {18}. По давней традиции величины, относящиеся к экстремуму (координата и момент), обозначаются звездочкой. Составляем сумму моментов {19} и, выражая из него неизвестный момент (это уравнение Елизавета Ильинична не выписала отдельно, делая выкладки в уме), подставляем найденную в {18} координату экстремума. Точное значение экстремума {20} равно ⁵⁹²⁹/₂₅₉₂ q·l². Погрешность указанного десятичного значения 2.3 q·l² составляет 0.

55%, так что отказ от громоздкой простой дроби выглядит вполне оправданным.
Эпюры поперечной силы {8} и изгибающего момента {9} показаны под расчетной схемой (Стр. 2), что очень удобно для визуальной проверки обеих эпюр.

Стр. 4, задача 3, изгиб шарнирно опёртой балки
Стр. 5, задача 3, продолжение
Стр. 6, задача 4, изгиб шарнирно опёртой балки
Стр. 7, задача 4, продолжение
Данные задачи решаются по тому же алгоритму и отдельных комментариев не требуют.

Стр. 8, задача 5, изгиб консольной балки
Здесь уместно обратить внимание на грамотный выбор Елизаветой Ильиничной направлений неизвестных реакций заделки.
Согласно правилам знаков, на левом конце расчётной схемы положительный момент направлен по часовой стрелке, а положительная сила – вверх. Внешние силовые факторы тех же направлений порождают положительные внутренние. Следовательно, если направить реакции именно так, то по их формальным знакам можно будет сразу судить о фактических знаках внутренних силовых факторов.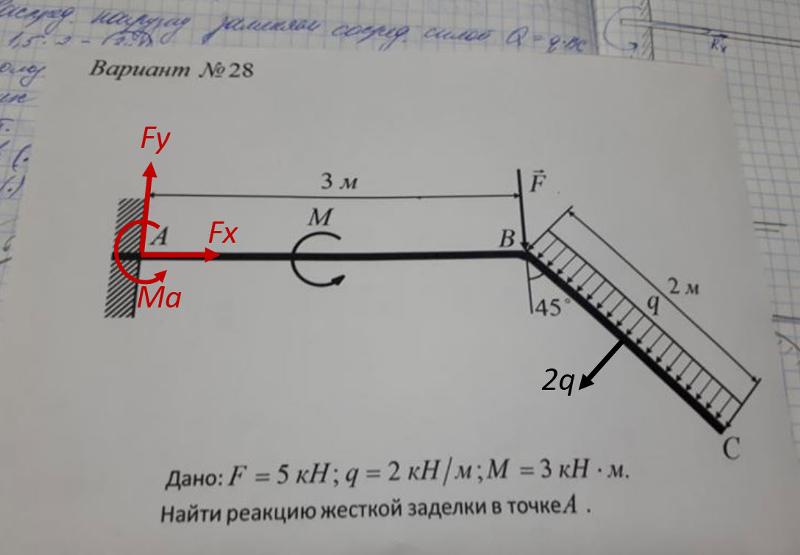
Отбросив заделку, Елизавета Ильинична направила реактивный момент по часовой {1}, а реактивную силу {2} – вверх. Реакции получили такие знаки: сила – плюс {3}, момент – минус {4}. Именно такие знаки автоматически оказались на эпюрах – {5} и {6} соответственно.

Стр. 9, задача 5, продолжение

Стр. 10, задача 6, изгиб шарнирно опёртой балки с врезанным шарниром
Данная задача была включена в задание, можно сказать, в виде шутки, или, точнее, розыгрыша. Дело в том, что решается она за считанные секунды и не требует ни рисунков, ни формул. Тем не менее подавляющее большинство студентов подходят к ней со всей серьёзностью и ответственностью, расписывая все уравнения и делая сечения. Более того, некоторые умудряются ещё и ошибаться. Ниже я покажу, как можно потратить на решение ровно столько времени, сколько требуется для выполнения одного рисунка – эпюры моментов.
Предельная простота задачи определяется наличием шарнира, врезанного над средней опорой. Во врезанном шарнире момент всегда равен нулю.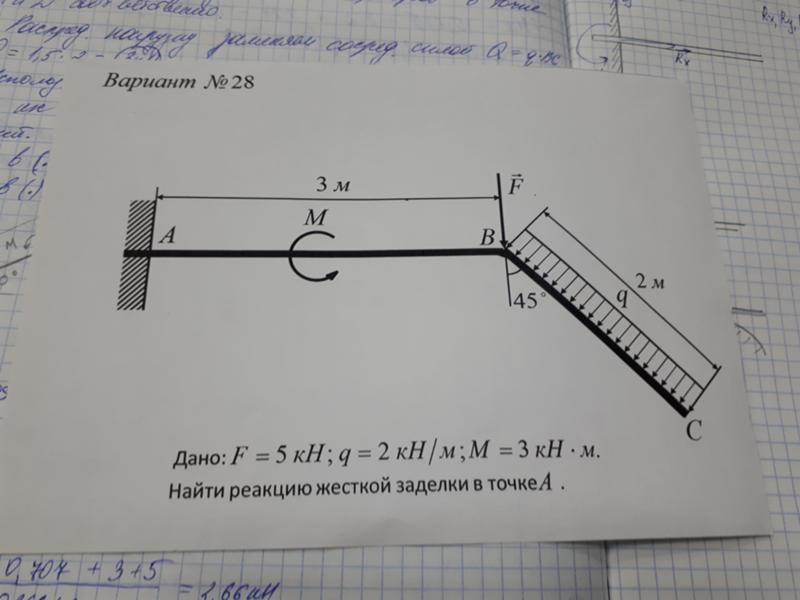 То есть мы сразу, во-первых, имеем одну точку эпюры над средней опорой. Во-вторых, расчётная схема разбивается на две независимых балки слева и справа от средней опоры. В-третьих, отпадает необходимость поиска не только реакции средней опоры, но и, как правило, реакций остальных опор.
Данная задача распадается на шарнирно опёртую балку АВ, нагруженную распределённой силой и моментом на левом конце, и на балку ВС с одним моментом на правом конце.
Начнем с участка АВ, а точнее, с момента. Согласно правилу знаков, ему будет отвечать отрицательный изгибающий момент в сечении А. Далее идёт парабола выпуклостью вверх, приходящая в сечении В, как мы уже знаем, в нуль. Поиск экстремума, правда, всё же требует определения реакции в опоре А, но без учёта участка ВС. Итак, составляя сумму моментов слева от врезанного шарнира, находим реакцию в опоре А – она равна ³/₂ q·l и направлена вверх. Нетрудно догадаться, что вся эпюра поперечной силы на данном участке будет расположена сверху оси и её не пересечёт. Значит, и экстремума на участке АВ нет. Рисуем эпюру и переходим к участку ВС.
А на нём и рассматривать-то нечего: слева нуль, справа +2 q·l². Соединяем точки прямой и всё – эпюра построена, задача решена.

Стр. 11, задача 7, изгиб балки с двумя врезанными шарнирами
В расчётной схеме пять неизвестных: в сечении А момент и две силы, горизонтальная и вертикальная, и по одной реакции в сечениях С и Е. Исходя из суммы на горизонталь, сразу исключаем из рассмотрения все горизонтальные силы, как реактивные, так и внутренние. Остаются 4 неизвестных. Уравнений будет больше, а именно:

Сумма сил на вертикаль;
Сумма моментов всех внешних силовых факторов слева от шарнира В, относительно него же;
То же, справа от В;
То же, слева от D;
То же, справа от D;
Сумма всех моментов относительно произвольной точки.

То есть имеем шесть уравнений для четырёх неизвестных. Значит, четыре уравнения используем для поиска реакций, одно – для необязательной проверки, а одно оказывается линейной комбинацией всех остальных уравнений и, таким образом, лишним.
Елизавета Ильинична выбрала уравнения №№5, 3, 1 и 2 ({1}-{4}), соответственно. Порядок решения выглядит разумным – каждое уравнение даёт новую, ранее неизвестную, величину, с учётом предыдущих результатов. Реакция R₄ вычисляется сразу {1}, что позволяет последовательно найти R₃ {2}, затем R₁ {3}, и, окончательно, R₂ {4}.
Далее, не делая сечения и не рисуя отсечённый кусочек (точнее, выполняя эти действия мысленно) {5}, Елизавета Ильинична ищет координату экстремума {6} и его величину {7}, на участке АВ.
Остальные расчёты выполняются аналогично.

Стр. 12, задача 7, продолжение

Стр. 13, задача 8, плоская рама
Задача также решена исключительно в уме. Сперва составляем сумму моментов относительно неподвижного шарнира. Обе внешние силы дают по моменту Fl против часовой стрелки. Чтобы уравновесить конструкцию, реакция в подвижном шарнире с плечом l должна быть направлена вниз и равняться 2F.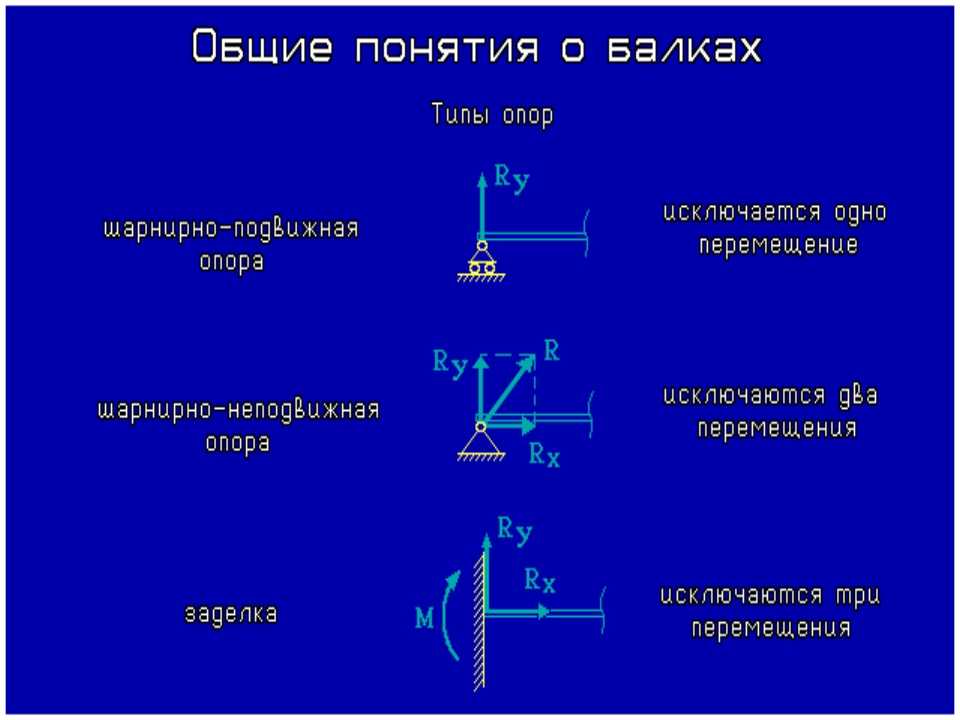 Сумма на горизонталь даёт нулевую горизонтальную реакцию в неподвижном шарнире. Вертикальная в нём же равна 2F и направлена вверх, хотя для построения эпюры она и не нужна.
Строим эпюру начиная, допустим, с правого верхнего угла. Вертикальная сила вызывает сжатие, а не изгиб, и может пока не учитываться. Горизонтальная сила сжимает левые (внутренние) слои и в правом нижнем углу даёт момент 2Fl. Из узла согласно правилу «с чем пришёл – с тем ушёл» мы уходим с тем же моментом, сжимающим те же внутренние слои. Но далее вертикальная сила заставляет эпюру момента идти вниз и прийти в нуль в левом нижнем углу. Задача решена.

Стр. 14, задача 9, плоская круговая рама
Постановка задачи {1}. Далее в уме находим реакции, составляя сперва сумму моментов относительно шарнира D. Обе внешних нагрузки дают момент Fr + 2F·r = 3Fr по часовой стрелке. Тогда сила в шарнире А с плечом r должна быть направленной вниз и быть равной 3F. Теперь из проекций на вертикаль и горизонталь находим реакции в самом шарнире D. Безопорная конструкция {2}.

Стр. 15, задача 9, продолжение
Разбиваем раму на участки DC и CA. На первом из них {1} произвольно выбираем направление изгибающего момента и правило знаков (вновь, на мой взгляд, неудобное).
В начале участка СА сила 5F {2} – внутренняя, найденная в уме из равновесия участка DC, а сила 2F {3} – внешняя. В уравнение равновесия попадает их сумма, точнее, разность 3F вместе с внутренним моментом 5Fr, также найденным на предыдущем участке.
Углу 180° в выбранной системе координат соответствует сечение А. Момент получился отрицательным и равным по модулю Fr {5}. Согласно выбранному правилу знаков {6} отрицательным считается момент, сжимающий внешние слои рамы. Именно таков по модулю и направлению внешний момент в сечении А – проверка сошлась.
Эпюра {3} показана на Стр. 14.

Стр. 16, задача 10, Т-образная плоская рама
Реакции заделки найдены на черновом рисунке внизу.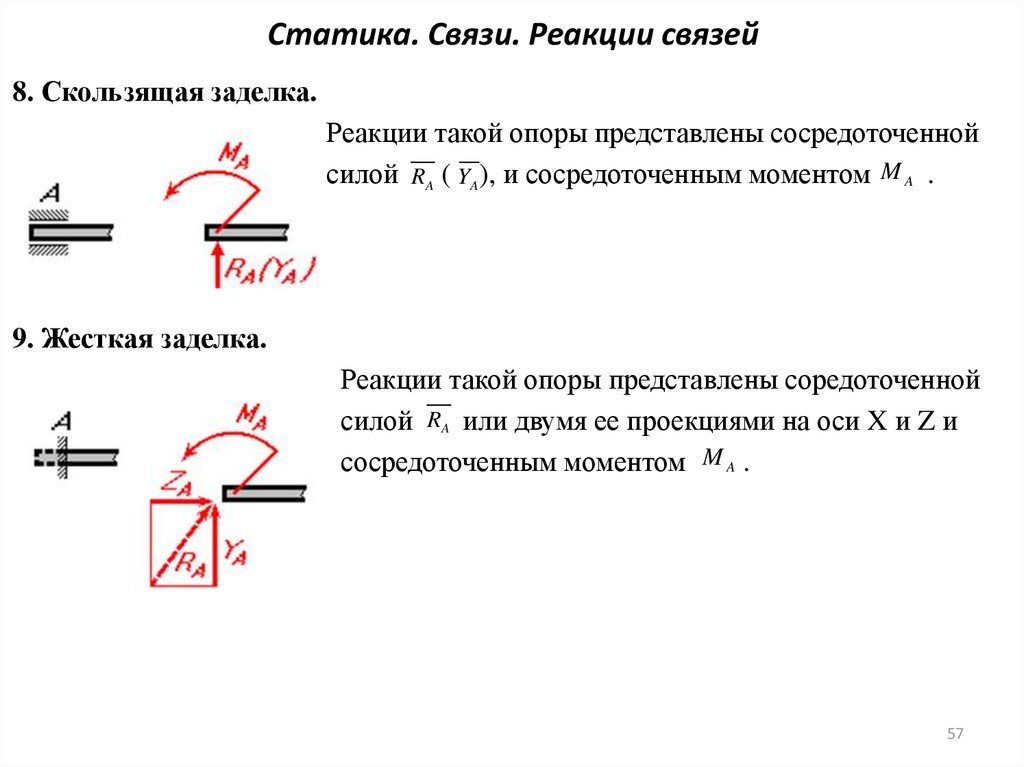 Построение эпюры очевидно.

Две остальные задачи (всего их в то время было 12) посвящены плоскопространственной и пространственной рамам, соответственно. В настоящее время эти задачи исключены из домашнего задания и здесь не рассматриваются.

Распространение распределения

в радикальных реакциях

Радикальные реакции

Распространение инициации в радикальных реакциях

Давайте обсудим хлорирование этана, чтобы проиллюстрировать Три важных шага радикальной галогена с гомолизом σ-связи с образованием двух радикалов. Это называется посвящение – начало радикальной цепной реакции. Мы разрываем связь в исходных материалах, поэтому этот шаг требует энергии света или тепла :

Обратите внимание, что в отличие от большинства других реакций в органической химии, таких как нуклеофильное замещение, отщепление или присоединение, показаны радикальных реакций половинчатых стрелок и одна стрелка показывает движение одного электрона.

Полуголовые стрелы , также известные как стрелы для рыболовных крючков , указывают на то, что σ-связь разрывается гомолитически, т. е. электроны ковалентной связи распределяются между двумя атомами.

Инициирование при умеренных температурах также может катализироваться пероксидами . Одной из особенностей пероксидов является наличие слабой связи О-О , которая при разрыве образует радикалы.

Вы когда-нибудь задумывались, почему одни лекарства продаются в темных бутылках, а другие в темных?

Ацилпероксиды особенно полезны для этой цели, поскольку образующиеся радикалы стабилизированы резонансом:

Простые пероксиды действуют аналогичным образом, образуя алкоксильные радикалы, которые затем используются в радикальных реакциях:

7 радикалы

, образующиеся на стадии инициирования , очень нестабильны .

Это атомы хлора, а из общей химии вы знаете, что галогены существуют в виде двухатомных молекул, а не атомов.

На следующем этапе эти реактивные радикалы быстро реагируют с этаном путем отрыва водорода :

радикал заключается в том, что создается новый радикал.

Отщепление водорода радикалом галогена является определяющей скоростью стадией радикального галогенирования.

9Алкильные радикалы 0007 также очень реакционноспособны , и они реагируют с газообразным хлором с образованием нового радикала хлора . Таким образом, процесс продолжается снова и снова без необходимости подачи энергии для повторного инициирования:

Вот почему радикальные реакции классифицируются как цепные реакции – для запускают реакцию, и однажды начавшись, процессы продолжаются многократно.

Стоит также отметить, что отщепление водорода отличается от реакций переноса протона , которые следуют ионному механизму. Абстрагирование водорода — это движение радикала H•, а перенос протона — это движение иона H ⁺:

Стадии инициации и распространения, которые мы рассмотрели до сих пор, представляют собой монохлорирование с образованием хлорэтана (этилхлорида). Однако , если Cl ₂ добавляют в избыточном или равном количестве, наблюдается полихлорирование .

Например, , при смешивании равных количеств метана и хлора и облучении светом с соответствующей длиной волны в результате реакции образуется смесь следующих продуктов: получение этой смеси моно- и полихлорированного метана заключается в изменении концентраций реагентов и продуктов по мере протекания реакции.

Первоначально присутствуют только хлор и метан, и их реакция дает хлорметан и хлороводород:

Однако в ходе реакции концентрация хлорметана в смеси увеличивается . Кроме того, хлорметан более реакционноспособен, чем метан, и, несмотря на более низкую концентрацию, он начинает реагировать с хлором с образованием дихлорметана :

. трихлорметан , который затем превращается в тетрахлорметан .

При хлорировании этана образуются 1,1-дихлорэтан и 1,2-дихлорэтан, а также смесь более высокохлорированных этанов:

Поэтому для достижения моногалогенирования всегда необходимо использовать алкан в избытке. Моногалогенирование важно, так как позволяет проводить селективное галогенирование с использованием брома и в целом более полезно для получения галогеналканов, используемых в органическом синтезе.

У вас может возникнуть один хороший вопрос:

Ответ на этот вопрос: да. Фактически, , когда встречаются два радикала, они реагируют очень быстро из-за своей нестабильности. Однако ключевое слово здесь — «когда» или «если» .

Концентрация радикалов очень низкая по сравнению с концентрацией нейтральных молекул, и у них просто нет возможности столкнуться. Таким образом, распространение продолжает повторять шаги тысячи раз, прежде чем в конце концов радикалы встретятся и прореагируют.

Когда два радикала реагируют, они начинают делиться неспаренными электронами и образуют новую σ-связь . Это стадия обрыва, которая завершает цепочку стадий распространения:

Обрыв не ограничивается реакцией конкретных радикалов. Любые два радикала, реагирующие с образованием нейтральных частиц, представляют собой реакцию обрыва.

Таким образом, терминация представляет собой комбинацию двух радикалов для образования стабильной связи, и в результате чистый результат переходит от двух радикалов к полному отсутствию радикалов.

Это может показаться слишком большим, если вы просматриваете это в первую очередь, но один быстрый способ идентифицировать эти стадии радикального галогенирования состоит в том, чтобы отслеживать количество радикалов:

0 радикалов к двум радикалам
Распространение – идет от 1 радикала к двум радикалам
Завершение – идет от 2 радикалов к 0 радикалам

Нарисуйте соответствующие стрелы для рыбного крючка для следующего радикального процесса и идентифицируйте их как распространение инициации или прекращение , и терминация в свободнорадикальных реакциях

В предыдущем посте о реакциях свободнорадикального замещения мы говорили о том, почему в свободнорадикальных реакциях требуется тепло или свет ( См. публикацию: Свободнорадикальные реакции – зачем нужны тепло или свет ). В этом посте мы рассмотрим механизм реакции свободно-радикального замещения, которая состоит из трех ключевых типов стадий: инициация, распространение и завершение.

Содержание

Механизм свободнорадикального замещения алкана Cl ₂
Стадия, на которой происходит чистое увеличение количества свободных радикалов, называется «инициацией»
Этап, на котором нет чистого прироста или потери свободных радикалов, называется «размножением»
Остерегайтесь этой распространенной ошибки при определении механизмов образования свободных радикалов
В свободнорадикальном галогенировании алканов существует два этапа размножения
Стадия, на которой происходит чистое уменьшение количества свободных радикалов, называется «прекращение»
Полный механизм свободнорадикального замещения алкана
Резюме: реакции свободнорадикального замещения
Примечания
(дополнительно) Ссылки и дополнительная литература

1.

Механизм свободнорадикального замещения алкана Cl ₂

Возможно, вы помните, что видели эту реакцию в предыдущем посте – это свободнорадикальное хлорирование. метана с Cl ₂ .

Это замена углерода, потому что связь C-H разрывается и образуется новая связь C-Cl. Побочным продуктом является HCl.

Теперь, когда мы знаем немного больше о том, что такое свободные радикалы и их ключевые свойства, сегодня мы ответим: как работает эта реакция? ».

Мы рассмотрим ключевые этапы этой реакции и узнаем, что они состоят из трех ключевых фаз: инициация , завершение и распространение .

2. Стадия, на которой происходит чистое увеличение количества свободных радикалов, называется «инициацией».

Свободнорадикальные реакции обычно требуют применения тепла или света. Это связано с тем, что любой из этих источников энергии может привести к гомолитическому расщеплению относительно слабых связей, таких как Cl-Cl, с образованием свободных радикалов [т. е. Кл• ]

Каждая свободнорадикальная реакция начинается со стадии образования свободных радикалов, и по этой причине этот начальный этап называется инициированием.

Вот уравнение для этого шага инициации. Следует отметить две вещи:

Реакция является равновесной – в любой момент времени присутствует только небольшая концентрация свободных радикалов (но этого будет достаточно, как мы увидим)
Обратите внимание, что существует чистая увеличение количества свободных радикалов в этой реакции. Мы идем от ноль (в реагентах) до два (в продуктах).

3. Этап, на котором нет чистого прироста или потери свободных радикалов, называется «размножением». Радикалы хлора очень реакционноспособны и могут соединяться с водородом из метана с образованием метильного радикала, • CH

₃

Если вы подсчитаете количество свободных радикалов в этом уравнении, вы заметите, что в реагентах есть один и один в продуктах. Так что есть нет чистого увеличения количества свободных радикалов.

Этот тип шага называется «распространением».

Если вы ведете подсчет, к этому моменту вы должны увидеть, что до завершения нашей реакции остается сформировать только одну связь. Все, что нам нужно сделать, это образовать связь C-Cl.

4. Остерегайтесь этой распространенной ошибки при определении механизмов действия свободных радикалов

Здесь легко допустить небольшую ошибку. Учитывая, что на стадии инициирования образуются два радикала хлора, было бы кажутся естественными для соединения радикала метила и радикала хлора с образованием CH ₃ –Cl . Верно?????

Нееет!

Обратите внимание, что количество свободных радикалов уменьшилось на , здесь, , а не , осталось прежним. Это не может быть распространением! (На самом деле это прекращение, о котором мы поговорим через минуту).

5.

В свободнорадикальном замещении есть две стадии размножения

На самом деле, мы можем сделать правильную стадию «размножения» следующим образом: возьмем метильный радикал, и он вступит в реакцию с Cl ₂ все еще присутствует. Это дает нам Ch4Cl и радикал хлора. Обратите внимание, что чистого изменения количества свободных радикалов не произошло, так что это все еще «распространение».

Еще раз обратите внимание, что мы образуем радикал хлора! Что в этом такого важного? Это очень важно, потому что этот радикал хлора может затем выполнить этап распространения № 1 на новой молекуле нашего субстрата (CH ₄ ), продолжая процесс. Это цепная реакция — после образования радикал хлора равен катализатор. Вот почему нам нужно лишь небольшое количество радикала хлора для протекания этой реакции. Нет ничего необычного в том, что 10 ⁴ или более из этих циклов продолжаются до того, как произойдет завершение. ( См. эту ссылку ниже )

6. Этап, на котором происходит чистое снижение количества свободных радикалов, называется «прекращением»

Может ли эта цепная реакция продолжаться вечно? №

Рассмотрим два предельных случая. Если концентрация Cl ₂ низкая относительно CH ₄ (другими словами, Cl ₂ является нашим ограничивающим реагентом), то скорость этапа распространения № 2 будет замедляться по мере уменьшения его концентрации. Без какого-либо Cl ₂, с которым можно было бы реагировать, наши радикалы •CH ₃ могут просто соединиться с другим свободным радикалом (таким как •Cl) с образованием, например, CH ₃ Cl. Для этой реакции практически нет препятствий. Обратите внимание, что здесь количество свободных радикалов уменьшается с 2 до нуля. Это называется завершением .

Две метильные группы также могут соединяться вместе, образуя CH ₃ –CH ₃ ; это тоже прекращение!

7.

Полный механизм свободно-радикального замещения алкана

Давайте объединим все эти этапы, чтобы мы могли четко видеть этапы инициации, распространения и завершения.

8. Резюме: реакции свободнорадикального замещения

Эти три типа стадий встречаются в каждой свободнорадикальной реакции.

Суть в том, что путем подсчета количества радикалов, созданных или уничтоженных на каждом этапе, можно определить, является ли этот этап инициацией, распространением или завершением.

Инициация -> чистое образование радикалов
Распространение -> отсутствие изменений в количестве свободных радикалов
Прекращение -> чистое разрушение свободных радикалов

Мы оставим два тизера для будущих постов.

Во-первых… обратите внимание, что здесь мы используем канал ₄ , где каждая связь C–H идентична. Что могло бы произойти, если бы мы использовали алкан, в котором все связи C–H не равны… как, например, пропан или пентан?

Во-вторых, эта реакция резко проваливается , когда Br ₂ используется вместо Cl ₂ для реакции CH ₄ . Однако мы увидим, что Br ₂ может работать в некоторых особых случаях.

Скоро еще!

Следующее сообщение: Изомеры из свободнорадикальных реакций

Примечания

БОНУСНЫЕ материалы.

Мы только что говорили о ситуации, когда используется один эквивалент хлора (Cl ₂ ). Что происходит, когда мы используем несколько эквивалентов или даже чрезмерное их количество?

Задумайтесь на секунду. Представьте, что у нас есть несколько эквивалентов Cl ₂ в присутствии CH ₃ Cl. Как вы думаете, что может произойти?

Атом Cl• может реагировать с CH ₃ Cl с образованием • CH ₂ Cl [и HCl], который затем может реагировать с Cl ₂ отдать CH ₂ Cl ₂ !

Аналогично, если у нас все еще есть избыток Cl ₂ , то мы будем наблюдать преобразование CH ₂ Cl ₂ в CHCl ₃ .

Наконец, при наличии достаточного количества Cl ₂ мы можем представить преобразование CHCl ₃ в CCl ₄ .

В этот момент больше нет связей C-H, чтобы реагировать с радикалом хлора, и, таким образом, наша реакция в конечном итоге прекратится.

Суть в том, что алканы, при достаточно большом избытке Cl ₂ , в конечном итоге заменят весь водород на хлор.

Этот путь фактически представляет собой промышленное производство дихлорметана (CH ₂ Cl ₂ – обычный лабораторный растворитель), хлороформа (CHCl ₃) и четыреххлористого углерода (CCl ₄). В течение многих десятилетий CCl ₄ выпускался в мегатонном масштабе для использования в качестве хладагента и растворителя для химической чистки, пока исследования не показали, что он и другие ХФУ разрушают озоновый слой.

(Дополнительно) Ссылки и дополнительная литература

Walling, C. in Free Radicals In Solution , Wiley and Sons, New York 1957 p. 352
Хлорирование метана
T. McBee, H. B. Hass, C. M. Neher и H. Strickland
Промышленная и инженерная химия 1942, 34 (3), 296-3009 _{9 : 111110 29111111110 29111111110 29111111110 29111111102020102020202021 (3). /ie50387a009
В этой статье показано, что хлорированием метана можно управлять с получением любого желаемого хлорметана с высоким выходом. Это важно, потому что CH ₃ Cl, CH ₂ Cl ₂, CHCl ₃ и CCl ₄ являются важным сырьем или растворителем, и именно так они производятся в промышленности.}
Кинетика термического хлорирования метана
Роберт Н. Пиз и Джордж Ф. Вальц
Журнал Американского химического общества 1931, 53 (10), 3728-3737 _{99020 53 (10), 3728-3737 _{: : 8: 8: 100008: : 8: 100008: 8: (10). /ja01361a016
В этой статье представлены кинетические доказательства того, что хлорирование метана 2 ^{и заказ} (первый заказ как по метану, так и по Cl ₂ ).}}
THE BROMINATION OF CYCLOHEXANE, METHYLCYCLOHEXANE, AND ISOBUTANE
M. S. KHARASCH, WILLIAM HERED, and FRANK R. MAYO
The Journal of Organic Chemistry 1941 06 (6), 818-829
DOI : 10.1021/jo01206a005
Природа механизма свободнорадикальной цепной реакции при замещении алканов не была полностью изучена до 1940-х годов. В этом новаторском 1941, Kharasch предлагает цепной механизм, который мы сейчас читаем в учебниках:
а) Br2 + hv -> 2 Br• (инициация)
б) R—H + Br• -> R• + HBr (стадия распространения 1)
c ) R• + Br2 -> R-Br + Br• (этап размножения 2)
Хараш сообщает, что свободнорадикальное замещение циклогексана на Br2 протекает очень медленно в темноте или в отсутствие кислорода.