Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.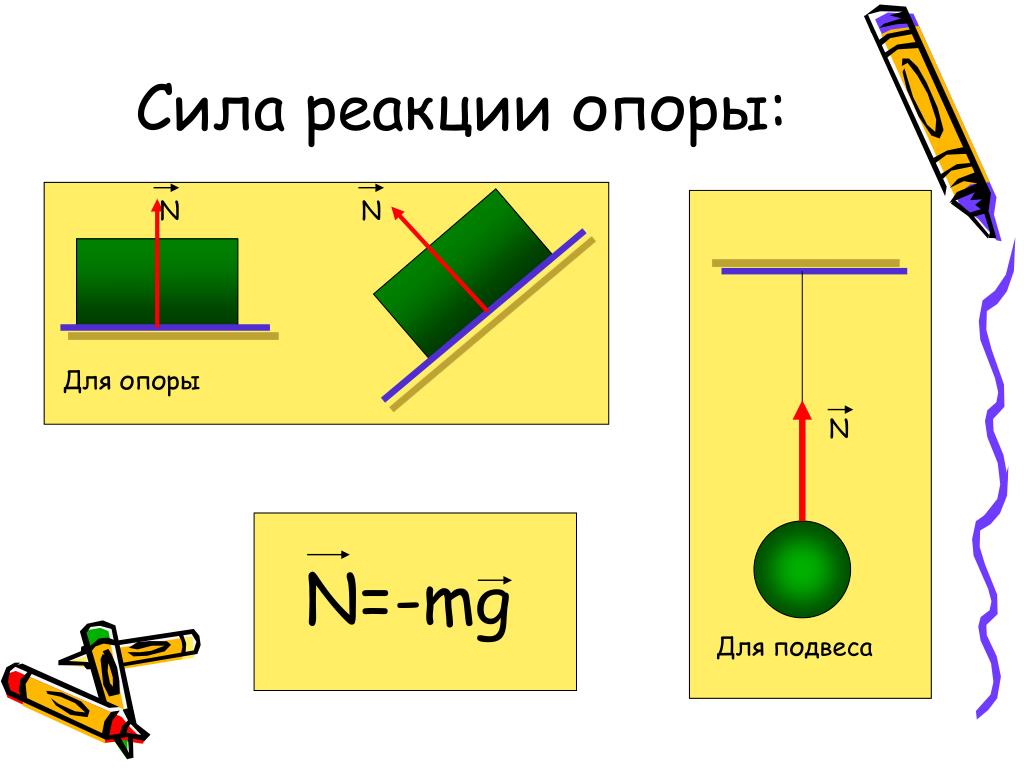
{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Силы в природе формулы.
 Школьная энциклопедия Необходимо знать точку приложения и направление каждой силы. Важно уметь определить какие именно силы действуют на тело и в каком направлении. Сила обозначается как , измеряется в Ньютонах. Для того, чтобы различать силы, их обозначают следующим образом
Школьная энциклопедия Необходимо знать точку приложения и направление каждой силы. Важно уметь определить какие именно силы действуют на тело и в каком направлении. Сила обозначается как , измеряется в Ньютонах. Для того, чтобы различать силы, их обозначают следующим образомНиже представлены основные силы, действующие в природе. Придумывать не существующие силы при решении задач нельзя!
Сил в природе много. Здесь рассмотрены силы, которые рассматриваются в школьном курсе физики при изучении динамики. А также упомянуты другие силы, которые будут рассмотрены в других разделах.
Сила тяжести
На каждое тело, находящееся на планете, действует гравитация Земли . Сила, с которой Земля притягивает каждое тело, определяется по формуле
Точка приложения находится в центре тяжести тела. Сила тяжести
Сила трения
Познакомимся с силой трения. Эта сила возникает при движении тел и соприкосновении двух поверхностей. Возникает сила в результате того, что поверхности, если рассмотреть под микроскопом, не являются гладкими, как кажутся. Определяется сила трения по формуле:
Возникает сила в результате того, что поверхности, если рассмотреть под микроскопом, не являются гладкими, как кажутся. Определяется сила трения по формуле:
Сила приложена в точке соприкосновения двух поверхностей. Направлена в сторону противоположную движению.
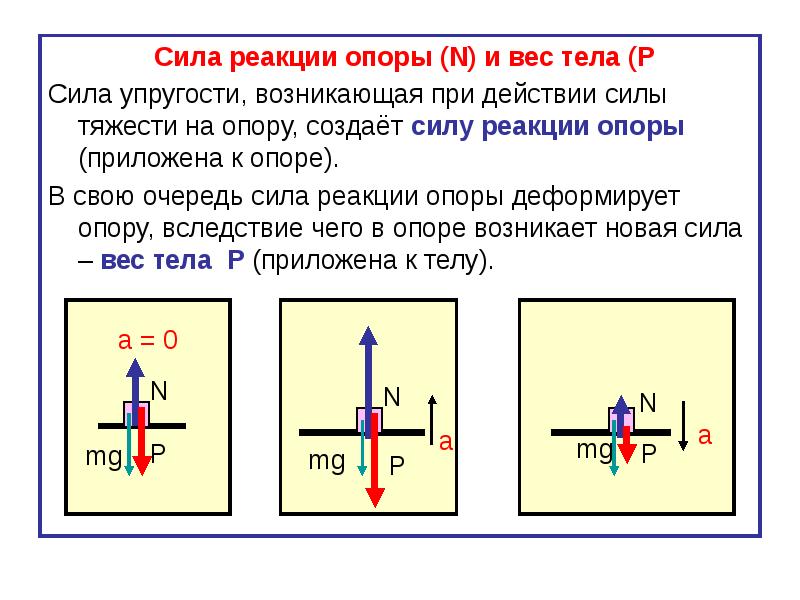
Сила реакции опоры
Представим очень тяжелый предмет, лежащий на столе. Стол прогибается под тяжестью предмета. Но согласно третьему закону Ньютона стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол. То есть вверх. Эта сила называется реакцией опоры. Название силы «говорит» реагирует опора . Эта сила возникает всегда, когда есть воздействие на опору. Природа ее возникновения на молекулярном уровне. Предмет как бы деформировал привычное положение и связи молекул (внутри стола), они, в свою очередь, стремятся вернуться в свое первоначальное состояние, «сопротивляются».
Абсолютно любое тело, даже очень легкое (например,карандаш, лежащий на столе), на микроуровне деформирует опору.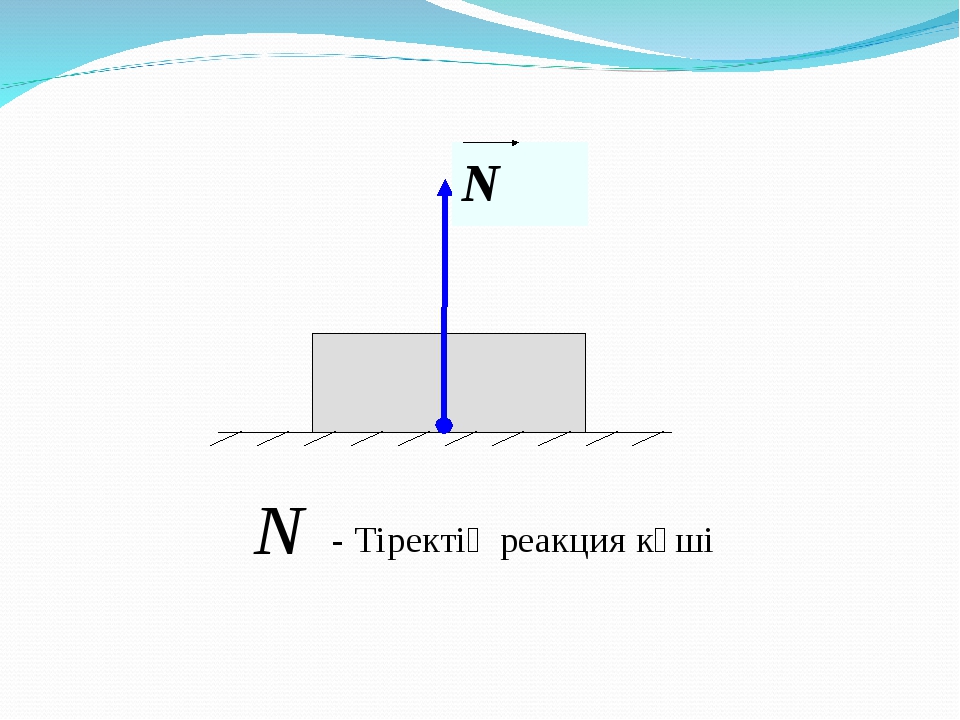 Поэтому возникает реакция опоры.
Поэтому возникает реакция опоры.
Специальной формулы для нахождения этой силы нет. Обозначают ее буквой , но эта сила просто отдельный вид силы упругости, поэтому она может быть обозначена и как
Сила приложена в точке соприкосновения предмета с опорой. Направлена перпендикулярно опоре.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
Сила упругости
Это сила возникает в результате деформации (изменения первоначального состояния вещества). Например, когда растягиваем пружину, мы увеличиваем расстояние между молекулами материала пружины. Когда сжимаем пружину — уменьшаем. Когда перекручиваем или сдвигаем. Во всех этих примерах возникает сила, которая препятствует деформации — сила упругости.
Закон Гука
Сила упругости направлена противоположно деформации.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
При последовательном соединении, например, пружин жесткость рассчитывается по формуле
При параллельном соединении жесткость
Жесткость образца. Модуль Юнга.
Модуль Юнга.
Модуль Юнга характеризует упругие свойства вещества. Это постоянная величина, зависящая только от материала, его физического состояния. Характеризует способность материала сопротивляться деформации растяжения или сжатия. Значение модуля Юнга табличное.
Подробнее о свойствах твердых тел .
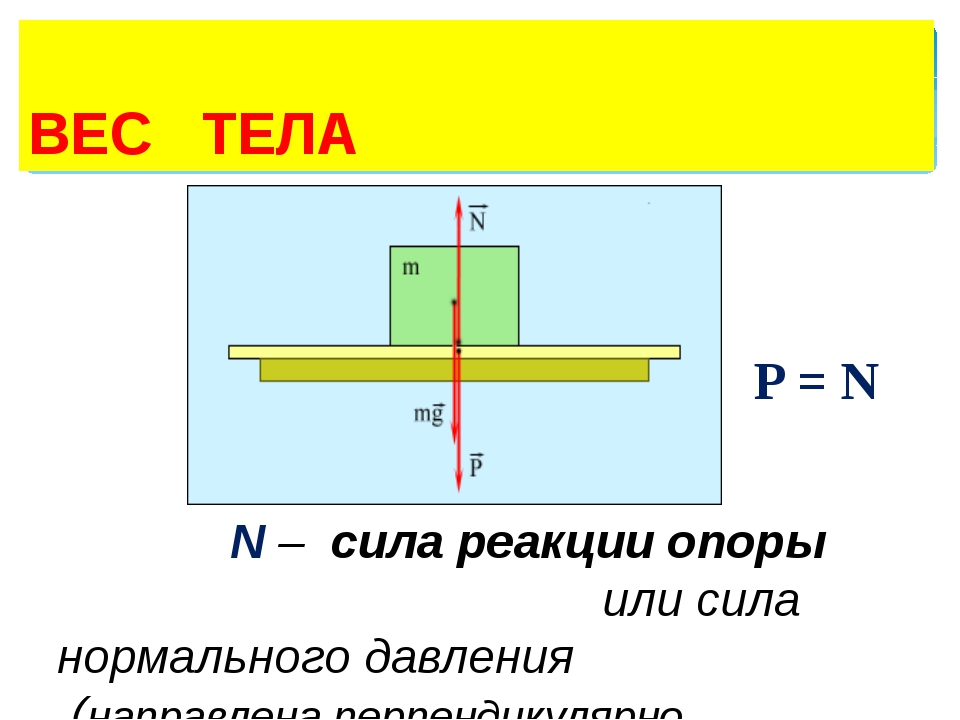
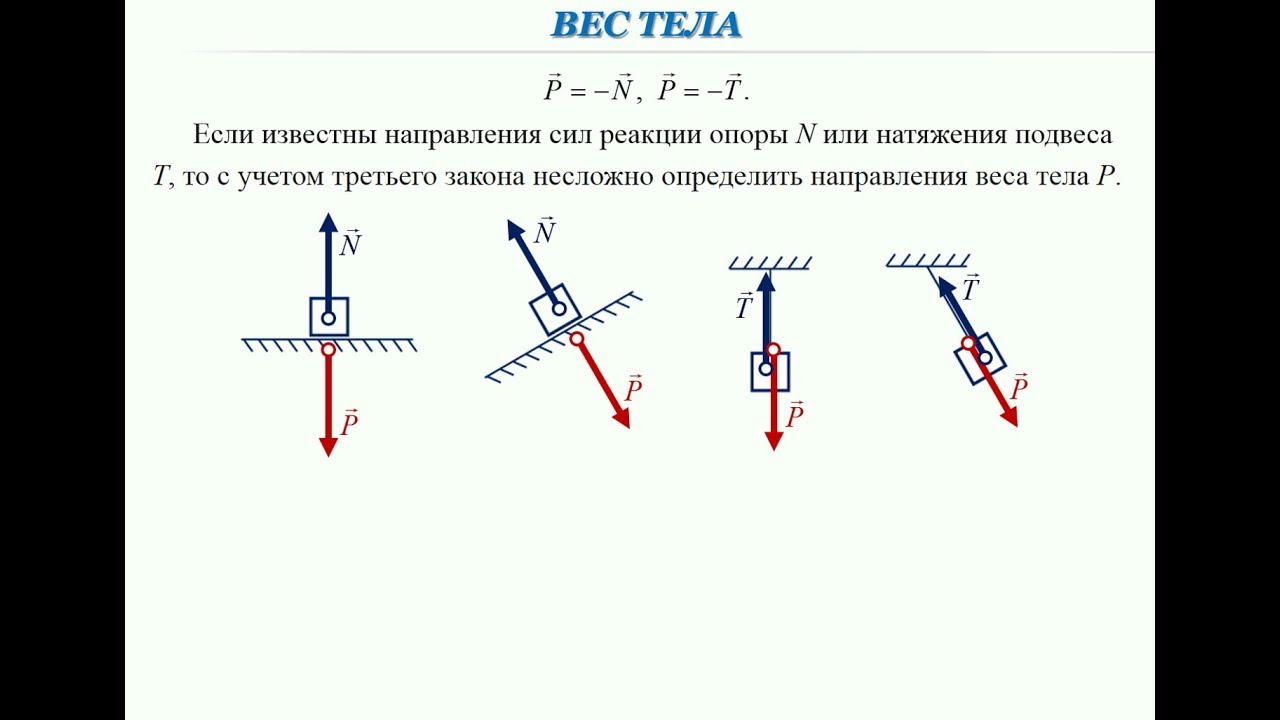
Вес тела
Вес тела — это сила, с которой предмет воздействует на опору. Вы скажете, так это же сила тяжести! Путаница происходит в следующем: действительно часто вес тела равен силе тяжести, но это силы совершенно разные. Сила тяжести — сила, которая возникает в результате взаимодействия с Землей. Вес — результат взаимодействия с опорой. Сила тяжести приложена в центре тяжести предмета, вес же — сила, которая приложена на опору (не на предмет)!
Формулы определения веса нет. Обозначается эта силы буквой .
Сила реакции опоры или сила упругости возникает в ответ на воздействие предмета на подвес или опору, поэтому вес тела всегда численно одинаков силе упругости, но имеет противоположное направление.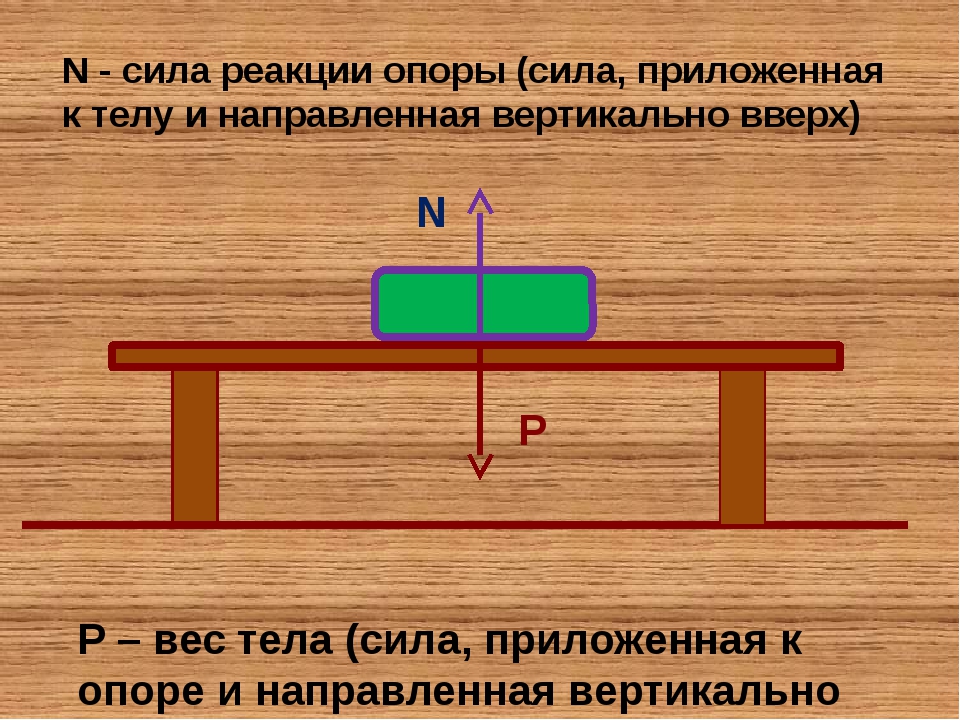
Сила реакции опоры и вес — силы одной природы, согласно 3 закону Ньютона они равны и противоположно направлены. Вес — это сила, которая действует на опору, а не на тело. Сила тяжести действует на тело.
Вес тела может быть не равен силе тяжести. Может быть как больше, так и меньше, а может быть и такое, что вес равен нулю. Это состояние называетсяневесомостью . Невесомость — состояние, когда предмет не взаимодействует с опорой, например, состояние полета: сила тяжести есть, а вес равен нулю!
Определить направление ускорения возможно, если определить, куда направлена равнодействующая сила
Обратите внимание, вес — сила, измеряется в Ньютонах. Как верно ответить на вопрос: «Сколько ты весишь»? Мы отвечаем 50 кг, называя не вес, а свою массу! В этом примере, наш вес равен силе тяжести, то есть примерно 500Н!
Перегрузка — отношение веса к силе тяжести
Сила Архимеда
Сила возникает в результате взаимодействия тела с жидкость (газом), при его погружении в жидкость (или газ).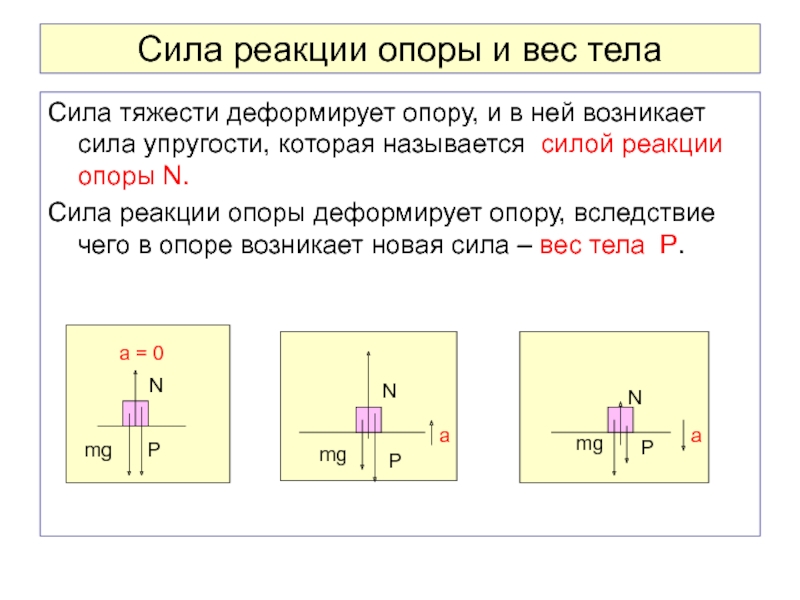 Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:
Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:
В воздухе силой Архимеда пренебрегаем.
Если сила Архимеда равна силе тяжести, тело плавает. Если сила Архимеда больше, то оно поднимается на поверхность жидкости, если меньше — тонет.
Электрические силы
Существуют силы электрического происхождения. Возникают при наличии электрического заряда. Эти силы, такие как сила Кулона , сила Ампера , сила Лоренца , подробно рассмотрены в разделе Электричество .
Схематичное обозначение действующих на тело сил
Часто тело моделируют материальной точкой . Поэтому на схемах различные точки приложения переносят в одну точку — в центр, а тело изображают схематично кругом или прямоугольником.
Для того, чтобы верно обозначить силы, необходимо перечислить все тела, с которыми исследуемое тело взаимодействует. Определить, что происходит в результате взаимодействия с каждым: трение, деформация, притяжение или может быть отталкивание.
Главное запомнить
Силы трения
Различают внешнее (сухое) и внутреннее (вязкое) трение. Внешнее трение возникает между соприкасающимися твердыми поверхностями, внутреннее — между слоями жидкости или газа при их относительном движении. Существует три вида внешнего трения: трение покоя, трение скольжения и трение качения.
Трение качения определяется по формуле
Сила сопротивления возникает при движении тела в жидкости или в газе. Величина силы сопротивления зависит от размеров и формы тела, скорости его движения и свойств жидкости или газа. При небольших скоростях движения сила сопротивления пропорциональна скорости тела
При больших скоростях пропорциональна квадрату скорости
Взаимосвязь силы тяжести, закона гравитации и ускорения свободного падения
Рассмотрим взаимное притяжение предмета и Земли.
Величина ускорения свободного падения зависит от массы Земли и ее радиуса! Таким образом, можно высчитать, с каким ускорением будут падать предметы на Луне или на любой другой планете, используя массу и радиус той планеты.
Расстояние от центра Земли до полюсов меньше, чем до экватора. Поэтому и ускорение свободного падения на экваторе немного меньше, чем на полюсах. Вместе с тем, следует отметить, что основной причиной зависимости ускорения свободного падения от широты местности, является факт вращения Земли вокруг своей оси.
При удалении от поверхности Земли сила земного тяготения и ускорения свободного падения изменяются обратно пропорционально квадрату расстояния до центра Земли.
Которая характеризует меру, с которой на тело воздействуют другие тела либо поля, называется силой. Согласно второму ускорение, которое получает тело, прямо пропорционально действующей на него силе.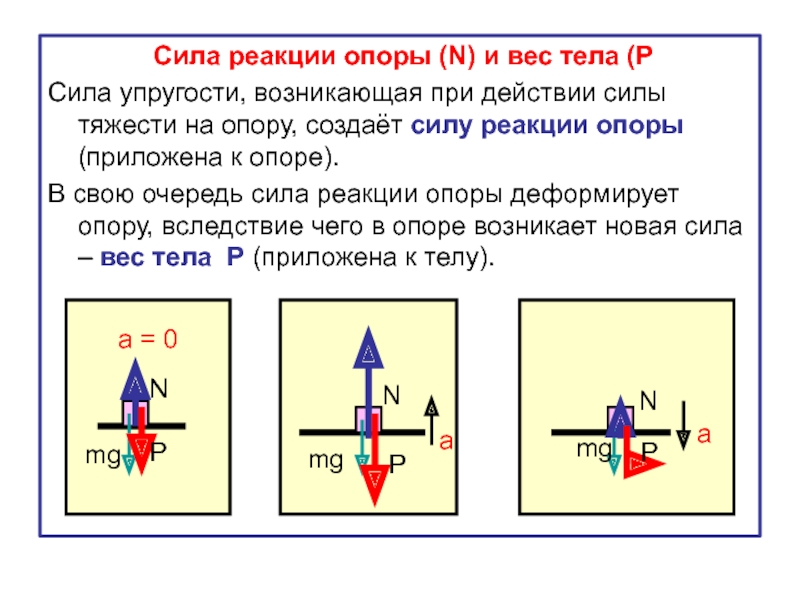
Инерциальные системы отсчета
Силы в природе являются векторными величинами, то есть они имеют модуль и направление. Две силы могут считаться одинаковыми лишь тогда, когда равны их модули, а их направления совпадают.
Если на тело не действуют силы, а также в том случае, когда геометрическая сумма сил, воздействующих на данное тело (эта сумма часто называется равнодействующей всех сил), равна нулю, то тело либо остается в состоянии покоя, либо продолжает движение в одном направлении с постоянной скоростью (то есть движется по инерции). Это выражение справедливо для инерциальных систем отсчета. Существование таких систем постулируется первым законом Ньютона. В природе таких систем нет, но они являются удобной Тем не менее, часто при решении практических задач систему отсчета, связанную с Землей, можно считать инерциальной.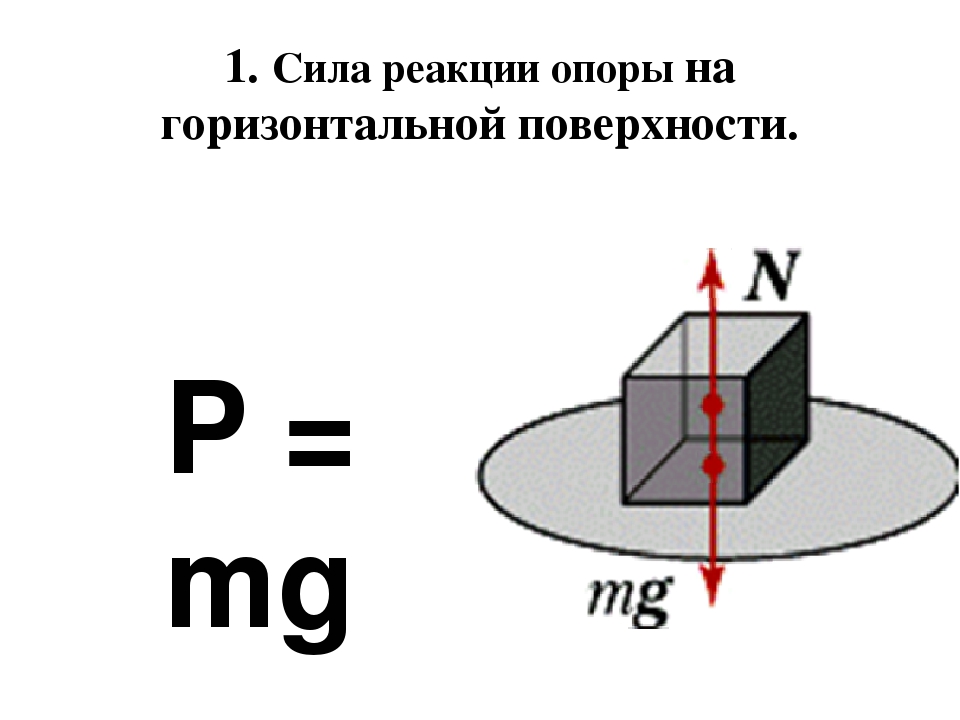
Земля — инерциальная и неинерциальная система отсчета
В частности при строительных работах, при расчете движения автомобилей и плавательного транспорта предположения о том, что Земля — инерциальная система отсчета, вполне достаточно, чтобы с необходимой для практического решения задач точностью описать действующие силы.
В природе также существуют задачи, не допускающие такого предположения. В частности, это относится к космическим проектам. При старте ракеты строго вверх она вследствие вращения Земли осуществляет видимое движение не только вдоль вертикали, но и в горизонтальном направлении против вращения Земли. В этом движении проявляется неинерциальность системы отсчета, связанной с нашей планетой.
Физически на ракету не действуют силы, отклоняющие ее. Тем не менее, для описания движения ракеты удобно использовать Эти силы не существуют физически, но предположение об их существовании позволяет представить неинерциальную систему инерциальной. Другими словами, при расчетах траектории ракеты считают, что система отсчета «Земля» является инерциальной, но при этом на ракету действует некоторая сила в горизонтальном направлении. Эта сила называется сила Кориолиса. В природе ее действие становится заметным, когда речь идет о телах, движущихся на некоторой высоте относительно нашей планеты в течение довольно большого времени либо с большой скоростью. Так, ее учитывают, не только описывая движение ракет и спутников, но и при расчетах движения артиллерийских снарядов, самолетов и т.д.
Эта сила называется сила Кориолиса. В природе ее действие становится заметным, когда речь идет о телах, движущихся на некоторой высоте относительно нашей планеты в течение довольно большого времени либо с большой скоростью. Так, ее учитывают, не только описывая движение ракет и спутников, но и при расчетах движения артиллерийских снарядов, самолетов и т.д.
Природа взаимодействий
Все силы в природе по характеру своего происхождения относятся к четырем фундаментальным гравитационное, слабое и сильное). В макромире заметным является лишь воздействие гравитации и электромагнитных сил. Слабые и сильные взаимодействия влияют на процессы, происходящие внутри атомных ядер и субатомных частиц.
Самым распространенным примером гравитационного взаимодействия является Это сила, с которой Земля действует на окружающие ее тела.
Электромагнитные силы, помимо очевидных примеров, включают в себя все упругие, связанные с давлением взаимодействия, которые тела оказывают друг на друга. Соответственно, такая сила природы, как вес (сила, с которой тело действует на подвес либо опору), имеет электромагнитную природу.
Соответственно, такая сила природы, как вес (сила, с которой тело действует на подвес либо опору), имеет электромагнитную природу.
До сих пор использовалось общее понятие силы, и не рассматривался вопрос о том, какие бывают силы и что они собой представляют. Несмотря на многообразие сил, встречающихся в природе, все их можно свести к четырем видам фундаментальных сил: 1) гравитационные; 2) электромагнитные; 3) ядерные; 4) слабые.
Гравитационные силы возникают между любыми телами. Их действие надо учитывать лишь в мире больших тел.
Электромагнитные силы действуют на заряды как неподвижные, так и движущиеся. Поскольку вещество построено из атомов, которые, в свою очередь состоят из электронов и протонов, то большинство сил, с которыми мы встречаемся в жизни — это электромагнитные силы. Ими являются, например, силы упругости, возникающие при деформации тел, силы трения.
Ядерные
и слабые силы проявляют себя на расстояниях, не
превышающих
м, поэтому эти силы заметны лишь в
микромире.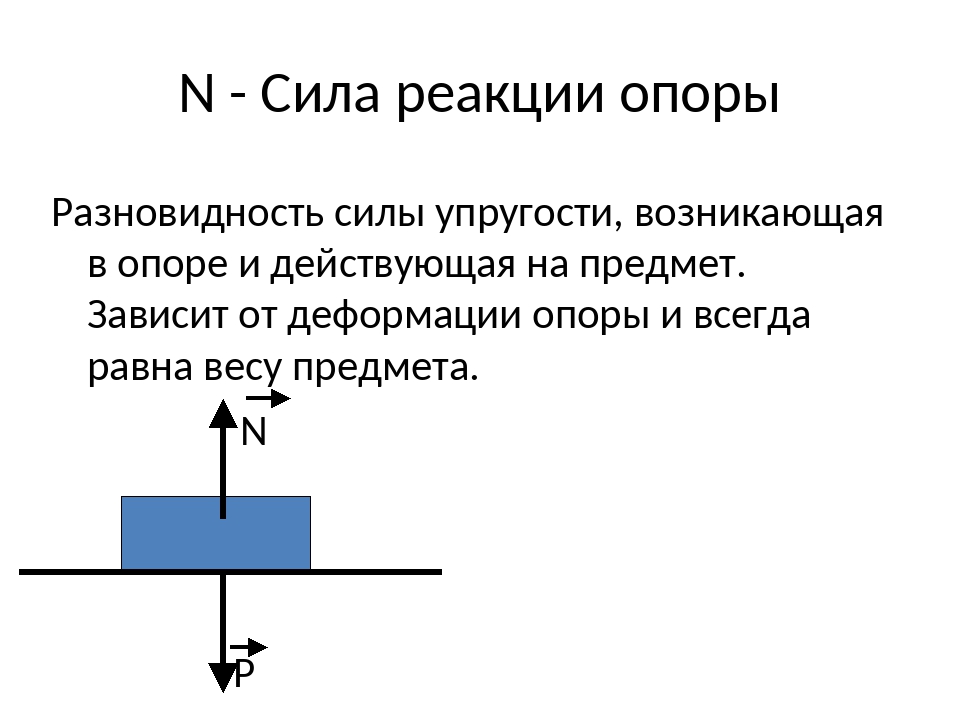 Вся классическая физика, а
вместе с ней и понятие силы, неприменимы
к элементарным частицам. Характеризовать
точным образом взаимодействие этих
частиц с помощью сил нельзя. Единственно
возможным здесь становится энергетическое
описание. Тем не менее, и в атомной физике
часто говорят о силах. В этом случае
терминсила становится синонимом слова взаимодействие .
Вся классическая физика, а
вместе с ней и понятие силы, неприменимы
к элементарным частицам. Характеризовать
точным образом взаимодействие этих
частиц с помощью сил нельзя. Единственно
возможным здесь становится энергетическое
описание. Тем не менее, и в атомной физике
часто говорят о силах. В этом случае
терминсила становится синонимом слова взаимодействие .
Таким образом, в современной науке слово сила употребляется в двух смыслах: во-первых, в смысле механической силы – точной количественной меры взаимодействия; во-вторых, сила означает наличие взаимодействия определенного типа, точной количественной мерой которого может быть только энергия .
В механике рассматриваются три типа сил: гравитационные, упругие и силы трения. Кратко остановимся на них.
1. Гравитационные
силы .
Все тела в природе притягиваются друг
к другу. Эти силы получили название
гравитационных. Ньютон установил закон,
названный законом
всемирного тяготения :
силы, с которыми притягиваются материальные
точки, пропорциональны произведению
их масс, обратно пропорциональны квадрату
расстояния между ними и направлены
вдоль прямой, соединяющих их, т. е.
е.
, (2.16)
где М и т – массы тел; r – расстояние между телами; гравитационная постоянная. Знак «» указывает на то, что это сила притяжения.
Из
формулы (2.16) следует, что при т = М = 1 кг
и r = 1 м,
= F ,
т.е. гравитационная постоянная равна
модулю силы притяжения материальных
точек единичной массы, находящихся на
единичном расстоянии друг от друга.
Впервые опытное доказательство закона
всемирного тяготения проведено
Кавендишем. Он сумел определить величину
гравитационной постоянной:
.
Очень малая величина
указывает на то, что сила гравитационного
взаимодействия значительна только в
случае тел с большими массами.
2. Силы
упругости .
При упругих деформациях возникают силы
упругости. Согласно закону
Гука ,
модуль упругой силы
пропорционален величине деформациих ,
т.е.
, (2.17)
где k
коэффициент упругости. Знак «»
определяет тот факт, что направление
силы и деформации противоположны.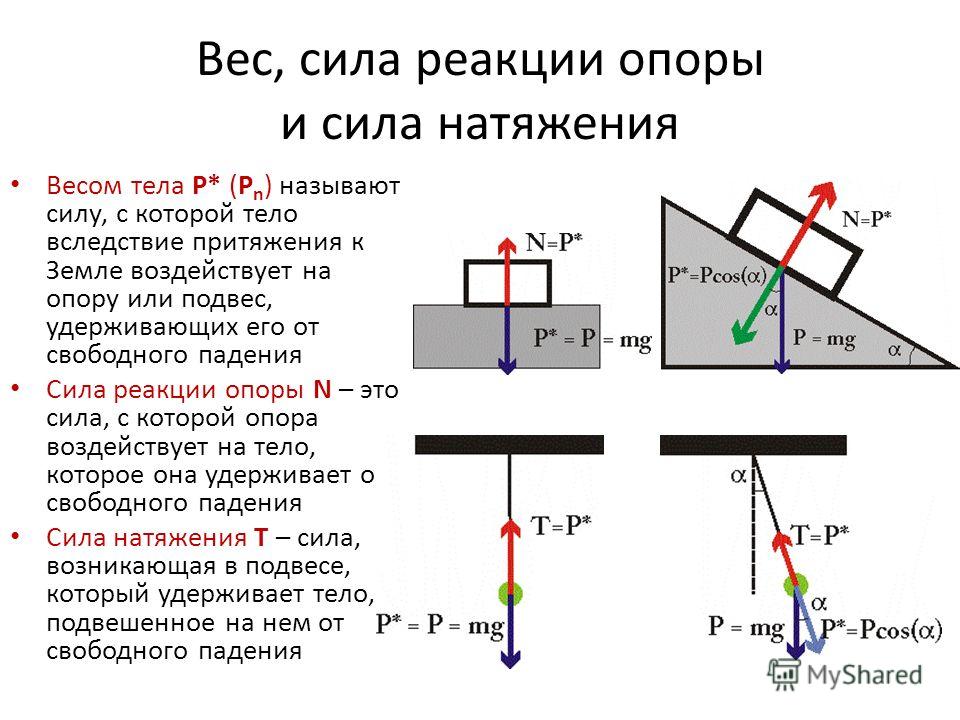
3. Силы трения . При перемещении соприкасающихся тел или их частей относительно друг друга возникают силы трения . Различают внутреннее (вязкое) и внешнее (сухое) трение.
Вязким трением называют трение между твердым телом и жидкой или газообразной средой, а также между слоями такой среды.
Внешним трением называют явление возникновения в месте контакта соприкасающихся твердых тел сил, препятствующих их взаимному перемещению. Если соприкасающиеся тела неподвижны, то между ними возникает сила при попытке сдвинуть одно тело относительно другого. Она называется силой трения покоя . Сила трения покоя не является однозначно определенной величиной. Она меняется от нуля до максимального значения силы, приложенной параллельно плоскости соприкосновения, при которой тело начинает двигаться (рис. 2.3).
Обычно
силой трения покоя и называют эту
максимальную силу трения. Модуль силы
трения покоя
пропорционален модулю силы нормального
давления, который по третьему закону
Ньютона равен модулю силы реакции опорыN ,
т. е.
е.
,
где
коэффициент трения покоя.
При
движении тела по поверхности другого
тела возникает сила трения скольжения .
Установлено, что модуль силы трения
скольжения
так
же пропорционален модулю силы нормального
давленияN
, (2.19)
где
коэффициент трения скольжения.
Установлено, что
,
однако при решении многих задач их
считают равными.
При решении задач учитывают следующие виды сил:
1. Сила
тяжести
сила, с которой гравитационное поле
Земли действует на тело (приложена эта
сила к центру масс тела).
В природе существует четыре типа сил: гравитационные, электромагнитные, ядерные и слабые.
Гравитационные силы, или силы тяготения, действуют между всеми телами. Но эти силы заметны, если хотя бы одно из тел имеет размеры, соизмеримые с размерами планет. Силы притяжения между обычными телами настолько малы, что ими можно пренебречь. Поэтому гравитационными можно считать силы взаимодействия между планетами, а также между планетами и Солнцем или другими телами, имеющими очень большую массу. Это могут быть звёзды, спутники планет и т.п.
Это могут быть звёзды, спутники планет и т.п.
Электромагнитные силы действуют между телами, имеющими электрический заряд.
Ядерные силы (сильные) являются самыми мощными в природе. Они действуют внутри ядер атомов на расстояниях 10 -13 см.
Слабые силы , как и ядерные, действуют на малых расстояниях порядка 10 -15 см. В результате их действия происходят процессы внутри ядра.
Механика рассматривает гравитационные силы, силы упругости и силы трения.
Гравитационные силы
Гравитация описывается законом всемирного тяготения. Этот закон был изложен Ньютоном в середине XVII в. в работе «Математические начала натуральной философии».
Гравитацией называют силу тяготения, с которой любые материальные частицы притягиваются друг у другу.
Сила, с которой материальные частицы притягиваются друг к другу, прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними .
G – гравитационная постоянная, численно равная модулю силы тяготения, с которой тело, имеющее единичную массу, действует на тело, имеющее такую же единичную массу и находящееся на единичном расстоянии от него.
G = 6,67384(80)·10 −11 м 3 ·с −2 ·кг −1 , или Н·м²·кг −2 .
На поверхности Земли сила гравитации (сила тяготения) проявляется в виде силы тяжести .
Мы видим, что любой предмет, брошенный в горизонтальном направлении, всё равно падает вниз. Падает вниз также и любой предмет, подброшенный вверх. Происходит это под действием силы тяжести, которая действует на любое материальное тело, находящееся вблизи поверхности Земли. Сила тяжести действует на тела и на поверхности других астрономических тел. Эта сила всегда направлена вертикально вниз.
Под действием силы тяжести тело движется к поверхности планеты с ускорением, которое называется ускорением свободного падения .
Ускорение свободного падения на поверхности Земли обозначается буквой g .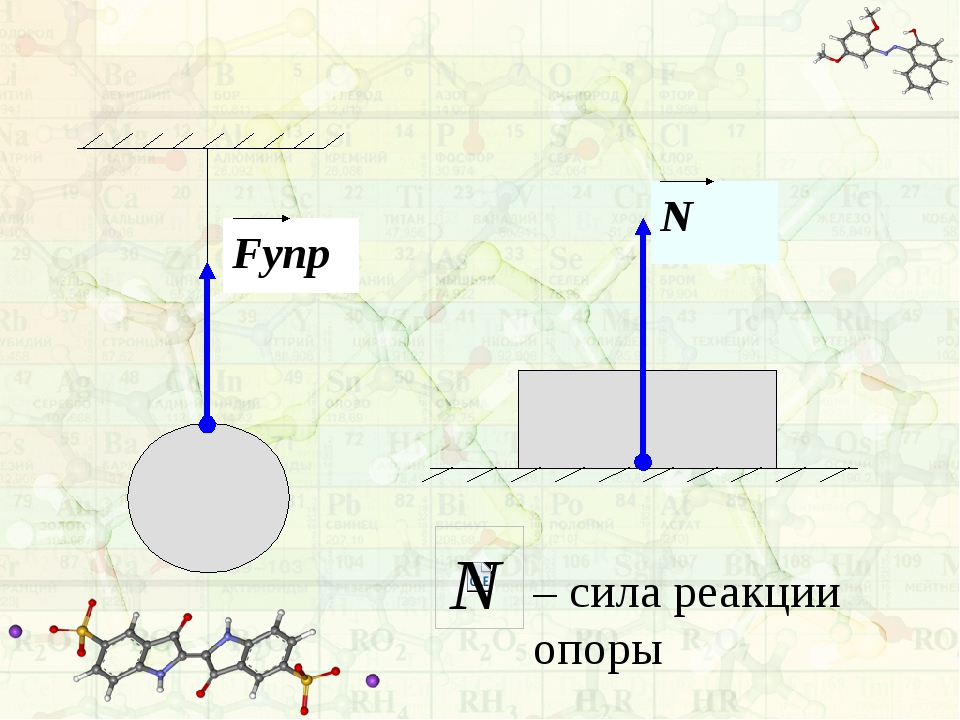
F t = mg ,
следовательно,
g = F t / m
g = 9, 81 м/с 2 на полюсах Земли, а на экваторе g = 9,78 м/с 2 .
При решении простых физических задач величину g принято считать равной 9,8 м/с 2 .
Классическая теория тяготения применима только для тел, имеющих скорость намного ниже скорости света.
Силы упругости
Силами упругости называются силы, которые возникают в теле в результате деформации, вызывающей изменение его формы или объёма. Эти силы всегда стремятся вернуть тело в его первоначальное положение.
При деформации происходит смещение частиц тела. Сила упругости направлена в сторону, противоположную направлению смещения частиц. Если деформация прекращается, сила упругости исчезает.
Английский физик Роберт Гук, современник Ньютона, открыл закон, устанавливающий связь между силой упругости и деформацией тела.
При деформации тела возникает сила упругости, прямо пропорциональная удлинению тела, и имеющая направление, противоположное перемещению частиц при деформации.
F = k ∆ l ,
где к – жёсткость тела, или коэффициент упругости;
∆ l – величина деформации, показывающая величину удлинения тела под воздействием сил упругости.
Закон Гука действует для упругих деформаций, когда удлинение тела мало, а тело восстанавливает свои первоначальные размеры после того, как исчезают силы, вызвавшие эту деформацию.
Если деформация велика, и тело не возвращается в свою исходную форму, закон Гука не применяется. При очень больших деформациях происходит разрушение тела.
Силы трения
Сила трения возникает, когда одно тело движется по поверхности другого. Она имеет электромагнитную природу. Это следствие взаимодействия между атомами и молекулами соприкасающихся тел. Направление силы трения противоположно направлению движения.
Это следствие взаимодействия между атомами и молекулами соприкасающихся тел. Направление силы трения противоположно направлению движения.
Различают сухое и жидкое трение. Сухим называют трение, если между телами нет жидкой или газообразной прослойки.
Отличительная особенность сухого трения – трение покоя, которое возникает при относительном покое тел.
Величина силы трения покоя всегда равна величине внешней силы и направлена в противоположную сторону. Сила трения покоя препятствует движению тела.
В свою очередь, сухое трение разделяется на трение скольжения и трение качения .
Если величина внешней силы превышает величину силы трения, то в этом случае появится проскальзывание, и одно из контактирующих тел начнёт поступательно перемещаться относительно другого тела. А сила трения будет называться силой трения скольжения . Её направление будет противоположно направлению скольжения.
Сила трения скольжения зависит от силы, с которой тела давят друг на друга, от состояния трущихся поверхностей, от скорости движения, но не зависит от площади соприкосновения.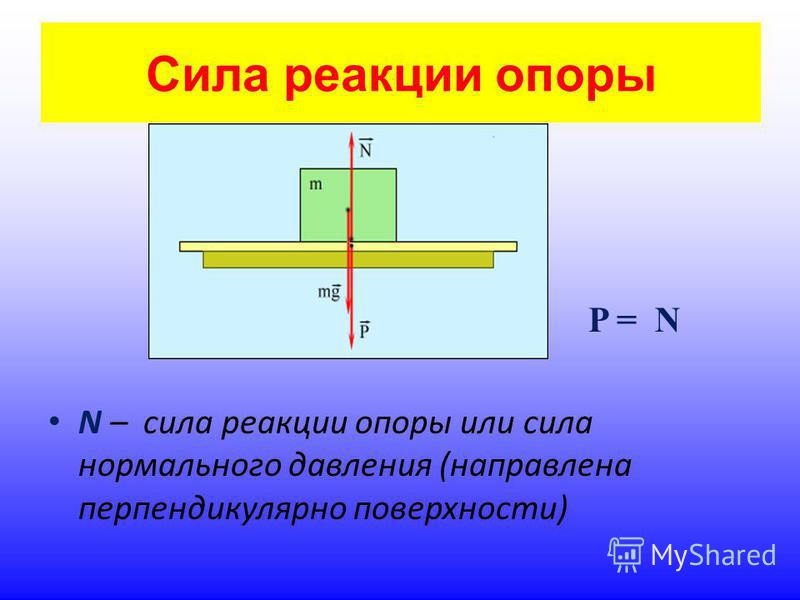
Сила трения скольжения одного тела по поверхности другого вычисляется по формуле:
F тр. = k · N ,
где k – коэффициент трения скольжения;
N – сила нормальной реакции, действующая на тело со стороны поверхности.
Сила трения качения возникает между телом, которое перекатывается по поверхности, и самой поверхностью. Такие силы появляются, например, при соприкосновении шин автомобиля с дорожным покрытием.
Величина силы трения качения вычисляется по формуле
где F t – сила трения качения;
f – коэффициент трения качения;
R – радиус катящегося тела;
N – прижимающая сила.
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.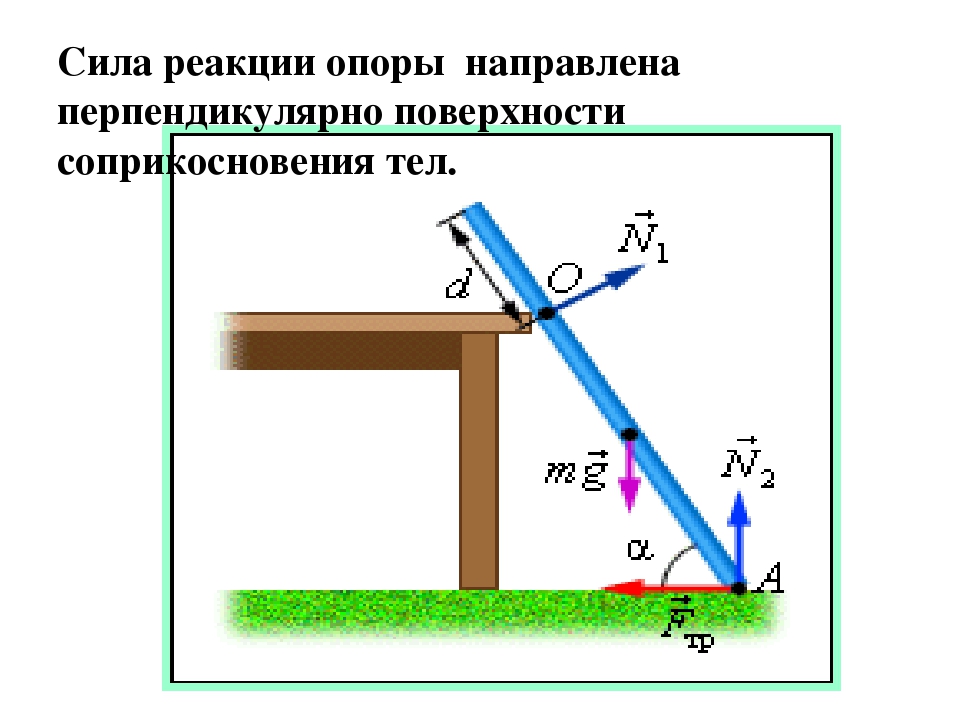
Размещено на http://www.allbest.ru/
Министерство образования и науки Российской Федерации
Федеральное государственное автономное образовательное
учреждение высшего образования
«Национальный исследовательский Томский политехнический университет»
Институт Кибернетики
Направление подготовки: Мехатроника и робототехника
Кафедра: Интегрированных компьютерных систем управления
Реферат
на тему: » Силы в природе »
Выполнил: Сергеев А.С.
Принял: доцент каф. ЭФ Кравченко Н.С.
Томск — 2016
Введение
Современные достижения физики высоких энергий все больше укрепляют представление, что многообразие свойств Природы обусловлено взаимодействующими элементарными частицами. Дать неформальное определение элементарной частицы, по-видимому, невозможно, поскольку речь идет о самых первичных элементах материи. На качественном уровне можно говорить, что истинно элементарными частицами называются физические объекты, которые не имеют составных частей.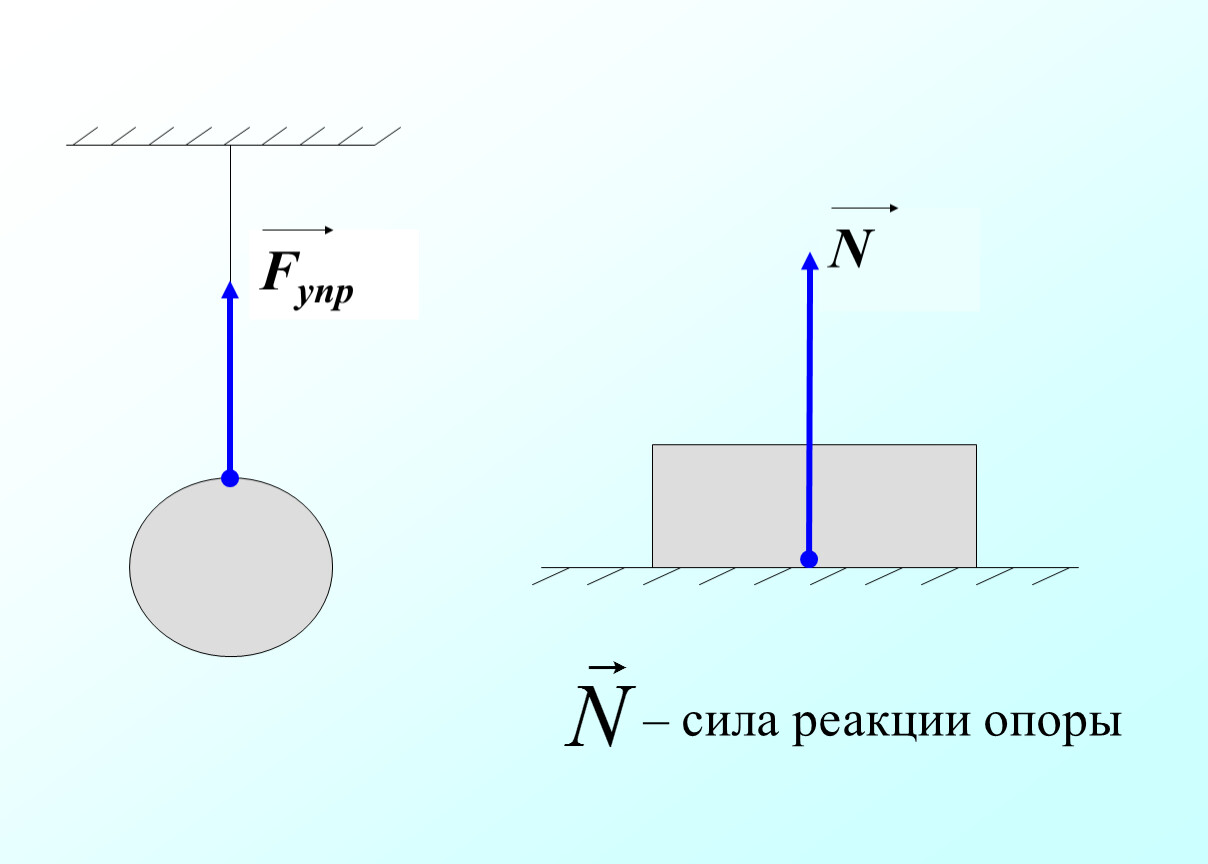
Очевидно, что вопрос об элементарности физических объектов — это в первую очередь вопрос экспериментальный. Например, экспериментально установлено, что молекулы, атомы, атомные ядра имеют внутреннюю структуру, указывающую на наличие составных частей. Поэтому их нельзя считать элементарными частицами. Сравнительно недавно открыто, что такие частицы, как мезоны и барионы, также обладают внутренней структурой и, следовательно, не являются элементарными. В то же время у электрона внутренняя структура никогда не наблюдалась, и, значит, его можно отнести к элементарным частицам. Другим примером элементарной частицы является квант света — фотон.
Современные экспериментальные данные свидетельствуют, что существует только четыре качественно различных вида взаимодействий, в которых участвуют элементарные частицы. Эти взаимодействия называются фундаментальными, то есть самыми основными, исходными, первичными. Если принять во внимание все многообразие свойств окружающего нас Мира, то кажется совершенно удивительным, что в Природе есть только четыре фундаментальных взаимодействия, ответственных за все явления Природы.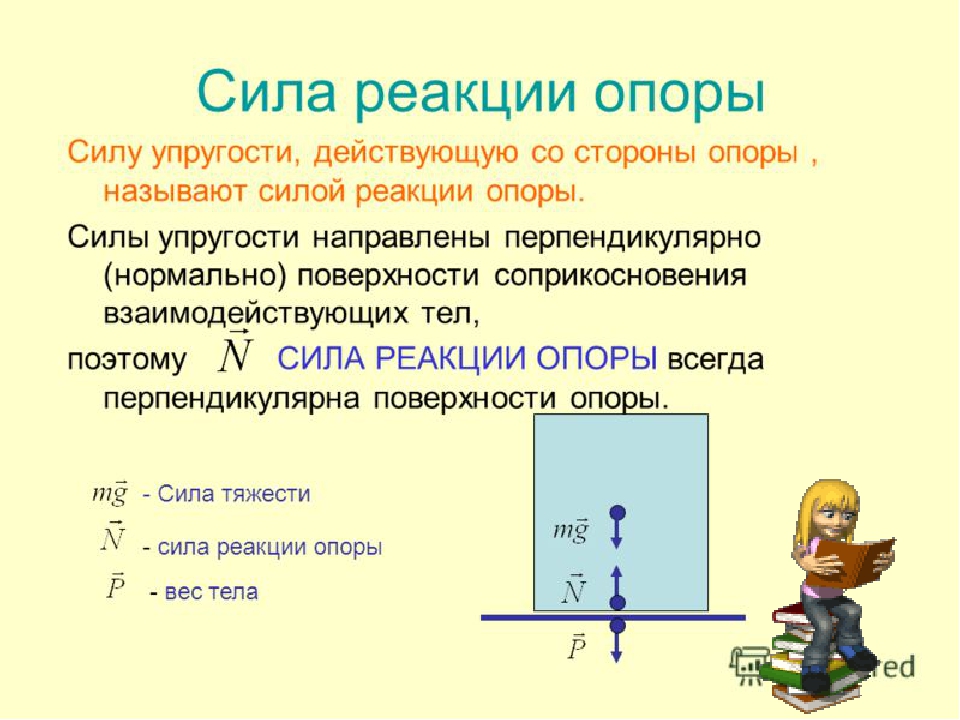
Помимо качественных различий, фундаментальные взаимодействия отличаются в количественном отношении по силе воздействия, которая характеризуется термином интенсивность. По мере увеличения интенсивности фундаментальные взаимодействия располагаются в следующем порядке: гравитационное, слабое, электромагнитное и сильное. Каждое из этих взаимодействий характеризуется соответствующим параметром, называемым константой связи, численное значение которого определяет интенсивность взаимодействия.
Каким образом физические объекты осуществляют фундаментальные взаимодействия между собой? На качественном уровне ответ на этот вопрос выглядит следующим образом. Фундаментальные взаимодействия переносятся квантами.
При этом в квантовой области фундаментальным взаимодействиям отвечают соответствующие элементарные частицы, называемые элементарными частицами — переносчиками взаимодействий. В процессе взаимодействия физический объект испускает частицы — переносчики взаимодействия, которые поглощаются другим физическим объектом. Это ведет к тому, что объекты как бы чувствуют друг друга, их энергия, характер движения, состояние изменяются, то есть они испытывают взаимное влияние.
Это ведет к тому, что объекты как бы чувствуют друг друга, их энергия, характер движения, состояние изменяются, то есть они испытывают взаимное влияние.
В современной физике высоких энергий все большее значение приобретает идея объединения фундаментальных взаимодействий. Согласно идеям объединения, в Природе существует только одно единое фундаментальное взаимодействие, проявляющее себя в конкретных ситуациях как гравитационное, или как слабое, или как электромагнитное, или как сильное, или как их некоторая комбинация. Успешной реализацией идей объединения послужило создание ставшей уже стандартной объединенной теории электромагнитных и слабых взаимодействий. Идет работа по развитию единой теории электромагнитных, слабых и сильных взаимодействий, получившей название теории великого объединения. Предпринимаются попытки найти принцип объединения всех четырех фундаментальных взаимодействий.
C ила
Скорость тела относительно Земли изменяется, когда на него действуют другие тела.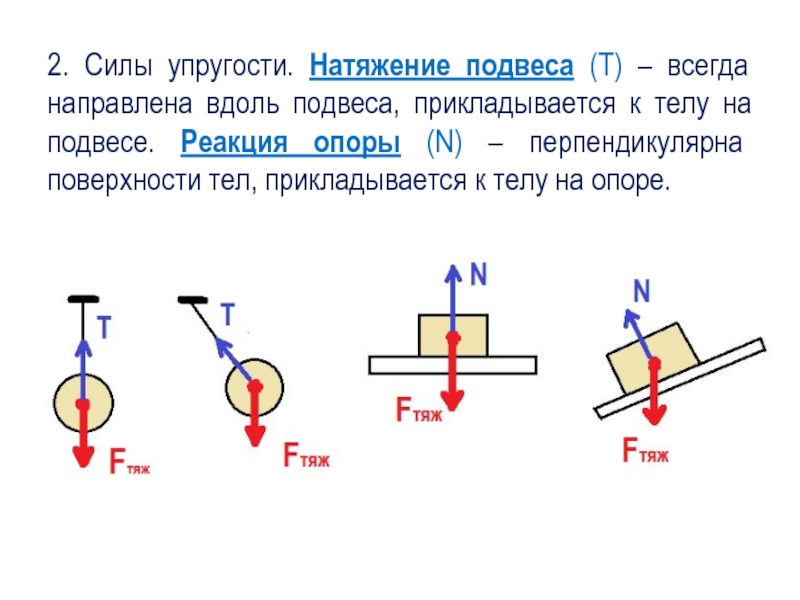 К примеру:
К примеру:
Человек, когда толкает вагонетку, приводит её в движение. В этом случае скорость вагонетки будет изменяться под действием силы руки человека.
Рассмотрим другой пример:
Когда взаимодействует рука с шаром мы наблюдаем, что витки пружины начинают двигаться, и пружина сжимается. Отпустив ее, мы увидим, как пружина, распрямляясь, приводит в движение шар. Сначала действующим телом здесь была рука человека. Затем стала пружина.
Во всех вышеприведенных примерах причиной изменения скорости тела было действие, оказываемое на него другими телами. Мерой этого действия является векторная физическая величина, называемая силой .
Сила векторная величина, как и другие векторные величины. Сила характеризуется не только числовым значением, но и своим направлением.
Силу обычно обозначают буквой F .
Если сила к телу не приложена (F = 0), то это означает, что никакого действия на него не оказывается, и потому скорость такого тела относительно Земли не изменяется.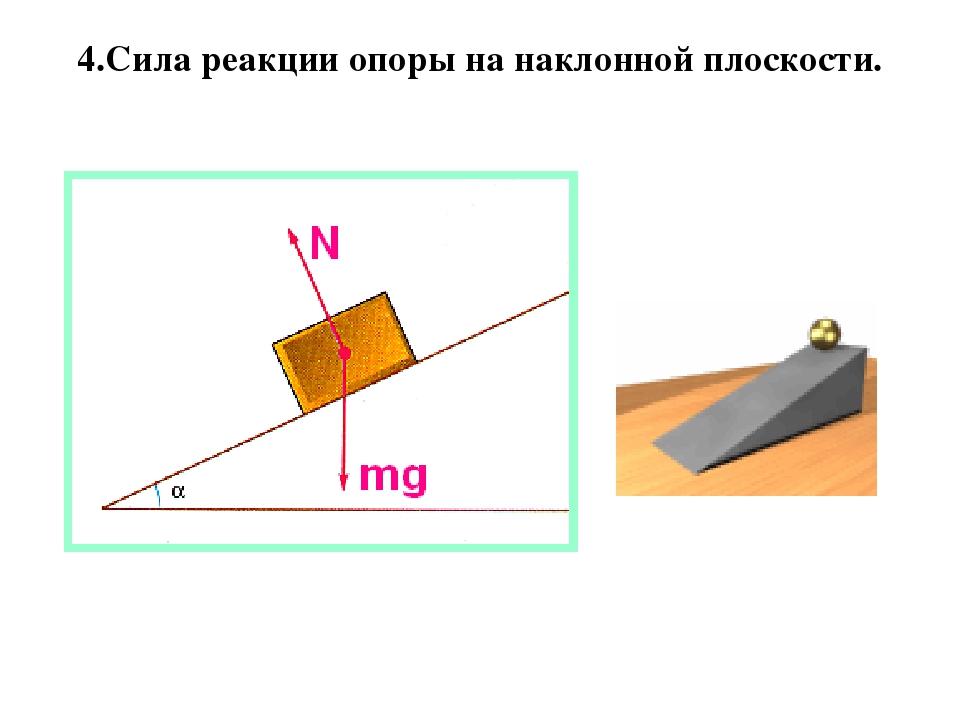 Если же, наоборот, сила F ? 0, то тело испытывает некоторое воздействие, и его скорость изменяется. При этом, чем больше сила F, тем значительнее изменяется скорость тела относительно Земли.
Если же, наоборот, сила F ? 0, то тело испытывает некоторое воздействие, и его скорость изменяется. При этом, чем больше сила F, тем значительнее изменяется скорость тела относительно Земли.
Единицей силы в СИ является ньютон . H — это сила, которая за 1 секунду изменяет скорость тела массой 1 килограмм на 1 м/с. Эта единица названа в честь великого ученого И. Hьютона.
Рассмотрим наиболее известные силы.
Равнодействующая сила
Обычно на любое движущееся тело действует не одно, а сразу несколько окружающих его тел.
Например: Когда тело падает, на него действует не только Земля, но и воздух.
Когда на материальную точку действует несколько тел, их общее действие характеризуется равнодействующей силой.
Для нахождения равнодействующей силы есть несколько правил.
1) Если к телу приложены две силы F(1) и F(2), направленные по одной прямой в одну сторону, то их равнодействующая F находится по формуле
При этом направление равнодействующей силы совпадает с направлением приложенных сил
2) Если к телу приложены две силы F(1) и F(2), направленные по одной прямой в противоположные стороны, то при F
F(1) > F(2) их равнодействующая F находится по формуле
F = F(1) — F(2).
Направление равнодействующей силы в этом случае совпадает с направлением большей из приложенных сил. Если при этом F(1) = F(2), то их равнодействующая F окажется равной нулю. В этом случае покоящееся тело так и будет покоиться, а движущееся тело будет совершать равномерное и прямолинейное движение с той скоростью, которая у него была.
Про две силы, равные по величине и направленные вдоль одной прямой в противоположные стороны, говорят, что они уравновешивают или компенсируют друг друга. Равнодействующая F таких сил всегда равна нулю и потому изменить скорость тела не может.
Для изменения скорости тела относительно Земли необходимо, чтобы равнодействующая всех приложенных к телу сил была отлична от нуля. В том случае, когда тело движется в направлении равнодействующей силы, его скорость возрастает; при движении в противоположном направлении скорость тела убывает.
Сила тяжести
Почему тело, брошенное в горизонтальном направлении, через несколько секунд оказывается на земле?
Почему тело, выпущенное из рук, падает вниз?
У этих явлений одна причина — притяжение Земли.
Сила притяжения к Земле называется силой тяжести . Сила тяжести направлена вертикально вниз. Когда тело под действием притяжения к Земле падает вниз, на него действует не только Земля, но и другие воздействия. В тех случаях, когда сила сопротивления воздуха пренебрежимо мала по сравнению с силой тяжести, падение тела называют свободным .
Чтобы определить силу тяжести, надо массу этого тела умножить на ускорение свободного падения:
Из этой формулы следует, что g = F(T)/m. Но F(T) измеряется в ньютонах, a m — в килограммах. Поэтому величину g можно измерять в ньютонах на килограмм:
g = 9,8 Н/кг?10 Н/кг.
С увеличением высоты над Землей ускорение свободного падения постепенно уменьшается. Уменьшение ускорения свободного падения означает, что и сила тяжести по мере увеличения высоты над Землей также уменьшается. Чем дальше тело находится от Земли, тем слабее она его притягивает.
Сила упругости
На все тела, находящиеся вблизи Земли, действует ее притяжение.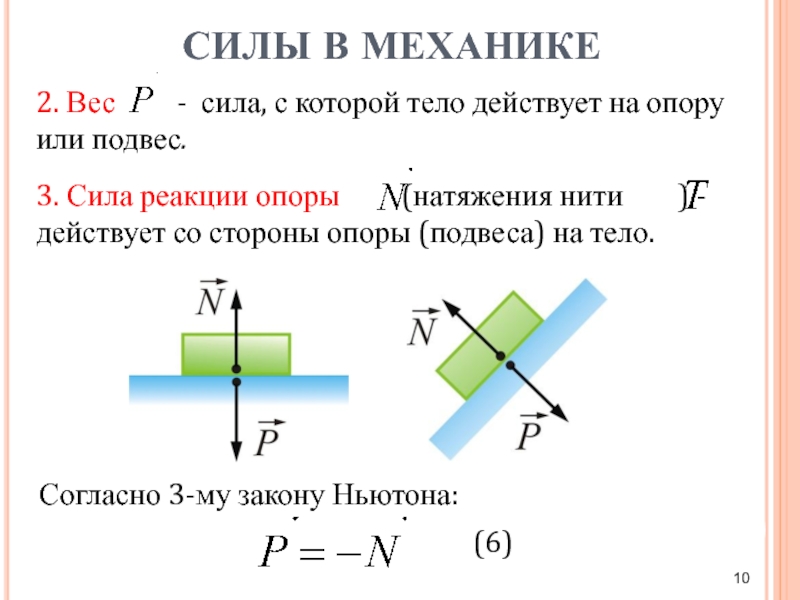 Под действием силы тяжести падают на Землю капли дождя, снежинки.
Под действием силы тяжести падают на Землю капли дождя, снежинки.
Но когда капли лежат на крыше, его притягивает Земля, однако он не проходит и не проваливается сквозь крышу, а остается в покое. Что препятствует его падению? Крыша. Она действует на капли с силой, равной силе тяжести, но направленной в противоположную сторону.
Рассмотрим один пример. Изображена доска, лежащая на двух подставках. Если на ее середину поместить тело, то под действием силы тяжести тело начнет продавливать доску, но через несколько минут, остановится. При этом сила тяжести станет уравновешенной силой, действующей на тело со стороны изогнутой доски и направленной вертикально вверх. Эта сила называется силой упругости.
Сила упругости возникает при деформации. Деформация — это изменение формы или размеров тела. Одним из видов деформации является изгиб. Чем больше прогибается опора, тем больше сила упругости, действующая со стороны этой опоры на тело. Перед тем как тело (гирю) положили на доску, эта сила отсутствовала. По мере движения гири, которая все сильнее и сильнее прогибала свою опору, возрастала и сила упругости. В момент остановки гири сила упругости достигла силы тяжести, и их равнодействующая стала равной нулю.
По мере движения гири, которая все сильнее и сильнее прогибала свою опору, возрастала и сила упругости. В момент остановки гири сила упругости достигла силы тяжести, и их равнодействующая стала равной нулю.
Если на опору поместить достаточно легкий предмет, то ее деформация может оказаться столь незначительной, что никакого изменения формы опоры мы не заметим. Но деформация все равно будет! А вместе с ней будет действовать и сила упругости, препятствующая падению тела, находящегося на данной опоре. В подобных случаях (когда деформация тела незаметна и изменением размеров опоры можно пренебречь) силу упругости называют силой реакции опоры.
Если вместо опоры использовать какой-либо подвес (нить, веревку, проволоку, стержень и т. д.), то прикрепленный к нему предмет также может удерживаться в покое. Сила тяжести и здесь будет уравновешена противоположно направленной силой упругости. Сила упругости при этом возникает из-за того, что подвес под действием прикрепленного к нему груза растягивается. Растяжение еще один вид деформации.
Растяжение еще один вид деформации.
Большой вклад внес в изучение силы упругости ученый Р. Гук. Закон Гука гласит:
Сила упругости , возникающая при растяжении или сжатии тела, пропорциональна его удлинению.
Если удлинение тела, т.е. изменение его длины, обозначить через х, а силу упругости — через F(упр), то по закону Гука можно придать следующую математическую форму:
где k — коэффициент пропорциональности, называемый жесткостью тела. У каждого тела своя жесткость. Чем больше жесткость тела (пружины, проволоки, стержня и т. д.), тем меньше оно изменяет свою длину под действием данной силы.
Единицей жесткости в СИ является ньютон на метр (1 Н/м).
Вес тела
Постоянно мы говорим: «весит 50 килограмм» и т.д. Но мы не знаем, что допускаем ошибку. Масса это мера инертности тела, каким образом тело реагирует на приложенное к нему воздействие, либо же само воздействует на другие тела. А вес тела это сила, с которой тело действует на горизонтальную опору или вертикальный подвес под влиянием притяжения Земли.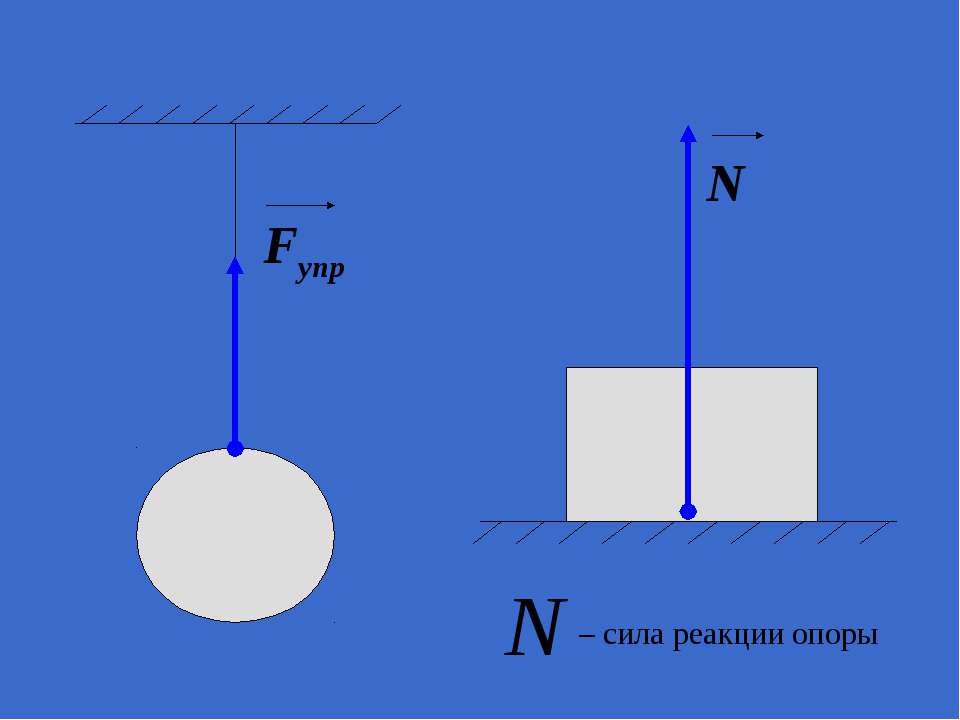
Масса измеряется в килограммах, а вес тела, как и любая другая сила в ньютонах. Вес тела имеет направление, как и любая сила, и является величиной векторной. А масса не имеет никакого направления и является величиной скалярной.
Вес тела как и сила тяжести направлена вниз.
Вес тела обычно обозначают буквой P .
Формула веса тела в физике записывается следующим образом:
где m — масса тела
Но, несмотря на совпадение с формулой и направлением силы тяжести, есть серьезное различие между силой тяжести и весом тела. Сила тяжести приложена к телу, то есть, грубо говоря, это она давит на тело, а вес тела приложен к опоре или подвесу, то есть, здесь уже тело давит на подвес или опору.
Но природа существования силы тяжести и веса тела одинакова притяжение Земли. Собственно говоря, вес тела является следствием приложенной к телу силы тяжести. И, так же как и сила тяжести, вес тела уменьшается с увеличением высоты.
Сила трения
Если вы попытаетесь сдвинуть с места шкаф, то сразу убедитесь, что это не так-то просто сделать. Его движению будет мешать взаимодействие ножек с полом, на котором он стоит.
Его движению будет мешать взаимодействие ножек с полом, на котором он стоит.
Взаимодействие, возникающее в месте соприкосновения тел и препятствующее их относительному движению, называют трением , а характеризующую это взаимодействие силу — силой трения .
Различают три вида трения: трение покоя, трение скольжения и трение качения.
1) Трение покоя . Положим тело на наклонную плоскость. При небольшом угле наклона плоскости тело может остаться на месте. Что будет удерживать его от соскальзывания вниз? Трение покоя. Сила трения покоя может быть любой.
Она изменяется вместе с силой, стремящейся сдвинуть тело с места. Но для любых двух взаимодействующих тел она имеет некоторое максимальное значение, больше которого быть не может.
Приложив к телу силу, превышающую максимальную силу трения покоя, мы сдвинем его с места, и тело начнет двигаться. Трение покоя при этом сменится трением скольжения. трение сила тяготение
2) Трение скольжения.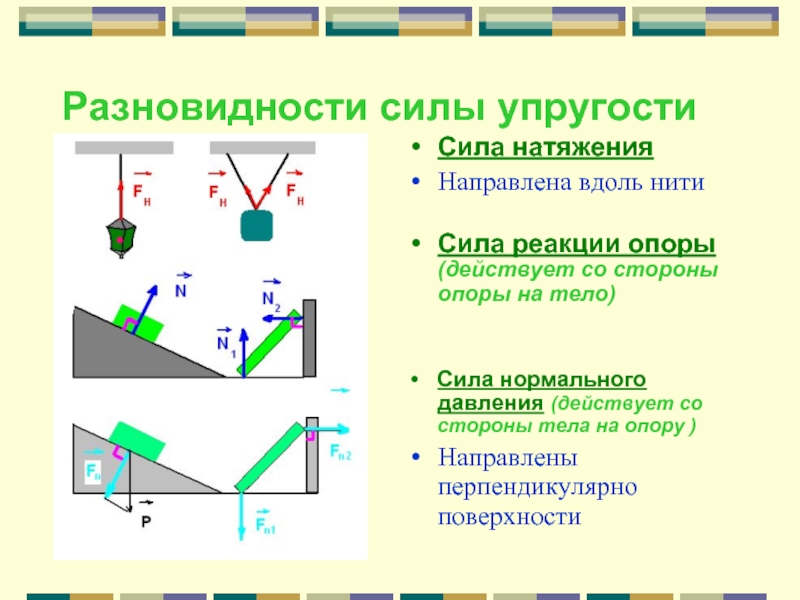 Из-за чего постепенно останавливаются санки? Из-за трения скольжения. Сила трения скольжения направлена всегда в сторону, противоположную направлению движения тела.
Из-за чего постепенно останавливаются санки? Из-за трения скольжения. Сила трения скольжения направлена всегда в сторону, противоположную направлению движения тела.
3) Трение качения . Если тело не скользит по поверхности другого тела, а как колесо или цилиндр, катится, то возникающее в месте их контакта трение называют трением качения.
Катящееся колесо несколько вдавливается в полотно дороги, и потому перед ним все время оказывается небольшой бугорок, который необходимо преодолевать. Именно тем, что катящемуся колесу постоянно приходится взбираться на появляющийся впереди бугорок, и обусловлено трение качения. При этом, чем дорога тверже, тем трение качения меньше.
Заключение
Итак, мы сделали обзор наиболее известных сил. Кратко описали каждую из сил, рассмотрели примеры из жизни.
Подведем итоги в виде таблицы:
Список литературы
1. http://phscs.ru/
2. http://bcoreanda.com/
3. http://bibliofond.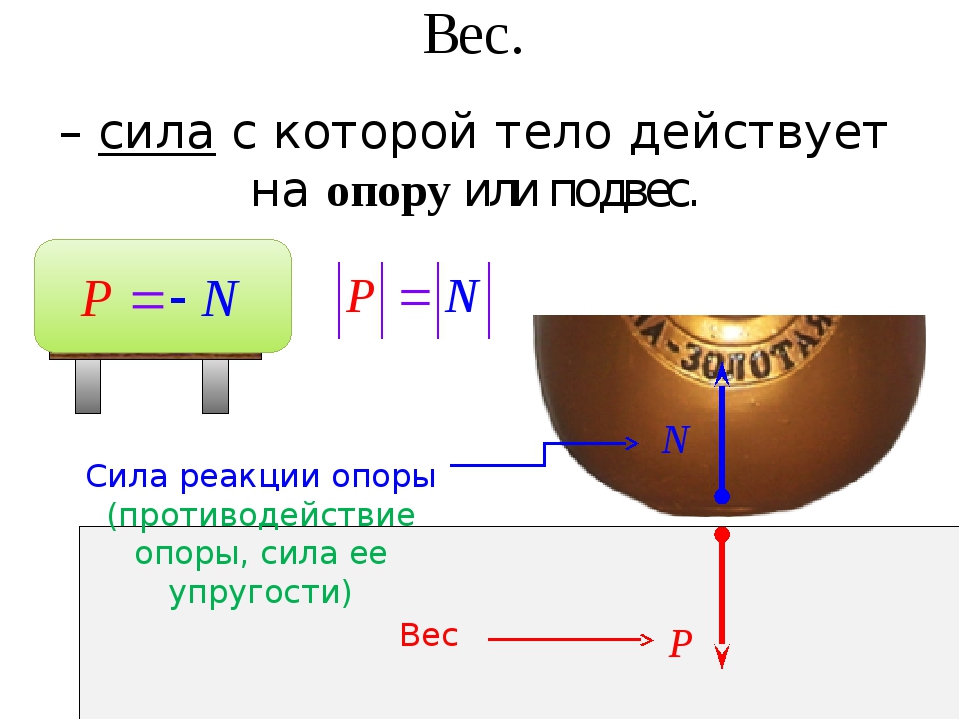 ru
ru
5. http://dic.academic.ru
6. http://interneturok.ru
7. https://ru.wikipedia.org
8. https://www.google.com/imghp?hl=ru
9. http://ru.solverbook.com/
10. http://www.fizika.ru
11. http://foxford.ru
12. http://infofiz.ru
13. http://multiurok.ru
Размещено на Allbest.ru
…Подобные документы
Движение тела по эллиптической орбите вокруг планеты. Движение тела под действием силы тяжести в вертикальной плоскости, в среде с сопротивлением. Применение законов движения тела под действием силы тяжести с учетом сопротивления среды в баллистике.
курсовая работа , добавлен 17.06.2011
Анализ зависимости веса тела от ускорения опоры, на которой оно стоит, изменения взаимного положения частиц тела, связанного с их перемещением друг относительно друга. Исследование основных видов деформации: кручения, сдвига, изгиба, растяжения и сжатия.
презентация , добавлен 04.12.2011
Изучение понятия «вес тела» — силы, с которой это тело действует на опору или подвес, вследствие действия на него силы тяжести. Обозначение и направление веса тела. Характеристика принципа работы и видов динамометров – приборов для измерения силы (веса).
Обозначение и направление веса тела. Характеристика принципа работы и видов динамометров – приборов для измерения силы (веса).
презентация , добавлен 13.12.2010
Гравитационные, электромагнитные и ядерные силы. Взаимодействие элементарных частиц. Понятие силы тяжести и тяготения. Определение силы упругости и основные виды деформации. Особенности сил трения и силы покоя. Проявления трения в природе и в технике.
презентация , добавлен 24.01.2012
Механическое движение. Относительность движения. Взаимодействие тел. Сила. Второй закон Ньютона. Импульс тела. Закон сохранения импульса в природе и технике. Закон всемирного тяготения. Сила тяжести. Вес тела. Невесомость.
шпаргалка , добавлен 12.06.2006
Явление тяготения и масса тела, гравитационное притяжение Земли. Измерение массы при помощи рычажных весов. История открытия «Закона всемирного тяготения», его формулировка и границы применимости. Расчет силы тяжести и ускорения свободного падения.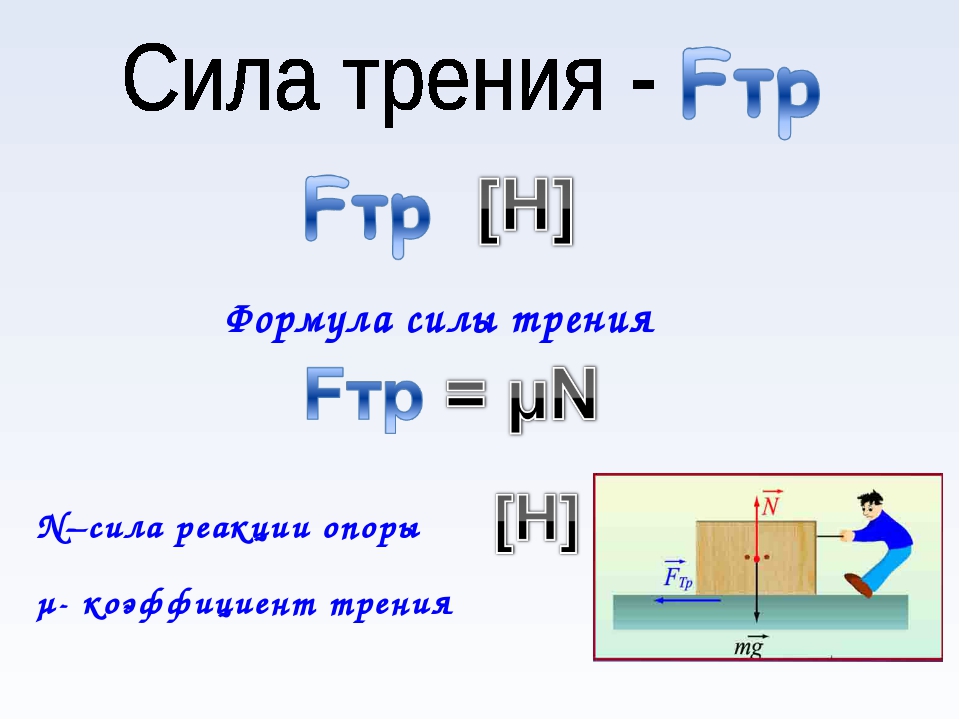
конспект урока , добавлен 27.09.2010
Запись второго закона Ньютона в векторной и скалярной форме. Определение пути прохождения тела до остановки при заданной начальной скорости. Расчет времени движения данного тела, если под действием силы равной 149 Н тело прошло путь равный 200 м.
презентация , добавлен 04.10.2011
Различие силы тяжести и веса. Момент инерции относительно оси вращения. Уравнение моментов для материальной точки. Абсолютно твердое тело. Условия равновесия, инерция в природе. Механика поступательного и вращательно движения относительно неподвижной оси.
презентация , добавлен 29.09.2013
Сущность закона определения максимальной силы трения покоя. Зависимость модуля силы трения скольжения от модуля относительной скорости тел. Уменьшение силы трения скольжения тела с помощью смазки. Явление уменьшения силы трения при появлении скольжения.
презентация , добавлен 19.12.2013
Законы движения планет Кеплера, их краткая характеристика. История открытия Закона всемирного тяготения И. Ньютоном. Попытки создания модели Вселенной. Движение тел под действием силы тяжести. Гравитационные силы притяжения. Искусственные спутники Земли.
История открытия Закона всемирного тяготения И. Ньютоном. Попытки создания модели Вселенной. Движение тел под действием силы тяжести. Гравитационные силы притяжения. Искусственные спутники Земли.
Чему равна сила опоры. Как найти силу реакции опоры
Равномерное движение
S = v * t
S – путь, расстояние [м] (метр)
v – скорость [м/с] (метр в секунду)
t – время [ c ] (секунда)
Формула перевода скорости:
х км/ч= font-family:Arial»> м/с
Средняя скорость
v сред = EN-US»>s в – весь путь
t в – всё время
Плотность вещества
ρ= EN-US»>ρ – плотность
m – масса [кг] (килограмм)
V – объем [м3] (метр кубический)
Сила тяжести, вес и сила реакции опоры
Сила тяжести – сила притяжения к Земле. Приложена к телу. Направлена к центру Земли.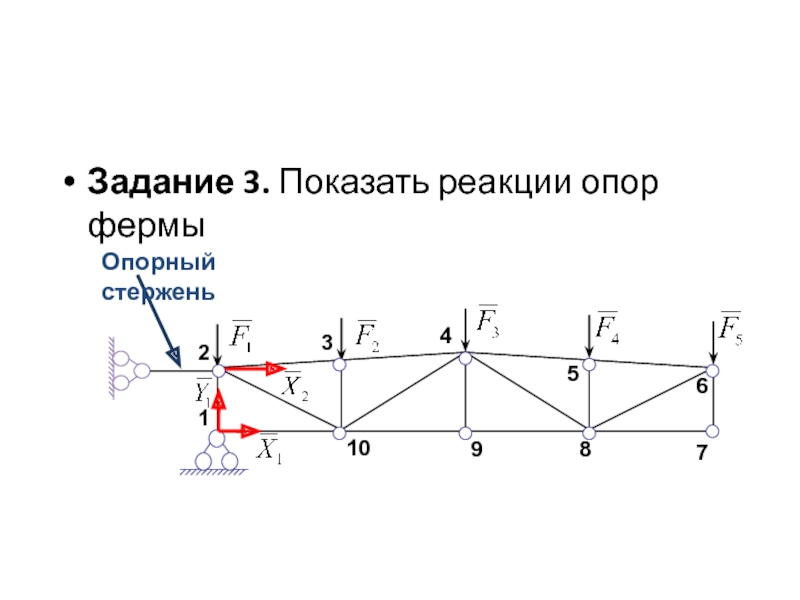
Вес – сила, с которой тело давит на опору или растягивает подвес. Приложена к телу. Направлена перпендикулярно опоре и параллельно подвесу вниз.
Сила реакции опоры – сила, с которой опора или подвес сопротивляется давлению или растяжению. Приложена к опоре или подвесу. Направлена перпендикулярно опоре или параллельно подвесу вверх.
F т =m*g; P=m*g*cosα; N=m*g*cosα
F т – сила тяжести [Н] (Ньютон)
P – вес [ Н ]
N – сила реакции опоры [Н]
m – масса [кг] (килограмм)
α – угол между плоскостью горизонта и плоскостью опоры [º,рад] (градус, радиан)
g≈9,8 м / с2
Сила упругости (Закон Гука)
F упр = k * x
F упр — сила упругости [Н] (Ньютон)
k – коэффициент жёсткости [Н/м] (Ньютон на метр)
x – удлинение/сжатие пружины [м] (метр)
Механическая работа
A=F*l*cosα
A – работа [Дж] (Джоуль)
F – сила [Н] (Ньютон)
l – расстояние, на котором действует сила [м] (метр)
α – угол между направлением силы и направлением движения [º,рад] (градус, радиан)
Частные случаи:
1)α=0, т. е. направление действия силы совпадает с направлением движения
е. направление действия силы совпадает с направлением движения
A=F*l;
2) α = π /2=90 º, т. е. направление силы перпендикулярно направлению движения
A=0;
3) α = π =180 º, т. е. направление силы противоположно направлению движения
A =- F * l ;
Мощность
N = EN-US»>N – мощность [Вт] (Ватт)
A – работа [Дж] (Джоуль)
t – время [с] (секунда)
Давление в жидкостях и твёрдых телах
P = font-family:Arial»>; P = ρ * g * h
P – давление [Па] (Паскаль)
F – сила давления [Н] (Ньютон)
s – площадь основания [м2] (квадратный метр)
ρ – плотность материала/жидкости [кг/м3] (килограмм на метр кубический)
g – ускорение свободного падения [м/с2] (метр на секунду в квадрате)
h – высота предмета/столба жидкости [м] (метр)
Сила Архимеда
Сила Архимеда – сила, с которой жидкость или газ стремятся вытолкнуть погруженное в них тело.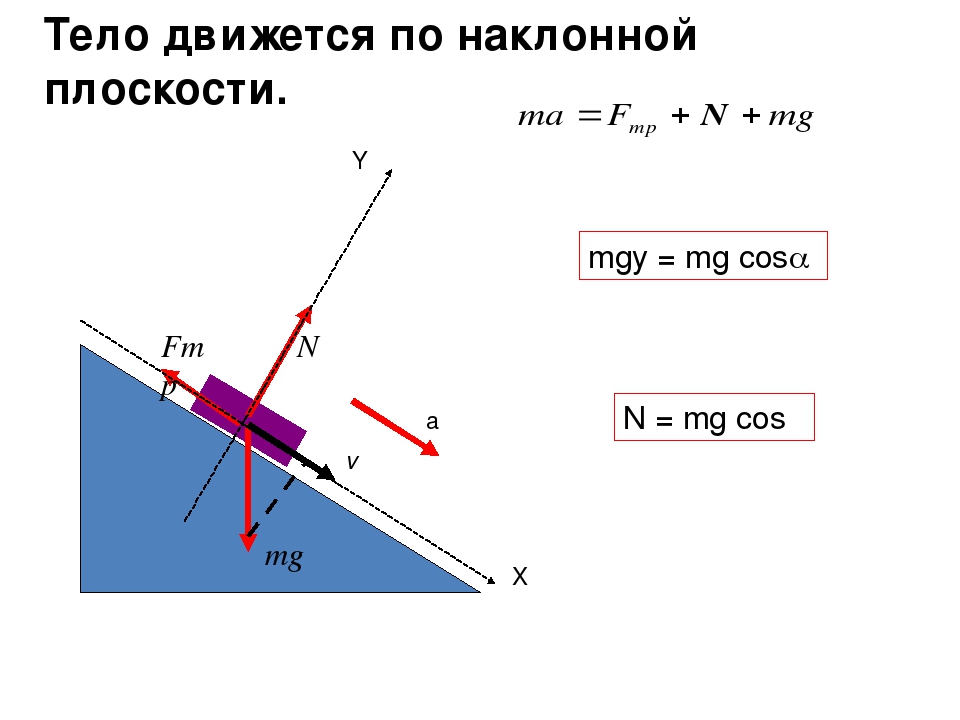
F Арх = ρ ж * V погр * g
F Арх – сила Архимеда [Н] (Ньютон)
ρ ж – плотность жидкости/газа [кг/м3] (килограмм на метр кубический)
V погр – объем погруженной части тела [м3] (метр кубический)
g – ускорение свободного падения [м/с2] (метр на секунду в квадрате)
Условие плавания тел:
ρ ж ≥ρ т
ρ т – плотность материала тела [кг/м3] (килограмм на метр кубический)
Правило рычага
F 1 * l 1 = F 2 * l 2 (равновесие рычага)
F 1,2 – сила, действующая на рычаг [Н] (Ньютон)
l 1,2 – длина плеча рычага соответствующей силы [м] (метр)
Правило моментов
M = F * l
M – момент силы [Н*м] (Ньютон-метр)
F – сила [Н] (Ньютон)
l – длина (рычага) [м] (метр)
M1=M2 (равновесие)
Сила трения
F тр =µ* N
F тр – сила трения [Н] (Ньютон)
µ — коэффициент трения [ , %]
N – сила реакции опоры [Н] (Ньютон)
Энергия тела
E кин = font-family:Arial»>; E п = m * g * h
E кин – кинетическая энергия [Дж] (Джоуль)
m – масса тела [кг] (килограмм)
v – скорость тела [м/с] (метр в секунду)
Еп – потенциальная энергия [Дж] (Джоуль)
g – ускорение свободного падения [м/с2] (метр на секунду в квадрате)
h – высота над землей [м] (метр)
Закон сохранения энергии: Энергия не исчезает в никуда и не появляется из ниоткуда, она лишь переходит из одних форм в другие.
Необходимо знать точку приложения и направление каждой силы. Важно уметь определить какие именно силы действуют на тело и в каком направлении. Сила обозначается как , измеряется в Ньютонах. Для того, чтобы различать силы, их обозначают следующим образом
Ниже представлены основные силы, действующие в природе. Придумывать не существующие силы при решении задач нельзя!
Сил в природе много. Здесь рассмотрены силы, которые рассматриваются в школьном курсе физики при изучении динамики. А также упомянуты другие силы, которые будут рассмотрены в других разделах.
Сила тяжести
На каждое тело, находящееся на планете, действует гравитация Земли . Сила, с которой Земля притягивает каждое тело, определяется по формуле
Точка приложения находится в центре тяжести тела. Сила тяжести всегда направлена вертикально вниз .
Сила трения
Познакомимся с силой трения. Эта сила возникает при движении тел и соприкосновении двух поверхностей.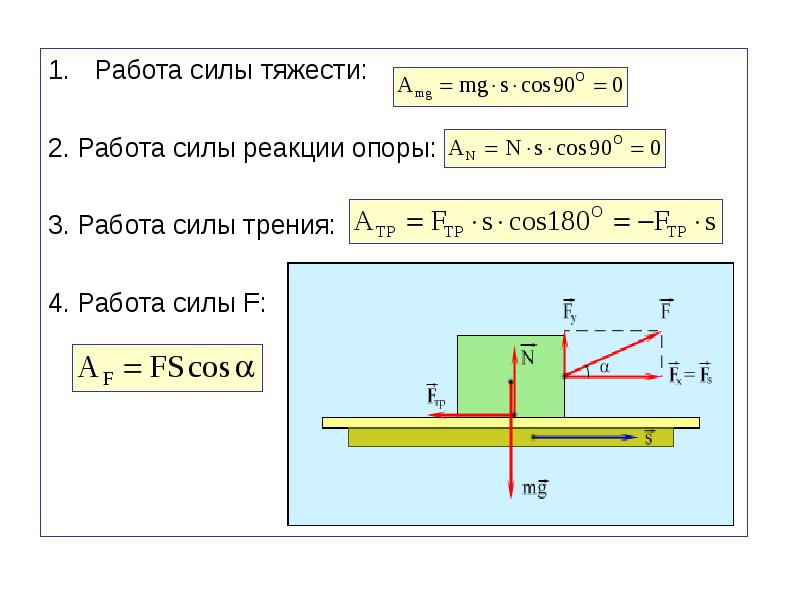 Возникает сила в результате того, что поверхности, если рассмотреть под микроскопом, не являются гладкими, как кажутся. Определяется сила трения по формуле:
Возникает сила в результате того, что поверхности, если рассмотреть под микроскопом, не являются гладкими, как кажутся. Определяется сила трения по формуле:
Сила приложена в точке соприкосновения двух поверхностей. Направлена в сторону противоположную движению.
Сила реакции опоры
Представим очень тяжелый предмет, лежащий на столе. Стол прогибается под тяжестью предмета. Но согласно третьему закону Ньютона стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол. То есть вверх. Эта сила называется реакцией опоры. Название силы «говорит» реагирует опора . Эта сила возникает всегда, когда есть воздействие на опору. Природа ее возникновения на молекулярном уровне. Предмет как бы деформировал привычное положение и связи молекул (внутри стола), они, в свою очередь, стремятся вернуться в свое первоначальное состояние, «сопротивляются».
Абсолютно любое тело, даже очень легкое (например,карандаш, лежащий на столе), на микроуровне деформирует опору.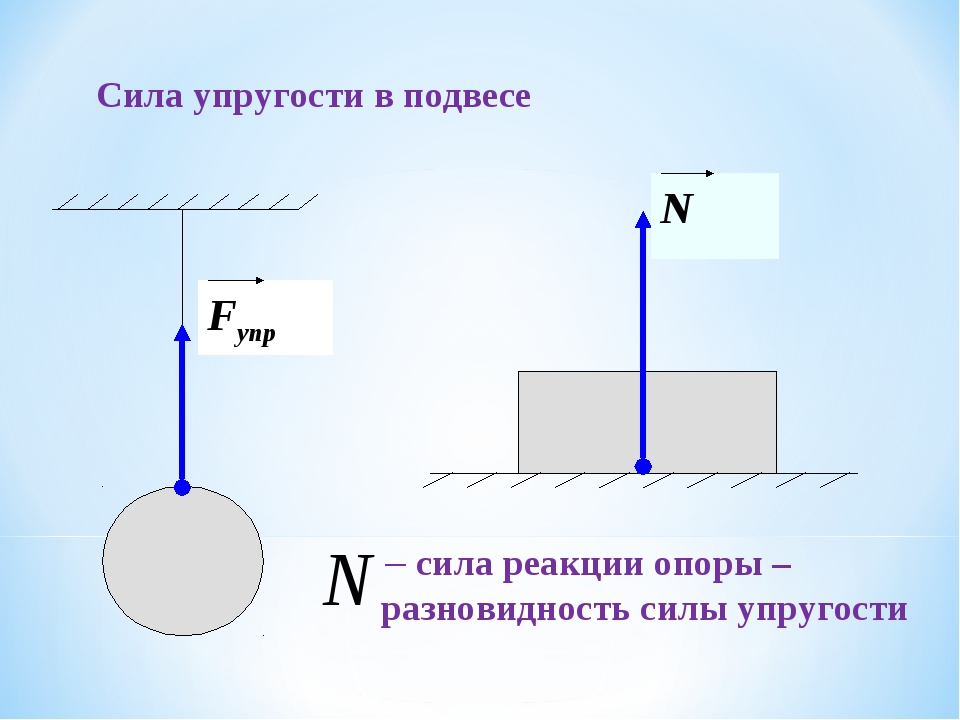 Поэтому возникает реакция опоры.
Поэтому возникает реакция опоры.
Специальной формулы для нахождения этой силы нет. Обозначают ее буквой , но эта сила просто отдельный вид силы упругости, поэтому она может быть обозначена и как
Сила приложена в точке соприкосновения предмета с опорой. Направлена перпендикулярно опоре.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
Сила упругости
Это сила возникает в результате деформации (изменения первоначального состояния вещества). Например, когда растягиваем пружину, мы увеличиваем расстояние между молекулами материала пружины. Когда сжимаем пружину — уменьшаем. Когда перекручиваем или сдвигаем. Во всех этих примерах возникает сила, которая препятствует деформации — сила упругости.
Закон Гука
Сила упругости направлена противоположно деформации.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
При последовательном соединении, например, пружин жесткость рассчитывается по формуле
При параллельном соединении жесткость
Жесткость образца. Модуль Юнга.
Модуль Юнга.
Модуль Юнга характеризует упругие свойства вещества. Это постоянная величина, зависящая только от материала, его физического состояния. Характеризует способность материала сопротивляться деформации растяжения или сжатия. Значение модуля Юнга табличное.
Подробнее о свойствах твердых тел .
Вес тела
Вес тела — это сила, с которой предмет воздействует на опору. Вы скажете, так это же сила тяжести! Путаница происходит в следующем: действительно часто вес тела равен силе тяжести, но это силы совершенно разные. Сила тяжести — сила, которая возникает в результате взаимодействия с Землей. Вес — результат взаимодействия с опорой. Сила тяжести приложена в центре тяжести предмета, вес же — сила, которая приложена на опору (не на предмет)!
Формулы определения веса нет. Обозначается эта силы буквой .
Сила реакции опоры или сила упругости возникает в ответ на воздействие предмета на подвес или опору, поэтому вес тела всегда численно одинаков силе упругости, но имеет противоположное направление.
Сила реакции опоры и вес — силы одной природы, согласно 3 закону Ньютона они равны и противоположно направлены. Вес — это сила, которая действует на опору, а не на тело. Сила тяжести действует на тело.
Вес тела может быть не равен силе тяжести. Может быть как больше, так и меньше, а может быть и такое, что вес равен нулю. Это состояние называется невесомостью . Невесомость — состояние, когда предмет не взаимодействует с опорой, например, состояние полета: сила тяжести есть, а вес равен нулю!
Определить направление ускорения возможно, если определить, куда направлена равнодействующая сила
Обратите внимание, вес — сила, измеряется в Ньютонах. Как верно ответить на вопрос: «Сколько ты весишь»? Мы отвечаем 50 кг, называя не вес, а свою массу! В этом примере, наш вес равен силе тяжести, то есть примерно 500Н!
Перегрузка — отношение веса к силе тяжести
Сила Архимеда
Сила возникает в результате взаимодействия тела с жидкость (газом), при его погружении в жидкость (или газ).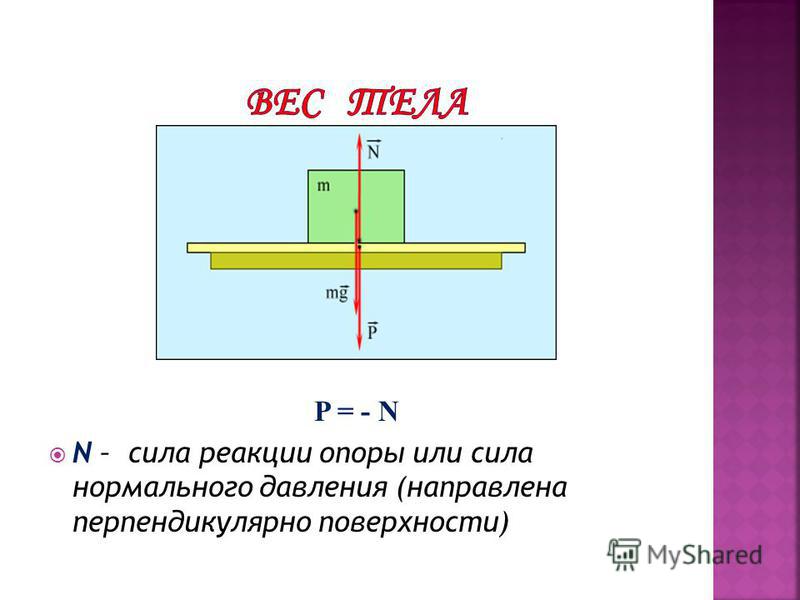 Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:
Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:
В воздухе силой Архимеда пренебрегаем.
Если сила Архимеда равна силе тяжести, тело плавает. Если сила Архимеда больше, то оно поднимается на поверхность жидкости, если меньше — тонет.
Электрические силы
Существуют силы электрического происхождения. Возникают при наличии электрического заряда. Эти силы, такие как сила Кулона , сила Ампера , сила Лоренца , подробно рассмотрены в разделе Электричество .
Схематичное обозначение действующих на тело сил
Часто тело моделируют материальной точкой . Поэтому на схемах различные точки приложения переносят в одну точку — в центр, а тело изображают схематично кругом или прямоугольником.
Для того, чтобы верно обозначить силы, необходимо перечислить все тела, с которыми исследуемое тело взаимодействует. Определить, что происходит в результате взаимодействия с каждым: трение, деформация, притяжение или может быть отталкивание. Определить вид силы, верно обозначить направление. Внимание! Количество сил будет совпадать с числом тел, с которыми происходит взаимодействие.
Определить вид силы, верно обозначить направление. Внимание! Количество сил будет совпадать с числом тел, с которыми происходит взаимодействие.
Главное запомнить
1) Силы и их природа;
2) Направление сил;
3) Уметь обозначить действующие силы
Различают внешнее (сухое) и внутреннее (вязкое) трение. Внешнее трение возникает между соприкасающимися твердыми поверхностями, внутреннее — между слоями жидкости или газа при их относительном движении. Существует три вида внешнего трения: трение покоя, трение скольжения и трение качения.
Трение качения определяется по формуле
Сила сопротивления возникает при движении тела в жидкости или в газе. Величина силы сопротивления зависит от размеров и формы тела, скорости его движения и свойств жидкости или газа. При небольших скоростях движения сила сопротивления пропорциональна скорости тела
При больших скоростях пропорциональна квадрату скорости
Рассмотрим взаимное притяжение предмета и Земли. Между ними, согласно закону гравитации возникает сила
Между ними, согласно закону гравитации возникает сила
А сейчас сравним закон гравитации и силу тяжести
Величина ускорения свободного падения зависит от массы Земли и ее радиуса! Таким образом, можно высчитать, с каким ускорением будут падать предметы на Луне или на любой другой планете, используя массу и радиус той планеты.
Расстояние от центра Земли до полюсов меньше, чем до экватора. Поэтому и ускорение свободного падения на экваторе немного меньше, чем на полюсах. Вместе с тем, следует отметить, что основной причиной зависимости ускорения свободного падения от широты местности, является факт вращения Земли вокруг своей оси.
При удалении от поверхности Земли сила земного тяготения и ускорения свободного падения изменяются обратно пропорционально квадрату расстояния до центра Земли.
Сила реакции опоры относится к силам упругости, и всегда направлена перпендикулярно поверхности. Она противостоит любой силе, которая заставляет тело двигаться перпендикулярно опоре. Для того чтобы рассчитать ее нужно выявить и узнать числовое значение всех сил, которые действуют на тело, стоящее на опоре.
Для того чтобы рассчитать ее нужно выявить и узнать числовое значение всех сил, которые действуют на тело, стоящее на опоре.
Вам понадобится
- — весы;
- — спидометр или радар;
- — угломер.
Инструкция
- Определите массу тела с помощью весов или любым другим способом. Если тело находится на горизонтальной поверхности (причем неважно, движется оно или пребывает в состоянии покоя), то сила реакции опоры равна силе тяжести действующей на тело. Для того чтобы рассчитать ее умножьте массу тела на ускорение свободного падения, которое равно 9,81 м/с² N=m g.
- Когда тело движется по наклонной плоскости, направленной под углом к горизонту, сила реакции опоры находится под углом в силе тяжести. При этом она компенсирует только ту составляющую силы тяжести, которая действует перпендикулярно наклонной плоскости. Для расчета силы реакции опоры, с помощью угломера измерьте угол, под которым плоскость располагается к горизонту. Рассчитайте силу реакции опоры, перемножив массу тела на ускорение свободного падения и косинус угла, под которым плоскость находится к горизонту N=m g Cos(α).

- В том случае, если тело движется по поверхности, которая представляет собой часть окружности с радиусом R, например, мост, пригорок то сила реакции опоры учитывает силу, действующую по направлению из центра окружности, с ускорением, равным центростремительному, действующую на тело. Чтобы рассчитать силу реакции опоры в верхней точке, от ускорения свободного падения отнимите отношение квадрата скорости к радиусу кривизны траектории.
- Получившееся число умножьте на массу движущегося тела N=m (g-v²/R). Скорость должна быть измерена в метрах в секунду, а радиус в метрах. При определенной скорости значение ускорения, направленного от центра окружности, может сравняться, и даже превысить ускорение свободного падения, в этот момент сцепление тела с поверхностью пропадет, поэтому, например, автомобилистам, нужно четко контролировать скорость на таких участках дороги.
- Если же кривизна направлена вниз, и траектория тела вогнутая, то рассчитайте силу реакции опоры, прибавив к ускорению свободного падения отношение квадрата скорости и радиуса кривизны траектории, а получившийся результат умножьте на массу тела N=m (g+v²/R).

- Если известна сила трения и коэффициент трения, силу реакции опоры рассчитайте, поделив силу трения на этот коэффициент N=Fтр/μ.
Положим камень на горизонтальную крышку стола, стоящего на Земле (рис. 104). Поскольку ускорение камня относительно Земли равно пулю, то по второму закону Ньютона сумма действующих на него сил равна нулю. Следовательно, действие на камень силы тяжести m · g должно компенсироваться какими-то другими силами. Ясно, что под действием камня крышка стола деформируется. Поэтому со стороны стола на камень действует сила упругости. Если считать, что камень взаимодействует лишь с Землей и крышкой стола, то сила упругости должна уравновешивать силу тяжести: F упр = -m · g. Эту силу упругости называют силой реакции опоры и обозначают латинской буквой N. Так как ускорение свободного падения направлено вертикально вниз, сила N направлена вертикально вверх – перпендикулярно поверхности крышки стола.
Поскольку крышка стола действует на камень, то по третьему закону Ньютона и камень действует на крышку стола силой P = -N (рис. 105). Эту силу называют весом .
105). Эту силу называют весом .
Весом тела называют силу, с которой это тело действует на подвес или опору, находясь относительно подвеса или опоры в неподвижном состоянии.
Ясно, что в рассмотренном случае вес камня равен силе тяжести: P = m · g. Это будет верно для любого тела, покоящегося на подвесе (опоре) относительно Земли (рис. 106). Очевидно, что в этом случае точка крепления подвеса (или опора) неподвижна относительно Земли.
Для тела, покоящегося на неподвижном относительно Земли подвесе (опоре), вес тела равен силе тяжести.
Вес тела также будет равен действующей на тело силе тяжести в случае, если тело и подвес (опора) движутся относительно Земли равномерно прямолинейно.
Если же тело и подвес (опора) движутся относительно Земли с ускорением так, что тело остается неподвижным относительно подвеса (опоры), то вес тела не будет равен силе тяжести.
Рассмотрим пример. Пусть тело массой m лежит на полу лифта, ускорение a которого направлено вертикально вверх (рис.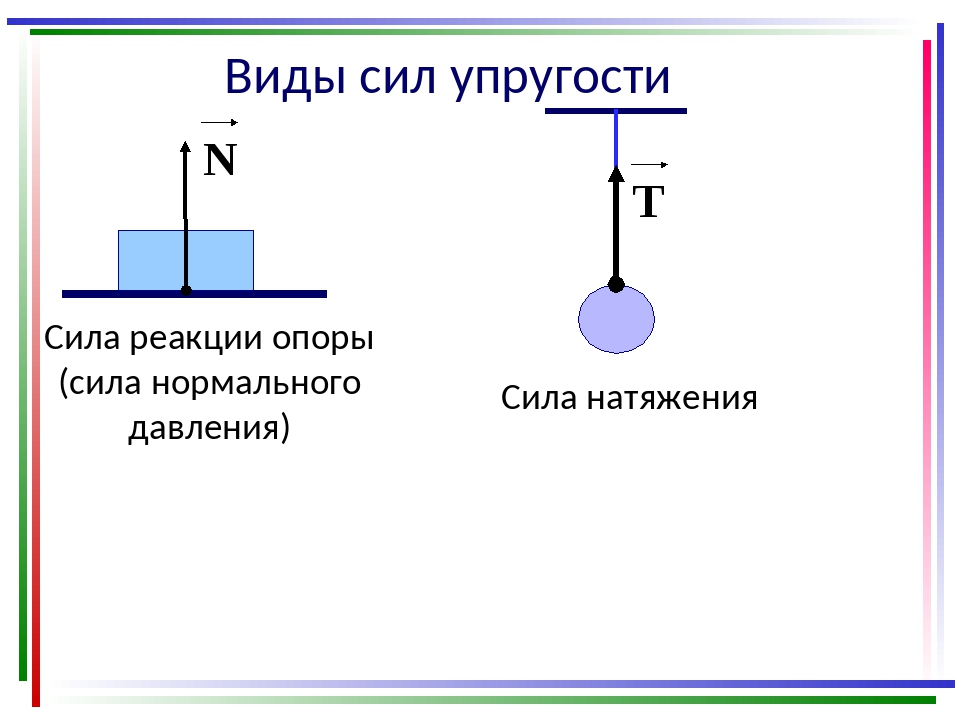 107). Будем считать, что на тело действуют только сила тяжести m · g и сила реакции пола N. (Вес тела действует не на тело, а на опору – пол лифта.) В системе отсчета, неподвижной относительно Земли, тело на полу лифта движется вместе с лифтом с ускорением a. В соответствии со вторым законом Ньютона произведение массы тела на ускорение равно сумме всех действующих на тело сил. Поэтому: m · a = N — m · g.
107). Будем считать, что на тело действуют только сила тяжести m · g и сила реакции пола N. (Вес тела действует не на тело, а на опору – пол лифта.) В системе отсчета, неподвижной относительно Земли, тело на полу лифта движется вместе с лифтом с ускорением a. В соответствии со вторым законом Ньютона произведение массы тела на ускорение равно сумме всех действующих на тело сил. Поэтому: m · a = N — m · g.
Следовательно, N = m · a + m · g = m · (g + a). Значит, если лифт имеет ускорение, направленное вертикально вверх, то модуль силы N реакции пола будет больше модуля силы тяжести. В самом деле, сила реакции пола должна не только скомпенсировать действие силы тяжести, но и придать телу ускорение в положительном направлении оси X.
Сила N – это сила, с которой пол лифта действует на тело. По третьему закону Ньютона тело действует на пол с силой P, модуль которой равен модулю N, но направлена сила P в противоположную сторону. Эта сила является весом тела в движущемся лифте. Модуль этой силы P = N = m · (g + a). Таким образом, в лифте, движущемся с направленным вверх относительно Земли ускорением, модуль веса тела больше модуля силы тяжести .
Таким образом, в лифте, движущемся с направленным вверх относительно Земли ускорением, модуль веса тела больше модуля силы тяжести .
Такое явление называют перегрузкой .
Например, пусть ускорение а лифта направлено вертикально вверх и его значение равно g, т. е. a = g. В этом случае модуль веса тела – силы, действующей на пол лифта, – будет равен P = m · (g + a) = m · (g + g) = 2m · g. То есть вес тела при этом будет в два раза больше, чем в лифте, который относительно Земли покоится или движется равномерно прямолинейно.
Для тела на подвесе (или опоре), движущемся с ускорением относительно Земли, направленным вертикально вверх, вес тела больше силы тяжести.
Отношение веса тела в движущемся ускоренно относительно Земли лифте к весу этого же тела в покоящемся или движущемся равномерно прямолинейно лифте называют коэффициентом перегрузки или, более кратко, перегрузкой .
Коэффициент перегрузки (перегрузка) – отношение веса тела при перегрузке к силе тяжести, действующей на тело.
В рассмотренном выше случае перегрузка равна 2. Понятно, что если бы ускорение лифта было направлено вверх и его значение было равно a = 2g, то коэффициент перегрузки был бы равен 3.
Теперь представим себе, что тело массой m лежит на полу лифта, ускорение которого a относительно Земли направлено вертикально вниз (противоположно оси X). Если модуль a ускорения лифта будет меньше модуля ускорения свободного падения, то сила реакции пола лифта по-прежнему будет направлена вверх, в положительном направлении оси X, а ее модуль будет равен N = m · (g — a). Следовательно, модуль веса тела будет равен P = N = m · (g — a), т. е. будет меньше модуля силы тяжести. Таким образом, тело будет давить на пол лифта с силой, модуль которой меньше модуля силы тяжести.
Это ощущение знакомо каждому, кто ездил на скоростном лифте или качался на больших качелях. При движении вниз из верхней точки вы чувствуете, что ваше давление на опору уменьшается. Если же ускорение опоры положительно (лифт и качели начинают подниматься), вас сильнее прижимает к опоре.
Если ускорение лифта относительно Земли будет направлено вниз и равно по модулю ускорению свободного падения (лифт свободно падает), то сила реакции пола станет равной нулю: N = m · (g — a) = m · (g — g) = 0. В этом случае пол лифта перестанет давить на лежащее на нем тело. Следовательно, согласно третьему закону Ньютона и тело не будет давить на пол лифта, совершая вместе с лифтом свободное падение. Вес тела станет равным нулю. Такое состояние называют состоянием невесомости .
Состояние, при котором вес тела равен нулю, называют невесомостью.
Наконец, если ускорение лифта, направленное к Земле, станет больше ускорения свободного падения, тело окажется прижатым к потолку лифта. В этом случае вес тела изменит свое направление. Состояние невесомости исчезнет. В этом можно легко убедиться, если резко дернуть вниз банку с находящимся в ней предметом, закрыв верх банки ладонью, как показано на рис. 108.
Итоги
Весом тела называют силу, с которой это тело действует на поднес или опору, находясь относительно подвеса или опоры в неподвижном состоянии.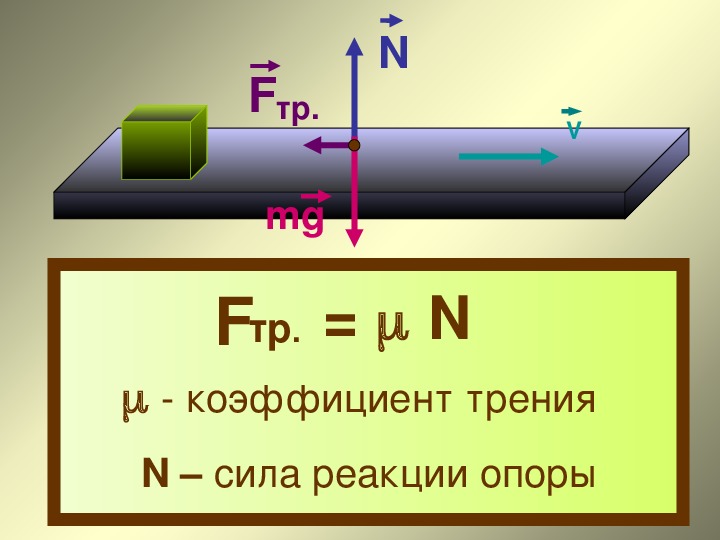
Вес тела в лифте, движущемся с направленным вверх относительно Земли ускорением, по модулю больше модуля силы тяжести. Такое явление называют перегрузкой .
Коэффициент перегрузки (перегрузка) – отношение веса тела, при перегрузке к силе тяжести, действующей на это тело.
Если вес тела равен нулю, то такое состояние называют невесомостью .
Вопросы
- Какую силу называют силой реакции опоры? Что называют весом тела?
- К чему приложен вес тела?
- Приведите примеры, когда вес тела: а) равен силе тяжести; б) равен нулю; в) больше силы тяжести; г) меньше силы тяжести.
- Что называют перегрузкой?
- Какое состояние называют невесомостью?
Упражнения
- Семиклассник Сергей стоит на напольных весах в комнате. Стрелка прибора установилась напротив деления 50 кг. Определите модуль веса Сергея. Ответьте на остальные три вопроса об этой силе.
- Найдите перегрузку, испытываемую космонавтом, который находится в ракете, поднимающейся вертикально вверх с ускорением a = Зg.
- С какой силой действует космонавт массой m = 100 кг на ракету, указанную в упражнении 2? Как называется эта сила?
- Найдите вес космонавта массой m = 100 кг в ракете, которая: а) стоит неподвижно на пусковой установке; б) поднимается с ускорением a = 4g, направленным вертикально вверх.
- Определите модули сил, действующих на гирю массой m = 2 кг, которая висит неподвижно На легкой нити, прикрепленной к потолку комнаты. Чему равны модули силы упругости, действующей со стороны нити: а) на гирю; б) на потолок? Чему равен вес гири? Указание: для ответа на поставленные вопросы воспользуйтесь законами Ньютона.
- Найдите вес груза массой m = 5 кг, подвешенного на нити к потолку скоростного лифта, если: а) лифт равномерно поднимается; б) лифт равномерно опускается; в) поднимающийся вверх со скоростью v = 2 м/с лифт начал торможение с ускорением a = 2 м/с 2 ; г) опускающийся вниз со скоростью v = 2 м/с лифт начал торможение с ускорением a = 2 м/с 2 ; д) лифт начал движение вверх с ускорением a = 2 м/с 2 ; е) лифт начал движение вниз с ускорением a = 2 м/с 2 .
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка браузера на прием файлов cookie
Существует множество причин, по которым файл cookie не может быть установлен правильно. Ниже приведены наиболее распространенные причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки браузера, чтобы принять файлы cookie, или спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файл cookie.
- Ваш браузер не поддерживает файлы cookie. Попробуйте другой браузер, если вы подозреваете это.
- Дата на вашем компьютере в прошлом.
 Если часы вашего компьютера показывают дату до 1 января 1970 г.,
браузер автоматически забудет файл cookie. Чтобы это исправить, установите правильное время и дату на своем компьютере.
Если часы вашего компьютера показывают дату до 1 января 1970 г.,
браузер автоматически забудет файл cookie. Чтобы это исправить, установите правильное время и дату на своем компьютере. - Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Предоставить доступ без файлов cookie потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в файле cookie; никакая другая информация не фиксируется.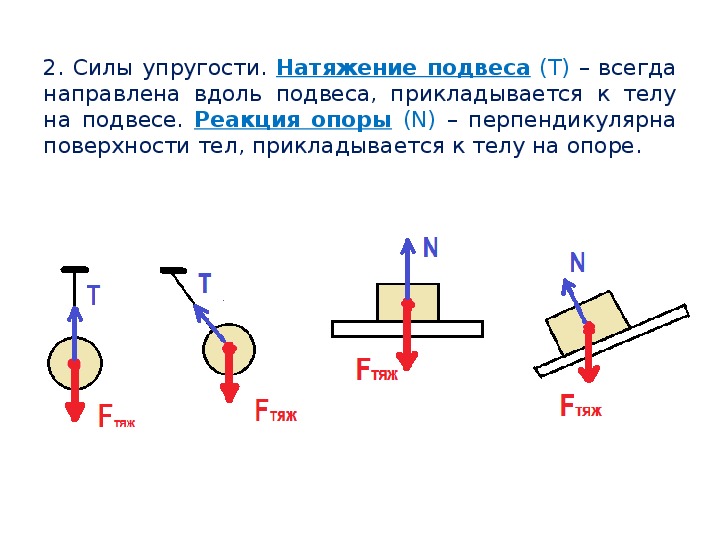
Как правило, в файле cookie может храниться только та информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, если вы не решите ввести его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступ к остальной части вашего компьютера, и только сайт, создавший файл cookie, может его прочитать.
Примеры прикладных расчетов | Основные сведения о подшипниках
[Пример 1] Срок службы подшипника (время) с надежностью 90 %
(Условия)
Глубокий шариковый подшипник: 6308
радиальная нагрузка F R = 3500 N
осевая нагрузка не применяется ( F A = 0)
скорость вращения N = 800min -1
① Базовая динамическая грузоподъемность (
C r ) получена из таблицы спецификаций подшипников.C r = 50,9 кН
② Динамическая эквивалентная радиальная нагрузка (
P r ) рассчитывается с использованием уравнения (5-32).
P r = F r = 3500 N
③Срок службы подшипника (
л 10 ч ) рассчитывается по уравнению (5-2).[Пример 2] Срок службы подшипника (время) с надежностью 96 %
(Условия)
Глубокий шариковый подшипник: 6308
радиальная нагрузка F R = 3500N
осевая нагрузка F A = 1000N
скорость вращения N = 800min -1
①Из таблицы спецификаций подшипников;
Номинальная грузоподъемность (
C r , C 0r ) ƒ 0 Коэффициент получен. C r = 50,9 кН P R = XF R + R + YF A = (0,56 × 3500) + (1,82 × 1000) = 3780 N (Условия) Из таблицы спецификаций подшипников получается делительный диаметр D pw = (40 + 90)/2 = 65. Рабочая температура составляет 70 °C, поэтому согласно рис. 12-3, Зависимость между вязкостью смазочного масла и температурой (индекс вязкости: 100), вязкость при эксплуатации составляет ν = 20 мм 2 / с Следовательно, согласно рис. B l 4m 4m = α 1 α ISO L 10 = 0,55 × 7,7 × 50900 ≒ 216000 ч Рис. А Рис. В Коэффициент α ISO также можно рассчитать на нашем веб-сайте. (Условия) [Примечание] 1) Используются те значения, где F a / F r > e . (см. уравнение 5-33, таблица 5-9) (Условия) Результирующее значение, F a / F r = 300/2000 = 0.15, меньше любых других значений e в таблице спецификаций подшипников. где C 0R из 62042 R 9,3 кН, а ƒ 0 12.8 Затем можно вычислить значение e с помощью пропорциональной интерполяции. В результате можно подтвердить, что (Условия) Начиная с F a / F r = 2400/4000 = 0.6 намного больше, чем значение e , указанное в таблице спецификаций подшипников, это предполагает, что осевая нагрузка влияет на динамическую эквивалентную нагрузку. Где ƒ 0 F A / A / C 0R = 13,3 × 2400/29500 = 1,082 Таким образом, F a / F r = 0,6 > e . (Условия) Из значений, перечисленных в Таблице 5-11, коэффициент ƒ a , связанный с повторно-кратковременной нагрузкой: ƒ a = 2 серия диаметров 3: ƒ b = 1.0 F AP AP = 9,8 ƒ A · ƒ B · ƒ P · D M 2 = 9. (Условия)
ƒ 0 = 13,2
C 0r 90 043 =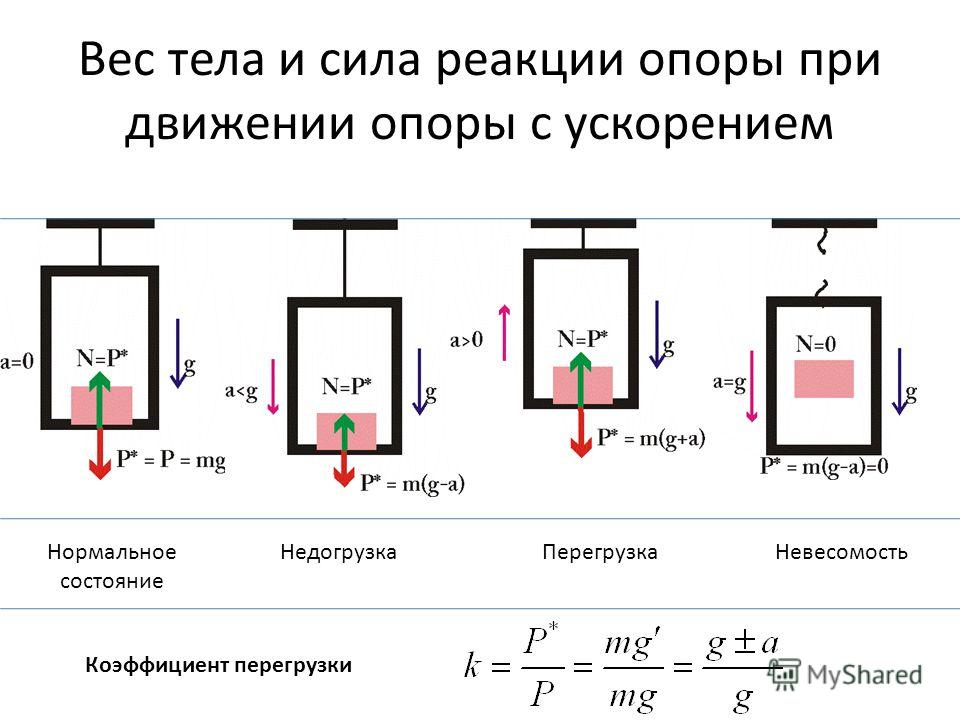
②Динамическая эквивалентная нагрузка (
P r ) рассчитывается с использованием уравнения (5-32). ③Срок службы с надежностью 90 % (
л 10 ч ) определяется с помощью уравнения (5-2). [Пример 3] Расчет коэффициента
α ISO с условиями примера 2
Масляная смазка (Масло, отфильтрованное фильтром тонкой очистки)
Рабочая температура 70℃
Надежность 96% ④Выбор смазочного масла
d mn = 65 × 800 = 52 000. Следовательно, выберите VG 68 из Таблицы 12-8, Надлежащие значения кинематической вязкости в зависимости от условий работы подшипника. ⑤ Расчет коэффициента
α ISO
Согласно Рис.
2, ν 1 1 = 21,7 мм 2
κ = ν / ν 1 = 20 / 21,7 = 0,92
Масло было фильтровано тонким фильтром, так что стол 5-4 показывает e c от 0,5 до 0,6.
Чтобы строго оценить значение, e c = 0,5.
α ISO = 7.7 ⑥Срок службы с надежностью 96 % (
L нм ) получен с использованием уравнения (5-8) .
Согласно таблице 5-3, α 1 = 0,55.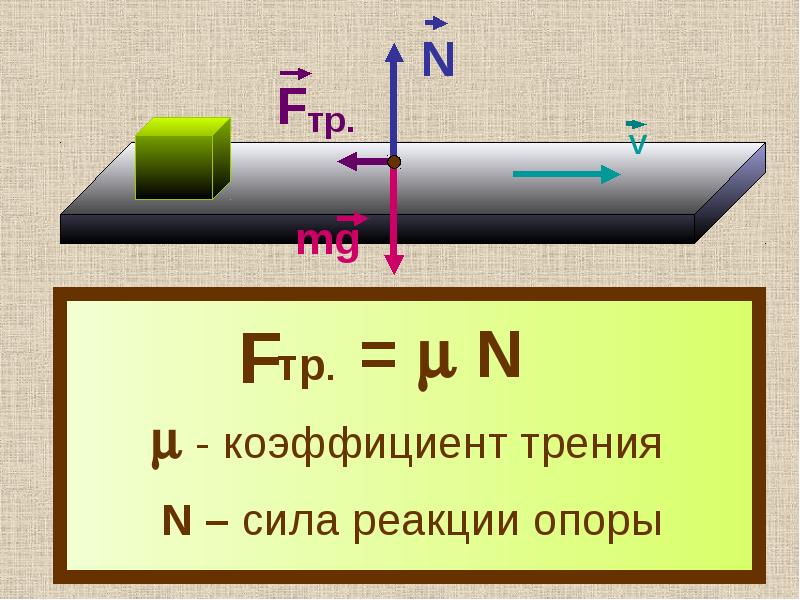
[Пример 4] Срок службы подшипника (полный оборот)
Конический роликовый подшипник
Подшипник A: 30207 JR
Подшипник B: 30207 JR
радиальная нагрузка
F RA = 5200 N
F RB = 6800 N
Осевая нагрузка K а = 1600 Н ①Из таблицы спецификаций подшипников получены следующие характеристики.
Базовый динамический рейтинг нагрузки E 1) 1) 1) 1) 1)
( C R ) Подшипник 68,8 кН 0,37 0,4 1,60 Подшипник В 83,9 кН 0,40 0,4 1,48 
Где F a / F r ≦ e , X = 1, Y = 0. ②Аксиальную нагрузку, воздействующую на валы, необходимо рассчитывать с учетом того факта, что составляющая сила в осевом направлении возникает, когда радиальная нагрузка прикладывается к коническим роликоподшипникам.
③Эквивалентная динамическая нагрузка (
P r ) получена из Таблицы 5-9. ④Срок службы каждого подшипника (
L 10 ) рассчитывается по уравнению (5-1). [Пример 5] Выбор размера подшипника
Грозные шариковые подшипники: 62 серии
требуемый срок службы: более 10000 ч
радиальная нагрузка F R = 2000 N
осевая нагрузка F A = 300 N
скорость вращения N = 1600 мин -1 ①Эквивалентная динамическая нагрузка (Pr) рассчитана гипотетически.

Следовательно, JTEKT может считать, что P r = F r = 2000 N. ②Требуемая номинальная базовая динамическая грузоподъемность (
C r ) рассчитывается в соответствии с уравнением (5-4). ③Среди тех, которые указаны в таблице спецификаций подшипников, подшипник серии 62 с
C r , превышающим 19730 Н, представляет собой 6205R с диаметром отверстия 25 мм. ④Динамическая эквивалентная нагрузка, полученная на шаге ①, подтверждается получением значения
e для 6205 R.
ƒ 0 F A / C 0R = 12,8 × 300/9300 = 0,413
F a / F r = 0.15 < и .
Следовательно, P r = F r . [Пример 6] Выбор размера подшипника
Глубокий шариковый подшипник: 63 серии
требуемый срок службы: более 15 000 ч
радиальная нагрузка F R = 4000 N
осевой нагрузка F A = 2400 N
скорость вращения n = 1000 мин -1 ①Рассчитана гипотетическая динамическая эквивалентная нагрузка (
P r ):
, следовательно, предполагая, что x = 0,56, y = 1,6
(приблизительное среднее значение y ), используя уравнение (5-32) ,
P R = XF R + XF a = 0,56 × 4000 + 1,6 × 2400 = 6080 N ②Используя уравнение (5-4), требуемая базовая номинальная динамическая грузоподъемность (
C r ) составляет: ③Из таблицы спецификаций подшипников 6309 с диаметром отверстия 45 мм выбран как подшипник серии 63 с
C r превышающим 58700 Н.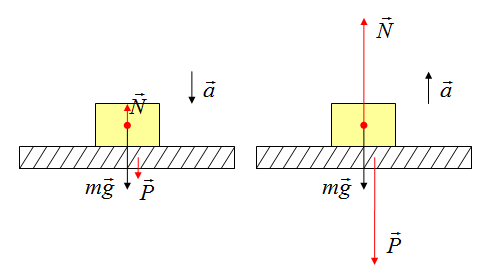
④Эквивалентная динамическая нагрузка и номинальный срок службы подтверждены путем расчета значения
и для 6309.
Значения, полученные с использованием пропорциональной интерполяции:
E = 0,283, y = 1,54.
Используя полученные значения, можно рассчитать эквивалентную динамическую нагрузку и номинальный срок службы следующим образом: ⑤ Базовый номинальный срок службы модели 6308 при использовании тех же шагов составляет:
л 10 ч ≒ 11500 ч, что не соответствует требованиям к сроку службы. [Пример 7] Расчет допустимой осевой нагрузки для цилиндрических роликоподшипников
Однорядный цилиндрический роликоподшипник: NUP 310
Частота вращения n = 1500 мин -1
Масляная смазка
Осевая нагрузка периодически прикладывается.
①Используя таблицу спецификаций подшипников, значение
d m для NUP 310 можно рассчитать следующим образом: ②Каждый коэффициент, используемый в уравнении (5-45).
Согласно рис. 5-13, коэффициент ƒ P для допустимого ребра поверхность давления, связанные с
D M N = 80 × 150043, является: 4 , является: ƒ р = 0,062 ③Используя уравнение (5-45), допустимая осевая нагрузка
F ap составляет: 8 × 2 × 1,0 × 0,062 × 80 2 ≒ 7780 Н
8 × 2 × 1,0 × 0,062 × 80 2 ≒ 7780 Н [Пример 8] Расчет срока службы подшипников вала цилиндрической шестерни
Конический роликовый подшипник
Подшипник A: 32309 JR
Подшипник B: 32309 JR
Подшипник B: 32310 JR
Тип передачи: SPUR Gear (нормально обработанный)
Угол давления передач α 1 = α 2 = 20 °
Круг передач Диаметр диаметр
D P1 = 360 мм
= 360 мм
D P2 = 180 мм
Power передач W = 150 кВт
Скорость вращения N = 1000 мин -1
Условие эксплуатации : сопровождается воздействием
Место установки α 1 = 95 мм, α 2 = 265 мм, B 1 = 245 мм, B 2 = 115 мм, C = 360 мм
①С помощью уравнений (5-14) и (5-15) рассчитываются теоретические нагрузки, приложенные к зубчатым колесам (тангенциальная нагрузка,
K t ; радиальная нагрузка, K r ).
[Шестерня 1]
[Шестерня 2]
②Рассчитана радиальная нагрузка, приложенная к подшипнику,
, где коэффициент нагрузки определяется как ƒ w = 1,5 из таблицы 5-6 , а коэффициент передачи как ƒ g = 1,2 из таблицы 5-8 .
[Подшипник А]
Нагрузка, состоящая из
K t1 и K t2 :Нагрузка, состоящая из
K r1 и K r2 :Комбинируя нагрузки
K tA и em>K rA , радиальную нагрузку ( F rA ), приложенную к подшипнику А, можно рассчитать следующим образом:[Подшипник Б]
*Нагрузка, состоящая из K
t1 и K t2 :Нагрузка, состоящая из K
r1 и K r2 :Радиальная нагрузка (
F rB ), приложенная к подшипнику B, может быть рассчитана с использованием тех же шагов, что и для подшипника A.
③Следующие характеристики можно получить из таблицы спецификаций подшипников.
| Базовый динамический рейтинг нагрузки ( C R ) | E 1) 1) 1) 1) 1) ||||
|---|---|---|---|---|
| Подшипник | 183 кН | 0,35 | 0,4 | 1,74 |
| Подшипник В | 221 кН |
[Примечание] 1) Используются те значения, где F a / F r > e .
Где F a / F r ≦ e , X = 1, Y = 0,
④Когда осевая нагрузка не приложена извне, если радиальная нагрузка приложена к коническому роликоподшипнику, создается осевая составляющая силы.

Принимая во внимание этот факт, необходимо рассчитать осевую нагрузку, приложенную к валу и периферийным частям:
(уравнение 5-33, таблица 5-9)
Из результата видно, что осевая составляющая сила ( F rB /2 Y B ), приложенная к подшипнику B, также приложена к подшипнику A как осевая нагрузка, приложенная от вала и периферии части.
⑤Используя значения, указанные в Таблице 5-9, рассчитывается динамическая эквивалентная нагрузка, где
K a = 0 :⑥Используя уравнение (5-2), рассчитывается номинальный срок службы каждого подшипника:
[Подшипник А]
[Подшипник Б]
Артикул
Используя уравнение (5-11), срок службы системы ( л 10 часов ) с использованием пары подшипников:
Формула напряжения | Задачи с решаемыми примерами
Натяжение относится к тянущей силе, передаваемой в осевом направлении посредством веревки, троса, цепи или подобного одномерного непрерывного объекта, или каждым концом стержня или подобного трехмерного объекта; напряжение можно также описать как пару сил действие-противодействие, действующую на каждом конце указанных элементов.
Что такое сила натяжения?
В переводе с латыни слово «натяжение» означает «растяжение». Сила, приложенная к длине гибкого участка, такого как веревка, трос или цепь, в физике называется силой формулы натяжения. Мы знаем, что на толчок или натяжение указывает сила натяжения. В физике мы имеем дело с несколькими типами сил, такими как вес, нормальная сила, толчок, столкновение и т. д. Сила или мощность, основанная на том, как она работает и передается, может быть контактной или бесконтактной.Сила натяжения – это сила контакта, которая передается гибкой среде по длине.
Часто называемая силой «пары действие-реакция», напряжение применяется к каждому компоненту адаптивного объекта. Если рассматривать любую сшивку, то часть струны с одной стороны в поперечном сечении будет использовать силу действия на часть струны с другой стороны в поперечном сечении. Точно так же вторая часть троса использует реактивную мощность первой части. Таким образом, в любом поперечном сечении мы можем видеть силы натяжения, действующие с обеих сторон.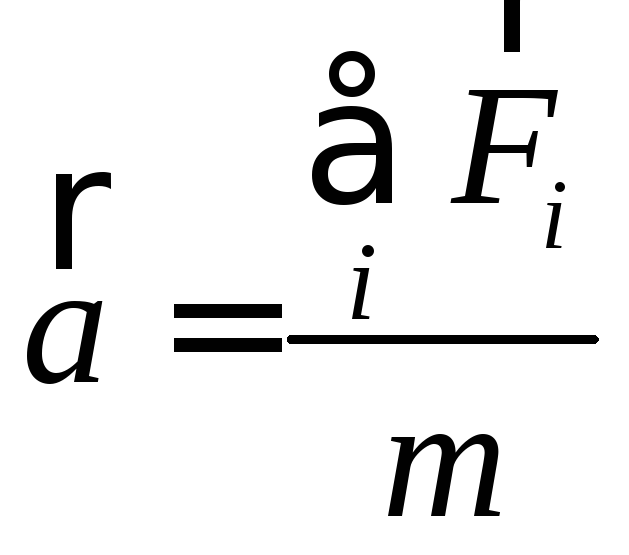 На концах шнур будет оказывать давление на связанный с ним предмет (сила тяжести), а предмет будет использовать силу реакции веревки на него. Направление этой силы соответствует длине шнура.
На концах шнур будет оказывать давление на связанный с ним предмет (сила тяжести), а предмет будет использовать силу реакции веревки на него. Направление этой силы соответствует длине шнура.
Что следует помнить
Натяжение — это сила, действующая на средние длины, особенно на гибкие, такие как веревка или шнур.
Сила натяжения остается силой гравитации.
Полная энергия может быть рассчитана как: Fnet = T − W = 0
T = W ± ma
Если тело движется вверх, то напряжение будет обозначаться как T = W + ма.
Когда тело опускается, толщина такая же, как T = W — ma.
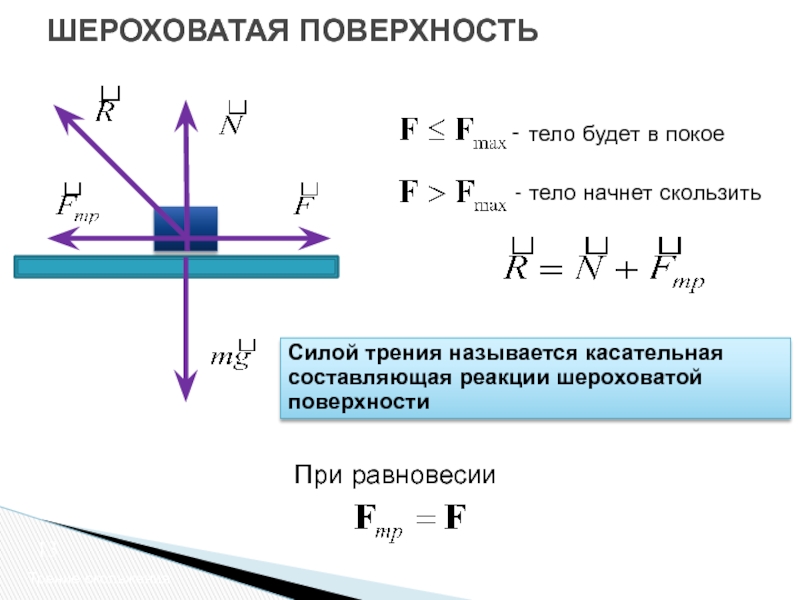
T = W, если дискомфорт равен массе тела.
На атомарном уровне, когда атомы или молекулы отделяются друг от друга и получают потенциальную энергию при еще существующей восстанавливающей силе, восстанавливающая сила может создавать напряжение. Каждый конец струны или стержня под таким натяжением может тянуть объект, к которому он прикреплен, чтобы восстановить длину струны / стержня до ее расслабленной длины.
Натяжение можно легко объяснить в случае тел, подвешенных на цепи, тросе, веревке и т. д. Оно обозначается буквой T (иногда также обозначается как Ft).
Если такое подвешенное тело движется вертикально с ускорением a, то;
T = W ± ma
Где W — вес тела, а m — масса тела.
Случай (i) Если тело движется вверх с ускорением a, напряжение; T = W + ma
Случай (ii) Если тело движется вниз с ускорением a, напряжение; T = W – ma
Случай (iii) Если тело просто подвешено (не движется), натяжение; Т = Вт.
Случай (iv) Если тело движется вверх или вниз с постоянной скоростью, напряжение; T = W
Вес объекта W = мг.
Следовательно, формулу натяжения можно изменить следующим образом:
T=m(g±a)
Где m = масса тела, g = ускорение свободного падения, a = ускорение движущегося тела.
Поскольку натяжение представляет собой силу, ее единицей измерения в системе СИ является ньютон (Н).
Пример:
Легкая и нерастяжимая струна поддерживает тело массой 15 кг, подвешенное к ее нижнему концу.Если верхний конец нити прочно прикреплен к крюку на крыше, то каково натяжение нити?
Решение:
Поскольку тело не движется, а просто подвешено, натяжение нити будет равно весу тела. m = 15 кг
T = W = mg = 15 × 9,8 = 147 N
Пример:
Обезьяна массой 10 кг карабкается по легкой вертикальной веревке, подвешенной на крюке, с ускорением 2 м/с2.