1) Определение реакции опоры а при шарнирном соединении в точке с.

Рассмотрим систему уравновешивающихся сил, приложенных ко всей конструкции (рис.11). Составим уравнение моментов сил относительно точки B.

Рис.11

 

                                        (1)

где  кН.

После подстановки данных и вычислений уравнение (26) получает вид:

                                                                                                     (2)

Второе уравнение с неизвестными   и   получим, рассмотрев систему уравновешивающихся сил, приложенных к части конструкции, расположенной левее шарнира С (рис. 12):

Рис. 12

 

                 .

Отсюда находим, что

                  кН.

Подставив найденное значение   в уравнение (2) найдем значение  :

                    кН.

Модуль реакции опоры А при шарнирном соединении в точке С равен:

                    кН.

2) Расчетная схема при соединении частей конструкции в точке с скользящей заделкой, показанной на рис. 13.

 

Рис. 13

 

Системы сил, показанные на рис. 12 и 13, ничем друг от друга не отличаются. Поэтому уравнение (2) остается в силе. Для получения второго уравнения рассмотрим систему уравновешивающихся сил, приложенных к части конструкции, расположенной левее скользящей заделки С (рис. 14).

Рис. 14

 

Составим уравнение равновесия:

                       

откуда

                

и из уравнения (2) находим:

              

           

Следовательно, модуль реакции при скользящей заделке в шарнире С равен:

             

                кН.

Итак, при соединении в точке С скользящей заделкой модуль реакции опоры А меньше, чем при шарнирном соединении ( ).

Найдем составляющие реакции опоры В и скользящей заделки.

Для левой от С части

                                   ,

откуда

               кН.

Составляющие реакции опоры В и момент в скользящей заделке найдем из уравнений равновесия, составленных для правой от С части конструкции.

                            

              кНм

                             кН

                     ;          кН

 

Ответ:  Результаты расчета приведены в таблице.              

	Силы, кН						Момент, кНм
	XA	YA	RA	XC	XB	YB		MC
Для схемы на рис. 11	-7,5	-18,4	19,9	—	—	—		—
Для схемы на рис.13	-14,36	-11,09	17,35	-28,8	28,8	12,0		-17,2

 

Пример 6.

Дано: вариант расчетной схемы (рис.15).

Р₁ = 14 кН; Р₂ = 8 кН; q = 10 кн/м;  М = 6 кНм; АВ = 0,5 м; ВС = 0,4 м; CD = 0,8 м; DE = 0,3 м; 

EF = 0,6 м.

                Определить реакции в опорах А и F.

                Решение. Используя рекомендации примера 3, расставляем реакции в опорах. Их получается четыре ( ,  ,  ,  ). Так как в плоской статике для одного тела можно составить только три уравнения равновесия, то для определения реакций необходимо разбить конструкцию на отдельные твердые тела так, чтобы число уравнений и неизвестных совпало. В данном случае можно разбить на два тела АВСD и DEF. При этом в месте разбиения, т. е. в точке Dдля каждого из двух тел появляются дополнительные реакции, определяемые по виду, числу и направлению так же, как и для точек А и F. При этом по третьему закону Ньютона они равны по значению и противоположно направлены для каждого из тел. Поэтому их можно обозначить одинаковыми буквами (см. рис. 16).

Рис. 15

 

                Далее, как и в примере 3, заменяем распределенную нагрузку q сосредоточенной силой  и находим её модуль  . Затем выбираем оси координат и раскладываем все силы на рис. 15 и 16 на составляющие параллельные осям. После этого составляем уравнения равновесия для каждого из тел. Всего их получается шесть и неизвестных реакций тоже шесть ( ,  ,  ,  ,  ,  ),  поэтому система уравнений имеет решение, и можно найти модули, а с учетом знака модуля и правильное направление этих реакций (см. пример 3).

Рис. 16. Разбиение конструкции на два тела в точке D, т. е. в месте их соединения скользящей заделкой (трение в ней не учитывается)

 

                Целесообразно так выбирать последовательность составления уравнений, чтобы из каждого последующего можно было определить какую-то одну из искомых реакций. В нашем случае удобно начать с тела DEF, т. к. для него имеем меньше неизвестных. Первым составим уравнение проекций на ось х, из которого найдем R_F. Далее составим уравнения проекций на оси у и найдем Y_D, а затем уравнение моментов относительно точки F и определим M_D. После этого переходим к телу ABCD. Для него первым можно составить уравнения моментов относительно точки А и найти М_А, а затем последовательно из уравнений проекций на оси найти X_A, Y_A. Для второго тела необходимо учитывать свои реакции Y_D

, M_D, взяв их из рис.16, но значения этих реакций уже будут известны из уравнений для первого тела.

                При этом значения всех ранее определенных реакций подставляются в последующие уравнения со своим знаком. Таким образом, уравнения запишутся так:

                для тела DEF

                

                для тела ABCD

                

                В некоторых вариантах задан коэффициент трения в какой-то точке, например  . Это означает, что в этой точке необходимо учесть силу трения  , где N_A реакция плоскости в этой точке. При разбиении конструкции в точке, где учитывается сила трения, на каждое из двух тел действует своя сила трения и реакция плоскости (поверхности). Они попарно противоположно направлены и равны по значению (как и реакции на рис.16).

                Реакция N всегда перпендикулярна плоскости возможного скольжения тел либо касательной к поверхностям в точке скольжения, если там нет плоскости. Сила трения же направлена вдоль этой касательной либо по плоскости против скорости возможного скольжения. Приведенная выше формула для силы трения справедлива для случая предельного равновесия, когда скольжение вот-вот начнется (при непредельном равновесии сила трения меньше этого значения, а определяется её величина из уравнений равновесия). Таким образом, в вариантах задания на предельное равновесие с учетом силы трения к уравнениям равновесия для одного из тел необходимо добавить еще одно уравнение  . Там, где учитывается сопротивление качению и задан коэффициент сопротивления качения  , добавляются уравнения равновесия колеса (рис.

17).

                При предельном равновесии

               

Рис.17

 

                Из последних уравнений, зная G,  , R, можно найти N, F_тр, T для начала качения без проскальзывания.

                В заключение отметим, что разбиение конструкции на отдельные тела проводят в том месте (точке), где имеет место наименьшее число реакций. Часто это невесомый трос или невесомый ненагруженный рычаг с шарнирами на концах, которые соединяют два тела (рис 18).

Рис. 18

 

 

Пример 7. Жесткая рама ABCD (рис. 19) имеет в точке А неподвижную шарнирную опору, а в точке 

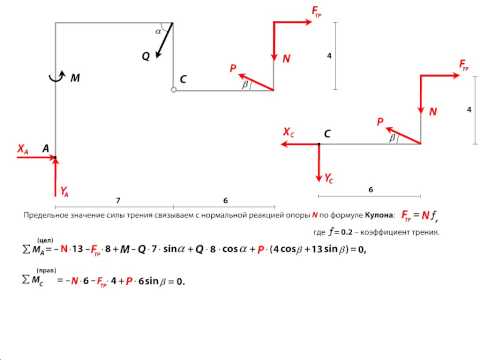б — подвижную шарнирную опору на катках. Все действующие нагрузки и размеры показаны на рисунке.

Дано: F=25 кН,  =60º, Р=18 кН,  =75º, М=50 кНм, =30°, а=0,5 м.

Определить: реакции в точках A и В, вызы­ваемое действующими нагрузками.

Рис. 19

   

Указания. Задача – на равновесие тела под действием произвольной плоской системы сил. При ее решении учесть, что натяжения обеих ветвей нити, перекинутой через блок, когда трением пренебрегают, будут одинаковыми. Уравнение моментов будет более простым (содержать меньше неизвестных), если составлять уравнение относительно точки, где пересекаются линии действия двух реакций связей. При вычислении момента силы F часто удобно разложить ее на составляющие F’ и F”, для которых плечи легко определяются, и воспользоваться теоремой Вариньона; тогда  

 

Решение.  1. Рассмотрим равновесие пластины. Проведем коорди­натные оси ху и изобразим действующие на пластину силы: силу , пару сил с моментом М, натяжение троса   (по модулю T = Р) и реакции связей  (реакцию неподвижной шарнирной опоры A изображаем двумя ее составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости).

2. Для полученной плоской системы сил составим три уравнения  равновесия. При вычислении момента силы   относительно точки A воспользуемся теоремой Вариньона, т.е. разложим силу  на состав­ляющие F΄, F˝ ( , )  и учтем, что по теореме Вариньона:   Получим:

                

Подставив в составленные уравнения числовые значения заданных величин и решив эти уравнения, определим искомые реакции.

Ответ: X=-8,5кН; Y =-23,3кН; R=7,3кН. Знаки указывают, что силы X_A и Y_A  направлены противоположно силам, показан­ным на рис. 19.

 

Пример 8. Жесткая рама АBCD (рис.20) имеет в т. А неподвижную шарнирную опору, а т. D прикреплена к невесомому стержню. В т. С к раме привязан трос, перекинутый через блок и несущий на конце груз весом Р =20 кН. На раму действует пара сил  с моментом    М = 75 кНм и две силы F₁ =10 кН и F₂=20 кН, составляющие со стержнями рамы углы  =30⁰ и  =60⁰ соответственно. При определении размеров рамы принять a =0,2 м. Определить реакции связей в точках А и D, вызванные действием нагрузки.

Дано: Р =20 кН, М =75 кНм, F₁ =10 кН, F₂ =20 кН,   =30⁰,   =60⁰,   =60⁰, a= 0,2 м.

Определить: Х_А, У_А, R_D.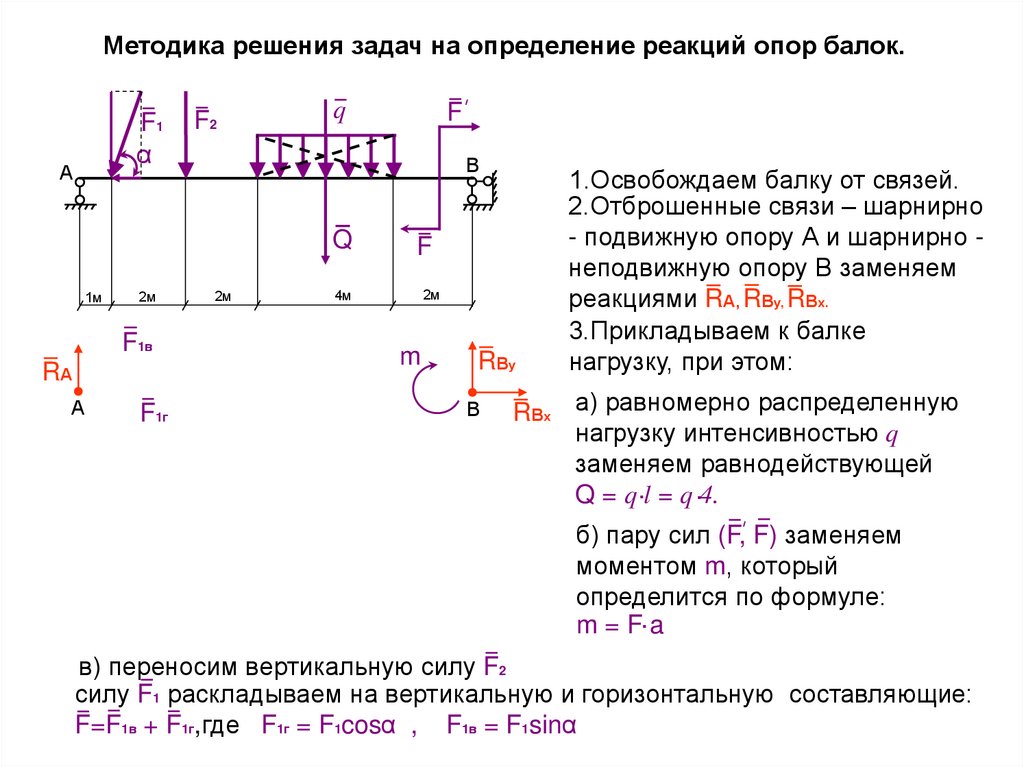

          Рис. 20

 

 

             Указания. Задача – на равновесие тела под действием произвольной плоской системы сил. При ее решении следует учесть, что натяжения обеих ветвей нити, перекинутой через блок, когда трением пренебрегают, будут одинаковыми. Уравнение моментов будет более простым (содержать меньше неизвестных), если брать моменты относительно точки, где пересекаются линии действия двух реакций связей. При вычислении момента силы   часто удобно разложить ее на составляющие   и , для которых плечи легко определяются, и воспользоваться теоремой Вариньона; тогда 

 

           Решение.

1.Рассмотрим равновесие рамы. Проведем координатные оси х, у и изобразим действующие на раму силы: силы   и  , пару сил с моментом М, натяжение троса   (по модулю Т = Р) и реакции связей   (реакцию неподвижной шарнирной опоры А представляем в виде составляющих ; стержневая опора препятствует перемещению т.  D рамы в направлении вдоль стержня,  поэтому  в  том  же  направлении  будет  действовать  и реакция опоры  ).

2. Составим уравнения равновесия рамы. Для равновесия произвольной плоской системы сил достаточно, чтобы сумма проекций всех сил на каждую из двух координатных осей и алгебраическая сумма моментов всех сил относительно любой точки на плоскости равнялись нулю.

При вычислении моментов сил   и   относительно точки А воспользуемся теоремой Вариньона, т.е. разложим силы на составляющие  ,   ;  ,      и учтем, что  .

Получим:

                      ;    ,                                                                                                                        (1)

                      ;    ,                                                                                                                          (2)

                       ;   .         (3)

Подставив в составленные уравнения числовые значения заданных величин, и решив эти уравнения, определим искомые реакции.

Из уравнения (3) определяем R_D =172,68 кН.

Из уравнения (1) определяем Х_А = -195,52 кН.

Из уравнения (2) определяем У_А = -81,34 кН.

Знаки «-» при величинах Х_А и У_А означают, что истинное направление этих реакций противоположно указанному на рисунке.

Проведем проверку.

Найдем

          ,

т.к.  , то реакции опор найдены правильно.

Ответ: Х_А = -195,52 кН, У_А = -81,34 кН_, R_D = 172,68 кН.

 

 

Пример 9. Конструкция (рис. 21) состоит из жесткого угольника и стержня, которые в точке С свободно опираются друг о друга. Внешними связями, наложенными на конструкцию, являются: в точке А – жесткая заделка, в точке В – шарнир. На конструкцию действуют: пара сил с моментом М =80 кН·м, равномерно распределенная нагрузка интенсивности q =10 кН/м и силы:  =15 кН и  =25кН. При определении размеров конструкции принять а =0,35 м.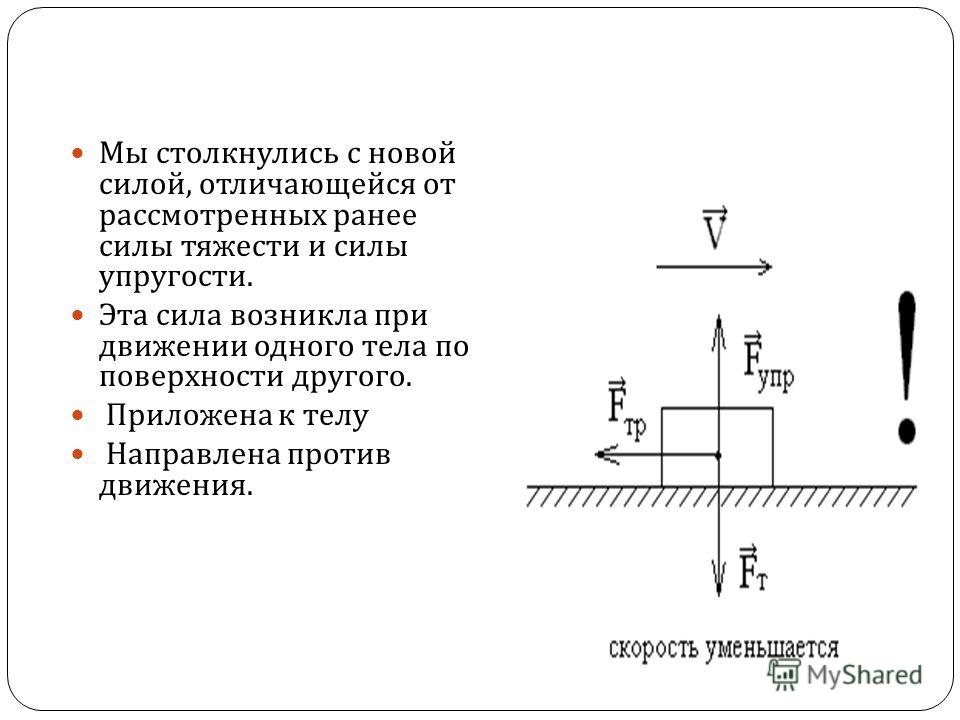 Определить реакции связей в точках А, В и С.

Дано: М =80 кН·м, q =10 кН/м, F₁=15 кН, F₂=25 кН, а =0,35 м.

Определить: R_A, M_A, R_B, R_C.

Указания. Задача – на равновесие системы тел, находящихся под действием плоской системы сил. При ее решении можно или рассмотреть сначала равновесие всей системы, а затем равновесие одного из тел системы, изобразив его отдельно, или же сразу расчленить систему и рассмотреть равновесие каждого из тел в отдельности, учтя при этом закон о равенстве действия и противодействия. В задачах, где имеется жесткая заделка, следует учесть, что ее реакция представляется силой, модуль и направление которой неизвестны, и парой сил, момент которой также неизвестен.

Решение.

Выполняем его в соответствии с изложенной выше методикой.

1. В данной задаче изучается равновесие системы, состоящей из жесткого угольника и стержня.

2. Выбираем систему координат ХАУ (см. рис. 21).

3. Активными нагрузками на данную систему являются: распределенная нагрузка интенсивностью q,  ,   и момент М.

Рис.21

 

          Изобразим на чертеже предполагаемые реакции связей. Так как жесткая заделка (в сечении А) препятствует перемещению этого сечения стержня вдоль направлений Х и У, а также повороту стержня вокруг точки А, то в данном сечении в результате действия заделки на стержень возникают реакции  ,  ,  . Шарнирная опора в точке В препятствует перемещению данной точки стержня вдоль направлений Х и У. Следовательно, в точке В возникают реакции _, и  . В точке С опоры стержня на угольник возникают реакция   действия угольника на стержень и реакция   действия стержня на угольник. Эти реакции направлены перпендикулярно плоскости угольника, причем R_C = R_С(согласно закону о равенстве действия и противодействия).

1. Задачу решаем способом расчленения. Рассмотрим сначала равновесие стержня ВС (рис. 21, б). На стержень действуют реакции связей  ,  ,  , сила   и момент . Для полученной плоской системы сил можно составить три уравнения равновесия, при этом сумму моментов внешних сил и реакций связей удобнее считать относительно точки В:

                ;                ;                                     (1)

                ;                 ;                           (2)

                 ;     .              (3)

Из уравнения (3) получим: R_C =132,38 кН.

Из уравнения (1) получим: Х_В = -12,99 кН.

Из уравнения (2) получим: У_В = -139,88 кН.

Реакция шарнира в точке В:

                   .

Теперь рассмотрим равновесие угольника СА (рис. 21, в). На угольник действуют: реакции связей  , сила   и распределенная нагрузка q. Заметим, что R^/_C = R_C =132,38 кН. Для данной плоской системы сил можно составить три уравнения равновесия, при этом сумму моментов сил будем считать относительно точки С:

                   ;         ;                                                                                                                  (4)

                   ;         ;                                                                                             (5)

                    ;      .      (6)

Из уравнения (4) получим: Х_А = 17,75 кН.

Из уравнения (5) получим: У_А= -143,13 кН.

                  .

Из уравнения (6) получим: М_А= -91,53 кНм.

Задача решена.

А теперь для наглядного доказательства того, какое значение имеет правильный выбор точки, относительно которой составляется уравнение моментов, найдем сумму моментов всех сил относительно точки А (рис. 21, в):

                .                                                 (7)

Из этого уравнения легко определить М_А:

М_А = -91,53 кНм.

Конечно, уравнение (6) дало то же значение М_А, что и уравнение (7), но уравнение (7) короче и в него не входят неизвестные реакции Х_А и У_А, следовательно, им пользоваться удобнее.

Ответ: R_A =144,22 кН_,, M_A = -91,53 кНм, R_B =140,48 кН,  R_C =R_C =132,38 кН.

 

 

Пример 10. На угольник АВС ( ), конец А которого жестко заделан, в точке С опирается стержень DE (рис. 22, а). Стержень имеет в точке D неподвижную шарнирную опору, и к нему приложена сила  , а к угольнику — равномерно распределенная на участке KB нагрузка интенсивности q и пара с моментом М.

 

Рис. 22

 

Д а н о:  F=10 кН,  М=5 кНм,  q=20 кН/м,  а=0,2 м.

О п р е д е л и т ь: реакции в точках А, С, D, вызванные заданными нагрузками.

Указания.  Задача — на равновесие системы тел, находящихся под действием плоской системы сил. При её решении можно или рассмотреть сначала равновесие всей системы в целом, а затем — равновесие одного из тел системы, изобразив его отдельно, или же сразу расчленить систему и рассмотреть равновесие каждого из тел в отдельности, учитывая при этом закон о равенстве действия и противодействия. В задачах, где имеется жесткая заделка, учесть, что её реакция представляется силой, модуль и направление которой неизвестны, и парой сил, момент которой тоже неизвестен.

Решение. 1. Для определения реакций расчленим систему и рассмотрим сначала равновесие стержня DE (рис. 22, б). Проведем координатные оси XY и изобразим действующие на стержень силы: силу  , реакцию  , направленную перпендикулярно стержню и составляющие   и   реакции шарнира D. Для полученной плоской системы сил составляем три уравнения равновесия:

            ,                    ;                                 (1)

            ,                    ;                                          (2)

           ,          .                             (3)

2. Теперь рассмотрим равновесие угольника (рис. 22, в). На него действуют сила давления стержня  ’, направленная противоположно реакции  , равномерно распределенная нагрузка, которую заменяем силой  , приложенной в середине участка KB (численно  ), пара сил с моментом М и реакция жесткой заделки, складывающаяся из силы, которую представим составляющими  ,  , и пары с моментом 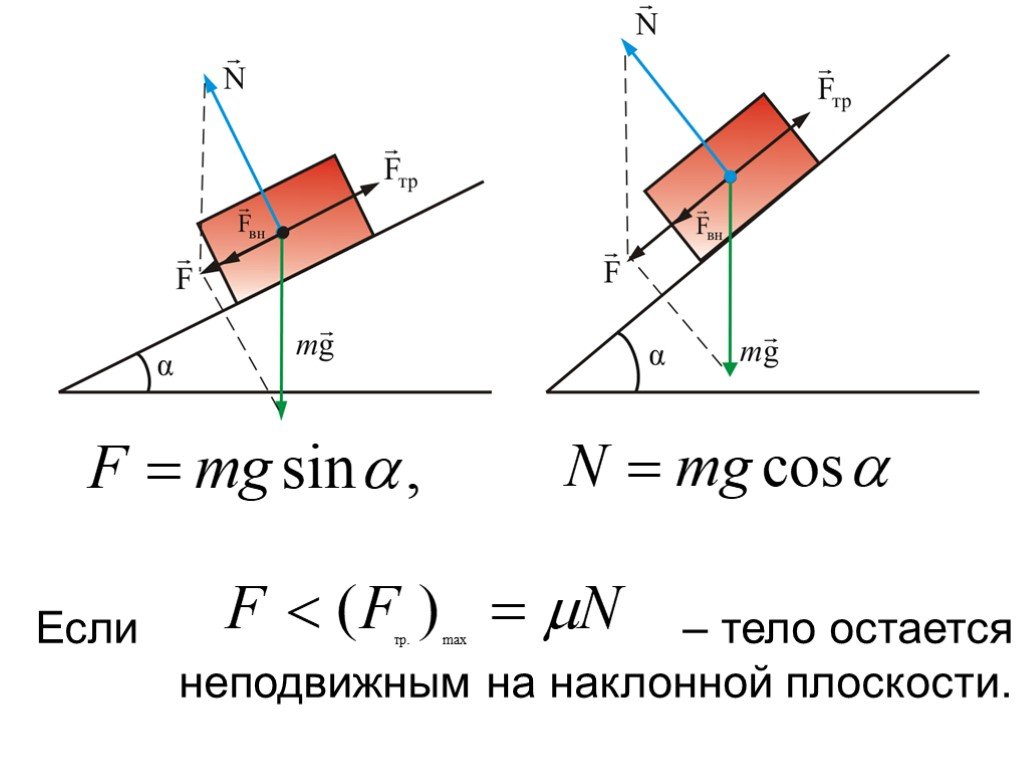 . Для этой плоской системы сил тоже составляем три уравнения равновесия:

            ,             ;                                                                     (4)

            ,             ;                                                                       (5)

             ,         .             (6)

При вычислении момента силы  ’ разлагаем её на составляющие  ’₁ и  ’₂ и применяем теорему Вариньона. Подставив в составленные уравнения числовые значения заданных величин и решив систему уравнений (1) — (6), найдем искомые реакции. При решении учитываем, что численно N = N в силу равенства действия и противодействия.

Ответ:  N= 21,7 кН;  Y_D= -10,8 кН;  Х_D= 8,8 кН;  Х_A= -26,8 кН; y_A= 24,7 кН;  М_A= -42,6 кНм.                     

Знаки указывают, что силы  , _A и момент М_A направлены противоположно показанным на рисунках.

 

Пример 11.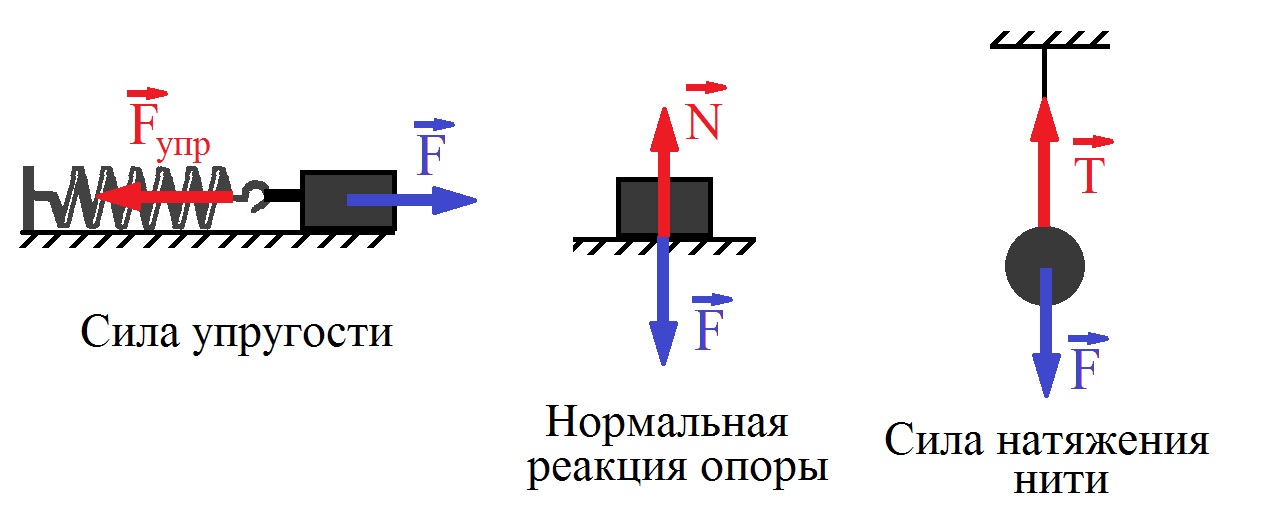  Найти реакции опор конструкции. Схема конструкции показана на рисунке 23.

Дано: Q=2 кН, G=1 кН, а=15 см, b=10 см, с=20 см, R=20 см, r=5 см,  ,  ,  ,  .

 

Рис. 23

 

Решение: К конструкции приложены сила тяжести  , силы   и реакции опор  шарниров   и  :   (рис. 24)

Рис. 24

 

Из этих сил пять неизвестных. Для их определения можно составить пять уравнений равновесия.

Уравнения моментов сил относительно координатных осей:

           ;

           ;

           ;            кН.

           ;

            ;        кН.

            ;

             ;               кН.

Уравнения проекций сил на оси координат:

             ;

              кН

            ;

            кН.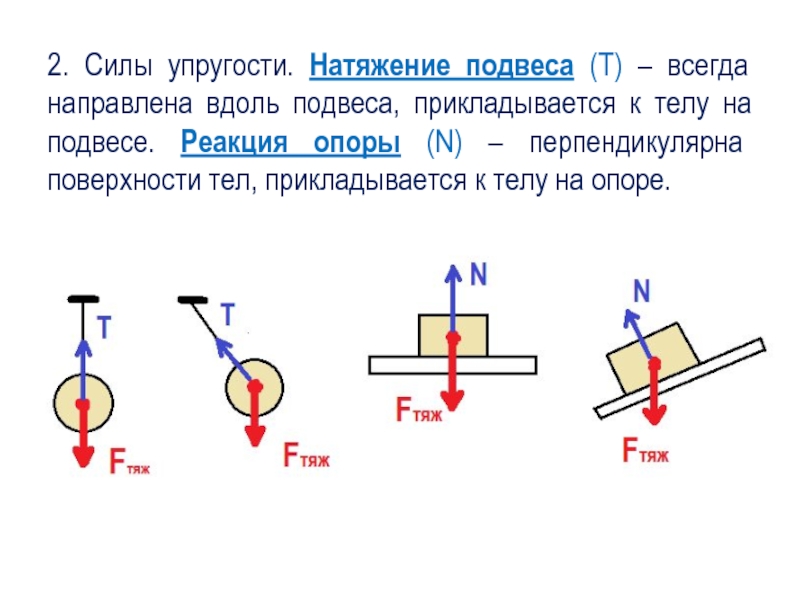

Ответ:    =0,43 кН,  =1,16 кН,  =3,13 кН,  =-0,59 кН,  =3,6 кН

 

 

Пример 12.

Конструкция состоит из жесткого угольника АЕС и стержня СК, которые в точке С (рис. 25) соединены друг с другом с помощью цилиндрического шарнира. Внешними связями являются: в точке А  шарнирно-неподвижная опора, в точке В  невесомый стержень ВВ, в точке D  шарнирно-подвижная опора. К конструкции приложена сила  , пара сил с моментом М и равномерно распределенная на участке  КВ  нагрузка интенсивности q.

Дано: F = 10 кН,  = 60, q = 20 кН/м, М = 50 кНм, а = 0,5 м.

Определить реакции связей в точках А, В, С и D, вызванные заданными нагрузками.

 

Рис.  25

 

Решение.   Для определения реакций расчленим систему по шарниру С и рассмотрим сначала равновесие стержня КС (рис. 26). Проведем координатные оси ху и изобразим действующие на стержень силы: равномерно распределенную нагрузку заменим силой  , приложенной в середине участка ВК (численно   кН), реакцию   стержня ВВ направим вдоль этого стержня, а действие отброшенного угольника АЕС представим составляющими    и  реакции шарнира С.

Рис. 26

 

Для полученной плоской системы сил составляем три уравнения равновесия:

                                      (1)

                                       (2)

                                     (3)

При вычислении момента силы   разлагаем ее на составляющие   и   и применяем теорему Вариньона ( ,  ) из уравнения (3) находим:

                 

                 

Из уравнения (1) следует:

                   

                

Из уравнения (2) следует:

              

               

КОЕ-КАКИЕ РАСЧЕТЫ | Наука и жизнь

На камень, скользящий по воде, действуют сила тяжести P, сила трения Fтр и сила нормального давления N. Она раскладывается на силу сопротивления Fc и силу реакции опоры Fр, которая компенсирует вес камня и не дает ему утонуть.

Открыть в полном размере

‹

›

Оценим минимальную скорость броска, необходимую для того, чтобы камень подпрыгнул хотя бы один раз.

Если камень массой m брошен со скоростью V, то в момент удара о поверхность воды на него действуют сила тяжести Р = mg и сила реакции опоры F_р = kSV², где S — площадь контакта камня с поверхностью воды, k — коэффициент, имеющий размерность плотности. Его величина зависит от формы камня, угла наклона плоскости камня к поверхности воды и угла между траекторией полета и поверхностью воды (угол падения α).

Если считать углы малыми, то для круглого камня радиусом r можно приближенно записать F_р = kr²V², где k 500 кг/м³. Камень подскочит, если сила реакции опоры больше силы тяжести: F^p > Р. Отсюда получаем условие подпрыгивания камня: V > V_min = √Mg/kr², где V_min — минимальная скорость броска.

Таким образом, чем тяжелее камень и чем меньше его радиус, тем с большей скоростью надо его бросать. Вот почему лучше брать довольно большие, но легкие камни. Пример. Чтобы камень радиусом 5 см и массой 100 г подпрыгнул хотя бы раз, его нужно бросить со скоростью больше 0,5 м/с (2 км/ч), камень радиусом 2,5 см и той же массой — больше 1 м/с (4 км/ч). А если взять камень радиусом 2,5 см и массой 50 г, его начальная скорость должна быть больше 0,7 м/с (2,8 км/ч).

Теперь оценим максимально возможное число подпрыгиваний камня при заданной скорости броска.

При каждом ударе о воду камень теряет энергию ∆Е (в основном за счет трения о воду), величину которой можно считать постоянной для каждого удара, так как она не зависит от скорости полета камня и определяется только его массой (по типу сухого трения). Не будет большой ошибкой предположить, что после последнего N-го удара кинетическая энергия камня станет равна 0 (хотя в действительности это не совсем так), то есть: N∆E = mV²/2.

Отсюда получаем формулу для оценки максимального числа подскоков камня: N = mV2/2∆E. Из этой формулы следует, что, бросив камень вдвое быстрее, можно учетверить количество подскоков.

Расчеты, выполненные Л. Боке, показали, что для камня радиусом 5 см и массой 100 г, брошенного так, что угол наклона его плоскости к поверхности воды α = 10°, потеря энергии при каждом ударе ∆E = 0,2 Дж. Тогда, если начальная скорость V = 6,3 м/с, максимальное число подскоков N = 10. Чтобы повторить мировой рекорд (N = 40) с помощью такого камня, надо запустить его со скоростью примерно 12,6 м/с с углом наклона 10°.

Оценим теперь, как влияет скорость вращения камня на максимальное число подскоков. Несмотря на стабилизирующее действие гироскопического эффекта, каждый удар о воду смещает положение оси вращения камня на угол δθ, приближенно равный g/rω2, где r — радиус камня, ω — скорость его вращения. Для многократного подпрыгивания необходимо, чтобы угол δθ был очень малым, то есть ω >> √g/r. Поэтому следует брать камень большого радиуса и закручивать его как можно сильнее.

После N-го удара ось оказывается смещена на угол Nδθ. Если в качестве условия полной дестабилизации положить угол смещения оси 90° – α (камень повернулся ребром к поверхности воды), то Nδθ = /2–α, то максимальное число подскоков N = (/2–α)δθ. Как показали эксперименты Боке, для оценки числа подскоков достаточно положить Nδθ = 1. Отсюда N = 1/δθ = rω2/g, ω = √gN/r.

Согласно полученной оценке, для достижения мирового рекорда камень радиусом 5 см нужно закрутить со скоростью не меньше 14 оборотов в секунду (полный оборот равен 2 радиан). Проверьте!

Использованная литература

Bocquet L., Witkowski N. L’art des ricochets // La Recherche, № 365, 2003.

Bocquet L. Physics of stone skipping // American Journal of Physics, 2002.

См. в номере на ту же тему

А. ЗАЙЦЕВА — «Блинчики» на воде по-научному.

«Прыгающая» бомба.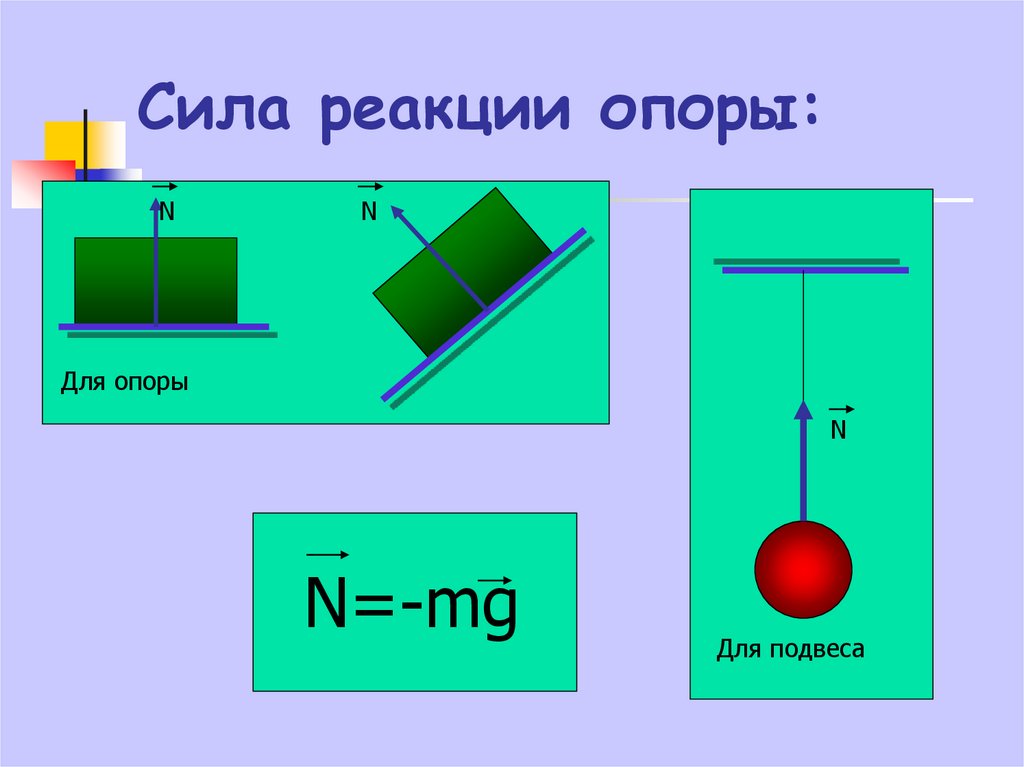

Вокруг света «прыжками».

Фиксированная балка – определение, прогиб, формула и преимущества

Что такое фиксированная балка?

Неподвижная балка — это балка, закрепленная на обоих концах фиксированными опорами. Фиксированные балки используются в конструкции, потому что они имеют много преимуществ по сравнению с обычными балками. Это неопределенный луч, потому что он имеет более одной избыточной реакции.

Фиксированная балка обеспечивает дополнительную устойчивость конструкции. Таким образом, конструкция становится более жесткой и устойчивой. Такие балки используются, чтобы выдерживать горизонтальные и вертикальные нагрузки на конструкцию.

Загрузить заметки/формулы для исследования структурного анализа

Преимущества неподвижной балки

Неподвижные балки имеют много преимуществ по сравнению с свободно опертыми балками. Здесь упоминаются некоторые преимущества.

• Обладает большей грузоподъемностью, чем свободно опертая балка при тех же условиях нагрузки.
• Имеет меньшее значение максимального прогиба, чем у свободно опертой балки.
• Максимальный изгибающий момент меньше, чем у свободно опертой балки.
• Наклон неподвижных балок на обоих концах равен нулю.

Прогиб в неподвижной балке

В фиксированной балке прогиб является важным параметром, определяющим грузоподъемность балки. Прогиб такой балки зависит от типа нагрузки и распределения нагрузки по балке. Прогиб балки также зависит от свойств поперечного сечения балки и свойств материала.

Прогиб неподвижных балок под действием равномерно распределенной нагрузки-

Формула изгибающего момента для неподвижных балок

Изгибающий момент неподвижной балки — это расчетный параметр, представляющий общую прочность балки на изгиб. Изгибающий момент – это сопротивление балки ее вращению вокруг продольной оси.

Изгибающий момент для неподвижной балки при равномерно распределенной нагрузке-

Что такое Степень неопределенности неподвижных балок?

Поскольку мы знаем, что неподвижные балки опираются на неподвижную опору с обоих концов, а также мы знаем, что неподвижная опора в общем случае имеет три числа реакций. Эти реакции включают одномоментную реакцию, одну горизонтальную реакцию и одну вертикальную реакцию.

Степень неопределенности — превышение количества реакций, не найденных при числе уравнений равновесия. Так, для наклонного нагружения Степень неопределенности равна (3+3)-3=3, а для вертикального нагружения Степень неопределенности равна (2+2)-2=2.

Условия совместимости в фиксированных балках

Для понимания параметра используются неопределенные уравнения совместимости балок. Условия совместимости неподвижных балок — это те уравнения, которые необходимы для решения неизвестных балок; эти условия учитывают равновесие смещения балки или конструкции. Совместимость просто означает, что не должно быть отклонений более чем в одном направлении в конкретном соединении неопределенной конструкции.

Условия совместимости в фиксированных балках используются для решения параметра отклонения балки. Эти уравнения включают уравнения смещения и наклона в любой точке балки. Эти уравнения основаны на критериях уклона на неподвижной опоре балки и прогиба на защемленных опорах, равных нулю.

Фиксированная балка с внутренним шарниром

Фиксированная балка — это балка, поддерживаемая с обоих концов фиксированной опорой. Следовательно, это так называемый неопределенный луч. Неопределенный луч – это луч, степень определенности которого больше единицы. Внутренний шарнир представляет собой простой шарнир, расположенный в центре балки. Внутренний шарнир обеспечивает свободное вращение балки вокруг точки, в которой она находится.

Внутренний шарнир в неподвижной балке обеспечивает дополнительное уравнение совместимости; с его помощью в пучке можно найти еще одну реакцию. Таким образом, внутренний шарнир уменьшает неопределенность балки за счет уменьшения избыточной реакции балки.

SFD и BMD для фиксированных балок

SFD и BMD для фиксированных балок представляют собой диаграммы поперечной силы и изгибающего момента соответственно по длине балки. SFD и BMD для фиксированных балок будут зависеть от изменения нагрузки по длине балки. Форма SFD и BMD зависит от условий нагружения и типа нагрузки на балку.

Напишите уравнение или формулу

Используйте Word для школы

Справка и обучение Word

Используйте Word для школы

Используйте Word для школы

Напишите уравнение или формулу

• Напишите уравнение или формулу
  Статья
• Отступ первой строки абзаца
  Статья
• Двойной интервал между строками в документе
  Статья
• Создайте библиографию, цитаты и ссылки
  Статья
• Вставка сносок и концевых сносок
  Статья

Следующий: Улучшить доступность и простоту использования

1. org/ListItem»>

   Выберите Вставьте > Уравнение или нажмите Alt + =.

2. Выберите нужное уравнение.

3. Подробнее см. на ленте Конструкции и Преобразование вариантов .

Чтобы ввести уравнение с нуля, нажмите Alt += на клавиатуре.

или

Вставить > Уравнение > Вставить новое уравнение .

Используйте палец, стилус или мышь, чтобы написать уравнение.

Дополнительные параметры Structures и Convert см. на ленте.

Добавить уравнение в галерею уравнений

org/ItemList»>

1. Выберите уравнение, которое хотите добавить.

2. Щелкните стрелку вниз и выберите Сохранить как новое уравнение… .

3. Введите имя уравнения в поле Диалоговое окно «Создать новый стандартный блок» .

4. Выберите Уравнения в списке галереи.

5. Выберите OK .

Чтобы изменить или отредактировать ранее написанное уравнение,

1. Выберите уравнение, чтобы увидеть Инструменты для уравнений на ленте.

   Примечание. Если вы не видите Инструменты для формул , формула могла быть создана в более старой версии Word. Если это так, см. раздел Изменение уравнения, написанного в предыдущей версии Word.

2. Выберите Дизайн , чтобы увидеть инструменты для добавления различных элементов в уравнение. Вы можете добавить или изменить следующие элементы в своем уравнении.

   • В группе Символы вы найдете математические символы. Чтобы увидеть все символы, нажмите кнопку Еще . Чтобы увидеть другие наборы символов, нажмите на стрелку в правом верхнем углу галереи.

   • Группа Структуры содержит структуры, которые можно вставлять. Просто выберите структуру, чтобы вставить ее, а затем замените заполнители, маленькие прямоугольники с пунктирными линиями, своими собственными значениями.

   • Professional 9Опция 0121 отображает уравнение в профессиональном формате, оптимизированном для отображения. Параметр Linear отображает уравнение как исходный текст, который можно использовать для внесения изменений в уравнение, если это необходимо. Линейная опция будет отображать уравнение либо в формате UnicodeMath, либо в формате LaTeX, который можно установить в блоке Conversions.

   • Можно преобразовать все уравнения в документе в профессиональный или линейный форматы или только одно уравнение, если выбрана математическая зона или курсор находится в уравнении.

На устройствах с сенсорным экраном и пером вы можете писать уравнения с помощью стилуса или пальца. Чтобы писать уравнения чернилами,

1. org/ListItem»>

   Выберите Draw > Ink to Math Convert и затем нажмите Ink Equation в нижней части встроенной галереи.

2. Используйте стилус или палец, чтобы написать математическое уравнение от руки. Если вы не используете сенсорное устройство, используйте мышь, чтобы написать уравнение. Вы можете выбирать части уравнения и редактировать их по ходу работы, а также использовать окно предварительного просмотра, чтобы убедиться, что Word правильно интерпретирует ваш почерк.

3. Когда вы будете удовлетворены, нажмите Вставьте , чтобы преобразовать уравнение рукописного ввода в уравнение в вашем документе.