По расчетным схемам определить реакции опор

Автор admin На чтение 10 мин Просмотров 2 Опубликовано 8 апреля 2023 Обновлено 8 апреля 2023

Содержание

1. Как определить реакции опор или найти опорные реакции: для балки или рамы
2. Что такое реакция опоры или опорная реакция?
3. Зачем определять реакции опор?
4. Пример определения опорных реакций для балки
5. Первое уравнение равновесия
6. Второе уравнение равновесия
7. Третье уравнение равновесия
8. Вычисление реакций опор
9. iSopromat.ru
10. Задача
11. Пример решения
12. Определение реакций опор балки – решение задачи
13. Как определить реакции опор балки
14. Пример решения задачи на определение реакций опор балки
15. Решение задачи
16. Уравнения равновесия для сил
17. Уравнения равновесия для моментов
18. Решение уравнений равновесия
19. Проверка правильности решения
20. Второй способ решения

Как определить реакции опор или найти опорные реакции: для балки или рамы

Что такое реакция опоры или опорная реакция?

Реакция опоры или опорная реакция – это силовой фактор, возникающий в опоре, от действия на конструкцию внешней нагрузки. В опорах, как правило, возникают реактивные силы, которые для удобства ручного расчета раскладываются на две составляющие: вертикальную и горизонтальную проекции. В жестких заделках, которые ограничивают все степени свободы конструкций, в том числе поворот сечений, также могут появляться реактивные моменты.

Зачем определять реакции опор?

На элементы конструкций всегда наложены какие-то связи, в виде опор, жестких заделок, стержней, которые ограничивают степени свободы конструкций. Под действием внешней нагрузки в этих связях возникают реакции. И эти реакции опор нужно обязательно учитывать при расчетах на прочность, жесткость и т. д., так как они являются внешними нагрузками. Практически любая задача по сопромату начинается с нахождения реакций связей, именно поэтому статья будет одной из первых на этом сайте.

Пример определения опорных реакций для балки

Давайте рассмотрим пример, на котором я покажу как определяются реакции опор. Причем, постараюсь объяснить максимально просто, буквально на пальцах.

Возьмем простую балку, загруженную сосредоточенной силой F, под действием которой в опорах появляются реакции R_A и R_B. Также сразу вводим систему координат x, y:

Чтобы узнать численное значение эти реакций, воспользуемся первой формой уравнений равновесия:

Первое уравнение равновесия

Записываем первое уравнение. Так как оси x не параллельна ни одна из сил, то соответственно сумма проекций сил на эту ось будет равна нулю:

Таким будет первое уравнение для этой расчетной схемы.

Второе уравнение равновесия

Второе уравнение, связанно с проекциями на вертикальную ось. Здесь все намного лучше, все силы параллельны этой оси, а значит дадут проекции. Вопрос только с каким знаком, каждая сила пойдет в уравнение. Если направление силы, совпадает с направлением оси, то в уравнение она пойдет со знаком «плюс» (R_A и R_B). Если же сила направленна в противоположную сторону, как F, в нашем случае, то в уравнении будем записывать ее с минусом.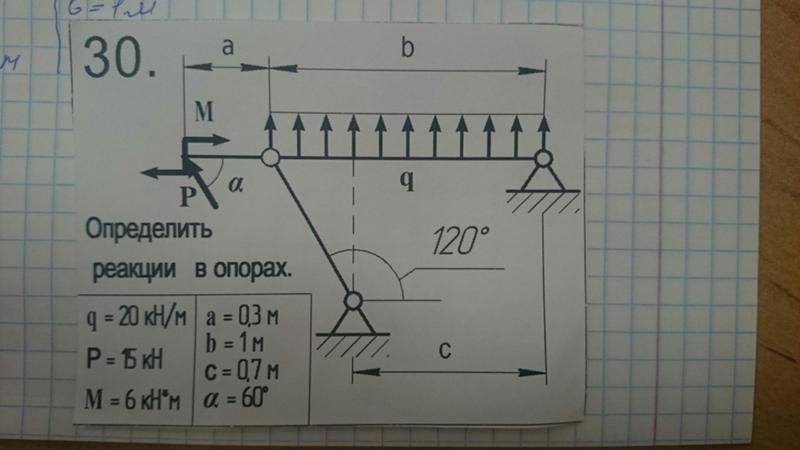 Таким образом, получим второе уравнение равновесия:

Как видите, во втором уравнении у нас находится 2 неизвестные реакции. Чтобы, наконец, решить задачу, давайте запишем третье уравнение равновесия.

Третье уравнение равновесия

Это уравнение отличается от первых двух, так как тут речь идет о моментах. Напомню, момент – это произведение силы на плечо. В свою очередь, плечо – это перпендикуляр, опущенный от центра момента до линии действия силы. То есть это кратчайшее расстояние от центра момента до силы. В качестве центра моментов у нас назначена точка A, по условию сумма моментов всех сил должна быть равна нулю относительно этой точки.

Начинаем рассуждать и записывать уравнение. Реакция R_A не дает момента, относительно точки А, так как линия действия этой силы пересекает эту точку и соответственно плечо равно нулю. А там, где нет плеча, нет и момента.

Сила F, относительно точки А, создает момент равный:

Обратите внимание, плечо в данном случае равно 2 метрам. Кроме того, важен знак момента, для этого традиционно используется правило, которое продвинутым студентам известно еще с теоретической механики:

• Если сила, относительно произвольного центра, поворачивает ПРОТИВ часовой стрелки, то момент силы положительный;
• Если сила, относительно произвольного центра, поворачивает ПО часовой стрелке, то момент силы отрицательный.

Для силы F, как видите, момент отрицательный:

Реакция опоры — R_B, создает момент равный R_B · 4, так как сила поворачивает против часовой стрелки, то в уравнение записываем его со знаком плюс:

Вычисление реакций опор

Вот собственно и все, все уравнения составлены. Теперь осталось только решить их и найти искомые значения реакций опор (F=2 кН):

В этой статье, мы рассмотрели достаточно простой пример. Если вы хотите развить свои навыки по определению реакций опор, узнать различные хитрости по их нахождению, научится определять реакции, когда на конструкцию действуют силы под различными углами, учитывать в уравнениях сосредоточенные моменты и распределенную нагрузку, приступайте к изучению статьи – как определить реакции опор для балки.

Источник

iSopromat.ru

Пример решения задачи по расчету опорных реакций балки, закрепленной на двух шарнирных опорах и нагруженной сосредоточенной силой F, моментом m и равномерно распределенной нагрузкой q.

Задача

Для заданной двухопорной балки с консольной частью, нагруженной комплексом нагрузок: силой F, моментом m и распределенной нагрузкой q, определить величину и направление опорных реакций.

Длина пролета балки 3м. Длина консольной части – 1,5м.

Пример решения

Рекомендуем посмотреть наш видеоурок. В нем мы постарались подробно показать порядок расчета реакций в опорах балки.

Для решения задачи, обозначим характерные точки (сечения) балки (точки A, B, C и D) и определим положение системы координат y-z, выбрав ее начало например в т. A (рис.2)

Обе опоры балки являются шарнирными, поэтому в каждой из них будет возникать только сила, обозначим их соответственно R_A и R_C

Так как все заданные нагрузки раположены исключительно в вертикальной плоскости (плоский поперечный изгиб) и не дают проекций на ось z, то опорные реакции будут тоже только вертикальными.

Вообще говоря, реакции в опорах являются такими силами, которые необходимы для удержания балки с приложенными к ней нагрузками, в статичном (неподвижном) состоянии. В данном случае эти силы не позволяют ей вращаться и перемещаться в вертикальной плоскости.

Данная балка является статически определимой, т.к. уравнений равновесия достаточно для определения неизвестных усилий в опорах балки.

Для составления уравнений статики, опорные реакции R_A и R_C предварительно направляются произвольно, например, вверх (рис.3).

Для определения двух неизвестных реакций потребуется два уравнения.

Здесь сумму моментов лучше записывать относительно точки расположенной на опоре (например, A), т.к. в этом случае соответствующая реакция R_A в уравнении не участвует.

Из выражения (2) определяем R_C:

и подставив его в выражение (1) находим R_A:

Направление и величина реакций, как правило, необходимы для дальнейших расчетов балки на прочность и жесткость, поэтому во избежание возможных ошибок рекомендуется выполнять проверку найденных значений.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Определение реакций опор балки – решение задачи

Как определить реакции опор балки

Пример решения задачи на определение реакций опор балки

Жесткая балка, линейные размеры которой указаны на рисунке 1, закреплена в точках А и В. На балку действуют пара сил с моментом М, равномерно распределенная нагрузка интенсивностью q и две силы P и G, место приложения которых показано на рисунке.
Определить реакции опор балки в точках A и B, вызываемые указанными нагрузками.

Дано:
P = 20,2 Н ; G = 22,6 Н ; q = 2 Н/м ; M = 42,8 Н·м ; a = 1,3 м ; b = 3,9 м ; α = 45° ;

Решение задачи

Проводим оси x и y системы координат. Начало системы координат поместим в точку A . Ось x направим горизонтально, вдоль балки. Ось y – вертикально. Ось z перпендикулярна плоскости рисунка и направлена на нас.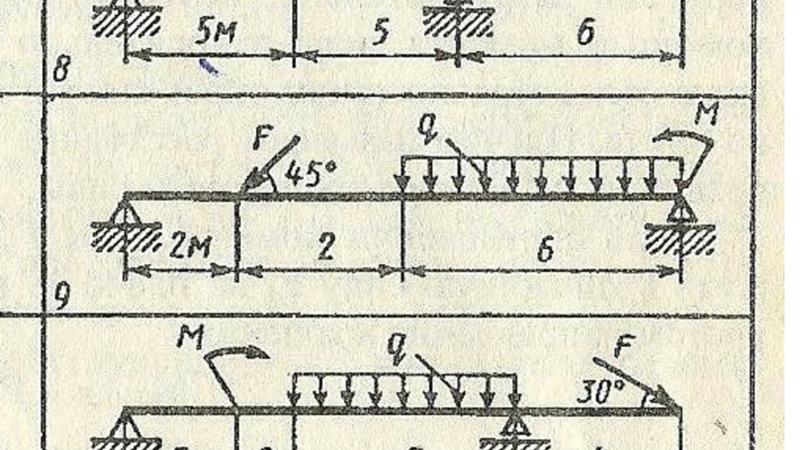 На рисунке она не указана.

Силы, действующие на балку.

Отбрасываем опоры и заменяем их силами реакций.
В шарнире A , разложим силу реакции на составляющие и вдоль осей координат.
Реакция , в подвижной опоре на катках, направлена вертикально. Предполагаемые направления реакций опор выбираем по своему усмотрению, наугад. Если ошибемся с направлением реакции, то получим отрицательное значение, что будет говорить о том, что соответствующая сила реакции направлена в противоположную сторону.

Заменим равномерно распределенную нагрузку q равнодействующей . Абсолютное значение равнодействующей равно площади эпюры:
Н .
Точка приложения равнодействующей находится в центре тяжести эпюры. Поскольку эпюра представляет собой прямоугольник, то ее центр тяжести находится в точке C – посередине отрезка AD :
AC = CD = b/2 = 1,95 м .

Уравнения равновесия для сил

Определяем проекции сил на оси координат.

Разложим силу на составляющие вдоль координатных осей:
.
Абсолютные значения составляющих:
.
Вектор параллелен оси x и направлен в противоположную от нее сторону. Вектор параллелен оси y и также направлен в противоположную сторону. Поэтому проекции силы на оси координат имеют следующие значения:
.

Остальные силы параллельны осям координат. Поэтому они имеют следующие проекции:
;
;
;
;
.

Составляем уравнения равновесия для сил.
Сумма проекций всех сил на ось x равна нулю:
;
;
;
(П1) .

Сумма проекций всех сил на ось y равна нулю:
;
;
;
(П2) .

Уравнения равновесия для моментов

Итак, мы уже составили два уравнения для сил: (П1) и (П2). Но в них есть три неизвестные величины: , и . Чтобы их определить, нам нужно составить еще одно уравнение.

Составим уравнение равновесия для моментов сил. Для этого нам нужно выбрать ось, относительно которой мы будем вычислять моменты. В качестве такой оси возьмем ось, проходящую через точку A , перпендикулярно плоскости рисунка. За положительное направление выберем то, которое направлено на нас. Тогда, по правилу правого винта, положительным направлением закручивания будет направление против часовой стрелки.

Находим моменты сил относительно выбранной оси.
Силы , и пересекают ось. Поэтому их моменты равны нулю:
; ; .

Сила перпендикулярна плечу AB . Ее момент:
.
Поскольку, относительно оси A , сила направлена против часовой стрелки, то ее момент положительный.

Сила перпендикулярна плечу AK . Поскольку, относительно оси A , эта сила направлена по часовой стрелки, то ее момент имеет отрицательное значение:
.

Аналогичным способом находим моменты остальных сил:
;
.
Момент от пары сил M не зависит от точек приложения сил, входящих в пару:
.

Составляем уравнение равновесия. Сумма моментов сил относительно оси A равна нулю:
;

;
;
(П3) .

Решение уравнений равновесия

Итак, для трех неизвестных величин, мы получили три уравнения:
(П1) .
(П2) .
(П3) .

Решаем эти уравнения. Вычисляем расстояния.
м;
м;
м;
м.

Из уравнения (П1) находим:
Н.
Из уравнения (П3) находим:

Н.
Из уравнения (П2) имеем:
Н.
Абсолютное значение реакции опоры в точке A :
Н.

Проверка правильности решения

Чтобы проверить, правильно ли мы определили реакции опор балки, найдем сумму моментов сил относительно другой оси. Если мы нашли реакции правильно, то она должна равняться нулю.

Возьмем ось, проходящую через точку E . Вычисляем сумму моментов сил относительно этой оси:

.
Найдем погрешность вычисления суммы моментов. Найденные силы мы округлили до двух знаков после запятой. То есть погрешность определения реакций опор составляет 0,01 Н . Расстояния, по порядку величины, примерно равны 10 м. Тогда погрешность вычисления суммы моментов составляет около 10·0,01 = 0,1 Нм . Мы получили значение -0,03 Нм . Эта величина отличается от нуля не более, чем на величину погрешности. То есть, с учетом погрешности вычислений, сумма моментов относительно другой оси равна нулю. Значит решение правильное, силы реакций найдены верно.

Второй способ решения

Первым способом мы составили два уравнения для сил и одно – для моментов. Задачу можно решить другим способом, составив два уравнения для моментов и одно для сил.

Воспользуемся тем, что сумма моментов сил равна нулю относительно любой оси. Возьмем вторую ось, которая проходит через точку B перпендикулярно плоскости рисунка. Сумма моментов сил относительно этой равна нулю:
.
Вычисляем моменты сил относительно оси B .
; ; ;
;
;
;
;
.

Сумма моментов сил относительно оси B равна нулю:
;

;
;
(П4) ;

Итак, вторым способом, мы также имеем три уравнения:
(П1) .
(П3) ;
(П4) .

Здесь каждое уравнение содержит только одну неизвестную величину. Реакции и определяются из тех же уравнений, что и ранее.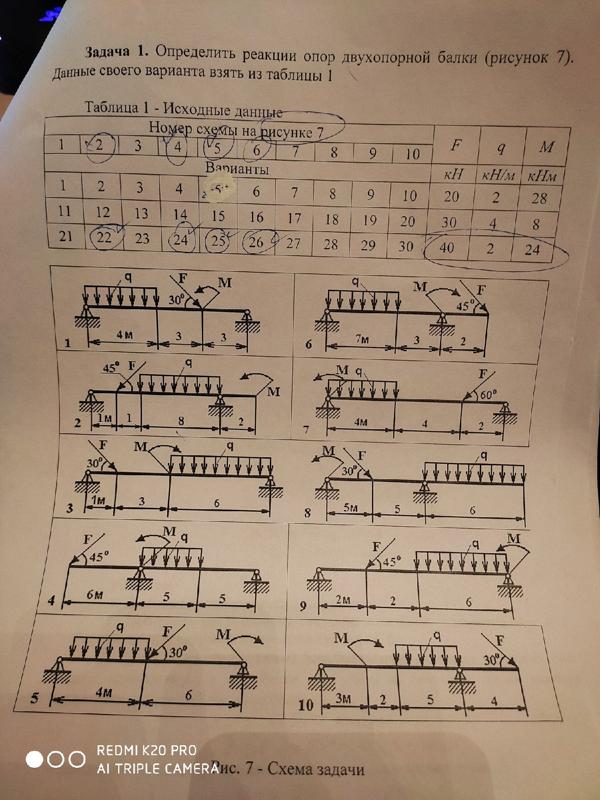 Находим силу из уравнения (П4):

Н.

Значение реакции совпало со значением, полученным первым способом из уравнения (П2).

Автор: Олег Одинцов . Опубликовано: 14-10-2017 Изменено: 28-12-2021

Источник

Как определить реакции на опорах при расчете в ПК Лира

Есть такая сложность в проектировании, о которой я не раз писала. Это конструирование узлов опирания. Как бы правильно ни был посчитан и законструирован несущий элемент, если с опорами просчет – конструкция рискует стать аварийной. И чем легкомысленней относиться к узлам, тем больше риск.

Думала я думала, и решила показать, как нагрузка в местах опирания выглядит в тоннах. Солидно выглядит, я вам скажу. На видео ниже вы сами убедитесь: обыкновенная, не особо массивная монолитная лестница (толщина всего-то 150 мм) дает вертикальную нагрузку на одной опоре в размере 7 тонн! И эти семь тонн должна воспринять стена, не разрушившись. Мало того, лестница давит вниз именно с силой 7 тонн, и если опора не надежна (допустим, повесили на забитых в стену арматурных стержнях), вся эта масса будет настойчиво и упорно пытаться рвануть к земле.

И дай Бог, чтобы у нее не получилось!

Зачем я пишу эту статью? Чтобы вы запомнили: всегда, при любых конструкциях, нужно выяснять реакции на опорах и конструировать узлы с учетом этих реакций. В видео я дала инструмент, как можно определить реакцию в Лире. Вводите в расчет конечный элемент КЭ56, который моделирует опору (связи при этом нужно убрать), выполняете расчет и смотрите реакции в каждом элементе (оптимально, если сгенерированы РСН, а то придется суммировать реакции по всем загружениям). Если элементов больше одного, суммируете. И получаете искомую реакцию.

А подробнее в видео.

Есть и другие способы определить реакции на опорах. Не так важно, каким именно вы пользуетесь. Главное — пользуйтесь!

Видео-курсы

Видео-курс «Расчет столбчатых фундаментов на естественном основании»

Этот курс записан после того, как за довольно короткий срок я узнала, как много проектировщиков не знают элементарного и не делают тех расчетов, которые обязаны делать. Ситуация, честно говоря, отвратительная и ведет к медленному, но верному разрушению того, что вот так вот, спустя рукава, напроектировано.

Подробнее

Видео-курс «Расчет каркаса просто и быстро»

Видео-курс Ирины Михалевской, записанный для чертежника, который никогда не делал расчеты. Сразу после курса он начал брать заказы и зарабатывать совсем другие деньги за свою работу, хотя пришел ко мне с сомнениями — не имея опыта, он боялся, что расчеты в Лире чересчур сложны для начинающих (и не зря, но есть обходной путь).

Подробнее

Видео-курс «Азы проектирования коттеджей»

Видео-практикум по проектированию коттеджа с рассмотрением различных вариантов обогатит ваш опыт и даст возможность получить комплексное представление обо всех этапах расчета, отработав его на практике. Авторский курс Ирины Михалевской сделает для вас проектирование коттеджей понятным и доступным, даже если вы только начинаете свой путь конструктора.

Подробнее

Видео-курс «Интересные лестницы из монолитного железобетона»

31 видео, раскрывающие суть проектирования монолитных лестниц сложной формы. Цикл видео, в котором я делюсь опытом проектирования непростых лестниц — расчеты, конструирование, решение проблем. Концентрация полезной информации, которая не будет пылиться без дела. Проектировщики таких лестниц востребованы как никогда, конкуренции нет, а спрос всегда имеется. Успейте занять пустующую нишу и пополнить свою копилку знаний непростыми решениями.

Подробнее

Видео-курс «Грамотные чертежи КЖ»

Курс про то, что должно быть в чертежах КЖ, чтобы они были исчерпывающе качественными, грамотными и без критических ошибок. Упор на конструирование и содержание чертежей.

Подробнее

Видео-курс «Инструкция по сбору нагрузок»

Авторский курс Ирины Михалевской сделает для вас сбор нагрузок понятным и простым, даже если вы до этого никогда не пытались вникнуть в эту тему. Что вы откроете для себя в курсе? Принципы сбора нагрузок для любой расчетной схемы — вы не просто получите много примеров для разных конкретных случаев, но и поймете в общем, как действовать в любых ситуациях.

Подробнее

Последняя статья на сайте

Видео-курс «Инструкция по сбору нагрузок»

Авторский курс Ирины Михалевской сделает для вас сбор нагрузок понятным и простым, даже если вы до этого никогда не пытались вникнуть в эту тему.

Что вы откроете для себя в курсе?

Принципы сбора нагрузок для любой расчетной схемы — вы не просто получите много примеров для разных конкретных случаев, но и поймете в общем, как действовать в любых ситуациях.

Прочитать статью

Новые статьи

• Видео-курс «Инструкция по сбору нагрузок»
• Видео-курс «Грамотные чертежи КЖ»
• Видео-курс «Интересные лестницы из монолитного железобетона»
• Видео-курс «Азы проектирования коттеджей»
• Видео-курс «Расчет каркаса просто и быстро»
• Видео-курс «Расчет столбчатых фундаментов на естественном основании»
• Как выполнить расчет каркаса и ничего не упустить
• Мономах просто. Обучающий видео-курс. Урок 5. Колонны, балки, стены, проемы в стенах и перегородках
• Опирание монолитных плит на стены. Ответы на вопросы
• Проверка чертежей железобетонной лестницы входа. Видео с комментариями
• Проверка чертежей бассейна. Видео с комментариями
• Конструирование железобетонных лестниц с пояснениями: опалубка, армирование, примеры выполнения чертежей
• Конструирование железобетонных балок с пояснениями: опалубка, армирование, примеры выполнения чертежей.
• Мономах просто. Обучающий видео-курс. Урок 4. Перекрытия

Новое в блоге

Странные отношения с заказчиком

Иногда случаются странные вещи, и я не могу их объяснить.

Работа – работой, но отношения с людьми для меня всегда на первом месте. Нет нормальных отношений – работа тоже нормальной не будет.

Не так давно был  у меня случай. Человек нашел мой сайт, написал мне письмо и попросил помочь с двумя расчетами. Ок. Договорились о цене, сроках, выяснила все исходные данные и принялась за работу. Когда работа была выполнена, написала заказчику и сказала, что работа готова, после оплаты вышлю результаты.

Обычная вроде бы схема, никогда не подводила.

Прочитать статью

Изменение по ходу проекта – чем аукается?

Ох уж эти переделки… Иногда выучишь наизусть и содержимое чертежей, и ход их выполнения, пока десять раз переделаешь.

А знаете, чем чревато? Ошибками. Переделка – это всегда незамеченные замыленным глазом, не отловленные ошибки. Причем и проверщик не поможет: у проверщика тоже глаз замыливается…

Прочитать статью

Как у Бога за пазухой

Интересное дело. Конструктор чаще всего получает работу от архитектора, ну или от человека, выполняющего роль ГИПа – координатора между заказчиком и всеми исполнителями проекта. Напрямую от заказчика работа поступает редко и мимолетно – это обычно те люди, которые строят без проекта, но особо ответственные конструкции сами «проектировать» не рискуют.

Прочитать статью

Популярные статьи

• Как подобрать перемычки в кирпичных стенах
• Расчет металлического косоура лестницы
• Сбор нагрузок для расчета конструкций — основные принципы
• Собираем нагрузки на ленточный фундамент дома
• Как рассчитать стены из кладки на устойчивость
• Подбираем перемычки в несущих кирпичных стенах — примеры расчета
• Монолитное перекрытие
• В чем разница между шарнирным опиранием и жестким защемлением
• Расчет сечения стропил
• Монолитное перекрытие по металлическим балкам
• Чертеж котлована. Пример выполнения
• Первое и второе предельное состояние при расчете конструкций
• Сборное перекрытие или монолит?
• Монолитный пояс — что это такое и зачем он нужен?
• Как пробить проем в существующей стене?
• Как определить нагрузку на крышу в вашем районе
• Как выполнить армирование перекрытия частного дома
• Расчет кладки из газобетона на смятие под действием нагрузки от перекрытия
• Мономах просто. Обучающий видео курс.
• Армирование монолитных перекрытий в районе отверстий

Последние комментарии

Машиностроение — как определить направление опорных реакций в ферме?

$\begingroup$

Привет, я не знаю как определить направление опорных реакций в точках А и К. Я знаю, что точка А имеет штифтовую опору, поэтому она может воспринимать горизонтальные и вертикальные нагрузки, а точка К имеет роликовую опору , поэтому может воспринимать только вертикальную нагрузку. Но я не уверен, в каком направлении должны быть силы для обеих точек. Помощь будет высоко оценена.

• машиностроение
• строительство зданий
• строительство
• статика
• механика твердого тела

$\endgroup$

4

$\begingroup$

Я бы предположил, что система находится в равновесии, а точка K является опорой для фермы.

В этих расчетах ферма обычно рассматривается как единое целое, поэтому создание простой диаграммы сил значительно поможет уменьшить кажущуюся сложность.

Точка A имеет момент против часовой стрелки, а точка K — нет.

Диаграмма будет похожа на балку длиной 20… Оттуда и работайте.

$\endgroup$

$\begingroup$

Выберите направление горизонтальной и вертикальной реакции в точке A и вертикальной реакции в точке K.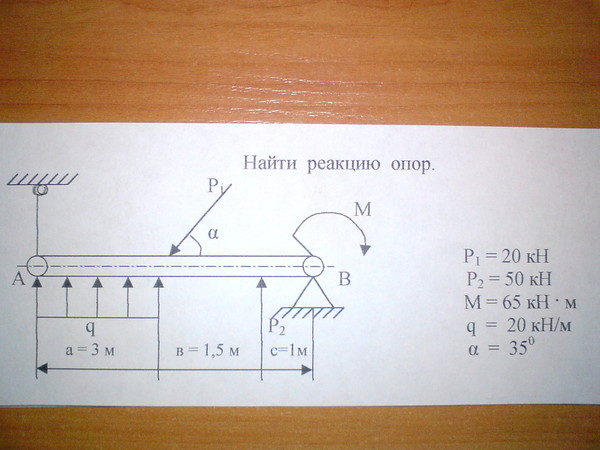 Если ответ отрицательный, вы ставите стрелку в неправильном направлении. Вам не нужно правильно выбирать направление для начала.

$\endgroup$

$\begingroup$

Другие ответы подскажут вам, как найти (мгновенно) очевидные силы в точках A и K. каждой силы и члена (это называется обозначением Боу) и построить диаграмму Кремоны

https://www.northernarchitecture.us/allowable-stress/truss-analysis.html

Преимущество этого в том, что он самоконтролируемый, элегантный и имеет всю информацию в одном сюжете

https://en.wikipedia.org/wiki/Cremona_diagram

Другими распространенными методами являются соединения (похожие на это, но немного) и сечения, которые запутывают сложные структуры. Обе верны, но диаграммы Кремоны труднее преподавать, но они гораздо более удовлетворительны. ИМХО.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Расчет реакций Задачи и решения – Гражданское строительство X

Определите реакции опор для рамы, показанной на рис. 3.20(а).

Решение
Схема свободного тела См. рис. 3.20(b).
Статическая детерминированность Рама внутренне устойчива с r =3. Следовательно, она статически определима.
Реакции опор

Определите реакции опор балки, показанной на рис. 3.21(а).

Решение
Диаграмма свободного тела См. рис. 3.21(b).
Статическая детерминированность Балка внутренне неустойчива. Он состоит из трех жестких элементов, AB; BE и EF, соединенных двумя внутренними шарнирами в точках B и E. Структура имеет r = 5 и ec = 2; поскольку r =3 + ec, структура статически определима.

Оставшиеся два уравнения равновесия теперь можно применить для определения оставшихся двух неизвестных,
Cy и Dy:

Важно понимать, что уравнения равновесия моментов включают моменты всех сил, действующих на всю конструкции, тогда как уравнения состояния моментов включают только моменты тех сил, которые действуют на часть конструкции с одной стороны внутреннего шарнира.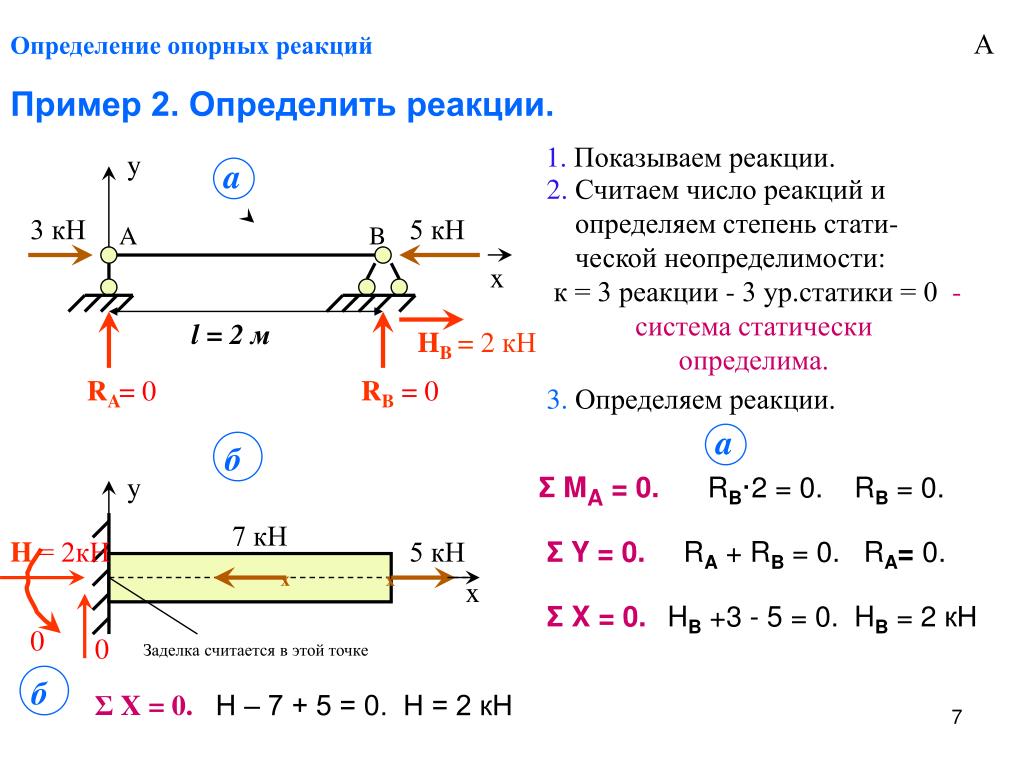
Наконец, мы вычисляем Dy, используя уравнение равновесия,

Альтернативный метод Реакции балки можно определить альтернативно, применяя три уравнения равновесия к каждой из трех жестких частей AB, BE и EF балки. Диаграммы свободного тела этих жестких частей показаны на рис. 3.21 (c). На этих диаграммах показаны внутренние силы, воздействующие на внутренние шарниры в точках B и E, в дополнение к приложенным нагрузкам и опорным реакциям. Обратите внимание, что внутренние силы, действующие на каждом конце B участков AB и BE и на каждом конце E участков BE и EF, имеют одинаковые величины, но противоположные направления, согласно закону действия и противодействия Ньютона.

Всего неизвестных (включая внутренние силы) девять. Поскольку существует три уравнения равновесия для каждой из трех жестких частей, общее количество доступных уравнений также равно девяти (r + fi = 3nr = 9). Следовательно, все девять неизвестных (реакции плюс внутренние силы) могут быть определены из уравнений равновесия, и балка статически определима. Применяя три уравнения равновесия к участку АВ, получаем следующее:

Определить реакции в опорах трехшарнирной арки, показанной на рис. 3.22(а).

Решение
Диаграмма свободного тела См. рис. 3.22(b).
Статическая детерминированность Арка внутренне неустойчива; она состоит из двух жестких частей, AB и BC, соединенных внутренним шарниром в B. Арка имеет r = 4 и ec = 1; поскольку r =3 þ ec, оно статически определимо.
Реакции опор

Определите реакции опор балки, показанной на рис. 3.23(а).,

Решение
Схема свободного тела Схема свободного тела всей конструкции показана на рис. 3.23(b).
Статическая определенность Балка внутренне неустойчива, при r = 5 и ec = 2. Поскольку r = 3 þ ec, конструкция статически определима.
Опорные реакции Используя диаграмму свободного тела всей балки, показанную на рис. 3.23(b), мы определяем реакции следующим образом:

Альтернативный метод уравнения равновесия для каждой из трех жестких частей, AC, CD и DF балки.