Растяжение (сжатие) прямого стержня — Студопедия
Поделись с друзьями:
1. Определение внутренних сил в растягиваемых и сжимаемых стержнях.
2. напряжения при растяжении (сжатии) прямого стержня. Понятие о допускаемом напряжении.
3. Определение деформаций и перемещений. Закон Гука.
4. Опытное изучение свойств материалов.
Растяжение и сжатие – это простой и часто встречающийся случай напряженного состояния элементов конструкции и деталей машин.
В таких условиях работает буксировочный канат или трос подъемного механизма, колонна здания.
Чистое (центральное) растяжение или сжатие возникает в элементе конструкции, если внешняя нагрузка вызывает в нем только одно внутреннее усилие, которое сопротивляется этой внешней нагрузке, — нормальную продольную силу.
При определении значений внутренних нормальных сил, действующих в поперечных сечениях стержней, примем следующее правило знаков:
— нормальная сила положительна, если сопротивляется растяжению стержня;
— нормальная сила отрицательна – если сопротивляется сжатию.
Для определения значений внутренней нормальной силы в любом из поперечных сечений используется метод сечений.
Пусть прямой стержень постоянной толщиной в одном конце закреплен, а к его другому торцу приложена растягивающая его вдоль оси стержня внешняя сила F.
Какое по величине внутреннее продольное усилие возникает в некотором поперечном сечении стержня n-n?
Прежде всего, отметим, что под действием закрепления и внешней силы стержень растягивается (деформируется), но никуда не движется, т.е. остается в равновесии.
Удобно вначале мысленно «снять» со стержня закрепление. Заменим его влияние на стержень эквивалентно действующей внешней силой. Эта сила равна реакции закрепления.
Т.е. в закреплении возникает некоторое усилие, благодаря которому верхний край стержня остается неподвижным. Это усилие называют реакцией закрепления на внешнюю нагрузку, передающееся на это закрепление через деформируемый стержень.
Незакрепленный стержень, теперь уже под действием двух внешних воздействий: известной силы и неизвестной пока реакции также никуда не движется, т.е. находится в равновесии.
Определить величину реакции поможет математическая формулировка этого факта.
Проведем координатную ось Оz, для удобства совпадающую с осью стержня. Стержень никуда не движется под действием силы и реакции в частности, не движется и вдоль оси, потому что проекции этих внешних сил на ось уравновешивают друг друга.
Такого рода факт в механике формулируется уравнением общего равновесия стержня: суммарная проекция на ось Оz всех действующих на стержень внешних сил, равна нулю:
При построении уравнений общего равновесия механики принято использовать следующее правило знаков:
· Проекция усилия на ось положительна, если ее направление совпадает с выбранным направлением этой оси;
· И наоборот – проекция отрицательна, если направлена в противоположную сторону.
Эпюры – графики внутренних усилий, напряжений, перемещений, деформаций, возникающих в элементах конструкций и деталях машин под воздействием внешней нагрузки.
Напряжения при растяжении (сжатии) прямого стержня
Предположим, растягивающую брус внешнюю силу удалось распределить равномерно по его торцам.
Опыты показывают. Что в этом случае каждое продольное волокно бруса подвержено только растяжению и в любом его поперечном сечении внутренние силы действуют только по нормали к этим сечениям.
Поперечные сечения бруса, плоские до деформации, под действием внешних сил перемещаются параллельно своему начальному положению и остаются постоянными.
Растягивающие стержень внешние силы не всегда удается распределить по площади стержня равномерно.
Но опыты показывают, что поведение поперечных сечений растягиваемых стержней, расположенных на некотором расстоянии от места приложения внешней нагрузки, уже не зависит от способа приложения этих сил и всегда соответствует гипотезе плоских сечений.
При рассмотрении деформаций растяжения или сжатия, а также при рассмотрении последующих простых деформаций нами будет рассматриваться принцип Сен-Венана, названный по имени французского ученого XIX века, который заключается в том, что внутренние силовые факторы, возникающие в результате действия внешних сил, распределяются по сечениям рассматриваемого тела равномерно.
Рассмотрим стержень, подверженный действию продольных сил
Если на поверхность призматического стержня нанести сетку линий параллельных и перпендикулярных оси стержня, и приложить к нему растягивающую силу, то можно убедиться в том, что линии сетки и после деформации останутся взаимно-перпендикулярными, но расстояние между ними изменятся.
Все горизонтальные линии, например, cd, переместятся вниз, оставаясь горизонтальными и прямыми.
Можно предположить, что и внутри стержня будет происходить то же самое, т.е. поперечные сечения стержня плоские и нормальные к его оси до деформации, останутся плоскими и нормальными к оси и после деформации.
Эту гипотезу называют гипотезой плоских сечений (гипотезой Бернулли).
Продольная сила N есть равнодействующая нормальных напряжений в поперечном сечении:
поскольку , то
, отсюда
В частном случае, когда на стержень действует одна внешняя сила, из уравнения равновесия получим:
И вместо общей формулы получим частный вид формулы для растяжения:
Эти формулы справедливы и для сжатия, с той только разницей, что сжимающие напряжения считаются отрицательными.
Кроме того, сжатые стержни помимо расчета на прочность рассчитываются также и на устойчивость.
Очевидно, что эти напряжения в реальных условиях нельзя создавать больше или много меньше определенной величины. Поэтому вводится понятие допускаемого напряжения: — условие прочности.
Определение деформаций и перемещений. Закон Гука.Опыты показывают, что при растяжении длина стержня увеличивается, а поперечные размеры уменьшаются, при сжатии – наоборот.
Для многих материалов при нагружении до определенных пределов опыты показали следующую зависимость между относительным удлинением стержня и напряжением :
, где
— абсолютное удлинение стержня
— длина образца до деформации
— длина образца после деформации
Эта зависимость носит название закона Гука и формулируется следующим образом: линейные деформации прямо пропорциональны нормальным напряжениям.
— коэффициент, зависящий от материала, т.е. его способность сопротивляться деформированию. Он характеризует жесткость материала, т.е. его способность сопротивляться деформированию.
Для ст.3 .
Для других материалов значение можно найти в справочниках.
Имея ввиду, что для стержня постоянного сечения:
, а
Можно получить формулу для определения полного (абсолютного) удлинения (укорочения) стержня:
Между продольным удлинением и поперечным существует зависимость:
Здесь — коэффициент поперечной деформации (коэффициент Пуассона), который характеризует способность материала к поперечным деформациям.
При пользовании этой формулой удлинение считается положительным, а укорочение – отрицательным.
Для всех материалов .
Для стали при упругих деформациях можно принимать =0,3.
Зная можно определить полное поперечное сужение или расширение стержня : , где — поперечный размер стержня до деформации
— поперечный размер стержня после деформации.
В стержнях переменного сечения напряжения в поперечных сечениях можно считать распределенными равномерно (если угол конусности ) и определять их по той же формуле, что и для стержня постоянного сечения.
Для определения деформаций стержня переменного сечения, в поперечных сечениях которого действует продольная сила N, найдем сначала удлинение элемента длиной , которое является дифференциалом полного удлинения .
Согласно закону Гука, имеем:
Полное удлинение стержня получим, интегрируя выражение в пределах :
, если и — величины постоянные, то
Чтобы воспользоваться этой формулой, необходимо знать закон изменения в зависимости от .
Для ступенчатых стержней интегрирование заменяется суммирование, и полное изменение длины бруса определяется как алгебраическая сумма деформаций его отдельных частей, в пределах которых :
Например, для стержня изображенного на схеме, имеем:
Определим теперь удлинение стержня постоянного сечения под действием силы тяжести, которая представляет собой нагрузку, равномерно распределенную вдоль стержня.
Удельный вес материала обозначим через .
Рассмотрим деформацию элемента , выделенного на расстоянии от нижнего конца.
Удлинение элемента равно:
Интегрируя это выражение в пределах, получим
Это выражение можно представить в другом виде, если учесть, что сила тяжести бруса равна: или , тогда получим — формула по определению перемещения с учетом собственного веса при известной длине
Следовательно, удлинение бруса постоянного сечения от собственной силы тяжести в два раза меньше удлинения от действия силы, равной силе тяжести и приложенной к его концу.
Для изучения свойств материалов и установления значения предельных (по разрушению или по пластическим деформациям) производят испытания образцов материала вплоть до разрушения. По виду деформации различают испытания на растяжение, сжатие, кручение и изгиб.
Испытания производят при статической и ударной (испытание на усталость и выносливость) нагрузках на ГМС – 50.
Цель испытания на растяжение – определение механических характеристик материала.
При проведении испытания автоматически записывается диаграмма зависимости между растягивающей силой и удлинением образца.
Условия и порядок выполнения работы
1. Стальной стержень ступенчатого сечения находится под действием внешней силы и собственного веса.
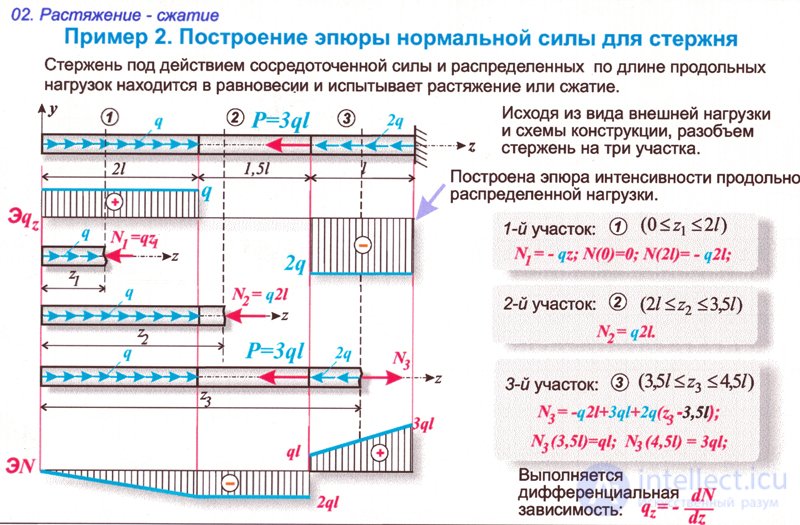
2. Необходимо построить эпюры:
· нормальных продольных сил
· нормальных напряжений
· перемещения сечений стержня относительно жесткой заделки.
Площадь большего поперечного сечения стержня в 2 раза превышает меньшую.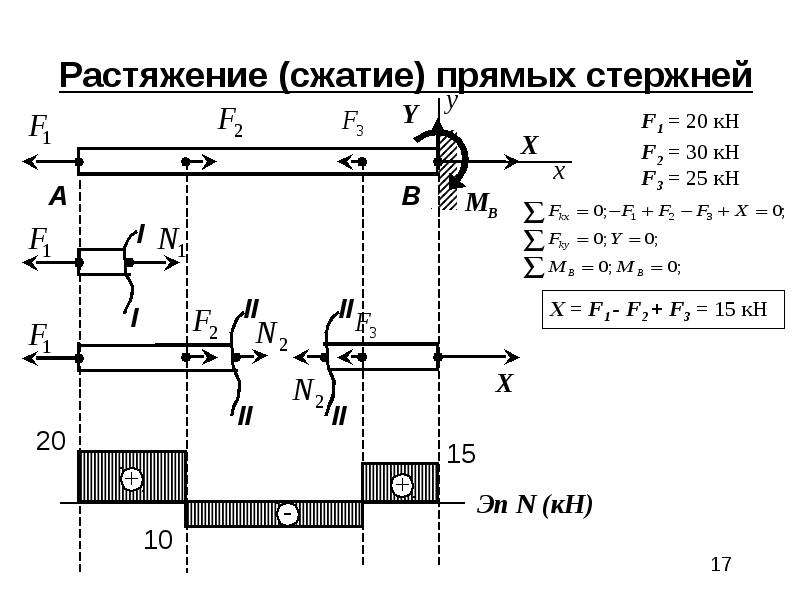
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
| Растяжение и сжатие | Fiziku5
Для простых конструктивных схем используется метод по разрушающим нагрузкам. В этом методе определяется предельная нагрузка, которую может выдержать конструкция без разрушения и без больших деформаций. Предельная (разрушающая) нагрузка сравнивается с рабочей, и на основании этого делается вывод о прочности конструкции в рабочих условиях.
В том случае, когда к конструкции предъявляются требования минимальных деформаций, её элементы рассчитываются на жёсткость.
Вопросы для самопроверки
1. В чём отличие реального объекта от расчётной схемы?
2. Назовите основные формы моделей физических объектов, их отличие.
3. Каким образом схематизируют внешние нагрузки?
4. Назовите гипотезы, используемые при выборе расчётной схемы материала.
5. Назовите внутренние силовые факторы, возникающие в сечениях тела, их размерности.
6. Запишите уравнения равновесия, которые позволяют определить внутренние силовые факторы.
7. Что называется деформацией? Формы деформаций. Виды деформации в зависимости от вида внутреннего силового фактора. Размерности деформаций.
8. Напряжение, его размерность. Виды напряжений. Чем они отличаются друг от друга?
2. Растяжение и сжатие
2.1.Определение продольной силы
Растяжением (сжатием) называется такой вид деформации стержня, при котором в поперечных сечениях возникает только продольная сила. Её вектор перпендикулярен к поперечному (перпендикулярному к оси стержня) сечению. Растяжение (сжатие)
Определение продольной силы проиллюстрируем на примере растяжения стержня (рис.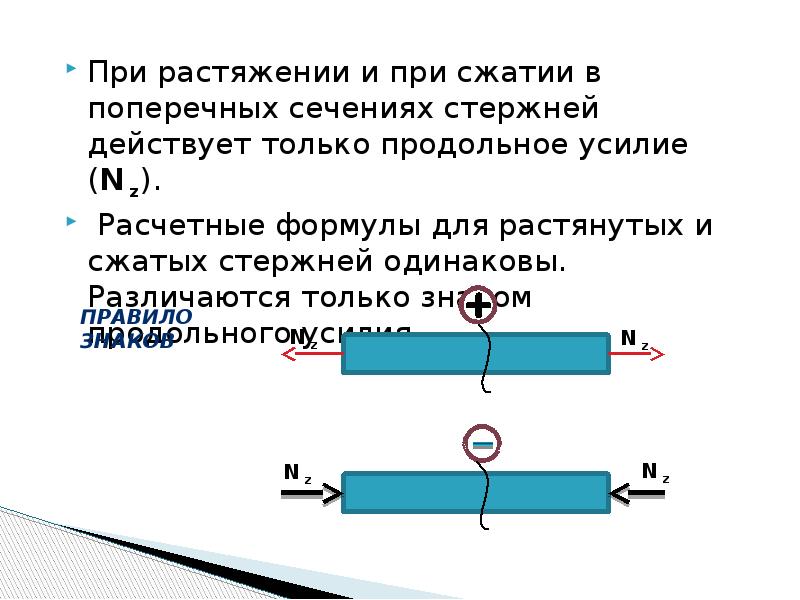
6а). Прямой стержень постоянного сечения (например, квадратного со стороной а), жёстко закреплён в верхней его
части и нагружен осевыми силами и в точках 1 и 2. Весом стержня пренебрежём.
Разбиваем стержень вдоль его длины на участки, определяемые точками приложения сил: первый участок 1–2, второй – 2–3.
Применим метод сечений (РОЗУ) – рассекаем стержень в произвольном сечении I−I на первом участке, отбрасываем верхнюю часть. Действие внутренних силовых факторов заменяем равнодействующей силой в сечении ( рис. 6б).
Уравновешивание рассматриваемой части стержня показывает, что продольная сила (согласно уравнению (1.1)) равна
и направлена от сечения. По правилу знаков в сопротивлении материалов продольная сила считается положительной, если она направлена от сечения (рассматриваемый участок стержня работает на растяжение). Если бы продольная сила была направлена к сечению, то она считалась бы отрицательной (рассматриваемый участок стержня работает на сжатие).
Поскольку сечение I−I на первом участке было выбрано произвольно, продольная сила по длине стержня на этом участке будет постоянной.
Рассматривая аналогично сечение II−II (рис. 6в), находим продольную силу на втором участке:
.
Аналогично первому участку, продольная сила на втором участке постоянна.
По полученным значениям продольных сил строим график зависимости – эпюру продольных сил, показанную на рис. 6г.
2.2. Определение напряжения
Если на поверхности призматического стержня нанести сетку линий, параллельных и перпендикулярных оси стержня (рис. 7а), и приложить к нему растягивающую силу (рис. 7б) , то можно убедиться в том, что линии сетки после деформации останутся взаимно перпендикулярными.
Можно предположить, что и внутри стержня будет такая же картина, т. е. поперечные сечения стержня, плоские и нормальные к его оси до деформации, останутся плоскими и нормальными к оси и после деформации.
Эта гипотеза называется гипотезой плоских сечений или гипотезой Бернулли. Формулы, полученные на основе этой гипотезы, подтверждаются результатами опытов.
Такая картина деформаций позволяет считать, что в поперечных сечениях стержня действуют только нормальные напряжения, равномерно распределённые по сечению, а касательные – равны нулю.
Продольная сила – равнодействующая нормальных напряжений в поперечном сечении:
. (2.1)
Так как (по гипотезе Бернулли), то
, (2.2)
откуда
, (2.3)
где А – площадь сечения стержня.
Эта формула справедлива и при сжатии, с той лишь разницей, что сжимающее напряжение считается отрицательным.
2.3. Определение деформаций. Закон Гука
Анализ деформации стержня при растяжении (рис. 7) показывает, что весь стержень удлинится на ∆l = l1 – l (абсолютная деформация), а его поперечные размеры уменьшатся на ∆b = b1 – b (абсолютное сужение).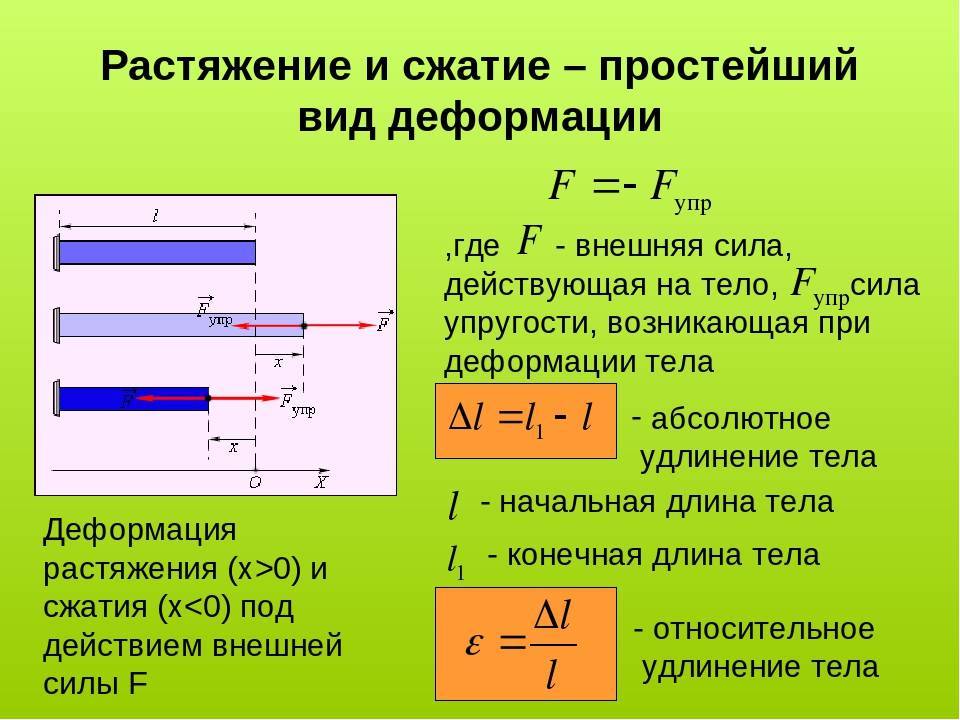
. (2.4)
Относительная деформация – величина безразмерная (иногда задаётся в %).
Закон Гука, вытекающий из гипотезы упругости (физической связи между напряжениями и деформациями), в случае растяжения (сжатия) стержневого элемента имеет вид:
, (2.5)
где Е − модуль упругости материала (первого рода), или модуль Юнга – характеризует упругие свойства материала; определяется опытным путём.
Из (2.5) с учётом (2.3) относительная продольная деформация равна:
. (2.6)
Величина ЕА – жёсткость стержня на растяжение (сжатие).
Абсолютная поперечная деформация , а относительная
. (2.7)
Эксперименты показывают, что отношение величин поперечной деформации к продольной ε для изотропных материалов практически постоянно и оценивается коэффициентом Пуассона (физическая характеристика материала – коэффициент поперечной деформации):
.
(2.8)
Величина μ для широкого класса конструкционных материалов изменяется в диапазоне:
. (2.9)
Полное удлинение стержня: при постоянном значении N и площади сечения А найдём, подставив (2.6) в формулу (2.4):
. (2.10)
Для стержня со ступенчатым изменением площади поперечного сечения и продольной силы удлинения вычисляются на участках с постоянными А и N и результаты алгебраически суммируются:
. (2.11)
Перемещение δ какого-либо сечения стержня вдоль оси z, отстоящего от точки отсчёта на расстоянии z, определяют по формуле, представляющей собой аналитическую линейную зависимость:
. (2.12)
ньютоновская механика. Есть ли натяжение у объектов, кроме струн, веревок и стержней?
спросил
Изменено 3 года, 11 месяцев назад
Просмотрено 1к раз
$\begingroup$ Почему мы определяем натяжение только струн, веревок, стержней и т.
п.? Разве каждый объект не должен испытывать силу натяжения? Например, когда вы тянете бумагу с противоположных сторон, она натягивается и испытывает состояние, похожее на напряжение. Если каждый объект испытывает напряжение, можете ли вы определить напряжение?
- ньютоновская механика
- силы
Натяжение не определено только для струн.
Однако уникальность идеальных струн заключается в том, что они могут испытывать ТОЛЬКО растяжение, тогда как твердые тела могут испытывать растяжение и сжатие. Идеальные струны разрушились бы.
Надеюсь, это поможет
$\endgroup$ 0 $\begingroup$Вы можете думать о натяжении как о силе, которая помогает поддерживать структурную целостность под действием растягивающей силы (здесь это довольно расплывчато, но подождите).
Представьте себе прочный цилиндрический стержень.
Вы можете сжать его концы, и есть нормальная реакция, которую вы должны преодолеть. Эта нормальная реакция пытается сохранить структурную целостность стержня. Напряжение в некотором смысле эквивалентно нормальной реакции, но в противоположном направлении — если вместо сжатия вы пытаетесь тянуть за оба конца стержня, вам приходится преодолевать другую силу, пытаясь сохранить структуру вашего стержня (путем предотвращения его от разрыва). Эта сила и есть то, что обычно называют «напряжением».
Я подчеркнул сходство между нормальной реакцией и силами натяжения, потому что они имеют одно и то же происхождение — они возникают в результате межмолекулярных взаимодействий, описывающих структуру вашего объекта. Для всех практических целей нормальную реакцию можно назвать «напряжением сжатия». Смысл этого обсуждения в том, что объекты пытаются сохранить свою структурную целостность, и вопрос семантики состоит в том, чтобы назвать эту «восстанавливающую» силу нормальной реакцией, или напряжением, или чем-то еще.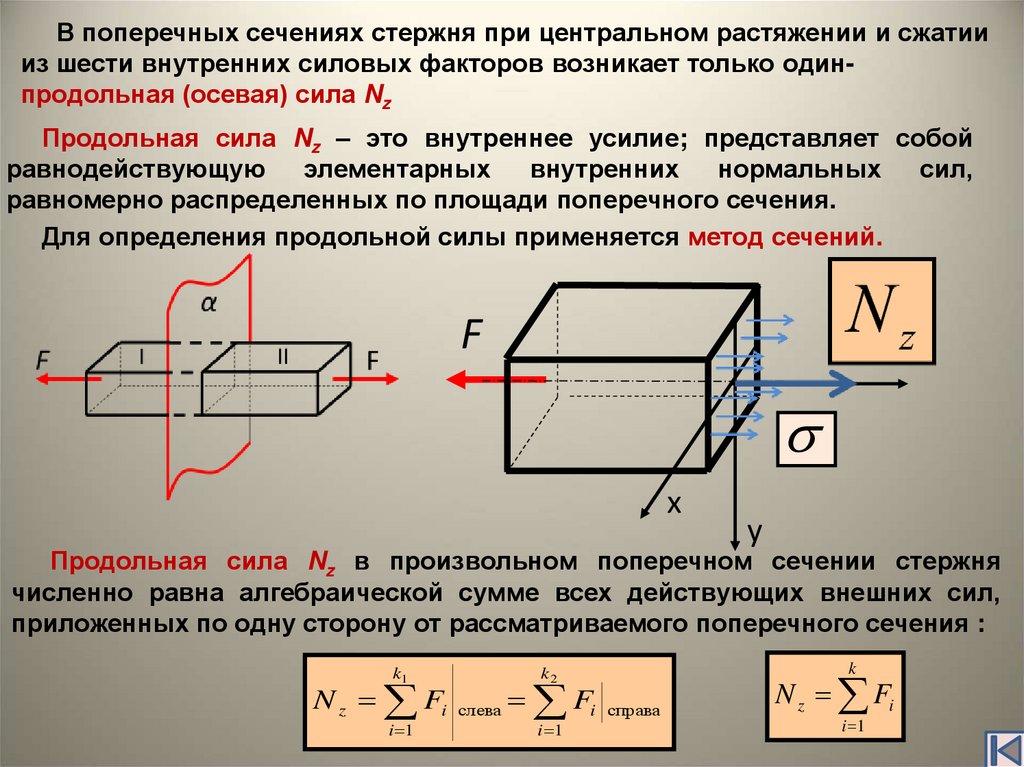
Молекулярное происхождение этих сил идентично.
Тем не менее, иногда полезно сохранить это различие для интуитивной ясности. Трудно сжимаемый предмет, например струна, по всей своей длине почти не будет давать нормальной реакции (струну очень легко сдавить), но ее растяжение непременно вызовет натяжение, которое необходимо преодолеть, прежде чем она порвется (т.е. потеряет силу). это целостность).
$\endgroup$ $\begingroup$«Напряжение» — простой частный случай напряженное состояние в любом твердом объекте.
Но обычно вы начинаете изучать механику, используя простые ситуации, когда здравые идеи, такие как «натяжение», — это все, что вам нужно, вместо того, чтобы начинать с изучения тензоров напряжений и деформаций и определяющих уравнений в механике сплошной среды!
$\endgroup$ $\begingroup$ Если вы думаете о чем-то действительно фундаментальном, то есть только четыре признанных фундаментальных силы, а «натяжение» (что-то вроде струны) обычно рассматривалось как результат электромагнитного взаимодействия (электромагнитной силы) атомов или частиц.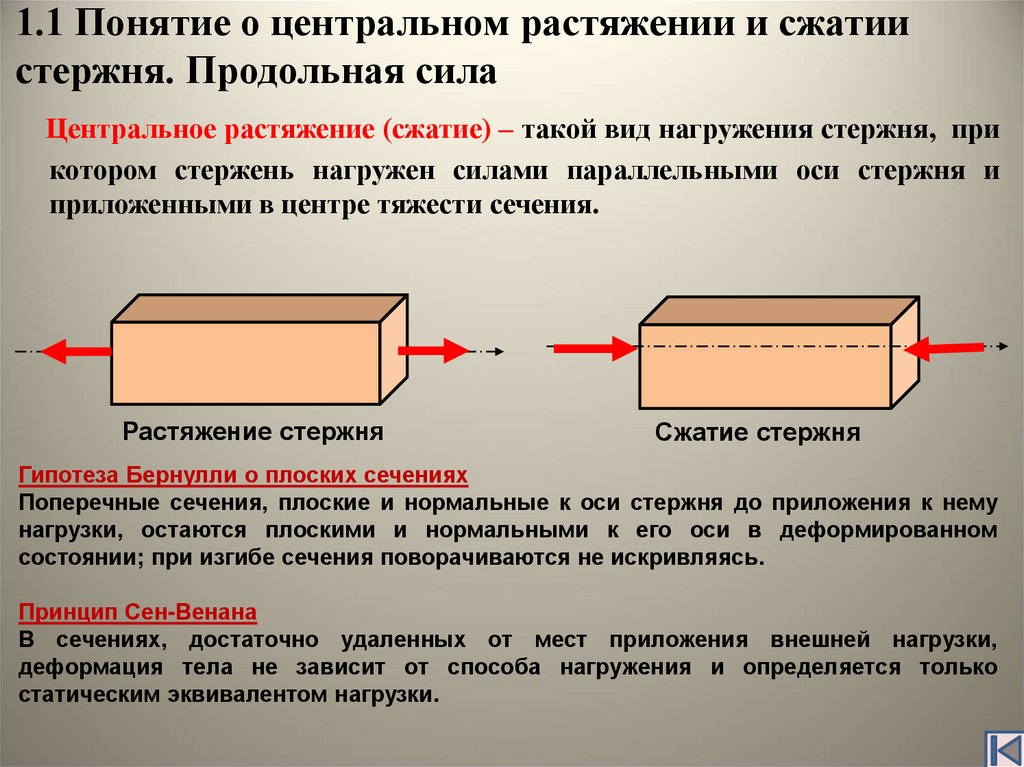
Однако напряжение на уровне субчастиц также может возникать из-за сильного взаимодействия, как протоны внутри ядра.
Зависит от того, напряжение — это просто более формальная формулировка обычного слова «растяжение», это слово, обычно используемое физиками для упоминания понятным для физиков способом.
$\endgroup$ $\begingroup$Поднимите кирпич. Попробуйте разобрать. Что мешает разобрать? Это напряжение в кирпиче. Откуда берется напряжение в кирпиче? Это происходит из-за межмолекулярных сил внутри кирпича.
То же самое и со строками. Вот второй пример. Если вы внимательно посмотрите на толстую веревку, то увидите, что она состоит из множества маленьких нитей, намотанных друг на друга. Почему это? Таким образом, трение между струнами увеличивает доступное натяжение всей веревки. Другими словами, межмолекулярные силы (в данном случае трение) внутри веревки увеличиваются, заставляя веревку больше «хотеть» оставаться вместе; чем больше веревка хочет оставаться вместе, тем больше силы она может выдержать, когда вы пытаетесь ее разорвать.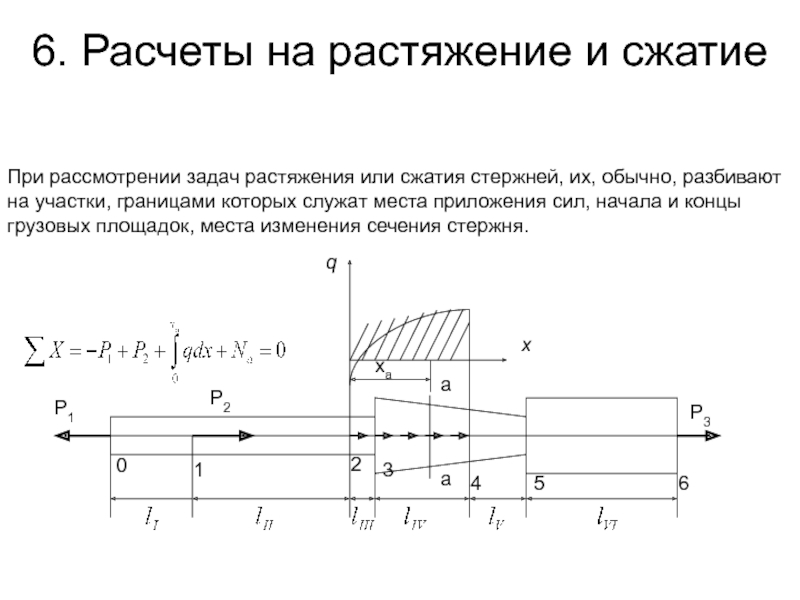
Точно так же, как нормальная сила — это сила отталкивания электронных оболочек друг от друга (из-за принципа запрета Паули), напряженность также возникает из микромасштабной силы.
$\endgroup$Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя адрес электронной почты и парольОпубликовать как гость
Электронная почтаТребуется, но никогда не отображается
Опубликовать как гость
Электронная почтаТребуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения.
Удлинители для испытаний на растяжение и сжатие — G1024, G1024-1, G1024-2, G1031, G1031-1, G1031-2
005
Г1024, Г1024-1, Г1024-2, Г1031, Г1031-1, Г1031-2
Просмотреть все
Г1024, Г1024-1, Г1024-2, Г1031, Г1031-1, Г1031-2
Для использования между датчиками силы, датчики, захваты, и вложения. Не рекомендуется для приложений сжатия.
Есть вопрос?
| Модель | Грузоподъемность фунт-сила [Н] | Вес фунт [кг] | Код ТН ВЭД | ECCN | Страна происхождения | |
|---|---|---|---|---|---|---|
| Г1024 | 200 [1000] | 0,05 [0,023] | 00000 | EAR99 | США | |
| G1024-1 | 200 [1000] | 0,02 [0,009] | ||||
| G1024-2 | 200 [1000] | 0,01 [0,005] | ||||
| Г1031 | 500 [2500] | 0,25 [0,113] | ||||
| G1031-1 | 500 [2500] | 0,10 [0,045] | ||||
| G1031-2 | 500 [2500] | 0,05 [0,023] |
| Модель | А | ØВ | С | Д |
|---|---|---|---|---|
| Г1024 | 5,0 [127,0] | 0,25 [6,4] | № 10-32F | #10-32М |
| G1024-1 | 2,0 [50,8] | |||
| G1024-2 | 1,0 [25,4] | |||
| Г1031 | 5,0 [127,0] | 0,50 [12,7] | 5/16-18F | 5/16-18М |
| G1031-1 | 2,0 [50,8] | |||
| G1031-2 | 1,0 [25,4] |
Информация для заказа
| Модель | Описание | Цена в США |
|---|---|---|
| Г1024 | Удлинитель, 5″, #10-32 | 20,00 $ |
| G1024-1 | Удлинитель, 2″, #10-32 | 20,00 $ |
| G1024-2 | Удлинитель, 1″, #10-32 | 20,00 $ |
| Г1031 | Удлинитель, 5″, 5/16-18 | 25,00 $ |
| G1031-1 | Удлинитель, 2″, 5/16-18 | 25,00 $ |
| G1031-2 | Удлинитель, 1″, 5/16-18 | 25,00 $ |
Mark-10 определяет точность в процентах от полной шкалы
инструмент.
Для определения погрешности измерения как фактической
значение нагрузки, умножьте процент точности на мощность прибора.
Пример 1 – манометр M5-50:
Точность составляет ±0,1% от полной шкалы (FS). Умножьте ±0,1% на 50 фунтов силы, что равно ±0,05 фунта-силы. Это означает, что любое отображаемое значение может быть выше или ниже на 0,05 фунт-силы. Например, если отображается значение составляет 30,00 фунтов-силы, истинное показание будет ≥290,95 фунта силы и ≤30,05 фунта силы.
Пример 2 – Plug & Test
® Индикаторы и датчики : Точности датчика и индикатора должны быть сложены.
Индикаторы моделей 7i и 5i имеют значения точности ±0,1% полной шкалы,
в то время как модель 3i рассчитана на ± 0,2% полной шкалы. На примере а
Датчик крутящего момента серии R50 с индикатором модели 3i, прибавка от ±0,35% до ±0,2%,
что равно ±0,55%. В конкретном примере для модели MR50-12,
точность становится ±0,55% x 135 Нсм = ±0,7425 Нсм.