Растяжение-сжатие
Растяжением или сжатием брусьев называют такой вид деформации, при котором в их поперечных сечениях возникает единственный внутренний силовой фактор – продольная сила N.
Брус при растяжении-сжатии называют стержнем.
Для определения продольной силы используется метод сечений:
В сечениях бруса, удаленных более чем на величину h (рис. 2.1) от торцов (мест нагружения), усилие N на основании принципа Сен-Венана равномерно распределяется по площади поперечного сечения, вызывая нормальные напряжения:
В наклонном сечении возникают нормальные σα и касательные τα напряжения:
причем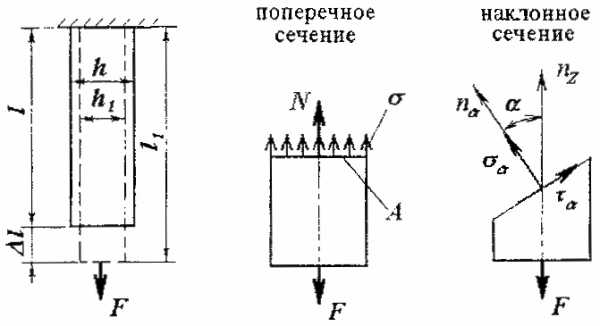
Рис. 2.1
При растяжении (сжатии) имеют место только линейные деформации:
— абсолютная продольная деформация (удлинение/укорочение)
— абсолютная продольная деформация (сужение/утолщение)
— относительная продольная деформация
— относительная поперечная деформация
Отношение
называется коэффициентом поперечной деформации (коэффициентом Пуассона).
Напряжения и деформации взаимосвязаны законом Гука
где:
E – модуль упругости I рода (модуль Юнга), является постоянной величиной для данного материала и характеризует его жесткость, для стали E=200ГПа.
Изменение длины участка бруса постоянного сечения вычисляется по формуле
Величина EiAi называется жесткостью поперечного сечения бруса при растяжении (сжатии).
Полное удлинение (укорочение) бруса с несколькими силовыми участками:
Условие прочности при растяжении/сжатии выражается неравенством:
Здесь
— допускаемое напряжение;
σпред — предельное (опасное) для данного материала напряжение, равное пределу текучести (σТ или σ0,2) для пластичных материалов или пределу прочности σ пч для хрупких материалов;
[n] – нормативный коэффициент запаса прочности.
Условие прочности позволяет решать три типа задач:
1. Проверка прочности (проверочный расчет)
2. Подбор сечения (проектировочный расчет)
3. Определение грузоподъемности (допускаемой нагрузки)
При расчете на жесткость растянутого (сжатого) бруса обычно определяют величину продольной деформации, которая не должна превышать допустимых значений, т.е.
Примеры решения задач >
Лекции по сопромату >
isopromat.ru
Осевое растяжение-сжатие
Осевым (центральным) растяжением (сжатием) брусьев называют такой вид деформирования, при котором в их поперечных сечениях возникает единственный внутренний силовой фактор – продольная сила N.
Для определения продольной силы используется метод сечений (Рис. 4.1,б).
Напряжения
N
В наклонном сечении возникают нормальные σα и касательные τα напряжения (рис. 4.1,в).
причем
Условие прочности
Условие прочности при растяжении (сжатии) выражается неравенством:
где [σ] – допускаемые напряжения, определяются как:
n – коэффициент запаса прочности, устанавливаемый нормативными документами.
Условие прочности позволяет решать три типа задач:
- Проверка прочности (проверочный расчет)
- Подбор сечения (проектировочный расчет)
- Определение грузоподъемности (допускаемой нагрузки)
Примеры решения задач >
Деформации и условие жесткости при растяжении и сжатии >
isopromat.ru
2 Растяжение и сжатие
2.1 Внутренние усилия и напряжения при растяжении (сжатии)
Растяжение (сжатие) — простой вид сопротивления, при котором стержень нагружен силами, параллельными продольной оси стержня и приложенными в центр тяжести его сечения.Рассмотрим стержень, упруго растянутый центрально приложенными сосредоточенными силами P.
Прежде чем перейти к исследованию внутренних усилий и напряжений, возникающих в растянутом стержне, рассмотрим некоторые гипотезы, связанные с характером деформирования такого стержня и имеющие в сопротивлении материалов исключительно важное значение.
Принцип Сен-Венана: в сечениях, достаточно удаленных от мест приложения сил, распределение напряжений и деформаций мало зависит от способа приложения нагрузок.
Принцип Сен-Венана дает возможность вести расчет без учета местных (локальных) деформаций, возникающих вблизи точек приложения внешних сил и отличающихся от деформаций основного объема материала, что в большинстве случаев упрощает решение задачи.
Гипотеза плоских сече-ний (гипотеза Я.Бернулли): поперечные сечения стержня плоские и перпендикулярные его оси до деформации остаются плоскими и перпендикулярными оси, и после деформации.
Мысленно рассекая стер-жень, определим внутренние силы в растянутом стержне:
а) стержень, нагруженный растя-гивающими силами P и находя-щийся в равновесии, рассекаем произвольным сечением;
б)
отбрасываем одну из частей стержня, а
ее действие на дру-гую часть компенсируем
вну-тренними усилиями интенсив-ностью ;
;
в) осевое внутреннее усилие N, возникающее в сечении стержня, определим, составляя уравнения равновесия для отсеченной части:
. (2.1)
Проецируя внешнюю силу P, действующую на отсеченную часть стержня, на другие оси (z и y), а также составляя уравнения моментов относительно координатных осей, легко убедится, что осевое усилие N является единственным внутренним усилием, возникающим в сечении стержня (остальные тождественно равны нулю).
Таким образом, при растяжении (сжатии) из шести внутренних усилий в сечении стержня возникает только одно — продольная сила N.
Нормальные
напряжения 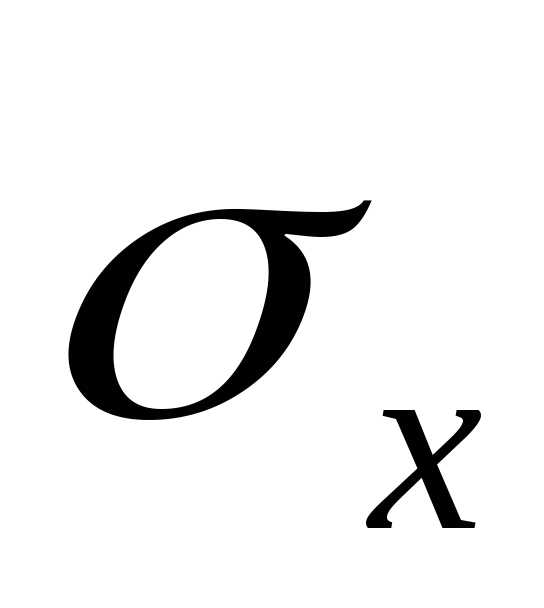 ,
возникающие в сечении стержня, связаны
с осевым усилием N следующим образом:
,
возникающие в сечении стержня, связаны
с осевым усилием N следующим образом:
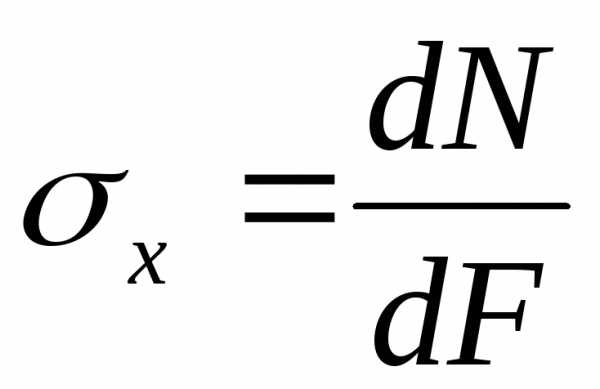 ,
или
,
или  . (2.2)
. (2.2)
Учитывая,
что в соответствии с гипотезой Бернулли
напряжения равномерно распределены по
поперечному сечению (т.е. 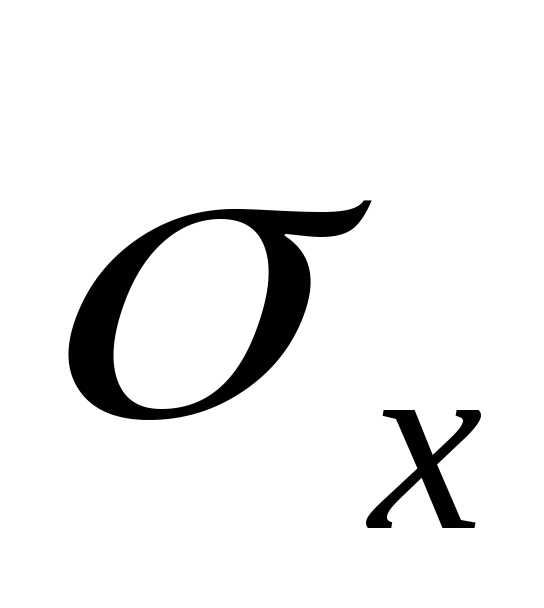
. (2.3)
Таким образом, нормальные напряжения при растяжении (сжатии) определяются как
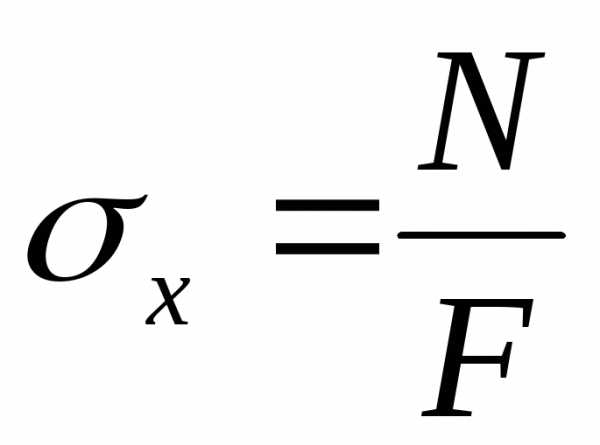 . (2.4)
. (2.4)
2.2 Перемещения и деформации при растяжении (сжатии)
Рассмотрим стержень, находящийся под действием растягивающей нагрузки. Выделим (до деформации) двумя произвольными сечениями А-А и В-В бесконечно малый участок длинойdx на расстоянии x от свободного конца. Под действием внешней силы P сечение А-А переместиться в положение А1-А1 на расстояние u, а сечение В-В — в положение В1-В1 на расстояние u+du (du — бесконечно малая величина) Следовательно, абсолютное удлинение отрезка dx равно разности его размеров до и после деформации Δdx = du.
Относительная продольная деформация точек сечения А-А стержня при растяжении
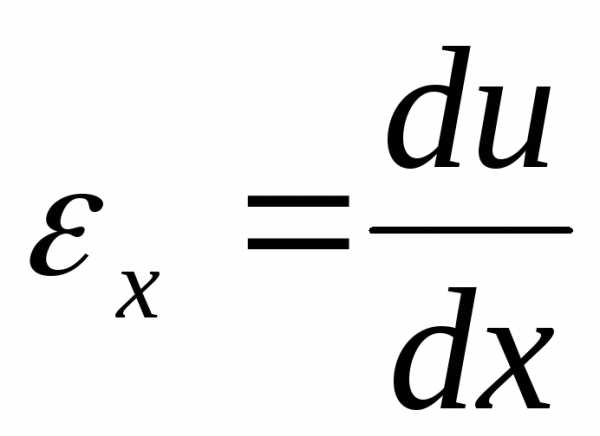 (2.5)
(2.5)
Для линейно-упругого матери-ала связь между нормальными напряжениями и относительной деформацией при растяжении определяется законом Гука:
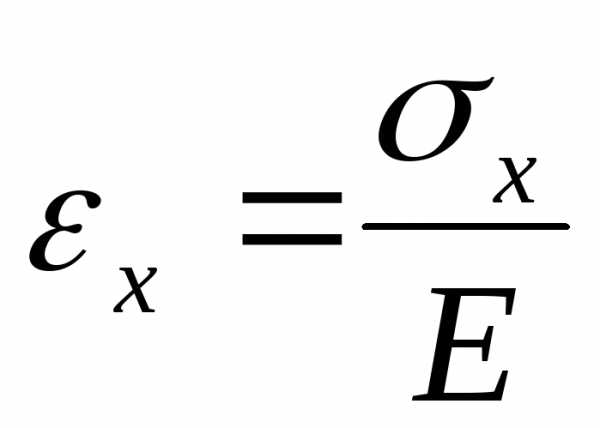 ,
(2.6)
,
(2.6)
или, учитывая, что ,
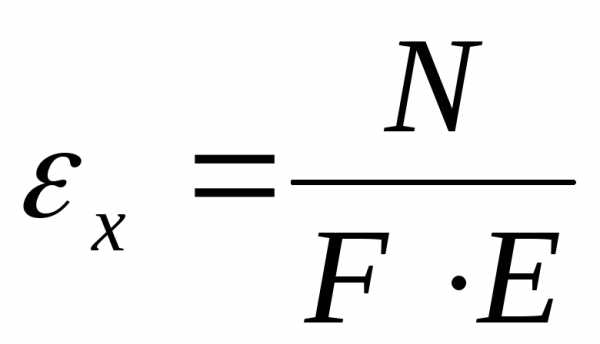 ,
(2.7)
,
(2.7)
где
Е — модуль нормальной упругости (модуль
Юнга), постоянный коэффициент, который
является константой материала (например,
для стали Е=2∙10
Исходя из этих формул, можно записать выражение для перемещений точек растягиваемого стержня в рассматриваемом сечении
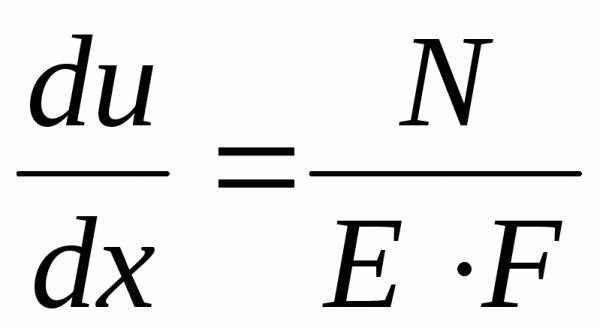 ,
, 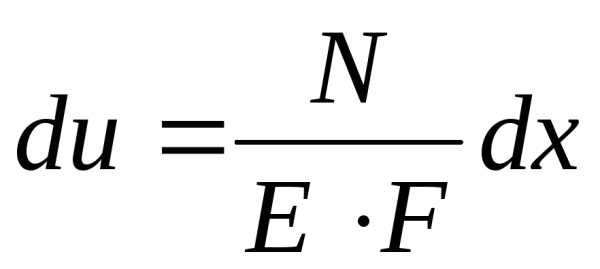 ,
(2.8)
,
(2.8)
Тогда
полное удлинение стержня при растяжении  ,
равное перемещению точек правого
крайнего сечения, относительно левого
крайнего:
,
равное перемещению точек правого
крайнего сечения, относительно левого
крайнего:
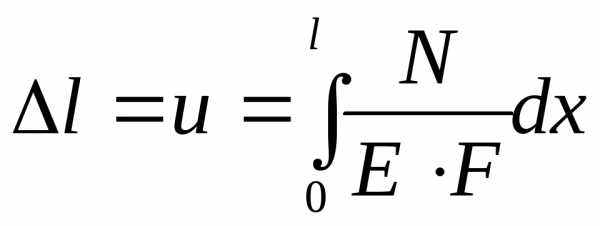 (2.9)
(2.9)
При постоянстве величин N, F, Е вдоль оси стержня, абсолютное удлинение можно найти так:

При растяжении стержень деформируется не только в продольном направлении, но и в поперечном.
Абсолютная поперечная деформация стержня опреде-ляется как разность его поперечных размеров до и после деформации:
;
.
Относительная поперечная деформация стержня определяется отношением абсолютной поперечной деформации к соответствующему первоначальному размеру.
Относительная поперечная деформация при растяжении (сжатии) для изотропных материалов во всех направлениях одинакова:
(2.11)
.
Между относительной поперечной и продольной деформациями прирастяжении (сжатии) в пределах применимости закона Гука существует постоянное соотношение, которое называется коэффициентом поперечных деформаций (коэффициентом Пуассона
Коэффициент Пуассона равен абсолютной величине отношения поперечной деформации к продольной
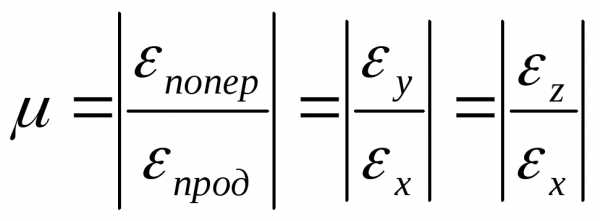 .
(2.12)
.
(2.12)
Коэффициент Пуассона – безразмерная величина.
Так как продольная и поперечная деформация для конструкционных материалов имеют противоположные знаки, можем записать
(2.13)
или,
учитывая, что, согласно закону Гука, 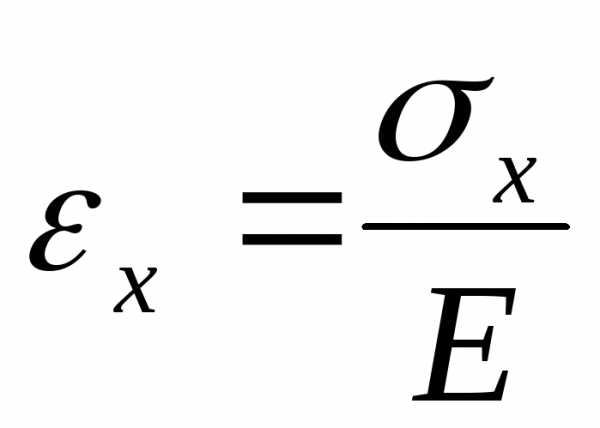 запишем
запишем
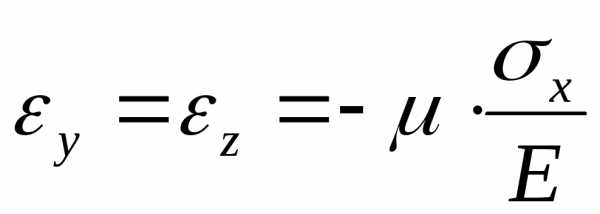 (2.14)
(2.14)
Коэффициент
Пуассона µ также как и модуль Юнга Е характеризует упругие свойства материала.
Для изотропных материалов коэффициент
Пуассона находится в пределах от 0 до
0,5 (сталь  ;
каучук
;
каучук ).
).
studfiles.net
Расчет опорной реакции при растяжении-сжатии
Задача
Для прямого ступенчатого стержня нагруженного системой продольных сил (рис. 1), где F1=25кН, F2=50кН, F3=30кН, требуется определить величину и направление опорной реакции в заделке.
рис. 1
Пример решения
Проведем координатную ось z совпадающую с продольной осью стержня.
Так как при растяжении-сжатии все внешние силы приложенные к стержню расположены вдоль его оси, то из возможных для заделки шести усилий здесь будет только одно — продольная реакция R.
Для того чтобы записать уравнение статики зададим этой силе произвольное направление, например влево (рис. 2).
рис. 2
Запишем уравнение равновесия (неподвижности) стержня.
Для этого, спроецируем все силы на ось z, сума которых должна быть равна нулю.
При этом, силы направление которых совпадает с направлением оси z примем положительными, а силы, имеющие обратное направление — соответственно отрицательными:
Отсюда находим величину опорной реакции R:
Положительный знак реакции R означает что изначально выбранное направление оказалось правильным.
Проверка решения
Для проверки правильности полученного результата, можно просто сложить все силы направленные вправо:
и силы направленные влево (включая опорную реакцию R):
Эти суммы должны совпадать.
Построение эпюры внутренних продольных сил >
Другие примеры решения задач >
isopromat.ru
Лекция по Сопромату на тему «Растяжение и сжатие» (11 класс)
№1 Центральное растяжение и сжатие. Метод сечений. Внутренние силы в поперечных сечениях. Правило знаков. Построение эпюр нормальных сил.
Центральным растяжением (или центральным сжатием) называется такой вид деформации, при котором в поперечном сечении бруса возникает только продольная сила (растягивающая или сжимающая), а все остальные внутренние усилия равны нулю. Иногда центральное растяжение (или центральное сжатие) кратко называют растяжением (или сжатием) .
Понятие о внутренних силах (метод сечений).Под действием внешних нагрузок в поперечных сечениях элементов конструкций и деталей машин возникают внутренние силы упругости, характеризующие связи между молекулами и его отдельными частицами. Возникновение внутренних сил сопровождается деформацией материала. Эти силы противодействуют внешним силам и стремятся восстановить прежнюю форму тела. Одна из задач сопротивления материалов состоит в определении величин внутренних сил.
Для этого широко используется метод сечений, сущность которого заключается в следующем:
1. В рассматриваемом месте элемент сооружения или деталь условно рассекается на две части.
2. Одна из частей условно отбрасывается.
3. Оставшаяся часть уравновешивается внутренними силами упругости.
Правило знаков Растягивающие продольные усилия принято считать положительными, а сжимающие — отрицательными.
Продольная сила в любом напряженном сечении бруса определяется методом сечений: она равна алгебраической сумме проекций всех внешних сил, приложенных по одну сторону от рассматриваемого сечения, на продольную ось.
Если продольная сила по всей длине бруса не постоянна, то строят эпюру «N». Эпюра – это график изменения внутреннего силового фактора по длине бруса.
Правила построения эпюр продольных сил:
Разбиваем брус на участки, границами которых являются сечения, где приложены внешние силы.
В пределах каждого участка применяют метод сечений и определяют продольную силу. При этом если внешняя сила растягивает оставленную часть стержня, т.е. направлена от сечения — продольная сила положительна; если внешняя сила сжимает оставленную часть стержня, т.е. направлена к сечению – продольная сила отрицательна.
Откладываем полученные значения и строим эпюру продольных сил. Если на участке не действует равномерно распределенная нагрузка, то эпюра ограничена прямой, параллельной нулевой линии.
Правильность построения эпюр продольных сил определяется следующим образом: в сечениях, где приложена внешняя сила, на эпюре есть «скачки», равные по величине приложенной силе.
№2 Центральное растяжение и сжатие. Удлинение стержня. Абсолютная и относительная продольная и поперечная деформации. Коэффициент Пуассона.
Центральным растяжением (или центральным сжатием) называется такой вид деформации, при котором в поперечном сечении бруса возникает только продольная сила (растягивающая или сжимающая), а все остальные внутренние усилия равны нулю. Иногда центральное растяжение (или центральное сжатие) кратко называют растяжением (или сжатием) .
Как определить удлинение или укорочение стержня (бруса) под действием внешней нагрузки. Будем разбираться сразу на примерах.
Возьмем брус круглого и постоянного поперечного сечения, который нагружен
растягивающей силой.

При таком раскладе, очевидно, что брус удлинится на какую-то величину дельта.
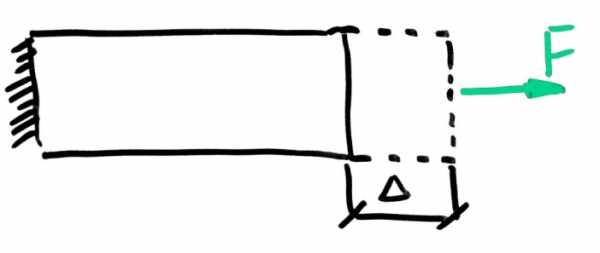
Как ее найти? Вычислить удлинение можно по формуле:
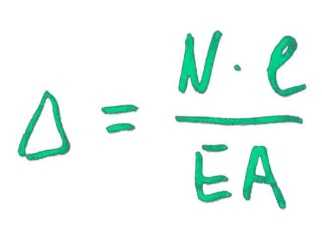
В формуле есть уже знакомая вам буква N – продольная сила, l – длина недеформированного бруса, то есть до действия внешней нагрузки, E – модуль упругости и A – площадь поперечного сечения. Если проанализировать формулу, то можно сделать вывод, что, по сути, по ней площадь эпюры продольных сил делится на произведение модуля упругости и площади поперечного сечения.
Вернемся к нашему примеру. Слегка модифицируем формулу, подставив исходные данные и площадь поперечного сечения – круга. Вот что получим:
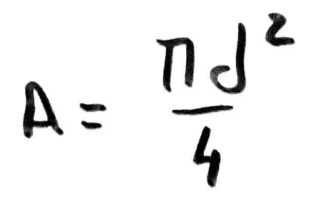
Вот так просто можно найти удлинение или укорочения брусьев.
А что делать, если, например брус ступенчатый или на него действуют несколько внешних сил? В этом случае обязательно строится эпюра продольных сил, разбивается на кусочки, так чтобы на этих кусочках внутренняя сила была одна, вычисляются уже относительные удлинения (укорочения) по вышеприведенной формуле для этих кусочков и результат складывают.
Посмотрим эту технику на примере двухступенчатого бруса загруженного парой сил. Найдем перемещение свободного торца бруса. Как и обговаривалось ранее, сначала строим эпюру внутренних усилий: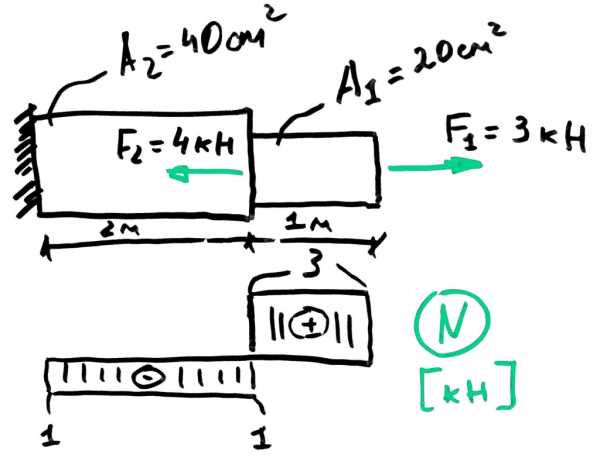
Дальше эпюру бьем на два участка и вычисляем относительные перемещения с учетом знака продольной силы. Потом складываем эти два значения.Так как в итоге получили положительное значение, то значит, что брус удлинился, если бы получили отрицательное значение, то соответственно это значило, что он укоротился.
На практике на стержни помимо сосредоточенных сил могут действовать и распределенные нагрузки. Как быть в таком случае? Ответ нам даст эпюра продольной силы. Рассмотрим стержень, загруженный только распределенной нагрузкой, построим для него эпюру.

Как видно, эпюрой продольных сил от распределенной нагрузки является прямоугольной треугольник. Что есть равно половина от прямоугольника. Тогда вычисляя перемещение, выражение нужно дополнительно помножить на ½.
Если под действием силы P брус длиной L изменил свою продольную величину на +/- дельта l, то эта величина называется абсолютной продольной деформацией (абсолютное удлинение или укорочение). При этом наблюдается и поперечная абсолютная деформация +/- дельта b .Отношение называется относительной продольной деформацией, а отношение — относительной поперечной деформацией.
Коэффициент Пуассона (обозначается как или ) — величина отношения относительного поперечного сжатия к относительному продольному растяжению. Этот коэффициент зависит не от размеров тела, а от природы материала, из которого изготовлен образец.
Отношение называется коэффициентом Пуассона, который характеризует упругие свойства материала.
Коэффициент Пуассона имеет значение . (для стали он равен )
infourok.ru
Лекция . Задачи и метод сопротивления материалов. Растяжение и сжатие. Общие понятия.
Возведение сооружений и строительство машин (которые далее будем называть конструкциями) начинается с составления проекта, в котором определяют форму, размеры и материал конструкции. Каждая конструкция составляется из отдельных деталей, взаимно соединенных между собой. Эти детали будем называть элементами конструкций. В процессе эксплуатации элементы в той или иной степени участвуют в работе и подвергаются действию различных внешних факторов: нагрузок, изменений температуры[1].
Под влиянием внешних сил элементы конструкций изменяют свою первоначальную геометрическую форму, объем и размеры. Такое изменение называют деформацией.
Величина деформации может при определенных условиях нарушить нормальную работу конструкции и даже оказаться опасной для целости того или иного элемента.
Для обеспечения нормальной и безопасной работы конструкция должна удовлетворять условиям прочности, жесткости и надежности.
Прочность– это способность конструкции выдерживать заданную нагрузку, не разрушаясь.
Жесткость– способность конструкции под действием внешних сил сопротивляться возникновению деформации.
Надежность – свойство конструкции выполнять заданные функции, сохраняя свои эксплуатационные показатели в определенных нормативных пределах в течение требуемого промежутка времени.
Этими вопросами и занимается наука сопротивление материалов.
Сопротивление материалов – наука, в которой изложены принципы и методы расчета элементов конструкций на прочность, жесткость и надежность.
Кроме этих требований, проектируемые сооружения должны удовлетворять требованиям наибольшей экономичности и долговечности.
Основные формы элементов конструкций
При всем разнообразии видов элементов конструкций их можно свести к сравнительно небольшому числу основных форм[2].
Стержень или брус– тело, у которого один размер (длина) значительно превышает два других (поперечных) размера (рис. 1).
В машиностроении встречаются стержни как прямолинейные (рис. 1, а), так и криволинейные (рис. 1, б), как постоянного (рис. 1, а), так и переменного (рис. 1, в) сечения.
Стержни, у которых толщина стенки значительно меньше габаритных размеров поперечного сечения, называют тонкостенными (рис. 1, г). В настоящее время они широко применяются в строительных конструкциях, судо- и особенно в авиастроении.
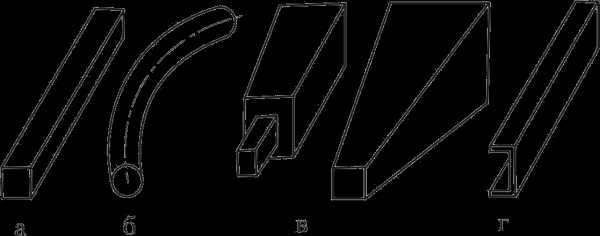
Рис. 1
Оболочка представляет собой тело, ограниченное криволинейными поверхностями, расположенными на близком расстоянии друг отдруга.
Поверхность, которая делит толщину оболочки на равные части, называется срединной. По форме срединной поверхности различают оболочки цилиндрические (рис. 2, а), конические (рис. 2,б),сферические (рис. 2, в) и др. К оболочкам относятся неплоские стенки тонкостенных резервуаров, котлов, купола зданий, обшивки фюзеляжа, крыла и других частей летательных аппаратов, корпуса подводных лодок и т. д.
Если срединная поверхность представляет собой плоскость, то расчетный объект называют пластинкой (рис. 2,г). Встречаются пластинки круглые (рис. 2, д), прямоугольные (рис. 2, г) и другихочертаний. К пластинкам могут быть отнесены плоские днища и крышки резервуаров, перекрытия инженерных сооружений, диски турбомашин и т. п.
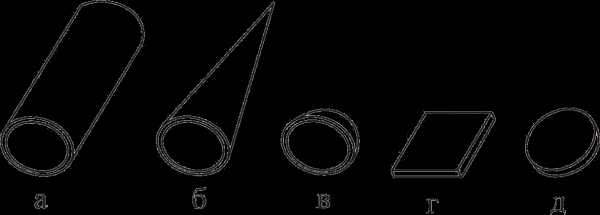
Рис. 2
Тела, у которых все три размера одного порядка, называют массивными телами. К ним относятся фундаменты сооружений, подпорные стенки и т. п.
studfiles.net
Растяжение-сжатие в сопротивлении материалов | Сопромат и Строймех онлайн обучение
/ Растяжение — сжатие, Сопротивление материалов онлайн/ 0 комментариев
Первая тема сопротивления материалов — это растяжение-сжатие. Задачи на растяжение-сжатие в сопротивлении материалов — довольно простая тема сопромата. И сейчас я это докажу.
Прежде всего растяжение — мы интуитивно понимаем — удлинение, увеличение размеров. А сжатие — уменьшение длины, укорочение.
При изучении растяжения-сжатия используется один и тот же подход ко всем задачам, ко всем расчетным схемам. А именно — метод сечений. О нем мы расскажем в отдельной записи. А пока, ниже вы видите видео уроки на эту тему. Надеюсь вам будет полезно и удобно изучать эту тему со мной.
Что такое растяжение-сжатие
Прежде всего нужно сказать, что растяжение-сжатие — это такой вид деформации (относительного изменения размеров), при котором одно плоское сечение относительно другого удаляется параллельно исходному положению.
Пример деформации растяжения-сжатия. Схема приложения нагрузок.
Все это звучит сложно, но посмотрите видео и Вы все поймете!
Подход в решении задач на растяжение-сжатие
В первом видео уроке объясняется сам процес возникновения деформации растяжения-сжатия. Как отличить растяжение от сжатия. Приводится объяснение основного метода расчета задач по сопротивлению материалов — метод сечений.
Здесь рассмотрены задачи для стержня, имеющего сплошное поперечное сечение. На такой стержень может действовать как одна сила, так и несколько.
Внутренние усилия при растяжении-сжатии, метод сечений. Видео урок.
Растяжение-сжатие в стержневых конструкциях
Видео урок по определению внутренних усилия для нескольких стержней при растяжении-сжатии.
Во втором видео уроке приводится решение задачи на растяжение-сжатие для системы стержневых конструкций. Приведены методика и план решения задачи по сопротивлению материалов на тему растяжение-сжатие.
Учет собственного веса в задачах сопротивления материалов на растяжение-сжатие
Видео урок по расчету стержня на растяжение-сжатие с учетом собственного веса.
Третья задача на растяжение-сжатие стержней с учетом собственного веса. Приведен пример решения задачи и доступно рассказывается как можно учесть собственный вес конструкции при расчете на растяжение-сжатие.
stroymex.online