Расчетные характеристики бетона: Нормативные и расчетные характеристики бетона и арматуры

Содержание

Нормативные и расчетные характеристики бетона и арматуры

Основными показателями прочности и деформативности бетона являются нормативные значения их прочностных и деформационных характеристик.

Основными прочностными характеристиками бетона являются нормативные значения:

сопротивления бетона осевому сжатию R_b,n;
сопротивления бетона осевому растяжению R_bt,n.

Нормативное значение сопротивления бетона осевому сжатию (призменная прочность) следует устанавливать в зависимости от нормативного значения прочности образцов-кубов (нормативная кубиковая прочность) для соответствующего вида бетона и контролируемого на производстве.

Нормативное значение сопротивления бетона осевому растяжению при назначении класса бетона по прочности на сжатие следует устанавливать в зависимости от нормативного значения прочности на сжатие образцов-кубов для соответствующего вида бетона и контролируемого на производстве.

Соотношение между нормативными значениями призменной и кубиковой прочностями бетона на сжатие, а также соотношение между нормативными значениями прочности бетона на растяжение и прочности бетона на сжатие для соответствующего вида бетона следует устанавливать на основе стандартных испытаний.

При назначении класса бетона по прочности на осевое растяжение нормативное значение сопротивления бетона осевому растяжению принимают равным числовой характеристике класса бетона по прочности на осевое растяжение, контролируемой на производстве.

Основными деформационными характеристиками бетона являются нормативные значения:

предельных относительных деформаций бетона при осевом сжатии и растяжении ε_bo,n и ε_bto,n ;
начального модуля упругости бетона Е_b,n.
Кроме того, устанавливают следующие деформационные характеристики:
начальный коэффициент поперечной деформации бетона v;
модуль сдвига бетона G;
коэффициент температурной деформации бетона α_bt;
относительные деформации ползучести бетона ε_сг (или соответствующие им характеристику ползучести φ_b,cr меру ползучести C_b,cr;
относительные деформации усадки бетона ε_shr.

Нормативные значения деформационных характеристик бетона следует устанавливать в зависимости от вида бетона, класса бетона по прочности на сжатие, марки бетона по средней плотности, а также в зависимости от технологических параметров бетона, если они известны (состава и характеристики бетонной смеси, способов твердения бетона и других параметров).

В качестве обобщенной характеристики механических свойств бетона при одноосном напряженном состоянии следует принимать нормативную диаграмму состояния (деформирования) бетона, устанавливающую связь между напряжениями σ_b,n (σ_bt,n) и продольными относительными деформациями ε

b,n (ε_bt,n) сжатого (растянутого) бетона при кратковременном действии однократно приложенной нагрузки (согласно стандартным испытаниям) вплоть до их нормативных значений.

Основными расчетными прочностными характеристиками бетона, используемыми в расчете, являются расчетные значения сопротивления бетона:

осевому сжатию R_b;
осевому растяжению R_bt.

Расчетные значения прочностных характеристик бетона следует определять делением нормативных значений сопротивления бетона осевому сжатию и растяжению на соответствующие коэффициенты надежности по бетону при сжатии и растяжении.

Значения коэффициентов надежности следует принимать в зависимости от вида бетона, расчетной характеристики бетона, рассматриваемого предельного состояния, но не менее:

для коэффициента надежности по бетону при сжатии:

1.3 — для предельных состояний первой группы;
1.0 — для предельных состояний второй группы;

для коэффициента надежности по бетону при растяжении:

1,5 — для предельных состояний первой группы при назначении класса бетона по прочности на сжатие;
1.3 — то же, при назначении класса бетона по прочности на осевое растяжение;
1.0 — для предельных состояний второй группы.

Расчетные значения основных деформационных характеристик бетона для предельных состояний первой и второй групп следует принимать равными их нормативным значениям.

Влияние характера нагрузки, окружающей среды, напряженного состояния бетона, конструктивных особенностей элемента и других факторов, не отражаемых непосредственно в расчетах, следует учитывать в расчетных прочностных и деформационных характеристиках бетона коэффициентами условий работы бетона γ

bi.

Расчетные диаграммы состояния (деформирования) бетона следует определять путем замены нормативных значений параметров диаграмм на их соответствующие расчетные значения.

Значения прочностных характеристик бетона при плоском (двухосном) или объемном (трехосном) напряженном состоянии следует определять с учетом вида и класса бетона из критерия, выражающего связь между предельными значениями напряжений, действующих в двух или трех взаимно перпендикулярных направлениях.

Деформации бетона следует определять с учетом плоского или объемного напряженных состояний.

Характеристики бетона — матрицы в дисперсно-армированных конструкциях следует принимать как для бетонных и железобетонных конструкций.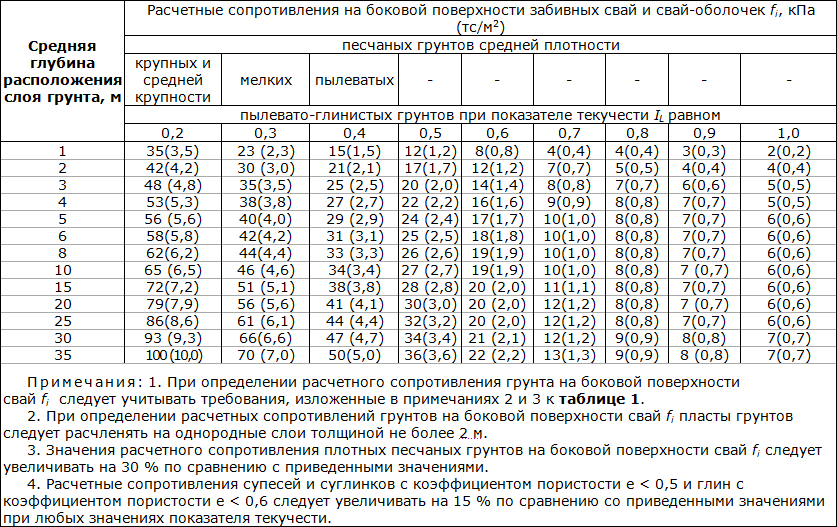

Характеристики фибробетона в фибробетонных конструкциях следует устанавливать в зависимости от характеристик бетона, относительного содержания, формы, размеров и расположения фибр в бетоне, ее сцепления с бетоном и физико-механических свойств, а также в зависимости от размеров элемента или конструкции.

Основными показателями прочности и деформативности арматуры являются нормативные значения их прочностных и деформационных характеристик.

Основной прочностной характеристикой арматуры при растяжении (сжатии) является нормативное значение сопротивления R_s,n, равное значению физического предела текучести или условного, соответствующего остаточному удлинению (укорочению), равному 0,2%. Кроме того, нормативные значения сопротивления арматуры при сжатии ограничивают значениями, отвечающими деформациям, равным предельным относительным деформациям укорочения бетона, окружающего рассматриваемую сжатую арматуру.

Основными деформационными характеристиками арматуры являются нормативные значения:

относительных деформаций удлинения арматуры ε_s0,n при достижении напряжениями нормативных значений R_s,n;
модуля упругости арматуры E_s,n.

Для арматуры с физическим пределом текучести нормативные значения относительной деформации удлинения арматуры ε_s0,n определяют как упругие относительные деформации при нормативных значениях сопротивления арматуры и ее модуля упругости.

Для арматуры с условным пределом текучести нормативные значения относительной деформации удлинения арматуры ε_s0,n определяют как сумму остаточного удлинения арматуры, равного 0,2%, и упругих относительных деформаций при напряжении, равном условному пределу текучести.

Для сжатой арматуры нормативные значения относительной деформации укорочения принимают такими же, как при растяжении, за исключением специально оговоренных случаев, но не более предельных относительных деформаций укорочения бетона.

Нормативные значения модуля упругости арматуры при сжатии и растяжении принимают одинаковыми и устанавливают для соответствующих видов и классов арматуры.

В качестве обобщенной характеристики механических свойств арматуры следует принимать нормативную диаграмму состояния (деформирования) арматуры, устанавливающую связь между напряжениями σ_s,n и относительными деформациями ε_s,n арматуры при кратковременном действии однократно приложенной нагрузки (согласно стандартным испытаниям) вплоть до достижения их установленных нормативных значений.

Диаграммы состояния арматуры при растяжении и сжатии принимают одинаковыми, за исключением случаев, когда рассматривается работа арматуры, в которой ранее были неупругие деформации противоположного знака.

Характер диаграммы состояния арматуры устанавливают в зависимости от вида арматуры.

Расчетные значения сопротивления арматуры R_s определяют делением нормативных значений сопротивления арматуры на коэффициент надежности по арматуре.

Значения коэффициента надежности следует принимать в зависимости от класса арматуры и рассматриваемого предельного состояния, но не менее:

при расчете по предельным состояниям первой группы — 1,1;
при расчете по предельным состояниям второй группы — 1,0.

Расчетные значения модуля упругости арматуры E_s принимают равными их нормативным значениям.

Влияние характера нагрузки, окружающей среды, напряженного состояния арматуры, технологических факторов и других условий работы, не отражаемых непосредственно в расчетах, следует учитывать в расчетных прочностных и деформационных характеристиках арматуры коэффициентами условий работы арматуры γ_si.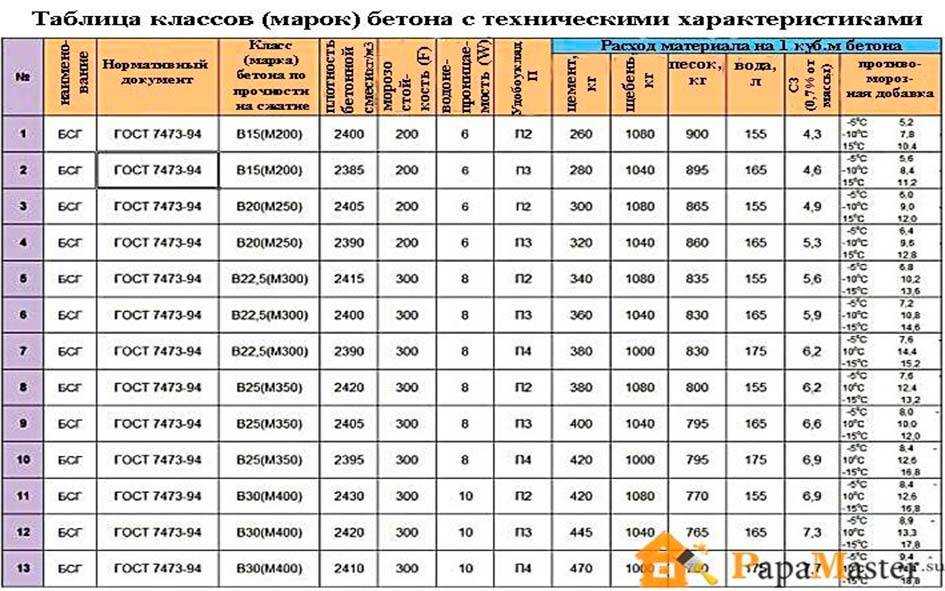

Расчетные диаграммы состояния арматуры следует определять путем замены нормативных значений параметров диаграмм на их соответствующие расчетные значения.

Нормативные и расчетные значения характеристик бетона

2.6.Основными прочностными характеристиками бетона являются нормативные значения:

сопротивления бетона осевому сжатию (призменная прочность) R_b_,_n;

сопротивления бетона осевому растяжению R_bt_,_n.

Нормативные значения сопротивления бетона R_b_,_n и R_bt_,_nв зависимости от класса бетона В даны в табл.2.3

Таблица 2.3

Вид сопротивления	Нормативные значения сопротивления бетона R_b_,_nиR_bt_,_nи расчетные значения сопротивления бетона для предельных состояний второй группыR_b_,_serиR_bt_,_ser, МПа (кгс/см²), при классе бетона по прочности на сжатие
Вид сопротивления	В15	В20	В25	В30	В35	В40	В45	В50	В55	В60
Сжатие осевое (призменная прочность) R_b_,_n,R_b_,_ser	11,0 (112)	15,0 (153)	18,5 (188)	22,0 (224)	25,5 (260)	29,0 (296)	32,0 (326)	36,0 (367)	39,5 (403)	43,0 (438)
Растяжение осевое R_bt_,_n,R_bt_,_ser	1,10 (11,2)	1,35 (13,8)	1,55 (15,8)	1,75 (17,8)	1,95 (19,9)	2,10 (21,4)	2,25 (22,9)	2,45 (25,0)	2,60 (26,5)	2,75 (28,0)

2. 7.Расчетные значения сопротивления бетона осевому сжатию и осевому растяжению для предельных состояний первой группыR_b иR_btопределяются делением нормативных сопротивлений на коэффициенты надежности по бетону, принимаемые равными: при сжатии γ_b= 1,3; при растяжении γ_bt= 1,5.

Расчетные значения сопротивления бетона осевому сжатию и осевому растяжению для предельных состояний второй группы R_b_,_serиR_bt_,_serпринимаются равными нормативными сопротивлениямиR_b_,_nиR_bt,_n.

Расчетные значения сопротивления бетона R_b,R_bt,R_b_,_serиR_bt_,_ser(с округлением) в зависимости от их классов по прочности на сжатие приведены: для предельных состояний первой группы — в табл. 2.4, второй группы — в табл.2.3.

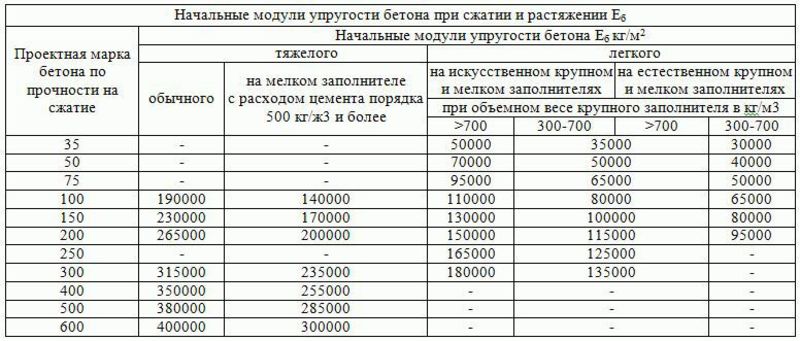
Таблица 2.4

Вид сопротивления	Расчетные значения сопротивления бетона для предельных состояний первой группы R_bиR_bt,МПа (кгс/см²), при классе бетона по прочности на сжатие
Вид сопротивления	В15	В20	В25	В30	В35	В40	В45	В50	В55	В60
Сжатие осевое (призменная прочность) R_b	8,5 (86,6)	11,5 (117)	14,5 (148)	17,0 (173)	19,5 (199)	22,0 (224)	25,0 (255)	27,5 (280)	30,0 (306)	33,0 (336)
Растяжение осевое R_bt	0,75 (7,6)	0,90 (9,2)	1,05 (10,7)	1,15 (11,7)	1,30 (13,3)	1,40 (14,3)	1,50 (15,3)	1,60 (16,3)	1,70 (17,3)	1,80 (18,3)

2. 8.При расчете на действие только постоянных и временных длительных нагрузок расчетные сопротивления бетонаR_bиR_btумножаются на коэффициент условий работы γ_b₁= 0,9.

2.9.Значения начального модуля упругости бетона при сжатии и растяжении принимают в зависимости от класса бетона по прочности на сжатие В согласно табл.2.5.

Таблица 2.5

Значения начального модуля упругости бетона при сжатии и растяжении E_b· 10^-3, МПа (кгс/см²), при классе бетона по прочности на сжатие
В15	В20	В25	В30	В35	В40	В45	В50	В55	В60
24,0 (245)	27,5 (280)	30,0 (306)	32,5 (331)	34,5 (352)	36,0 (367)	37,0 (377)	38,0 (387)	39,0 (398)	39,5 (403)

При продолжительном действии нагрузки значение начального модуля деформаций бетона определяют по формуле

(2. 1)

где φ_b_,_cr-коэффициент ползучести, принимаемый в зависимости от относительной влажности воздуха и класса бетона согласно табл. 2.6.

Таблица 2.6

Относительная влажность воздуха окружающей среды, %	Значения коэффициента ползучести φ_b_,_crпри классе бетона на сжатие
Относительная влажность воздуха окружающей среды, %	В15	В20	В25	В30	В35	В40	В45	В50	В55	В60
выше 75 (повышенная)	2,4	2,0	1,8	1,6	1,5	1,4	1,3	1,2	1,1	1,0
40 — 75 (нормальная)	3,4	2,8	2,5	2,3	2,1	1,9	1,8	1,6	1,5	1,4
ниже 40 (пониженная)	4,8	4,0	3,6	3,2	3,0	2,8	2,6	2,4	2,2	2,0
Примечание. Относительную влажность воздуха окружающей среды принимают по СНиП 23-01-99как среднюю месячную относительную влажность наиболее теплого месяца для района строительства.

2.10.Значения коэффициента поперечной деформации бетона (коэффициент Пуассона) допускается приниматьv_b_,_p= 0,2, а модуль сдвига бетонаG= 0,4E_b.

2.11. Значения коэффициента линейной температурной деформации бетона при изменении температур от минус 40 до плюс 50 °С принимаются α_b_,_t= 1 · 10^-5°С.

2.12. Для определения массы железобетонной конструкции плотность тяжелого бетона принимается равной 2400 кг/м³. Плотность железобетона при содержании арматуры 3 % и менее может приниматься равной 2500 кг/м³, а при содержании арматуры более 3 % плотность определяется как сумма масс бетона и арматуры на единицу объема железобетонной конструкции. При этом масса 1 м арматурной стали принимается по приложению1, а полосовой, угловой и фасонной стали — по государственным стандартам.

При определении нагрузки от собственного веса удельный вес конструкции в кН/м³допускается принимать равным 0,01 от плотности в кг/м³.

2.13. Значения относительных деформаций бетона, характеризующих диаграмму состояния сжатого бетона (ε_b_1,_red, ε_b₂) и растянутого бетона (ε_bt_1,_red, ε_bt₂) приведены в пп.3.26и4.7.

6 СВОЙСТВА БЕТОНА, ИСПОЛЬЗУЕМЫЕ КОНСТРУКТОРАМИ

Сурьяканта | 9 января 2018 г. | Строительство зданий, технология бетона, строительство, дорожное строительство | 6 комментариев

Схема испытания прочности на изгиб

Ниже приведены свойства бетона в затвердевшем состоянии, используемые проектировщиком в процессе проектирования железобетонной конструкции.

1. Прочность на сжатие

Характеристическая прочность определяется как прочность бетона, ниже которой ожидается падение не более 5% результатов испытаний. В соответствии с IS: бетонная смесь 456 всегда рассчитана на целевую прочность, рассчитанную как,

Целевая прочность: Характеристики прочности + (1,65 x стандартное отклонение)

M20 — минимальная марка бетона для использования в железобетонных работах.

2. Прочность на растяжение

Прочность на изгиб является одним из показателей прочности бетона на растяжение. В бетонной конструкции один набор видимых трещин возникает при изгибе, чтобы вычислить коэффициент нагрузки против растрескивания. Согласно IS: 456 прочность бетона на растяжение может быть рассчитана из прочности на сжатие с использованием эмпирического соотношения, определяемого:

Прочность на изгиб: f _cr =0,7 √fck Н/мм ²

3. Модуль упругости

Модуль упругости бетона, на который существенно влияют следующие факторы.

Тип используемых заполнителей,
Тип цемента и
Смешайте пропорции

Это свойство требуется для расчета прогибов железобетонных элементов конструкции, которые формируют важное предельное состояние при расчете железобетонных элементов. При отсутствии данных испытаний модуль упругости бетона обычно связывают с прочностью на сжатие и рассчитывают по эмпирическому соотношению, рекомендованному нормами IS: 456-2000, и выражают как,

E _C = 5000 √fck

, где E _C является краткосрочным статическим модулем эластичности бетона, выраженной в N/MM ²

F _{2 CK}. бетона в Н/мм ² .

4. Усадка бетона

Состав бетона и условия окружающей среды, такие как температура и влажность, влияют на общую усадку бетона. Содержание воды в бетоне существенно влияет на усадку. IS: 456-2000 рекомендует общую деформацию усадки как 0,0003 при отсутствии тестовых данных.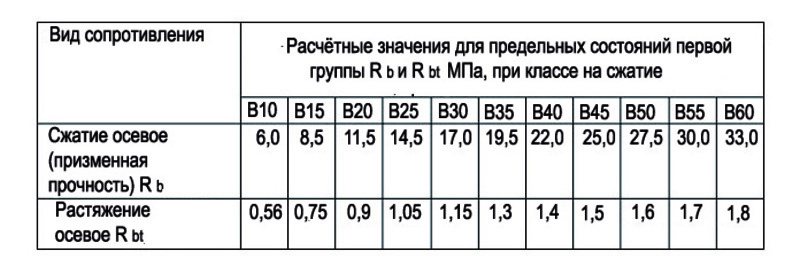 Усадка при высыхании простого бетона может привести к образованию поверхностных трещин. Усадка бетона также влияет на прогиб железобетонных элементов.

5. Ползучесть бетона

Неупругая зависящая от времени деформация, возникающая в бетонном элементе под длительной нагрузкой, называется ползучестию бетона. На ползучесть бетона влияют следующие факторы.

Содержание цемента,
В/Ц отношение,
Температура и влажность,
Размер структурного элемента,
Тип загрузки и период загрузки.

При отсутствии надежных экспериментальных данных коэффициент ползучести выражается как отношение предельной деформации ползучести/упругой деформации при различных возрастных нагрузках в соответствии с рекомендациями МС: 456-2000, приведенными ниже.

Возраст при загрузке	Коэффициент ползучести
7 дней	2,2
28 дней	1,6
1 год	1,1

Ползучесть бетона существенно влияет на прогиб железобетонных изгибаемых элементов. Более высокий коэффициент ползучести приводит к большим прогибам. Значение коэффициента ползучести полезно при расчете зависящих от времени прогибов железобетонных элементов.

6. Коэффициент теплового расширения

Коэффициент теплового расширения бетона, на который в основном влияет тип заполнителя, используемого в бетоне, требуется для проектирования конструкций, таких как дымоходы, резервуары для воды, силосы и т. д. Значения, рекомендуемые в МС: 456-2000 собраны ниже.

Тип заполнителя	Коэффициент теплового расширения для бетона
Кварцит	от 1,2 до 1,3 x 10 ^-5
Песчаник	от 0,9 до 1,2 x 10 ^-5
Гранит	от 0,7 до 0,95 x 10 ^-5
Базальт	от 0,8 до 0,95 x 10 ^-5
Известняк	от 0,6 до 0,9 x 10 ^-5

Теги:Свойства бетона

Об авторе

Сурьяканта

Инженер-геотехник-материаловед. Вы можете связать меня в Google +. Чтобы узнать обо мне больше, просто посетите страницу AboutMe

Тема от MyThemeShop.

Формулы для расчета различных свойств бетона

Содержание

Самым основным испытанием бетона является испытание на прочность при сжатии. Иногда для целей проектирования необходимы другие свойства бетона, такие как предел прочности при растяжении, модуль упругости, значения усадки и т. д.

Исследователи и специалисты установили различные взаимосвязи между прочностью бетона на сжатие и другими свойствами. В этой статье мы собираемся показать формулы, которые связывают прочность бетона на сжатие с другими свойствами, применимыми к Еврокодам.

Нормативная прочность бетона (f _ck )

Нормативная прочность – это такая прочность, ниже которой можно ожидать падение 5% результатов при испытании на прочность на сжатие. Индивидуальные результаты ниже f _ck могут быть получены, но, как правило, их необходимо исследовать только в том случае, если они падают более чем на 4 МПа ниже f _ck (BS EN 206-1, кл. 8.2, таблица 14).

Расчетная прочность (f _cd )

Расчетная прочность бетона на сжатие определяется по формуле;

f _cd = α _cc f _ck /γ _c ——– (1)

где;
f _ck = характеристическая прочность бетона на сжатие в цилиндре через 28 дней
γ _c = частичный коэффициент запаса прочности для бетона (принимается равным 1,5 для Национального приложения Великобритании) неблагоприятные эффекты, связанные с тем, как применяется нагрузка (консервативно принято за 0,85).

Целевая средняя прочность (f _см )

Целевая средняя прочность, f _см , также является значением, используемым для определения состава смеси и предназначенным для учета нормальной изменчивости, которая будет иметь место в производство бетона. Этот предел в 8 МПа для цилиндров согласуется с нормальным распределением со стандартным отклонением (SD) около 5 МПа:

f _ck = f _см – 1,64SD ——- (2)

Где 1,64SD = 8
Следовательно, SD = 8/1,64 ≈ 5 МПа

N/B: Для кубов предел равен 10 МПа что дает стандартное отклонение около 6 МПа.

Изменение прочности на сжатие с течением времени

В то время как расчет обычно основан на 28-дневной прочности, BS EN 1992-1-1, подраздел 3.1.2(6), дает выражение для развития среднего прочность бетона на сжатие во времени при 20°С составляет:

f _см (t) = [β _куб.см (t)]f _см ——— (3)

где;
f _см (t) – средняя прочность на сжатие в возрасте t дней.
β _куб.см (t) = exp{s[1 – (28/t) ^0,5 ]} ——— (3a)

где;
s – коэффициент, который зависит от марки цемента
= 0,20 для цемента классов прочности СЕМ 42,5R, СЕМ 52,5N и СЕМ 52,5R (Класс R)
= 0,25 для цемента классов прочности СЕМ 32,5R, ЦЕМ 42,5N (Класс R) N)
= 0,38 для цемента классов прочности ЦЕМ 32,5Н (Класс S)
(где класс R = высокая ранняя прочность; класс N = нормальная ранняя прочность; класс S = медленная ранняя прочность).

Прочность на растяжение

Прочность на растяжение обычно определяется одним из трех способов: прочность на прямое растяжение, прочность на разрыв при растяжении или прочность на изгиб. Для обычных конструкций средняя прочность на растяжение, f _ctm , связана с прочностью цилиндра выражениями:

Классы прочности ≤ C50/60
f _ctm = 0,30 F _CK ^(2/3) МПа ——— (4)

классы прочности> C50/60
F _CTM = 2,12LOG _E [1 + (F _C 33333. )/10] МПа ——— (5)

Прочность на растяжение при изгибе

Прочность на растяжение при изгибе также может быть рассчитана из средней прочности на растяжение с помощью следующих выражений.

Прочность на изгиб больше:

f _ctm,fl = (1,6 – h/1000)f _ctm ——— (6)
или,
f _ctm,fl = f _ctm

где;
h общая глубина элемента в мм

Развитие прочности при растяжении

BS EN 1992-1-1 содержит выражения для расчета прочности при растяжении при различных сроках созревания:

f _ctm (t) = [t] β _куб.