Что такое расчетное сопротивление грунта? — MIDAS IT
В этой статье вы найдете ответы на следующие вопросы: что такое расчетное сопротивление, как его определить аналитически, как его определить численно с помощью midas GTS NX, и что происходит с грунтом при превышении давления по подошве фундамента расчетного сопротивления.
Аналитическое определение расчетного сопротивления грунта
Вывод формулы расчетного сопротивления
Зависимость, которая представлена на рисунке 1, была получена Н. П. Пузыревским, и, как правило, называется его именем. Данная зависимость была преобразована в формулу в СП 22.13330 для определения расчетного сопротивления грунта по подошве фундамента, см. рисунок 2.
Рисунок 1. Начальная критическая нагрузка на грунт по формуле Н. П. Пузыревского
Рисунок 2. Формула расчетного сопротивления по СП 22.13330
Допущения для формулы расчетного сопротивления
Формула расчетного сопротивления имеет ряд допущений:
- При незначительном развитии зон пластических деформаций принимается линейная зависимость между деформациями и напряжениями;
- Формула выведена из решения плоской задачи, при которой напряжения будут зависеть только от координат x — y;
- В решении формулы заложен равный тензор напряжений от собственного веса грунта (гидростатическое давление), что не совпадает с действительностью.

Определение расчетного сопротивления грунта по СП 22.13330
По СП 22.13330.2016 расчет расчетного сопротивления относится к пункту 5.6. А пункт 5.6 — это расчет оснований по деформациям. Целью расчета оснований по деформациям является ограничение абсолютных или относительных перемещений пределами, при которых гарантируется нормальная эксплуатация сооружения и не снижается его долговечность. Важно понимать, что расчетное сопротивление — это проверка по II-ой группе предельных состояний, а не по I-ой.
Согласно пункту 5.6.6 — «расчет деформаций основания фундамента при среднем давлении под подошвой фундамента р, не превышающем расчетное сопротивление грунта R (см. 5.6.7), следует выполнять, применяя расчетную схему в виде линейно-деформируемого полупространства (см. 5.6.31) с условным ограничением глубины сжимаемой толщи Нс (см. 5.6.41)». Этот пункт означает, что величина расчетного сопротивления — это ограничение значения давления по подошве фундамента, при превышении которого нельзя считать осадку по пункту 5.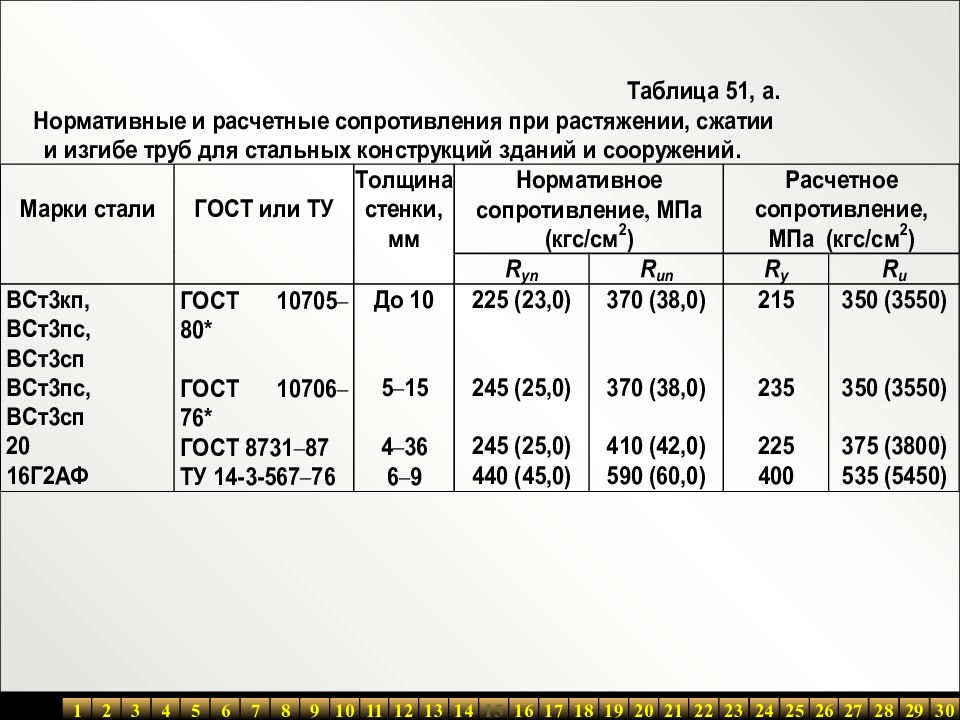
Было определено расчетное сопротивление ленточного фундамента без подвала с глубиной заложения 2 м, шириной подошвы 2 м, с опиранием в водонасыщенный грунт с углом внутреннего трения 18 градусов, с удельным сцеплением 10 кПа и с удельным весом 20.3 кН/м3 и 11.1 кН/м3 во взвешенном состоянии. По аналитическому расчету было получено значение расчетного сопротивления в 190 кПа.
Рисунок 3. Определение расчетного сопротивления аналитическим способом
Численное определение расчетного сопротивления грунта в midas GTS NX
Для численного расчета была реализована плоская задача. На рисунке 3 представлены стадии расчета в трехмерной постановке для наглядной визуализации (данную задачу нет смысла решать в трехмерной постановке): первая стадия — начальная, вторая стадия — откопка котлована, третья стадия — это активация ленточного фундамента с нагрузкой по обрезу и обратная засыпка пазух котлована, см.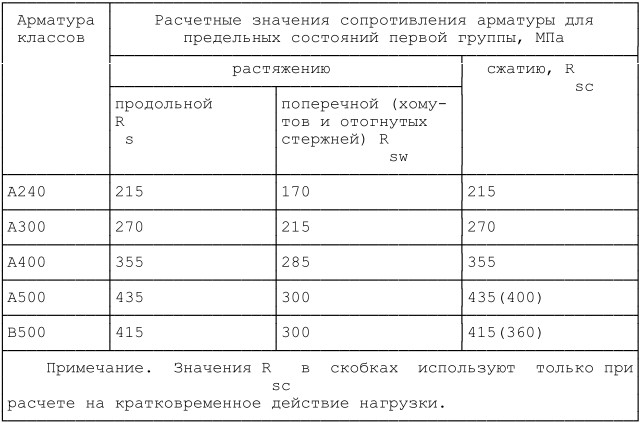 рисунок 4. При решении данной задачи использовалась модель грунта Мора-Кулона.
рисунок 4. При решении данной задачи использовалась модель грунта Мора-Кулона.
Рисунок 4. Стадийность в midas GTS NX
Расчетное сопротивление численным методом можно получить двумя способами:
- измерить величину пластических зон под подошвой фундамента. Расчетное сопротивление — это такая нагрузка по подошве фундамента, при которой пластические зоны под подошвой фундамента распространяется на глубину, равную величине четверти ширины подошвы фундамента;
- построить график давления от осадки для точки, расположенной по центру подошвы фундамента, и давление, при котором график начнет изменяться нелинейно, это и есть величина расчетного сопротивления.
Для того чтобы определить расчетное сопротивление, на обрез фундамента была приложена нагрузка в 190 кПа, и в настройках последней стадии данная нагрузка была разделена на 20 шагов нагружения. Для того чтобы в выводе результатов присутствовал каждый шаг нагружения, в настройках нужно выставить пункт «Every Increment» (см. рисунок 5). Параметры решателя для конкретной стадии приоритетнее настроек, заданных в расчетном случае. Поэтому необходимо изменить и другие параметры решателя для стадии с пригрузом, чтобы задача была рассчитана корректно: «Convergence Criteria», «Advanced Nonlinear Setting».
рисунок 5). Параметры решателя для конкретной стадии приоритетнее настроек, заданных в расчетном случае. Поэтому необходимо изменить и другие параметры решателя для стадии с пригрузом, чтобы задача была рассчитана корректно: «Convergence Criteria», «Advanced Nonlinear Setting».
Рисунок 5. Разделение нагрузки на инкременты
Для каждой подстадии была измерена зона пластических деформаций под подошвой фундамента. За величину расчетного сопротивления было принято давление на последней стадии, на которой пластическая зона не превышает b/4 (0.5 м). На 12-ой подстадии размер пластических зон под подошвой фундамента составил 0.5 м (см. рисунок 6), это соответствует нагрузке 114 кПа (190*12/20=114 кПа), а на следующей ступени для нагрузки 123 кПа (190*13/20=123 кПа) размер пластических зон равен 0.75 м (см. рисунок 7). Это означает, что расчетное сопротивление по численному методу составляет 114 кПа, так как на 13-й ступени условие по пластическим деформациям уже не выполняется.
Рисунок 6. Пластические зоны (красные кружки) при нагрузке 114кПа
Рисунок 7. Пластические зоны (красные кружки) при нагрузке 123 кПа
Рисунок 8. Пластические зоны (красные кружки) при нагрузке 190 кПа
Далее значение расчетного сопротивления необходимо проверить графическим способом. Чтобы построить график, нужно извлечь результаты для точки по центру подошвы фундамента с помощью команды «Extract», см. рисунок 9. И далее эти данные необходимо скопировать в Excel и построить график нагрузки от перемещения.
Для визуальной оценки отклонений была построена линия тренда по первым точкам графика, и, если увеличить данный график, то видно, что после 114 кПа график имеет значительные отклонения от линии тренда, то есть график начинает изменяться нелинейно, и при каждой следующей итерации эти отклонения все больше и больше, см. рисунок 10. Данный график был продлен до уровня вертикального напряжения в 400 кПа для наглядности.
Рисунок 9. Извлечение результатов расчета
Рисунок 10. График вертикального давления по подошве фундамента от осадки P(S)
Выводы
- Расчетное сопротивление, определенное в midas GTS NX, на 40% меньше аналитического. Это происходит из-за ряда допущений при расчете по СП 22.13330. Допущения перечислены выше в настоящей статье.
- Оценивать расчетное сопротивление по численному методу нужно по величине пластических зон и по графику давления по подошве фундамента от его осадки.
- Если давление по подошве больше значения расчетного сопротивления, то недопустимо считать осадку методом послойного суммирования, нужно использовать другие методики расчета осадки, например численное моделирование в midas GTS NX.
Сопротивление грунта — НПКБ «СТРОЙПРОЕКТ»
- Главная >
- Информация >
- Расчетное сопротивление грунта
В случае связного грунта и небольших нагрузках деформация основания будет иметь упругий характер. На этом этапе не происходит уплотнения грунта и изменения структурной прочности σstr. Следует отметить, что сыпучие (несвязанные) грунты или глинистые грунты нарушенной структуры не обладают структурной прочностью.
На этом этапе не происходит уплотнения грунта и изменения структурной прочности σstr. Следует отметить, что сыпучие (несвязанные) грунты или глинистые грунты нарушенной структуры не обладают структурной прочностью.
При увеличении нагрузки Р, больше σstr, развивается процесс уплотнения. При этом возникает перемещение частиц грунта, снижается его пористость. Связь деформаций и нагрузки имеет близкую к линейной зависимость. Развивающиеся осадки несут стабилизированный характер, т.е. не развиваются во времени. При этом касательные напряжения значительно ниже предельных, т.е. отсутствует предельные области в любой точке основания. Наибольшая нагрузка на этом участке называется начальной критической нагрузкой Рн.кр. См. рисунок.
Нормативное сопротивление грунта
Опытным путем и продолжительными наблюдениями за осадками зданий и сооружений было установлено, что если допустить под фундаментом развитие зон предельного равновесия ну глубину не более 1/4 от ширины фундамента, то несущая способность основания остается обеспеченной, а развитие осадок во времени имеет стабилизированный характер, т. е. стремящийся к постоянной величине. При этом связь напряжений и деформаций в грунтовом массиве остается приближенной к линейной зависимости, т.е. возможно применение математического аппарата теории линейно деформируемого грунта.
е. стремящийся к постоянной величине. При этом связь напряжений и деформаций в грунтовом массиве остается приближенной к линейной зависимости, т.е. возможно применение математического аппарата теории линейно деформируемого грунта.
Таким образом, еще в середине 20-го века было введено понятие нормативного сопротивления грунта, соответствующего наибольшему значению среднего сжимающего напряжения, до достижении которого сохраняется относительно линейная зависимость между напряжениями и деформациями грунта.
Расчетное сопротивление грунта
Дальнейшее развитие строительной науки и практики позволило еще дальше отодвинуть предел линейной работы грунта. Было введено понятие расчетного сопротивления грунта основания R.
Сегодня расчетное сопротивление грунта широко используется в проектной и строительной практике. Эта величина подлежит нормированию и должна рассчитываться строго в соответствии с действующими нормами и правилами в строительстве. Как правило, его используют для предварительного определения габаритов фундаментов и для расчета деформаций основания, когда средние напряжения под подошвой фундамента не должны превышать значения R.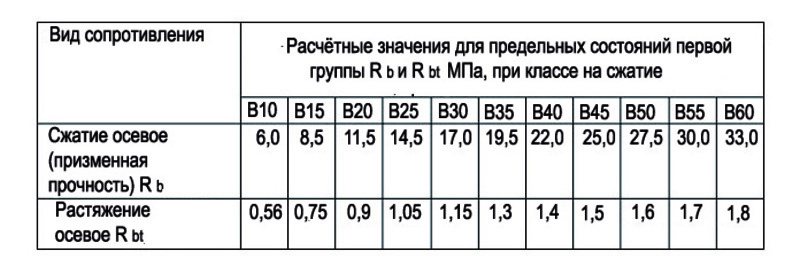
Определить расчетное сопротивление грунта основания, в режиме онлайн, можно здесь.
Предельная критическая нагрузка
При увеличении нагрузки Р, больше значения расчетного сопротивления R, в основании формируются развитые области предельного равновесия. В некоторых случаях, это явление проявляется в виде валов выпирания около подошвы фундамента. Как правило, при таких нагрузках происходит полная потеря устойчивости грунта основания, а называется такая нагрузка — предельная критическая нагрузка Рu, см. рисунок, т.е. это нагрузка при которой происходит исчерпание несущей способности грунтов.
В практике проектирования оснований и фундаментов, предельные критические нагрузки на фундаменты определяются при расчетах оснований по несущей способности. Цель таких расчетов, в соответсвии со строительными нормами и правилами, является обеспечение прочности и устойчивости оснований, а также недопущение сдвига фундамента по подошве.
Методика определения критических нагрузок различна для скальных, дисперсных и нестабилизированных глинистых грунтов.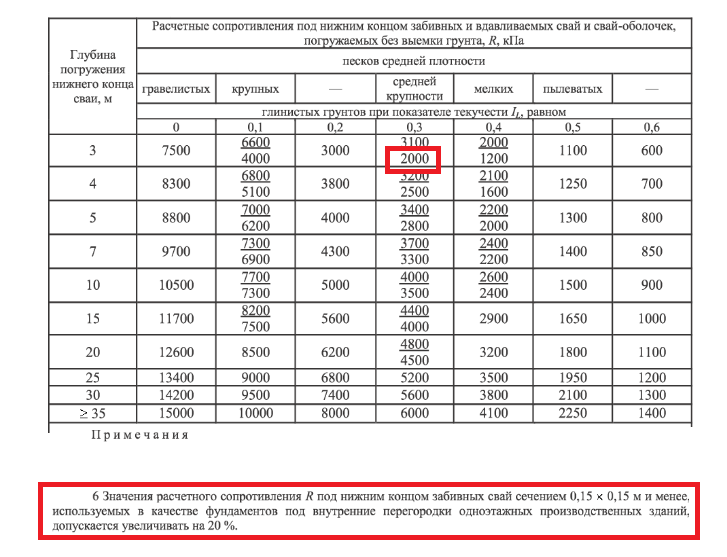
Расчет конструкций фундаментов
Проектирование фундаментов
характеристических сопротивлений или расчетных сопротивлений?
Засов Великобритания | 31 августа 2022 г.
В этой статье обсуждаются расчетные данные, предоставленные BlindBolt, которые представляют собой расчетные сопротивления и должны сравниваться непосредственно с расчетными нагрузками (предельными нагрузками), приложенными к креплению. Расчетные сопротивления были определены на основе обширной серии физических испытаний болтов различного диаметра из нержавеющей и углеродистой стали, из материалов различной толщины и прочности.
Расчет расчетных сопротивлений в EN 1993
В EN 1993 расчетное сопротивление определяется как характеристическое сопротивление, деленное на частичный коэффициент безопасности, γ M .
Различные частичные коэффициенты безопасности подходят для различных компонентов в соединении – Таблица 2.
В БС 59 ситуация несколько иная50, где расчетное сопротивление рассчитывается напрямую. Поскольку расчетные сопротивления в обоих кодах очень похожи, подразумевается, что частичный коэффициент запаса прочности применяется в пределах прочности конструкции, используемой в BS 5950, а не является явным.
Разработчики иногда запрашивают у BlindBolt характеристическое значение сопротивления для использования с конструкциями в соответствии с Еврокодом, но для этого разработчику потребуется выбрать соответствующее значение γ M для расчета расчетного сопротивления. Уникальная форма BlindBolt явно отличается от обычного болта, то есть γ Значение M для стандартных компонентов может быть неподходящим.
Для изготовленных на заказ креплений, таких как BlindBolt, единственным надежным способом определения расчетного сопротивления является физическое испытание.
Свяжитесь с нашей командой сегодня по телефону +44 (01299) 272 955
Расчетные сопротивления, определенные в результате испытаний
Приложение D стандарта EN 1990 облегчает определение как характеристических, так и расчетных сопротивлений на основе результатов испытаний. Основной подход заключается в определении среднего сопротивления на основе ряда испытаний и уменьшении среднего значения на заданное число стандартных отклонений. По мере проведения большего количества тестов количество стандартных отклонений, которые необходимо вычесть из среднего значения, уменьшается.
Если расчетное сопротивление должно быть рассчитано, уменьшение является более высоким штрафом, чем если должно быть рассчитано характеристическое сопротивление. Например, если проводится шесть испытаний, для расчета характеристического сопротивления необходимо вычесть 1,77 стандартного отклонения.
Для расчета расчетного сопротивления необходимо вычесть более штрафные 3,33 стандартных отклонения, но этот подход устраняет неопределенность в отношении того, какое значение γM следует применять к характеристическому сопротивлению. Сопротивления, указанные BlindBolt, являются расчетными сопротивлениями — не следует применять частичный коэффициент безопасности. Приведенные значения сопротивления можно непосредственно сравнить с предельной нагрузкой на крепление.
Сопротивление сдвигу – неожиданный результат испытаний
В соответствии с BS 5950 и EN 1993, сопротивление сдвигу крепежного изделия по понятным причинам зависит от площади поперечного сечения. Сопротивление сдвигу, определенное в результате испытания, проведенного в соответствии с описанной выше процедурой, привело к более высокому сопротивлению, чем можно было бы рассчитать в соответствии со стандартом проектирования. BlindBolt пришел к выводу, что, несмотря на результаты испытаний, сопротивление сдвигу должно быть ограничено значением, соответствующим выражениям в стандарте проектирования, исходя из площади поперечного сечения. В этом случае расчетное сопротивление сдвигу точно соответствует положениям стандарта проектирования. Для конструкций по Еврокоду указанное значение M применяется к расчетному характеристическому сопротивлению. Для исполнений по BS 5950 принимается указанная прочность.
В этом случае расчетное сопротивление сдвигу точно соответствует положениям стандарта проектирования. Для конструкций по Еврокоду указанное значение M применяется к расчетному характеристическому сопротивлению. Для исполнений по BS 5950 принимается указанная прочность.
Свяжитесь с нашей командой сегодня по телефону +44 (01299) 272 955
Сопротивления BlindBolt
Сопротивления, предоставляемые BlindBolt, являются расчетными сопротивлениями (или «предельными» сопротивлениями), а не характеристическими сопротивлениями. Нет необходимости делить приведенные в таблице сопротивления на любое значение γ M .
Узнайте больше, поговорив с членом нашей дружной, экспертной команды сегодня по телефону +44 (01299) 272 955 или по электронной почте [email protected]. Мы с нетерпением ждем вашего ответа
Расчетное сопротивление стального соединения (EN)
Учебники
EN (Еврокод)
CBFEM
Сопротивление
Связь
Этот артикул также доступен на:
В этом учебном пособии показано, как использовать IDEA StatiCa Connection для моделирования, проектирования и проверки соединения конструкционной стали, а также для расчета расчетного сопротивления соединения.
1 Новый проект
Давайте запустим IDEA StatiCa Connection и откроем файл проекта для этого руководства.
2 Анализ напряжения и деформации
Чтобы увидеть разницу между двумя типами анализа, давайте сначала выполним анализ напряжения/деформации. Рассчитать модель — используйте кнопку на верхней ленте.
Вы можете непосредственно увидеть общие результаты анализа напряжения/деформации, отображаемые в верхнем левом углу сцены.
3 Расчетное сопротивление соединения
Сначала скопируйте элемент проекта, чтобы сохранить предыдущую работу и изменить тип анализа на DR (Расчетное сопротивление соединения) для нового элемента проекта (Соединение 2).
Теперь запустите анализ расчетного сопротивления соединения с помощью команды Рассчитать на верхней ленте.
4 Результаты
Перейдите к вкладке Проверить и Расчетное сопротивление соединения в таблицах результатов. Приложение рассчитывало коэффициент (процент) приложенной нагрузки для достижения расчетного сопротивления соединения. Под таблицей отображается путь загрузки.
Приложение рассчитывало коэффициент (процент) приложенной нагрузки для достижения расчетного сопротивления соединения. Под таблицей отображается путь загрузки.
Для лучшего понимания результатов см. Теоретические основы.
Хотите улучшить свои навыки? Посетите наш кампус
Узнайте, как эффективно использовать IDEA StatiCa, с помощью наших онлайн-курсов для самостоятельного обучения.
Начать обучение
ДОПОЛНИТЕЛЬНОЕ СОДЕРЖИМОЕ
Учебники
Расчет пропускной способности стального соединения (EN)
Связь
EN (Еврокод)
Учебники
Анализ жесткости стального соединения (EN)
Связь
EN (Еврокод)
Вебинары
Решение IDEA StatiCa Connection — основы
30 июня 2021 г.
