Расчет жб балки: Расчёт железобетонной балки

Содержание

РАСЧЕТ СЛОЖНОНАПРЯЖЕННОЙ ЖЕЛЕЗОБЕТОННОЙ БАЛКИ КОРОБЧАТОГО СЕЧЕНИЯ | БУЛКИН

1. Байков В.Н., Елагин Э.Г., Вернигор В.А., Туров А.И. Влияние ядра сечения на деформативность железобетонного стержня прямоугольного поперечного сечения при кручении // Сопротивление железобетонных элементов силовым воздействиям. Ростов н/д: РИСИ. 1985. С. 42-48.

2. Гвоздев А.А. Расчет несущей способности по методу предельного равновесия. М.: Стройиздат, 1949. 279 с.

3. Морозов В.И., Бахотский И.В. К расчету фиброжелезобетонных конструкций, подверженных совместному воздействию кручения с изгибом // Современные проблемы науки и образования. 2013. № 5. С.109.

4. Федоров В.С., Колчунов Вл.И., Покусаев А.А. Расчет расстояния между пространственными трещинами и ширины их раскрытия в железобетонных конструкциях при кручении с изгибом (случай 2) // Жилищное строительство. 2016. №5. С. 16–21

5. Adheena Thomas, Afia S Hameed. An Experimental Study On Combined Flexural And Torsional Behaviour Of RC Beams // International Research Journal of Engineering and Technology. 2017. Vol. 04. No. 05. Pp.1367–1370.

6. Mostofinejad D., Talaeitaba S.B. Nonlinear Modeling of RC Beams Subjected to Torsion using the Smeared Crack Model // Procedia Engineering 14 (2011) 1447-1454. Elsevied Ltd. 2011. Pp.1447-1454.

7. G. Klein, G. Lucier, S. Rizkalla, P. Zia and H. Gleich. Torsion simplified: a failure plane model for desigh of spandrel beams // ACI Concrete International Journal, February 2012. Pp.1-8.

8. Ilker Kalkan, Saruhan Kartal. Torsional Rigidities of Reinforced Concrete Beams Subjected to Elastic Lateral Torsional Buckling // International Journal of Civil and Environmental Engineering. 2017. Vol. 11. No.7. Pp.969–972.

9. Булкин С.А. Кручение с изгибом сталефиброжелезобетонной балки прямоугольного сечения // Строительство и реконструкция. 2021. № 2. С. 3-13.

10. Демьянов А.И., Алькади С.А. Статико-динамическое деформирование железобетонных элементов пространственной рамы при их сложном сопротивлении // Известия высших учебных заведений. Строительство. 2018. № 11 (719). С. 20-33.

11. Травуш В.И., Карпенко Н.И., Колчунов В.И., Каприелов С.С., Демьянов А.И., Конорев А.В. Результаты экспериментальных исследований конструкций квадратного и коробчатого сечений из высокопрочного бетона при кручении с изгибом // Строительство и реконструкция. 2018. №6(80). С. 32-43.

12. Травуш В.И., Карпенко Н.И., Колчунов В.И., Каприелов С.С., Демьянов А.И., Булкин С.А., Московцева В.С. Результаты экспериментальных исследований сложнонапряженных балок круглого поперечного сечения из высокопрочного фиброжелезобетона // Строительная механика инженерных конструкций и сооружений. 2020. №16 (4). С.290-297.

13. Травуш В.И., Карпенко Н.И., Колчунов В.И., Каприелов С.С., Демьянов А.И., Конорев А.В. Основные результаты экспериментальных исследований железобетонных конструкций из высокопрочного бетона В100 круглого и кольцевого сечений при кручении с изгибом // Строительная механика инженерных конструкций и сооружений. 2019. №1. С.51-61.

14. Демьянов А.И., Сальников А.С., Колчунов Вл. И. Экспериментальные исследования железобетонных конструкций при кручении с изгибом и анализ их результатов // Строительство и реконструкция. 2017. №4(72). С. 17–26.

15. Демьянов А.И., Колчунов В.И., Покусаев А.А. Экспериментальные исследования деформирования железобетонных конструкций при кручении с изгибом // Строительная механика инженерных конструкций и сооружений. 2017. №6. С. 37–44.

16. Демьянов А.И., Наумов Н.В., Колчунов Вл.И. Некоторые результаты экспериментальных исследований составных железобетонных конструкций при кручении с изгибом // Строительство и реконструкция. 2018. №5(79). С. 13–23.

17. Колчунов Вл.И., Федоров В.С. Понятийная иерархия моделей в теории сопротивления строительных конструкций // Промышленное и гражданское строительство. 2020. №8. С. 16–23. doi:10.33622/0869-7019.2020.08.16-23.

18. Карпенко Н.И. Общие модели механики железобетона. М.: Стройиздат, 1996. 410 с.

19. Karpenko N. I., Kolchunov Vl.I., Kolchunov V.I., Travush V.I. Calculated model of a complex-stressed reinforced concrete element under torsion with bending // International Journal for Computational Civil and Structural Engineering. 2021. Т. 17. No. 1. Pp. 34-47.

20. Карпенко Н.И. Теория деформирования железобетона с трещинами. М., Стройиздат, 1976. 208 с.

21. Методическое пособие «Статически неопределимые железобетонные конструкции. Диаграммные методы автоматизированного расчета и проектирования». Федеральный центр нормирования, стандартизации и оценки соответствие в строительстве. М.. 2017. 197 с.

22. Чистова Т.П. Экспериментальное исследование деформаций обычных железобетонных элементов коробчатого и сплошного прямоугольного сечения при чистом кручении. Прочность и жесткость железобетонных конструкций. Под редакцией С.А. Дмитриева и С.М. Крылова. М., Стройиздат, 1971.

Расчет прочности балки прямоугольного сечения (СП)

Цель: Проверка режима экспертизы железобетона в постпроцессоре «Железобетон» вычислительного комплекса SCAD

Задача: Проверить прочность сечения балки при заданном армировании

Ссылки: Пособие по проектированию бетонных и железобетонных конструкций из тяжелого бетона без предварительного напряжения арматуры (к СП 52-101-2003), 2005, с. 28.

Файл с исходными данными:

SCAD 6 SP.spr
отчет – SCAD 6 SP.doc

Соответствие нормативным документам: СП 52-101-2003.

Исходные данные:

Макс. 0 Т
Привязка 0 м

M_y

Макс. 0 кН*м
Привязка 0 м

Макс. 630 кН*м
Привязка 3 м

M_z

M_k

Q_z

Макс. 42,81 Т
Привязка 0 м

Макс. -42,81 Т
Привязка 6 м

Q_y

Длина стержня 6 м
Длина гибкой части 6 м
Загружение L1 — «140 кН/м»

Конструктивная группа Балка

Расстояние между арматурными стержнями в первом ряду S1 меньше допускаемого (см.

п. 8.3.3 СП 52-101-2003) .
Элементы: 1

Коэффициент надежности по ответственности γ_n = 1
Тип элемента — Изгибаемый
Напряженное состояние — Одноосный изгиб

Коэффициенты учета сейсмического воздействия
Нормальные сечения	0
Наклонные сечения	0

Расстояние до ц.т. арматуры
a₁	a₂
мм	мм
70	30

Арматура	Класс	Коэффициент условий работы
Продольная	A400	1
Поперечная	A240	1

Бетон
Вид бетона: Тяжелый
Класс бетона: B20

Коэффициенты условий работы бетона
γ_b1	учет нагрузок длительного действия	1
γ_b2	учет характера разрушения	1
γ_b3	учет вертикального положения при бетонировании	1
γ_b4	учет замораживания/оттаивания и отрицательных температур	1

Влажность воздуха окружающей среды — 40-75%

Трещиностойкость
Ограниченная ширина раскрытия трещин
Требования к ширине раскрытия трещин выбираются из условия сохранности арматуры
Допустимая ширина раскрытия трещин:

Непродолжительное раскрытие 0,4 мм
Продолжительное раскрытие 0,3 мм

Конструктивная группа Балка. Элемент № 1
Длина элемента 6 м

Заданное армирование

Участок	Арматура	Сечение
1	S₁ — 6Ø32 S₂ — 3Ø12

Участок

Арматура

Сечение

S₁ — 6Ø32

S₂ — 3Ø12

Результаты расчета
Участок	Коэффициент использования	Проверка	Проверено по СНиП
1	1,02	Прочность по предельному моменту сечения

Сравнение решений:

Проверка	Прочности сечения
Пособие	630/606,2 = 1,039
SCAD	1,02
Отклонение, %	1,9 %

Бесплатное онлайн-программное обеспечение для проектирования бетонных профилей.

Расчет шага арматуры и площади арматуры для железобетона.

Проанализируйте конструкцию железобетонной балки или колонны в соответствии с Еврокодом 2 с помощью этого калькулятора арматуры.

НовыйСохранить Открыть Загрузить отчет в формате PDF

Профиль раздела
М/Н участок
Сводка результатов
Детали арматуры
Теория

Бетонный профиль

Прочность бетона f _ck МПа

Введите прочность больше 0 и меньше 60 МПа.

Ширина секции мм

Введите ширину больше 0 и меньше 3000 мм.

Глубина сечения мм

Введите глубину больше 0 и меньше 3000 мм.

Нижняя арматура

Кол-во стержней 2345678910

Диаметр прутка 810121620253240 мм

Крышка (вниз) мм

Введите покрытие больше 0 и меньше глубины/2

Расширенные настройки:

Укажите верхнюю арматуру

Кол-во стержней 02345678910

Диаметр стержня 810 мм

Крышка (сверху) мм

Введите защитный слой больше 0 и меньше глубины/2

4. Свойства армирования:

Прочность стали f _yk МПа

Введите прочность больше 0 и меньше 700 МПа

Крышка до краев мм

Введите крышку больше 0 и меньше ширины/2

Расширенные настройки

Теория расчета

Для чего используется бетон в строительстве?

Прочность, стоимость и доступность бетона сделали его наиболее широко используемым строительным материалом 21 века. Бетон производится из цемента, смешанного с водой. Часто в смесь добавляют каменный заполнитель и химические добавки для улучшения структурных характеристик и обрабатываемости материала. Чаще всего используется смесь цемента, заполнителей и воды в соотношении 1:2:4.

Зачем нужно армирование бетона?

Бетон слаб на растяжение и сдвиг. Стальная арматура образует связь с бетоном и придает бетону прочность на растяжение, предотвращает опасное хрупкое разрушение материала. Хрупкое разрушение опасно в неармированном бетоне, так как происходит внезапно и не предупреждает о скором разрушении материала.

Как найти нейтральную ось железобетона?

Когда балка изгибается, одна сторона балки испытывает растягивающее напряжение, а другая — сжимающее. Образуется нейтральная ось, вдоль которой напряжение равно нулю. Положение нейтральной оси зависит от положения и характеристик любой стальной арматуры и характера приложенной нагрузки.

Как рассчитать сопротивление бетона на изгиб и осевое сопротивление?

Каждое нейтральное положение оси в бетонной секции будет иметь результирующее осевое сопротивление и сопротивление изгибу. График зависимости осевого сопротивления от сопротивления изгибу для каждого нейтрального положения оси создает огибающую, которая представляет мощность бетонной секции.

Как рассчитать площадь и сопротивление сдвигу бетона?

Срезные звенья используются для сопротивления поперечному усилию, воздействующему на бетон. Уравнение несущей способности бетонной стойки используется для определения площади звеньев сдвига, необходимой для обеспечения необходимого сопротивления звеньев сдвигу.

Как рассчитать минимальную площадь армирования бетона?

Минимальная площадь армирования должна составлять 0,24% площади бетонного сечения в качестве типичного значения.
Чтобы обеспечить контроль трещин и удовлетворить требования SLS, в бетоне должна быть предусмотрена минимальная площадь армирования. Величину можно оценить из уравнения равновесия между усилием растяжения в бетоне до образования трещин и усилием растяжения в арматуре при текучести.
Минимальную площадь железобетонной стали можно рассчитать по уравнению
As,min·σs = kc · k · fct,eff · Act
Где As,min эквивалентно минимальной площади, требуемой в зоне растяжения.
Акт – это площадь бетона в зоне растяжения.
σs — напряжение в стали после образования трещины, его можно принять за предел текучести стали
fct,eff — предел прочности бетона при растяжении
k – коэффициент, учитывающий влияние неравномерных самоуравновешивающихся напряжений, приводящих к уменьшению удерживающих сил

= 1,0 для стенок с h ≤ 300 мм или полок шириной менее 300 мм
= 0,65 для стенок с h ≥ 800 мм или полок шириной более 800 мм
kc — коэффициент, учитывающий распределение напряжения в сечении непосредственно перед растрескиванием и изменение плеча рычага:
Для чистого напряжения kc можно принять равным 1,0, это также можно использовать во всех случаях как консервативное значение.

Как рассчитать максимальную площадь армирования бетона?

Максимум от 1% до 2% площади бетона должно быть предусмотрено в качестве арматуры

Как найти расстояние между арматурными стержнями?

Минимальное расстояние между стержнями должно быть больше, чем размер стержня, максимальный размер заполнителя + 5 мм или 20 мм в соответствии с Еврокодом 2 (EC2)
Минимальное горизонтальное расстояние между стержнями должно быть больше, чем размер стержня или максимальный размер заполнителя + 5 мм. Минимальное вертикальное расстояние между стержнями должно быть больше размера стержня или 2/3 максимального размера заполнителя в соответствии с BS8110

Как рассчитать ширину трещины в бетоне?

Напряжение сжатия в бетоне должно быть ограничено, чтобы избежать продольных трещин, микротрещин или высоких уровней ползучести, где они могут привести к неприемлемому влиянию на функцию конструкции.
Продольные трещины могут возникать, если уровень напряжения при характерном сочетании нагрузок превышает критическое значение. Такое растрескивание может привести к снижению долговечности. При отсутствии других мер, таких как увеличение покрытия арматуры в сжимаемой зоне или ограничение поперечной арматурой, может быть целесообразным ограничить сжимающее напряжение до более низкого значения для бетона, подвергающегося суровым условиям воздействия.

Как спроектировать железобетонную колонну

Диаграммы грузоподъемности бетонной колонны можно использовать для расчета требуемой площади армирования по высоте, ширине, приложенной осевой силе и изгибу.

Для чего нужен этот калькулятор?

Этот бесплатный калькулятор может использоваться инженерами-строителями для проектирования железобетона. Этот инструмент можно использовать для расчета площади арматуры и арматурных стержней, а также расчета расстояния между стержнями в соответствии с европейскими нормами (Еврокод 2). Рассчитайте нейтральную ось железобетонной балки и по ней определите растягивающие и сжимающие напряжения, возникающие в результате действия изгибающего момента. Спроектируйте арматуру, работающую на сдвиг, и убедитесь, что краткосрочная и долговременная ширина трещин в бетоне соответствует предельному состоянию.

Внесите свой вклад в этот код

Этот код является открытым исходным кодом, и вы можете внести свой вклад в его разработку.

Вы можете найти исходный код на GitHub здесь:

Concrete-Properties

Зарегистрируйтесь, чтобы разблокировать все наши бесплатные инженерные калькуляторы аккаунт? Войти

Я согласен с условиями.

Расчет перемещений для рабочих нагрузок железобетонных балок и плит с использованием физически нелинейного анализа

. 2022 23 ноября; 15 (23): 8307.

дои: 10.3390/ma15238307.

Антонио Ренато Бичелли ¹ , Педро Кантор ¹ , Рафаэль Вонг ² , Марио Руи Арруда ³

Принадлежности

¹ Instituto Superior Técnico, Universidade de Lisboa, 1049-001 Лиссабон, Португалия.
² Faculdade de Ciências e Tecnologia, Universidade Nova de Lisboa (UNL), 2825-149 Caparica, Portugal.
³ CERIS-Instituto Superior Técnico, 1049-001 Лиссабон, Португалия.

PMID: 36499804
PMCID: PMC9741035
DOI: 10. 3390/ma15238307

Бесплатная статья ЧВК

Антонио Ренато Бичелли и др. Материалы (Базель). 2022 .

Бесплатная статья ЧВК

. 2022 23 ноября; 15 (23): 8307.

дои: 10.3390/ma15238307.

Авторы

Антонио Ренато Бичелли ¹ , Педро Кантор ¹ , Рафаэль Вонг ² , Марио Руи Арруда ³

Принадлежности

¹ Instituto Superior Técnico, Universidade de Lisboa, 1049-001 Лиссабон, Португалия.
² Faculdade de Ciências e Tecnologia, Universidade Nova de Lisboa (UNL), 2825-149 Caparica, Portugal.
³ CERIS-Instituto Superior Técnico, 1049-001 Лиссабон, Португалия.

PMID: 36499804
PMCID: PMC9741035
DOI: 10.3390/ma15238307

Абстрактный

Эта статья направлена на использование нелинейного физического анализа для расчета смещения балок и плит в состоянии с трещинами. В этом исследовании используется коммерческое программное обеспечение SAP2000 для выполнения численного анализа с использованием формулы конечных элементов с применением многослойного метода. Первоначально было проведено параметрическое исследование для оценки вертикального смещения при эксплуатационных нагрузках железобетонных балок и плит с использованием различных пролетов, условий крепления и геометрии. Чтобы проверить модель конечных элементов, в исследовании сравнивались значения смещения для линейного анализа с использованием таблиц Бареса. В последующем применяются упрощенные методы расчета водоизмещения в перспективе с использованием счетов от Euro-International du Béton (CEB). Затем эти значения сравниваются с физически нелинейным анализом в состоянии длительного взлома с помощью SAP2000. В числовых и аналитических методах использовались два структурных кода, Regulamento de Estruturas de Betão Armado e Pré-Esforçado (REBAP) и Еврокод 2 (EC2), чтобы оценить их различия в контроле за деформацией. Таким образом, основная цель состоит в том, чтобы установить сравнения между двумя методами анализа, чтобы показать, что нелинейное моделирование методом конечных элементов дает значения, которые ниже, чем аналитический расчет, что позволяет добиться большей экономии при проектировании железобетонных элементов конструкции. Кроме того, можно отметить, что EC2 имеет некоторые несоответствия в конструкции свободно опертых плит, требующих большей толщины, чем плоская квадратная плита, и что непрямая деформация для REBAP занижена для балок и, в некоторых случаях, для плит.

Ключевые слова: треснувшее состояние; расчет водоизмещения; многослойный метод; физически нелинейный анализ.

Заявление о конфликте интересов

Авторы заявляют об отсутствии конфликта интересов.

Цифры

Рисунок 1

( a ) Минимальная толщина…

Рисунок 1

( a ) Минимальная толщина свободно опертой плиты и ( b…

Рисунок 1

( a ) Минимальная толщина свободно опертой плиты и ( b ) минимальная высота поддерживаемой балки.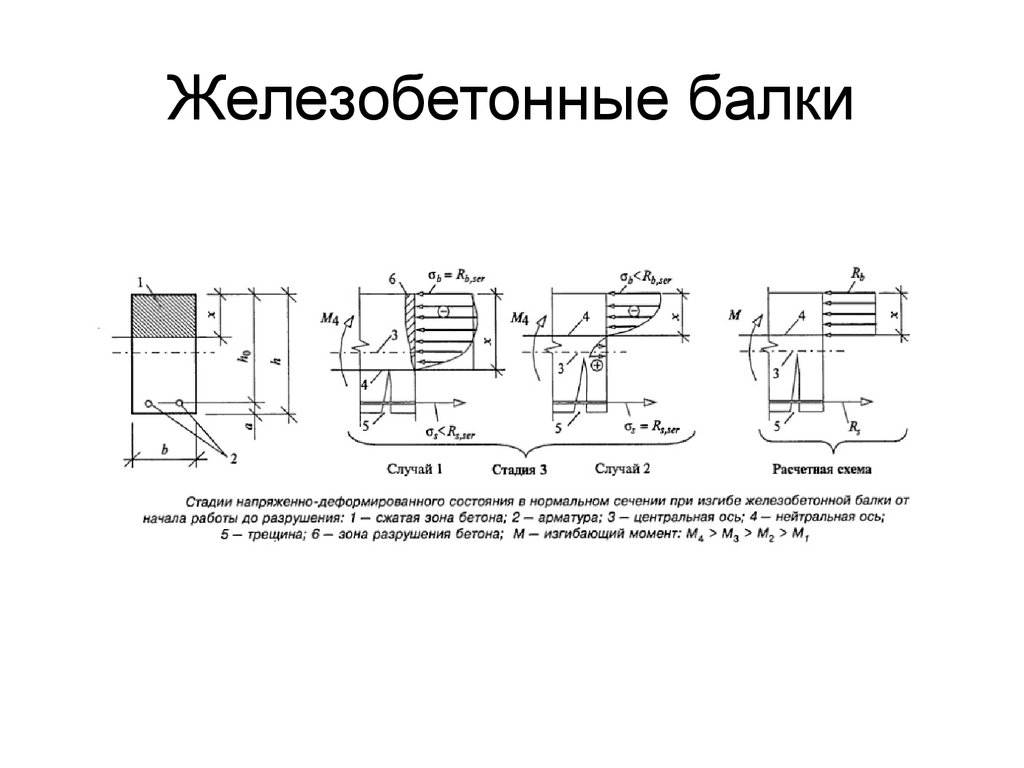

Рисунок 2

( a ) Минимальная толщина…

Рисунок 2

( a ) Минимальная толщина опорной плиты с фиксированным концом и ( b…

фигура 2

( a ) Минимальная толщина плиты с фиксированным концом и ( b ) плиты с фиксированным концом.

Рисунок 3

Минимальная толщина квадрата…

Рисунок 3

Минимальная толщина квадратной плоской плиты.

Рисунок 3

Минимальная толщина квадратной плоской плиты.

Рисунок 4

Кривые напряжения-деформации для ( а…

Рисунок 4

Кривые напряжения-деформации для ( a ) бетона и ( b ) стали, оба…

Рисунок 4

Кривые напряжения-деформации для ( a ) бетона и ( b ) стали, обе адаптированы из [21].

Рисунок 5

( a ) Кривая импульс-кривизна…

Рисунок 5

( a ) Кривая импульс-кривизна железобетона, адаптированная из [21], ( b…

Рисунок 5

( a ) Кривая импульс-кривизна железобетона, адаптированная из [21], ( b ) Иллюстративный график ползучести, адаптированный из [22]. 1 – безтрещинный режим, 2 – переходный режим, 3 – трещинный режим.

Рисунок 6

( a ) Просто поддерживается…

Рисунок 6

( a ) Свободно опертая балка с распределенной нагрузкой, ( b ) поперечное сечение…

Рисунок 6

( a ) Свободно опертая балка с распределенной нагрузкой, ( b ) поперечное напряжение в состоянии I и ( c ) в состоянии II.

Рисунок 7

( a ) Просто…

Рисунок 7

( a ) Плита с простой опорой и ( b ) с фиксированной опорой…

Рисунок 7

( a ) Просто поддерживаемая плита и ( b ) поддерживаемая неподвижная плита.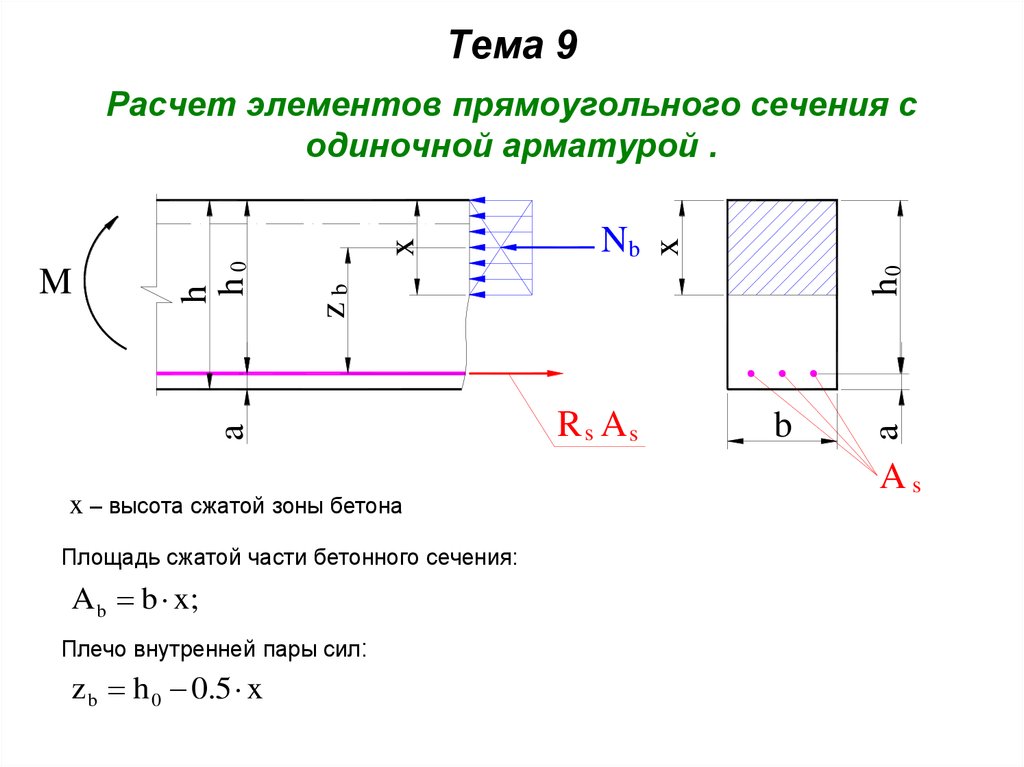

Рисунок 8

( a ) Плита с фиксированным концом…

Рисунок 8

( a ) Плита с фиксированным концом и ( b ) плоская плита.

Рисунок 8

( a ) Плита с фиксированным концом и ( b ) плоская плита.

Рисунок 9

Совместимость по рабочему объему в одной точке…

Рисунок 9

Совместимость смещения в одной точке для плиты с одним фиксированным краем.

Рисунок 9

Совместимость смещения в одной точке для плиты с одной фиксированной границей.

Рисунок 10

k коэффициент для ( a…

Рисунок 10

k коэффициент для ( a ) свободно опертой плиты, ( b ) поддерживаемой…

Рисунок 10

k коэффициент для ( a ) просто опертая плита, ( b ) поддерживаемая плита с фиксированными концами и ( c ) плита с фиксированными концами.

Рисунок 11

Сечение для ( и )…

Рисунок 11

Сечение для ( a ) железобетонной плиты и ( b ) нелинейных…

Рисунок 11

Поперечное сечение ( a ) железобетонной плиты и ( b ) нелинейного элемента оболочки.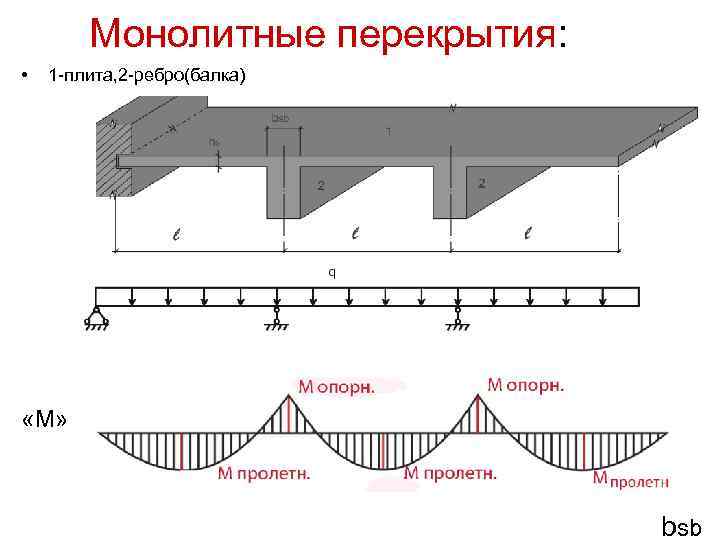

Рисунок 12

Сечение для ( и )…

Рисунок 12

Сечение для ( a ) железобетонной балки и ( б ) нелинейный…

Рисунок 12

Поперечное сечение ( a ) железобетонной балки и ( b ) нелинейного элемента оболочки.

Рисунок 13

Распределение напряжения в трещине…

Рисунок 13

Распределение напряжений в поперечном сечении ж/б с трещинами с 10 слоями в SAP 2000.

Рисунок 13

Распределение напряжения в поперечном сечении ж/б с трещинами с 10 слоями в SAP 2000.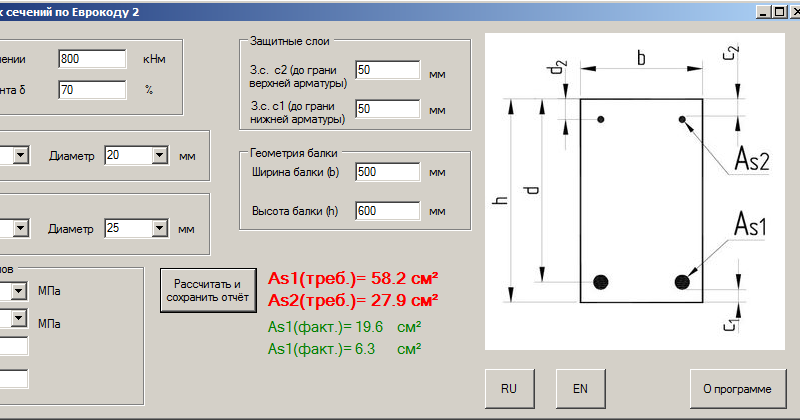

Рисунок 14

Кривые напряжения-деформации для ( a…

Рисунок 14

Кривые напряжения-деформации для ( a ) LM; ( б ) 1НЛМ; ( с…

Рисунок 14

Кривые напряжения-деформации для ( a ) LM; ( б ) 1НЛМ; ( c ) 2NLM и ( d ) стали, используемые в SAP2000 (значения в МПа и м/м).

Рисунок 15

Сетки конечных элементов для (…

Рисунок 15

Сетки конечных элементов для ( a ) балки и ( b ) плиты…

Рисунок 15

Сетки конечных элементов для моделей балок ( a ) и плит ( b ).

Рисунок 16

Схема соединения плиты с…

Рисунок 16

Схема соединения плиты с балкой в конечно-элементной модели.

Рисунок 16

Схема соединения плиты с балкой в конечно-элементной модели.

Рисунок 17

Схема для ( и )…

Рисунок 17

Схема для ( a ) просто опертая плита; ( b ) фиксированный с опорой…

Рисунок 17

Схема для ( a ) свободно опертой плиты; ( b ) плита с фиксированным концом; ( c ) плита с фиксированным концом и ( d ) плоская плита.

Рисунок 18

Значения соотношений для ( a…

Рисунок 18

Значения соотношений для ( a ) LM, ( b ) 1NLM и (…

Рисунок 18

Значения соотношений для ( a ) LM, ( b ) 1NLM и ( c ) 2NLM для свободно опертой плиты.

Рисунок 19

Значения деформации 2NLM: (…

Рисунок 19

Значения деформации 2NLM: ( a ) аналитические и ( b ) числовые,…

Рисунок 19

Значения деформации 2NLM: ( a ) аналитические и ( b ) числовые, с их предельными значениями, для свободно опертой плиты.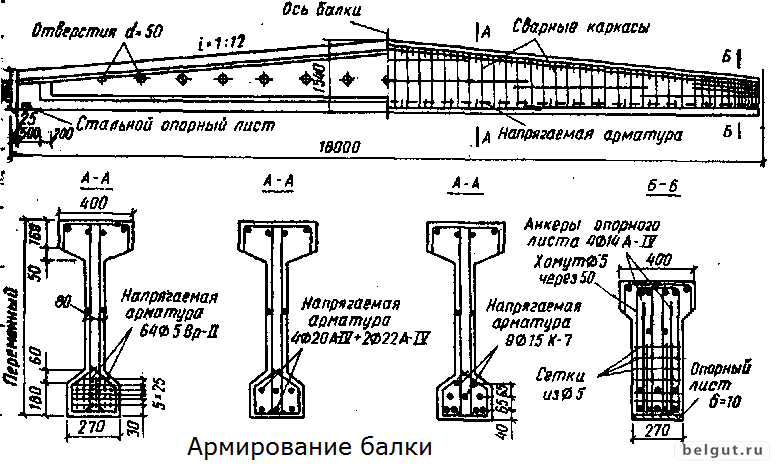

Рисунок 20

Значения соотношений для ( a…

Рисунок 20

Значения соотношений для ( a ) LM, ( b ) 1NLM и (…

Рисунок 20

Значения соотношений для ( a ) LM, ( b ) 1NLM и ( c ) 2NLM для плиты с фиксированным концом.

Рисунок 21

Значения деформации 2NLM: (…

Рисунок 21

Значения деформации 2NLM: ( a ) аналитические и ( b ) числовые,…

Рисунок 21

Значения деформации 2NLM: ( a ) аналитические и ( b ) числовые, с их предельными значениями, для плиты с фиксированными концами.

Рисунок 22

Значения соотношений для ( a…

Рисунок 22

Значения соотношений для ( a ) LM, ( b ) 1NLM и (…

Рисунок 22

Значения отношений для ( a ) LM, ( b ) 1NLM и ( c ) 2NLM, для плиты с фиксированным концом.

Рисунок 23

Значения деформации 2NLM: (…

Рисунок 23

Значения деформации 2NLM: ( a ) аналитические и ( b ) числовые,…

Рисунок 23

Значения деформации 2NLM: ( a ) аналитический и ( b ) числовой, с их предельными значениями, для плиты с фиксированным концом.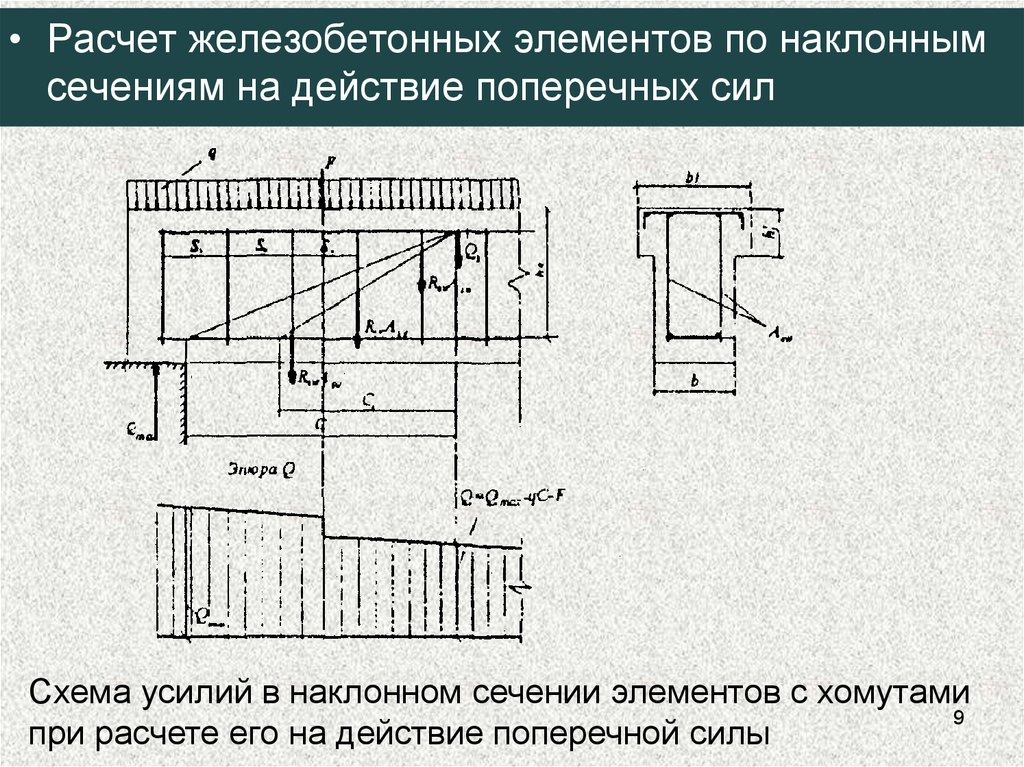

Рисунок 24

Значения соотношений для ( a…

Рисунок 24

Значения соотношений для ( a ) LM, ( b ) 1NLM и (…

Рисунок 24

Значения коэффициентов для ( a ) LM, ( b ) 1NLM и ( c ) 2NLM для плоской плиты.

Рисунок 25

Значения деформации 2NLM: (…

Рисунок 25

Значения деформации 2NLM: ( a ) аналитические и ( b ) числовые,…

Рисунок 25

Значения деформации 2NLM: ( a ) аналитические и ( b ) числовые, с их предельными значениями, для плоской плиты.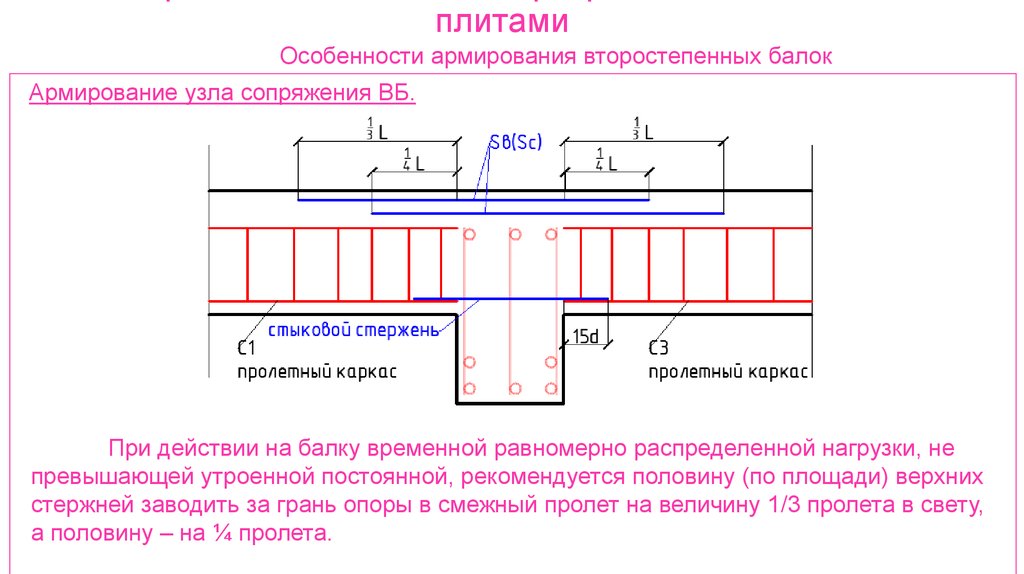

Рисунок 26

Значения соотношений для ( a…

Рисунок 26

Значения соотношений для ( a ) LM, ( b ) 1NLM и (…

Рисунок 26

Значения соотношений для ( a ) LM, ( b ) 1NLM и ( c ) 2NLM, для опорной балки.

Рисунок 27

Значения деформации 2NLM: (…

Рисунок 27

Значения деформации 2NLM: ( a ) аналитические и ( b ) числовое,…

Рисунок 27

Значения деформации 2NLM: ( a ) аналитические и ( b ) числовые, с их предельными значениями, для поддерживаемой балки.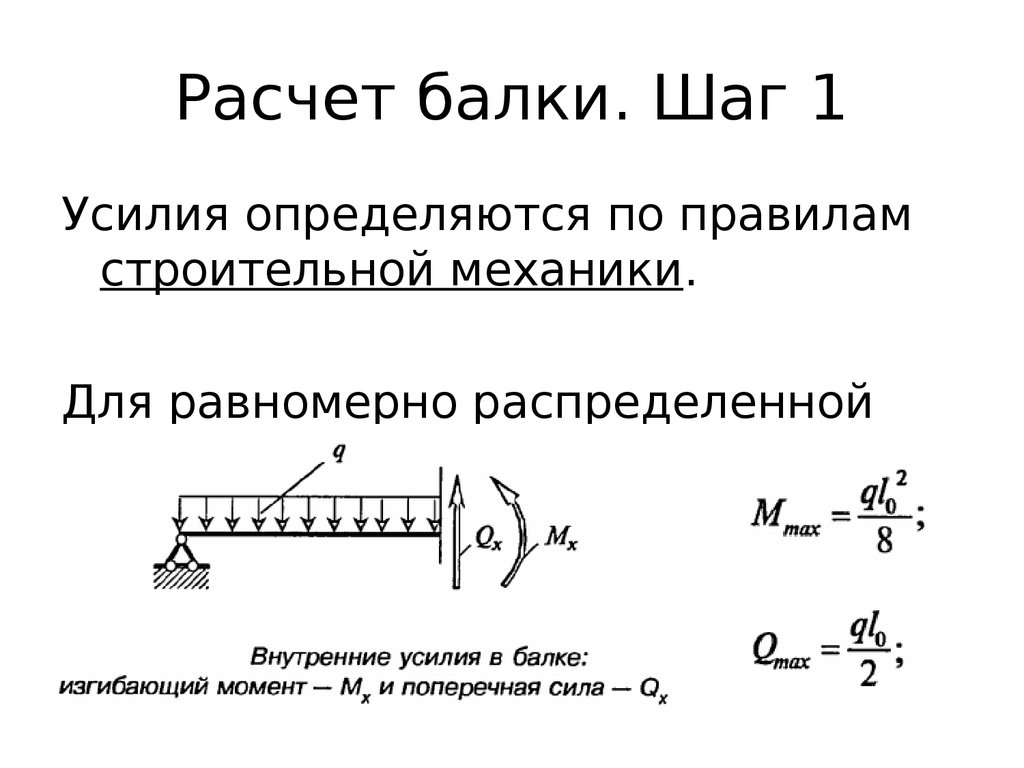

Рисунок 28

Сетка конечных элементов…

Рисунок 28

Сетка конечных элементов первого случая исследования.

Рисунок 28

Сетка конечных элементов первого случая исследования.

Рисунок 29

Сетка конечных элементов…

Рисунок 29

Сетка конечных элементов второго случая исследования.

Рисунок 29

Сетка конечных элементов второго случая исследования.

Рисунок 30

Сетка конечных элементов…

Рисунок 30

Сетка конечных элементов третьего случая исследования.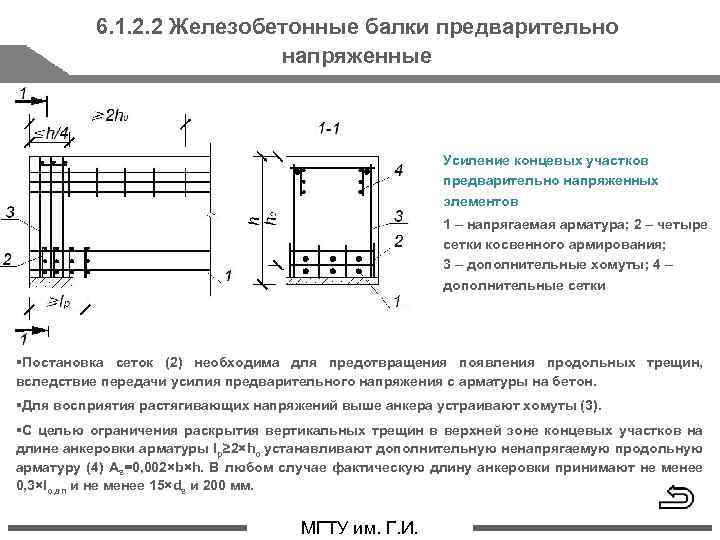

Рисунок 30

Сетка конечных элементов третьего случая исследования.

См. это изображение и информацию об авторских правах в PMC

Похожие статьи

Конечно-элементное исследование структурного поведения армированного базальтовым волокном полимера (BFRP) — армированного самоуплотняющегося бетона (SCC) плит настила моста Томпсона.
Чжоу Л., Чжэн Ю., Тейлор С.Э. Чжоу Л. и др. Полимеры (Базель). 2018 18 июня; 10 (6): 678. doi: 10.3390/polym10060678. Полимеры (Базель). 2018. PMID: 30966712 Бесплатная статья ЧВК.
Исследование ударопрочности железобетонных балок, усиленных полимерной сеткой, армированной углеродным волокном, и инженерными цементными композитами.
Си З., Лю Ф., Пан Дж., Донг Х. Си З и др. Полимеры (Базель). 2022 11 мая; 14 (10): 1951. doi: 10.3390/polym14101951. Полимеры (Базель). 2022. PMID: 35631833 Бесплатная статья ЧВК.
Анализ прогиба многослойных плит с пластиковыми вставками.
Масенас Ю., Шална Р., Юкнявичюс Л., Валивонис Ю. Масенас Дж. и др. Материалы (Базель). 2021 13 октября; 14 (20): 6050. дои: 10.3390/ma14206050. Материалы (Базель). 2021. PMID: 34683642 Бесплатная статья ЧВК.
Влияние геометрических ограничений на четырехточечное испытание удельного электрического сопротивления железобетонных плит Веннера.
Роблес КПВ, Йи Дж.Дж., Ки Ш.Х. Роблес КПВ и др. Датчики (Базель). 2021 5 июля; 21 (13): 4622. дои: 10.3390/s21134622. Датчики (Базель). 2021. PMID: 34283169 Бесплатная статья ЧВК.
Экспериментальные данные и подтверждение поведения при кручении фибробетонных балок: обзор.
Awoyera PO, Effiong JU, Olalusi OB, Prakash Arunachalam K, de Azevedo ARG, Martinelli FRB, Monteiro SN. Awoyera PO и соавт. Полимеры (Базель). 2022 15 марта; 14 (6): 1171. дои: 10.3390/polym14061171. Полимеры (Базель). 2022. PMID: 35335504 Бесплатная статья ЧВК. Обзор.

Посмотреть все похожие статьи