Расчет фермы со шпренгелями от неподвижной нагрузки, построение линий влияния

Ниже приведено решение задачи. Закачка решения в формате doc начнется автоматически через 10 секунд.

 

                                        1. Исходные данные

Согласно задания: Неподвижная нагрузка: Постоянная нагрузка – узловая нагрузка F = 40 кН, приложенная к узлам верхнего и нижнего пояса, исключая опорные. Длинна панели d = 3,6 м . Высота t = 2,4 м. Исследуемые стержни – первая и вторая панель слева.

  2. Кинематический анализ.

 

W=2У – Сф – Соп =  2 · 16 – 31 – 3 = 0,

Следовательно, ферма статически определима.

Здесь

У=16 – число узлов фермы, включая опорные;

Сф = 29 – число стержней фермы;

Соп = 3 – число опорных связей.

 

 

 

      Рис.1

 

 

 

 

3. Определение опорных реакций от неподвижной нагрузки.

Поскольку ферма симметрична и нагружена симметричной нагрузкой:

 

Рис.

2 Расчетная схема заданной фермы.

 

  4. Определение усилий в стержнях фермы. (аналитически)   

Стержни шпренгельной фермы бывают трех категорий

1. Стержни принадлежат только основной ферме. Усилия в этих стержнях определяются расчетом только основной фермы.

В нашей ферме – это исследуемые стержни (2-4, 4-5, 5-7, 7-9, 6-9, 8-9).

2. Стержни принадлежащие одновременно, как основной ферме, так и дополнительной  (шпренгелю). Усилия в этих стержнях определяются как сумма двух усилий. Одно усилие, возникающее в стержне основной фермы, второе – в слившемся с ним шпренгеле.

В нашей ферме – это исследуемые стержни (1-3, 1-2, 3-5, 4-6, 4-8).

     3. Стержни принадлежащие только дополнительной ферме (шпренгелю).

         Шпренгель рассматриваем как самостоятельную двухопорную ферму.

 

         Усилие в этих стержнях определяется только от нагрузки приложенной

          непосредственно к шпренгелю.

В нашей ферме – это исследуемые стержни (2-3, 2-5, 6-7, 6-8).

Разделим ферму на основную и дополнительные (шпренгели).

 Рис.3. Основная ферма.

Рис.4. Дополнительные фермы (шпренгели).

 Определим усилия в основной ферме.

Предварительно определим функции углов в ферме.

 

   

 

  

  

 

 

 

Усилие в стержне (1-4). Усилие находим методом сечений. Рассекаем ферму (сечение I-I)(рис.3) и рассматриваем равновесие левой части фермы. Составим уравнение равновесия относительно моментной точки 5.(рис. 5).
 

   Рис.5 

Плечо силы относительно т. 5:

 

Усилие в стержне 1-5. Усилие находим методом сечений. Рассекаем    ферму (сечение I-I)(рис.3) и рассматриваем равновесие левой части фермы. Составим уравнение равновесия относительно моментной точки 4. (рис5).

Плечо силы относительно т. 4:

 

  

Усилие в стержне 4-5)’. Усилие находим методом сечений. Рассекаем ферму (сечение II-II)(рис.3) и рассматриваем равновесие левой части фермы. Составим уравнение равновесия относительно моментной точки С.(рис. 6).

   Рис.6

  Плечо силы относительно т. С:

 

 

Усилие в стержне 4-9’. Усилие находим методом сечений. Рассекаем ферму (сечение III-III)(рис.3) и рассматриваем равновесие левой части фермы. Составим уравнение равновесия относительно оси У. (рис.7).

 

 

    Рис.7

     

Усилие в стержне 5-9’. Усилие находим методом сечений. Рассекаем ферму (сечение III-III)(рис.3) и рассматриваем равновесие левой части фермы. Составим уравнение равновесия относительно моментной точки 4.(рис. 7).

Плечо силы относительно т. 4:

 

Усилие в стержне 4-8’. Усилие находим методом сечений. Рассекаем ферму (сечение III-III)(рис.3) и рассматриваем равновесие левой части фермы. Составим уравнение равновесия относительно моментной точки 9.(рис. 7).

Плечо силы относительно т. 9:

 

Усилие в стержне 8-9’. Усилие находим методом сечений. Вырезаем узел 8 (рис.3) и рассматриваем его равновесие. Составим уравнение равновесия относительно осей хОу. (рис.8).

   Рис.8

 

 

Определим усилия в стержнях дополнительной фермы.

Из заданной расчетной схемы (рис.2) выделим шпренгель первой панели слева (рис.9.1.).

 Рис.9.1.       Рис.9.2.      Рис.9.3.

Рассмотрим его как ферму на двух опорах ( опоры – узлы 1 и 5).

  

Усилие в стержне 1-2”(2-5”). Усилие находим методом сечений. Вырезаем узел 1 и рассматриваем его равновесие. Составим уравнение равновесия относительно осей хОу. (рис.9.2.).

 

Усилие в стержне 1-3”(3-5”). Усилие находим методом сечений. Вырезаем узел 1 и рассматриваем его равновесие. Составим уравнение равновесия относительно осей хОу. (рис.9.2.).

 

 Усилие в стержне 2-3”. Усилие находим методом сечений. Вырезаем узел 3 и рассматриваем его равновесие. Составим уравнение равновесия относительно осей хОу. (рис.9.3.).

 

 

 

 

 

Из заданной расчетной схемы (рис.2) выделим шпренгель второй панели слева (рис.10.1.).

 Рис.10.1.       Рис.10.2.       Рис.10.3.   Рис.10.4.

 Усилие в стержне 4-8”, 4-6”. Усилия находим методом сечений. Вырезаем узел 4 и рассматриваем его равновесие. Составим уравнения равновесия относительно осей хОу. (рис.10.2.).

Тогда,  

Усилие в стержне 6-7”. Усилие находим методом сечений. Вырезаем узел 7 и рассматриваем его равновесие. Составим уравнение равновесия относительно оси у. (рис.10.3.).

 

Усилие в стержне 6-8”. Усилие находим методом сечений. Вырезаем узел 8 и рассматриваем его равновесие. Составим уравнение равновесия относительно оси у. (рис.10.4.).

 

 

Определим усилия в заданной расчетной схеме.

 

Стержень	Основная ферма	Шпренгель	Заданная ферма
1-3	135	15	150
3-5	135	15	150
1-2	-225	-25	-250
2-4	-225	—	-225
2-3	—	40	40
2-5	—	-25	-25
4-5	-30	—	-30
5-7	162,41	—	162,41
7-9	162,41	—	162,41
4-6	108,17	18,03	126,2
6-9	108,17	—	108,17
4-8	-216,54	-18,03	-234,57
6-7	—	40	40
6-8	—	14,28	14,28
8-9	160,23	—	160,23

 

 

 

6. Построение линий влияния.

Линии влияния для полной фермы строим как геометрическую сумму линии влияния  основной фермы и линии влияния              от дополнительной фермы (шпренгеля).

Линия влияния усилия в опоре А.

Груз на опоре А

Груз на опоре В

Над опорой А откладываем единицу и соединяем с нулем над опорой В.

Получили линию влияния усилия в опоре 17.

Линия влияния усилия в опоре В.

Груз на опоре А

Груз на опоре В

Над опорой В откладываем единицу и соединяем с нулем над опорой А.

Получили линию влияния усилия в опоре В.

 

 Линия влияния N1-2.

Основная ферма.

Используем метод сечений. Рассекаем ферму (сечение I-I) Составим уравнение равновесия относительно моментной точки 5.(рис. 11).

Груз справа. Рассматриваем равновесие левой части фермы (рис.11). Составляем уравнение равновесия – сумма моментов относительно моментной точки 5.

 

То есть линия влияния представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (-1,25). Над опорой А откладываем (-1,25), соединяем с нулем над опорой В.

Получили правую ветвь линии влияния усилия .

Груз слева. Рассматриваем равновесие правой части фермы (рис.11). Составляем уравнение равновесия – сумма моментов относительно моментной точки 5.

  

То есть линия влияния представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (-3.75). Над опорой В откладываем

(-3,75), соединяем с нулем над опорой А.

Получена левая ветвь линии влияния .

Строим передаточную прямую, расположенную под рассеченной панелью. Левый узел 1 рассеченной панели сносим на левую ветвь, правый узел 4  на правую ветвь. Соединяем эти точки и получаем передаточную прямую.

Ветви пересекаются под моментной точкой 5.

Шпренгель.

Из заданной расчетной схемы (рис.2) выделим шпренгель первой панели

 

слева (рис.9.1.). Усилие находим методом сечений. Вырезаем узел 1 и рассматриваем его равновесие. Составим уравнение равновесия относительно оси у. (рис.9.2.).

Единичная сила в узле 1. 

Единичная сила в узле 5. 

Единичная сила в узле 3.

Геометрически суммируем линии влияния основной и дополнительной ферм.

Определение значения усилия по линиям влияния.

 

 

Рис.11

 

Линия влияния N2-4.

Основная ферма.

Используем метод сечений. Рассекаем ферму (сечение I-I) Составим уравнение равновесия относительно моментной точки 5.(рис. 12).

Груз справа. Рассматриваем равновесие левой части фермы (рис.12). Составляем уравнение равновесия – сумма моментов относительно моментной точки 5.

 

То есть линия влияния представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (-1,25). Над опорой А откладываем (-1,25), соединяем с нулем над опорой В.

Получили правую ветвь линии влияния усилия .

Груз слева. Рассматриваем равновесие правой части фермы (рис.12). Составляем уравнение равновесия – сумма моментов относительно моментной точки 5.

  

То есть линия влияния представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (-3.75). Над опорой В откладываем

(-3,75), соединяем с нулем над опорой А.

Получена левая ветвь линии влияния .

Строим передаточную прямую, расположенную под рассеченной панелью. Левый узел 1 рассеченной панели сносим на левую ветвь, правый узел 4  на правую ветвь. Соединяем эти точки и получаем передаточную прямую.

Ветви пересекаются под моментной точкой 5.

Шпренгель.

Стержень 2-4 принадлежит только основной ферме.

 

Линия влияния N2-5.

Основная ферма.

Стержень 2-5 принадлежит только шпренгелю.

Шпренгель.

Из заданной расчетной схемы (рис.2) выделим шпренгель первой панели

слева (рис.9.1.). Усилие находим методом сечений. Вырезаем узел 5 и рассматриваем его равновесие. Составим уравнение равновесия относительно оси у. (рис.9.2.).

Единичная сила в узле 1. 

Единичная сила в узле 5.  

Единичная сила в узле 3.

 

 

Рис.12

 

Линия влияния N1-3(N3-5).

Основная ферма.

Используем метод сечений. Рассекаем ферму (сечение I-I) Составим уравнение равновесия относительно моментной точки 4.(рис. 13).

Груз справа. Рассматриваем равновесие левой части фермы (рис.13). Составляем уравнение равновесия – сумма моментов относительно моментной точки 4.

  

То есть линия влияния представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (0.75). Над опорой А откладываем (0.75), соединяем с нулем над опорой В.

Получили правую ветвь линии влияния усилия .

Груз слева. Рассматриваем равновесие правой части фермы (рис.13). Составляем уравнение равновесия – сумма моментов относительно моментной точки 4.

  

То есть линия влияния представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (2.25). Над опорой В откладываем

(2. 25), соединяем с нулем над опорой А.

Получена левая ветвь линии влияния .

Строим передаточную прямую, расположенную под рассеченной панелью. Левый узел 1 рассеченной панели сносим на левую ветвь, правый узел 4  на правую ветвь. Соединяем эти точки и получаем передаточную прямую.

Ветви пересекаются под моментной точкой 4.

Шпренгель.

Из заданной расчетной схемы (рис.2) выделим шпренгель первой панели

слева (рис.9.1.). Усилие находим методом сечений. Вырезаем узел 1 и рассматриваем его равновесие. Составим уравнение равновесия относительно оси у. (рис.9.2.).

Единичная сила в узле 1. 

 

Единичная сила в узле 5. 

Единичная сила в узле 3.

 Учитывая что

 

Геометрически суммируем линии влияния основной и дополнительной ферм.

Определение усилия по линиям влияния

 

Рис.13

 

Линия влияния N4-5.

Основная ферма.

Используем метод сечений. Рассекаем ферму (сечение II-II) Составим уравнение равновесия относительно моментной точки C. (рис. 14).

Груз справа. Рассматриваем равновесие левой части фермы (рис.14). Составляем уравнение равновесия – сумма моментов относительно моментной точки 4.

  

То есть линия влияния представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (-0,5). Над опорой А откладываем (-0,5), соединяем с нулем над опорой В.

Получили правую ветвь линии влияния усилия .

Груз слева. Рассматриваем равновесие правой части фермы (рис.14). Составляем уравнение равновесия – сумма моментов относительно моментной точки C.

  

То есть линия влияния представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (2,5). Над опорой В откладываем (2,5), соединяем с нулем над опорой А.

Получена левая ветвь линии влияния .

Передаточная прямая при езде по верху.

Строим передаточную прямую, расположенную под рассеченной панелью. Левый узел 2 рассеченной панели сносим на левую ветвь, правый узел 4  на правую ветвь.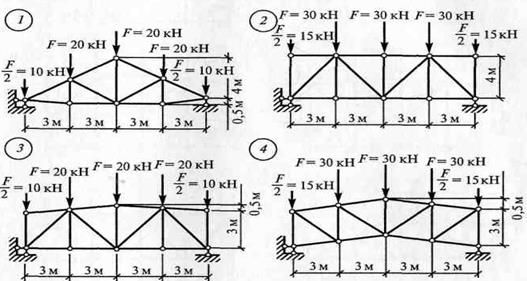 Соединяем эти точки и получаем передаточную прямую.

Ветви пересекаются под моментной точкой С.

Передаточная прямая при езде по низу.

Строим передаточную прямую, расположенную под рассеченной панелью. Левый узел 5 рассеченной панели сносим на левую ветвь, правый узел 7  на правую ветвь. Соединяем эти точки и получаем передаточную прямую.

Ветви пересекаются под моментной точкой С.

Шпренгель.

Стержень 4-5 принадлежит только основной ферме.

 

Линия влияния N2-3.

Основная ферма.

Стержень 2-3 принадлежит только шпренгелю.

Шпренгель.

Из заданной расчетной схемы (рис.2) выделим шпренгель первой панели

слева (рис.9.1.). Усилие находим методом сечений. Вырезаем узел 3 и рассматриваем его равновесие. Составим уравнение равновесия относительно оси у. (рис.9.2.).

Единичная сила в узле 1. 

Единичная сила в узле 5. 

Единичная сила в узле 3.

Рис.14

 

Линия влияния N5-7(N7-9).

Основная ферма.

Используем метод сечений. Рассекаем ферму (сечение III-III) Составим уравнение равновесия относительно моментной точки 4.(рис. 15).

Груз справа. Рассматриваем равновесие левой части фермы (рис.15). Составляем уравнение равновесия – сумма моментов относительно моментной точки 4.

  

То есть линия влияния представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (0.902). Над опорой А откладываем (0.902), соединяем с нулем над опорой В.

Получили правую ветвь линии влияния усилия .

Груз слева. Рассматриваем равновесие правой части фермы (рис.15). Составляем уравнение равновесия – сумма моментов относительно моментной точки 4.

  

То есть линия влияния представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (2,707). Над опорой В откладываем

(2,707), соединяем с нулем над опорой А.

Получена левая ветвь линии влияния .

Строим передаточную прямую, расположенную под рассеченной панелью.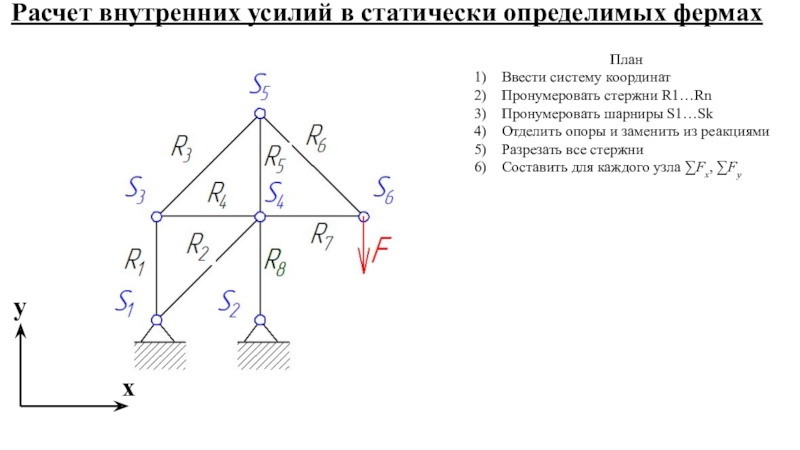 Левый узел 5 рассеченной панели сносим на левую ветвь, правый узел 9  на правую ветвь. Соединяем эти точки и получаем передаточную прямую.

Ветви пересекаются под моментной точкой 4.

Шпренгель.

Стержень 5-7(7-9) принадлежит только основной ферме.

 

Определение усилия по линиям влияния

 

 

Линия влияния N6-7.

Основная ферма.

Стержень 6-7 принадлежит только шпренгелю.

Шпренгель.

Из заданной расчетной схемы (рис.2) выделим шпренгель второй панели

слева (рис.10.1.). Усилие находим методом сечений. Вырезаем узел 7 и рассматриваем его равновесие. Составим уравнение равновесия относительно оси у. (рис.10.3.).

Единичная сила в узле 5. 

Единичная сила в узле 9. 

Единичная сила в узле 3.

Рис.15

 

Линия влияния N4-6

Основная ферма.

Используем метод сечений. Рассекаем ферму (сечение III-III) Составим уравнение равновесия относительно оси у. (рис. 16).

Груз справа. Рассматриваем равновесие левой части фермы (рис.16). Составляем уравнение равновесия – сумма проекций всех сил на ось у.

       

То есть линия влияния представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (1,803). Над опорой А откладываем (1,803), соединяем с нулем над опорой В.

Получили правую ветвь линии влияния усилия .

Груз слева. Рассматриваем равновесие правой части фермы (рис.16). Составляем уравнение равновесия – сумма проекций всех сил на ось у.

  

То есть линия влияния представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (-1,803). Над опорой В откладываем

(-1,803), соединяем с нулем над опорой А.

Получена левая ветвь линии влияния .

Строим передаточную прямую, расположенную под рассеченной панелью. Левый узел 5 рассеченной панели сносим на левую ветвь, правый узел 9  на правую ветвь. Соединяем эти точки и получаем передаточную прямую.

Шпренгель.

Из заданной расчетной схемы (рис.2) выделим шпренгель второй панели

слева (рис.10.1.). Усилие находим методом сечений. Вырезаем узел 7 и рассматриваем его равновесие. Составим уравнение равновесия относительно осей хоу. (рис.10.2.).

 

Единичная сила в узле 5. 

Единичная сила в узле 9. 

Единичная сила в узле 7.

Геометрически суммируем линии влияния основной и дополнительной ферм

 

 

 

 

 

Рис.16

 

Линия влияния N6-9

Основная ферма.

Используем метод сечений. Рассекаем ферму (сечение III-III) Составим уравнение равновесия относительно оси у.(рис. 17).

Груз справа. Рассматриваем равновесие левой части фермы (рис.17). Составляем уравнение равновесия – сумма проекций всех сил на ось у.

       

То есть линия влияния представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (1,803). Над опорой А откладываем (1,803), соединяем с нулем над опорой В.

Получили правую ветвь линии влияния усилия .

Груз слева. Рассматриваем равновесие правой части фермы (рис.17). Составляем уравнение равновесия – сумма проекций всех сил на ось у.

  

То есть линия влияния представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (-1,803). Над опорой В откладываем

(-1,803), соединяем с нулем над опорой А.

Получена левая ветвь линии влияния .

Строим передаточную прямую, расположенную под рассеченной панелью. Левый узел 5 рассеченной панели сносим на левую ветвь, правый узел 9  на правую ветвь. Соединяем эти точки и получаем передаточную прямую.

Шпренгель.

Стержень 6-9 принадлежит только основной ферме.

Определение усилия по линиям влияния.

Линия влияния N6-8 (рис. 17)

Основная ферма.

Стержень 6-8 принадлежит только шпренгелю.

Шпренгель.

Из заданной расчетной схемы (рис.2) выделим шпренгель второй панели

слева (рис.10. 1.). Усилие находим методом сечений. Вырезаем узел 7 и рассматриваем его равновесие. Составим уравнение равновесия относительно осей хоу. (рис.10.4.).

 

Единичная сила в узле 5. 

Единичная сила в узле 9. 

Единичная сила в узле 7.

Учитывая, что:

 

Определение усилия по линиям влияния.

Рис.17

 

Линия влияния N4-8

Основная ферма.

Используем метод сечений. Рассекаем ферму (сечение III-III) Составим уравнение равновесия относительно моментной точки 9.(рис. 18).

Груз справа. Рассматриваем равновесие левой части фермы (рис.18).

  

То есть линия влияния представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (-1,803). Над опорой А откладываем (-1,803), соединяем с нулем над опорой В.

Получили правую ветвь линии влияния усилия .

Груз слева. Рассматриваем равновесие правой части фермы (рис.18).

  

То есть линия влияния представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (-1,803).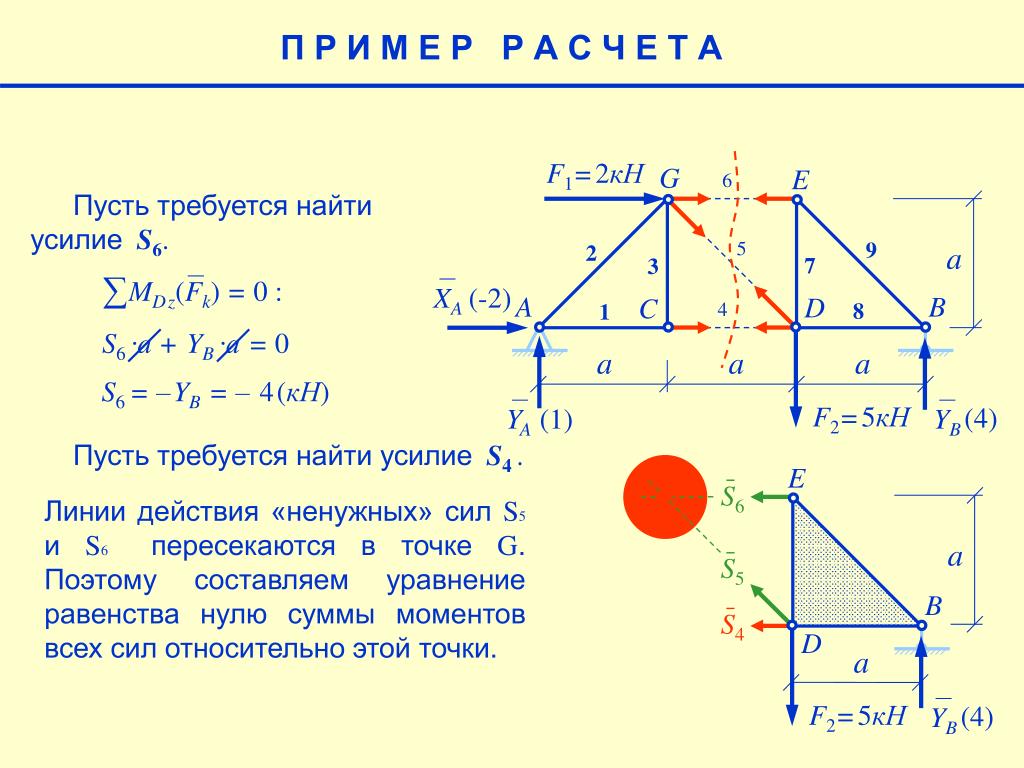 Над опорой В откладываем

(-1,803), соединяем с нулем над опорой А.

Получена левая ветвь линии влияния .

Строим передаточную прямую, расположенную под рассеченной панелью. Левый узел 5 рассеченной панели сносим на левую ветвь, правый узел 9  на правую

ветвь. Соединяем эти точки и получаем передаточную прямую.

Шпренгель.

Из заданной расчетной схемы (рис.2) выделим шпренгель второй панели

слева (рис.10.1.). Усилие находим методом сечений. Вырезаем узел 5 и рассматриваем его равновесие. Составим уравнение равновесия относительно осей хоу. (рис.10.2.).

Единичная сила в узле 5. 

Единичная сила в узле 9. 

 

Единичная сила в узле 7.

Геометрически суммируем линии влияния основной и дополнительной ферм

Определяем значение усилия по линиям влияния.

Рис.18

 

Линия влияния N8-9 (езда по верху)

Основная ферма.

Используем метод сечений. Рассекаем ферму (сечение III-III) Составим уравнение равновесия относительно моментной точки 9.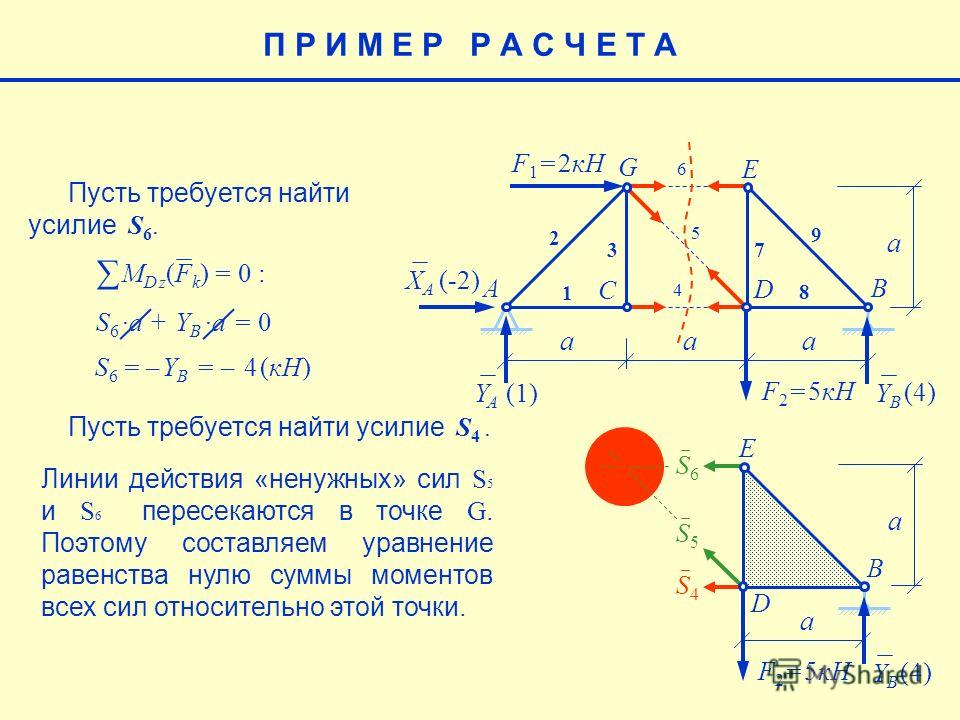 (рис. 19).

Груз слева от узла 8. Рассматриваем равновесие левой части фермы (рис.19).

Учитывая что:  

То есть линия влияния представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (2). Над опорой А откладываем

(2), соединяем с нулем над опорой В.

Получили правую ветвь линии влияния усилия .

Груз слева. Рассматриваем равновесие правой части фермы (рис.19).

  

Учитывая что:  

То есть линия влияния представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (2). Над опорой В откладываем

(2), соединяем с нулем над опорой А.

Получена левая ветвь линии влияния .

 Груз в узле 8.

Учитывая что:  

То есть линия влияния (езда по верху) в точке 8 равна (-1).

Шпренгель.

Стержень 8-9 принадлежит только основной ферме.

 

Линия влияния N8-9 (езда по низу)

Основная ферма.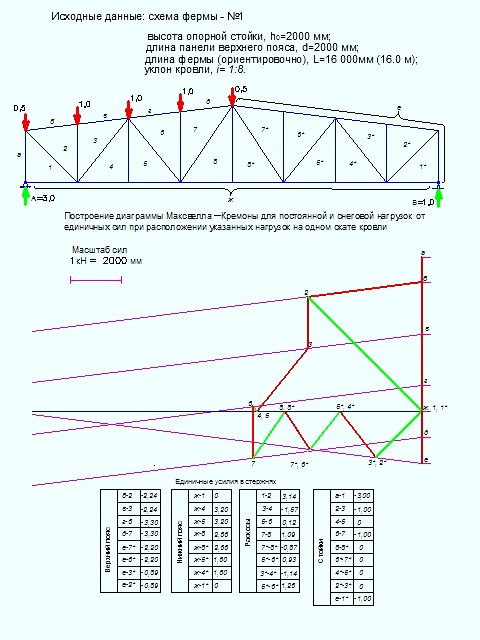

Используем метод сечений. Рассекаем ферму (сечение III-III) Составим уравнение равновесия относительно моментной точки 9.(рис. 19).

Груз слева от узла 8. Рассматриваем равновесие левой части фермы (рис.19).

Учитывая что:  

То есть линия влияния представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (2). Над опорой А откладываем

(2), соединяем с нулем над опорой В.

Получили правую ветвь линии влияния усилия .

Груз слева. Рассматриваем равновесие правой части фермы (рис.19).

  

Учитывая что:  

То есть линия влияния представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (2). Над опорой В откладываем

(2), соединяем с нулем над опорой А.

Получена левая ветвь линии влияния .

 

 

Шпренгель.

Стержень 8-9 принадлежит только основной ферме.

Определение усилия по линиям влияния.

     Рис. 19

 

 

 

 

 

 

 

 

 

Сравнительная таблица

 

Стержень	Определение аналитически	По линиям влияния	Невязка %
1-3	150	150	0
3-5	150	150	0
1-2	-250	-250	0
2-4	-225	-225	0
2-3	40	40	0
2-5	-25	-25	0
4-5	-30	-30	0
5-7	162,41	162,4	0,006
7-9	162,41	162,4	0,006
4-6	126,2	126,08	0,1
6-9	108,17	108,08	0,08
4-8	-234,57	-234,08	0,2
6-7	40	40	0
6-8	11,18	11,2	0,18
8-9	160,23	160	0,14

 

 

Стропильные фермы

Содержание материала

• Стропильные фермы
• Системы решетки ферм
• Порядок расчета стропильных ферм
• Определение усилий в стержнях фермы
• Определение расчетных длин и предельных гибкостей стержней фермы
• Предельные гибкости
• Выбор типа сечений стержней фермы
• Подбор сечений элементов фермы
• Расчетная и геометрическая схема фермы
• Сечение пояса
• Расчетная схема и сечение пояса
• Коэффициент влияния формы сечения η
• Сечение стержней растянутого нижнего пояса стропильной фермы
• Сечение сжатого среднего раскоса фермы по расчетному усилию
• Расчет и конструирование узлов фермы
• Все страницы

Страница 1 из 15

5. 1. Общая характеристика и классификация ферм

Фермой называют решетчатую конструкцию, образуемую из отдельных прямолинейных стержней, связанных в узлах в геометрически неизменяемую систему.

Ферма в целом работает преимущественно на изгиб, а ее элементы (если нагрузка приложена в узлах, оси элементов пересекаются в центре узлов) на осевые усилия (растяжение или сжатие). Жесткость узлов в легких фермах несущественно влияет на работу конструкции, поэтому в большинстве случаев их можно рассматривать как шарнирные.

Фермы бывают плоскими (все стержни лежат в одной плоскости) и пространственными. Плоские фермы могут воспринимать нагрузку, приложенную в их плоскости, и нуждаются в закреплении из своей плоскости связями или другими элементами.

Основными элементами фермы являются пояса, образующие ее контур, и решетка, состоящая из раскосов и стоек.

Пояса фермы работают в основном на продольные усилия и полностью воспринимают изгибающий момент. Решетка объединяет пояса в одно целое, обеспечивает неизменяемость системы и воспринимает поперечную силу.

Максимальное усилие в элементах пояса при шарнирном опирании однопролетной фермы действует в середине ее пролета, в раскосах – у опоры.

Соединение элементов в узлах фермы осуществляют путем непосредственного примыкания одних элементов к другим или с помощью узловых фасонок.

Классифицируются фермы по назначению, статической схеме, очертанию поясов, системе решетки, способу соединения элементов в узлах и на опоре, величине усилия в элементах, напряженному состоянию.

По назначению фермы подразделяются на стропильные, фермы мостов, подъемных кранов, опор линий электропередачи и другие.

По статической схеме фермы подразделяются на балочные (разрезные, неразрезные, консольные), рамные, арочные и вантовые. Балочные разрезные системы наиболее просты в изготовлении и монтаже, но весьма металлоемки. Неразрезные фермы экономичнее по расходу материала, обладают большей жесткостью, что позволяет уменьшить их высоту, но они, как статически неопределимые системы, чувствительны к осадке опор. Рамные и арочные системы экономичны по расходу стали. Их применение рационально для большепролетных зданий. В вантовых фермах все стержни работают только на растяжение и могут быть выполнены из гибких элементов (стальных тросов).

Промежуточными между фермой и сплошной балкой являются комбинированные системы, состоящие из балки, подкрепленной снизу шпренгелем или раскосами, либо сверху аркой. Подкрепляющие элементы уменьшают изгибающие моменты в балке и повышают жесткость системы.

В зависимости от очертания поясов фермы бывают с параллельными поясами, треугольные, трапецеидальные, полигональные.

Выбор очертания ферм зависит от назначения сооружения, типа и материала кровли, системы водоотвода (малоуклонные рубероидные кровли или металлические и из асбестоцементных листов, которые требуют больших уклонов), типа и размеров фонаря, типа соединения фермы с колоннами (шарнирное или жесткое), статической схемы, вида нагрузок, определяющих эпюру изгибающих моментов (теоретически наиболее экономичной по расходу стали является ферма, очерченная по эпюре моментов).

Фермы с параллельными поясами благодаря распространению кровель с рулонным покрытием являются основными для покрытий зданий. По своему очертанию они далеки от эпюры моментов и по расходу стали не экономичны, однако имеют существенные конструктивные преимущества. Равные длины стержней поясов и решетки, одинаковая схема узлов, наибольшая повторяемость элементов и деталей и возможность унификации способствуютт индустриализации их изготовления.

Фермы треугольного очертания рациональны для консольных систем, а также для балочных систем при сосредоточенной нагрузке в середине пролета (подстропильные фермы). К конструктивным недостаткам треугольных ферм можно отнести сложный острый опорный узел, допускающий только шарнирное сопряжение с колоннами, длинные средние раскосы, подбираемые по предельной гибкости (вызывают перерасход металла). Применение треугольных ферм под распределенную нагрузку диктуется необходимостью обеспечения большого уклона кровли.

Фермы трапецеидального очертания занимают промежуточное место между треугольными и фермами с параллельными поясами, они больше соответствуют эпюре изгибающих моментов, имеют конструктивные преимущества перед треугольными фермами за счет упрощения узлов и возможности устроить жесткий рамный узел, что повышает жесткость каркаса.

Фермы полигонального очертания рационально применять для тяжелых ферм больших пролетов, так как очертание их наиболее близко соответствует параболическому очертанию эпюры изгибающих моментов, что дает значительную экономию металла. Элементы верхнего пояса таких ферм прямолинейны между узлами, криволинейное очертание достигается переломами пояса в узлах.

Руководство по регулировке анкерного стержня гитары

Руководство по регулировке анкерного стержня гитары

В этой статье представлен общий обзор того, как работает анкерный стержень и как регулировать анкерный стержень. Регулировка анкерного стержня гитары является ключевой частью поддержания оптимальной играбельности.

Знакомство с анкерным стержнем

ПРЕЖДЕ ЧЕМ ЧТО-НИБУДЬ ДЕЛАТЬ С ВАШИМ АНИЛЬНЫМ стержнем , вам необходимо иметь достаточно хорошее представление о анкерных стержнях. Не смейтесь над этим. Вы имеете дело со спроектированной системой и должны понимать конструкцию анкерного стержня и принцип работы анкерного стержня.

Все гитарные анкерные стержни одинаковы только в том, что касается их предполагаемой функции — регулировки рельефа грифа. Однако все анкерные стержни сделаны из стали; состав используемой стали неодинаков. Различия в составе стали, диаметре стержня и качестве изготовления приводят к большим различиям в прочности любого анкерного стержня.

Почему важна прочность анкерного стержня? Регулируя анкерный стержень в любом направлении, вы изменяете силу, приложенную к стержню. На анкерный стержень действуют силы сжатия, растяжения и крутящего момента.

Ослабление анкерного стержня (поворот против часовой стрелки) облегчает (уменьшает натяжение) гриф, что приводит к увеличению (большей) высоте струны. Ослабление анкерного стержня делается для исправления обратного изгиба.

Затягивание анкерного стержня (поворот по часовой стрелке) увеличивает сжатие, тем самым подталкивая центр грифа к струнам. Веб-сайт MusicPlayers.com описывает это следующим образом: «Это выпрямляет изогнутую вверх шею, оттягивая головку грифа от натяжения струн. Это уменьшает рельефность, снижая действие струны (высоту струны над ладами). Поверните гайку по часовой стрелке, чтобы затянуть стержень». ¹ Затяжка анкерного стержня выполняется для корректировки изгиба.

Что произойдет, если перетянуть анкерный стержень? Когда вы перетягиваете анкерный стержень, вы приближаетесь к приложению большей силы, чем он может выдержать. Эта сила фактически становится крутящим моментом, который срезает (скручивает/ ломает) шток или регулировочную гайку. Однако большинство сломанных анкерных стержней можно отремонтировать; стоимость ремонта сломанного анкерного стержня часто превышает стоимость гитары. Стоимость замены анкерного стержня гитары обычно составляет от 400 до 700 долларов, в зависимости от типа гитары и места вашего проживания. Возможный вариант ремонта — купить замену, но это недешево и приносит еще один набор проблем.

Сколько существует типов анкерных стержней для гитар? Существует множество типов анкерных стержней для акустических и электрогитар. Европейский мастер Маргарита Пастелла из Fret Not Guitar Repair определила пять типов анкерных стержней, обычно используемых при сборке электрических и акустических гитар. ²

В этой статье мы собираемся обсудить два наиболее распространенных типа анкерных стержней, используемых для электрогитар и бас-гитар . Два общих анкерных стержня — это Анкерный стержень одинарного действия и Анкерный стержень двойного действия .

Анкерный стержень одинарного действия

Анкерный стержень одинарного действия является наиболее распространенным анкерным стержнем в промышленных приборах. Эти стержни предназначены для затягивания, тем самым увеличивая давление на заднюю часть шеи. Это приводит к тому, что шея вынуждена изгибаться назад. Целью этого обычно является противодействие натяжению струн для выпрямления грифа.

Анкерный стержень двойного действия

Анкерный стержень двойного действия позволяет регулировать положение шеи в обоих направлениях (вверх или вниз). Уникально то, что анкерные стержни двойного действия могут создавать рельеф с натяжением струны или без него. Двухсторонние анкерные стержни имеют точки регулировки (гайки) на каждом конце.

Анкерный стержень одинарного действия и анкерный стержень двойного действия

В какую сторону поворачивать анкерный стержень

В какую сторону поворачивать анкерный стержень, зависит от желаемого эффекта. Прежде чем затягивать анкерный стержень, всегда рекомендуется немного повернуть его против часовой стрелки, чтобы ослабить. Чтобы сделать профессиональная настройка гитары или профессиональная настройка баса, гриф должен быть ровным (ровным). Чтобы компенсировать нежелательное искривление шеи, вы можете отрегулировать шею вверх или вниз.

Уменьшение рельефа Затягивание анкерного стержня путем поворота его по часовой стрелке заставляет гриф изгибаться вверх по направлению к струнам (выпуклость).

Увеличение рельефа Ослабление анкерного стержня путем его поворота против часовой стрелки влияет на отрыв грифа от струн (вогнутость).

Проверка сброса

Проверяйте величину сброса на протяжении всего процесса регулировки. Начните с проверки рельефа шеи, чтобы получить представление о том, насколько необходима регулировка. Важно отметить, что полный эффект от регулировки анкерного стержня проявляется не сразу. Шея обычно имеет немного отсроченный ответ. Чтобы свести к минимуму нагрузку на шею, не поворачивайте анкерный стержень более чем на 1/4 оборота в течение 24 часов. Еще раз проверьте рельеф и при необходимости отрегулируйте его.

Как проверить рельеф очень просто.

Для электрогитары просто зажмите верхнюю струну на первом и последнем ладу. (Вы можете захотеть поставить каподастр на первую струну). На 7-м ладу измерьте расстояние между низом струны и верхом 7-го лада. Это измерение и есть ваше облегчение. В статье 2019 года сотрудники Sweetwater Sound обсудили важность возможности также видеть гриф гитары перед регулировкой анкерного стержня. Они специально заявили: «Первый шаг в любой настройке — это взглянуть на гриф и посмотреть, какие исправления нам могут понадобиться. Глядя на гриф, мы получаем представление о том, как гриф реагирует на натяжение струны и рельеф анкерного стержня. На данный момент мы просто пытаемся понять, прямая шея или нет». ³

Для бас-гитары зажмите верхнюю струну (нижняя ми) на первом и 15-м ладах. (Вы можете захотеть поставить каподастр на первую струну). На 7-м или 8-м ладу измерьте расстояние между нижней частью струны и верхней частью 7-го лада. Это измерение и есть ваше облегчение. Как автор блога Premier Guitar Тони Нэги прокомментировал: «Скорее всего, вы думаете о настройке, потому что каким-то образом ваш инструмент не работает так, как вам хотелось бы. Чтобы выявить любые проблемы, нам нужно рассмотреть все факторы, влияющие на общую играбельность, звук и функционирование вашего инструмента». ⁴

Не существует единого стандарта измерения, подходящего для каждой гитары. В качестве руководства вы можете использовать от 0,008″ до 0,015″. Оптимальное количество рельефа во многом зависит от личных предпочтений.

После того, как вы это сделаете, если вам все еще не нравится игра струн, вам может потребоваться отрегулировать высоту седла бриджа. После внесения этих корректировок необходимо проверить и отрегулировать интонацию. Поскольку гриф реагирует медленно, через несколько дней вы можете обнаружить, что интонацию необходимо сбросить.

Что делать, если мой анкерный стержень не поворачивается или не затягивается?

Всегда соблюдайте осторожность при регулировке анкерного стержня. Если у вас есть какие-либо опасения по поводу невозможности повернуть анкерный стержень, пришло время проконсультироваться с мастером или местным гитарным техником.

Какие инструменты нужны для регулировки анкерного стержня?

Список инструментов, необходимых для регулировки анкерного стержня, относительно невелик. Вам может не понадобиться все, что здесь перечислено. Например, не у каждой гитары есть крышка анкерного стержня, поэтому отвертка не нужна.

• Малая отвертка (если нужно снять крышку анкерного стержня)
• Регулировочный ключ, подходящий для гайки анкерного стержня вашей гитары
• Измеритель высоты струны с отметками 1/32″ и 1/64″
• Электронный тюнер (цифровой тюнер на зажиме или в стойке)

Не существует гаечного ключа стандартного типа или размера для всех анкерных стержней гитары. Возможные варианты: шестигранный ключ, накидной ключ, гаечный ключ или отвертка. Анкерные ключи изготавливаются в метрических и SAE (британских) размерах.

Для некоторых гитар требуется более специализированный инструмент. Джон ЛеВан, писатель и эксперт по ремонту гитар в Premier Guitar, заявил: «У меня есть как минимум 20 различных гаечных и шестигранных ключей, предназначенных для регулировки грифа гитары, но я все еще сталкиваюсь с одной гитарой, для которой требуется инструмент, которого у меня нет. Существует так много различных инструментов, предназначенных для регулировки анкерных стержней, что почти невозможно иметь их все». ⁵

ИСПОЛЬЗОВАНИЕ КЛЮЧА НЕПРАВИЛЬНОГО РАЗМЕРА МОЖЕТ ПОВРЕДИТЬ ГАЙКУ АНИЛЬНОЙ ТЯГИ. Всегда убедитесь, что вы используете правильный ключ для вашей конкретной гайки анкерного стержня.

Должен ли я самостоятельно регулировать анкерный стержень?

В идеале было бы здорово, если бы вы знали, как выполнять базовое техническое обслуживание и настройку. Вы можете смотреть видео и читать статьи, но вам нужен опыт.

Получение этого опыта включает определенный уровень риска поломки анкерного стержня, а также снятия или поломки цилиндрической гайки анкерного стержня. Имейте в виду, что профессиональная настройка гитары стоит около 75-150 долларов. Ремонт сломанной анкерной штанги стоит от 400 до 700 долларов и выше.

Не расстраивайтесь. Даже лучшие мастера в мире в свое время не знали, что такое анкерный стержень, а тем более, как его регулировать. Если вы несколько склонны к механике, вы можете научиться регулировать анкерный стержень.

---

Улучшите эту статью для других! Оставьте комментарий о своем опыте регулировки анкерного стержня и поделитесь своими советами.

СНОСКИ

• ¹ Дэн Эрлевин, «Guitar 201: Adjusting the Truss Rod» , 3 мая 2017 г., доступно на сайте MusicPlayers.com
• ² Маргарита Пастелла, «Типы анкерных стержней» , 3 мая 2011 г. , доступна в компании Fret Not Guitar Repair
• ³ Sweetwater Writer, «Как настроить электрогитару: регулировка анкерного стержня» , 22 марта 2019 г., доступно в Sweetwater Sound
• ⁴ Тони Надь, «Сделай сам: как настроить бас-гитару» , 12 декабря 2012 г., доступно в Premier Guitar
• ⁵ Джон ЛеВан, «Guitar Shop 101: Демистификация анкерных инструментов» , 13 июня 2014 г., доступно в Premier Guitar
.

Отводы для трубопроводов — усилия упорных блоков

Engineering ToolBox — Ресурсы, инструменты и базовая информация для проектирования и проектирования технических приложений!

Усилия упорных блоков на анкеры изгибов труб из-за скоростей жидкости и внутренних давлений — онлайн-калькулятор результирующей силы.

Рекламные ссылки

В конструкции трубопровода без надлежащей поддержки потока жидкости и внутреннего давления могут возникать недопустимые силы и напряжения.

Результирующая сила — или необходимая опорная сила — на упорный блок — или анкер — для изгиба зависит от

• массового расхода жидкости или скорости потока
• изменения направления потока
• внутреннего давления

Без потока и давления нет силы.

Онлайн-калькулятор результирующей силы изгиба трубы

Приведенный ниже калькулятор можно использовать для расчета результирующей силы в изгибе трубы:

Метрические единицы

ρ — плотность жидкости (кг/м ³ )

d — внутр. диаметр труба или колено (м)

v — скорость жидкости (м/с)

β — угол поворота колена ( ^o )

p — манометрическое давление (кПа) 9 0201

Имперский Единицы измерения

SG — удельный вес жидкости

d — внутр. диаметр труба или изгиб (дюймы)

v — скорость жидкости (фут/с)

β — угол поворота изгиба ( ^o )

p — манометрическое давление (psi)

• Сделать ярлык для этого калькулятора на главном экране?

Результирующая сила из-за массового расхода и скорости потока

Результирующая сила в направлении x из-за массового расхода и скорости потока может быть выражена как:

R _x = m v (1 — cosβ)                         (1 )

    = ρ A v ² (1 — cosβ)                          (1b)

    = ρ π (d / 2) ² v 9002 5 2 (1 — cosβ)                           (1c)

где

R _x = результирующая сила в направлении x (Н)

m = массовый расход (кг/с)

v = скорость потока (м/с)

β = поворотный изгиб угол (градусы)

ρ = плотность жидкости (кг/м ³ )

d = внутренний диаметр трубы или колена (м) скорость может быть выражена как :

R _y = m v sinβ                          (2)

    = ρ A v ^{2 9002 6 sinβ                        (2b)}

    = ρ π (d / 2) ² v ² sinβ (2с)   

R _y = результирующая сила в направлении y (Н)

Результирующая сила на изгибе из-за силы в направлениях x и y может быть выражена как:

R = ( Р _x ² + R _y ² ) ^1/2                            (3)

900 08 , где

R = результирующая сила на изгиб (Н)

Пример — Результирующая сила на изгибе из-за массового расхода и скорости потока

Результирующая сила на изгибе 45 ^o с внутренним диаметром

• 102 мм = 0,102 м
• вода плотностью 1000 кг/м ³
• скорость потока 20 м/с

может быть рассчитано как 02 м) / 2) ² (20 м/с) ² (1 — cos(45))

    = 957 Н

Результирующая сила в направлении Y:

R _y = (1000 кг/м ³ ) π ((0,102 м) / 2) ² (20 м/с) ² sin(45)

    = 2311 Н

Результирующая сила на изгибе

R = (957 Н) ² + (2311 Н) ² ) ^1/2  

    = 2501 Н

Примечание. Если β равно 90 ^o , результирующие силы в направлениях x и y одинаковы.

Результирующая сила статического давления

Давление, «действующее» на торцевые поверхности изгиба, создает результирующие силы в направлениях x и y.

Результирующая сила в направлении x может быть выражена как

R _px = p A (1- cos β)                           (4)   

9 0008     = p π (d / 2) ² ( 1- cos β)                           (4b)

, где

R _{px 9025 7 = результирующая сила давления в направлении x (Н)}

p = манометрическое давление внутри трубы ( Па, Н/м ² )

Результирующая сила в направлении y может быть выражена как β                             (5)

где

R _py = результирующая сила от давления в направлении y (Н)

Результирующая сила на изгибе от силы в направлениях x и y может быть выражена как:

R _p = (R _px ² + R _py ² ) ^1/2                           (6)

где

R _p = результирующая сила на изгиб из-за статического давления (Н)

Пример — Результирующая сила на изгибе из-за давления

Результирующая сила на изгибе 45 ^o с внутренним диаметром

• 102 мм = 0,102 м
• давление 100 кПа

можно рассчитать как

Результирующая сила в направлении x:

R _x = (100 10 ³ Па) π ((0,102 м) / 2) ^{2 90 026 (1 — cos(45) ))}

    = 239 Н

Результирующая сила в направлении Y:

R _y = (100 10 ³ Па) π ( (0,102 м) / 2) ² sin(45)

    = 578 Н

Результирующая сила на изгибе

R = ((239 Н) ² + (577 Н) ² ) ^1/2  

    = 625 Н

Рекламные ссылки

Похожие темы

• Стратегии проектирования

  Стратегии проектирования трубопроводных систем — документация, P&ID, блок-схемы — пропускная способность и ограничения.

• Номинальное давление

  Номинальное давление труб и трубок и их фитингов — углеродистая сталь, нержавеющая сталь, пластик, медь и т.д.

Связанные документы

• Трубы из эпоксидной смолы — опорное расстояние

  Расстояние между опорами для труб из армированного эпоксидного стекловолокна.

• Опоры для подвески горизонтальных труб — расстояние и размер стержня

  Рекомендуемый максимальный промежуток между подвесками — и размеры стержня для прямых горизонтальных труб.

• Горячая гибка труб из меди и медных сплавов

  Гибка медных труб и труб при температуре.

• Горячая гибка труб из никеля и никелевых сплавов

  Температурные диапазоны для гибки труб и трубок из никеля и никелевых сплавов.

• Реактивное движение

  Рассчитайте тяговую силу выброса или тягу, создаваемую несжимаемым реактивным потоком.

• Жидкости. Плотность

  Плотность обычных жидкостей, таких как ацетон, пиво, масло, вода и др.

• Жидкости — Удельный вес

  Удельный вес обычных жидкостей, таких как ацетон, спирт, скипидар, масло и т.д.

• Трубы и трубки — Температурное расширение

  Трубы расширяются при нагревании и сжимаются при охлаждении, и это расширение можно выразить с помощью уравнения расширения.

• Пресс-фитинги — опоры

  Максимальное расстояние между опорами прессовой посадки.

• Трубы из ПВХ — контуры температурного расширения

  Расчет температурного расширения и сжатия в системах трубопроводов из ПВХ.

• Трубы из ПВДФ — расстояние между опорами

  Максимальное расстояние между опорами для труб из ПВДФ.

• Ограниченное тепловое расширение — сила и напряжение

  Напряжение и сила при ограничении теплового расширения трубы, балки или аналогичного изделия.

• Стальные трубы — Расчет петель теплового расширения

  Расчет и определение размеров петель теплового расширения стальных труб.

• Резьбовые стержни – пробные нагрузки в метрических единицах

  Расчетная грузоподъемность стальных стержней с метрической резьбой.

• Подземные трубы — давление грунта

  Давление, действующее на подземные трубы из-за веса грунта и транспорта.

• Гидравлический удар

  Быстрое закрытие или открытие клапанов или запуск насосов с остановкой может вызвать скачки давления в трубопроводах, известные как гидравлические удары.

Рекламные ссылки

Engineering ToolBox — Расширение SketchUp — 3D-моделирование онлайн!

Добавляйте стандартные и настраиваемые параметрические компоненты, такие как балки с полками, пиломатериалы, трубопроводы, лестницы и т. д., в свою модель Sketchup с помощью Engineering ToolBox — расширения SketchUp, которое можно использовать с потрясающими, увлекательными и бесплатными программами SketchUp Make и SketchUp Pro. . Добавьте расширение Engineering ToolBox в свой SketchUp из хранилища расширений SketchUp Pro Sketchup!

Перевести

О Engineering ToolBox!

Мы не собираем информацию от наших пользователей.