Онлайн калькулятор расчет стойки из швеллера, двутавра, тавра и уголка на прочность, устойчивость и допустимую гибкость

Главная » Онлайн калькуляторы

На чтение 2 мин. Просмотров 9.5k. Обновлено 28 сентября, 2021

Калькулятор предназначен для расчёта центрально-нагруженных стоек (колонн) из горячекатаного и другого проката следующей номенклатуры:

1. Уголка равнополочного;
2. Уголка неравнополочного;
3. Швеллера с уклоном и с параллельными гранями полок;
4. Двутавров с уклоном полок и с параллельными гранями полок различных модификаций, а также тавровых балок (тавров).

Предлагаем воспользоваться онлайн калькулятором для расчета массы швеллера

Вид проката Уголок равнополочныйУголок неравнополочныйШвеллер с уклоном полокШвеллер с паралельными гранями полокДвутавр с уклоном полокДвутавр с паралел. гранями полок нормальныйДвутавр с паралел. гранями полок широкопол.Двутавр с паралел. гранями полок колнныйДвутавр с паралел. гранями полок доп.сери(Д)Тавр с паралелными гранями полок нормальныйТавр с паралел. гранями полок широкополочныйТавр с паралелными гранями полок колнный

Вид и назначение стоек (колонн) Стойки и раскосы передаюшие реакции опорОсновные колонныВторостепенные колонны

Сталь С235 (Ст3кп2)Сталь С245 (Ст3пс5,Ст3сп5)Сталь С255 (СтГпс,Ст3Гсп)Сталь С285 (Ст3сп,Ст3Гпс,Ст3Гсп)Сталь С345 (12Г2С,09Г2С)Сталь С345К (10ХНДП)Сталь С375 (12Г2С)Сталь С390 (14Г2АФ)Сталь С390Д (14Г2АФД)Сталь С440 (16ГАФ)Сталь С590 (12Г2СМФ)

Если Вашего материала нет в таблице, но Вам известно его расчётное сопротивление, введите его значение в это поле (кг/см2):

РАЗМЕРЫ ВЫБРАННОГО ПРОФИЛЯ:

Выберите схему крепления стойки

Заделка-консоль      Заделка-заделка      Заделка-шарнир      Шарнир-шарнир

Введите параметры для расчёта

Длина стойки L, м :

Нагрузка P, кг :

Размеры проката углового профиля оговариваются ГОСТ 8509-93 и ГОСТ 8510-86; швеллеров ГОСТ 8240-97; двутавров ГОСТ 26020-83; тавров — ТУ 14-2-685-86; (получаемых продольной разрезкой пополам горячекатаных двутавров с параллельными гранями полок по ГОСТ 26020-83).

При проектировании строительных конструкций необходимо принимать схемы, обеспечивающие прочность, устойчивость и пространственную неизменяемость сооружения в целом, а также его отдельных элементов при монтаже и эксплуатации.

Поэтому стойку,находящуюся под действием сжимающей её нагрузки необходимо проверять:

• на прочность;
• устойчивость;
• допустимую гибкость.

Согласно Актуализированной редакция СНиП II-23-81 (CП16.13330, 2011) расчет на прочность элементов из стали при центральном растяжении или сжатии силой P следует выполнять по формуле:

P/Fp*Ry*Yc <= 1, где

• P — действующая нагрузка,
• Fp — плошадь поперечного сечения стойки,
• Ry — расчётное сопротивление материала (стали стойки), выбирается по таблице В5 Приложения «В» того же СНиПа;
• Yc — коэффициент условий работы по таблице 1 СНиПа (0.9-1.1). В соответствии с примечанием к этой таблице (пункт 5) в калькуляторе принято Yc=1.

Проверку на устойчивость элементов сплошного сечения при центральном сжатии силой P следует выполнять по формуле:

P / Fi*Fp*Ry*Yc <= 1, где

Fi — коэффициент продольного изгиба центрально-сжатых элементов.

Коэффициент Fi введён в расчёт в качестве компенсации возможности некоторой не прямолинейности стойки, недостаточной жесткости её крепления и неточности в приложении нагрузки относительно оси стойки. Значение Fi зависит от марки стали и гибкости колонны и часто берётся из таблицы 72 СНиП II-23-81 1990г. исходя из гибкости стойки и расчётного сопротивления выбранной стали сжатию, растяжению и изгибу.

Это несколько упрощает и огрубляет расчёт, так как СНиП II-23-81* предусматривает специальные формулы для определения Fi. Гибкость (Lambda) — некоторая величина, характеризующая свойства рассматриваемого стержня в зависимости от его длины и параметров поперечного сечения, в частности радиуса инерции:

Lambda = Lr / i; здесь

• Lr — расчётная длина стержня;
• i — радиус инерции поперечного сечения стержня (стойки,колонны).

Радиус инерции сечения i равен корню квадратному из выражения I / Fp, где

• I — момент инерции сечения,
• Fp — его площадь.

Lr (расчётная длина) определяется как MuL;

здесь L- длина стойки,а Mu — коэфф., зависящий от схемы её крепления:

• «заделка-консоль»(свободный конец) — Mu = 2;
• «заделка-заделка»-Mu = 0.5;
• «заделка-шарнир» -Mu = 0.7;
• «шарнир-шарнир»-Mu=1.

Следует иметь ввиду,что при наличии у формы поперечного сечения 2-ух радиусов инерции (например, у швеллера, двутавра, тавра — относительно осей x-x и y-y), при расчёте Lambda используется меньший.

Уголки (как равнополочные так, и неравнополочные) имеют минимальный радиус инерции относительно оси z-z, который и используется в расчётах. Кроме того,сама Lambda (гибкость стойки), рассчитанная по формуле Lambda=Lr/i не должна превышать 220-ти в соответствии с табл. 19.СНиП II-23-81*; там же содержатся ограничения на предельную гибкость центрально-сжатых стержней.

Для их использования необходимо сделать выбор в таблице калькулятора «Вид, назначение стоек…». Предельная гибкость стоек, кроме их геометрических параметров, зависит также от коэфф. продольного изгиба (Fi), действующей нагрузки(P), расчётного сопротивления материала стойки (Ry) и условий её работы (Yc).

ПРИМЕЧАНИЕ. Размеры выбранного швеллера, двутавра и тавра указываются в строке «РАЗМЕРЫ ВЫБРАННОГО ПРОФИЛЯ»; размеры полок уголков-в их таблицах; толщина уголков выбирается отдельно после появления возможных толщин выбранного номера уголка в вышеуказанной строке.

Поделиться

Оцените автора

( 3 оценки, среднее 5 из 5 )

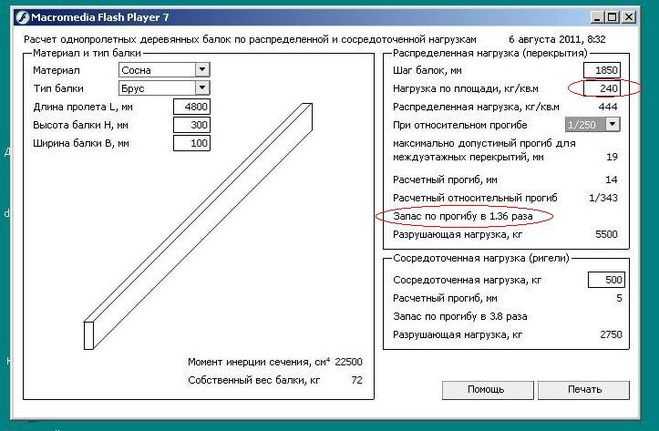
Расчет двутавра на прогиб и изгиб

Калькулятор

Пример расчета

Калькуляторы по теме:

• Сбор нагрузок на балки перекрытия онлайн
• Расчет прямоугольной трубы
• Расчет квадратной трубы
• Расчет швеллера
• Расчет уголка
• Расчет деревянной балки
• Расчет двутавра на устойчивость.

Разновидности

Металлические конструкции отличаются по многим признакам. Это рекомендуется учитывать при выборе изделия.

По назначению

С помощью металлических балок можно создать качественное прочное перекрытие, выбрав один из вариантов.

1. 
   Монолитное. В опалубку заливается бетон, производится усиление решеткой из арматуры. Поверхность получается бесшовной, отличается высокой прочностью.
2. Монолитно-сборное. В этом случае помимо металлических балок используются бетонные блоки, которые укладываются на стальной профиль. Участки стыков заливаются бетоном.
3. Составное. Используется комбинация материалов, то есть на несущие металлические изделия укладываются плиты, доски, панели. Этот вариант предполагает создание дополнительного утепления и звукоизоляции поверхности.

По материалу: стальные и алюминиевые

Металлические конструкции могут изготовляться из разных материалов. Самыми популярными являются стальные и алюминиевые балки для перекрытий.

• Стальные изделия изготавливаются из сплава стали способом холодного или горячего катания. Стальные конструкции бывают нескольких видов: уголок, швеллер, двутавр. Из преимуществ стальных балок можно выделить огнеустойчивость, устойчивость к гниению и внешним факторам, высокую прочность.
  Основными недостатками являются: высокая стоимость, низкие показатели тепло и звукоизоляции, риск образования коррозии. Монтаж стальных конструкций невозможно осуществлять без привлечения специальной техники.
• Алюминиевые балки. При их изготовлении используется не просто алюминий, а его сплавы. В строительстве такие изделия применяются реже, чем стальные аналоги, так как они уступают по показателям устойчивости при сильных нагрузках. Чаще всего алюминиевые балки применяют при строительстве малогабаритных зданий. При возведении промышленных объектов изделия из данного металла применяются только в комбинации со стальными конструкциями.

По конструкции

В современном строительстве применяют несколько разновидностей металлических балок, различных по конструкции.

1. 
   Тавровые. Основное сечение представляет собой стенку и полку в виде буквы «Т».
2. Двутавровые. Сечение металлопроката выглядит как буква «Н». Изделие отличается большей жесткостью, чем тавровое, за счет того, что с противоположной стороны имеет дополнительную полку.
   Двутавровые элементы подразделяются на несколько видов, каждый из которых имеет маркировку:
3. У – узкополочные конструкции.
4. Д – среднеполочные изделия.
5. К – колонные балки. Ширина полки такого элемента может равняться высоте изделия.

Существуют двутавры не с параллельными, а с наклонными полками. Их классифицируют на специальные и обычные. Их характеристики регламентирует ГОСТ 19425-74.

6. Швеллер. Сечение элемента представляет собой букву «П». Эти балки считаются универсальными, применяются во всех сферах промышленности.

Инструкция к калькулятору

Обращаю ваше внимание, что в нецелых числах необходимо ставить точку, а не запятую, то есть, например, 5.7 м, а не 5,7. Также двутавр необходимо проверять на устойчивость (на заваливание от момента). Это можно сделать с помощью калькулятора, ссылка на который расположена выше (в списке «Калькуляторы по теме»). Если что-то не понятно, задавайте свои вопросы через форму комментариев, расположенную в самом низу.

Исходные данные

Расчетная схема:

Длина пролета (L) — минимальное расстояние между двумя крайними опорами или длина консоли.

Расстояния (A и B) — расстояния от опор до мест приложения нагрузок. Для 3 схемы А равна длине консоли балки, опирающейся на 2 опоры.

Нормативная и расчетная нагрузки — нагрузки, на которые рассчитывается квадратная труба. Рассчитать их можно с помощью следующих материалов:

• калькулятор по сбору нагрузок на балку перекрытия;
• пример сбора нагрузок на балку перекрытия.

Fmax — максимально возможный прогиб согласно таблицы E.1 СНиПа «Нагрузки и воздействия». Некоторые из них выписаны в таблицу 1.

Количество двутавров — этот показатель введен на случай, если балку перекрытия придется усилить еще такой же, положив ее рядом. То есть, если у вас одна балка, то указывается «один», если две рядом, то необходимо выбрать «две».

Расчетное сопротивление Ry— для каждой марки стали он свой. Наиболее распространенные значения приведены в таблице 2.

Размер двутавра — здесь следует выбрать профиль двутавра по тому или иному ГОСТу.

Что это такое и каких размеров бывают?

Балка является одним из основных элементов любой конструкции, ее функции – повысить устойчивость конструкции и укрепить ее. Балка (или ригель) состоит из полок и стенок различного размера, соединенных стыковыми швами с использованием сварки. Изготавливаются элементы на оборудованных предприятиях с использованием специальных станков.

Процедура изготовления осуществляется в несколько этапов, после чего готовое изделие проверяется на соответствие ГОСТам.

Металлические конструкции различаются по размерам, для удобства они имеют номера, с помощью которых можно подобрать необходимый материал для строительства.

• 
  «10» — небольшое по размерам изделие, применяется в качестве перекрытия для укрепления подвижных элементов в строительстве. Возможно использовать как направляющую для небольших подъемников.
• «12» — немного больший размер конструкции, выдерживающий большую нагрузку. Применяют за основу рам, используется в механизмах.
• «14» — изделия данного размера могут использоваться в промышленном производстве для устройства в ж/б конструкции.
• «16» — прочная конструкция, выполняющая роль полноценной опоры, может применяться для передвижения транспорта по цеху.
• «18» — надежный опорный элемент, применяется при возведении зданий, обеспечит устойчивость большой площади.
• «20» — большой элемент, который может служить основой для колонны или рамы. Часто используется в машиностроении.
• «25» — изделие может служить опорой для больших кранов и крупногабаритных подъемных механизмов.
• «30» — самая большая конструкция, не используемая в жилом строительстве. Является основой для подъемных механизмов.

Сфера применения

Металлические балки для перекрытий нашли свое применение в различных областях. Могут использоваться для:

• Укрепления кровли в жилом и промышленном строительстве.
• Создания межэтажных перекрытий.
• Устройства опор и различных колонн в промышленных сооружениях и архитектурных зданиях.
• Монтажа ангарных каркасов.
• Шахтовых стволов.
• Создания разнообразных железнодорожных вагонов.
• Строительства мостов, эстакад.
• Возведения металлических ферм.

На заметку: балки перекрытий из металла также можно использовать при строительстве малоэтажных частных домов.

Особенности процесса монтажа

Процедура устройства перекрытий с использованием металлических балок имеет определенные особенности, которые необходимо знать и четко соблюдать.

1. 
   Обязательно наличие четкой схемы постройки с произведенными расчетами на прочность и изгиб изделий.
2. К боковым граням балок крепятся бруски сечением 60х60, после чего размещается накат из досок.
3. Накат накрывается слоем утеплителя, выполняющего функции звуко и теплоизоляции.
4. Шаг между стальными балками не должен превышать 150 см, оптимальное расстояние – 100 см.
5. Глубина опирания концов металлических конструкций на стены – максимум 25 см.
6. Чтобы добиться большей звукоизоляции можно использовать не обычные, а пружинные скобы.

Характеристики

Балки перекрытий, в зависимости от технологии производства, имеют различные характеристики.

1. 
   Двутавры с наклонными полками. Угол уклона 6-12 градусов. Основные параметры:
   длина – 10-60 см;
2. ширина – 5,5-19 см;
3. толщина полки – 7,2 мм-1,8 см;
4. толщина стенки – 4,5мм-1,2 см.
5. Двутавры с параллельными гранями (ГОСТ 26020, СТО АСЧМ 20-93) имеют иные характеристики:
   длина — Б-1 – 100 Б-4;
6. толщина полок – 5,7 мм-3,3 см;
7. ширина профиля – 55 мм-32 см;
8. толщина стенки – 4,1 мм-1,95 см.
9. Широкополочные металлические конструкции имеют следующие характеристики:
   длина — 20Ш1- 70Ш5;
10. ширина профиля – 15-32 см;
11. толщина стенки – 6,0 мм- 2,3 см;
12. толщина полок – от 9 мм -3,65 см.
13. Колонные балки имеют следующие показатели:
    длина – 20 К1-40 К5;
14. ширина профиля – от 20 до 40 см;
15. толщина стенки – от 6,5 до 2,3 см;
16. толщина полок – 1-3,55 см.

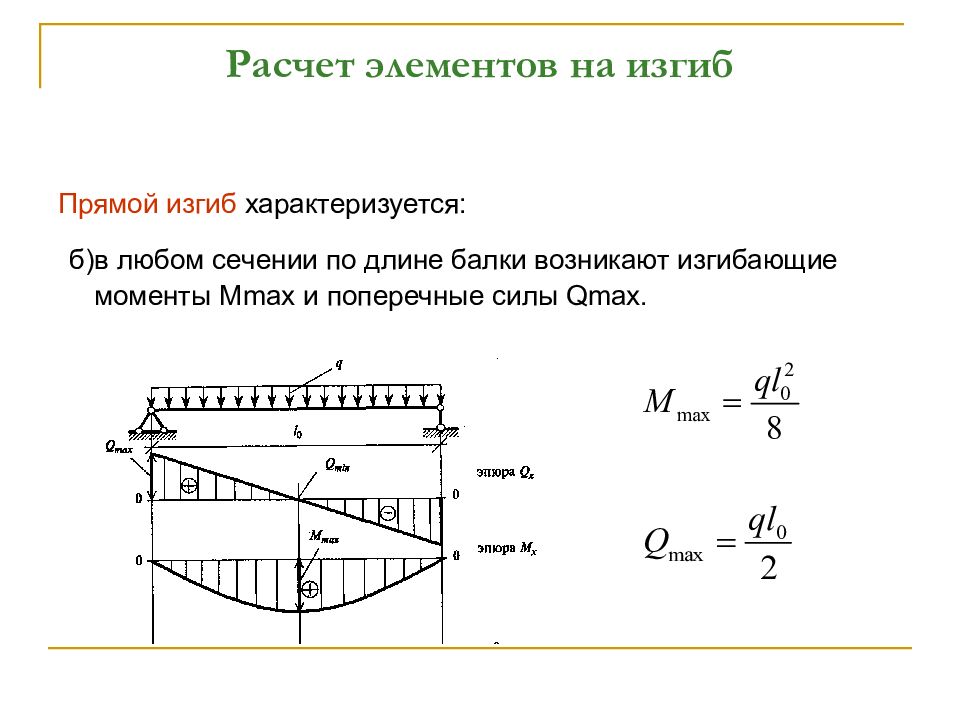
Построение эпюр изгибающего момента и поперечной силы при изгибе

Полученные значения изгибающего момента и поперечной силы в двух сечениях (при положении x=0 и x=l) откладываем соответствующие ординаты, т.е. буквально строим графики обеих функций.

Что мы видим из построенных эпюр, какие выводы мы можем сделать:

• из эпюры поперечной силы видно, что она не меняется по всей длине и равна внешней силе F
• так как в начале координат x (т. е. справа) мы видим на эпюре «скачок» на величину этой силы, то в конце, в заделке скачок говорит о том, что реакция в заделке равна силе F
• на эпюре моментов график выходит из нуля координаты x (справа на балке) и момент тоже равен нулю
• по мере удаления сечения от силы влево момент растет и достигает своей наибольшей величины в заделке, где наблюдается такой же скачок как и на эпюре поперечной силы и равен (- F x). Это говорит о том, что момент в заделке равен именно этому значению

Что такое «скачок» на эпюре

Когда график начинается не из нуля или не из значения полученного на предыдущем участке, а имеет в одном и том же сечении x два разных значения — такой разрыв функции называется скачок. Т.е. если рассматривать график бесконечно близко слева и бесконечно близко справа мы получаем два разных значения как поперечной силы, так и момента. И этот скачок для поперечной силы должен равняться приложенной сосредоточенной силе, а для момента приложенному сосредоточенному моменту.

Вот и все секреты построения эпюр для моментов и поперечных сил. Конечно дальше немного усложняется сам процесс, но принцип остается тот же.

Дальше в видео представлены примеры построения эпюр для распределенной нагрузки изгибающего момента. Чтобы было проще показать разницу все собрано в одном видео:

Рубрики

Изгиб, Сопромат онлайн

Метки

внутренние усилия, внутренние усилия при изгибе, задачи курса сопротивление материалов, изгиб, изгиб балки, изгибающий момент, Как построить эпюры изгибающих моментов и поперечных сил, краткий курс сопротивления материалов, поперечная сила, построение эпюр изгибающего момента, построение эпюр поперечной силы, правило знаков, правило знаков при изгибе, расчет балки, расчет балки на изгиб, Сопромат для чайников, Сопротивление материалов, сопротивление материалов краткий курс, сопротивление материалов примеры решения задач

• Сопротивление материалов
  Что такое сопромат
• Диаграмма растяжения стали на разрыв

Гипотезы сопротивления материалов Основные гипотезы сопротивления материалов

Виды опор и опорных реакций

Растяжение-сжатие

Как построить эпюры при растяжении-сжатии

Собственный вес при растяжении-сжатии

Растяжение сжатие сопромат

Изгиб

Эпюры моментов M(x) поперечных сил Q(x)

Расчет консольной балки на изгиб

Касательные напряжения и угол сдвига

Моменты инерции

Момент инерции сечения

Другие темы

Сложное сопротивление

Косой изгиб пример решения задач

Изгиб с растяжением — сжатием

Задачи на кручение

Репетитор по сопромату

Курсы по сопротивлению материалов

Отзывы

Отзывы про репетитора по сопромату и строймеху

Строймех

Строительная механика

Сказать спасибо

Помочь проекту

Форум

Курсы для инженера

Курсы для инженеров

Цены на все виды

В строительстве чаще всего используются двутавровые металлические балки. Средняя стоимость продукции представлена в таблице.

Наименование балки	Длина	Стоимость
двутавровая № 10	12 м	880
двутавровая № 10 Б-1	12 м	780
двутавровая № 12	12 м	900
двутавровая № 12 Б-1	12 м	660
двутавровая № 14	12 м	1050
двутавровая № 14 Б-1	12 м	740
двутавровая № 16	12 м	1300
двутавровая № 16 Б-1	12 м	980
двутавровая № 18	12 м	1280
двутавровая № 18 Б-1	12 м	1150
двутавровая № 20	12 м	1560
двутавровая № 25 Б-1	12 м	2150
двутавровая № 25 Ш-1	12 м	3500
двутавровая № 30	12 м	2600
двутавровая № 35	12 м	3300
двутавровая № 40	12 м	3500
двутавровая № 45 Б-1	12 м	5200

Выбор размера швеллера на примере

Пусть имеется швеллер, длина которой составляет 6 метров и он имеет шарнирное закрепление. На него действует распределенная нагрузка, величина которой составляет 250 кг/м. Расчет ведется в следующей последовательности:

1. Максимальное значение момента в профиле швеллера М = 9,81 х 250 х 6²/ 8 / 1000 = 11,04 кН∙м.
2. Необходимое значение момента сопротивления сечения швеллера, Wн = 11,04 х 1000 / 240 = 46,0 см3 (согласно СНиП 2-23-81 для стали С245 Ry = 240 МПа).
3. Подбираем по таблице ГОСТ размер швеллера с моментом сопротивления не ниже вычисленного значения 46,0 см3.

Это будет швеллер 12П (У) ГОСТ 8240-97 — значение момента сопротивления 50,8 см3 или швеллер гнутый 140х60х5 ГОСТ 8278-83 — значение момента сопротивления 47,8 см3.

Плюсы и минусы применения в зданиях

Конструкции из металла обладают рядом преимуществ, благодаря которым материал широко используется:

• повышенной прочностью;
• огнестойкостью;
• устойчивостью к внешним факторам;
• повышенной надежностью;
• большим периодом эксплуатации;
• возможностью усилить уже построенное здание;
• увеличенной несущей способностью.

Однако такие балки имеют и свои недостатки, которые также следует учитывать:

• сложность проведения строительных работ;
• необходимость задействовать тяжелую технику;
• металл может подвергаться коррозии;
• требуется производить сложные подсчеты, с чем у новичка могут возникнуть серьезные сложности.

Способы выполнить расчет и проверку на прогиб

Причина, по которой СНиПы устанавливают столь драконовские ограничения, проста и очевидна. Чем меньше деформация, тем больше запас прочности и гибкости конструкции. Для прогиба менее 0,5% несущий элемент, балка или плита все еще сохраняет упругие свойства, что гарантирует нормальное перераспределение усилий и сохранение целостности всей конструкции. С увеличением прогиба каркас здания прогибается, сопротивляется, но стоит, с выходом за пределы допустимой величины происходит разрыв связей, и конструкция лавинообразно теряет жесткость и несущую способность.

Просчитать прогиб конструкции можно несколькими способами:

• Воспользоваться программным онлайн-калькулятором, в котором «зашиты» стандартные условия, и не более того;
• Использовать готовые справочные данные для различных типов и видов балок, для различных опор схем нагрузок. Нужно только правильно идентифицировать тип и размер балки и определить искомый прогиб;
• Посчитать допустимый прогиб руками и своей головой, большинство проектировщиков так и делают, в то время как контролирующие архитектурные и строительные инспекции предпочитают второй способ расчета.

К сведению! Чтобы реально представлять, почему так важно знать величину отклонения от первоначального положения, стоить понимать, что измерение величины прогиба является единственным доступным и достоверным способом определить состояние балки на практике.
Измерив, насколько просела балка потолочного перекрытия, можно с 99% уверенностью определить, находится ли конструкция в аварийном состоянии или нет.

Требования

Все требования, предъявляемые к балкам из металла, четко обозначены в ГОСТах и СНиПах. Основными требованиями являются:

• Прочность. В зависимости от типа материала, используемого при изготовлении изделия, показатели прочности могут отличаться, но они должны соответствовать значениям, указанным в нормативных документах.
• Период эксплуатации. Металлические конструкции, согласно ГОСТ, должны прослужить минимум 80 лет.
• Устойчивость к коррозии. Готовые элементы должны быть дополнительно обработаны составами, предотвращающими образование коррозии.

Deflection Angle given Length of Curve Calculator

✖Length of curve is defined as the arc length in a parabolic curves.ⓘ Length of curve [L]		AlnAngstromArpentAstronomical UnitAttometerAU of LengthBarleycornBillion Light YearBohr RadiusCable (International )Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (Long)Cubit (UK)DecameterDecimeterEarth Distance from MoonEarth Distance from SunEarth Equatorial RadiusEarth Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsec MeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (ткань)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck L engthPointPoleQuarterReedReed (Long)RodRoman ActusRopeRussian ArchinSpan (ткань)Sun RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter	+10% -10%
✖Радиус кривой – это радиус окружности, часть которой, скажем, дуга принимается во внимание. ⓘ Радиус кривой [R] 8 AlnAngstromArpentAstronomical UnitAttometerAU of LengthBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (Long)Cubit (UK)DecameterDecimeterEarth Distance from MoonEarth Distance from SunEarth Equatorial RadiusEarth Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth) FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPica ПикометрPlanck LengthPointPoleQuarterReed (Long)RodRoman ActusRopeRussian ArchinSpan (ткань)Sun RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaЯрдYoctometerYottameterZeptometerZettameter	+10% -10%

✖ Центральный угол — это угол, вершина (вершина) которого является центром O окружности, а катеты (стороны) — это радиусы, пересекающие окружность в двух различных точках A и B. ⓘ Угол отклонения при заданной длине кривой [∠ Central ]

КругЦиклГрадусГрадМилмиллирадианМинутаМинуты дугиТочкаКвадрантЧетвертькругРадианОборотПрямой УголСекундаПолукругСекстантаЗнакПоворот

⎘ Копировать

👎

Формула

Перезагрузить

👍

Угол отклонения при заданной длине кривой Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1: Преобразование входных данных в базовые единицы

Длина кривой: 100 метров —> 100 метров Преобразование не требуется
Радиус кривой: 50 метров —> 50 метров Преобразование не требуется

ШАГ 2: Вычислите формулу

ШАГ 3: Преобразуйте результат в единицу измерения

2 Радиан —> 114,591559026186 Градус (проверьте преобразование здесь)

< 10+ калькуляторов кривых

Угол отклонения при заданной длине кривой Формула

Центральный угол = длина кривой/радиус кривой
∠ _{центральный}

= Л/П

Что означает построение кривой?

Разметка кривой означает размещение различных точек на равных и удобных расстояниях по длине кривой. Расстояние между любыми двумя последовательными точками называется интервалом привязки. Поскольку измерять интервал колка по дуге нецелесообразно, его измеряют по хорде.

Как рассчитать угол отклонения, учитывая длину кривой?

Угол отклонения при заданной длине кривой Калькулятор использует центральный угол = длина кривой/радиус кривой для расчета центрального угла. Угол отклонения при заданной длине кривой также называется внутренним центральным углом. Центральный угол — это угол, вершина которого является центром окружности, а катеты (стороны) — это радиусы, пересекающие окружность в двух различных точках. Центральный угол обозначается символом

∠ _{центральный} .

Как рассчитать угол отклонения при заданной длине кривой с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для угла отклонения с учетом длины кривой, введите длину кривой (L) и радиус кривой (R) и нажмите кнопку расчета. Вот как можно объяснить расчет угла отклонения с учетом длины кривой с заданными входными значениями -> 114,5916 = 100/50 .

Часто задаваемые вопросы

Что такое угол отклонения с учетом длины кривой?

Угол отклонения при заданной длине кривой также называется внутренним центральным углом. Центральный угол — это угол, вершина которого является центром окружности, а катеты (стороны) — это радиусы, пересекающие окружность в двух различных точках. кривая/радиус кривой

. Длина кривой определяется как длина дуги в параболических кривых, а радиус кривой — это радиус окружности, часть которой, например, дуга, принимается во внимание.

Как рассчитать угол отклонения, учитывая длину кривой?

Угол отклонения при заданной длине кривой также называется внутренним центральным углом. Центральный угол — это угол, вершина которого является центром окружности, а катеты (стороны) — это радиусы, пересекающие окружность в двух различных точках. Он рассчитывается по формуле Центральный угол = длина кривой/радиус кривой . Чтобы рассчитать угол отклонения с учетом длины кривой, вам потребуется длина кривой (L) и радиус кривой 9.0101 (R) . С помощью нашего инструмента вам нужно ввести соответствующие значения для длины кривой и радиуса кривой и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.

Доля

Скопировано!

Torpedo Vorhaltrechner Project — Счетные диски торпед

Расположение руля торпеды в другом месте, чем торпедный аппарат, привело к разделению расчета угла отклонения и функции прицеливания. В случае с надводными кораблями на торпедных аппаратах устанавливались обычные торпедные прицельные приспособления, которые настраивались на углы отклонения, полученные от командного пункта. Вычислительные устройства, называемые 9На командных постах располагались 0143 диски расчета угла директора (нем. Torpedorechenscheibe ), которые решали торпедный треугольник. В случае с подводными лодками при атаках в надводном положении использовался общий торпедный аппарат, расположенный на мостике. При атаке из подводного положения наведение производилось перископом, а угол отклонения рассчитывался в БПУ с помощью торпедных счетных дисков или таблиц.

Расчетный диск торпеды использовал теорию треугольника торпеды, основанную на двух известных переменных: угол на носу и скорость цели, чтобы определить угол отклонения торпеды. Кроме того, торпедные счетные диски могли иметь шкалы, определяющие (для предполагаемого угла на носу и скорости цели) максимальное расстояние до цели в момент пуска торпеды, чтобы цель находилась в зоне досягаемости торпеды.

 

Чертеж 1. Реплика немецкого торпедного счетного диска

Диск состоит из круглого циферблата со шкалой (от 0 до 180º левого и правого борта) на краю, которая представляет угол прицеливания на носу.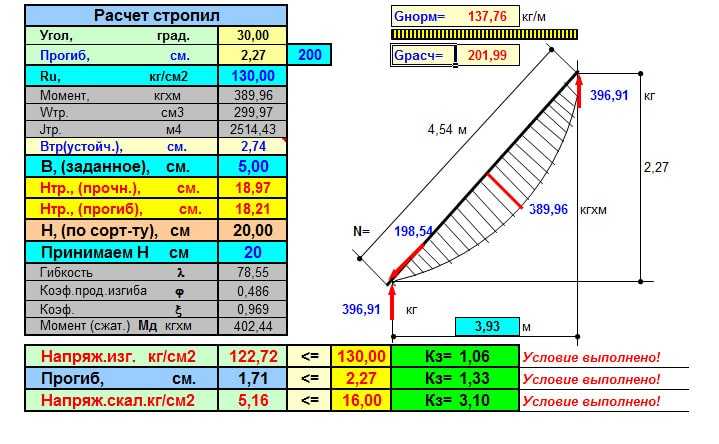 Он также используется для считывания угла отклонения. Циферблат содержит параллельные линии, которые представляют целевой пеленг. Эти линии находятся внутри меньшего круга и соединяют соответствующие значения угла на этом круге, то есть: 10º и 170º, 20º и 160º, 30º и 150º и так далее.

Над циферблатом находится линейка, которую можно вращать вокруг центра. На этом линеале находится шкала установки целевой скорости – в диапазоне от 6 до 30 узлов.
Для расчета угла отклонения линеал необходимо повернуть так, чтобы его край (пересекающий центр циферблата) указывал на угол изгиба на внешней шкале циферблата. Затем необходимо считать целевой пеленг, который пересекает линейную относительно соответствующей целевой скорости. Угол, который соответствует целевому пеленгу, является углом отклонения.
На циферблате нарисованы дуги, представляющие собой части окружностей того же радиуса, что и окружность, охватывающая линии пеленга цели, но их центры смещены. Каждая дуга описывается числом, представляющим расстояние до цели в момент пуска торпеды.
Для определения максимального расстояния до цели (для предполагаемого угла наклона лука и скорости цели) используется дуга, которая пересекает линеал относительно соответствующей скорости цели (при необходимости с интерполяцией).
Шкалы представленного счетного диска верны для торпед, движущихся со скоростью 30 узлов и максимальной дальностью 12500 метров (данные для торпеды G7a). В случае с другими торпедами приходится переделывать шкалы.

Принцип действия диска расчета торпеды следующий: торпедный треугольник строится таким образом, что точка А представляет собой корабль, выпускающий торпеду, точка В — цель в момент пуска торпеды, а точка С — точку где торпеда пересечет (поразит) цель. Длина стороны треугольника AC равна длине вектора скорости торпеды (т.е. при 30 узлах) — она же равна радиусу окружности, на которой расположены точки A и D. Шкала скорости цели на lineal имеет тот же масштаб, что и скорость торпеды, со значением 0 в центре циферблата. Длина стороны треугольника BC равна вектору целевой скорости.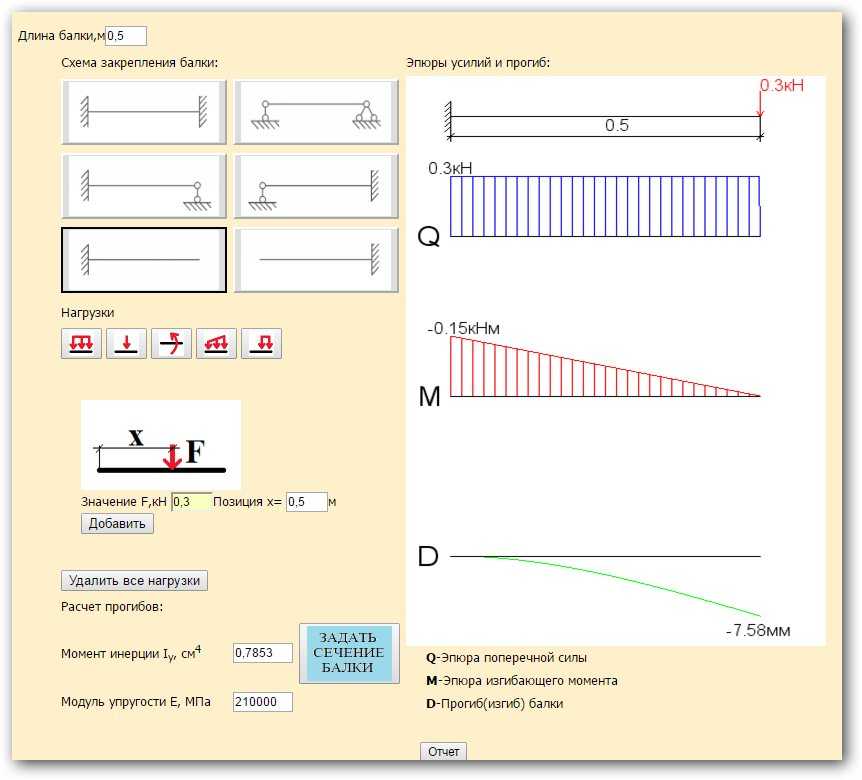

Сторона AB параллельна диаметру окружности, соединяющей точки, представляющие пеленги 0 и 180°.
Угол дуги γ между сторонами треугольника AB и BC равен углу между стороной BC и диаметром окружности, который соединяет точки, представляющие пеленги 0 и 180º, поэтому угол дуги можно легко установить, совместив линейную с соответствующее положение на внешней шкале циферблата.
Угол отклонения β между сторонами AC и AB такой же, как угол между сторонами AD и CD, равный углу между стороной CD и диаметром окружности, которая соединяет точки, представляющие пеленги 0 и 180º. Таким образом, угол отклонения можно легко прочитать по внешней шкале циферблата (для облегчения этого описаны линии целевого азимута).

 

Чертеж 2. Принцип работы счетного диска торпеды

Определение максимальной дальности до цели в момент пуска торпеды работает по следующему принципу: радиус окружности, на которой расположены точки А и D, соответствует (в некотором масштабе) максимальной дальности полета торпеды (то есть 12500 метров для торпеды G7a). На циферблате расположены дуги, являющиеся частями кругов одинакового диаметра со смещенными вниз (в том же масштабе) центрами с шагом 2500 метров. Точка А расположена на окружности «0», а точка В – возле окружности «7». Таким образом, точки A и B, расположенные на одной опорной линии (которая параллельна линии, соединяющей центры смещенных окружностей), находятся на таком же расстоянии друг от друга, как и центры соответствующих окружностей — «0» и «7», т. е. примерно 7 * 2500 метров = 17500 метров. Так, если в момент пуска торпеды цель находится на расстоянии менее 17500 метров, то цель достигает торпеда с максимальной дальностью 12500 метров.

Демонстрация работы такого вычислительного диска доступна здесь.

Рисунок 3. Британский диск расчета торпед времен Первой мировой войны
(диск управления торпедами Mark I)  [1]

 

Чертеж 4. Диск расчета американских торпед времен Второй мировой войны
( Torpedo Angle Solver Mark 7 ) [2]

 

Фото 1.