Расчет стального уголка | Характеристики гнутого металлического уголка
Стальной уголок – наиболее востребованный вид фасонного проката. По способу производства он разделяется на горячекатаный и гнутый. Исходные материалы: углеродистые стали обыкновенного качества Ст3 пс/сп (для рядового применения), качественные, низколегированные 09Г2С, 17Г1С, 10ХСНД, 15 ХСНД (для изделий, используемых при повышенных нагрузках, в сложных температурных условиях, при контакте с агрессивными средами).
Характеристики горячекатаного металлического уголка
Равнополочный горячекатаный стальной уголок производят в соответствии с ГОСТом 8509-93 из квадрата, являющегося исходной заготовкой. Наиболее массово используется угловой профиль обычной точности «В», для ответственных конструкций – продукция высокой точности «А». Размеры полки, согласно стандарту, – от 20 до 250 мм.
Сортамент неравнополочных уголков определяется ГОСТом 8510-86. Наименьшие размеры полок – 16 и 25 мм, максимальные – 125 и 200 мм.
Эта продукция применяется при создании конструкций сложной формы, например, арок.
Для горячекатаной продукции характерна высокая прочность, что позволяет использовать ее в конструкциях, предназначенных для работы в условиях высоких нагрузок. В производстве углового профиля массово используют углеродистую сталь обыкновенного качества и качественную. Изделия из низколегированных сталей применяют для создания конструкций ответственного назначения корпусов, рам и других деталей сельскохозяйственной техники, локомотивов, вагонов, крупногабаритных строительных машин и механизмов. Изделия из такого профиля могут сохранять рабочие характеристики в широком температурном интервале – от -70° до +70°C, при серьезных суточных и сезонных температурных перепадах.
Горячекатаную продукцию поставляют партиями, размер которых обычно не превышает 70 тонн. Каждая партия имеет сертификат соответствия требованиям нормативной документации.
Расчет количества стального равнополочного уголка
При определении массы партии проката углового профиля необходимо знать массу погонного метра, которую вы можете определить по таблице, и общий метраж.
Таблица весов равнополочного стального горячекатаного уголка наиболее распространенных размеров
|
Размер полки, мм |
Толщина стенки, мм |
Масса 1 м, кг |
Размер полки, мм |
Толщина стенки, мм |
Масса 1 м, кг |
|
Толщина стенки, мм |
Масса 1 м, кг |
|
20 |
3 |
0,89 |
35 |
4 |
2,1 |
50 |
4 |
3,05 |
|
4 |
1,15 |
5 |
2,58 |
5 |
3,77 |
|||
|
25 |
3 |
1,12 |
40 |
3 |
1,85 |
6 |
4,47 |
|
|
4 |
1,46 |
4 |
2,42 |
63 |
4 |
3,9 |
||
|
30 |
3 |
1,36 |
5 |
2,98 |
5 |
4,81 |
||
|
4 |
1,78 |
45 |
3 |
2,08 |
6 |
5,72 |
||
|
32 |
3 |
1,46 |
4 |
2,73 |
70 |
5 |
5,38 |
|
|
4 |
1,91 |
5 |
3,37 |
6 |
6,39 |
|||
|
35 |
3 |
1,6 |
50 |
3 |
2,32 |
7 |
7,39 |
Характеристики гнутого стального уголка
Эту продукцию получают на профилегибочных станках из горяче- или холоднокатаного листового проката.
Процесс проходит без нагрева. В холодногнутой продукции сохраняются остаточные напряжения, ухудшающие рабочие свойства. Для устранения остаточных явлений применяют отпуск – нагрев до определенной температуры с последующим медленным охлаждением. Визуальное отличие двух видов продукции: горячекатаный уголок имеет четкий прямой внешний угол, для гнутого характерен скругленный угол.
Размеры металлического равнополочного гнутого уголка определяются ГОСТом 19771-93, неравнополочного – ГОСТом 19772-93. Эта продукция имеет меньшую прочность, по сравнению с горячекатаной. Применяется в мебельном производстве, в качестве ребер жесткости, вспомогательных элементов при креплении конструкций, для изготовления деталей машин и механизмов.
расчет массы партии, характеристики, таблица
Горячекатаный уголок – вид фасонного стального проката, изготавливаемый горячей деформацией при температурах, которые превышают температуру рекристаллизации стали. Наиболее востребованный вариант – равнополочный профиль.
Такая металлопродукция востребована в строительстве, машино- и станкостроении, для изготовления нестандартного технологического оборудования, ворот, калиток, устройства козырьков, навесов, ограждений. Сортамент стального горячекатаного уголка соответствует ГОСТу 8509-93. Марка стали для производства этой металлопродукции выбирается, в зависимости от запланированного эксплуатационного назначения.
Характеристики стального горячекатаного уголка
Для изготовления металлоизделий рядового применения востребованы углеродистые стали обыкновенного качества. Для использования углового профиля под высокими нагрузками и в сложных эксплуатационных условиях при его производстве применяют углеродистые качественные конструкционные марки и низколегированные стали, стойкие к пониженным температурам. С целью повышения коррозионной стойкости металлоизделия из «черной» углеродистой стали покрывают цинковым, керамоцинковым или алюмоцинковым слоем. Металлопокрытия обеспечивают более высокую степень защиты, по сравнению с лакокрасочными материалами.
Благодаря форме профиля, металлоизделия устойчивы к усилиям на изгиб и растяжение, но плохо противостоят скручиванию. Продукция может иметь разные показатели точности размеров:
- «А» – профильные изделия высокой точности;
- «В» – продукция обычной точности.
Определение массы партии стального уголка
Для расчета примерной массы партии углового профиля можно воспользоваться следующей формулой:
M = 2A*s*7,85*L, в которой:
M – масса профильного изделия, кг;
A – ширина полки, м;
s – толщина, мм;
7,85 – средняя плотность стали, кг/дм3;
L – длина изделия.
Для определения массы партии равнополочного стального уголка по таблице вес одного погонного метра умножают на общий метраж.
Таблица размеров и весов 1 м равнополочного уголка
| Номер (ширина полки, мм) | Толщина стенки, мм | Масса 1 м, кг | Номер уголка | Толщина стенки, мм | Масса 1 м, кг |
| 20 | 3 | 0,887 | 80 | 5,5 | 6,777 |
| 20 | 4 | 1,146 | 80 | 6 | 7,360 |
| 25 | 3 | 1,123 | 80 | 7 | 8,513 |
| 25 | 4 | 1,46 | 80 | 8 | 9,652 |
| 25 | 5 | 1,782 | 80 | 10 | 11,88 |
| 28 | 3 | 1,269 | 80 | 12 | 14,05 |
| 30 | 3 | 1,364 | 90 | 6 | 8,327 |
| 30 | 4 | 1,78 | 90 | 7 | 9,638 |
| 30 | 5 | 2,18 | 90 | 8 | 10,93 |
| 32 | 3 | 1,463 | 90 | 9 | 12,21 |
| 32 | 4 | 1,911 | 90 | 10 | 13,48 |
| 35 | 3 | 1,604 | 90 | 12 | 15,96 |
| 35 | 4 | 2,099 | 100 | 7 | 10,79 |
| 35 | 5 | 2,578 | 100 | 8 | 12,25 |
| 40 | 3 | 1,846 | 100 | 10 | 15,1 |
| 40 | 4 | 2,419 | 100 | 12 | 17,9 |
| 40 | 5 | 2,976 | 100 | 14 | 20,63 |
| 40 | 6 | 3,518 | 100 | 15 | 21,97 |
| 45 | 3 | 2,081 | 100 | 16 | 23,3 |
| 45 | 4 | 2,733 | 120 | 8 | 14,74 |
| 45 | 5 | 3,369 | 120 | 10 | 18,23 |
| 45 | 6 | 3,989 | 120 | 12 | 21,65 |
| 50 | 3 | 2,324 | 120 | 15 | 26,67 |
| 50 | 4 | 3,054 | 140 | 9 | 19,41 |
| 50 | 5 | 3,769 | 140 | 10 | 21,45 |
| 50 | 6 | 4,467 | 140 | 12 | 25,5 |
| 50 | 7 | 5,150 | 150 | 10 | 23,02 |
| 50 | 8 | 5,818 | 150 | 12 | 27,39 |
| 60 | 4 | 3,707 | 150 | 15 | 33,82 |
| 60 | 5 | 4,578 | 150 | 18 | 40,11 |
| 60 | 6 | 5,434 | 160 | 11 | 27,02 |
| 60 | 8 | 7,098 | 160 | 12 | 29,35 |
| 60 | 10 | 8,700 | 160 | 14 | 33,97 |
| 63 | 4 | 3,896 | 160 | 16 | 38,52 |
| 63 | 5 | 4,814 | 160 | 18 | 43,01 |
| 63 | 6 | 5,717 | 160 | 20 | 47,44 |
| 70 | 5 | 5,382 | 180 | 11 | 30,47 |
| 70 | 6 | 6,395 | 180 | 12 | 33,12 |
| 70 | 7 | 7,392 | 180 | 15 | 40,96 |
| 70 | 8 | 8,373 | 180 | 18 | 48,66 |
| 70 | 10 | 10,29 | 180 | 20 | 53,72 |
| 75 | 5 | 5,797 | 200 | 12 | 36,97 |
| 75 | 7 | 7,964 | 200 | 20 | 60,08 |
| 75 | 9 | 10,07 | 200 | 30 | 87,56 |
В продажу стальной уголок поступает хлыстами длиной – 4-12 м, по заказу длина отрезков может быть увеличена.
Препарирование сгибов и отверстий штампов
Рис. 1. При расчете допуска на изгиб используется дополнительный угол изгиба.
Примечание редактора: Это первая статья из серии, посвященной основам работы листогибочного пресса. Информация получена из онлайн-программы обучения Fundamentals of Press Brake Operations e-Fab, представленной Стивом Бенсоном из ASMA LLC и доступной в Ассоциации изготовителей и производителей. Материал также происходит из программы сертификации прецизионных листогибочных прессов FMA, представленной Бенсоном и проводимой в местах по всей стране. Для получения дополнительной информации посетите сайт www.fmanet.org/training или позвоните по телефону 888-39.4-4362. Рисунки предоставлены ASMA LLC, 2952 Doaks Ferry Road N.W., Salem, OR 97304, 503-399-7514, www.asmachronicle.com, смартфон www.asmachronicle.com/mobi.htm.
Дно и чеканка с помощью листогибочного пресса достигли своего расцвета.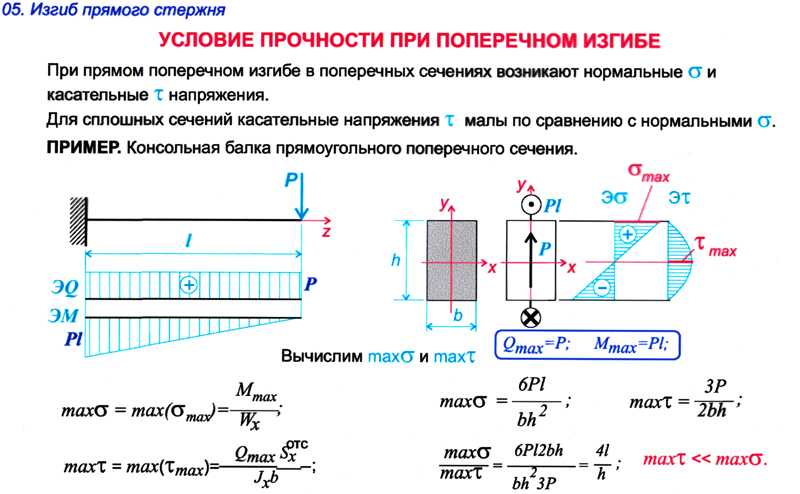
Но за последние несколько десятилетий воздушное формование стало отраслевым стандартом. Итак, при воздушной формовке, как вы выбираете отверстие в нижней части штампа? Вы выбираете отверстие штампа, которое в 6 раз превышает толщину материала, в 8 раз, в 10 раз или даже в 12 раз?
Чем уже отверстие штампа, тем больше тоннажа потребуется для гибки детали. Если вы новичок или беспокоитесь о превышении пределов тоннажа, вы можете выбрать отверстие, которое в 10–12 раз превышает толщину материала; если вы не беспокоитесь о тоннаже, вы можете получить отверстие матрицы, толщина которого всего в 6 раз больше.
Почти каждый листогибочный пресс поставляется с таблицей грузоподъемности, и многие производители инструментов публикуют информацию о максимальной грузоподъемности для каждого производимого ими инструмента. Вы используете формулу для расчета требований к тоннажу для конкретной работы, чтобы убедиться, что вы не толкаете свой станок за пределы предела нагрузки на инструмент, а также того, что указано в пределе нагрузки на поршень производителя листогибочного пресса (см.
Тоннаж имеет значение боковая панель).
Важную роль играют размещение инструмента на станине, тип операции гибки и другие факторы.
Но при пневматическом формовании листогибочных прессов открытие штампа не только влияет на доступный тоннаж на фут. Так какое же идеальное отверстие матрицы — в 6, 8, 10 или 12 раз больше толщины материала? Широко распространено эмпирическое правило, согласно которому 8-кратная толщина материала является идеальным раскрытием штампа. Что ж, это правильно, но только тогда, когда между толщиной материала и желаемой внутренней стороной имеется взаимосвязь один к одному. радиус. Но если вы хотите поставить 3-в. радиуса в материал толщиной 0,036 дюйма, эмпирическое правило 8-кратной толщины материала просто не сработает.
Вот почему. В нижней части профиль пуансона эффективно проштамповывает материал чуть больше, чем толщина материала. При чеканке пуансон так сильно вдавливается в материал, что он утончает материал и фактически перестраивает молекулярную структуру металла, поэтому чеканка в наши дни редко выполняется, по крайней мере, намеренно.
Однако при воздушной штамповке отверстие штампа задает радиус
изгиба .
Это становится очевидным, когда вы видите формирование воздуха в действии. Для воздушной формы пуансон опускается до определенной точки, но, в отличие от дна, заготовка не плотно прилегает к радиусу пуансона; скорее, внутренний радиус рассчитывается в процентах от отверстия штампа. Если вы измените отверстие матрицы, вы измените внутренний радиус изгиба, который вы производите, иногда значительно. Если вы измените внутреннюю радиус изгиба, вы изменяете величину удлинения материала в пределах каждого изгиба; вычитание изгиба (BD), в свою очередь, изменяет вашу деталь, и тогда вы не сможете сформировать деталь до желаемых размеров.
Правило 20 процентов
Правило 20 процентов показывает, насколько резко небольшие изменения отверстия штампа влияют на результирующий внутренний радиус изгиба. Это правило гласит, что внутренний радиус изгиба детали, формованной воздухом, будет составлять 20 процентов отверстия штампа.
В отличие от большинства эмпирических правил в торговле, это не основано на холоднокатаной стали, а вместо этого использует нержавеющую сталь 304 в качестве основы. В холоднокатаной стали от 15 до
17 процентов, мягкий алюминий (серия 50) от 14 до 16 процентов, нержавеющая сталь 304 от 20 до 22 процентов и горячекатаный травленый и промасленный 12-14 процентов.
Здесь по-прежнему полезно использовать холоднокатаную сталь с пределом прочности при растяжении 60 000 фунтов на квадратный дюйм в качестве базового уровня. Если вы работаете с другим материалом, вы можете умножить растяжение на эту базовую линию. Итак, если ваш металл имеет предел прочности при растяжении 120 000 фунтов на квадратный дюйм, это в два раза превышает предел прочности на растяжение холоднокатаной стали. Таким образом, вы умножаете 15 процентов на 2 и обнаруживаете, что ваш внутренний радиус будет примерно равен 30 процентам площади кубика. открытие.
Поскольку характеристики сплава могут различаться, правило охватывает диапазон процентов, поэтому вы можете начать со среднего значения и со временем корректировать его по мере необходимости.
Предположим, у вас есть три пробных образца холоднокатаной стали 16-го калибра (все с одинаковым направлением волокон) и согните их с помощью пуансона с радиусом 1⁄32 дюйма, используя среднее процентное значение для трех различных отверстий штампа. 0,473 дюйма. открытие может
получить внутренний радиус изгиба 0,70 дюйма. A 0,551 дюйма. отверстие дает внутренний радиус изгиба 0,082 дюйма и 0,984 дюйма открытие может привести к внутреннему радиусу изгиба 0,147 дюйма. Это огромная вариация радиуса, и ширина штампа изменилась примерно на полдюйма .
Рисунок 2: Каждый изгиб имеет два внешних отступа (OSSB). Таким образом, чтобы рассчитать вычет изгиба, умножьте OSSB на 2, а затем вычтите допуск изгиба (BA), который представляет собой длину изгиба вдоль нейтральной оси.
Основы определения изгиба
Каждый изгиб удлиняется — его часто называют рост или растяжение , хотя технически точным термином является удлинение.
Из-за этого вы должны вычесть определенное количество этого значения из размера плоской заготовки, чтобы при изгибе материала он удлинялся до размера, необходимого для печати. Удлинение происходит потому, что нейтральная ось изгиба смещается в сторону внутреннего радиуса.
Каждый изгиб состоит из угла изгиба и внутреннего радиуса изгиба. Если два сгиба детали имеют одинаковый угол сгиба и внутренний радиус, оба будут иметь одинаковый вычет сгиба. Если другой изгиб детали имеет другую комбинацию угла/внутреннего радиуса, для него потребуется собственный расчет вычета изгиба.
Несмотря на то, что современные таблицы вычета изгибов относительно точны, старые диаграммы имеют серьезные расхождения. За десятилетия было опубликовано более 100 диаграмм дедукции изгибов, и ни одна из них полностью не согласуется с другой. Допустим, вы ставите 0,063 дюйма. радиус из холоднокатаной стали толщиной 0,060 дюйма. Одна диаграмма может давать вычет изгиба 0,106, другая 0,136—, то есть разница 0,030.
в . Это может не иметь большого значения, если вы работаете со слабыми допусками и имеете ограниченное количество изгибов. Но в части с несколькими изгибами 0,030 дюйма. дисперсия будет накапливаться, что в конечном итоге сделает невозможным формирование детали для печати.
Правда, клиентам может быть наплевать на внутренний радиус. На печати детали может быть указан определенный радиус, но пока деталь соответствует и работает так, как предполагалось, они, вероятно, не собираются доставать свои измерители радиуса для измерения каждого изгиба. Но если вы определите точный вычет изгиба, необходимый для определенного радиуса, вы эффективно упростите производство и уменьшите количество неотъемлемых ошибки. Следовательно, ваша пропускная способность увеличивается, и вы намного более продуктивны.
Для начала нужно знать, что происходит с листовым металлом, когда он изгибается. При каждом изгибе нейтральная ось материала, при которой материал не сжимается и не расширяется, смещается внутрь к внутреннему радиусу.
припуск на изгиб — это длина изгиба, измеренная по нейтральной оси материала.
Здесь вступают в игру геометрия и тригонометрия. Припуск на изгиб = [(0,017453 × внутренний радиус изгиба) + (0,0078 × толщина материала)] × дополнительный угол изгиба . Вы можете вставить значение внутреннего радиуса изгиба в соответствии с правилом 20 процентов. Для угла сгиба используется дополнительный угол (см. Рисунок 1 ). (Эта формула включает коэффициент K и другие математические функции, которые будут рассмотрены в следующих статьях этой серии.)
Далее вам необходимо знать отступ изгиба снаружи, который представляет собой расстояние от вершины, где две плоскости изгиба пересекаются на внутренних поверхностях, до точки касания изгиба, где плоский металл переходит в изогнутый металл. Вот формула, которую легко вычислить с помощью любого научного калькулятора: Внешний отступ = [тангенс (градус угла изгиба / 2)] × (толщина материала + внутренний
радиус изгиба).
К этому моменту вам известен внешний отступ и припуск на изгиб. Теперь вы готовы к расчету вычета изгиба: опять же, количество материала, вычитаемого из плоской заготовки для учета удлинения материала при каждом изгибе (см. 9).0013 Фигуры 2 и 3 ).
Вот формула: Вычет изгиба = (2 × Внешний отступ) — Припуск изгиба . Имея в руках вычет изгиба, вы можете определить подходящий размер плоской заготовки и запрограммировать листогибочный пресс так, чтобы пальцы заднего упора приспосабливались к удлинению материала при каждом изгибе.
Основа гибки
Подобные геометрические и тригонометрические расчеты составляют основу работы листогибочного пресса. Конечно, современные средства управления и программное обеспечение могут автоматизировать многие из этих вычислений. Но в вашей производственной карьере такое современное оборудование может быть не всегда доступно. Более того, только потому, что машина старая, не означает, что она не может быть производительной.
Рис. 3: Здесь показаны основы разработки плоских заготовок. Размеры x и y идут к вершине. Чтобы учесть удлинение изгиба, добавьте x и y, а затем вычтите вычет изгиба. Вычет изгиба равен двойному внешнему отступу (OSSB + OSSB) за вычетом припуска на изгиб.
И это только начало. Вам как оператору листогибочного пресса приходится беспокоиться о многих переменных. Какой это изгиб — крутой, радиусный или глубокий? Каково направление зерна? Список можно продолжить. (Примечание редактора: эти и другие темы будут рассмотрены в следующих частях этой серии.)
Самое главное, если вы знаете математику, вы точно знаете, что входит в каждый изгиб. Диаграммы и эмпирические правила полезны, но в прецизионном производстве металла вы должны быть точными . Чем больше у вас знаний, тем лучше и продуктивнее вы можете работать.
Тоннаж имеет значение
Когда вы выбираете отверстие для штампа, вы, конечно, по-прежнему изменяете доступный тоннаж.
Чтобы убедиться, что приложение не выходит за пределы тоннажа вашей машины или инструмента, вам нужно знать, сколько тоннажа действительно занимает работа.
Вернемся к математике. Обратите внимание, как в следующем уравнении толщина материала возводится в квадрат. Немного большая толщина материала может иметь большое значение для увеличения требуемой грузоподъемности.
[(575 × толщина материала в квадрате)/V ширина штампа]/12 × коэффициенты материала × коэффициенты метода гибки = тонна на дюйм. В этом расчете базовым является воздушная формовка мягкой стали. Другие методы гибки и материалы находятся выше или ниже этой базовой линии.
Существенные факторы
Мягкая сталь, 1,0
Медь, 0,5
Алюминий серии H, 0,5
Алюминий серии T6, 1,28
нержавеющая сталь 304, 1,4
Факторы метода
Воздушная формовка, 1.0
Уретановые инструментальные операции, 4.
0
Нижний изгиб, 5.0+
Чеканка, 10+
Зная количество тонн на дюйм, вы можете рассчитать тоннаж, необходимый для данной работы: Длина изгиба × Тонны на дюйм = Общий тоннаж.
Все это коренится в изгибе на 90 градусов в стандартной плашке. Максимальный тоннаж достигается не сразу. В большинстве случаев около 80 процентов общего тоннажа достигается в пределах первых 20 градусов угла изгиба. Другими словами, даже под небольшим углом изгиб может оказывать огромное давление на инструменты и оборудование.
Как всегда, последнее слово остается за производителями инструментов и листогибочных прессов, когда речь заходит о грузоподъемности их оборудования. Вы никогда — никогда — не должны превышать максимально допустимую массу для набора инструментов или листогибочного пресса.
Вычисление допусков на изгиб, уменьшения изгиба и К-фактора
В моем предыдущем посте я говорил о К-факторе, припуске на изгиб и уменьшении изгиба, а также о том, что они означают при проектировании листового металла.
Теперь давайте посмотрим, как мы можем получить эти значения для конкретного листа.
Как я упоминал в своем последнем посте, вам нужно выполнить несколько тестов, чтобы вычислить эти значения для конкретного листа. Эти тесты включают в себя изгибание некоторых образцов, а затем выполнение некоторых измерений и расчетов.
Рассмотрим лист толщиной 20 мм и длиной 300 мм, как показано на рис. 1. Мы рассмотрим три сценария изгиба с тремя разными углами изгиба; 60, 90 и 120, и мы рассчитаем для них К-фактор, допуск на изгиб и вычитание изгиба. Инструмент для гибки имеет радиус 30 мм, что означает, что наш внутренний радиус изгиба (R) равен 30 мм. Начнем с изгиба на 90 градусов, это самый простой сценарий.
Рисунок 1: Плоский лист
Угол изгиба 90 градусов
На рисунке 2 показан лист, согнутый под углом 90 градусов. Начнем с расчета допуска на изгиб. Оттуда мы можем рассчитать К-фактор и вычитание изгиба. После сгибания листа нам нужно сделать некоторые измерения, как показано на рисунке 2.
9.0003
Рисунок 2: Изгиб под углом 90 градусов
Мы можем рассчитать длину отрезка 1 и 2 следующим образом:
На нейтральной оси имеем:
В этой формуле начальная длина равна 300 мм. Заменив Initial Length, Leg Length 1 и 2 в приведенном выше уравнении, мы можем рассчитать допуск на изгиб следующим образом:
Мы знаем, что BA — это длина дуги на нейтральной оси. Длина дуги для этого сценария может быть рассчитана как:
Где R’ — радиус дуги на нейтральной оси. Вставив значение допуска изгиба в приведенное выше уравнение, мы получаем:
Теперь, если мы вычтем R из R’, мы можем найти расстояние нейтральной оси (t) от внутренней поверхности:
От K -Факторное уравнение у нас есть:
Javelin SOLIDWORKS Service Advertisement
Наши эксперты SOLIDWORKS могут настроить вашу среду, чтобы ваша команда использовала комплексный набор из шаблоны , столы и библиотека формовочных инструментов
Углы изгиба менее 90 градусов
Для нашего второго сценария мы собираемся обсудить расчеты для углов изгиба менее 90 градусов.
В качестве примера мы собираемся использовать 60 градусов в качестве угла изгиба. Мы снова должны сделать некоторые измерения, как показано на Рисунке 3. Затем мы должны рассчитать длину опоры 1 и длину опоры 2.
Рис. 3: Изгиб 60 градусов
0002 Начнем с расчета длины полки 1. Из рисунка 3 мы знаем, чтоГде R — внутренний радиус изгиба, который в данном примере равен 30 мм. Мы можем рассчитать длину отвода 1 с помощью нескольких простых уравнений:
Теперь давайте рассчитаем длину отвода 2:
Теперь, когда у нас есть длина отвода 1 и 2, мы можем снова использовать следующее уравнение для расчета изгиба. Допуск:
Для расчета R’, который является радиусом дуги на нейтральной оси, мы можем использовать следующее уравнение:
A — это угол изгиба в приведенном выше уравнении, поэтому
Чтобы рассчитать расстояние нейтральной оси от внутренней поверхности (t), мы можем вычесть внутренний радиус изгиба из R’:
И имея t и Толщина листа (T) мы можем рассчитать K-фактор следующим образом:
Углы изгиба более 90 градусов
Как и в предыдущих сценариях, начнем с расчета длины полки 1.