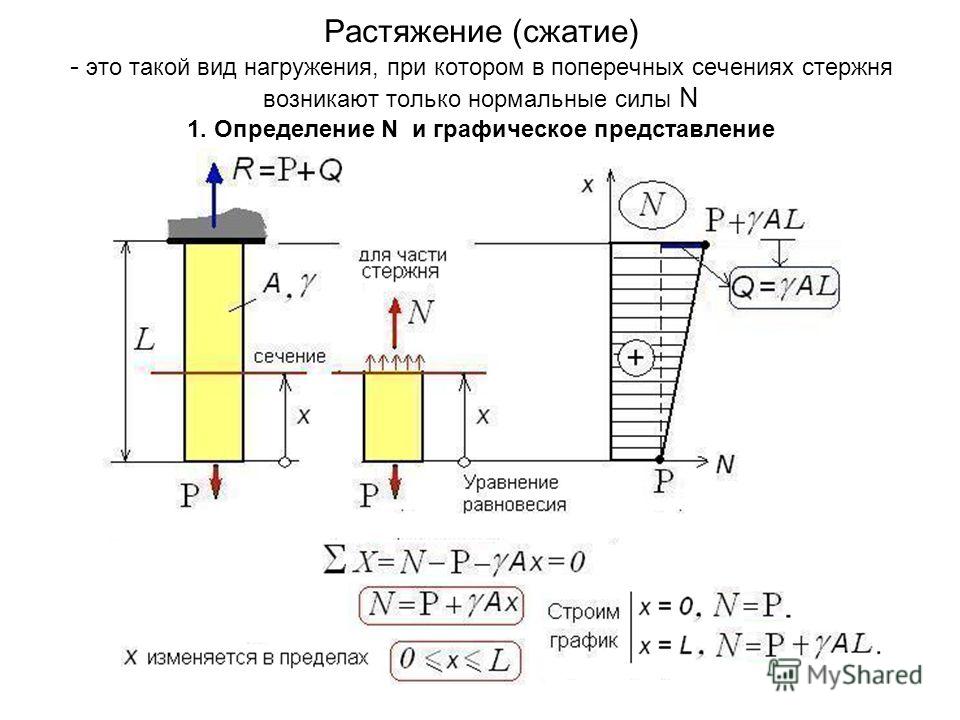
Расчет стержня на растяжение сжатие: Формулы для расчетов на растяжение-сжатие

Содержание

Расчет стержня на прочность

Пример решения задачи по расчету размеров поперечного сечения прямого стального стержня по условию прочности на растяжение-сжатие.

Задача

Для прямого стержня постоянного сечения подобрать размер стороны a квадратного сечения по условию прочности. Материал стержня – сталь. Допустимые напряжения [σ]=160 МПа.

Полученные размеры принять согласно ГОСТ 6636.

Другие примеры решений >
Помощь с решением задач >

Пример решения

Предыдущие пункты решения задачи

Определение опорных реакций.
Построение эпюр внутренних продольных сил.

Рассматриваемый стержень нагружен исключительно продольными силами, поэтому для подбора размеров его поперечного сечения воспользуемся условием прочности при растяжении-сжатии.

где N – внутренние продольные силы (найдены ранее),
A — площадь поперечного сечения стержня.

Чтобы найти размеры поперечного сечения стержня рассчитаем площадь A.

Для этого запишем условие прочности относительно площади:

Площадь сечения в данном случае постоянна по всей длине стержня и должна обеспечивать прочность на всех его силовых участках. Поэтому расчет будем вести по самому нагруженному из них, т.е. где внутренняя сила максимальна (N_max).

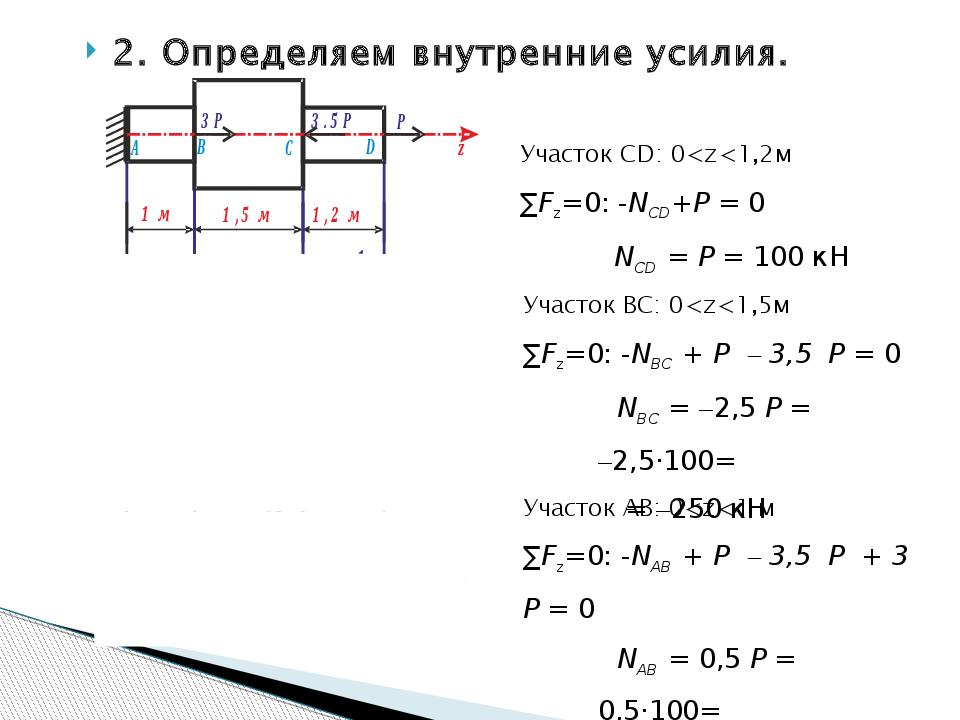
По построенной эпюре внутренних сил видно, что наиболее нагруженным является II участок, где N=N_max=70кН.

Тогда расчетная площадь сечения стержня:

Таким образом для обеспечения необходимой прочности стержня площадь его поперечного сечения должна быть не менее 437,5 мм².

Теперь, зная площадь квадрата, рассчитаем его сторону

Это соответственно минимальный размер поперечного сечения стержня, обеспечивающий его прочность.

В случаях, когда в задании не ставится дополнительных условий полученный размер можно округлить до целого миллиметра, но только в большую сторону.

По ГОСТ 6636 окончательно принимаем ближайший в сторону увеличения линейный размер а=22мм.

Все дальнейшие расчеты стержня будем вести по этому размеру.

Расчет и построение эпюры нормальных напряжений >
Другие примеры решения задач >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

На нашем сайте можно бесплатно скачать:

— Рамки A4 для учебных работ
— Миллиметровки разного цвета

— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Сохранить или поделиться с друзьями

Заказать решение

Поиск формул и решений задач

Манжосов В.К. Расчет стержня при растяжении-сжатии.

Методические указания

Файлы
Академическая и специальная литература
Механика
Сопротивление материалов

Сопротивление материалов

Задачники и решебники по сопротивлению материалов

Механика

История механики
Механика деформируемого твердого тела
Механика жидкостей и газов

Механика сплошных сред
Периодика по механике
Сопротивление материалов
Строительная механика

Теоретическая механика
Теория колебаний

формат pdf
размер 430. 25 КБ
добавлен 16 апреля 2010 г.

— Ульяновск: УлГТУ, 2001. — 20 с.
Методические указания составлены в соответствии с учебными программами по дисциплинам «Сопротивление материалов» и «Механика деформируемого твердого тела» для направлений 55.29 — «Технология, оборудование и автоматизация машиностроительных производств», 55.14 — «Наземные транспортные системы», 55.01 — «Строительство».
Указания предназначены для выполнения расчетно-проектировочных и контрольных заданий, предусмотренных рабочими программами по дисциплинам.
Работа подготовлена на кафедре «Теоретическая и прикладная механика».
УДК 539.9(076) ББК30.12я7
Рецензент канд. техн. наук, доцент И. Н. Карпунина
Одобрено секцией методических пособий научно-методического совета университета.
Учебное издание
МАНЖОСОВ Владимир Кузьмин.
Расчет стержня при растяжении — сжатии.
Методические указания.

Редактор Н. А. Евдокимова.

Похожие разделы

Академическая и специальная литература
Металлургия
Металловедение
Механические и физические свойства металлов
Дефекты металлов
Усталость металлов

Смотрите также

формат pdf
размер 1.1 МБ
добавлен 15 апреля 2010 г.

Примеры решения задач к выполнению расчетно-проектировочных работ по сопротивлению материалов. Часть 1. Пример 1.1 Эпюры внутренних сил при центральном растяжении-сжатии.

Пример 1.2 Построение эпюры крутящих моментов. Пример 1.3 Эпюры внутренних усилий при изгибе консольной балки. Пример 1.4 Эпюры при изгибе двухопорной балки. Пример 1.5 Эпюры при изгибе балки с подвесным пролетом. Пример 1.6 Растяжение с учетом собственного веса стержня. Пример…

Практикум

формат pdf
размер 416.41 КБ
добавлен 28 ноября 2011 г.

Методические указания к расчетно-графической работе Краснодар: Изд. КубГТУ, 2001. — 17 с. Для студентов 2-го курса очной формы обучения всех строительных специальностей Содержание Введение Расчёт на прочность статически определимого ступенчатого стержня по допускаемым напряжениям Расчёт статически неопределимого ступенчатого стержня Расчёт плоской, статически неопределимой стержневой системы

Практикум

формат doc
размер 452. 44 КБ
добавлен 02 февраля 2012 г.

Методические указания к выполнению расчетно-графических работ для студентов механических специальностей. – Омск: Изд-во СибАДИ, 2008. – 28 с. Содержатся основные теоретические положения по расчету на прочность и жесткость при растяжении, сжатии, кручении и изгибе. В приведенных числовых примерах на предложенных схемах показывается последовательность выполнения задания, приводятся результаты расчетов и их графическая интерпретация. Примеры соотве…

Практикум

формат pdf
размер 5.87 МБ
добавлен 20 января 2012 г.

— Омск, Изд-во СибАДИ, 1999. — 28 с. Даны расчетные схемы для трех заданий: определение геометрических характеристик для плоских сечений; построение эпюр внутренних усилий при растяжении-сжатии, кручении и изгибе; расчёты на прочность и жесткость при растяжении-сжатии, кручении и изгибе. Излагается последовательность выполнения каждого задания; приводятся расчетные схемы для каждого варианта; сформулированы контрольные вопросы для самопроверки;…

формат doc
размер 2.22 МБ
добавлен 02 апреля 2010 г.

В этом пособии ясно и конкретно описаны примеры решения задач по таким темам как: Растяжение и сжатие. Расчет статически неопределимых систем при растяжении и сжатии. Напряженное состояние в точке тела. Кручение стержня круглого поперечного сечения. Геометрические характеристики плоских сечений. Прямой поперечный изгиб. Расчет статически неопределимой балки. Внецентренное сжатие. Косой изгиб. Изгиб с кручением. Устойчивость стержней. Удар. Хорошо…

Практикум

формат pdf
размер 385. 31 КБ
добавлен 04 марта 2011 г.

Метод. указания. – 2-е изд., испр. и доп. – Ульяновск: УлГТУ, 2009. – 20 с. Составлены в соответствии с учебными программами по дисциплинам «Сопротивление материалов» для направлений «Машиностроительные технологии и оборудование», «Строительство». Методические указания предназначены для выполнения расчетно-проектировочных и контрольных заданий, предусмотренных рабочими программами по дисциплине. Работа подготовлена на кафедре теоретической и прик…

Практикум

формат pdf
размер 330.72 КБ
добавлен 05 марта 2011 г.

Метод. указания. – 2-е изд., испр. и доп. – Ульяновск: УлГТУ, 2009. – 24 с. Составлены в соответствии с учебными программами по дисциплинам «Сопротивление материалов» для направлений «Машиностроительные технологии и оборудование», «Строительство». Методические указания предназначены для выполнения расчетно-проектировочных и контрольных заданий, предусмотренных рабочими программами по дисциплине. Работа подготовлена на кафедре теоретической и прик…

формат jpg
размер 16.91 МБ
добавлен 03 декабря 2009 г.

Красноярск, КрасГАСА. 2005. -98 с. Расчет стержня на прочность и жесткости при растяжении и сжатии. Расчеты на прочность. Геометрические характеристики плоских сечений. Прямой изгиб бруса. Сдвиг. Кручение. Теория напряженного состояния и теория прочности. Сложное сопротивление. Устойчивость сжатых стержней. Расчет статически неопределимых систем. Динамические задачи.rn

формат doc
размер 1004. 73 КБ
добавлен 15 апреля 2010 г.

Расчет стержневых статически неопределимых систем при растяжении (сжатии). Расчет валов и пружин на жесткость и прочность при кручении. Построение эпюр внутренних силовых факторов для балок и рам. Задачи на прочность и жесткость при изгибе статически определимых систем. Расчет статически неопределимых систем по методу сил. Расчеты на прочность при сложном напряженном состоянии. Задачи на прочность при циклических напряжениях. Расчеты элементов ко…

Практикум

формат pdf
размер 395.14 КБ
добавлен 26 января 2011 г.

Методические указания. Издательство: Хабаровск, ДВГУПС. Год: 2001 Методические указания включают в себя краткое описание метода сил для расчета статически неопределимых систем. Рассмотрен ряд характерных примеров расчета методом сил при одноосном растяжении или сжатии, кручении и изгибе, а также приведен расчет один раз статически неопределимой плоской системы при растяжении и сжатии. Методические указания предназначены для студентов строительн…

Сжатие (или растяжение) стержня

Рассмотрим стержень с прямоугольным поперечным сечением, так что можно использовать декартовы координаты в трех измерениях. Пусть больший размер стержня проходит вдоль оси z , с сжимающей силой на единицу площади f , приложенной к обоим концам. Представьте, что стержень достаточно толстый, чтобы не согнуться под действием приложенной силы.

Предположим, что сила равномерно приложена к поверхности на концах стержня, так что нет изменений углов любых пересекающихся плоскостей, которые могут быть проведены через стержень.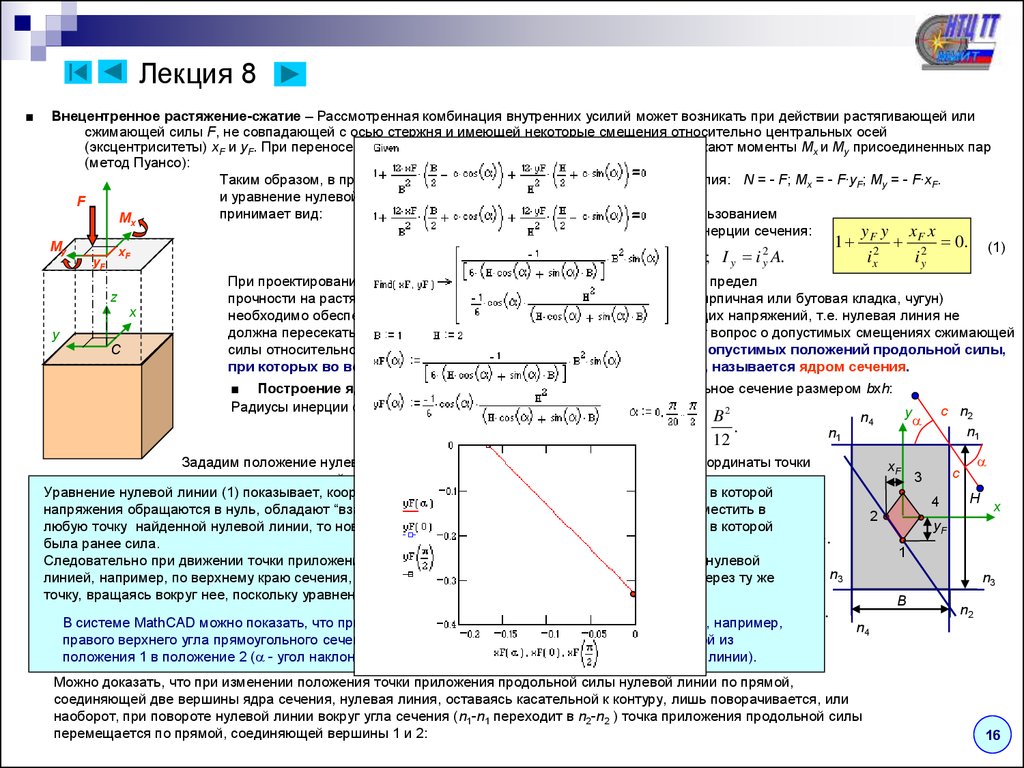 Следовательно, из определения деформации сдвига все недиагональные члены тензора деформации равны нулю.

Из обсуждения в блоге от 10 марта «баланс сил в материале под напряжением» мы знаем, что мы можем разрезать стержень в любом месте, чтобы сформировать новые плоские поверхности, перпендикулярные оси Z, и поскольку силы, воздействующие на каждую из две части должны уравновеситься, сила на любой такой поверхности равна приложенной силе f . По тому же аргументу сила на любой плоскости, перпендикулярной осям x или y, должна быть равна нулю.

Следовательно, величина вектора напряжения на любой плоскости z через стержень равен f, и вектор напряжения на любой плоскости x или y должен быть равен нулю. Из другого предыдущего блога (4 марта, «Теорема Коши о напряжениях») мы знаем, что

Применяя это уравнение к поверхности стержня (или, исходя из приведенного выше обсуждения, любой части стержня, ограниченной x-, y — и z-плоскости) и заменив z -компоненту вектора напряжения на f , а поскольку к сторонам стержня (которые имеют единичные векторы нормали в x и y направления), мы имеем

Поскольку компонента x вектора напряжения и компоненты напряжения сдвига равны нулю, компонента xx- тензора напряжений также равна нулю. Аналогично, yy — компонента тензора напряжений также равна нулю, но zz -компонента равна приложенной силе — f . Знак минус указывает, что сила приложена вдоль вектора нормали внутрь .

Теперь мы можем использовать формулу закона Гука для тензора деформации, приведенную в предыдущем блоге:

Подставляя компоненты тензора напряжений, находим

Мы видим, что хотя неосевые напряжения равны нулю, неосевые деформации — нет. Предположительно, когда мы сжимаем стержень с концов, он становится «толще», но не настолько, насколько сжимаются концы (мы скоро это проверим). Это та часть, которую мы упустили из предыдущего обсуждения куска натянутой резиновой трубки. Наконец, zz — компонент деформации явно отрицательный, что указывает на сжатие.

Обратите внимание, что, хотя это чисто нормальные деформации без сдвига, вышеприведенные выражения, которые будут использоваться для расчета их числовых значений, содержат как модуль объемного сжатия, так и модуль сдвига — не то, что можно было бы ожидать от разделения этих свойств материала в модели Гука.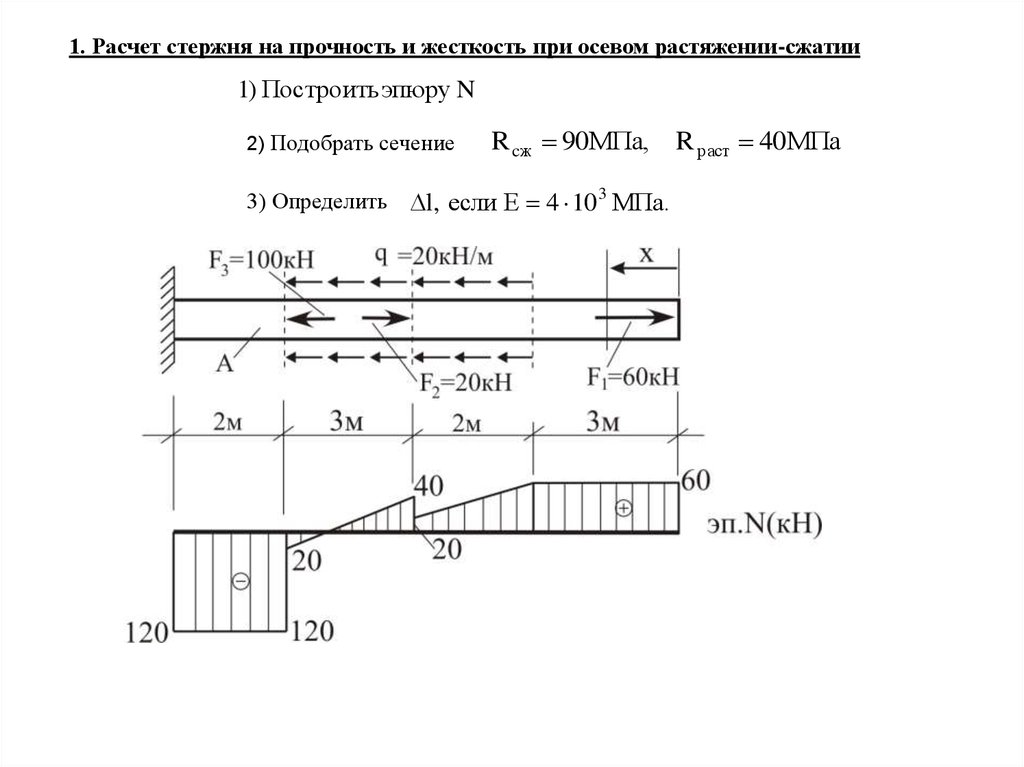 закон.

В отличие от модели чистого сжатия, используемой для записи первого члена закона Гука, стержень одновременно сжимается в осевом направлении и расширяется в поперечном направлении. Возможно, именно поэтому для описания каждой из составляющих деформации требуются оба свойства материала.

В примере с резиновой трубкой мы ввели модуль Юнга, который можно записать здесь как

Таким образом, коэффициент сжатия (или растяжения) — константа пропорциональности, связывающая осевое напряжение и осевую деформацию — или модуль Юнга, представляет собой комбинацию Объемный модуль и модуль сдвига. Следуя Ландау и Лифшицу, мы можем ввести другую материальную константу, называемую коэффициентом Пуассона , используя греческую букву nu , что снова позволяет записать закон Гука только с двумя константами.

Коэффициент Пуассона – это безразмерное число, определяемое как отношение поперечного расширения (сжатия) к продольному сжатию (растяжению):

Для большинства материалов nu находится в диапазоне от 0,2 до 0,3, что указывает на поперечную нормальную деформацию компоненты всегда меньше деформации в направлении приложенных сил, как и следовало ожидать.

Подставляя компоненты деформации используя результаты из набора шести уравнений, перечисленных выше, мы находим коэффициент Пуассона с точки зрения K и mu .:

Прежде чем мы сможем переписать закон Гука, у нас есть еще одна задача — найти K и mu через E и nu , что можно сделать, обратив два только что полученных выражения для последняя пара терминов.

Подстановка этого последнего уравнения в любое из первых двух в этом наборе в конечном итоге дает нам объемный модуль с точки зрения
модуля Юнга и коэффициента Пуассона:

В следующем блоге нам понадобится тензор деформации с точки зрения тензора напряжений с Е и nu, и тогда мы можем записать, вероятно, наиболее полезную и понятную версию закона Гука в компонентной форме.

Напряжение и деформация) – x-Douglas College Physics 1107 Fall 2019 Custom учебник

Глава 4 Динамика: сила и законы движения Ньютона

Резюме

Закон штата Гука.
Объясните закон Гука, используя графическое представление между деформацией и приложенной силой.
Обсудите деформации, такие как изменение длины
Определите изменение длины, зная массу, длину и радиус.

Силы могут влиять на форму объекта. Если бульдозер втолкнет машину в стену, то машина не сдвинется с места, но заметно изменит форму. Изменение формы из-за приложения силы представляет собой деформацию . Известно, что даже очень малые силы вызывают некоторую деформацию. При малых деформациях наблюдаются две важные характеристики. Во-первых, объект возвращается к своей первоначальной форме при снятии силы, то есть деформация является упругой при малых деформациях. Во-вторых, величина деформации пропорциональна силе, т. е. при малых деформациях Закон Гука соблюдается. В форме уравнения закон Гука имеет вид

[латекс]\boldsymbol{F = k\Delta{L},}[/латекс]

, где Δ L — величина деформации (например, изменение длины), вызванная силой F , а k — константа пропорциональности, которая зависит от формы и состава объект и направление силы. Обратите внимание, что эта сила является функцией деформации Δ L — не постоянна, как кинетическая сила трения. Иногда мы используем Δ x вместо Δ L. Деформация может быть вдоль любой оси. Переставить это на

[латекс]\boldsymbol{\Delta{L}\: = }[/латекс][латекс]\boldsymbol{\frac{F}{k}}[/латекс]

дает понять, что деформация пропорциональна приложенной силе. На рис. 1 показана зависимость по закону Гука между расширением Δ L пружины или человеческой кости. Для металлов или пружин прямолинейная область, к которой относится закон Гука, намного больше. Кости хрупкие, эластичная область мала, а перелом внезапный. В конце концов, достаточно большое напряжение на материале приведет к его разрыву или разрушению. Прочность на растяжение — это разрушающее напряжение, вызывающее необратимую деформацию или разрушение материала.

ЗАКОН ГУКА

[латекс]\boldsymbol{F = k\Delta{L},}[/латекс]

, где Δ L — величина деформации (например, изменение длины), вызванная силой F , а k — константа пропорциональности, зависящая от формы и состава объекта и направления силы.

[латекс]\boldsymbol{\Delta{L}\:=}[/латекс][латекс]\boldsymbol{\frac{F}{k}}[/латекс]

Рис. 1. График деформации Δ L в зависимости от приложенной силы Ф . Прямой отрезок — это линейный участок, на котором соблюдается закон Гука. Наклон прямой области равен 1/k . Для больших сил график искривлен, но деформация остается упругой — Δ L вернется к нулю, если усилие будет устранено. Еще большие силы постоянно деформируют объект, пока он окончательно не сломается. Форма кривой вблизи разрушения зависит от нескольких факторов, в том числе от того, как сила F применяется. Обратите внимание, что на этом графике наклон увеличивается непосредственно перед разрывом, указывая на то, что небольшое увеличение F приводит к большому увеличению L вблизи разрыва.

Константа пропорциональности k зависит от ряда факторов материала. Например, гитарная струна из нейлона при натяжении растягивается, и удлинение Δ L пропорционально приложенной силе (по крайней мере, при малых деформациях). Более толстые нейлоновые струны и те, что сделаны из стали, меньше растягиваются при одном и том же приложенном усилии, что означает, что они имеют большее 9-кратное усилие.0123 к (см. рис. 2). Наконец, все три струны возвращаются к своей нормальной длине после снятия силы при условии, что деформация невелика. Большинство материалов ведут себя таким образом, если деформация составляет менее примерно 0,1% или примерно 1 часть на 10 ³ .

Рисунок 2. Одна и та же сила, в данном случае вес ( w ), приложенная к трем разным гитарным струнам одинаковой длины, приводит к трем разным деформациям, показанным заштрихованными сегментами. Струна слева из тонкого нейлона, та, что посередине, из нейлона потолще, а та, что справа, из стали.

НЕМНОГО ПОТЯНИТЕСЬ

Как бы вы измерили константу пропорциональности k резиновой ленты? Если резиновая лента растянулась на 3 см, когда к ней прикреплен груз массой 100 г, то насколько сильно она растянется, если две одинаковые резиновые ленты будут прикреплены к одной и той же массе, даже если их сложить параллельно или, наоборот, связать вместе последовательно?

Решения

Задачи и упражнения

1) 110 Н/м

2) 0,0101 м = 1,01 см

3) 1,11 ньютона

4) 6,0 см По соотношению и пропорции 12 Н/4,0 см? так ? = 18 х 4 / 12 =

Теперь рассмотрим тип деформации, вызывающий изменение длины (растяжение и сжатие). Существуют также боковые силы, вызывающие сдвиг (напряжение) и изменение объема, но мы не будем подробно останавливаться на них в этом курсе.

Изменение длины Δ L образуется, когда к проволоке или стержню прикладывают силу, параллельную его длине L ₀ , либо растягивая его (растяжение), либо сжимая его. (См. рис. 3.)

Рис. 3. (а) Натяжение. Стержень растянут на длину Δ L , когда сила приложена параллельно его длине. (б) Сжатие. Тот же стержень сжимается силами одинаковой величины в противоположном направлении. Для очень малых деформаций и однородных материалов Δ L примерно одинаковы при одинаковой величине растяжения или сжатия. При больших деформациях площадь поперечного сечения изменяется при сжатии или растяжении стержня.

Эксперименты показали, что изменение длины ( Δ L ) зависит лишь от нескольких переменных. Как уже отмечалось, Δ L пропорционально силе F и зависит от вещества, из которого сделан объект. Кроме того, изменение длины пропорционально исходной длине L ₀ и обратно пропорциональна площади поперечного сечения проволоки или стержня. Например, длинная гитарная струна растянется больше, чем короткая, а толстая струна растянется меньше, чем тонкая. Мы можем объединить все эти факторы в одно уравнение для Δ L :

[латекс]\boldsymbol{\Delta{L}\:=}[/латекс][латекс]\boldsymbol{\frac{1}{Y}\frac{\vec{\textbf{F}}}{A} }[/латекс][латекс]\boldsymbol{L_0},[/латекс]

где Δ L изменение длины, F приложенная сила, Y коэффициент, называемый модулем упругости или модулем Юнга, который зависит от вещества, A площадь поперечного сечения, а L ₀ — исходная длина. В таблице 3 приведены значения Y для нескольких материалов. Говорят, что материалы с большим значением Y имеют большую жесткость при растяжении, поскольку они меньше деформируются при заданном растяжении или сжатии. 92)}[/латекс] Алюминий 70 25 75 Кость – растяжение 16 80 8 Кость – компрессия 9 Латунь 90 35 75 Кирпич 15 Бетон 20 Стекло 70 20 30 Гранит 45 20 45 Волосы (человеческие) 10 Твердая древесина 15 10 Чугун, литой 100 40 90 Свинец 16 5 50 Мрамор 60 20 70 Нейлон 5 Полистирол 3 Шелк 6 Паутинная резьба 3 Сталь 210 80 130 Сухожилие 1 Ацетон 0,7 Этанол 0,9 Глицерин 4,5 Меркурий 25 Вода 2,2 Таблица 3. Модули упругости ¹ .

Модули Юнга для жидкостей и газов не указаны в таблице 3, поскольку они не могут растягиваться или сжиматься только в одном направлении. Обратите внимание, что существует предположение, что объект не ускоряется, так что на самом деле есть две приложенные силы величиной F действуют в противоположных направлениях. Например, струны на Рисунке 3 тянут вниз силой величины w и удерживаются потолком, который также оказывает силу величиной w .

Пример 1: натяжение длинного троса

Подвесные тросы используются для перевозки гондол на горнолыжных курортах. (См. рис. 4) Рассмотрим подвесной трос с неподдерживаемым пролетом длиной 3 км. Рассчитайте величину растяжения стального троса. Предположим, что кабель имеет диаметр 5,6 см и максимальное натяжение, которое он может выдержать, равно 3,0 × 10 ⁶ Н .

Рис. 4. Гондолы перемещаются по подвесным тросам на горнолыжном курорте Гала Юдзава в Японии. (кредит: Rudy Herman, Flickr)
Стратегия
Сила равна максимальному натяжению, или F = 3,0 × 10 ⁶ Н . Площадь поперечного сечения π r ² = 2,46 × 10 ^-3 м ² . Уравнение [латекс]\жирныйсимвол{\Delta{L} = \frac{1}{Y}\frac{F}{A}L_0}[/latex] можно использовать для определения изменения длины. 92})(3020\textbf{ m})}[/latex]
[latex]\boldsymbol{=18\textbf{ m}}.[/latex]
Обсуждение
Это довольно натянуто, но только около 0,6% длины без поддержки. Влияние температуры на длину может быть важным в этих условиях.
Кости в целом не ломаются при растяжении или сжатии. Скорее, они обычно ломаются из-за бокового удара или изгиба, что приводит к сдвигу или хрусту кости. Поведение костей при растяжении и сжатии важно, поскольку оно определяет нагрузку, которую кости могут нести. Кости классифицируются как несущие конструкции, такие как колонны в зданиях и деревьях. Несущие конструкции имеют особенности; колонны в здании имеют стальные арматурные стержни, а деревья и кости — волокнистые. Кости в разных частях тела выполняют разные структурные функции и подвержены разным нагрузкам. Таким образом, кость в верхней части бедренной кости располагается тонкими пластинками, разделенными костным мозгом, тогда как в других местах кости могут быть цилиндрическими и наполненными костным мозгом или просто сплошными. Люди с избыточным весом склонны к повреждению костей из-за постоянного сжатия в суставах и сухожилиях.
Другой биологический пример закона Гука происходит в сухожилиях. Функционально сухожилие (ткань, соединяющая мышцу с костью) должно сначала легко растягиваться при приложении силы, но обеспечивать гораздо большую восстанавливающую силу при большем напряжении. На рис. 5 показана зависимость между напряжением и деформацией сухожилия человека. Некоторые сухожилия имеют высокое содержание коллагена, поэтому напряжение или изменение длины относительно невелики; другие, такие как опорные сухожилия (как в ноге), могут изменять длину до 10%. Обратите внимание, что эта кривая напряжения-деформации нелинейна, поскольку наклон линии изменяется в разных областях. В первой части растяжения, называемой областью пальцев, волокна сухожилия начинают выстраиваться в направлении напряжения — это называется 9.0123 разжимной . В линейной области фибриллы будут растягиваться, а в области разрушения отдельные волокна начинают рваться. Простую модель этой взаимосвязи можно проиллюстрировать параллельными пружинами: разные пружины активируются при разной длине растяжения. Примеры этого приведены в задачах в конце этой главы. Связки (ткань, соединяющая кость с костью) ведут себя аналогичным образом.
Рисунок 5. Типичная кривая напряжения-деформации для сухожилий млекопитающих. Показаны три области: (1) область носка (2) линейная область и (3) область разрушения.
В отличие от костей и сухожилий, которые должны быть прочными и эластичными, артерии и легкие должны быть очень растяжимыми. Эластические свойства артерий необходимы для кровотока. Давление в артериях увеличивается, и стенки артерий растягиваются, когда кровь выталкивается из сердца. Когда аортальный клапан закрывается, давление в артериях падает, и стенки артерий расслабляются, чтобы поддерживать кровоток. Когда вы чувствуете свой пульс, вы чувствуете именно это — эластичное поведение артерий по мере того, как кровь течет через них при каждом толчке сердца. Если бы артерии были жесткими, вы бы не почувствовали пульс. Сердце также является органом с особыми эластическими свойствами. Легкие расширяются за счет мышечного усилия, когда мы вдыхаем, но свободно и эластично расслабляются, когда мы выдыхаем. Наша кожа особенно эластична, особенно у молодых. Молодой человек может похудеть со 100 кг до 60 кг без видимых провисаний кожи. Эластичность всех органов с возрастом снижается. Постепенное физиологическое старение за счет снижения эластичности начинается в начале 20-летнего возраста.
Пример 2. Расчет деформации: насколько укорачивается ваша нога, когда вы стоите на ней?
Рассчитайте изменение длины бедренной кости голени, когда мужчина массой 70,0 кг поддерживает на ней 62,0 кг своего веса, предполагая, что кость эквивалентна однородному стержню длиной 40,0 см и радиусом 2,00 см . 2) = 607.6\textbf{N}},[/латекс]
, а площадь поперечного сечения равна π r ² = 1,257 × 10 ^-3 м ² . Уравнение [латекс]\жирныйсимвол{\Delta{L} = \frac{1}{Y}\frac{F}{A}L_0}[/latex] можно использовать для определения изменения длины.
Раствор
Все количества, кроме Δ L , известны. Обратите внимание, что здесь необходимо использовать значение сжатия для модуля Юнга кости. Таким образом,
[латекс]\boldsymbol{\Delta{L}=(\frac{1}{9{-5}\textbf{ м}}.[/latex]
Обсуждение
Это небольшое изменение длины кажется разумным, согласующимся с нашим опытом, что кости жесткие. На самом деле, даже довольно большие силы, возникающие при напряженной физической работе, не сильно сжимают или сгибают кости. Хотя кость жесткая по сравнению с жиром или мышцами, некоторые из веществ, перечисленных в таблице 3, имеют более высокие значения модуля Юнга Y . Другими словами, они более жесткие.
Уравнение изменения длины традиционно перестраивается и записывается в следующем виде:
[латекс]\boldsymbol{\frac{F}{A}}[/latex][латекс]\boldsymbol{=Y}[/latex][латекс]\boldsymbol{\frac{\Delta{L}}{L_0 }}.[/латекс]
Отношение силы к площади [латекс]\boldsymbol{\frac{F}{A}},[/латекс] определяется как напряжение (измеряется в Н/м ² ), а отношение изменения длины в длину,[латекс]\жирныйсимвол{\гидроразрыва{\Delta{L}}{L_0}},[/латекс]определяется как штамм (безразмерное количество). Другими словами,
[латекс]\boldsymbol{\textbf{стресс}=Y\times\textbf{штамм}}.[/латекс]
В этой форме уравнение аналогично закону Гука, где напряжение аналогично силе, а деформация аналогична деформации. Если мы снова перепишем это уравнение к виду
[латекс]\boldsymbol{F=YA}[/латекс][латекс]\boldsymbol{\frac{\Delta{L}}{L_0}},[/latex]
видим, что это то же самое, что и закон Гука с константой пропорциональности
[латекс]\boldsymbol{k\:=}[/латекс][латекс]\boldsymbol{\frac{YA}{L_0}}. [/latex]
Эта общая идея о том, что сила и вызываемая ею деформация пропорциональны малым деформациям, применима к изменениям длины, боковому изгибу и изменениям объема.
НАПРЯЖЕНИЕ
Отношение силы к площади [латекс]\boldsymbol{\frac{F}{A}},[/латекс] определяется как напряжение, измеренное в Н/м ² .
НАПРЯЖЕНИЕ
Отношение изменения длины к длине [латекс]\boldsymbol{\frac{\Delta{L}}{L_0}},[/латекс] определяется как напряжение (безразмерная величина). Другими словами,
[латекс]\boldsymbol{\textbf{стресс}=Y\times\textbf{штамм}}.[/латекс]
Закон Гука определяется выражением
[латекс]\boldsymbol{F=k\Delta{L}},[/latex] или [латекс]\boldsymbol{F=k\Delta{x}},[/latex]
, где Δ L — величина деформации (изменение длины), F — приложенная сила, а k — константа пропорциональности, зависящая от формы и состава объекта. и направление силы. Связь между деформацией и приложенной силой также можно записать как
[латекс]\boldsymbol{\Delta{L}\:=}[/латекс][латекс]\boldsymbol{\frac{1}{Y}\frac{F}{A}}[/latex][латекс] \boldsymbol{L_0},[/латекс]
, где Y — это модуль Юнга , зависящий от вещества, A — площадь поперечного сечения, а L ₀ — исходная длина.
Отношение силы к площади [латекс]\boldsymbol{\frac{F}{A}},[/латекс] определяется как напряжение , измеренное в Н/м ² .
Отношение изменения длины к длине [латекс]\boldsymbol{\frac{\Delta{L}}{L_0}},[/латекс] определяется как штамм (безразмерная величина). Другими словами,
[латекс]\boldsymbol{\textbf{стресс}=Y\times\textbf{штамм}}.[/латекс]
Сноски
1 Приблизительные и средние значения. Модули Юнга Y для растяжения и сжатия иногда различаются, но здесь они усреднены.