Расчет стойки на прочность и устойчивость
Расположенный ниже онлайн калькулятор предназначен для расчёта центрально-нагруженной стойки (колонны) из стального проката круглого, квадратного, прямоугольного и шестигранного сечения на прочность, устойчивость и изгиб. Если Вам нужно рассчитать онлайн прочность, изгиб и устойчивость стойки из СТАЛЬНЫХ ТРУБ, смотрите ТУТ . Или расчет стойки из ШВЕЛЛЕРА, ДВУТАВРА, ТАВРА и УГОЛКА на прочность, устойчивость и гибкость.При проектировании строительных конструкций, необходимо принимать схемы, обеспечивающие прочность, устойчивость и пространственную неизменяемость сооружения в целом, а также его отдельных элементов при монтаже и эксплуатации.
Поэтому стойку, находящуюся под действием сжимающей её нагрузки необходимо проверять:
- На прочность;
- Устойчивость;
- Допустимую гибкость.
Для расчета предлагаем вам воспользоваться онлайн калькулятором, специально разработанным для нашего сайта!
| Укажите вид проката | |||
| Круг | Квадрат | Полоса | Шестигранник |
| Выберите схему крепления стойки | Заделка-консоль | Заделка-заделка | Заделка-шарнир | Шарнир-шарнир |
| Материал проката | Вид и назначение стоек (колонн) | Сталь С235 (Ст3кп2)Сталь С245 (Ст3пс5,Ст3сп5)Сталь С255 (СтГпс,Ст3Гсп)Сталь С285 (Ст3сп,Ст3Гпс,Ст3Гсп)Сталь С345 (12Г2С,09Г2С)Сталь С345К (10ХНДП)Сталь С375 (12Г2С)Сталь С390 (14Г2АФ)Сталь С390Д (14Г2АФД)Сталь С440 (16ГАФ)Сталь С590 (12Г2СМФ) | Стойки и раскосы передаюшие опорные реакции Основные колонныВторостепенные колонны |
Если Вашего материала нет в таблице, но Вам известно рассчётное
сопротивление этого материала, ведите его значение в это поле (кг/см2):
Введите параметры для расчёта
| Длина стойки L, м | Размер D или Dv, или A, им | ||
| Размер B, мм | Нагрузка на стойку P, кг |
Логика онлайн расчета на прочность и устойчивость стойки из стального проката
Согласно Актуализированной редакция СНиП II-23-81 (CП16. 13330, 2011) рассчитывая на прочность элементов из стали при центральном растяжении или сжатии силой P следует выполнять по формуле:
13330, 2011) рассчитывая на прочность элементов из стали при центральном растяжении или сжатии силой P следует выполнять по формуле:
P / Fp * Ry * Yc <= 1
- где P — действующая нагрузка.
- Fp — площадь поперечного сечения колонны.
- Ry — подсчетное сопротивление материала (стали колонны), выбирается по таблице В5 Приложения «В» того же СНиПа.
- Yc — коэффициент условий работы по таблице 1 СНиПа (0.9-1.1). В соответствии с примечанием к этой таблице (пункт 5) в калькуляторе принято Yc=1.
Проверку на устойчивость элементов сплошного сечения при центральном сжатии силой P следует выполнять по формуле:
P / Fi * Fp * Ry * Yc <= 1
где Fi — коэффициент продольного изгиба центрально — сжатых элементов.
Коэффициент Fi введён в качестве компенсации возможности некоторой не прямолинейности колонны, недостаточной жесткости её крепления и неточности в приложении нагрузки относительно оси стойки.
Значение Fi зависит от марки стали и гибкости колонны и часто берётся из таблицы 72 СНиП II-23-81 1990г., исходя из гибкости колонны и расчётного сопротивления выбранной стали сжатию, растяжению и изгибу.
Это несколько упрощает и огрубляет вычисления, так как СНиП II-23-81* предусматривает специальные формулы для определения Fi. Гибкость (Lambda) — некоторая величина, характеризующая свойства рассматриваемого стержня в зависимости от его длины и параметров поперечн. сечения, в частности радиуса инерции:
Lambda = Lr / i
- здесь Lr — расчётная длина стержня,
- i — радиус инерции поперечного сечения стержня (колонны).
Радиус инерции сечения i равен корню квадратному из выражения I / Fp, где I — момент инерции, Fp — его площадь.
Lr (расчётная длина) определяется как Mu*L; здесь L — длина стойки, а Mu — коэфф., зависящий от схемы её крепления:
- «заделка-консоль»(свободный конец) — Mu=2;
- «заделка-заделка» — Mu = 0.
 5;
5; - заделка — шарнир» — Mu = 0.7;
- «шарнир — шарнир» — Mu = 1.
Следует иметь ввиду,что при наличии у формы поперечн. сечения 2-ух радиусов инерции (например, у прямоугольника), при вычислении Lambda используется меньший.
Кроме того, сама Lambda (гибкость колонны), рассчитанная по формуле Lambda = Lr / i не должна превышать 220-ти в соответствии с таблицей 19. СНиП II-23-81*; там же содержатся ограничения на предельную гибкость центрально — сжатых стержней.
Для их использования необходимо сделать выбор в таблице онлайн калькулятора «Вид, назначение стоек». Предельная гибкость стоек, кроме их геометрических параметров, зависит также от коэффициента продольного изгиба (Fi), действующей нагрузки (P), расчётного сопротивления материала стоики (Ry) и условий её работы (Yc).
Предельная гибкость, устойчивость и прочность стоек, кроме их геометрических параметров, зависит также от коэффициента продольного изгиба (Fi), действующей нагрузки (P), расчётного сопротивления материала стойки (Ry) и условий её работы (Yc).
Если возникнут трудности при расчетах онлайн калькулятором прочности и устойчивости, рекомендуем предварительно ознакомиться с инструкцией.
Механика материалов и конструкций — Библиотека — Кафедра прочности ЛА (102)
| 1. | Построение эпюр внутренних силовых факторов при растяжении и сжатии. М.Б. Зайцева. – Методические указания к выполнению домашнего задания. – Х: «Харьк. авиац. ин-т», 1988. – 34 с. | |
| 2. | Построение эпюр внутренних силовых факторов при кручении. М.Б. Зайцева. – Методические указания к выполнению домашнего задания. – Х: «Харьк. авиац. ин-т», 1988. – 34 с. | |
| 3. | Построение эпюр внутренних силовых факторов при изгибе консольной балки. М.Б. Зайцева. – Методические указания к выполнению домашнего задания. – Х: «Харьк. авиац. ин-т», 1988. – 36 с. | |
| 4. | Построение эпюр внутренних силовых факторов при изгибе балки на двух опорах. С.А. Полтарушников, М.Б. Зайцева. – Методические указания к выполнению домашнего задания. – Х: «Харьк. авиац. ин-т», 1988. – 38 с. | |
| 5. | Построение эпюр внутренних силовых факторов для плоских рам. М.Б. Зайцева, С.А. Полтарушников. – Методические указания к выполнению домашнего задания. – Х: «Харьк. авиац. ин-т», 1988. – 38 с. | |
| 6. | Побудова епюр внутрішніх силових факторів при розтяганні й стисканні. О.Г. Дібір, М.І. Пекельний, М.М. Гребенніков, А.О. Кірпікін. – Навч. посіб. – Х.: Нац. аерокосм. ун-т ім. М.Є. Жуковського «Харк. авіац. ін-т», 2013. – 32 с.Викладено методику побудови епюр внутрішніх силових факторів при розтяганні й стисканні. Наведено приклади розв’язання і оформлення задач, а також рекомендації до виконання домашнього завдання. | |
| 7. | Геометрические характеристики плоских сечений. М.Н. Гребенников, Н.И. Пекельный. – Учеб. пособие. – Х. : Нац. аэрокосм. ун-т им. Н.Е. Жуковского «Харьк. авиац. ин-т», 2015. – 92 с.Изложена методика определения центра тяжести, моментов инерции составных плоских фигур. Приведены таблицы справочных данных, примеры решения задач и рекомендации к выполнению домашнего задания по данной теме с учетом кинематической проверки правильности решения. : Нац. аэрокосм. ун-т им. Н.Е. Жуковского «Харьк. авиац. ин-т», 2015. – 92 с.Изложена методика определения центра тяжести, моментов инерции составных плоских фигур. Приведены таблицы справочных данных, примеры решения задач и рекомендации к выполнению домашнего задания по данной теме с учетом кинематической проверки правильности решения. | |
| 8. | Геометричні характеристики плоских перерізів. М.М. Гребенніков, М.І. Пекельний. – Учеб. пособие. – Харків: Нац. аерокосм. ун-т ім. М.Є. Жуковського «Харків. авіац. ін-т», 2018. – 92 с.Викладено методику визначення центра ваги, моментів інерції складових плоских фігур. Наведено таблиці довідкових даних, приклади розв’язання задач і рекомендації до виконання домашнього завдання з даної теми з урахуванням кінематичної перевірки правильності розв’язання. | |
| 9. | Расчет статически неопределенного стержня при растяжении-сжатии. М.Б. Зайцева, С.А. Полтарушников. – Методические указания к выполнению домашнего задания. | |
| 10. | Расчет брусьев на прочность и жесткость. Л.В. Литовский, М.Н. Гребенников. – Методические указания к выполнению домашнего задания. – Х.: Нац. аэрокосм. ун-т «Харьк. авиац. ин-т», 2004. – 35 с. | |
| 11. | Теории прочности. Сложное сопротивление. М.Н. Гребенников, Н.И. Пекельный. – Учеб. пособие. – Х.: Нац. аэрокосм. ун-т им. Н.Е. Жуковского «Харьк. авиац. ин-т», 2016. – 140 с.Рассмотрены основные теории прочности. Изложена методика расчета на прочность элементов конструкций, находящихся в сложном напряженном состоянии. Описаны частные случаи сложного сопротивления — внецентренное растяжение-сжатие и косой изгиб. Приведены таблицы справочных данных, примеры решения задач и рекомендации к выполнению домашнего задания по данной теме. | |
| 12. | Теорії міцності. Складний опір. М. М. Гребенніков, В. Ю. Мірошніков, М. І. Пекельний. – Харків: Нац. аерокосм. ун-т ім. М. Є. Жуковського «Харків. авіац. ін-т», 2022. – 162 с.Розглянуто основні теорії міцності. Викладено методику розрахунку на міцність елементів конструкцій, що перебувають у складному напруженому стані. Описано окремі випадки складного опору – позацентрове розтягнення-стиснення і косий згин. Наведено таблиці довідкових даних, приклади розв’язання задач і рекомендації щодо виконання домашнього завдання з даної теми. – Харків: Нац. аерокосм. ун-т ім. М. Є. Жуковського «Харків. авіац. ін-т», 2022. – 162 с.Розглянуто основні теорії міцності. Викладено методику розрахунку на міцність елементів конструкцій, що перебувають у складному напруженому стані. Описано окремі випадки складного опору – позацентрове розтягнення-стиснення і косий згин. Наведено таблиці довідкових даних, приклади розв’язання задач і рекомендації щодо виконання домашнього завдання з даної теми. | |
| 13. | Расчет статически неопределимых рам. М.Н. Гребенников, А.Г. Дибир, Л.В. Литовский, О.В. Макаров, Н.И. Пекельный, Г.И. Юдин. – Учеб. пособие. – Х.: Нац. аэрокосм. ун-т «Харьк. авиац. ин-т», 2013. – 48 с.Изложена методика раскрытия статической неопределимости конструктивных элементов типа рама методом сил. Приведены таблицы справочных данных, примеры решения задач и рекомендации к выполнению домашнего задания по данной теме с учетом кинематической проверки правильности решения. | |
14. | Розрахунок статично невизначених рам. М.М. Гребенніков, О.Г. Дібір, М.І. Пекельний, А.О. Кірпікін. – Учеб. пособие. – Х.: Нац. аэрокосм. ун-т «Харьк. авиац. ин-т», 2020. – 48 с.Викладено методику розкриття статичної невизначеності конструктивних елементів типу рама методом сил. Наведено таблиці довідкових даних, приклади розв’язання задач і рекомендації до виконання домашнього завдання з даної теми з урахуванням кінематичної перевірки одержаного розв’язку. | |
| 15. | Расчет многопролетных неразрезных балок. Уравнение трех моментов. М.Н. Гребенников, А.Г. Дибир, Н.И. Пекельный. – Учеб. пособие. – Х.: Нац. аэрокосм. ун-т «Харьк. авиац. ин-т», 2010. – 46 с.Изложена методика раскрытия статической неопределимости конструктивных элементов типа «балка» с помощью уравнения трех моментов. Оговорены особенности наличия жесткой заделки, консоли и момента на промежуточной опоре. Приведены таблицы справочных данных и примеры решения задач. | |
| 16. | Расчет на прочность при действии повторно-переменных нагрузок. Н.И. Пекельный, А.Г. Дибир. – Учеб. пособие. – Харьков: Нац. аэрокосм. ун-т «Харьк. авиац. ин-т», 2004. – 74 с.Изложена методика расчета на прочность при действии повторно-переменных нагрузок на отдельные конструктивные элементы типа вала при реализации изгиба с кручением и наличии различных концентраторов напряжений. Приведены таблицы и графики справочных данных для некоторых материалов, типов концентраторов напряжений и видов поверхностной обработки деталей. Даны рекомендации по использованию этих данных, а также примеры выполнения домашнего задания по указанной теме. | |
| 17. | Устойчивость продольно сжатых стержней. А.Г. Дибир, О.В. Макаров, Н.И. Пекельный. – Учеб. пособие. – Харьков: Нац. аэрокосм. ун-т «Харьк. авиац. ин-т», 2008. – 43 с.Представлен расчет на устойчивость продольно сжатых стержней с учетом условий закрепления концов стержня. Даны пределы применимости формулы Эйлера и формулы Ясинского. Рассмотрена несущая способность элементов конструкции крыла самолета. Выведены уравнения приближенных расчетов на прочность и жесткость при продольно-поперечном изгибе стержня. Для сравнения уравнение Эйлера и перемещения сечений выведены с использованием энергетического метода и приведена оценка точности формул. Кроме теоретических сведений по расчету на устойчивость стержней приведены примеры их практических расчетов. Даны пределы применимости формулы Эйлера и формулы Ясинского. Рассмотрена несущая способность элементов конструкции крыла самолета. Выведены уравнения приближенных расчетов на прочность и жесткость при продольно-поперечном изгибе стержня. Для сравнения уравнение Эйлера и перемещения сечений выведены с использованием энергетического метода и приведена оценка точности формул. Кроме теоретических сведений по расчету на устойчивость стержней приведены примеры их практических расчетов. | |
| 18. | Практические расчеты на прочность конструктивных элементов. Часть 1. А.Г. Дибир, О.В. Макаров, Н.И. Пекельный, Г.И. Юдин, М.Н. Гребенников. – Учеб. пособие. – Харьков: Нац. аэрокосм. ун-т «Харьк. авиац. ин-т», 2007. – 102 с.Представлен расчет на прочность элементов конструкций, представляющих собой толстостенный цилиндр под действием внутреннего, наружного или одновременно внутреннего и наружного давлений. Решена задача Ляме — определение напряжений в толстостенной трубе, в том числе с эксцентричным отверстием. Определены напряжения в толстостенной сфере. Для составных цилиндров решена задача Гадолина. Проведено сравнение прочностей составного и сплошного цилиндров. Даны конструктивно-технологические рекомендации по повышению прочности в технике высоких давлений.Кроме теоретических выкладок по определению напряженно-деформированного состояния материала цилиндра рассмотрены примеры реальных расчетов элементов конструкций как в упругой, так и в пластической зоне. Определены напряжения в толстостенной сфере. Для составных цилиндров решена задача Гадолина. Проведено сравнение прочностей составного и сплошного цилиндров. Даны конструктивно-технологические рекомендации по повышению прочности в технике высоких давлений.Кроме теоретических выкладок по определению напряженно-деформированного состояния материала цилиндра рассмотрены примеры реальных расчетов элементов конструкций как в упругой, так и в пластической зоне. |
Калькулятор натяжения
Создано Кеннетом Аламбра
Отзыв от Bogna Szyk и Jack Bowater
Последнее обновление: 05 июня 2023 г.
Содержание:- Что такое сила натяжения?
- Второй закон движения Ньютона
- Как вычислить натяжение в канатах, приостановленное объект
- Как найти натяжение в веревках при тяге объекта
- FAQ
Этот калькулятор натяжения научит вас, как найти силу напряжения в канате или струнке, используемой для поднятия объекта. В этой статье вы также узнаете, как найти натяжение веревок, которыми тянут объект на поверхности без трения. Вы также увидите в этом калькуляторе натяжения веревки или струны различные диаграммы свободного тела, чтобы лучше понять, как рассчитать силы натяжения. Если вы хотите узнать больше о натяжении и формуле силы натяжения, читайте дальше!
В этой статье вы также узнаете, как найти натяжение веревок, которыми тянут объект на поверхности без трения. Вы также увидите в этом калькуляторе натяжения веревки или струны различные диаграммы свободного тела, чтобы лучше понять, как рассчитать силы натяжения. Если вы хотите узнать больше о натяжении и формуле силы натяжения, читайте дальше!
Что такое сила натяжения?
Представьте, что вы поднимаете с земли баскетбольный мяч. Вы почувствуете вес мяча в своих руках из-за силы тяжести, действующей на массу мяча. Теперь представьте, что вы обвязываете мяч веревкой, которую затем используете, чтобы снова поднять мяч. Вы по-прежнему чувствовали бы вес мяча через веревку. В этой ситуации канат теперь находится в натяжении . То, что удерживает веревку вместе, называется силой натяжения . Разрезание веревки ослабит силу натяжения и отправит мяч в свободное падение.
Сила натяжения — это осевая сила, действующая на объект, который тянет, например веревку, веревку или цепь. Мы также можем наблюдать силу натяжения в других материалах, таких как стержни и стержни, при условии, что они подвергаются внешнему растяжению или растяжению. Материалы с высокой прочностью на растяжение делают лучшие стержни и стержни, так как они не ломаются под действием сил растяжения. Вы можете проверить наш калькулятор напряжения, в котором обсуждается эластичность, чтобы узнать больше о прочности на растяжение.
Мы также можем наблюдать силу натяжения в других материалах, таких как стержни и стержни, при условии, что они подвергаются внешнему растяжению или растяжению. Материалы с высокой прочностью на растяжение делают лучшие стержни и стержни, так как они не ломаются под действием сил растяжения. Вы можете проверить наш калькулятор напряжения, в котором обсуждается эластичность, чтобы узнать больше о прочности на растяжение.
Сила натяжения также является прекрасным примером Третьего закона движения Ньютона . Третий закон движения Ньютона гласит, что когда одно тело воздействует на другое тело, то второе тело действует с такой же силой в противоположном направлении обратно на исходное тело. Сила натяжения представляет собой реактивную силу, противодействующую внешней силе притяжения.
Второй закон движения Ньютона
Чтобы рассчитать натяжение, действующее на веревку, нам сначала нужно понять Второй закон движения Ньютона . Второй закон Ньютона гласит, что сумма сил, действующих на объект постоянной массы, равна массе этого объекта, умноженной на его ускорение. Мы также можем выразить это утверждение в виде уравнения:
Мы также можем выразить это утверждение в виде уравнения:
ΣF = m × a
, где:
- Σ (сигма) обозначает сумму сил F ;
- м — масса объекта; и
- это ускорение.
Для объекта, подвешенного на веревке, мы можем использовать ускорение свободного падения g в качестве его ускорения. Гравитационное ускорение дает нам значение его веса с точки зрения силы, например, ньютонов или фунт-сила . Если объект движется с другим ускорением, мы должны использовать его фактическое ускорение для расчета. Однако этот калькулятор натяжения определяет силы натяжения только в случаях
Это утверждение означает, что этот инструмент учитывает только объектов в покое в данной системе. В этом калькуляторе натяжения мы также предполагаем, что веревки не имеют массы и, следовательно, не вносят никакого вклада в силы натяжения. Мы также предполагаем, что массы или объекты находятся в вакууме и не испытывают трения или сопротивления воздуха по отношению к окружающей их среде.
Мы также предполагаем, что массы или объекты находятся в вакууме и не испытывают трения или сопротивления воздуха по отношению к окружающей их среде.
Как рассчитать натяжение веревок, подвешивающих объект
На приведенном ниже рисунке видно, что сила F, необходимая для подъема объекта, равна весу объекта W. Эта идея является фундаментальной концепцией, лежащей в основе нашей формулы силы натяжения. Ниже также показана диаграмма свободного тела объекта, которая показывает силы натяжения T, действующие на струну. Как видите, силы натяжения приходят парами и в противоположных направлениях:
Следуя второму закону движения Ньютона, мы можем выразить сумму сил, используя диаграмму свободного тела объекта, как показано в правой части иллюстрации выше. Мы используем диаграммы свободного тела , чтобы показать различные направления и величины сил, действующих на тело. В равновесии все эти силы должны равняться нулю. Считая все восходящие силы положительными, а направленные вниз отрицательными, получаем следующее уравнение:
ΣF↑ = 0 = T + (-W)
T = W
где вес W становится отрицательным, поскольку он направлен вниз. Перенося W в другую часть уравнения, мы теперь видим, что сила натяжения веревки равна весу предмета, который она несет, как это также показано выше.
Перенося W в другую часть уравнения, мы теперь видим, что сила натяжения веревки равна весу предмета, который она несет, как это также показано выше.
Если мы используем больше веревок для подъема объекта, общая сила натяжения делится на веревки. Сила натяжения каждой веревки зависит от ее угла по отношению к направлению силы, которой она противодействует. Чтобы лучше понять это, давайте рассмотрим другую диаграмму свободного тела объекта, подвешенного на двух веревках, как показано ниже:0003
На диаграмме свободного тела, показанной выше, мы можем видеть горизонтальную и вертикальную составляющие сил натяжения, T₁ и T₂. Силы являются векторами, что означает, что они всегда имеют как величин, так и направлений. Как и все векторы, силы могут быть выражены в этих компонентах, которые дают влияние силы вдоль горизонтальной и вертикальной осей. T₁ₓ и T₂ₓ — вертикальные компоненты T₁ и T₂ соответственно. С другой стороны, T 1y и T 2y являются вертикальными составляющими одних и тех же сил соответственно. Поскольку гравитация действует на объект по вертикальной оси, нам необходимо учитывать вертикальные составляющие сил натяжения для нашего суммирования сил следующим образом:
Поскольку гравитация действует на объект по вертикальной оси, нам необходимо учитывать вертикальные составляющие сил натяжения для нашего суммирования сил следующим образом:
ΣF↑ = 0 = T 1 год + T 2 года + (-W)
W = T 1 год + T 2 года 90 102
Поскольку нам также известны углы сил растяжения, мы можем выразить T 1y и T 2y через T₁ и T₂ соответственно с помощью тригонометрических функций:
T 1y 9 0102 = T₁ × sin(α)
T 2y = T₂ × sin(β)
W = T₁ × sin(α) + T₂ × sin(β)
Можно также сказать, что для того, чтобы система находилась в равновесии, объект не должен двигаться ни горизонтально, ни вдоль оси x. Следовательно, горизонтальные компоненты T₁ и T₂ должны равняться нулю. Также с помощью тригонометрии мы можем выразить T₁ₓ и T₂ₓ через T₁ и T₂ соответственно:
T₁ₓ = T₂ₓ
T₁ × cos(α) = T₂ × cos(β)
Если мы разделим обе стороны на cos(α) , мы получим уравнение, в котором T₁ выражается через T₂ и углы:
T₁ = T₂ × cos(β) / cos(α)
Затем мы можем использовать это уравнение для решения T₂, подставив T₂ × cos(β) / cos(α) в качестве T₁ в наше уравнение суммирования сил, как показано ниже: 9 0003
W = T₁ × sin(α) + T₂ × sin(β)
W = T₂ × [cos(β) / cos(α)] × sin(α) + T₂ × sin(β)
W = T ₂ × [cos(β) × sin(α) / cos(α) + sin(β)]
T₂ = W / [cos(β) × sin(α) / cos(α) + sin(β)]
Наконец, если мы умножим все это уравнение на cos(β) / cos(α) , поскольку мы получили значение T₁ через T₂, а затем все упростим, мы получим следующее уравнение:
T₁ = W / [cos(β) × sin(α) / cos(α) + sin(β)] × [cos(β) / cos(α)]
T₁ = W / [cos(α) × sin(β) / cos(β) + sin(α)]
Теперь все, что вам нужно знать, это углы натяжения канатов по отношению к горизонтали. Если задан угол от вертикали, просто вычтите этот угол из 90°. Это даст вам угол от горизонтали. Однако, если вам даны другие значения углов, которые могут быть больше 90° или даже 180°, вы можете воспользоваться нашим калькулятором эталонного угла, который поможет вам определить нужный угол. После определения значений переменных в наших формулах силы натяжения мы теперь можем найти силы натяжения.
Если задан угол от вертикали, просто вычтите этот угол из 90°. Это даст вам угол от горизонтали. Однако, если вам даны другие значения углов, которые могут быть больше 90° или даже 180°, вы можете воспользоваться нашим калькулятором эталонного угла, который поможет вам определить нужный угол. После определения значений переменных в наших формулах силы натяжения мы теперь можем найти силы натяжения.
Как найти натяжение веревки при вытягивании объекта
Как найти силу натяжения на объекте, который тянут так же, как когда объект подвешен. Единственное отличие состоит в том, что сначала нам нужно вычислить ускорение всей системы и сумма всех сил по горизонтали. Если веревка находится под углом к уровню пола, нам также необходимо вычислить горизонтальную составляющую тягового усилия.
Давайте рассмотрим пример ниже, чтобы лучше понять, как найти силу натяжения веревки, тянущей за собой один или два объекта. В этом примере два объекта тянутся одной приложенной силой тяги. Другая веревка тянет второй объект, который прикреплен к первому объекту, как показано ниже:
Другая веревка тянет второй объект, который прикреплен к первому объекту, как показано ниже:
На этом рисунке показано, что массы m₁ и m₂ равны 3 кг и 2 кг соответственно. Сумма этих двух масс дает общую массу системы 5 кг . Нам также необходимо определить горизонтальную составляющую силы тяги, T = 24 N , то есть под углом θ = 60° . Если снова использовать тригонометрические функции, то можно сказать, что горизонтальная составляющая силы тяги равна 24 Н × cos(60°) , что равно 12 Н . Теперь, когда мы знаем горизонтальную составляющую силы тяги и полную массу системы, мы можем рассчитать ускорение a системы следующим образом: 0026
После того, как мы нашли ускорение системы, мы можем снова использовать второй закон Ньютона для расчета натяжения веревки или струны системы. Для этого умножьте ускорение на массу, которую тянет веревка. Для T₂ его диаграмма свободного тела показывает нам, что он отвечает только за массу m₂; мы можем сказать, что Т₂ = а × м₂ . При этом Т₂ = (2,4 м/с²) × (2 кг) = 4,8 Н . С другой стороны, T₁ — это сила натяжения, которая притягивает вес m₁ и m₂. Однако у нас уже есть значение T₁, которое просто равно T = 24,0 Н. Следовательно, T₁ = 24,0 Н .
Для T₂ его диаграмма свободного тела показывает нам, что он отвечает только за массу m₂; мы можем сказать, что Т₂ = а × м₂ . При этом Т₂ = (2,4 м/с²) × (2 кг) = 4,8 Н . С другой стороны, T₁ — это сила натяжения, которая притягивает вес m₁ и m₂. Однако у нас уже есть значение T₁, которое просто равно T = 24,0 Н. Следовательно, T₁ = 24,0 Н .
В нашем примере, если бы левая и правая веревки были просто одной веревкой, мы могли бы сравнить эту установку с системой шкивов. Блок — это простая машина, которая использует силы натяжения канатов для получения механического преимущества. Вы можете воспользоваться нашим калькулятором шкивов и калькулятором длины ремня (который представляет собой систему с двумя шкивами), чтобы узнать больше о механических преимуществах и натяжении.
Часто задаваемые вопросы
Как рассчитать натяжение веревки под углом?
Чтобы рассчитать натяжение веревки под углом:
- Найдите угол от горизонтали, на которую установлена веревка.

- Найдите горизонтальную составляющую силы натяжения, умножив приложенную силу на косинус угла.
- Рассчитайте вертикальную составляющую силы натяжения, умножив приложенную силу на синус угла.
- Сложите эти две силы вместе, чтобы найти общую величину приложенной силы.
- Учтите любые другие приложенные силы , например, другую веревку, силу тяжести или трение, и решите уравнение силы обычным образом.
Как рассчитать натяжение, создаваемое 10-килограммовым ящиком на двух веревках, подвешенных под углом 60 градусов?
Для определения натяжения в этом случае:
- Определить вертикальную и горизонтальную составляющие сил натяжения канатов:
- Т₁ = Т₁ sin(60) + Т₁ cos(60)
- T₂ = T₂ sin(60) + T₂ cos(60)
- Вертикальные (синусоидальные) составляющие уравновешивают вес :
- T₁ sin(60) + T₂ sin(60) = √3 (T₁ + T₂)/2 = 98 Н
- Горизонтальные (косинусные) составляющие силы натяжения уравновешивают друг друга :
- T₁ cos(60) = T₂ cos(60) или T₁ = T₂
- Решите уравнения:
- 98 Н = √3 Т₁ или, Т₁ = Т₂ = 56,58 Н
Как найти натяжение двух канатов при одинаковом угле подвески?
Когда углы подвески (α) одинаковы для двух веревок, величина натяжения (T) становится одинаковой для обеих веревок.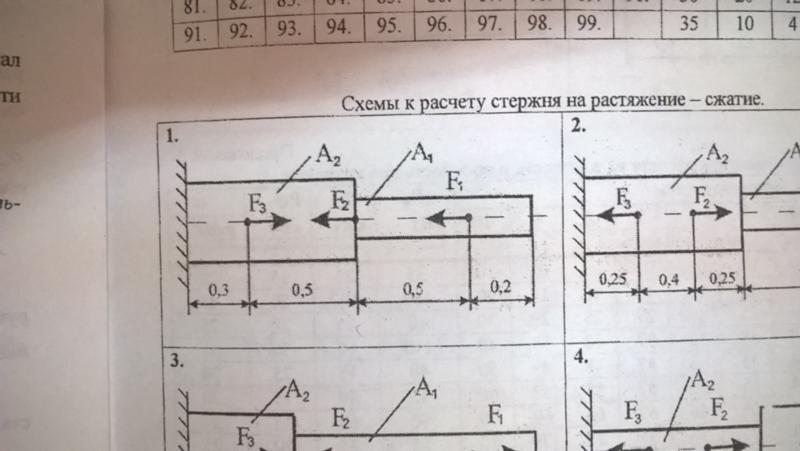 Чтобы определить величину натяжения, используйте уравнение 2T sin(α) = m × g , где m × g представляет вес подвешенного объекта.
Чтобы определить величину натяжения, используйте уравнение 2T sin(α) = m × g , где m × g представляет вес подвешенного объекта.
Является ли напряжение контактной силой?
Да, натяжение — это контактная сила. Натяжение возникает в канате или канате при его растяжении, и растягивающие усилия передаются по канату от одного конца к другому.
Кеннет Аламбра
Сценарий натяжения
Количество канатов
Входные значения
Масса объекта, м
Вес, Вт
Выходное значение
Натяжение каната, T
Посмотрите 10 похожих калькуляторов динамики — почему вещи движутся ➡️
Угол наклона ускорения Сила удара автомобиля… 7 more
Приведенное растягивающее напряжение Калькулятор растягивающей нагрузки
✖Растягивающая нагрузка — это сила растяжения, действующая на материал и обычно приводящая к растягивающему напряжению и деформации растяжения в образце. | Атомная единица силыАттоньютонСентиньютонДеканьютонДециньютонДайнЭксаньютонФемтоньютонГиганьютонГрамм-силаГрейв-силаГектоньютонДжоуль на сантиметрДжоуль на метрКилограмм-силаКилоньютон КилопондКилофунт-силаКип-силаМеганьютонМикроньютонМиллигрейв-силаМиллиньютонНаноньютонНьютонУнция-силаПетаньютонПиконьютонПундФунт-фут на квадратную секундуФунт-силаСтенеТераньютонТон-сила (длинная)Тонна-сила (метрическая)Тон-сила (короткая)Йоттаньютон | +10% -10% | |
✖Площадь поперечного сечения стержня — это площадь двумерной формы, которая получается, когда трехмерная фигура разрезается перпендикулярно некоторой заданной оси в точке.ⓘ Площадь поперечного сечения of Bar [A] | АкрАкр (исследование США)AreArpentBarnCarreauCircular InchCircular MilCuerdaDecareDunamЭлектронное сечениеГектарHomesteadMuPingPlazaPyongRoodSabinSectionSquare AngstromSquare CentimeterSquare ChainSquare DecameterSquare Deci метрКвадратный футКвадратный фут (исследование США)Квадратный гектометрКвадратный дюймКвадратный километрКвадратный метрКвадратный микрометрКвадратный милКвадратная миляКвадратная миля (римская)Квадратная миля (статут)Квадратная миля (исследование США)Квадратный миллиметрКвадратный нанометрКвадратный окуньКвадратный столб корабльVaras Castellanas CuadVaras Conuqueras Cuad | +10% -10% |
✖Растягивающее напряжение на тело можно определить как величину силы, приложенной к упругому стержню, которая делится на площадь поперечного сечения стержня в направлении, перпендикулярном приложенной силе. | Атмосфера ТехническаяАттопаскальБарБарьеСантиметр ртутного столба (0 °C)Сантиметр водяного столба (4 °C)СентипаскальДекапаскальДеципаскальДин на квадратный сантиметрЭксапаскальФемтопаскальФут Морская вода (15 °C)ФемтопаскальФут Морская вода (15 °C)ФемтопаскальФутовая вода (60 °F)ГигапаскальГрамм-сила на квадратный сантиметрГектопаскальДюйм ртутного столба (32 °F)In ch Ртуть (60 °F)Дюйм воды (4 °C)Дюйм воды (60 °F)Килограмм-сила на квадратный сантиметрКилограмм-сила на квадратный метрКилограмм-сила на квадратный миллиметрКилоньютон на квадратный метрКилопаскальКилофунт на квадратный дюймКип-сила на квадратный дюймМегапаскаль-метр Морская водаСчетчик воды (4 °C)МикробарМикропаскальМиллибарМиллиметр ртути (0 °C) C) Миллиметр водяного столба (4 °C) МиллипаскальНанопаскальНьютон на квадратный сантиметрНьютон на квадратный метрНьютон на квадратный миллиметрПаскальПетапаскальПикопаскальPiezeФунт на квадратный дюймФунт на квадратный футФунт-сила на квадратный футФунт-сила на квадратный дюймФунт на квадратный футСтандартная атмосфераТерапаскальТон-сила (длинная) на квадратный футТонна-сила (длинная) на Квадратный дюйм-тонна-сила (короткий) на квадратный фут-тонна-сила (короткий) на квадратный дюйм-торр | ⎘ Копировать |
👎
Формула
Перезагрузить
👍
Растягивающее напряжение при заданной растягивающей нагрузке
ШАГ 0: Сводка предварительного расчета
ШАГ 1: Преобразование входных данных в базовые единицы
Растягивающая нагрузка: 9,61 килоньютон —> 9610 ньютон (проверьте преобразование здесь)
Площадь поперечного сечения стержня: 64000 квадратных миллиметров —> 0,064 квадратных метра ( Проверьте преобразование здесь)
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицы измерения
150156,25 Паскаль —> 0,15015625 Мегапаскаль (Проверьте преобразование здесь)
< 14 типов калькуляторов напряжений
Напряжение сжатия с учетом силы сопротивления
Идти Сжимающее напряжение на корпусе = сила сопротивления/площадь поперечного сечения стержня
Сила сопротивления при сжимающем напряжении
Идти Сила сопротивления = сжимающее напряжение на корпусе * площадь поперечного сечения стержня
Растягивающее напряжение с учетом силы сопротивления
Идти Растягивающее напряжение на корпусе = сила сопротивления/площадь поперечного сечения стержня
Сила сопротивления при заданном растягивающем напряжении
Идти Сила сопротивления = растягивающее напряжение на корпусе * площадь поперечного сечения стержня
Сжимающее напряжение при осевом толчке, действующем на тело
Идти Сжимающее напряжение на корпусе = осевое усилие/площадь поперечного сечения стержня
Осевой толчок, действующий на тело при напряжении сжатия
Идти Осевое усилие = сжимающее напряжение на корпусе*площадь поперечного сечения стержня
Растягивающее напряжение при заданной растягивающей нагрузке
Идти Растягивающее напряжение на корпусе = растягивающая нагрузка/площадь поперечного сечения стержня
Растягивающая нагрузка при заданном растягивающем напряжении
Идти Растягивающая нагрузка = растягивающее напряжение на корпусе * площадь поперечного сечения стержня
Деформация сжатия тела
Идти Деформация сжатия = уменьшение длины/начальной длины
Растягивающая деформация тела
Идти Деформация растяжения = увеличение длины стержня/начальной длины
Поперечное смещение с учетом деформации сдвига
Идти Поперечное смещение = Деформация сдвига * Высота тела
Деформация сдвига при поперечном смещении
Идти Деформация сдвига = поперечное смещение/высота тела
Сопротивление сдвигу с учетом напряжения сдвига
Идти Сопротивление сдвигу = Напряжение сдвига в теле * Площадь сдвига
Напряжение сдвига с учетом сопротивления сдвигу
Идти Напряжение сдвига в теле = сопротивление сдвигу/площадь сдвига
Растягивающее напряжение с учетом формулы растягивающей нагрузки
Растягивающее напряжение на корпусе = растягивающая нагрузка/площадь поперечного сечения стержня
σ t = P нагрузка /A
Что такое растягивающее напряжение?
Растягивающее напряжение определяется как сопротивление материала разрушению при растяжении. При равновесии приложенная нагрузка равна силе сопротивления. Эта сила сопротивления на единицу площади равна растягивающему напряжению.
При равновесии приложенная нагрузка равна силе сопротивления. Эта сила сопротивления на единицу площади равна растягивающему напряжению.
Как рассчитать растягивающее напряжение при растягивающей нагрузке?
Растягивающее напряжение с учетом растягивающей нагрузки Калькулятор использует Растягивающее напряжение на корпусе = Растягивающая нагрузка/площадь поперечного сечения стержня для расчета растягивающего напряжения на корпусе. Растягивающее напряжение с учетом растягивающей нагрузки можно рассчитать путем деления растягивающей нагрузки, действующей на образец, на площадь поперечного сечения. Растягивающее напряжение на корпусе обозначается символом σ t .
Как рассчитать растягивающее напряжение при заданной растягивающей нагрузке с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для расчета напряжения растяжения с учетом нагрузки растяжения, введите значение растягивающей нагрузки 9. 0507 (P нагрузка ) и площадь поперечного сечения стержня (A) и нажмите кнопку расчета. Вот как можно объяснить вычисление растягивающего напряжения с учетом растягивающей нагрузки с заданными входными значениями -> 1,5E-7 = 9610/0,064 .
0507 (P нагрузка ) и площадь поперечного сечения стержня (A) и нажмите кнопку расчета. Вот как можно объяснить вычисление растягивающего напряжения с учетом растягивающей нагрузки с заданными входными значениями -> 1,5E-7 = 9610/0,064 .
Часто задаваемые вопросы
Что такое растягивающее напряжение при растягивающей нагрузке?
Напряжение растяжения при заданной растягивающей нагрузке можно рассчитать путем деления растягивающей нагрузки, действующей на образец, на площадь поперечного сечения, и оно представлено как σ t = P нагрузка /A или Растягивающее напряжение на корпусе = растягивающая нагрузка/площадь поперечного сечения стержня . Растягивающая нагрузка — это сила растяжения, действующая на материал, которая обычно приводит к растягивающему напряжению и деформации растяжения в образце, а площадь поперечного сечения стержня — это площадь двумерной формы, которая получается, когда трехмерная форма разрезается перпендикулярно некоторой заданной оси в точке.

 – Х: «Харьк. авиац. ин-т», 1988. – 40 с.
– Х: «Харьк. авиац. ин-т», 1988. – 40 с. ⓘ Растягивающая нагрузка [P load ]
ⓘ Растягивающая нагрузка [P load ] ⓘ Растягивающее напряжение при заданной растягивающей нагрузке [σ t ]
ⓘ Растягивающее напряжение при заданной растягивающей нагрузке [σ t ]