23.4. Расчет статически неопределимых балок по предельному состоянию. Кинематический и статический способ.

При расчете статически определимой балки было установлено, что ее несущая способность исчерпается, когда, хотя бы в одном, т.е. в наиболее опасном сечении пластическая область заполняет все сечение, т.е. когда в этом сечении образуется пластический шарнир и система становится геометрически изменяемой.

Для статически неопределимых балок образование одного пластического шарнира не приводит к исчерпанию несущей способности, т.к. в этом случае степень кинематической определимости сис­темы снижается на одну единицу. В случае n раз статически неопределимой балки исчерпание несущей способности происходит при формировании n + 1 пластических шарниров. Однако в ряде случаев часть балки может стать геометрически изменяемой при значительно меньшем числе пластических шарниров.

Рис.23. 5

Например, в статически многократно неопределимой балке с консолью (рис.23.5), несущая способность заданной системы исчерпается в случае возникновения первого же пластического шарнира над крайней правой опорой.

Для расчета статически неопределимых систем по теории предельного равновесия можно воспользоваться одним из двух способов — кинематическим или статическим.

При применении кинематического способа, в предельном состоянии составляется уравнение работы всех внешних и внутренних усилий на основе принципа возможных перемещений. Этот принцип формулируется так: если система твердых тел находится в равновесии под действием системы сил, то работа, совершаемая этими силами на любом малом возможном перемещении системы, должна быть равна нулю.

Рис.23.6

При применении статического способа при отсутствии упругого расчета, на основе которого, предварительно можно определить наиболее вероятную схему разрушения конструкции, задаются различные схемы разрушения предельной стадии работы рассматриваемой системы, и для каждой из них составляются уравнения равновесия и определяются предельные значения внешних сил.

Из их числа, наименьшая является расчетной величиной предельной силы.

Из числа рассмотренных схем разрушения, на основании которых определяется предельная сила, является наиболее вероятной схемой, разрушения конструкции.

Рассмотрим несколько характерных примеров для определения предельной нагрузки для статически неопределимых балок, принимая диаграмму растяжения-сжатия материалов без упрочнения, т.е. диаграмму Прандтля (см. рис.22.3, в).

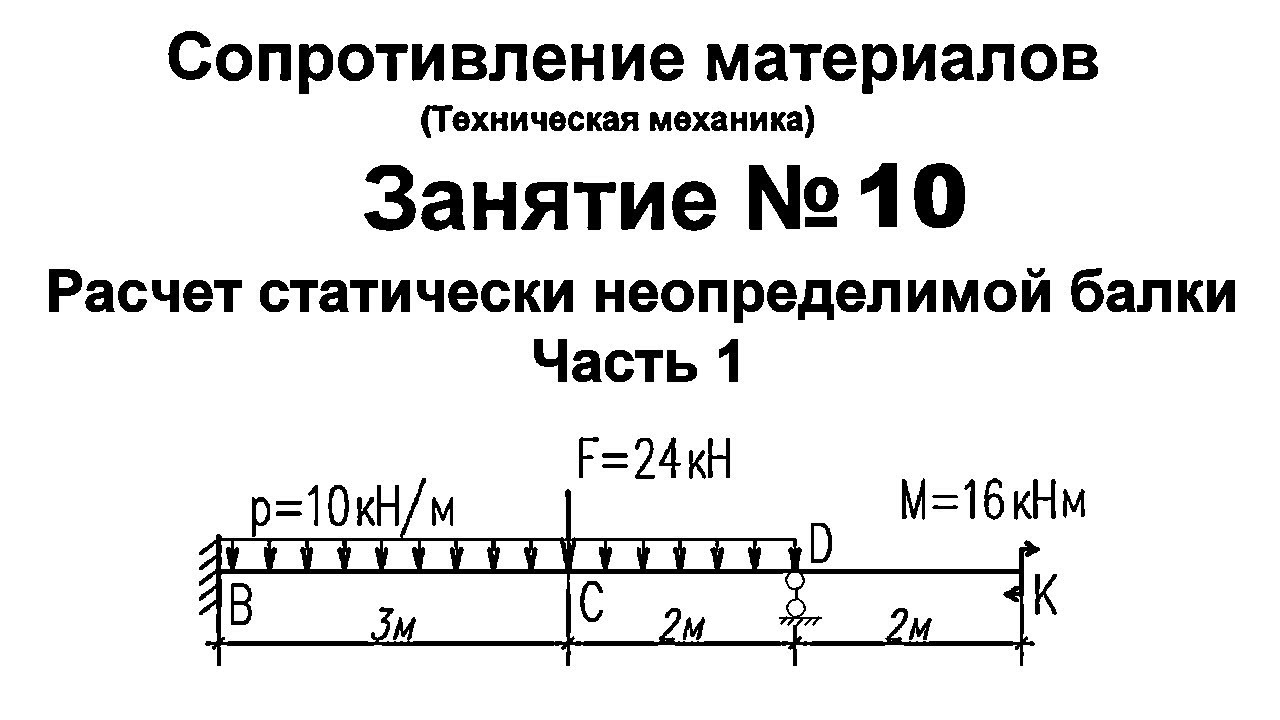
Пусть трехопорная балка (рис.23.6, а) нагружена силой величиной Р. Эта балка один раз статически неопределимая. На рис.23.6, 

б изображена эпюра изгибающих моментов, при упругой стадии деформирования. Для решения этой задачи применим статический способ.

Значение силы , при которой в наиболее опасной точке балки напряжение достигает предела текучести, и может быть установлено из равенства наибольшего момента, действующего в опасном сечении, допускаемому:. Откуда, получим:

.

Если балка имеет прямоугольное поперечное сечение, то

,

и, следовательно,

. (23.15)

Рис.23.7

Наращивая величину внешней силы , пластическая область в опасном сеченииВ балки увеличивается. При некотором значении силы в сечении В возникает пластический шарнир, тогда величина изгибаю­щего момента в этом сечении становится равной . При дальнейшем росте внешней силы

Р, момент в сечении В остается постоянным и равным . Это означает, что трехопорная балка приобретает пластический шарнир в т.В. При этом она нагружена силой Р и двумя моментами , приложенных в разных торцах сеченияВ (рис.23.7, а). Следовательно, в данном случае возникновение одного пластического шарнира превращает один раз статически неопределимую балку в балку статически определимую.

При дальнейшем росте силы Р изгибающие моменты в сечении В и на участке АВ не возрастают, а изгибающие моменты на участке ВСD, с ростом величины силы Р, растут. При указанных предположениях, наибольшая величина изгибающего момента формируется в сечении С, где он раньше всего и достигает предельной величины .

Когда в сечении С изгибающий момент достигнет предельной величины , т.е. когда в этом сечении сформируется пласти­ческий шарнир, несущая способность балки исчерпается, вследствие чего, балка превращается в геометрически изменяемую систему.

Согласно статическому способу, и учитывая, что наиболее вероятная схема разрушения конструкции очевидна и изображена на рис.23.7, б, величина предельной силы определяется из уравнений равновесия и условий равенства изгибающего момента в сечениях пластического шарнира предельному моменту :

Решая совместно последнюю систему уравнений, получим:

, (23. 16)

откуда:

. (23.17)

При расчете по методу допускаемых напряжений расчетная величина допускаемой силы определяется:

, (13.18)

где n — коэффициент запаса по несущей способности конструкции.

В случае расчета по методу предельных состояний, величина допускаемой силы, принимает значение:

. (23.19)

Сопоставляя выражения (23.18) и (23.19), получим, что метод расчета по предельному состоянию дает величину допускаемой силы в раза больше, чем метод расчета по допускаемым напряжениям, при условии, что коэффициент запаса в обоих методах принят одинаковым.

В заключении рассмотрим балку с одним защемленным, а вторым шарнирно опертым концами, нагруженной двумя одинаковыми силами (рис.23.8, а).

Определим величину предельной силы кинематическим способом, предложенным А.А. Гвоздевым.

Рассматриваемая балка, один раз статически неопределима и, следовательно, ее несущая способность исчерпается в случае образования двух пластических шарниров.

Пластические шарниры могут формироваться в сечениях А, В и С. Для определения предельной нагрузки по кинематическому способу А.А. Гвоздева необходимо рассмотреть различные сочетания образования пластических шарниров в двух сечениях из трех. Число таких комбинаций равно трем, т.е. числу сочетаний из трех пластических шарниров по два.

Рис.23.8

Для различных вариантов расположения пластических шарниров составляются уравнения равновесия, при условии равенства изгибающего момента в сечениях пластического шарнира предельному моменту . Из полученных уравнений могут быть определены величины предельных нагрузок.

Действительной предельной нагрузкой будет наименьшая из вычисленных для различных сочетаний пластических шарниров.

Необходимо заметить, что при составлении уравнений предельного равновесия системы, можно использовать из трех уравнений статического равновесия всей системы в целом, только два из них. Третье уравнение автоматически будет удовлетворяться. Недостающие уравнения могут быть получены, из рассмотрения равновесия отсеченной части системы, предполагая, что рассматриваемое сечение проходит через пластический шарнир.

Рассмотрим различные возможные схемы предельной стадии работы конструкции.

Первая схема, предполагая, что пластические шарниры формируются в сечениях А и В (рис.23.8, б):

откуда

. (23.20)

Вторая схема, предполагая, что пластические шарниры формируются в сечениях А и С (рис. 23.8, в):

откуда

(23.21)

Третья схема, предполагая, что пластические шарниры формируются в сечениях В и С (рис.23.8, г):

откуда, решая совместно эту систему уравнений, получим значения изгибающего момента в заделке и значение предельной нагрузки:

(23.22)

Так как условие не может быть реализовано, то третью схему следует исключить из дальнейшего рассмотрения.

Сопоставляя предельные значения внешней силы, приведенные в (23.20)-(23.21), определяем, что наименьшая предельная нагрузка имеет место при второй схеме предельного равновесия, т.е. когда пластические шарниры формируются в сечениях 

А и С:

.

Далее рассмотрим применение кинематического способа — метода предельных состояний для определения величин продольных сил. Действительная схема разрушения системы показана на рис.23.9. Составим уравнения работ всех внутренних и внешних усилий на возможных перемещениях:

. (23.23)

Составляя уравнения совместности, получим:

(23.24)

Рис.23.9

Уравнение (23.23), с учетом (23.24), примет вид:

откуда:

. (23.25)

Сопоставляя выражения (23.25) и (23.21), заметим, что кинематический и статический способы дали идентичные результаты по значению предельной силы.

Расчет статически неопределимых балок. Способ сравнения деформаций

Лекция № 35. Расчет статически неопределимых балок. Способ сравнения деформаций.

Общие понятия и метод расчета.

До сих пор мы рассматривали только статически определимые балки, у которых три опорные реакции определялись из условий равновесия. Очень часто, по условиям работы конструкции, оказывается необходимым увеличить число опорных закреплений; тогда мы получаем так называемую статически неопределимую балку.

Рис.1. Схемы статически неопределимых балок

Например, для уменьшения пролета балки АВ на двух опорах (Рис.1, а) можно поставить опору еще посредине, а для уменьшения деформаций балки, защемленной одним концом (Рис.1, б), можно подпереть ее свободный конец.

Для подбора сечения таких балок, так же как и в рассмотренных ранее задачах, необходимо построить обычным порядком эпюры изгибающих моментов и поперечных сил, а стало быть, определить опорные реакции.

Во всех подобных случаях число опорных реакций, которые могут возникнуть, превышает число уравнений статики, например, для балок рис.2. Соответственно: четыре, четыре и пять опорных реакций.

Рис.2. Механизм появления дополнительных связей

Поэтому необходимо составить дополнительные уравнения, выражающие условия совместности деформаций, которые вместе с обычными уравнениями равновесия и дадут возможность определить все опорные реакции.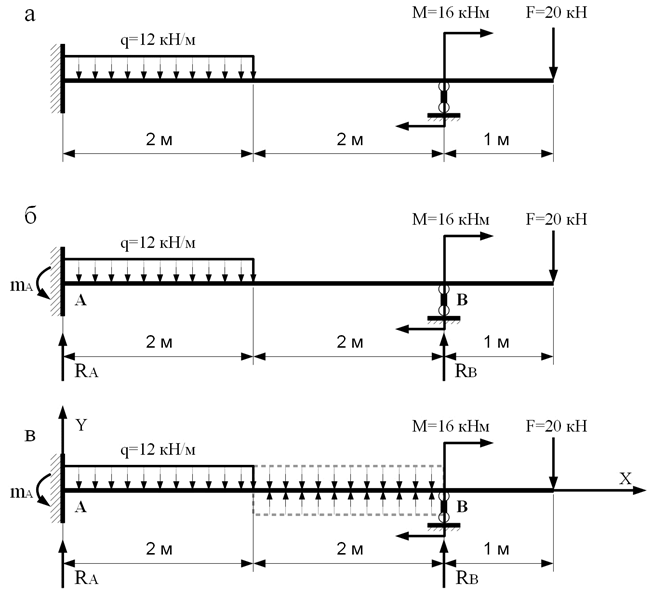

Определим опорные реакции и построим эпюру моментов для балки, находящейся под действием равномерно распределенной нагрузки q рис.3. Сначала изобразим все реакции, которые по устройству опор могут возникнуть в этой балке. Таких реакций может быть на опоре А три: вертикальная А, горизонтальная и опорный момент , на опоре В возможно появление лишь одной реакции В. Таким образом, число опорных реакций на одну больше, чем уравнений статики.

Одна из реакций является добавочной, как говорят, «лишней» неизвестной. Этот термин прочно укоренился в технической литературе; между тем, принять его можно лишь условно.

Рис.3. Исходная расчетная схема статически неопределимой балки.

Действительно, добавочная реакция и соответствующее ей добавочное опорное закрепление являются «лишними» только с точки зрения необходимости этих закреплений для равновесия балки как жесткого целого. С точки же зрения инженера добавленное закрепление во многих случаях не только не является лишним, а наоборот, позволяет осуществить такую конструкцию, которая без него была бы невозможна. Поэтому мы будем пользоваться термином «лишняя опорная реакция», «лишняя неизвестная» лишь условно.

Составим все уравнения статики для нашей балки, приравнивая нулю сумму проекций всех сил на направление оси балки, на перпендикуляр к ней, и сумму моментов относительно точки А. Получим систему:

,

Из первого уравнения сразу определяется опорная реакция Для определения трех других остаются лишь два уравнения.

За лишнюю реакцию можно взять любую из этих трех: попробуем взять реакцию опоры В. В таком случае мы должны считать, что рассматриваемая балка получилась из статически определимой балки АВ, защемленной концом А, у которой потом поставили добавочную опору в точке В. Эта статически определимая балка, которая получается из статически неопределимой при удалении добавочного, лишнего опорного закрепления, называется основной системой. Выбрав какую-либо из реакций за лишнюю неизвестную, мы тем самым выбираем основную систему.

Попробуем теперь превратить основную систему без опоры В в систему, полностью совпадающую с заданной статически неопределимой балкой (Рис.3).

Рис.4. Эквивалентная система

Для этого загрузим ее сплошной нагрузкой q и в точке В приложим лишнюю реакцию В (Рис.4).

Однако этого мало: в балке, представленной на рис.4, точка В может перемещаться по вертикали под действием нагрузок q и В; между тем, в нашей статически неопределимой балке точка В не имеет этой возможности, она должна совпадать с опорным шарниром. Поэтому, чтобы привести к окончательному совпадению, надо к последней добавить условие, что прогиб точки В основной системы под действием нагрузок q и В должен быть равен нулю:

Это и будет добавочное уравнение, определяющее реакцию В; оно является условием совместности деформаций в рассматриваемом случае: конец В балки не отрывается от опоры.

Решение этого добавочного уравнения возможно несколькими способами.

Способ сравнения деформаций.

Выполняя решение уравнения , названного уравнением совместности деформаций, можно рассуждать следующим образом.

Прогиб точки В основной системы под действием нагрузок q и В складывается из двух прогибов: одного , вызванного лишь нагрузкой q, и другого , вызванного реакцией В. Таким образом,

Остается вычислить эти прогибы. Для этого загрузим основную систему одной нагрузкой q (рис.4, а).

Рис.4. Расчет прогиба от исходной нагрузки — а) и реакции — б)

Тогда прогиб точки В будет равен:

При нагружении основной системы реакцией В (Рис.4,б) имеем:

Подставляя эти значения прогибов в уравнение (1), получаем:

Отсюда

В этом способе мы сначала даем возможность основной системе деформироваться под действием внешней нагрузки q, а затем подбираем такую силу В, которая бы вернула точку В обратно. Таким образом, мы подбираем величину неизвестной дополнительной реакции В с тем расчетом, чтобы уравнять прогибы от нагрузки q и силы В. Этот способ и называют способом сравнения деформаций.

Рис.5. Эпюры поперечных сил и внутренних изгибающих моментов.

Подставляя значение лишней реакции В в уравнения статики, получаем

Выражение изгибающего момента получаем, рассматривая правую часть балки (Рис.4) и подставляя значение В:

Информация в лекции «1 Монголо-татарское иго и его последствия для Руси» поможет Вам.

Поперечная сила Q выражается формулой

Эпюры моментов и поперечных сил изображены на рис.5. Сечение с наибольшим положительным моментом соответствует абсциссе , определяемой равенством

т.е.

Отсюда соответствующая ордината эпюры моментов, равна:

Калькулятор луча

онлайн — Google Калькулятор

AlleBilderShoppingVideosMapsNewsBücher

suchoptionen

Бесплатный онлайн калькулятор луча | Реакции, сила сдвига и т. д. — SkyCiv

skyciv.com › free-beam-calculator

11.05.2023 · Бесплатный онлайн-калькулятор луча. Рассчитайте реакции, поперечную силу, изгибающий момент, прогиб и напряжение для консольных или свободно опертых балок.

Калькулятор балки онлайн (Расчет реакции, Рисует изгиб …

beamguru.com › онлайн › балка-калькулятор

Расчет реакций на опорах балки — статически определимых и статически неопределимых, автоматическое построение изгибающего момента, …

Примеры расчета · BEAMGURU Section Designer · Support

Бесплатный калькулятор луча — ClearCalcs

clearcalcs.com › freetools › beam-analysis

Самый мощный бесплатный онлайн-калькулятор луча. Простое моделирование сдвига, момента и прогиба с неограниченным количеством опор, интерактивными диаграммами …

Free Beam Calculator — Civils.ai

Civils.ai › free-beam-calculator

Этот бесплатный калькулятор может использоваться инженерами-конструкторами для расчета балок. Этот инструмент можно использовать для создания диаграмм изгибающих моментов, диаграмм поперечной силы, …

Калькулятор свободных балок для статически неопределимых балок

optimbeam.com › балка-калькулятор

Простой в использовании онлайн-калькулятор статически неопределимых балок. Обеспечивает опорные реакции, изгибающий момент, поперечную силу, прогиб и диаграммы напряжений.

Отклонение — калькулятор несущих балок

deflection.app

Отклонение — самое интерактивное, быстрое и точное приложение для расчета несущих балок. Визуальное проектирование и получение инженерных результатов, графиков, …

Калькулятор балки — MechaniCalc

Mechanicalc.com › калькуляторы › анализ балки

Калькулятор балки позволяет выполнять анализ напряжений и прогибов в прямых балках. Мы предлагаем бесплатную версию этого программного обеспечения.

Площадь: 0,7854 дюйма2
Длина: 10,00 дюйма
Инерция: 0,04909 дюйма4

Ähnliche Fragen

Как рассчитать необходимый размер балки?

Как рассчитать балки?

Как рассчитать, сколько может выдержать двутавровая балка?

Что такое лучевой калькулятор?

Бесплатный калькулятор балки онлайн

rascheta. net › beamuk

Граничное условие: Диаграммы: неподвижная-неподвижная балка. Закрепленный пучок. фиксированный луч. Диаграмма Q-поперечной силы. Диаграмма M-изгибающего момента. D-перемещения. неподвижно-штифтовая балка.

Калькулятор балки — WebStructural

webstructural.com › Beam-calculator

Калькулятор балки — отличный инструмент для быстрой проверки сил в балках. Используйте его для расчета стальных, деревянных и бетонных балок под различные нагрузки …

Калькулятор для балок: опорные реакции, изгибающий момент и напряжения

www.johannes-strommer.com › калькуляторы › расчет балок

Этот онлайн-калькулятор балки рассчитывает силы и моменты в двух опорах (= опорные реакции) и углы наклона статически …

Вариант нагрузки: точечная нагрузка точечная нагрузка – консольная равная нагрузка и точечная нагрузка дельта-нагрузка – справа дельта-нагрузка – слева
Подшипник B: подвижный подшипник с жестким зажимом на свободном конце

Калькулятор непрерывной балки

Калькулятор момента инерции

Калькулятор рамы

Формулы балки

Калькулятор напряжения изгиба

Оптимальная балка

калькулятор неопределенного луча — Googlesuche .

com › beam-calculator

Простой в использовании онлайн-калькулятор статически неопределимых балок. Обеспечивает опорные реакции, изгибающий момент, поперечную силу, прогиб и диаграммы напряжений.

Калькулятор луча | Оптимальный луч | Бесплатная пробная версия

absolutebeam.com

Простой в использовании онлайн-калькулятор статически неопределимой балки. Обеспечивает опорные реакции, изгибающий момент, поперечную силу, прогиб и диаграммы напряжений.

BEAMGURU.COM — Калькулятор балки и балки рамы/фермы …

beamguru.com

Этот калькулятор балки предназначен для расчета и построения изгибающего момента … Расчет статически неопределимых балок, рамы и фермы.

Перейти к расчету балки · Калькулятор рамы/фермы · Перейти к конструктору сечений · Поддержка

Калькулятор свободной балки — Civils.ai

Civils.ai › калькулятор свободной балки

Этот инструмент можно использовать для создания диаграмм изгибающих моментов, диаграмм поперечной силы, расчета сил реакции и измерения прогиба для неопределенной балки . ..

Бесплатный онлайн калькулятор луча | Реакции, сила сдвига и т. д. — SkyCiv

skyciv.com › free-beam-calculator

11.05.2023 · Бесплатный онлайн-калькулятор луча. Рассчитайте реакции, поперечную силу, изгибающий момент, прогиб и напряжение для консольных или свободно опертых балок.

Бесплатный калькулятор луча — ClearCalcs

clearcalcs.com › freetools › Анализ луча

Самый мощный бесплатный онлайн-калькулятор луча. Простое моделирование сдвига, момента и прогиба с неограниченным количеством опор, интерактивными диаграммами, …

Ähnliche Fragen

Как рассчитать реакцию балки?

Что такое лучевой калькулятор?

Отклонение — калькулятор несущих балок

deflection.app

Отклонение — самое интерактивное, быстрое и точное приложение для расчета несущих балок. Визуальное проектирование и получение инженерных результатов, графиков, …

Калькулятор для балок: опорные реакции, изгибающий момент и напряжения

www. johannes-strommer.com › калькуляторы › расчет балок

Расчет сил, моментов, напряжений, углов и прогиба статически определенных или неопределенных лучи. Графическое представление.

Вариант нагрузки: точечная нагрузка точечная нагрузка – консольная равная нагрузка равная нагрузка и точечная нагрузка дельта-нагрузка – правая треугольная нагрузка – левая
Подшипник B: подвижный подшипник с жестким зажимом на свободном конце

Калькулятор луча — PolyBeam прост и удобен в использовании!

www.polystruc.com › составная балка

Определяйте силы сечения и проектируйте статически неопределимые балки с помощью калькулятора балок PolyBeam! Загрузите БЕСПЛАТНУЮ версию PolyBeam уже сегодня!

Калькулятор балки — балка на 3 опорах под линейной нагрузкой — pickshares

pickshares.com › Начало › Инструменты › Калькуляторы балки

Рассчитайте статически неопределимую балку на 3 опорах с помощью нашего калькулятора прогиба.