Определение реакций опор балки, когда сила приложена под углом
Решение задачи по определению реакций шарнирных опор прямой двухопорной балки длиной 16м с пролетом и консольной частью, нагруженной силой F, приложенной под углом α=35° к продольной оси x, а также изгибающим моментом M и равномерно-распределенной нагрузкой q по одному силовому участку.
Задача
Балка опирается на две шарнирные опоры: подвижную (правая) и неподвижную (левая).
Требуется определить реакции в опорах.
Решение
Перед началом решения рекомендуется выполнить следующие действия:
- Изображаем балку в масштабе с опорами и действующими на нее нагрузками.
- Показываем оси системы координат х-y.
- Обозначаем характерные сечения балки буквами A, B, C и D.
Для некоторого упрощения расчетов силу F можно заменить её горизонтальной и вертикальной проекциями (составляющими):
а распределенную нагрузку q — её равнодействующей:

Далее, освобождаем балку от шарнирных опор, заменив их опорными реакциями.
Другие видео
В левой (шарнирно-неподвижной) опоре будет две составляющие полной реакции, а в правой (шарнирно-подвижной) — только одна.
Составляем уравнения равновесия статики и определяем неизвестные опорные реакции.
Другие видео
Из уравнения равенства нулю суммы моментов всех действующих на балку сил, составленного относительно одной из точек опор (например, точки B),
определяем одну из неизвестных вертикальных реакций RDY:
Другую вертикальную реакцию определяем из суммы моментов сил относительно точки в опоре D:
откуда RBY
Горизонтальную реакцию RBX в опоре B рассчитаем из уравнения суммы проекций всех сил на горизонтальную ось x:
Проверяем правильность найденных результатов, проецируя все силы на вертикальную ось y. В сумме должен получиться ноль:
Условие равновесия выполняется, следовательно, реакции опор найдены верно.

Другие примеры решения задач статики >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ
На нашем сайте можно бесплатно скачать:
— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку
Сохранить или поделиться с друзьями
Помощь с решением
Поиск формул и решений задач
sopromatguru.ru… СОПРОМАТ ГУРУ. Расчет балки онлайн. Построение эпюр. Реформал.
Основные сведения:
Рейтинг: | ||
Адрес: http://sopromatguru. | ||
О сайте: Анализ данных sopromatguru.ru показал, что у этого домена отсутствует рейтинг Alexa, а его посещаемость составляет около 35 тыс. в месяц. Лидирующую позицию по доле трафика занимает Россия (94,0%), а владельцем домена является Private Person. | ||
Заголовок: СОПРОМАТ ГУРУ. Расчет балки онлайн. Построение эпюр | ||
Мета-описание: Решение задач по сопромату и теоретической механике онлайн. Определение реакций опор, построение эпюр изгибающих моментов, эпюр поперечных сил бесплатно. Расчет статически определимой, статически неопределимой балки, рамы, фермы с решением. Валерия Иван Замечательнейший ресурс для студентов! Всё понятно, доступно, а главное — быстро. И по… | ||
Рейтинг Alexa Нет данных | Посетителей в день 1 004 | Просмотров в день 1 004 |
Статус: Онлайн | Дата последней проверки:
| |
Наиболее популярные страницы домена:
- СОПРОМАТ ГУРУ.
 Расчет балки онлайн. Построение эпюр
Расчет балки онлайн. Построение эпюрРешение задач по сопромату и теоретической механике онлайн. Определение реакций опор, построение эпюр изгибающих моментов, эпюр поперечных сил бесплатно. Расчет статически определимой, статически неоп…
- Расчет статически определимой балки с решением онлайн.
Расчет балки, опорные реакции балки, определение опорных реакций балки на двух опорах (двухопорной) и консольной балки, построение эпюр изгибающих моментов, эпюр продольных и поперечных сил, подбор се…
- Помощь проекту расчета статически определимых балок
Помощь в изучении сопромата, теоретической механики (термех, теормех). Рачет балки онлайн с решением. Эпюры.
Другие домены этого хостинг-провайдера (In-Solve/1Gb.ru hosting services provider):
second-hands.ru
nozbd. ru
ru
terra-minora.ru
zoomet.ru
bizrental.ru
kinospb.net
Географическое распределение аудитории для sopromatguru.ru:
| Страна | Доля посетителей | Рейтинг по стране |
|---|---|---|
| Россия | 94,0% | 78 370 |
Информация о домене:
| Возраст домена: | 8 лет |
| Владелец: | Private Person |
| Регистратор: | RU-CENTER-RU http://www.ripn.net |
Другие домены, которые могут быть вам интересны:
diymarketplace.net
touristsim.com
e-switch.com
en.fab.de
argentum. ua
ua
Онлайн калькулятор: Простые опорные реакции балки
Исследование Физика
Калькулятор вычисляет опорные реакции балки с двумя опорами при различных нагрузках.
Статьи, в которых описывается этот калькулятор
- Простая реакция поддержки луча
Простые реакции поддержки луча
Расстояние между опорами, M
Load
| 9004 9003 49. 49. 9. 9. 49. 9. 49. 9. 49. | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
9004 9003| 9004 | 9004 | . |  0031 0031 Load | Value | Direction | Moment direction | Range | Difference | |
51020501001000
Load
Расстояние до опоры A
Может быть отрицательным, если нагрузка приложена слева от опоры A
Сила нагрузки, кН Равномерно распределенная нагрузка, кН/м Линейно распределенная нагрузка, кН/м Момент, кН*м
НаправлениеВнизВверх
Направление момента По часовой стрелкеПротив часовой стрелки
РазницаУменьшениеУвеличение
Import dataImport error
«Один из следующих символов используется для разделения полей данных: табуляция, точка с запятой (;) или запятая (,)» Образец: -50,5;L;50,5;вверх;против часовой стрелки;50,5;увеличение
Загрузить данные из файла . csv.
csv.
Перетащите файлы сюда
Покажите подробную информацию
Точность расчета
цифры после десятичной точки: 2
Реакция поддержки A, KN
Реакция поддержки B, KN
Положительное направление моментов
по часовой промышленности
Ограничение
19 0001 Momentsпо часовой промышленности
. уравнение
Файл очень большой. Во время загрузки и создания может происходить замедление работы браузера.
Файл очень большой. Во время загрузки и создания может происходить замедление работы браузера.
Файл очень большой. Во время загрузки и создания может происходить замедление работы браузера.
Калькуляторы, использующие этот калькулятор
- Перерезывающая сила и изгибающий момент в двухопорной балке
Калькуляторы, используемые в этом калькуляторе
- Простые опорные реакции балки
URL, скопированный в буфер обмена
Аналогичные калькуляторы
- • Уравнение химического уравнения
- • Закон Кулона
- • Нормальная сила
- • Функциональный участок
- • Простая математика.
 )
)
балка Инженерная механика физика реакция статика поддержка
PLANETCALC, Простые опорные реакции балки
Антон 2021-07-24 07:38:07
‘; возврат рет; } }
Онлайн-калькулятор: Опорная реакция простой балки
Этот онлайн-калькулятор вычисляет опорные реакции простой балки при поперечных нагрузках. Простая балка представляет собой прямоугольную балку, закрепленную на двух опорах: одной — шкворневой (опора «А»), другой — роликовой (опора «Б»). Калькулятор отображает опорные реакции V A и V B , уравнения равновесия моментов и рисует балочную систему. Примечание. Расстояние до значения опоры «А» должно быть отрицательным для силы, действующей слева от опоры «А». Теория и расчетные формулы находятся под калькулятором.
Simple beam support reactions
Distance between supports, m
Load
| Distance to the support A | Load | Значение | Направление | Направление момента | .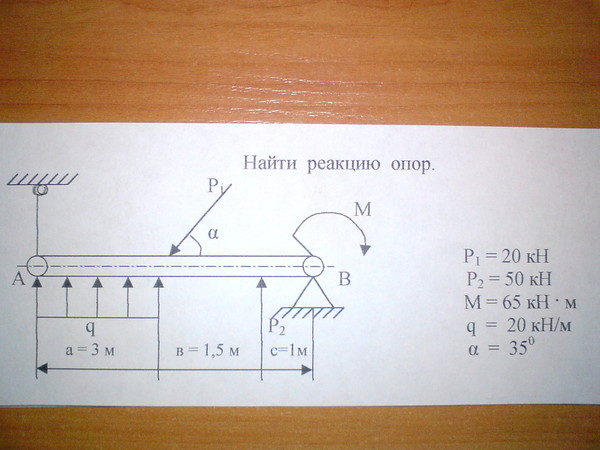 0031 0031 | |||
|---|---|---|---|---|---|---|---|---|
510501001000
. AНагрузкаСила, кНРавномерно распределенная нагрузка, кН/мЛинейно распределенная нагрузка, кН/мМомент, кН*м
НаправлениеВнизВверх0007
РазницаУменьшениеУвеличение
Import dataImport error
«Один из следующих символов используется для разделения полей данных: табуляция, точка с запятой (;) или запятая (,)» Образец: -50,5;L;50,5;вверх;против часовой стрелки;50,5;увеличение
Загрузка данные из файла .csv.
Перетащите файлы сюда
Показать подробности
Точность расчета
Знаки после запятой: 2
Реакция опоры A, кН
Реакция опоры B, кН
Положительное направление моментов
По часовой
Против часовой
Уравнение равновесия моментов
7 Файл очень большой Во время загрузки и создания может происходить замедление работы браузера.
Файл очень большой. Во время загрузки и создания может происходить замедление работы браузера.
Файл очень большой. Во время загрузки и создания может происходить замедление работы браузера.
Опорные реакции
Под действием нагрузок в опорах балки возникают противодействующие силы, называемые опорными реакциями. Эти силы зависят от вида нагрузки и типа опор.
Роликовая опора Роликовая опора (в нашей модели обозначена буквой «В») позволяет балке свободно перемещаться в горизонтальной плоскости и предотвращает вертикальное перемещение. Поэтому он имеет только вертикальную реакцию V B .
Штифтовая опора крепится к балке. Это предотвращает его горизонтальное и вертикальное перемещение. При наличии сил, действующих на балку в горизонтальной плоскости, эта опора дополнительно производит горизонтальную реакцию. В нашей модели на балку действуют только поперечные силы, поэтому горизонтальная реакция опоры «А» всегда будет равна нулю. Обозначим вертикальную реакцию опоры A через V А .
Обозначим вертикальную реакцию опоры A через V А .
Уравнения равновесия
Как известно из статики, все силы и моменты сил в неподвижной системе уравновешены. Поэтому суммы сил и моментов в любой точке этой системы равны нулю.
Все силы при поперечной нагрузке на простую балку действуют параллельно оси Y. Следовательно, можно составить только два независимых уравнения равновесия для проекции сил на ось Y. Достаточно найти две неизвестные опорные реакции: V А и В В .
При написании уравнений равновесия у нас есть выбор:
- составить одно уравнение равновесия проекции сил и одно уравнение баланса моментов в некоторой точке
- составить два уравнения равновесия моментов в двух точках.
Воспользуемся вторым способом, а первый оставим для проверки результата.
Удобнее всего составить уравнения точек опор А и В:
Напомним, что момент силы в некоторой точке есть произведение силы F на кратчайшее расстояние от этой точки до линии действия силы (рычага) l:
Исходя из этого, уравнения равновесия моментов в точках А и В для системы передаточных сил F 1 .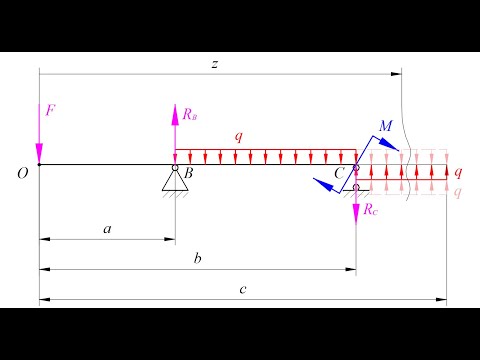 .. F n , действующих на балку, принимают вид:
.. F n , действующих на балку, принимают вид:
Где F i величина силы или реакции опоры в ньютонах. л и А и l i B — рычаг в метрах (кратчайшее расстояние от точки приложения силы i до опоры A или B соответственно). s i A и s i B — знак момента силы i в точках A или B соответственно.
Правило выбора знаков моментов: знак положительный (+1) для момента, изгибающего луч вокруг выбранной точки по часовой стрелке ↻ и отрицательный (-1) для противоположного направления ↺. Также можно выбрать противоположные значения, тогда уравнения примут немного другой вид, но конечный результат не изменится.
Например, для системы сил, показанной на рисунке выше, уравнения равновесия можно записать так:
Вычисляя, получаем значения опорных реакций: V А = 15,42 и В В = 14,58. Проверим, что сумма всех сил равна нулю (для сил, действующих вниз — знак положительный, для сил, действующих вверх — отрицательный):
Проверим, что сумма всех сил равна нулю (для сил, действующих вниз — знак положительный, для сил, действующих вверх — отрицательный):
При составлении уравнений принимаем, что реакции обеих опор направлены вверх. При расчете может оказаться, что реакция опоры окажется отрицательной. Это означает, что реакция такой опоры должна быть направлена в противоположную сторону. (Сумма моментов сил, действующих на балку, пытается оторвать ее от опоры.)
Распределенная нагрузка
Иногда требуется указать нагрузку, определенным образом распределенную по отрезку длиной a. Для целей расчета опорных реакций такую нагрузку можно заменить ее равнодействующей силой. Точка приложения такой силы находится в центре масс формы с распределенной нагрузкой. Модуль рассчитывается путем интегрирования функции распределения нагрузки в заданном диапазоне. Для простых функций модуль можно легко выразить через заданную скорость загрузки.
В таблице ниже приведены формулы для модуля сосредоточенной равнодействующей силы и точки ее приложения для всех типов распределенных нагрузок, поддерживаемых калькулятором:
| Загрузить | Модуль | Точка приложения |
|---|---|---|
| Униформа | 1/2 дюйма | |
| Линейно убывающая | 1/3 | |
| Линейно возрастающая | 2/3 а |
В приведенных выше формулах q — интенсивность нагрузки в Н/м, a — диапазон распределенной нагрузки.
 ru
ru