Решение задач с плоскими конструкциями.
Пример решения задачи по статике
На этой странице рассмотрены принципы и способы решения задач статики, в которых необходимо определить неизвестные реакции, возникающие в опорах плоской конструкции или рамы.
В основе решения таких задач лежит основной метод, используемый статикой, опирающийся на условие равновесия тел.
Расчет плоской конструкции
Задача:
Плоская статически определимая конструкция состоит из двух частей АС и ВС, соединенных шарнирно в узле С (см. рисунок 1).
Опора А неподвижна и представляет собой жесткую заделку, а опора В выполнена в виде подвижного шарнира, размещенного на наклонной плоскости.
К конструкции приложена сосредоточенная сила F = 73 Н, нагрузка интенсивностью q = 75 Н/м, равномерно распределенная на отрезке длиной b, и пара сил с моментом М = 3,5 Н×м.
Направление линий действия реакции опоры В и силы F определяются углами α = 37˚ и β = 41˚.
Размеры элементов конструкции: а = 0,35 м, b = 0,19 м, с = 0,54 м.
В задании предлагается определить реакции опор А и В плоской конструкции, состоящей из двух частей, соединенных шарнирно в точке С, а также силы, возникающие в самом шарнире С.
Решение:
1. Отбросим нижнюю часть конструкции до шарнира С, заменив ее реакцией RС.
Реакцию RС разложим на составляющие RСх и RСу , спроецировав ее на оси Х и Y.
Поскольку опора В является шарнирно-подвижной и размещена на наклонной плоскости (α = 37˚), момент в шарнире С возникать не будет, а реакция RВ направлена по перпендикуляру к наклонной плоскости и приложена к центру шарнира В (см. рис. 2).
2. Определим реакции опор С и В, составив уравнения равновесия сил и моментов сил относительно этих опор для звена СВ заданной конструкции.
∑МC = 0
F×sinβ×c — RВ× cosα×2с = 0,
откуда следует:
RВ = F×sinβ /(2× cosα) = 73×0,6560 /(2×0,7986) = 29,98 Н.
Суммарная реакция опоры В: RВ = 29,98 Н.
Реакцию RСх определим из условия равновесия проекций сил на ось Х:
∑FХ = 0
F×cosβ + RВ× sinα — RСх = 0, откуда:
RСх = F×cosβ + RВ× sinα = 73×0,7547 + 29,98×0,6018 = 73,14 Н.
Реакцию RСв определим из условия равновесия проекций сил на ось Y:
∑FY = 0
F× sinβ — RСу — RВ×cosα = 0,
RСу = F×sinβ — RВ×cosα = 73×0,6560 — 29,98×0,7986= 23,95 Н.
Суммарную реакцию опоры С определим, используя теорему Пифагора:
RС = √(RСх2 + RСу2) = √(73,142 + 23,952) = 76,96 Н.
Суммарная реакция опоры С: RС = 76,96 Н.
3. Отбросим от заданной конструкции верхнее звено до опоры С, заменив его известной нам реакцией RС, при этом направление данной реакции изменим на противоположное (см. рис. 3).
Разложим RС, как и в предыдущем случае, на проекции вдоль осей Х и Y.
4. Рассмотрим равновесие этой части конструкции и определим неизвестные реакции в опоре А.
Поскольку опора А представлена в виде жесткой заделки, ее реакция может быть представлена силой R А и моментом (парой сил) MА, которые по условию задания следует определить.
Реактивную силу RА разложим на проекции RАх и RАу по осям X и Y.
5. Для определения неизвестных реакций опоры А составим уравнение равновесия элемента конструкции:
∑FX = 0
q×b + RСх – RАх = 0,
откуда находим:
RАx = 75×0,19 + 73,14 = 87,39 Н.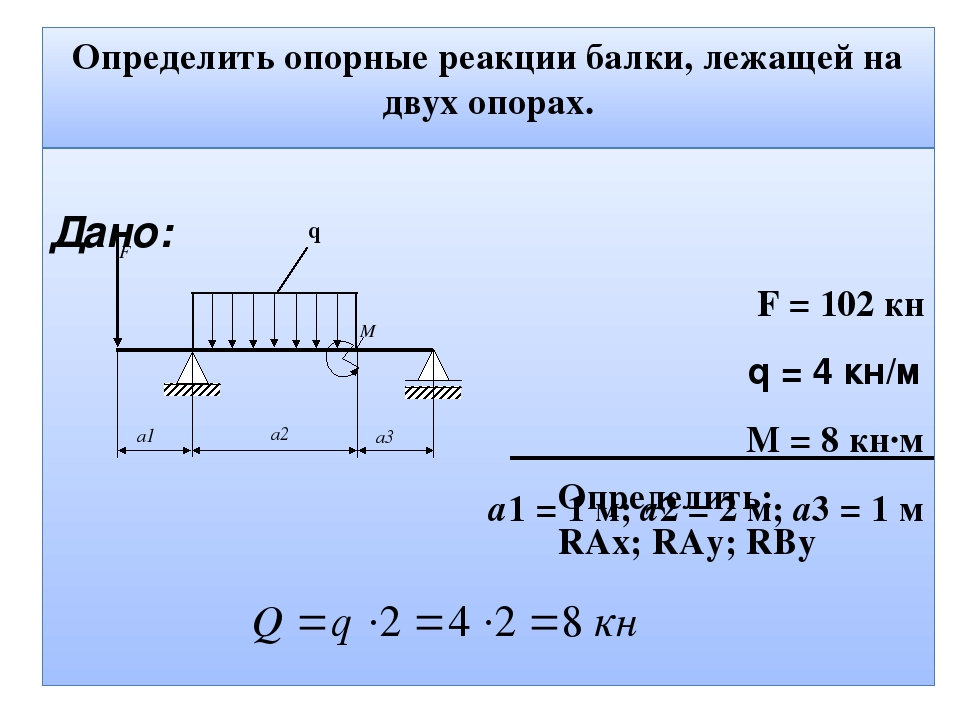
∑FY = 0
RСу — RАу = 0, откуда: RАу = RСу = 23,95 Н.
Суммарная реакция RА определится по теореме Пифагора:
RА = √(RАх2 + RАу
6. Для определения неизвестного момента МА составим уравнение равновесия моментов сил относительно опоры А:
∑МА = 0
МА – М + RСу×2а — RСх(а+b+а) – qb(а + b/2) = 0,
откуда находим момент МА:
МА = М — RСу×2а + RСх(а+b+а) + qb(а + b/2) = 3,5 — 23,95×0,70 + 73,14(0,35+0,19+0,35) + 75×0,19(0,35+0,19/2) = 58,17 Н×м.
Ответ:
- RВ = 29,98 Н;
- RС = 76,96 Н;
- RА = 90,61 Н;
- МА = 58,17 Н×м.

***
Задача по кинематике точки
Главная страница
Дистанционное образование
Специальности
Учебные дисциплины
Олимпиады и тесты
Статика. Определение реакций опор и усилий в стержнях плоской фермы способом РиттераДано:Определить реакции опор фермы от заданной нагрузки и усилия в стержнях. Решение: 1.Определение реакций опор. Рассмотрим внешние силы приложенные к ферме: силы Р1, Р2, Р3 и реакции опор . Для плоской системы сил составим три уравнения равновесия. Проверка 2.Определим усилия в стержнях фермы. Кроме внешних сил на каждый узел фермы действуют реакции сходящихся в ней стержней. 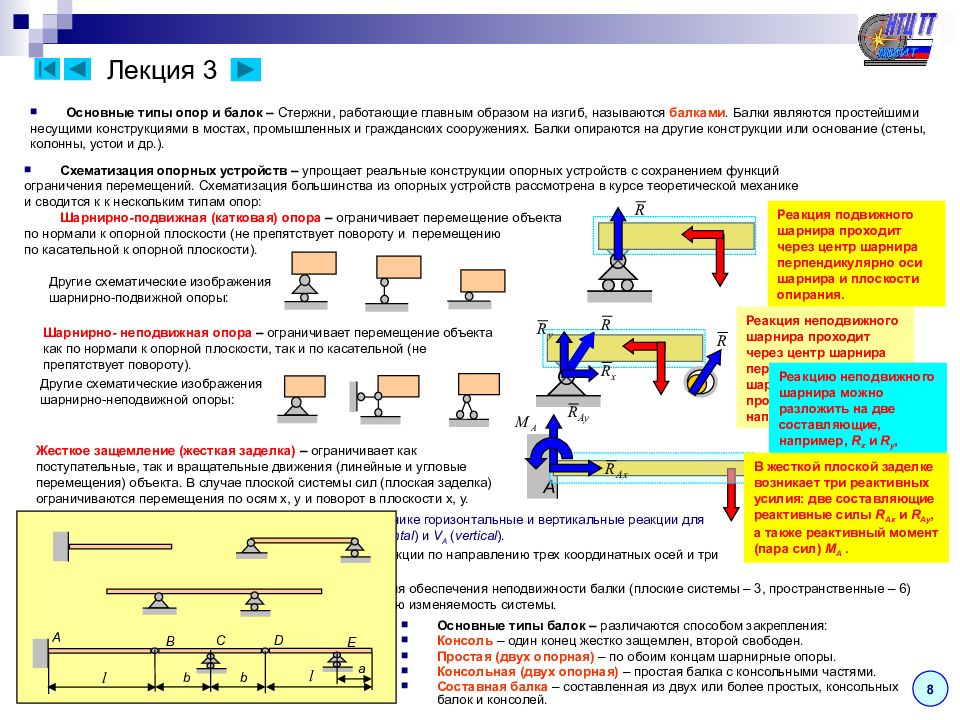 Эти реакции равны усилиям в стержнях. Эти реакции равны усилиям в стержнях.Рассмотрим равновесия сил приложенных к каждому узлу фермы, выбирая узлы в такой последовательности, чтобы число неизвестных сил в узле не превышало двух. Составим уравнения равновесия сил, приложенных к этому узлу: Стержень 1 сжат, а стержень 3 растянут. Для проверки расчета строим в масштабе треугольник сил. Треугольник сил получается замкнутым, следовательно, реакции определены правильно. Реакции остальных стержней определим аналогично. Расчет узла Н Составим уравнения равновесия сил, приложенных к этому узлу: Стержень 4 сжат, а стержень 2 растянут. Расчет узла С Составим уравнения равновесия сил, приложенных к этому узлу: Стержень 5 6 растянуты. Расчет узла Е Составим уравнения равновесия сил, приложенных к этому узлу: Стержень 7 сжат, а стержень 8 растянут. Расчет узла G Составим уравнения равновесия сил, приложенных к этому узлу: Стержень 9 растянут, а стержень 10 сжат.  Расчет узла F Составим уравнения равновесия сил, приложенных к этому узлу: Стержень 11 растянут, а стержень 13 сжат. Расчет начнем с узла B Составим уравнения равновесия сил, приложенных к этому узлу: Стержень 13 растянут. Таким реакции всех стержней фермы определены. Найдем напряжения в стержнях 4,5,8 способом Риттера. Проведем сечение I – I и составим для полученной системы три уравнения равновесия. Проведем сечение II – II и составим для полученной системы три уравнения равновесия. Решения обоими методами совподают. Cкачать бесплатно пример решения задач — Статика. Определение реакций опор и усилий в стержнях плоской фермы способом Риттера |
Определение реакций опор.
Механика Определение реакций опор.

просмотров — 640
Основные положения строительной механики
Основные исходные положения строительной механики при решении задач упругого расчёта сооружений те же, что и сопротивления материалов:
1. Предположение об идеальной упругости материала элементов сооружения.
2. Применение линейной связи между напряжениями и деформациями (закон Гука).
3. Применение принципа независимости действия, согласно которому результат действия системы сил равен сумме результатов действия отдельных сил системы.
Этот принцип применим только к относительно жёстким сооружениям и использование его при расчёте гибких систем в области больших деформаций недопустимо.
4. При расчетах рассматривается исходная недеформированная система.
2. Расчёт плоских статически определимых стержневых систем на неподвижную нагрузку
В данной главе рассматривается задача определения внутренних усилий в статически плоских определимых стержневых системах от заданной неподвижной нагрузки.
Алгоритм решения поставленной задачи для рассматриваемых систем включает:
· Кинематический анализ системы;
· Определение реакций опор;
· Определение внутренних усилий и построение при крайне важности их эпюр;
· Подбор или проверку размеров поперечных сечений стержней.
Вопросы кинематического анализа стержневых систем рассмотрены в главе 1. Далее рассматриваются остальные этапы указанного алгоритма.
Для определения реакции опор от заданной нагрузки крайне важно:
· Изобразить на расчётной схеме реакции опор или их составляющие;
· Наметить алгоритм расчёта для определения реакций опор;
· Задать правило знаков для записи уравнения равновесия;
· Записать уравнение равновесия;
· Определить реакции опор или их составляющие;
· Произвести проверку полученных результатов.
2.1.1 Типы опор и реакции опор.
Типы опор и реакции опор или их составляющие показаны на рис 2. 1.
1.
Рис. 2.1. Типы опор и реакции опор или их составляющие.
Необходимо отметить, что направление реакций опор или их составляющих, показанных на рис. 2.1, может быть изменено на противоположное.
Для краткости составляющие реакции опор будем называть реакциями опор.
2.1.2. Выбор алгоритма расчёта по определению реакции опор.
Для определения реакций опор плоской стержневой системы имеющей три опорных связи и, следовательно, три реакции опор используются три уравнения равновесия. Варианты уравнения равновесия показаны на рис. 2.2.
| Вариант 1. | Вариант 2. | Вариант 3. |
Рис. 2.2 Варианты систем уравнения равновесия
При записи уравнений равновесия на рис. 2.2 введены следующие обозначения:
или — алгебраическая сумма проекций заданной нагрузки и реакции опор соответственно на ось Х или Y;
— алгебраические суммы моментов от заданной нагрузки относительно точек А,В,С.
Для определения реакций опор можно использовать любой из указанных вариантов систем уравнений равновесия, задавать произвольным образом направление взаимно перпендикулярных осей Х, Y; задавать произвольно положение точек А,В,С для записи уравнений моментов. Но при этом следует иметь ввиду, что от выбора варианта уравнений равновесия, системы координат ХY и положения точек А,В,С зависит сложность полученных уравнений равновесия и трудоёмкость решения системы уравнений.
Читайте также
Проверочный расчет быстроходного вала Для проверочного расчета статической и усталостной прочности ступенчатого вала (быстроходного или тихоходного в соответствии с заданием) составим его расчетную схему (см. рис. 13). Поскольку подшипники прямозубой передачи,… [читать подробенее]
Рис.15.3
Пусть твердое тело вращается вокруг неподвижной оси z под действием приложенных к нему внешних активных сил и реакции связей и , приложенных в закрепленных точках тела А и В. Определим реакции связей и , как величины, зависящие от приложенных сил и… [читать подробенее]
Определим реакции связей и , как величины, зависящие от приложенных сил и… [читать подробенее]
Метод сечений (метод Риттера). Этим методом удобно пользоваться для определения усилий в отдельных стержнях фермы, в частности для проверочных расчетов. Идея метода состоит в том, что ферму разделяют на две части сечением, проходящим через три стержня, в которых (или в… [читать подробенее]
Основные положения строительной механики Основные исходные положения строительной механики при решении задач упругого расчёта сооружений те же, что и сопротивления материалов: 1. Предположение об идеальной упругости материала элементов сооружения. 2…. [читать подробенее]
Пример.
Для рамы, показанной на рис. 2.33, требуется построить эпюры усилий M, Q, N от заданной нагрузки. Исходные данные: М1=8 кНм, Р=6 кН, q=4кН/м, h=4 м, l=4 м.
h/2
h/2
l/2
l/2
P
q
… [читать подробенее]
Исходные данные: М1=8 кНм, Р=6 кН, q=4кН/м, h=4 м, l=4 м.
h/2
h/2
l/2
l/2
P
q
… [читать подробенее]
Пример1. Примеры выполнения задания (при действии на балку равномерно распределенной нагрузки и сосредоточенных сил и моментов). Разберем на конкретных примерах построение эпюр для балок, находящихся под действием равномерно распределенной нагрузки и… [читать подробенее]
Пример2.
Построить эпюры поперечных сил и изгибающих моментов для оси уравновешивающего механизма гаубицы Д-30, изображенной на рис.2.
Дано:
,
,
,
Решение:Из уравнения моментов всех сил относительно точки :
;
Из уравнения ; имеем
Полученное. .. [читать подробенее]
.. [читать подробенее]
Пример1. Примеры выполнения задания (при действии на балку равномерно распределенной нагрузки и сосредоточенных сил и моментов). Разберем на конкретных примерах построение эпюр для балок, находящихся под действием равномерно распределенной нагрузки и… [читать подробенее]
Пример2. Построить эпюры поперечных сил и изгибающих моментов для оси уравновешивающего механизма гаубицы Д-30, изображенной на рис.2. Дано: , , , Решение:Из уравнения моментов всех сил относительно точки : ; Из уравнения ; имеем Полученное… [читать подробенее]
Расчет реакции в узлах конструкции в программе SCAD Office
Расчет несущей способности здания не ограничивается только подбором основных конструктивных элементов. Немаловажным параметром расчета является расчет узловых соединений, а также предоставление данных об усилиях в узлах. Получить усилия в узле можно, проанализировав эпюры усилий в элементах, или воспользоваться специальным инструментом «Нагрузки от фрагмента схемы». Рассмотрим все возможности работы с этой функцией программного комплекса SCAD Office.
Получить усилия в узле можно, проанализировав эпюры усилий в элементах, или воспользоваться специальным инструментом «Нагрузки от фрагмента схемы». Рассмотрим все возможности работы с этой функцией программного комплекса SCAD Office.
Для начала стоит определиться с группой узлов (в которых необходимо получить реакцию) и группой элементов (с которых будет выполнен сбор усилий). Рассмотрим пример сбора нагрузок в основании колонны.
Исходные данные начинаем вводить с объединения в группы элементов и узлов:
Отметка группы узлов
Отметка группы элементов
В группу узлов попадают те узлы, в которых требуется получить реакцию (для базы колонн – узлы со связями). В группу элементов попадают элементы, усилие с которых требуется проанализировать при получении реакции. Если нет исключений (например, если в узел приходят два элемента, а реакцию надо получить только с одного элемента), то в группу элементов добавляется вся схема. Далее необходимо перейти в дерево процессов и указать, какие именно из множества групп узлов и элементов следует использовать при расчете. После этого жмем «Записать участок».
Далее необходимо перейти в дерево процессов и указать, какие именно из множества групп узлов и элементов следует использовать при расчете. После этого жмем «Записать участок».
Анализ результатов происходит в Графическом анализе – постпроцессы. Важно установить текущее направление реакции и загружение (комбинацию). При активации реактивной силы, на схеме будут отображены стрелки направления действия нагрузки на узел. С помощью инструмента «Оцифровка» можно подсветить значение реакции.
Для создания отчетной таблицы реакций по всем опорным узлам (например, для заполнения таблицы КМ в документации) необходимо обратиться в раздел документирования. В графе «Виды результатов выбрать «нагрузки от фрагмента схемы от комбинации загружений», выбрать нужные направления реакций, список узлов (по ранее сформированной группе), и заданную комбинацию.
Результатом может служить таблица в текстовом или табличном редакторе. Выбрав максимальные значения по нескольким комбинациям можно перенести их в таблицу документации раздела КМ.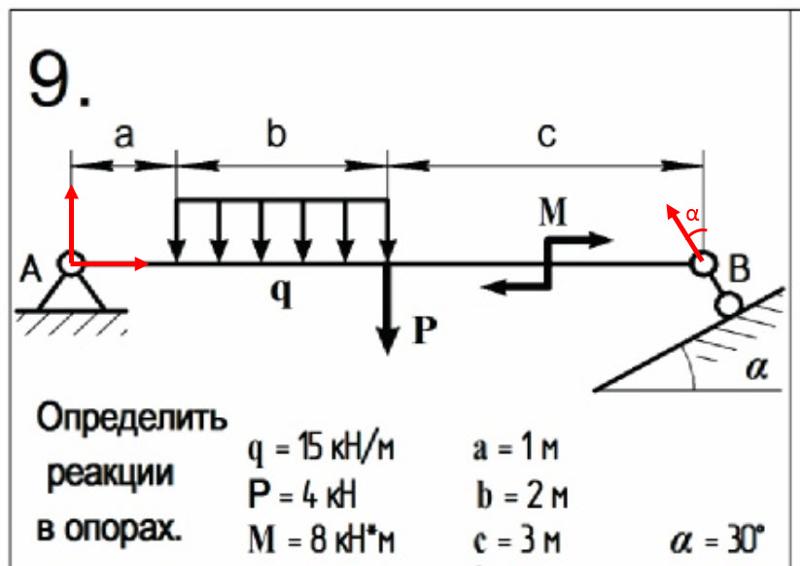
Пример:
Нагрузки от фрагмента схемы от комбинаций загружений
Единицы измерения:
- Силы: Т
- Единицы длины для силовых факторов: м
Параметры выборки:
Список узлов/элементов: 1 3 25 27 49 51 73 75 97 99 121 123
Список загружений/комбинаций: 1
Список факторов: RX, RY, RZ, RUX, RUY, RUZ
Нагрузки от фрагмента схемы от комбинаций загружений | |||||||
Узел | Комбинация | Значение | |||||
RX | RY | RZ | RUX | RUY | RUZ | ||
1 | 1 |
0. | 0.015 | 8.188 | -0.036 | 0.682 | -2.601e-004 |
3 | 1 | -0.099 | 0.015 | 8.188 | -0.036 | -0.682 | 2.601e-004 |
25 | 1 | 0.181 | 0.005 | 15.173 | -0.014 | 1.288 | -1.408e-004 |
27 | 1 | -0.181 | 0.005 |
15. | -0.014 | -1.288 | 1.408e-004 |
49 | 1 | 0.189 | 1.059 | 15.504 | 0.011 | 1.314 | -7.77e-005 |
51 | 1 | -0.189 | 1.061 | 15.504 | 0.011 | -1.314 | 7.777e-005 |
73 | 1 | 0.19 | -1.059 | 15.518 | -0.011 |
1. | -5.055e-005 |
75 | 1 | -0.19 | -1.061 | 15.569 | -0.011 | -1.323 | 5.048e-005 |
97 | 1 | 0.181 | -0.005 | 15.185 | 0.015 | 1.291 | 1.392e-004 |
99 | 1 | -0.181 | -0.005 | 15.236 | 0.015 | -1.291 |
-1. |
121 | 1 | 0.099 | -0.015 | 8.188 | 0.035 | 0.682 | 2.509e-004 |
123 | 1 | -0.099 | -0.015 | 8.188 | 0.035 | -0.682 | -2.509e-004 |
Следует отметить, что для узла может быть несколько различных сочетаний нагрузок, ориентироваться при этом нужно на максимальный изгибающий момент, поперечную и продольную силу при соответствующем действии остальных нагрузок.
Таким же способом можно получить реакцию в узле, не имеющим связевых закреплений.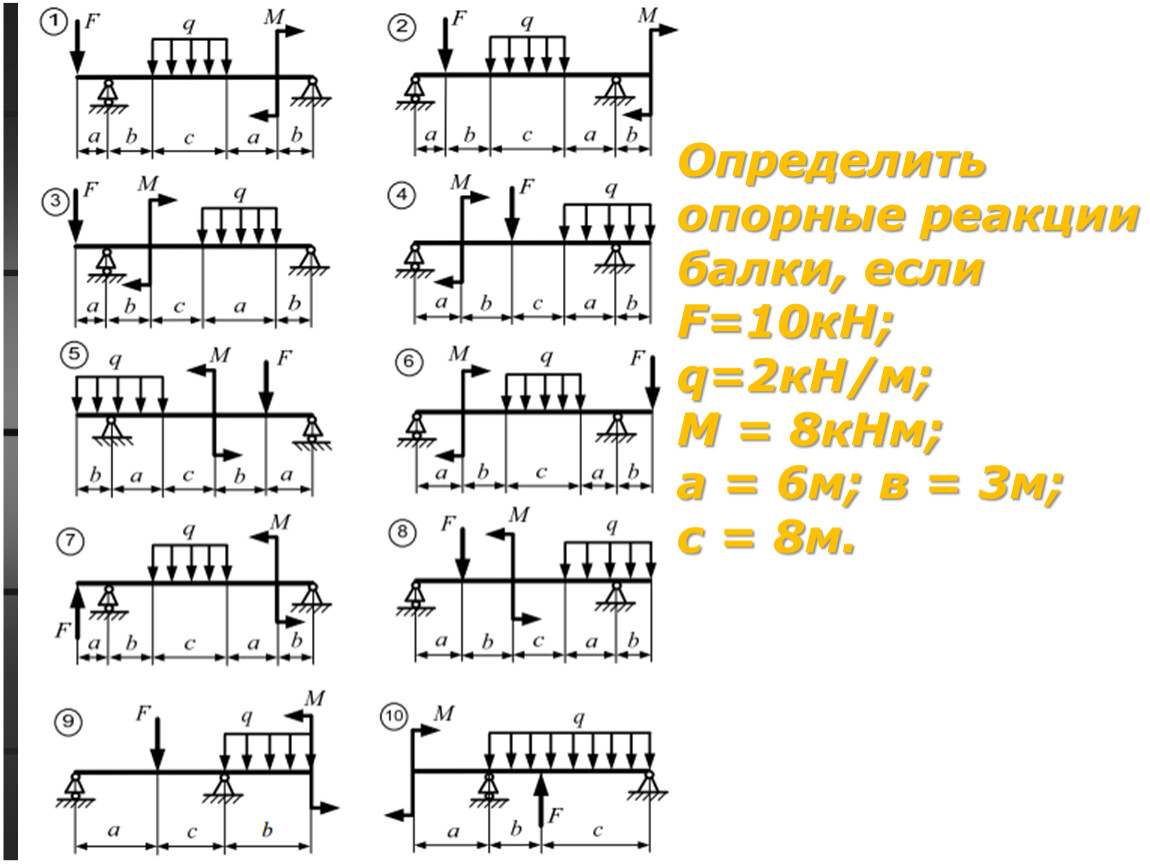 Для этого создаем новую группу узлов, в которую попадает нужный нам узел, и группу элементов, с которых хотим собрать усилия на этот узел. В примере ниже изображена колонна с консолью, я хочу получить изгибающий момент от действия крановой нагрузки, если я хочу также учесть вес конструкции выше, то выберу верхнюю часть колонны, если этого не нужно, то выделенным оставляем только консоль и добавляем ее в группу элементов.
Для этого создаем новую группу узлов, в которую попадает нужный нам узел, и группу элементов, с которых хотим собрать усилия на этот узел. В примере ниже изображена колонна с консолью, я хочу получить изгибающий момент от действия крановой нагрузки, если я хочу также учесть вес конструкции выше, то выберу верхнюю часть колонны, если этого не нужно, то выделенным оставляем только консоль и добавляем ее в группу элементов.
В нашем случае реакция момента консоли пригодится нам для расчета узла крепления консоли, продольная сила здесь нам не нужна, поэтому в нашем случае в группу элементов попадает только консоль.
Таким образом, можно вычислить реакцию в любом ферменном узле, узле крепления балки к колонне, стыковом узле балок и др. Полученные усилия можно использовать для формирования таблицы рабочей документации и, соответственно, для расчета самого узла, например, в программе КОМЕТА 2.
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings. REQUIRED_FIELD}})
REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings. LANGUAGE}}
{{$select.selected.display}}
LANGUAGE}}
{{$select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Балочные системы Определение реакций опор и моментов защемления
Балочные системы. Определение реакций опор и моментов защемления • 1. Виды нагрузок и разновидности опор • По способу приложения нагрузки делятся на сосредоточенные и распределенные. Если реально передача нагрузки происходит на пренебрежимо малой площадке (в точке), нагрузку называют сосредоточенной; если распределена по площадке или линии – распределенной.
Определение реакций опор и моментов защемления • 1. Виды нагрузок и разновидности опор • По способу приложения нагрузки делятся на сосредоточенные и распределенные. Если реально передача нагрузки происходит на пренебрежимо малой площадке (в точке), нагрузку называют сосредоточенной; если распределена по площадке или линии – распределенной.
Балочные системы • В задачах статики для абсолютно твердых тел распределенную нагрузку можно заменить равнодействующей сосредоточенной силой.
Разновидности балочных систем • Балка – прямой брус, закрепленный на опорах и изгибаемый приложенными к нему силами. Высота сечения балки незначительна по сравнению с длиной. • Жесткая заделка (защемление).
Разновидности балочных систем
Разновидности балочных систем
Разновидности балочных систем
Пример решения задач
Пример решения задач
Пример решения задач
Центр тяжести • Сила тяжести – равнодействующая сил притяжения Земли, она распределена по всему объему тела. • Силы притяжения, приложенные к частицам твердого тела, образуют систему мил, линии действия которых сходятся в центре Земли. Поскольку радиус Земли значительно больше размеров любого земного тела, силы притяжения можно считать параллельными. • Для определения точки приложения силы тяжести (равнодействующей параллельных сил) применим теорему Вариньона о моменте равнодействующей: • Момент равнодействующей относительно оси равен алгебраической сумме моментов относительно любой точки.
• Силы притяжения, приложенные к частицам твердого тела, образуют систему мил, линии действия которых сходятся в центре Земли. Поскольку радиус Земли значительно больше размеров любого земного тела, силы притяжения можно считать параллельными. • Для определения точки приложения силы тяжести (равнодействующей параллельных сил) применим теорему Вариньона о моменте равнодействующей: • Момент равнодействующей относительно оси равен алгебраической сумме моментов относительно любой точки.
Центр тяжести
Центр тяжести
Центр тяжести плоских тел (плоских фигур) • Для плоских фигур справедливо выражение: • V=Ah, • где А – площадь фигуры; h – ее высота. • Подставляем в формулы, получим:
Центр тяжести плоских тел (плоских фигур)
Уточненный расчет валов.
 Силы в зацеплении. Расчетная схема ведущего вала. Суммарные реакции в опорах. Расчетная схема промежуточного вала
Силы в зацеплении. Расчетная схема ведущего вала. Суммарные реакции в опорах. Расчетная схема промежуточного вала10. Уточненный расчет валов
Рисунок 4.Силы в зацеплении.
Для определения опорных
реакций и изгибающих моментов необходимо составить расчетную схему, основанием
которой является эскизная компоновка и схема сил в зацеплении. Опорные реакции
определяют, составляя уравнение равновесия в каждой из плоскостей действия сил. В цилиндрической прямозубой
передаче силу в зацеплении одной пары зубьев раскладывают на две взаимно
перпендикулярные составляющие (рисунок 4,а): окружную силу — Ft и радиальную — Fr. В цилиндрической косозубой передаче
силу в зацеплении раскладывают на три составляющие (рисунок 4, б): окружную — Ft, радиальную — Fr и осевую — Fa. Окружная
сила на шестерне направлена по касательной к делительному диаметру в
противоположном направлении вращения, а для колеса направление окружной силы
совпадает с направлением вращения. Радиальные силы направлены по радиусу к
центру колес. Радиальная сила в косозубой цилиндрической передаче направлена
по радиусу к центру колеса.
Радиальные силы направлены по радиусу к
центру колес. Радиальная сила в косозубой цилиндрической передаче направлена
по радиусу к центру колеса.
Рисунок 5 – Расчетная схема ведущего вала
Определяем реакции опор в вертикальной плоскости ведущего вала.
(10.1)
(10.2)
Проверяем правильность решения в вертикальной плоскости вала:
(10.3)
Реакции опор найдены верно!
Определяем реакции опор в горизонтальной плоскости ведущего вала:
(10. 4)
4)
(10.5)
Проверяем правильность решения в горизонтальной плоскости вала:
(10.6)
Реакции опор найдены верно!
Определяем суммарные реакции в опорах:
(10.7)
(10.8)
Рисунок 6.Расчетная схема промежуточного вала
Определяем реакции опор в вертикальной плоскости промежуточного вала:
(10.9)
(10. 10)
10)
Проверяем правильность решения в вертикальной плоскости вала:
(10.11)
Реакции опор найдены верно!
Определяем реакции опор в горизонтальной плоскости промежуточного вала.
(10.12)
(10.13)
Проверяем правильность решения в горизонтальной плоскости вала:
(10.14)
Реакции опор найдены верно!
Определяем суммарные реакции в опорах по формуле:
(10. 15)
15)
(10.16)
Рисунок 7. Расчетная схема выходного вала
Определяем реакции опор в вертикальной плоскости выходного вала.
(10.17)
(10.18)
Проверяем правильность решения в вертикальной плоскости вала:
(10.19)
Реакции опор найдены верно!
Определяем реакции опор в горизонтальной плоскости выходного вала.
(10.20)
(10.21)
Проверяем правильность решения в горизонтальной плоскости вала:
(10.22)
Реакции опор найдены верно!
Определяем суммарные реакции в опорах:
(10.23)
(10.24)
11. Проверочный расчет подшипников
Определяем эквивалентную нагрузку:
,
(11. 1)
1)
где Х – коэффициент радиальной нагрузки, принимаем X=1;
V – коэффициент, учитывающий вращение колец, принимаем V=1,0;
Frn – радиальная нагрузка подшипника;
Y – коэффициент осевой нагрузки;
Fan – осевая нагрузка;
- коэффициент безопасности, принимаем = 1,2;
- температурный коэффициент, принимаем = 1,0;
Вал I
Шарикоподшипник № 207
Так как на ведущем валу передача прямозубая, то, следовательно, осевая сила отсутствует.
Принимаем .
Вал II
Шарикоподшипник № 209.
На промежуточном валу передача косозубая, в зацеплении присутствует осевая нагрузка .
В зависимости от отношения , где С0-
статическая грузоподъемность подшипника, определяем коэффициент осевого
нагружения по табл. 7.3 [1], где выбираем X и Y.
С0=17,8 кН.
, данному значению соответствуют коэффициенты x=0,56; y=1,71.
Для дальнейшего расчета определяем отношение , где -реакция в опоре и -сила в зацеплении, и сравнить его с нормативным значением коэффициента е: если данное отношение больше е, то осевую нагрузку Fa учитываем при определении Pэкв , если меньше е, то не учитываем.
Данный расчет ведем для наиболее нагруженной опоры.
Принимаем
<-осевую нагрузкуне учитываем.
Принимаем
>-осевую нагрузку учитываем.
Принимаем .
Вал III
Шарикоподшипник № 215
На выходном валу передача косозубая, в зацеплении присутствует осевая нагрузка .
С0=41,1 кН.
, данному значению соответствуют коэффициенты x=0,56; y=1,99.
Для дальнейшего расчета определяем отношение , где -реакция в опоре и -сила в зацеплении, и сравнить его с
нормативным значением коэффициента е: если данное отношение больше е, то осевую
нагрузку Fa учитываем при определении Pэкв , если меньше е, то не учитываем.
Данный расчет ведем для наиболее нагруженной опоры.
Принимаем
<-осевую нагрузкуне учитываем.
Принимаем
>-осевую нагрузку учитываем.
Принимаем .
Определяем расчетную долговечность подшипников по формуле:
(12.1)
(12.2)
где L – долговечность, в млн. об;
LН – долговечность, в ч;
С – динамическая грузоподъемность подшипника;
m – коэффициент, равный для шариковых подшипников 3;
n – частота вращения вала;
Вал I
Вал II
Вал III
12. Расчет ведомого вала по
переменным напряжениям.
Расчет ведомого вала по
переменным напряжениям.
Рисунок 8.Эпюра моментов вычодного вала.
Расчет производим по выходному валу, так как он наиболее нагружен
Как рассчитать опорные реакции в балках
При проектировании зданий, каркасов, балок необходимо понимать величину и направление нагрузки, которая действует внутри опоры.
Все эти опоры расположены в любом месте вдоль конструктивного элемента. Они обнаруживаются на концах, в середине или в любых других промежуточных точках. Тип соединения опор определяет тип нагрузки, которой будет противостоять опора.Тип опоры также оказывает большое влияние на несущую способность каждого компонента.
Они обнаруживаются на концах, в середине или в любых других промежуточных точках. Тип соединения опор определяет тип нагрузки, которой будет противостоять опора.Тип опоры также оказывает большое влияние на несущую способность каждого компонента.
В этом эксклюзивном видеоруководстве по строительству вы узнаете, как измерять реакции в нагруженной (точечной нагрузке, UDL-нагрузке) балке, основанной на различных опорах, таких как шарнирная опора, роликовая опора, свободно опертая балка, шарнирная балка и т. д.
Предположим, что имеются две опоры: фиксированная или шарнирная опора и роликовая опора. Фиксатор или шарнирную опору обозначают точкой А, а роликовую опору — точкой В.
В точке А есть две реакции: вертикальная реакция и горизонтальная реакция. Горизонтальная реакция обозначается как RAH, а вертикальная реакция обозначается как RAV.
В точке B имеется только одна вертикальная реакция, и она обозначается как RBV.
Итак, есть три числа реакций, и вы должны измерить эти реакции. Здесь для расчета используются условия равновесия. Доступны следующие три типа условий равновесия: —
Здесь для расчета используются условия равновесия. Доступны следующие три типа условий равновесия: —
Ʃ В = 0
Ʃ Н = 0
Ʃ М = 0
Это означает, что сумма всех вертикальных сил в балке должна быть равна нулю.Итак, балка находится в равновесном состоянии. Кроме того, сумма всех горизонтальных усилий в балке также должна быть равна нулю.
Сумма моментов по любой точке должна быть равна нулю.
Чтобы изучить процесс расчета деталей, просмотрите следующий видеоурок.
Источник видео: Mission Civil engineering
Расчет опорной реакции, Машиностроение
Расчет опорной реакции:
Q: Балка длиной 8 м шарнирно закреплена в точке A и опирается на ролики на гладкую поверхность, наклоненную под углом 30° к горизонтали в точке B . Балка нагружена, как показано на рисунке ниже. Определите реакцию опоры.
Балка нагружена, как показано на рисунке ниже. Определите реакцию опоры.
Сол.: Диаграмма свободного тела показана на рисунке, который нам
∑Ч = 0
R AH + 8 cos45° — R B sin30° = 0
0,5 Р Б — Р АХ = 5.66 … ( I )
∑В = 0
R A V -10 — 8 cos45° — 10 + R B
R A V + 0,866 R B = 25.66 … ( II )
Принимая момент о A :
∑M A = 10 × 2 + 8 cos45° × 4 + 10 × 7 — R B cos30° 9 × 8= 0 0 0
R B = 16.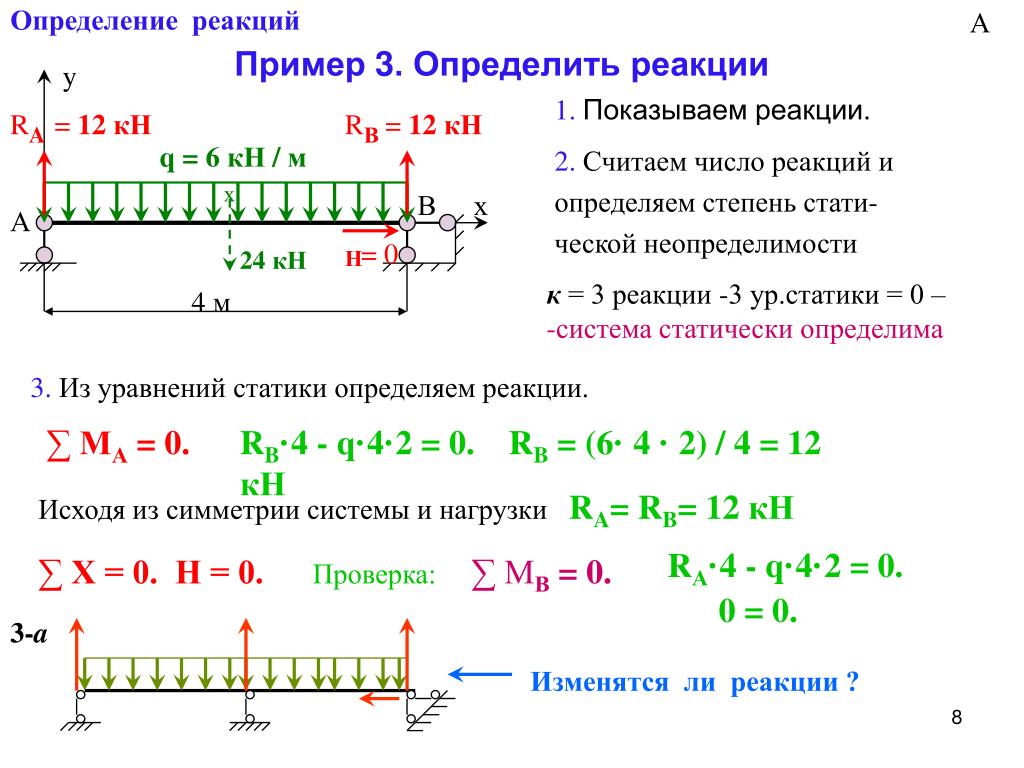 3kN…….АНС
3kN…….АНС
Из уравнения ( ii )
R A A V = 11.5kn ……. ANS
Из уравнения (1)
R AH = 2,5 кН …….ANS
Лабораторный отчет — РЕАКЦИЯ ОПОРНОЙ БАЛКИ И A
РЕАКЦИЯ ОПОРНОЙ БАЛКИ И A = w и принцип моментов
для нахождения реактивных балок и исследования реакций
двухпролетной неразрезной балки с тремя опорами.
ВВЕДЕНИЕ
Говорят, что балка находится в равновесии, когда она не стремится двигаться. Это жизненно важно
при анализе поддерживающих реакций[ CITATION JOB14 \l 1033 ]. Свободно опертая балка
— это балка, которая опирается на две поддерживающие опоры и может свободно перемещаться по горизонтали.
Обычные варианты использования свободно опертых балок с точечными нагрузками включают
удлинения, балки в конструкциях и станины машинных устройств. Сплошной является
Сплошной является
нижележащая часть, обеспечивающая сопротивление изгибу при приложении нагрузки или силы[
ЦИТАТА Dor13 \l 1033 ].В отличие от свободно опертой балки, которая
опирается на каждый конец и куча так или иначе распределена по ее длине, неразрезная балка
намного жестче и более заземлена. Неразрезная балка имеет большее
количество опор, чем необходимо для обеспечения баланса, и деформация
поведения под нагрузкой дополнительно учитывается при принятии решения о помощи. Концевые пролеты
могут быть консольными, могут быть свободно поддерживаемыми или фиксированными.
Метод – эксперимент 1
1. Откройте приложение (VDAS) и выберите эксперимент «STS13 Continuous and Indeterminate
Beams».
2. Выберите эксперимент «Просто поддерживаемая балка — точечные нагрузки».
3. Параметры по умолчанию соответствуют номенклатуре эксперимента, где
Длина балки 850 мм. Приложенная к балке масса будет равна 500 г. Эксперимент
Эксперимент
не требует I или E.
4. Переключите вкладки с «Сбор данных» на вкладку «Моделирование».Для эксперимента
требуется только W1, поэтому W2 и W3 имеют нулевые массы.
5. Результаты берутся из раздела «Результаты» VDAS.
6. Использовали принцип статического равновесия и моментов из «Результатов» для расчета
теоретических значений RA и RB.
3.4: Расчет опорных реакций для плоских конструкций
Опорные реакции для статически определимых и устойчивых конструкций на плоскости определяются с помощью уравнений равновесия.Процедура расчета описана ниже.
Процедура расчета опорных реакций
- Нарисуйте диаграмму конструкции в свободном теле, указав все неизвестные реакции с помощью стрелочной диаграммы.
- Проверьте устойчивость и определенность конструкции, используя уравнение 3.3 или 3.4. Если структура классифицируется как детерминированная, приступайте к анализу.
- Определите неизвестные реакции, применяя три уравнения равновесия.
 Если расчетная реакция приводит к отрицательному ответу, первоначально предполагаемое направление неизвестной реакции, как показано стрелкой на диаграмме свободного тела, неверно и должно быть исправлено, чтобы показать противоположное направление. После внесения поправки величина силы должна быть указана в виде положительного числа в скорректированном наконечнике стрелки на диаграмме свободного тела .
Если расчетная реакция приводит к отрицательному ответу, первоначально предполагаемое направление неизвестной реакции, как показано стрелкой на диаграмме свободного тела, неверно и должно быть исправлено, чтобы показать противоположное направление. После внесения поправки величина силы должна быть указана в виде положительного числа в скорректированном наконечнике стрелки на диаграмме свободного тела .
Пример 3.3
Консольная балка подвергается воздействию равномерно распределенной нагрузки и наклонной сосредоточенной нагрузки, как показано на рисунке 3.9а. Определить реакции на опоре A .
\(рис. 3.9\). Луч
Решение
Схема свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.9b. Опорные реакции, как показано на диаграмме свободного тела, равны \(A_{y \prime}\) \(A_{y \prime}\) и \(M\).
Расчет реакций. Перед расчетом опорных реакций распределенную нагрузку следует заменить единой равнодействующей силой, а наклонную нагрузку разложить на вертикальную и горизонтальную составляющие.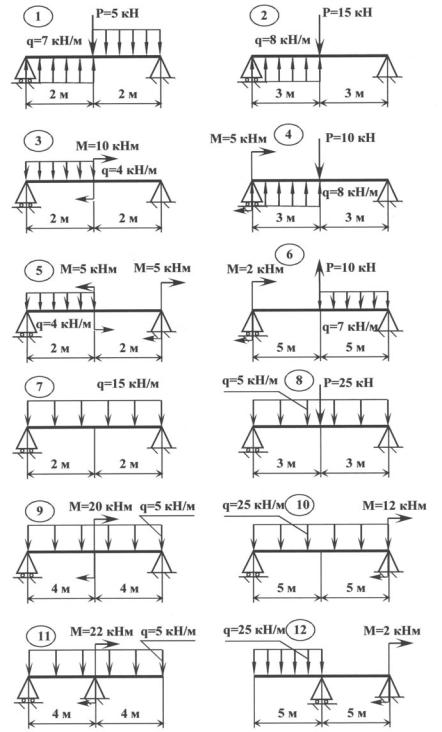 {\ circ} — (4 \ times 2) = 0 \\ A_ {y} = 23,45 \ mathrm {кН} \\ \ rightarrow + \ sum \ mathrm {F} _ {\ mathrm {x}} = 0 \\ \ mathrm{A}_{\mathrm{x}}=0 \end{array} \quad \begin{array}{c} A_{y}=23,45 \mathrm{kN} \uparrow \\ \mathrm{A}_ {\ mathrm {х}} = 0 \ конец {массив} \)
{\ circ} — (4 \ times 2) = 0 \\ A_ {y} = 23,45 \ mathrm {кН} \\ \ rightarrow + \ sum \ mathrm {F} _ {\ mathrm {x}} = 0 \\ \ mathrm{A}_{\mathrm{x}}=0 \end{array} \quad \begin{array}{c} A_{y}=23,45 \mathrm{kN} \uparrow \\ \mathrm{A}_ {\ mathrm {х}} = 0 \ конец {массив} \)
Пример 3.4
Простая балка длиной 12 футов несет равномерно распределенную нагрузку в 2 тысячи фунтов на фут по всему пролету и сосредоточенную нагрузку в 8 тысяч фунтов в середине пролета, как показано на рис. 3.10a. Определить реакции в опорах \(A\) и \(B\) балки.
\(Рис. 3.10\). Простой луч.
Решение
Схема свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.10b.
Расчет реакций. Распределенная нагрузка сначала заменяется единой равнодействующей силой, как показано на рис. 3.10c. Величина равнодействующей силы равна площади прямоугольного нагружения (распределенная сила). Таким образом, \(P=[(2 \mathrm{k} / \mathrm{ft})(12 \mathrm{ft})]\), и его расположение находится в центре тяжести прямоугольной нагрузки \(=\left[ \left(\frac{1}{2}\right)(12 \mathrm{ft})\right]\) Поскольку в этом примере нагрузка симметрична, реакции на обоих концах балки равны, и их можно определить с помощью уравнений статического равновесия и принципа суперпозиции следующим образом:
\(\begin{array}{l} +\стрелка вверх \sum F_{y}=0 \\ A_{y}=B_{y}=\left(\frac{2 \times 12}{2}\right )+\frac{2}{2}=13 \mathrm{kips} \\
+\стрелка вправо \sum \mathrm{F}_{\mathrm{x}}=0 \\ \mathrm{A}_{\ mathrm{x}}=0 \end{array} \quad \begin{array}{l} A_{y}=B_{y}=13 \mathrm{kips} \uparrow \\ \mathrm{A}_{\ матрм{х}}=0 \конец{массив}\)
Пример 3. 5
5
Балка с выступом подвергается переменной нагрузке, как показано на рис. 3.11а. Определить реакции на опорах \(A\) и \(B\).
\(рис. 3.11\). Балка с навесом.
Решение
Схема свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.11b.
Расчет реакций. Обратите внимание, что распределенная нагрузка в балке треугольная. Распределенная нагрузка сначала заменяется единой равнодействующей силой, как показано на рисунке 3.11в. Величина единой равнодействующей силы равна площади под треугольным нагружением. Таким образом, \(\rho=\left(\frac{1}{2}\right)(6 \mathrm{m})(10 \mathrm{kN} / \mathrm{m})\), а его центроид равен в центре загрузки (6м). Применение уравнений равновесия дает следующее:
\(\begin{array}{l} \curvearrowleft+\sum M_{A}=0 \\ -\left(\frac{1}{2}\right)(10)(6)(3)+3 B =0 \\ B_{y}=30 \mathrm{kN} \quad \quad B_{y}=30 \mathrm{kN} \\ \uparrow+\sum F_{y}=0 \\ 30+A_{y} -\left(\frac{1}{2}\right)(6)(10)=0 \quad \mathrm{A}_{\mathrm{y}}=0\\ \rightarrow+\sum \mathrm{F } _ {\ mathrm {x}} = 0 \\ \ mathrm {A} _ {\ mathrm {x}} = 0 \ quad \ quad \ mathrm {A} _ {\ mathrm {x}} = 0 \ end { массив}\)
Пример 3. 6
6
Балка с выступающими концами выдерживает три сосредоточенные нагрузки в 12 тысяч фунтов, 14 тысяч фунтов и 16 тысяч фунтов и момент 100 тысяч фунтов на фут, как показано на рисунке 3.12a. Определите реакции опор A и B .
\(рис. 3.12\). Брус с выступающими концами.
Решение
Схема свободного тела. Диаграмма свободного тела балки показана на рисунке 3.12b.
Расчет реакций. Применение уравнений равновесия дает следующее:
\(\begin{array}{l} +\curvearrowleft M_{A}=0 \\ -100+12(2)-14(2)-16(8)+4 B_{y}=0 \\ B_ {y}=58 \text { тысяч фунтов } \quad \quad B_{y}=58 \text { тысяч фунтов } \uparrow \\ +\uparrow \sum F_{y}=0 \\ 58+A_{y}-12 -14-16=0 \quad A_{y} = 26 \text { kips } \uparrow\\ +\rightarrow \sum F_{x}=0 \\ A_{x}=0 \quad \quad A_{x} \конец{массив}\)
Пример 3.7
Составная балка подвергается нагрузкам, показанным на рис. 3.13а. Найти опорные реакции в точках \(A\) и \(B\) балки.
\(рис. 3.13\). Составной луч.
Решение
Схема свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.13b.
Идентификация основных и дополнительных структур. Для правильного анализа составной структуры необходимо идентифицировать основные и дополнительные части структуры для правильного понимания их взаимодействия.Взаимодействие этих частей показано на рис. 3.13c. Первичная конструкция — это часть составной конструкции, которая может выдерживать приложенную внешнюю нагрузку без помощи дополнительной конструкции. С другой стороны, дополнительная конструкция является частью составной конструкции, которая зависит от основной конструкции для поддержки приложенной внешней нагрузки. Для данной структуры часть \(AC\) является первичной структурой, а часть \(CB\) является дополнительной структурой.
Расчет реакций.Анализ сложной структуры всегда должен начинаться с анализа дополнительной структуры, поскольку дополнительная структура поддерживается первичной структурой. Используя уравнения равновесия, опорные реакции балки определяются следующим образом:
Используя уравнения равновесия, опорные реакции балки определяются следующим образом:
Анализ дополнительной структуры \(CB\) .
Расчет опорной реакции. Диаграмма изолированного свободного тела комплементарной структуры показана на рис. 3.13c.Во-первых, распределенная нагрузка заменяется единой равнодействующей силой (\(P\)), которая равна площади прямоугольной нагрузки, как показано на рис. 3.13d и рис. 3.13e. Применяя уравнения равновесия и учитывая, что из-за симметрии нагрузки опорные реакции в точках C и B равны по величине, получаем следующее:
\(\begin{array}{l} +\стрелка вверх \sum F_{y}=0 \\ B_{y}=C_{y}=\frac{10(7)}{2}=35 \mathrm{ кН} \quad B_{y}=\mathrm{C}_{y}=\frac{10(7)}{2}=35 \mathrm{k} \end{массив}\)
Анализ первичной структуры \(AC\) .
Расчет опорной реакции. Заметим, что до расчета реакций реакция в точке \(С\) дополнительной структуры прикладывается к основной структуре в качестве нагрузки. Величина приложенной нагрузки такая же, как и у комплементарной конструкции, но противоположна по направлению. Применение уравнений равновесия предполагает следующее: \(\begin{array}{l} +\curvearrowleft \sum M_{A}=0 \\ -25(2)-35(4)+M_{A}=0 \ \
Величина приложенной нагрузки такая же, как и у комплементарной конструкции, но противоположна по направлению. Применение уравнений равновесия предполагает следующее: \(\begin{array}{l} +\curvearrowleft \sum M_{A}=0 \\ -25(2)-35(4)+M_{A}=0 \ \
M_{A}=190 \mathrm{kN} \cdot \mathrm{m} \quad M_{A}=190 \mathrm{kN} \cdot \mathrm{m} \curvearrowleft \\ +\uparrow \sum F_ {y}=0 \\ \mathrm{A}_{\mathrm{y}}-25-35=0 \\ \mathrm{A}_{\mathrm{y}}=60 \mathrm{кН} \quad \ mathrm {A} _ {\ mathrm {y}} = 60 \ mathrm {kN} \ uparrow \\ +\ rightarrow \ sum \ mathrm {F} _ {\ mathrm {x}} = 0 \\ \ mathrm {A } _ {\ mathrm {x}} = 0 \ quad \ mathrm {A} _ {\ mathrm {x}} = 0 \ конец {массив} \)
Пример 3.8
Найдите реакции опор \(A\), \(C\) и \(E\) составной балки, несущей равномерно распределенную нагрузку 10 тысяч фунтов/фут по всей длине, как показано на рис. 3.14a.
Рис. 3.14. Составной луч.
Решение
Схема свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3. 14b.
14b.
Идентификация основных и дополнительных структур. Диаграмма взаимодействия для данной структуры представлена на рис. 3.14в. AB является основной структурой, а BD и DE являются дополнительными структурами.
Расчет реакций.
Анализ дополнительной структуры \(DE\) .
Расчет опорной реакции. Диаграмма изолированного свободного тела показана на рис. 3.14c. Во-первых, распределенная нагрузка заменяется единой равнодействующей силой (\(P\)) равной площади прямоугольной нагрузки, как показано на рис. 3.14d.Применяя уравнения равновесия и отмечая, что из-за симметрии в нагружении опорные реакции в точках \(D\) и \(E\) равны по величине, находим следующее:
\(\begin{array}{l} +\стрелка вверх \sum F_{y}=0 \\ D_{y}=E_{y}=\frac{10(8)}{2}=40 \mathrm{ kips} \quad E_{y}=40 \mathrm{kips} \uparrow \end{массив}\)
Анализ дополнительной структуры \(BD\) .
Расчет опорной реакции. Диаграмма изолированного свободного тела показана на рисунке 3.14е. Во-первых, распределенная нагрузка заменяется единой равнодействующей силой (\(P\)), равной площади прямоугольной нагрузки, как показано на рис. 3.14f. Нагрузка от комплементарной конструкции приложена в точке \(D\). Применение уравнений равновесия позволяет сделать следующее:
Диаграмма изолированного свободного тела показана на рисунке 3.14е. Во-первых, распределенная нагрузка заменяется единой равнодействующей силой (\(P\)), равной площади прямоугольной нагрузки, как показано на рис. 3.14f. Нагрузка от комплементарной конструкции приложена в точке \(D\). Применение уравнений равновесия позволяет сделать следующее:
\(\begin{array}{l} +\curvearrowleft \sum M_{B}=0 \\ -10(8)\left(\frac{8}{2}\right)-40(8)+4 C_{y}=0 \\ C_{y}=160 \text { тыс.фунтов } \quad C_{y}=160 \text { тыс.фунтов } \uparrow \\ +\uparrow \sum F_{y}=0 \\ 160 -B_{y}-10(8)-40=0 \\ B_{y}=40 \text {кипов} \end{массив}\)
Анализ первичной структуры \(AB\) .
Расчет опорной реакции. Заметим, что до расчета реакций равномерная нагрузка заменяется единой равнодействующей силой, а реакция в точке \(B\) дополнительной конструкции прикладывается к основной конструкции как нагрузка. Применение требования равновесия дает следующее:
\(\begin{array}{l} \quad+\curvearrowleft \sum M_{A}=0 \\ \mathrm{M}-10(10)\left(\frac{10}{2}\right)+ 40(10)=0 \\ M_{A}=100 \mathrm{кипов} . \mathrm{ft} \quad \quad M_{A}=100 \mathrm{kips} . \mathrm{ft} \curvearrowleft \\ +\uparrow \sum F_{y}=0 \\ A_{y}-10(10)+40=0 \\ A_{\mathrm{y}}=60 \mathrm{ тысяч фунтов} \quad \quad A _{\mathrm{y}}=60 \mathrm{kips} \uparrow\\ +\rightarrow \sum \mathrm{F}_{\mathrm{x}}=0 \\ A_{x }=0 \quad \quad A_{x}=0 \end{массив}\)
\mathrm{ft} \quad \quad M_{A}=100 \mathrm{kips} . \mathrm{ft} \curvearrowleft \\ +\uparrow \sum F_{y}=0 \\ A_{y}-10(10)+40=0 \\ A_{\mathrm{y}}=60 \mathrm{ тысяч фунтов} \quad \quad A _{\mathrm{y}}=60 \mathrm{kips} \uparrow\\ +\rightarrow \sum \mathrm{F}_{\mathrm{x}}=0 \\ A_{x }=0 \quad \quad A_{x}=0 \end{массив}\)
Пример 3.9
Найдите реакции опор \(A\), \(B\), \(E\) и \(F\) нагруженной составной балки, как показано на рис. 3.15а.
\(Рис.3.15\). Составной луч.
Решение
Схема свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.15b.
Идентификация основной и дополнительной структуры. Диаграмма взаимодействия для данной структуры показана на рис. 3.15в. \(CD\) является дополнительной структурой, а \(AC\) и \(DF\) являются первичными структурами.
Расчет реакций.
Анализ дополнительной структуры \(CD\) .
Расчет опорной реакции.Диаграмма изолированного свободного тела показана на рис. 3.15c. Во-первых, распределенная нагрузка заменяется единой равнодействующей силой (\(P\)), равной площади прямоугольной нагрузки, как показано на рис. 3.15d. Применяя уравнения равновесия и отмечая, что из-за симметрии в нагружении опорные реакции в точках \(C\) и \(D\) равны по величине, находим следующее:
3.15c. Во-первых, распределенная нагрузка заменяется единой равнодействующей силой (\(P\)), равной площади прямоугольной нагрузки, как показано на рис. 3.15d. Применяя уравнения равновесия и отмечая, что из-за симметрии в нагружении опорные реакции в точках \(C\) и \(D\) равны по величине, находим следующее:
\(\begin{array}{l} +\стрелка вверх \sum F_{y}=0 \\ C_{y}=D_{y}=\frac{10(4)}{2}=20 \mathrm{ кН} \end{массив}\)
Анализ первичной структуры \(AC\) .
Расчет опорной реакции. Обратите внимание, что реакция в \(AC\) комплементарной структуры применяется как направленная вниз сила той же величины в той же точке первичной структуры. Применение уравнения равновесия позволяет сделать следующее:
\(\begin{array}{l} +\curvearrowleft \sum M_{A}=0 \\ -24(2)-20(5,5)+4 B_{y}=0 \\ B_{y}=39,5 \mathrm{kN} \quad \quad B_{y}=39,5 \mathrm{kN} \стрелка вверх\\ +\стрелка вверх \sum F_{y}=0 \\ \mathrm{A}_{y}+39.5-24-20=0 \\ A_{y}=4,5 \mathrm{kN} \quad \quad A_{y}=4,5 \mathrm{kN} \стрелка вверх\\ +\стрелка вправо \sum \mathrm{F}_ {\ mathrm{x}}=0 \\ A_{x}=0 \quad \quad A_{x} = 0 \end{массив}\)
Анализ первичной структуры \(DF\) .
Расчет опорной реакции. Диаграмма изолированного свободного тела показана на рис. 3.15f. Во-первых, распределенная нагрузка заменяется единой равнодействующей силой (\(P\)), равной площади треугольной нагрузки, как показано на рисунке 3.15г. Применяя уравнения равновесия и отмечая, что опорная реакция в точке \(D\) дополнительной конструкции действует как нагрузка на основную конструкцию, можно сделать следующее:
\(\begin{array}{l} +\curvearrowleft \sum M_{F} =0 \\ -20+\left(\frac{1}{2} \times 8 \times 10\right)\left( \frac{2}{3} \times 8\right)+20(8)-4 E_{y}=0 \\ E_{y}=88,33 \mathrm{kN} \quad E_{y}=88,33 \mathrm {kN} \uparrow \\ +\uparrow \sum F_{y}=0 \\ F_{y}+88,33-\left(\frac{1}{2} \times 8 \times 10\right)-20= 0 \\ F_{y}=28.33 \mathrm{кН} \quad F_{y}=28,33 \mathrm{кН}стрелка вверх \end{массив}\)
Пример 3.10
Определите реакции опор A и D рамы, показанной на рис. 3.16а.
\(рис. 3.16\). Рамка.
3.16\). Рамка.
Решение
Схема свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.16b.
Расчет реакций. Распределенные нагрузки в колонне \(AB\) и балке \(BC\) сначала заменяются одиночными равнодействующими силами, определяемыми как площадь их соответствующего оттенка нагрузки, как показано на рисунке 3.16в. Применение условий равновесия предполагает следующее:
\(\begin{array}{l} +\curvearrowleft \sum M_{A}=0 \\ D_{y}(6)-\left(\frac{1}{2}\right)(6)( 3)(3)-(2)(8)(4)=0 \\ D_{y}=15,7 \text { тыс.фунтов } \quad D_{y}=15,7 \mathrm{kips} \uparrow \\ +\uparrow \sum F_{y}=0 \\ \mathrm{A}_{y}+15,17-3(6)=0 \\ A_{y}=2,830 \mathrm{kips} \quad A_{y}=2,830 \ mathrm{kips} \uparrow \\ +\rightarrow \sum \mathrm{F}_{\mathrm{x}}=0 \\ -\mathrm{A}_{x}+(2 \times 8)=0 \ \ A_{x}=16 \mathrm{kips} \quad A_{x}=16 \mathrm{kips} \leftarrow \end{массив}\)
Пример 3.11
Жесткая рама нагружена, как показано на рис. 3. 17а. Определить реакции на опоре \(D\).
17а. Определить реакции на опоре \(D\).
\(рис. 3.17\). Жесткая рама.
Решение
Схема свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.17b.
Расчет реакций. Распределенная нагрузка в части AB рамы сначала заменяется единой равнодействующей силой, как показано на рис. 3.17c. Применение уравнений равновесия позволяет сделать следующее:
\(\begin{align} &+\curvearrowleft \sum M_{D}=0\\ &-M_{D}-16(8)+(4 \times 14)\left(\frac{14}{2 }\right)-10(10)=0\\ &M_{D}=164 \text { тыс.фунтов.} \mathrm{ft} \quad M_{D}=164 \text { тысяч фунтов. } \mathrm{ft} \curvearrowright \mathrm{A}\\ &+\uparrow \sum F_{y}=0\\ &D_{y}-4(14)-10=0\\ &D_{y}=66 \text { kips } \quad D_{y}=66 \text { kips } \uparrow\\ &+\rightarrow \sum \mathrm{F}_{\mathrm{x}}=0\\ &-D_{x }+16=0\\ &D_{x}=16 \text { тысяч фунтов } \quad D_{x}=16 \text { тысяч фунтов } \leftarrow \end{aligned}\)
Пример 3.12
Найдите реакции у опор E и F рамы, показанной на рисунке 3. 18а.
18а.
\(рис. 3.18\). Рамка.
Решение
Схема свободного тела. Схема свободного тела рамы показана на рисунке 3.18b.
Расчет реакций. Распределенные нагрузки сначала заменяются единичными равнодействующими силами, как показано на рис. 3.18c. Применение уравнений статического равновесия позволяет сделать следующее:
\(\begin{array}{l} +\curvearrowleft \sum M_{E}=0 \\ \left(\frac{1}{2} \times 4 \times 8\right)\left(\frac{ 1}{3} \times 4\right)-(4\times 7)\left(\frac{7}{2}\right)-\left(\frac{1}{2} \times 4 \times 8 \right)\left(\frac{7}{2}+\frac{1}{3} \times 4\right)+7 F_{y}=0 \\ F_{y}=22 \mathrm{kN} \quad F_{y}=22 \mathrm{kN} \uparrow \\ +\uparrow \sum F_{y}=0 \\ E_{y}+22-2\left(\frac{1}{2} \ умножить на 4 \times 8\right)-4(7)=0 \\ E_{y}=38 \mathrm{kN} \quad E_{y}=38 \mathrm{kN} \uparrow \\ +\rightarrow \sum \mathrm{F}_{\mathrm{x}}=0 \\ E_{x}=0 \quad E_{x}=0 \end{массив}\)
Пример 3.13
Определите реакции опоры A жесткой рамы, показанной на рис.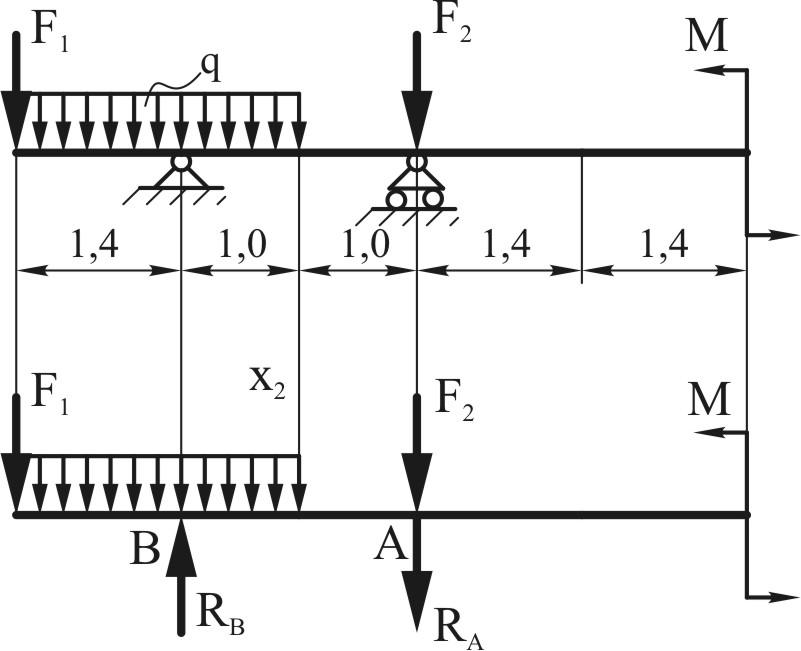 3.19а.
3.19а.
\(рис. 3.19\). Жесткая рама.
Решение
Схема свободного тела. Схема свободного тела рамы показана на рисунке 3.19b.
Расчет реакций. Распределенная нагрузка в столбце \(AB\) сначала заменяется одной равнодействующей силой, как показано на рис. 3.19c. Применение уравнений статического равновесия позволяет сделать следующее:
\(\begin{array}{l} +\curvearrowleft \sum M_{A}=0 \\ -M_{A}-20(3)-\left(\frac{1}{2} \times 10 \ умножить на 10\вправо)\влево(\frac{1}{3} \умножить на 10\вправо)=0 \\ M_{A}=-226.67 \mathrm{kN} \cdot \mathrm{m} \quad \quad M_{A}=226,67 \mathrm{kN} \cdot \mathrm{m} \curvearrowleft \\ +\uparrow \sum F_{y}=0 \\ A_{y}-20=0 \\ A_{y}=20 \mathrm{kN} \quad \quad A_{y}=20 \mathrm{kN} \uparrow\\ +\rightarrow \sum F_{x }=0 \\ -A_{x}+\left(\frac{1}{2} \times 10 \times 10\right)=0 \\ A_{x}=50 \mathrm{kN} \quad \quad A_{x}=50 \mathrm{кН} \leftarrow \end{массив}\)
Пример 3.14
Определите реакции опор \(A\) и \(E\) рамы, шарнирно закрепленной в \(C\), как показано на рис. 3.20а.
3.20а.
\(Рис. 3.20\). Рамка.
Решение
Схема свободного тела. Схема свободного тела рамы показана на рисунке 3.20b.
Расчет реакций. Реакции в составной раме рассчитываются с учетом диаграмм свободного тела как всей рамы, так и ее части. Перед расчетом реакций распределенную нагрузку в колонне заменяют единой равнодействующей силой. Вертикальные реакции в \(Е\) и \(А\) и горизонтальные реакции в \(А\) находятся путем применения уравнений статического равновесия и рассмотрения диаграммы свободного тела всей рамы.Горизонтальная реакция в \(E\) находится при рассмотрении части \(CDE\) диаграммы свободного тела.
\(\begin{array}{l} +\curvearrowleft \sum M_{A}=0 \\ 8 E_{y}-(2 \times 10)\left(\frac{10}{2}\right) -10(4)=0 \\ E_{y}=17,5 \text { тысяч фунтов } \quad \quad E_{y}=17,5 \mathrm{kips} \uparrow \\ +\uparrow \sum F_{y}=0 \\ A_{y}+17,5-10=0 \\ A_{y}=-7,5 \text { тысяч фунтов } \quad \quad A_{y}=7,5 \text { тысяч фунтов } \downarrow \end{array}\)
Знак минус означает, что изначально предполагаемое направление \(A_{y}\) было неправильным. Следовательно, \(A_{y}\) действует вниз, а не вверх, как первоначально предполагалось. Это должно быть исправлено при последующем анализе.
Следовательно, \(A_{y}\) действует вниз, а не вверх, как первоначально предполагалось. Это должно быть исправлено при последующем анализе.
Чтобы определить \(E_{x}\), рассмотрим момент сил в стержне \(CDE\) относительно шарнира.
\(\begin{array}{l} \curvearrowleft +\sum M_{C}=0 \\ 17,5(4)-10 E_{x}=0 \\ E_{x}=7 \text { тыс.фунтов} \ quad \quad E_{x}=7 \text { тысяч фунтов } \leftarrow \\ +\rightarrow \sum F_{x}=0 \\ -A_{x}-7+2 \times 10=0 \\ A_{x }=13 \text { тысяч фунтов } \quad \quad A_{x}=13 \text { тысяч фунтов } \leftarrow \end{массив}\)
Пример 3.15
Найдите реакции в опорах \(A\) и \(B\) нагруженной рамы на рис. 3.21а. Рама шарнирно закреплена в точке \(D\).
\(Рис. 3.21\). Загруженный кадр.
Решение
Схема свободного тела. Схема свободного тела рамы показана на рисунке 3.21b.
Расчет реакций. Распределенная нагрузка в столбце \(AC\) сначала заменяется единой результирующей силой путем нахождения области нагрузки, как показано на рис.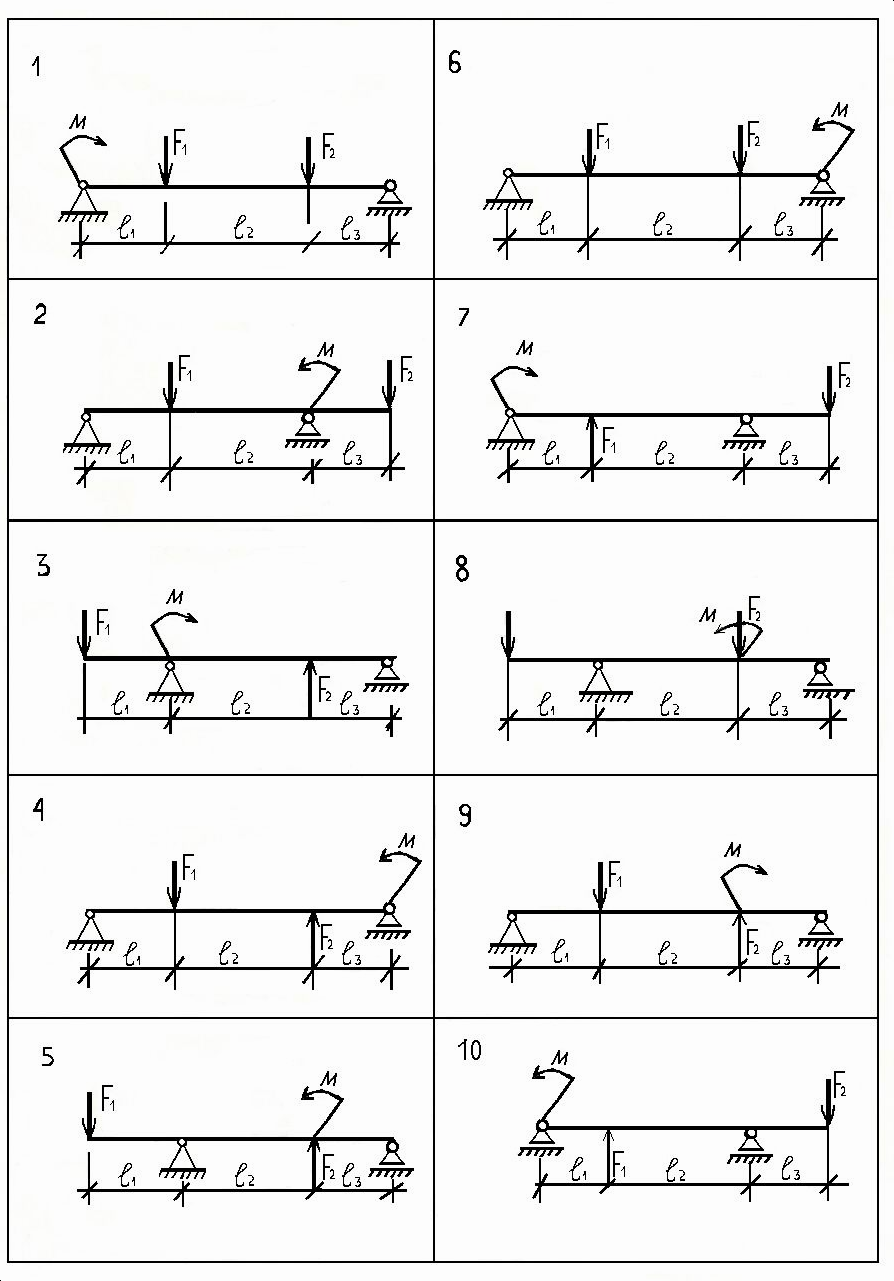 3.21.Реакция в точке \(B\) вычисляется путем принятия момента сил в части \(DB\) рамы относительно штифта в точке \(D\), а остальные реакции определяются путем применения других условий равновесия.
3.21.Реакция в точке \(B\) вычисляется путем принятия момента сил в части \(DB\) рамы относительно штифта в точке \(D\), а остальные реакции определяются путем применения других условий равновесия.
\(\begin{align} &+\curvearrowleft \sum M_{D}=0\\ &B_{y}(0)-15(4)=0\\ &B_{y}=0\\ &+n \ сумма M_{A}=0\\ &M_{A}+6 \times 0-\left(\frac{1}{2} \times 8 \times 20\right)\left(\frac{1}{3} \times 8\right)-12(3)+15(4)=0\\ &M_{A}=189,33 \mathrm{kN} \cdot \mathrm{m} \quad M_{A}=189.33 \mathrm{kN} \cdot \mathrm{m} \curvearrowright\\ &+\uparrow \sum F_{y}=0\\ &A_{y}+0-12=0\\ &A_{y}=-12 \mathrm{kN} \quad A_{y}=12 \downarrow \end{aligned}\)
Знак минус означает, что первоначально предполагаемое направление A y было неверным. Следовательно, A y действует вниз, а не вверх, как предполагалось изначально. Это должно быть исправлено при последующем анализе.
\(\begin{array}{l} +\стрелка вправо \сумма F_{x}=0 \\ -A_{x}-15+\left(\frac{1}{2} \times 8 \times 20\ справа)=0 \\ A_{x}=65 \mathrm{kN} \quad \quad A_{x}=65 \mathrm{kN} \rightarrow \end{array}\)
Краткое изложение главы
Условия статического равновесия: Конструкция находится в состоянии статического равновесия, если равнодействующая всех действующих на нее сил и моментов равна нулю.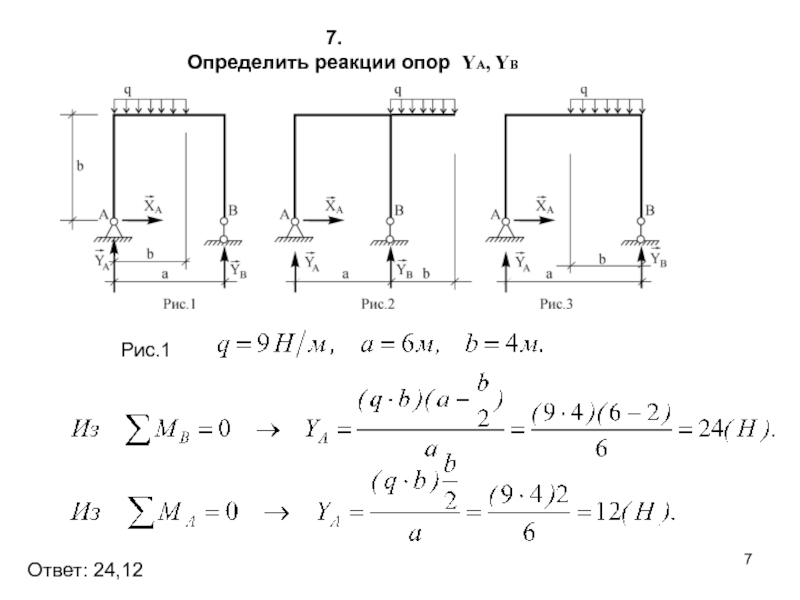 Математически это выражается следующим образом:
Математически это выражается следующим образом:
\(\Сигма F=0\) \(\Сигма M=0\)
Для тела на плоскости существуют следующие три уравнения равновесия:
\(\Sigma F_{X}=0\) \(\Sigma F_{Y}=0\)∑ \(\Sigma M_{0}=0\)
Типы опор: Различные символические представления используются для моделирования различных типов опор для конструкций. Ролик используется для моделирования опоры, которая препятствует вертикальному движению конструкции, но допускает горизонтальное перемещение и вращение.Штифт используется для моделирования опоры, которая предотвращает горизонтальные и вертикальные перемещения, но допускает вращение. Неподвижная опора моделирует опору, предотвращающую горизонтальные и вертикальные перемещения и повороты.
Детерминированность, неопределенность и устойчивость структур: Структура является детерминированной, если число неизвестных реакций равно числу статических равновесий. Таким образом, для определения опор такой конструкции достаточно уравнений статического равновесия. С другой стороны, статически неопределимая структура — это структура, в которой количество неизвестных реакций превышает уравнения равновесия. Для анализа неопределенной конструкции нужны дополнительные уравнения, и эти уравнения можно получить, рассматривая совместность конструкции. Неопределенные конструкции иногда необходимы, когда необходимо уменьшить размеры элементов или увеличить жесткость элементов. Стабильная структура — это структура, в которой опорные реакции не параллельны и не параллельны друг другу.Формулировка устойчивости и определенности балок и шпангоутов следующая:
С другой стороны, статически неопределимая структура — это структура, в которой количество неизвестных реакций превышает уравнения равновесия. Для анализа неопределенной конструкции нужны дополнительные уравнения, и эти уравнения можно получить, рассматривая совместность конструкции. Неопределенные конструкции иногда необходимы, когда необходимо уменьшить размеры элементов или увеличить жесткость элементов. Стабильная структура — это структура, в которой опорные реакции не параллельны и не параллельны друг другу.Формулировка устойчивости и определенности балок и шпангоутов следующая:
Балки и рамы: | \(3 m+r<3 j+C\) Структура неустойчива |
|
|
| \(3 m+r=3 j+C\) Структура детерминированная |
|
|
| \(3 m+r>3 j+C\)Структура не определена |
Практические задачи
3. 1 Классифицируйте конструкции, показанные на рисунках P3.1a–P3.1p, как статически определимые или неопределимые, а также статически устойчивые или неустойчивые. Если неопределенно, укажите степень неопределенности.
1 Классифицируйте конструкции, показанные на рисунках P3.1a–P3.1p, как статически определимые или неопределимые, а также статически устойчивые или неустойчивые. Если неопределенно, укажите степень неопределенности.
\(Рис. П3.1\). Структурная классификация.
3.2. Определите опорные реакции для балок, показанных на рис. P3.2–рис. P3.12.
\(Рис. П3.2\). Луч.
\(Рис. П3.3\). Луч.
\(Рис. П3.4\). Луч.
\(Рис. П3.5\). Луч.
\(Рис. П3.6\). Луч.
\(Рис. П3.7\). Луч.
\(Рис. П3.8\). Луч.
\(Рис. П3.9\). Луч.
\(Рис. П3.10\). Луч.
\(Рис. П3.11\). Луч.
\(Рис. П3.12\). Луч.
3.3.Определите опорные реакции для рам, показанных на рис. P3.13–рис. P3.20.
\(Рис. П3.13\). Рамка.
\(Рис. П3.14\). Рамка.
П3.14\). Рамка.
\(Рис. П3.15\). Рамка.
\(Рис. П3.16\). Рамка.
\(рис. 3.17\). Рамка.
\(рис. 3.18\). Рамка.
\(рис. 3.19\). Рамка.
\(Рис.3.20\). Рамка.
3.4 Определите опорные реакции для ферм, показанных на рис. P3.21–рис. P3.27.
\(рис. П3.21\). Ферма.
\(Рис. P3.22\). Ферма.
\(Рис. П3.23\). Ферма.
\(рис. П3.24\). Ферма.
\(Рис. P3.25\). Ферма.
\(рис. П3.26\). Ферма.
\(Рис. P3.27\). Ферма.
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка браузера на прием файлов cookie
Существует множество причин, по которым файл cookie не может быть установлен правильно. Ниже приведены наиболее распространенные причины:
Ниже приведены наиболее распространенные причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки браузера, чтобы принять файлы cookie, или спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файл cookie.
- Ваш браузер не поддерживает файлы cookie. Попробуйте другой браузер, если вы подозреваете это.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы это исправить, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.
Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.

Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Предоставить доступ без файлов cookie потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в файле cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только та информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт
не может определить ваше имя электронной почты, если вы не решите ввести его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступ к
остальной части вашего компьютера, и только сайт, создавший файл cookie, может его прочитать.
Расчет реакции прессы
Соберите блокнот, ручку и калькулятор. Во время этой процедуры необходимо учитывать линейную скорость, отображаемую на контроллере. Измерения должны производиться в порядке изготовления деталей станка. Может быть полезно иметь вспомогательный персонал для наблюдения и записи.
- Установите время реакции на нажатие равным нулю.
- Запрограммируйте две операции прессования (в случае ножниц две длины детали). Обязательно запрограммируйте их на достаточно длинном расстоянии, чтобы, когда XL200 запускает пресс в автоматическом режиме, линия работала на скорости.Если линия все еще разгоняется до скорости, тест будет недействителен. (Если станок поддерживает пробивку на линии, запрограммируйте ножницы и пробойник на одинаковое расстояние смещения для целей проверки. После проверки перепрограммируйте пробойник на правильное физическое расстояние).
- Выполнение операции прессования стоя (включите пресс вручную, когда материал остановлен).
- Проведите линию.
- После того, как контроллер дважды сработал жим, измерьте расстояние от жима стоя до первого автоматического жима.Затем измерьте от первого автоматического нажатия до второго.
- Вычесть вторую длину из первой.
- Разделите результат на линейную скорость в футах в минуту (метрах в минуту).
- Умножьте результат на 5 (0,06 при использовании метрической системы).
- Результатом является время реакции на нажатие.
Если длина деталей непостоянна из-за проблем с отслеживанием энкодера или отклонений реакции пресса, этот тест является пустой тратой времени. Несоответствия должны быть устранены в первую очередь, прежде чем можно будет выполнять измерения для устранения постоянных ошибок.Принимать любую другую методологию — это упражнение в бесполезности и разочаровании.
При выполнении процедуры расчета реакции на прессование в первый раз часто бывает полезно запустить не менее 5 деталей подряд. Первые две можно использовать для расчета времени реакции, если последние 4 части непротиворечивы.
Пример:
Технический специалист (Джо) вызывается для осмотра летающей штамповочной машины с разомкнутым контуром. Ларри, оператор станка, жалуется, что станок производит изделия разной длины при запуске, а иногда и во время производственного цикла.При осмотре Джо может увидеть, что XL200 никогда не был запрограммирован на значение реакции на сдвиг (или он подозревает, что значение было изменено).
Джо начинает с программирования 5 деталей размером 60 дюймов (1524 мм). Хорошо известно, что эта машина достигает скорости после небольшого расстояния, поэтому нет необходимости программировать более длинную деталь, которая потенциально может стать браком. Он настраивает линию на скорость 150 футов в минуту (46 миль в минуту) для целей теста.
Джо выполняет операцию «Ручной сдвиг», чтобы определить точку отсечки, а затем запускает линию.После изготовления 5 деталей он останавливает линию и измеряет детали в том порядке, в котором они были произведены, от первой до последней. Его результаты:
Его результаты:
Судя по числам, Джо видит, что существует общая разница в длине, которую он должен устранить, прежде чем продолжать какие-либо другие действия. Он знает, насколько критично отслеживание материала энкодером для точности процесса, поэтому он начинает с проверки выравнивания энкодера и кронштейна по отношению к материалу.
Джо обнаруживает, что колесо значительно не выровнено, и устраняет проблему.Он программирует еще 5 деталей, выполняет ручную резку и запускает второй комплект из 60-дюймовых (1524 мм) деталей. На этот раз его результаты:
По результатам Джо удовлетворен тем, что машина работает достаточно стабильно, и теперь он может использовать функции, встроенные в XL200, для устранения остальных проблем с длиной. Он выполняет процедуру расчета реакции на прессу, используя среднее значение последних 4 частей в качестве «второй длины»:
. 1-я длина – 2-я длина = 4,235 дюйма (107.6 мм)
4,235 дюйма (107,6 мм) / 150 футов в минуту (46 миль в минуту) = 0,02823 (2,3528)
0,028233 (2,3528) · 5 (0,06) = 0,1412 с
Джо вводит значение 0,1412 с в параметр Реакция на сдвиг в контроллере XL200. Он также знает, что может использовать функцию калибровки обрезки, чтобы устранить постоянную ошибку 0,265 дюйма (6,73 мм) из общей длины.
Он также знает, что может использовать функцию калибровки обрезки, чтобы устранить постоянную ошибку 0,265 дюйма (6,73 мм) из общей длины.
Теперь, когда Джо передает линию Ларри, производство может рассчитывать на постоянство и точность длины деталей от первой до последней, даже если Ларри меняет скорость во время производства.
Зеленая химия | Английский | Зеленая химия
Модуль «Зеленая химия»
Предлагаемое использование: курс органической химии (как лекция, так и лабораторная работа) при обсуждении различных реакций (замещение, удаление, присоединение, перегруппировка и т. д.)
АТОМНАЯ ЭКОНОМИКА: мера эффективности реакции
Майкл К. Канн, химический факультет, Скрэнтонский университет,
[email protected],
Доходность в процентах
Хотя эффективность реакции можно измерить многими способами, наиболее распространенным является расчет выхода (выход в процентах).Студентам часто требуется, особенно в лаборатории, определить теоретический выход на основе ограничивающего реагента, а затем рассчитать процентный выход на основе отношения фактического выхода к теоретическому X 100. Обычно химики-органики считают выходы 90% или лучше как отлично, в то время как 20% или менее являются плохими.
Обычно химики-органики считают выходы 90% или лучше как отлично, в то время как 20% или менее являются плохими.
Теоретический выход = (моль ограничивающего реагента)(стехиометрическое соотношение; желаемый продукт/ограничивающий реагент)(MW желаемого продукта)
Выход в процентах = (фактический выход/теоретический выход) X 100
Чтобы проиллюстрировать расчет процентного выхода (и измерение эффективности реакции), рассмотрим следующую реакцию нуклеофильного замещения, активируемую кислотой.Типичная процедура 1 для этой реакции начинается с растворения
Уравнение 1a
1,33 г бромида натрия (2) в 1,5 мл воды с последующим добавлением 0,80 мл 1-бутанола (1) и 1,1 мл (2,0 г) концентрированной серной кислоты (3). Следующая таблица реагентов (таблица 1) и таблица желаемого продукта (таблица 2) могут иметь значение
Таблица 1 Реагенты
| Реагент | МВт | Вес Используется (г) | Используемые моли | Теоретическая Необходимо моль | Плотность | Бп ( или С) |
| 1 С 4 Н 9 ОХ | 74. 12 12 | 0,80 | 0,0108 | 0,0108 | 0,810 | 118 |
| 2 NaBr | 102,91 | 1,33 | 0,0129 | 0,0108 | ||
| 3 H 2 SO 4 | 98,08 | 2,0 | 0,0200 | 0,0108 | 1,84 |
Таблица 2 Таблица желаемого продукта
| Соединение | МВт | Теоретический выход (моль) | Теоретический Выход (граммы) | Фактический выход (граммы) | % Выход | Плотность | Бп ( или С) |
| 4 С 4 Н 9 Бр | 137.03 | 0,011 | 1,48 (100%) | 1,20 | 81 | 1,275 | 101,6 |
установка. Разделив массу каждого используемого реагента на молекулярную массу реагента, вы получите количество молей каждого используемого реагента. Из стехиометрии реакции (уравнение 1а) видно, что для получения одного моля продукта (1-бромбутана) требуется один моль каждого реагента, а поскольку 1-бутанол (0,0108 моль) используется в наименьшем количестве, лимитирующий реагент.Расчет (как показано ниже) теоретического выхода 1-бромбутана дает 1,48 г. Это означает, что при использовании
Разделив массу каждого используемого реагента на молекулярную массу реагента, вы получите количество молей каждого используемого реагента. Из стехиометрии реакции (уравнение 1а) видно, что для получения одного моля продукта (1-бромбутана) требуется один моль каждого реагента, а поскольку 1-бутанол (0,0108 моль) используется в наименьшем количестве, лимитирующий реагент.Расчет (как показано ниже) теоретического выхода 1-бромбутана дает 1,48 г. Это означает, что при использовании
Теоретический выход = (моль ограничивающего реагента)(стехиометрическое соотношение; желаемый продукт/ограничивающий реагент)(ММ целевого продукта)
= (моль 1-бутанола) (стехиометрическое соотношение; 1-бромбутан/1-бутанол)( MW 1-бромбутана)
= (0,0180 моль) (1 моль/1 моль) (137,03 г/моль)
= 1.48 г
вышеуказанных количеств реагентов максимальное количество (при условии выхода 100%) 1-бромбутана, которое может быть получено, составляет 1,48 г. Фактически ни одна реакция никогда не протекает со 100%-ным выходом из-за таких факторов, как образование побочных продуктов, неполная конверсия исходных материалов, потери при обработке реакционной смеси и потери при выделении и очистке целевого продукта. Эта реакция обычно дает фактические выходы 1-1,2 г. Предполагая, что фактический выход составляет 1,20 г, расчет выхода в % осуществляется следующим образом.Таким образом, фактически выделяется 81% теоретического выхода, что является очень приличным выходом, который удовлетворил бы большинство химиков.
Фактически ни одна реакция никогда не протекает со 100%-ным выходом из-за таких факторов, как образование побочных продуктов, неполная конверсия исходных материалов, потери при обработке реакционной смеси и потери при выделении и очистке целевого продукта. Эта реакция обычно дает фактические выходы 1-1,2 г. Предполагая, что фактический выход составляет 1,20 г, расчет выхода в % осуществляется следующим образом.Таким образом, фактически выделяется 81% теоретического выхода, что является очень приличным выходом, который удовлетворил бы большинство химиков.
Выход в процентах = (фактический выход/теоретический выход) X 100
Как указывалось ранее, большинство химиков традиционно измеряют эффективность реакции процентным выходом, однако это лишь часть истории. Если учесть приведенную выше реакцию, где всего 4.Было использовано 13 г реагентов (0,8 г 1-бутанола, 1,33 г NaBr и 2,0 г H 2 SO 4 ), и что в лучшем случае эта реакция даст только 1,48 г целевого продукта, вопрос можно спросить: «Что происходит с массой (4,13 г — 1,48 г = 2,7 г ) массы реагентов?». Ответ заключается в том, что они попадают в побочные продукты (NaHSO 4 и H 2 O), которые могут быть нежелательными, неиспользованными, токсичными и/или непригодными для переработки/повторного использования. Побочные продукты часто рассматриваются как отходы и должны быть утилизированы или обработаны иным образом.В лучшем случае только 36% (1,48 г/4,13 г × 100) массы реагентов переходят в желаемый продукт. Если фактический выход составляет 81%, то только 29% (0,81 х 0,36 х 100) массы реагентов фактически превращается в желаемый продукт!
Ответ заключается в том, что они попадают в побочные продукты (NaHSO 4 и H 2 O), которые могут быть нежелательными, неиспользованными, токсичными и/или непригодными для переработки/повторного использования. Побочные продукты часто рассматриваются как отходы и должны быть утилизированы или обработаны иным образом.В лучшем случае только 36% (1,48 г/4,13 г × 100) массы реагентов переходят в желаемый продукт. Если фактический выход составляет 81%, то только 29% (0,81 х 0,36 х 100) массы реагентов фактически превращается в желаемый продукт!
Стремясь повысить осведомленность об атомах реагентов, которые включаются в желаемый продукт, и тех, которые тратятся впустую (включаются в нежелательные продукты), Барри Трост разработал концепцию атомной экономии . 2 В 1998 году компания Trost была удостоена президентской премии Green Chemistry Challenge Award за концепцию атомной экономики.В свете концепции экономии атомов вышеописанное нуклеофильное замещение, промотируемое кислотой, теперь необходимо пересмотреть. В уравнении 1b мы проиллюстрировали экономию атомов этой реакции, показав все атомы реагентов, которые включены в желаемый продукт, зеленым цветом,
В уравнении 1b мы проиллюстрировали экономию атомов этой реакции, показав все атомы реагентов, которые включены в желаемый продукт, зеленым цветом,
Уравнение 1b
, а те, которые потрачены впустую, показаны коричневым цветом. Точно так же атомы желаемого продукта отмечены зеленым, а атомы, составляющие нежелательные продукты, — коричневым. В таблице 3 представлен другой взгляд на экономию атомов в этой реакции.В столбцах 1 и 2 этой таблицы указаны формулы и формульные веса (FW) реагентов. Зеленым цветом (столбцы 3 и 4) показаны атомы и веса атомов реагентов, которые включаются в желаемый продукт (4), а коричневым цветом (столбцы 5 и 6) показаны атомы и веса атомов реагентов. реагенты, которые превращаются в нежелательные побочные продукты. Сосредоточив внимание на последней строке этой таблицы, можно увидеть, что из всех атомов реагентов (4C, 12H, 5O, 1Br, 1Na и 1S) только 4C, 9H и 1Br используются в целевом продукте и массе ( 3H, 5O, 1Na, 1S) выбрасываются как компоненты нежелательных продуктов. Это пример плохой атомной экономики! Логическим продолжением концепции атомной экономики Троста является вычисление
Это пример плохой атомной экономики! Логическим продолжением концепции атомной экономики Троста является вычисление
Таблица 3 Атомная экономия по уравнению 1
| Формула реагентов | Реагенты FW | Используемые атомы | Масса Использованных атомов | Неиспользованные атомов | Масса неиспользованных атомов |
| 1 C 4 H 9 OH | 74 | 4C,9H | 57 | HO | 17 |
| 2 NaBr | 103 | Br | 80 | Н/Д | 23 |
| 3 H 2 SO 4 | 98 | _____ | 0 | 2H, 4O, S | 98 |
| Итого 4C,12H,5O,BrNaS | 275 | 4C,9H,Br | 137 | 3H, 5O, Na, S | 138 |
процентная атомная экономика . 3 Это можно сделать, взяв отношение массы использованных атомов (137) к общей массе атомов всех реагентов (275) и умножив на 100. Как показано ниже, в этой реакции присутствует только 50% атомов экономика.
3 Это можно сделать, взяв отношение массы использованных атомов (137) к общей массе атомов всех реагентов (275) и умножив на 100. Как показано ниже, в этой реакции присутствует только 50% атомов экономика.
% Атомная экономия = (FW использованных атомов/FW всех реагентов) X 100
= (137/275) X 100 = 50% 9000
Таким образом, в лучшем случае (если реакция дает 100% выход) только половина массы реагентов будет включена в желаемый продукт, а остальная часть будет потрачена впустую на нежелательные побочные продукты.
ДОПОЛНИТЕЛЬНЫЙ МАТЕРИАЛ
Следующий необязательный материал касается двух новых терминов, называемых «экспериментальная» атомная экономика, и « Процентный выход X Экспериментальная атомная экономика». Эти два термина дополнительно объясняют эффективность реакции, однако этот материал можно опустить.
 Чтобы пропустить необязательный материал и вернуться к обсуждению атомной экономики и других экологических соображений, нажмите здесь.
Чтобы пропустить необязательный материал и вернуться к обсуждению атомной экономики и других экологических соображений, нажмите здесь.В действительности, если реакцию проводить в количествах, указанных в таблице 1, экономия атомов будет еще меньше. Это является результатом того факта, что в Таблице 3 предполагалось, что стехиометрические количества каждого реагента (1:1:1), как указано в уравнении 1b, будут израсходованы в этой реакции. Фактически количества реагентов 1, 2 и 3, которые использовались в реальной реакции, как показано в таблице 1, составляют 0,0108:0,0129:0,0200 = 1:1,11:1,85. Таблица 4 иллюстрирует введенный нами термин «экспериментальная» атомная экономия, основанный на фактических количествах реагентов, используемых в эксперименте.Таблица 4 аналогична таблице 3 за исключением того, что
Таблица 4 Экспериментальная экономия атома по уравнению 1: на основе фактического
| Формула реагентов | Масса реагента (используется FW X моль) | Используемые атомы | Вес использованных атомов (FW X моль) | Неиспользованные атомов | Масса неиспользованных атомов (FW X моль) |
| 1 C 4 H 9 OH | 74. 0 х 0,0108 = 0,80 0 х 0,0108 = 0,80 | 4C,9H | 57 X 0,0108 = 0,62 | HO | 17 X 0,0108=0,18 |
| 2 NaBr | 103 X 0,0129 = 1,33 | Br | 79,9X 0,0129=1,03 79,9X 0,0108=0,86 превышение 0,17 | Н/Д | 23 X 0,0129=0,30 превышение 0,17 промежуточный итог 0,47 |
| 3 H 2 SO 4 | 98 Х .0200= 2,0 | _____ | 0,00 | 2H, 4O, S | 98,1 х 0,0200=1,96 |
| Итого 4C,12H,5O,BrNaS | 4.13 | 4C,9H,Br | 1,48 | 3H, 5O, Na, S | 2,61 |
учитывается избыток любых используемых реагентов. В этом случае NaBr (реагент 2) используется в избытке (. 0129 моль) по сравнению с 1-бутанолом (0,0108 моль), который является лимитирующим реагентом. Таким образом, в Таблице 4 в четвертом столбце, где рассчитана масса фактически используемых реагентов, видно, что, хотя бром (из NaBr) используется в желаемом продукте, этот элемент находится в избытке и, следовательно, избыток необходимо добавить в неизрасходованную массу реагентов. Термин, который мы придумали и назвали Процент Экспериментальная атомная экономика , теперь можно рассчитать.Процентная экспериментальная экономия атома — это просто ожидаемая масса реагентов, которые используются в желаемом продукте (которая оказывается такой же, как теоретический выход), деленная на фактическую общую массу всех реагентов, использованных в эксперименте. В таблице 4 мы видим в столбце 4, строке 4, что используемая масса составляет 1,48 г, а общая масса реагентов составляет 4,13 г (строка 4, столбец 2), таким образом, % экспериментальной атомной экономии составляет (1,48/4,13 X 100)36.
0129 моль) по сравнению с 1-бутанолом (0,0108 моль), который является лимитирующим реагентом. Таким образом, в Таблице 4 в четвертом столбце, где рассчитана масса фактически используемых реагентов, видно, что, хотя бром (из NaBr) используется в желаемом продукте, этот элемент находится в избытке и, следовательно, избыток необходимо добавить в неизрасходованную массу реагентов. Термин, который мы придумали и назвали Процент Экспериментальная атомная экономика , теперь можно рассчитать.Процентная экспериментальная экономия атома — это просто ожидаемая масса реагентов, которые используются в желаемом продукте (которая оказывается такой же, как теоретический выход), деленная на фактическую общую массу всех реагентов, использованных в эксперименте. В таблице 4 мы видим в столбце 4, строке 4, что используемая масса составляет 1,48 г, а общая масса реагентов составляет 4,13 г (строка 4, столбец 2), таким образом, % экспериментальной атомной экономии составляет (1,48/4,13 X 100)36. %. Это конечно не что иное, как тот же расчет, что и был
%. Это конечно не что иное, как тот же расчет, что и был
% Экспериментальная экономная экономика = (масса реагентов, используемых в желаемом продукте / общую массу всех реагентов) x 100
= (теоретический выход / общая масса всех реагентов) x 100
= (1.48 г/4,13 г) х 100 = 36%
выполняется в начале обсуждения атомной экономии, и это представляет собой максимальный % массы реагентов, которые могут быть включены в желаемый продукт. Хотя тот же вывод был получен до обсуждения концепции экономии атомов, полезно составить таблицу, подобную Таблице 4, чтобы можно было увидеть, какие реагенты приводят к плохой экономии атомов.
Вместо того, чтобы рассматривать процентный выход и (экспериментальную) атомную экономию по отдельности, еще лучшим показателем эффективности реакции является рассмотрение их комбинации.Чтобы проиллюстрировать это, мы ввели термин Процентная доходность X Экспериментальная атомная экономика (%PE . EAE) . Это рассчитывается следующим образом:
EAE) . Это рассчитывается следующим образом:
% Выход X Экспериментальная атомная экономика = (фактический выход / теоретический выход) X (масса реагентов, используемых в желаемом
продукте / общей массы всех реагентов) x 100
% PE . EAE = (фактический выход / теоретический выход) X (теоретический выход / общая масса всех реагентов)
x 100
= (фактический выход / общая масса всех реагентов) x 100
= (1,20 г / 4,13 г) X 100
= 29%
Обратите внимание, что в этом расчете теоретический выход отменяется, оставляя отношение фактического выхода к общей массе всех реагентов X 100.Если снова предположить, что фактический выход составляет 1,20 г и разделить его на 4,13 г (общая масса всех реагентов из таблицы 4), то % выхода X экспериментальной атомной экономии составляет всего 29% (ранее мы пришли к такому же выводу в гораздо менее формальным способом; см. первый абзац этого раздела). Это означает, что только 29% от общей массы всех реагентов фактически выделяются в желаемый продукт, а 71% расходуется впустую! Измерение эффективности реакции таким образом открывает для нее совершенно новую перспективу.В то время как многие химики сочли бы выход 81% очень приемлемым, немногие сочли бы удовлетворительным выделение только 29% массы реагентов в желаемом продукте.
первый абзац этого раздела). Это означает, что только 29% от общей массы всех реагентов фактически выделяются в желаемый продукт, а 71% расходуется впустую! Измерение эффективности реакции таким образом открывает для нее совершенно новую перспективу.В то время как многие химики сочли бы выход 81% очень приемлемым, немногие сочли бы удовлетворительным выделение только 29% массы реагентов в желаемом продукте.
На этом дополнительный материал заканчивается
Другие экологические аспекты
Хотя учет как атомной экономии, так и % выхода дает гораздо более точную оценку эффективности реакции и ее приемлемости для окружающей среды, необходимо учитывать и другие факторы.Чтобы вызвать обсуждение приемлемости реакции для окружающей среды, целесообразно изучить некоторые из Двенадцати принципов зеленой химии (см. Ниже). Принципы номер 1 и 2 напрямую связаны с атомной экономикой и доходностью.
ДВЕНАДЦАТЬ ПРИНЦИПОВ ЗЕЛЕНОЙ ХИМИИ 4
1. Лучше предотвратить образование отходов, чем перерабатывать или убирать отходы после
Лучше предотвратить образование отходов, чем перерабатывать или убирать отходы после
образования.
2. Синтетические методы должны быть разработаны таким образом, чтобы обеспечить максимальное включение
всех материалов, используемых в процессе, в конечный продукт.
3. Везде, где это практически возможно, синтетические методологии должны быть разработаны для
использования и производства веществ, малотоксичных или совсем нетоксичных для
здоровья человека и окружающей среды.
4. Химические продукты должны быть разработаны таким образом, чтобы сохранить эффективность функции
при одновременном снижении токсичности.
5. Использование вспомогательных веществ (например, растворителей, разделителей и т. д.)
должно быть по возможности ненужным и безвредным при
.
6. Энергетические потребности должны признаваться в связи с их экологическими и
экономическими последствиями и должны быть сведены к минимуму. Синтетические методы
Синтетические методы
должны проводиться при температуре и давлении окружающей среды.
7. Сырье должно быть возобновляемым, а не истощаться
всякий раз, когда это технически и экономически целесообразно.
8. По возможности следует избегать ненужной дериватизации (блокирующая группа, защита/снятие защиты,
9. Каталитические реагенты (как можно более селективные) превосходят
стехиометрические реагенты.
10. Химические продукты должны быть разработаны таким образом, чтобы по окончании их
они не сохранялись в окружающей среде и не распадались на
безвредные продукты разложения.
11. Необходимо дальнейшее развитие аналитических методологий, чтобы обеспечить
мониторинг и контроль в режиме реального времени до образования
опасных веществ.
12. Вещества и форма вещества, используемые в химическом процессе
должны выбираться таким образом, чтобы свести к минимуму вероятность химических аварий,
, включая выбросы, взрывы и пожары.
Принципы 3 и 4 касаются токсичности всех веществ, используемых в реакции, включая реагенты и продукты. Из уравнения 1 становится ясно, что два атома водорода и один кислород, которые идут на образование воды, тратятся впустую. Однако если в результате реакции образуются отходы, то вода настолько безвредна для окружающей среды (нетоксична и не представляет проблем с утилизацией, если она чистая), насколько это можно себе представить.Однако все продукты и реагенты должны быть оценены на предмет их токсичности. Прекрасные примеры образования менее токсичных продуктов с такой же эффективностью можно увидеть в новых пестицидах, разработанных Ромом и Хаасом для борьбы с насекомыми и организмами, вызывающими морское обрастание. Каждый из этих новых образцов пестицидов получил награду Президентского конкурса «Зеленая химия».
Принцип № 5 требует рассмотрения вспомогательных веществ (растворителей, разделительных агентов, осушителей и т. д.).), которые используются в реакциях и синтезах. Хотя в качестве растворителя используется вода (окружающая среда плюс 5 ), в типичной экспериментальной процедуре 1 для выполнения уравнения 1 обработка продукта (1-бромбутана) после перегонки требует 1 мл концентрированной серной кислоты, 1 мл 3М гидроксида натрия, безводного хлорида кальция, 1 мл этанола, 1 мл ацетона и 2 мл п-ксилола, чтобы выделить всего 1-1,2 г 1-бромбутана! Таким образом, ясно, что отходы, образующиеся из этих вспомогательных веществ, значительны и превышают количество отходов (по крайней мере, с точки зрения массы), которые образуются непосредственно в результате реакции.Во многих органических реакциях используются большие количества органических растворителей, которые часто являются токсичными. Эти растворители часто попадают в воду, почву и воздух, что приводит к значительному загрязнению окружающей среды. Предпринимаются попытки заменить органические растворители водой, углекислым газом и ионными жидкостями при комнатной температуре.
Хотя в качестве растворителя используется вода (окружающая среда плюс 5 ), в типичной экспериментальной процедуре 1 для выполнения уравнения 1 обработка продукта (1-бромбутана) после перегонки требует 1 мл концентрированной серной кислоты, 1 мл 3М гидроксида натрия, безводного хлорида кальция, 1 мл этанола, 1 мл ацетона и 2 мл п-ксилола, чтобы выделить всего 1-1,2 г 1-бромбутана! Таким образом, ясно, что отходы, образующиеся из этих вспомогательных веществ, значительны и превышают количество отходов (по крайней мере, с точки зрения массы), которые образуются непосредственно в результате реакции.Во многих органических реакциях используются большие количества органических растворителей, которые часто являются токсичными. Эти растворители часто попадают в воду, почву и воздух, что приводит к значительному загрязнению окружающей среды. Предпринимаются попытки заменить органические растворители водой, углекислым газом и ионными жидкостями при комнатной температуре. На самом деле Джозеф Дезимоун из Университета Северной Каролины был удостоен президентской награды Green Chemistry Challenge за свою работу по разработке поверхностно-активных веществ для жидкого и сверхкритического диоксида углерода .В результате усилий доктора Дезимоуна был разработан процесс химической чистки одежды с использованием жидкой двуокиси углерода. Этот процесс перерабатывает двуокись углерода, полученную в качестве отходов в результате других химических процессов, и позволяет заменить перхлорэтилен, вред которого для здоровья вызывает сомнения.
На самом деле Джозеф Дезимоун из Университета Северной Каролины был удостоен президентской награды Green Chemistry Challenge за свою работу по разработке поверхностно-активных веществ для жидкого и сверхкритического диоксида углерода .В результате усилий доктора Дезимоуна был разработан процесс химической чистки одежды с использованием жидкой двуокиси углерода. Этот процесс перерабатывает двуокись углерода, полученную в качестве отходов в результате других химических процессов, и позволяет заменить перхлорэтилен, вред которого для здоровья вызывает сомнения.
Принцип № 6 учитывает энергетические потребности реакции. Предпочтительно проводить реакции при температуре и давлении окружающей среды, однако многие химические реакции требуют нагревания и/или охлаждения и давления, отличного от давления окружающей среды.Это требует использования некоторого источника энергии, и чаще всего этот источник энергии представляет собой ископаемое топливо. Чтобы провести реакцию и выделить 1-бромбутан, образовавшийся в уравнении 1, требуется кипячение с обратным холодильником и две перегонки.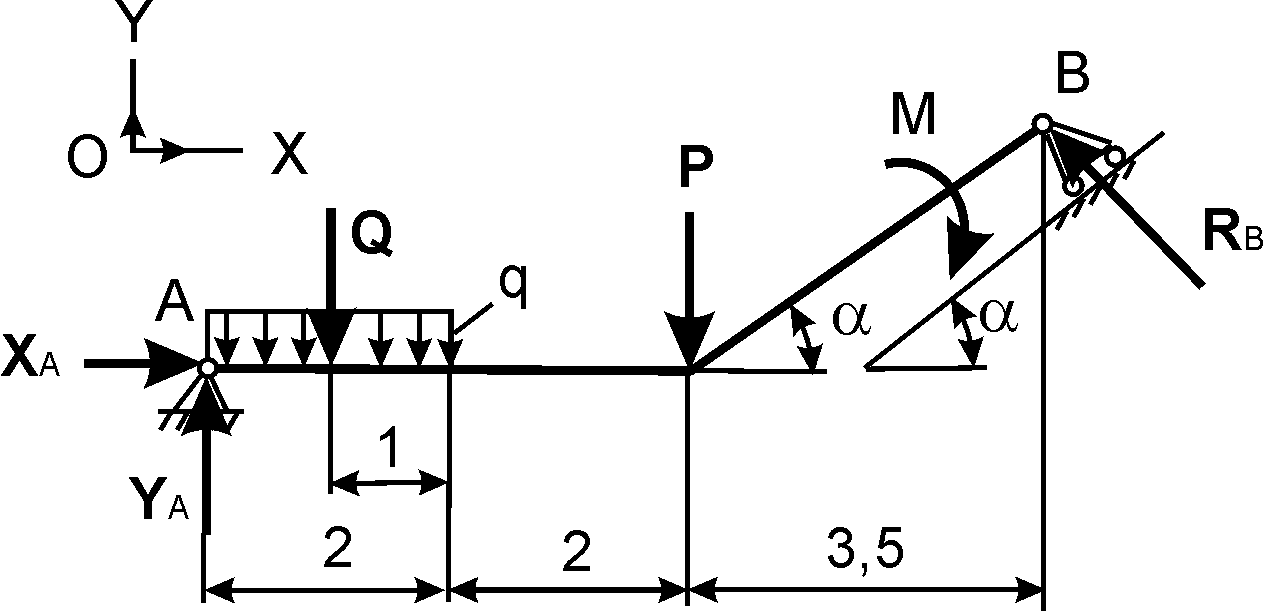 Таким образом, энергетические потребности этой реакции значительны.
Таким образом, энергетические потребности этой реакции значительны.
Большинство органических исходных материалов, таких как 1-бутанол в уравнении 1, в конечном итоге получают из сырой нефти, невозобновляемого (истощающегося) ресурса. Принцип № 7 побуждает нас задуматься о том, можно ли получить эти исходные материалы из возобновляемых ресурсов.Возобновляемые ресурсы обычно означают биологические и растительные материалы (биомасса). Углекислый газ и метан также обычно считаются возобновляемыми, поскольку их можно получать как естественными, так и синтетическими методами. Работа Дратса и Фроста из штата Мичиган, Марка Хольцэппла из Texas A&M и корпорации Biofine по созданию химического сырья из биомассы была отмечена наградой Президентского конкурса «Зеленая химия».
Некоторые могут ошибочно назвать реакцию, описанную в уравнении 1, реакцией, катализируемой кислотой, хотя на самом деле это реакция, активируемая кислотой.Это связано с тем, что серная кислота в этой реакции требуется в стехиометрическом, а не каталитическом количестве. Как показывает принцип №9, реагенты, используемые в каталитических количествах, предпочтительнее реагентов, используемых в стехиометрических количествах. Так как на потерю каждой молекулы воды в этой реакции требуется один моль серной кислоты, то будет достаточно только стехиометрических количеств этого реагента. Однако, даже если используются стехиометрические количества, восстановление/рециркуляция/повторное использование нежелательных продуктов должно иметь место всякий раз, когда это возможно.В последнее время были достигнуты значительные успехи в развитии реакций, которым способствуют нетоксичные и восстанавливаемые катализаторы. Биокаталитический процесс, открытый и разработанный Lilly Research Laboratories для производства потенциального противосудорожного препарата, получил награду Presidential Green Chemistry Challenge.
Как показывает принцип №9, реагенты, используемые в каталитических количествах, предпочтительнее реагентов, используемых в стехиометрических количествах. Так как на потерю каждой молекулы воды в этой реакции требуется один моль серной кислоты, то будет достаточно только стехиометрических количеств этого реагента. Однако, даже если используются стехиометрические количества, восстановление/рециркуляция/повторное использование нежелательных продуктов должно иметь место всякий раз, когда это возможно.В последнее время были достигнуты значительные успехи в развитии реакций, которым способствуют нетоксичные и восстанавливаемые катализаторы. Биокаталитический процесс, открытый и разработанный Lilly Research Laboratories для производства потенциального противосудорожного препарата, получил награду Presidential Green Chemistry Challenge.
Во всех оставшихся дискуссиях об эффективности реакции обсуждение будет ограничено атомной экономией, основанной на стехиометрии реакции. Когда кто-то сталкивается с этими реакциями в лаборатории, также может быть разумным рассчитать экономию атома на основе количества используемых реагентов (экспериментальная экономия атома).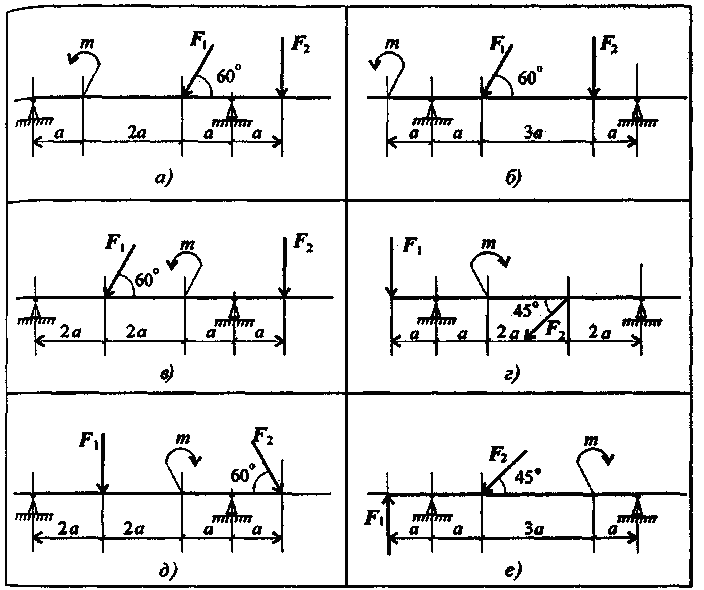 Кроме того, можно также рассмотреть такие вопросы, как токсичность, потребление энергии, использование вспомогательных веществ, каталитические и стехиометрические реагенты, а также возобновляемое и невозобновляемое сырье.
Кроме того, можно также рассмотреть такие вопросы, как токсичность, потребление энергии, использование вспомогательных веществ, каталитические и стехиометрические реагенты, а также возобновляемое и невозобновляемое сырье.
В приведенной выше реакции замещения (уравнение 1а) было обнаружено, что плохая экономия атомов является результатом того факта, что замещаемые атомы уходящей группы (ОН), противоиона (натрия) нашего нуклеофила (бромида) и вся серная кислота, необходимая для этой реакции, тратится впустую на образование нежелательных продуктов в этой реакции.В силу того факта, что реакции отщепления требуют только потери атомов (не приобретая их) из реагента, это означает, что реакции отщепления в целом даже хуже с точки зрения экономии атомов, чем реакции замещения.
В качестве примера рассмотрим атомы следующей реакции отщепления. Промотированное основанием дегидрогалогенирование алкилгалогенидов является распространенным методом получения алкенов из алкилгалогенидов путем отщепления.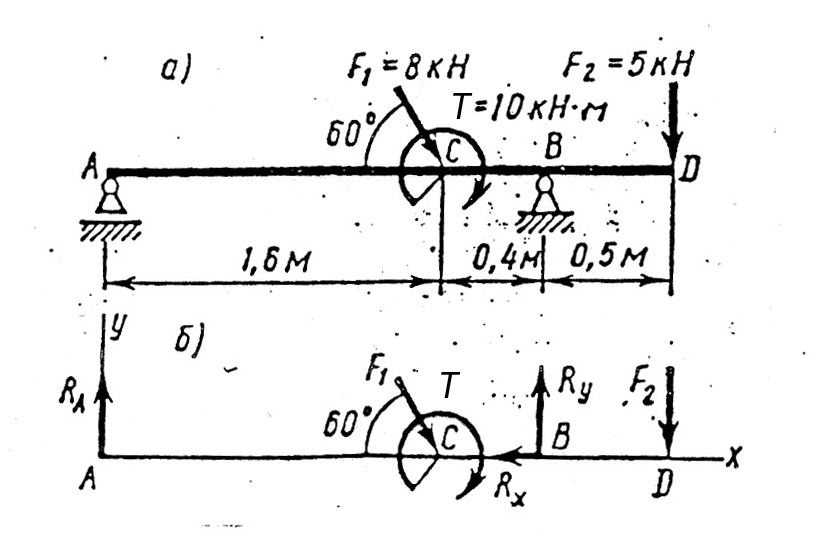 В уравнении 2 образование метилпропена осуществляется реакцией 2-бром-2-метилпропана (7) с этоксидом натрия (8).В этой реакции атомы реагентов, входящие в состав целевого продукта (9), и атомы целевого продукта обозначены зеленым цветом, а неиспользованные атомы реагентов показаны коричневым цветом, как и атомы в нежелательных продуктах. реакции. Таблица 5 иллюстрирует экономию атомов в этой реакции, и расчет % экономии атомов дает очень плохие 27%. Бедный атом
В уравнении 2 образование метилпропена осуществляется реакцией 2-бром-2-метилпропана (7) с этоксидом натрия (8).В этой реакции атомы реагентов, входящие в состав целевого продукта (9), и атомы целевого продукта обозначены зеленым цветом, а неиспользованные атомы реагентов показаны коричневым цветом, как и атомы в нежелательных продуктах. реакции. Таблица 5 иллюстрирует экономию атомов в этой реакции, и расчет % экономии атомов дает очень плохие 27%. Бедный атом
Уравнение 2
Таблица 5 Уравнение атомной экономики 2
| Формула реагентов | Реагенты FW | Используемые атомы | Масса Использованных атомов | Неиспользованные атомов | Масса неиспользованных атомов |
| 7 C 4 H 9 Br | 137 | 4C,8H | 56 | HBr | 81 |
| 8 C 2 H 5 ONa | 68 | ____ | 0 | 2C, 5H, O, Na | 68 |
| Итого 6C,14H,O,Br,Na | 205 | 4C,8H | 56 | 2C,6H,O,Br,Na | 149 |
% Атомная экономия = (FW использованных атомов/FW всех реагентов) X 100
Экономия
является результатом не только потери HBr, но и того, что это реакция, активируемая основанием, и все атомы основания этоксида натрия находятся в нежелательных побочных продуктах.
Поскольку реакции присоединения обычно приводят к включению всех атомов реагентов в конечные желаемые продукты, реакции присоединения приводят к высокой экономии атомов. Таким образом, с точки зрения атомной экономии реакции присоединения являются экологически более предпочтительными, чем реакции отщепления и замещения. В качестве примера рассмотрим следующее присоединение бромистого водорода к метилпропену. В этом примере все атомы реагентов (9 и 11) показаны зеленым цветом, поскольку все эти атомы используются в конечном желаемом продукте (7).Таблица экономии атомов (таблица 6) и расчет 100% экономии атомов еще больше подчеркивают превосходную экономию атомов этой реакции.
Уравнение 3
Таблица 6 Уравнение 3 атомной экономики
| Формула реагентов | Реагенты FW | Используемые атомы | Масса Использованных атомов | Неиспользованные атомов | Масса неиспользованных атомов |
| 9 С 4 Н 8 | 56 | 4C,8H | 56 | ____ | 0 |
| 11 HBr | 81 | HBr | 81 | ____ | 0 |
| Итого 4C,9H,Br | 137 | 4C,9H,Br | 137 | ____ | 0 |
% атомной экономии = (FW использованных атомов/FW всех реагентов) X 100
Реакции перегруппировки включают реорганизацию атомов молекулы.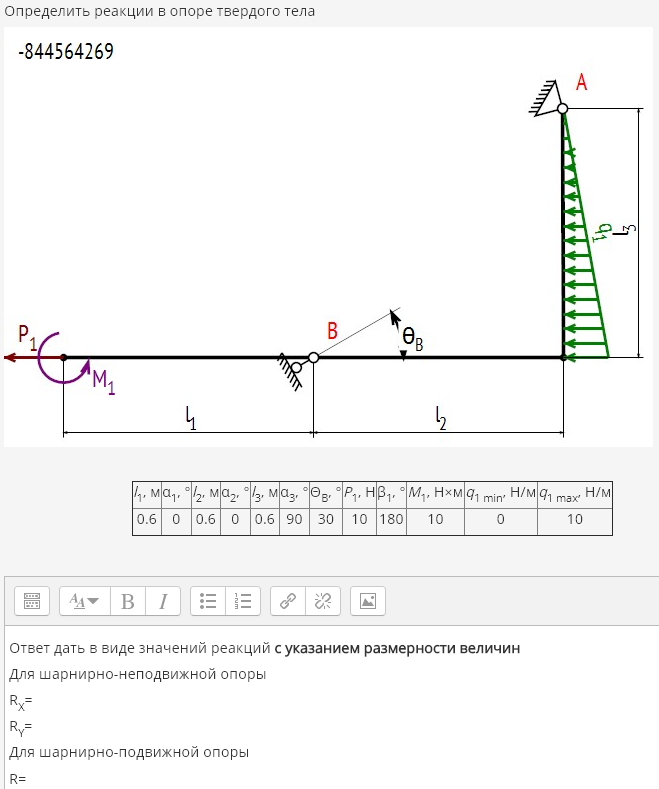 Поскольку в молекуле, подвергающейся перегруппировке, не происходит ни отщепления, ни добавления, ни замещения атомов, экономия атомов в реакциях перегруппировки составляет 100 %, и с точки зрения экономии атомов эти реакции являются предпочтительными для окружающей среды. Чтобы проиллюстрировать это, рассмотрим катализируемую кислотой перегруппировку 3,3-диметил-1-бутена (12) в 2,3-диметил-2-бутен (13). В этом случае все атомы реагента 12 показаны зеленым цветом, поскольку все они включены в желаемый продукт 13.Как и в предыдущих примерах, можно настроить таблицу атомной экономики и рассчитать % атомной экономики. Хотя кислота (H + ), используемая в этой реакции, не включается в желаемый продукт, она используется только в каталитических количествах и поэтому обозначена черным цветом (не зеленым или коричневым) и не учитывается в таблице экономии атомов или расчет атомной экономики. Как было предсказано выше для перегруппировок, % атомной экономии этой реакции составляет 100%.
Поскольку в молекуле, подвергающейся перегруппировке, не происходит ни отщепления, ни добавления, ни замещения атомов, экономия атомов в реакциях перегруппировки составляет 100 %, и с точки зрения экономии атомов эти реакции являются предпочтительными для окружающей среды. Чтобы проиллюстрировать это, рассмотрим катализируемую кислотой перегруппировку 3,3-диметил-1-бутена (12) в 2,3-диметил-2-бутен (13). В этом случае все атомы реагента 12 показаны зеленым цветом, поскольку все они включены в желаемый продукт 13.Как и в предыдущих примерах, можно настроить таблицу атомной экономики и рассчитать % атомной экономики. Хотя кислота (H + ), используемая в этой реакции, не включается в желаемый продукт, она используется только в каталитических количествах и поэтому обозначена черным цветом (не зеленым или коричневым) и не учитывается в таблице экономии атомов или расчет атомной экономики. Как было предсказано выше для перегруппировок, % атомной экономии этой реакции составляет 100%.
Уравнение 4
Таблица 7 Уравнение 4 атомной экономики
| Формула реагентов | Реагенты FW | Используемые атомы | Масса Использованных атомов | Неиспользованные атомов | Масса неиспользованных атомов |
| 12 С 6 Н 12 | 84 | 6C, 12H | 84 | ____ | 0 |
| Всего 6C,12H | 84 | 6C,12H | 84 | ____ | 0 |
% Атомная экономия = (FW использованных атомов/FW всех реагентов) X 100
Практически все органические реакции подпадают под категории реакций замещения, присоединения, отщепления или перегруппировки. С точки зрения экономии атомов реакции присоединения и перегруппировки являются экологически предпочтительными, за ними следуют реакции замещения, а реакции отщепления являются наименее предпочтительными с экологической точки зрения. Поскольку при изучении химии встречаются реакции, следует рассматривать каждую реакцию не только с точки зрения выхода, но и с точки зрения атомной экономии реакции.
С точки зрения экономии атомов реакции присоединения и перегруппировки являются экологически предпочтительными, за ними следуют реакции замещения, а реакции отщепления являются наименее предпочтительными с экологической точки зрения. Поскольку при изучении химии встречаются реакции, следует рассматривать каждую реакцию не только с точки зрения выхода, но и с точки зрения атомной экономии реакции.
Концепция атомной экономики также применима к синтезу. Чтобы определить атомную экономию синтеза, нужно просто определить, какие из атомов реагентов для всех стадий синтеза включаются в желаемый конечный продукт.
Чтобы проиллюстрировать концепцию экономии атомов в синтезе, рассмотрим промышленный синтез этиленоксида (19). Оксид этилена является исходным сырьем для синтеза этиленгликоля (используемого в антифризах), этоксилатов (поверхностно-активных веществ), а также эфиров и полимеров гликоля (таких как ПЭТФ). Ежегодно в мире производится около 8 800 миллионов фунтов этого соединения. Классический синтез (схема 1) этиленоксида (19) представляет собой двухстадийный синтез и известен как хлоргидриновый путь.Атомы реагентов, которые включаются в конечный желаемый продукт (19), и атомы желаемого продукта равны
Классический синтез (схема 1) этиленоксида (19) представляет собой двухстадийный синтез и известен как хлоргидриновый путь.Атомы реагентов, которые включаются в конечный желаемый продукт (19), и атомы желаемого продукта равны
Схема 1 Хлоргидриновый путь к этиленоксиду
зеленый, а те атомы показаны зеленым, а атомы реагентов, которые попадают в нежелательные продукты (вместе с атомами нежелательных продуктов), показаны коричневым. Таблица 8 представляет собой таблицу атомной экономии для хлоргидринового пути к этиленоксиду и позволяет рассчитать бедную атомную экономию (23%) этого пути.
Таблица 8 Атомная экономия Схемы 1, Путь хлоргидрина к оксиду этилена
| Формула реагентов | Реагенты FW | Используемые атомы | Масса Использованных атомов | Неиспользованные атомов | Масса неиспользованных атомов |
| 14 С 2 Н 4 | 28 | 2C, 4H | 28 | _____ | 0 |
| 15 Класс 2 | 71 | _____ | 0 | 2Cl | 71 |
| 6 В 2 О | 18 | О | 16 | 2H | 2 |
| 18 Са(ОН) 2 | 72 | _____ | 0 | Ca,4H,2O | 72 |
| Итого 2C,8H,3O,Ca,2Cl | 189 | 2C, 4H, O | 44 | 6H,2O,Ca,2Cl | 145 |
% атомной экономии = (FW использованных атомов/FW всех реагентов) X 100
= (44/189) X 100 = 200 = 2.
Разработан каталитический путь (схема 2) получения этиленоксида из этилена.В этом одностадийном синтезе единственным другим реагентом, помимо этилена, который используется, является 1/2 моля кислорода. Как видно из схемы 2 и таблицы 9, все атомы реагентов включаются в желаемый конечный продукт, и, таким образом, этот синтез имеет 100% экономию атомов. Экономия атомов 100 % для этой реакции неудивительна, поскольку это реакция присоединения, а, как было драгоценно указано, реакции присоединения имеют экономию атомов 100%.
Схема 2 Каталитический путь к оксиду этилена
Таблица 9 Атомная экономика схемы 2, каталитический путь к этиленоксиду
| Формула реагентов | Реагенты FW | Используемые атомы | Масса Использованных атомов | Неиспользованные атомов | Масса неиспользованных атомов |
| 14 С 2 Н 4 | 28 | 2C, 4H | 28 | _____ | 0 |
| 21 1/2 O 2 | 16 | О | 16 | _____ | 0 |
| Всего 2C,4H,1Ol | 44 | 2С, 4Н, О | 44 | _____ | 0 |
% Экономия атомов = (FW использованных атомов/FW всех реагентов) X 100
The Boots Company Синтез ибупрофена
Ибупрофен является активным ингредиентом ряда фирменных продуктов, включая Advil, Motrin и Nuprin. Ибупрофен действует как анальгетик (обезболивающее), а также эффективен как нестероидный противовоспалительный препарат (НПВП). НПВП уменьшают воспаление при таких состояниях, как артрит, остеоартрит и ревматизм. Ибупрофен упоминается как нестероидный противовоспалительный препарат, поскольку ибупрофен не является членом семейства стероидных соединений.
Ибупрофен действует как анальгетик (обезболивающее), а также эффективен как нестероидный противовоспалительный препарат (НПВП). НПВП уменьшают воспаление при таких состояниях, как артрит, остеоартрит и ревматизм. Ибупрофен упоминается как нестероидный противовоспалительный препарат, поскольку ибупрофен не является членом семейства стероидных соединений.
Мировое производство ибупрофена превышает 30 миллионов фунтов в год. Компания Boots Company PLC из Ноттингема, Англия, впервые запатентовала синтез ибупрофена в 1960-х годах (U.S. патент 3,385,886), и это служило основным методом синтеза в течение многих лет. Синтез ибупрофена в Boot представляет собой шестиэтапный синтез и показан на схеме 3. Как обычно, все
Схема 3. Сапоги Синтез ибупрофена
атома каждого реагента, которые включаются в конечный желаемый продукт (ибупрофен), показаны зеленым цветом, а те, которые попадают в нежелательные продукты, показаны коричневым цветом. Таблица 10 иллюстрирует атомную экономию синтеза Boots Company и позволяет рассчитать процентную атомную экономию, равную 40%. Как было указано выше, ежегодно производится около 30 миллионов фунтов ибупрофена. Если бы все мировые запасы ибупрофена производились по технологии Boots, то это привело бы к образованию около 35 миллионов фунтов отходов!
Как было указано выше, ежегодно производится около 30 миллионов фунтов ибупрофена. Если бы все мировые запасы ибупрофена производились по технологии Boots, то это привело бы к образованию около 35 миллионов фунтов отходов!
Таблица 10 Атомная экономика схемы 3, синтез ибупрофена компанией Boots
| Формула реагентов | Реагенты FW | Используемые атомы | Масса Использованных атомов | Неиспользованные атомов | Масса неиспользованных атомов |
| 1 С 10 Н 14 | 134 | 10C, 13H | 133 | Н | 1 |
| 2 C 4 H 6 O 3 | 102 | 2C,3H | 27 | 2C,3H,3O | 75 |
| 4 C 4 H 7 ClO 2 | 122.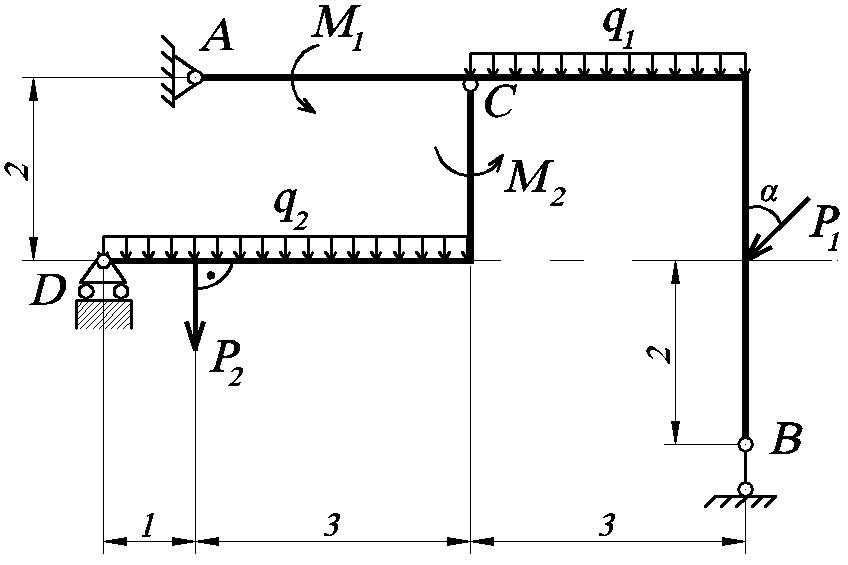 5 5 | C,H | 13 | 3C,6H,Cl,2O | 109,5 |
| 5 C 2 H 5 ONa | 68 | _____ | 0 | 2C, 5H, O, Na | 68 |
| 7 Н 3 О | 19 | _____ | 0 | 3H,O | 19 |
| 9 NH 3 О | 33 | _____ | 0 | 3H,N,O | 33 |
| 12 В 4 О 2 | 36 | H, 2O | 33 | 3H | 3 |
| Итого 20C,42H,N,10O, Cl,Na | 514.5 | Ибупрофен 13C,18H,2O | Ибупрофен 206 | Отходы 7C,24H,N,8O, Cl,Na | Отходы 308,5 |
% Атомная экономия = (FW использованных атомов/FW всех реагентов) X 100
В восьмидесятых годах ибупрофен был одобрен для безрецептурного отпуска, и срок действия патента компании Boots истек. Осознавая финансовые возможности, которые может предложить производство и продажа этого препарата, несколько компаний приступили к созданию предприятий и разработке новых методов приготовления ибупрофена. Корпорация Hoechst Celanese (Сомервилль, Нью-Джерси; теперь известная как Celanese Corporation) открыла новый трехэтапный синтез ибупрофена. Вместе с Boots Company они сформировали компанию BHC для производства (с помощью нового синтеза) и продажи ибупрофена. Синтез компании BHC показан на схеме 4, где использованные атомы показаны зеленым цветом, а неиспользованные атомы — коричневым.Атомная экономия дополнительно проиллюстрирована в таблице 11, и расчет % атомной экономии дает 77%, что является значительным улучшением по сравнению с 40% для
Осознавая финансовые возможности, которые может предложить производство и продажа этого препарата, несколько компаний приступили к созданию предприятий и разработке новых методов приготовления ибупрофена. Корпорация Hoechst Celanese (Сомервилль, Нью-Джерси; теперь известная как Celanese Corporation) открыла новый трехэтапный синтез ибупрофена. Вместе с Boots Company они сформировали компанию BHC для производства (с помощью нового синтеза) и продажи ибупрофена. Синтез компании BHC показан на схеме 4, где использованные атомы показаны зеленым цветом, а неиспользованные атомы — коричневым.Атомная экономия дополнительно проиллюстрирована в таблице 11, и расчет % атомной экономии дает 77%, что является значительным улучшением по сравнению с 40% для
Схема 4 Компания BHC Синтез ибупрофена
Таблица 11 Атомная экономия схемы 4, синтез ибупрофена компании BHC
| Формула реагентов | Реагенты FW | Используемые атомы | Масса Использованных атомов | Неиспользованные атомов | Масса неиспользованных атомов |
| 1 С 10 Н 14 | 134 | 10C, 13H | 133 | Н | 1 |
| 2 C 4 H 6 O 3 | 102 | 2C,3H,O | 43 | 2C,3H,2O | 59 |
| 4 Н 2 | 2 | 2H | 2 | _____ | 0 |
| 6 CO | 28 | CO | 28 | _____ | 0 |
| Итого 15C, 22H, 4O | 266 | Ибупрофен 13C,18H,2O | 206 | Отходы 2C, 3H, 2O | 60 |
% Атомная экономия = (FW использованных атомов/FW всех реагентов) X 100
Процесс компании Boots.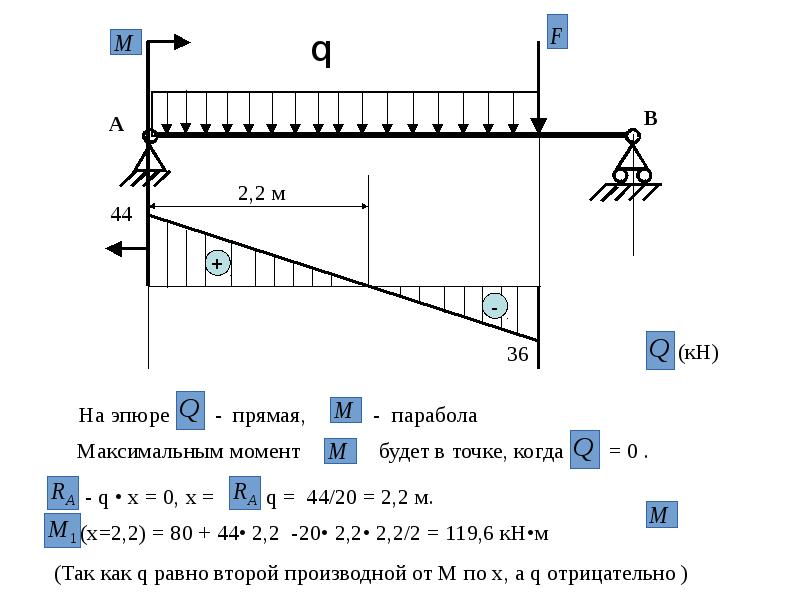 Атомная экономия процесса компании BHC подскакивает до >99%, если учесть, что уксусная кислота, полученная на этапе 1, извлекается и используется.
Атомная экономия процесса компании BHC подскакивает до >99%, если учесть, что уксусная кислота, полученная на этапе 1, извлекается и используется.
Процесс компании BHC предлагает не только значительное улучшение атомной экономики, но и другие экологические преимущества. К ним относятся трехстадийный каталитический процесс по сравнению с шестистадийным процессом Boots Company, для которого требуются вспомогательные реагенты в стехиометрических количествах. Например, на первой стадии каждого процесса получается один и тот же продукт (3) из одних и тех же реагентов (1 и 2).Однако в процессе компании Boots используется трихлорид алюминия в стехиометрических количествах (не учтено в таблице 10), в то время как в процессе компании BHC используется HF в каталитических количествах, который повторно извлекается и повторно используется. Трихлорид алюминия производит большое количество гидрата трихлорида алюминия в качестве отходов, которые обычно вывозятся на свалку. Никелевые и палладиевые катализаторы, используемые на этапах 2 и 3 процесса компании BHC, также извлекаются и используются повторно.
Поскольку процесс компании BHC состоит всего из трех шагов (по сравнению сшесть шагов для процесса Boots Company), и он имеет значительно улучшенную экономию атома, он не только приводит к резкому сокращению производимых отходов, но также обеспечивает большую производительность (больше ибупрофена за меньшее время и с меньшим количеством оборудования). Эти факторы превращаются в экономические выгоды для компании в результате того факта, что требуется меньше денег для обработки образующихся отходов и меньше капиталовложений требуется для производства того же количества ибупрофена. Таким образом, в результате более экологичного процесса не только выигрывает окружающая среда, но и укрепляется прибыль компании, а хорошие отношения с общественностью могут быть получены.
За разработку этого синтеза ибупрофена компания BHC получила престижную награду Presidential Green Chemistry Challenge в 1997 году, а также выдающуюся награду Кирпатрика за достижения в области химической инженерии 6 в 1993 году. Награда Кирпатрика присуждается раз в два года организацией Chemical Engineering журнал и отмечает выдающиеся усилия группы в разработке и коммерциализации технологических процессов.
Награда Кирпатрика присуждается раз в два года организацией Chemical Engineering журнал и отмечает выдающиеся усилия группы в разработке и коммерциализации технологических процессов.
Экономия атома и экспериментальная экономия атома выходят за рамки расчета выхода реакции и предлагают второй способ измерения эффективности реакции с учетом использованных и неиспользованных атомов реагентов.Процентная атомная экономия и процентная экспериментальная атомная экономия дают средства для количественной оценки атомной экономии и позволяют количественно сравнивать атомную экономию одной реакции (или синтеза) с другой. Возможно, наилучшей мерой эффективности реакции является учет как атомной экономии, так и выхода путем расчета процентного выхода X экспериментальной атомной экономии (PE . EAE). Конечно, при оценке экологической приемлемости реакции (или синтеза) следует учитывать не только эффективность реакции, но и (как обсуждалось выше) другие факторы, такие как токсичность, использование вспомогательных веществ, потребность в энергии, происхождение исходного сырья и т. д. каталитический против.стехиометрические реагенты.
д. каталитический против.стехиометрические реагенты.
1. Определите следующие термины
a) атомная экономия
b) % атомной экономии
c) % выхода
d) % экспериментальная атомная экономия
c) %PE . ЭАЭ
2. Какие термины в вопросе 1 имеют смысл только в отношении экспериментальных результатов? Какой экспериментальный результат необходим
, чтобы сделать эти термины значимыми?
3. Рассмотрим следующие реакции.
а) Обозначьте каждую реакцию как замещение, удаление, добавление или перестановку.
б) Перепишите каждую реакцию, убедившись, что она уравновешена. Покажите все атомы реагентов, входящие в состав
желаемого продукта, и атомы желаемого продукта зеленым цветом, а все остальные атомы коричневым цветом.
c) Составьте таблицу атомной экономии, аналогичную таблице 3, для каждой реакции.
d) Рассчитайте % атомной экономии каждой реакции.
4. Как указано в ссылке 3, Роджер Шелдон разработал термин, очень похожий на % атомную экономию, который называется % атома
Как указано в ссылке 3, Роджер Шелдон разработал термин, очень похожий на % атомную экономию, который называется % атома
использование.% использования атомов можно рассчитать по следующему уравнению.
% Использование атома = (МВт желаемого продукта/МВт всех продуктов) X 100
а) Сравните и сопоставьте это с % атомной экономикой.
б) С помощью информации, представленной на схемах 3 и 4, можете ли вы рассчитать % использования атомов для этих синтезов? Объясните свой
ответ.
c) Какая концепция, которую вы усвоили на первом курсе химии, делает фактические проценты, рассчитанные для %
использования атомов и % экономии атомов, равными (в большинстве случаев).Докажите это, рассчитав % использования атома для
каждой из реакций в вопросе 3 и сравнив ваши результаты с % атомной экономии, которую вы рассчитали в вопросе 3.
5. Рассмотрим следующий двухстадийный синтез 2-пентина.
а) Перепишите синтез, убедившись, что каждая реакция уравновешена. Покажите все атомы реагентов, которые включены
Покажите все атомы реагентов, которые включены
в желаемый продукт, и атомы желаемого продукта зеленым цветом, а все остальные атомы коричневым цветом.
c) Составьте таблицу экономии атомов для этого синтеза, аналогичную таблице 7.
d) Рассчитайте % экономии атомов этого синтеза.
e) Рассчитайте % использования атомов в этом синтезе.
.
6. Ваш преподаватель направит вас к эксперименту в вашем текущем лабораторном учебнике. Относительно этой лаборатории:
a) Напишите сбалансированное уравнение, показывающее атомы реагентов, входящих в состав желаемого продукта, и атомы
желаемого продукта зеленым цветом, а все остальные атомы коричневым цветом.
б) Постройте таблицу атомной экономии, аналогичную таблице 3.
в) Рассчитайте % атомной экономии.
d) Постройте таблицу экспериментальной экономии атома, аналогичную таблице 4.
e) Рассчитайте экспериментальную экономию атома.
f) Предположим, что эта реакция дает выход 80%. Рассчитайте %PE . ЕАЕ.
Рассчитайте %PE . ЕАЕ.
g) Какова потребность в энергии для этой реакции?
з) Используются ли в этой реакции вспомогательные вещества?
i) Какие реагенты используются в стехиометрических количествах?
j) Какие реагенты используются в каталитических количествах?
7.Поставка механизма для этапа 1 синтеза ибупрофена компанией BHC. Катализируется ли эта стадия кислотой или активируется кислотой?
8. Ниже показан третий синтез ибупрофена, называемый этиловым синтезом.
а) Перепишите синтез, показав все атомы реагентов, входящие в состав желаемого продукта, и атомы
желаемого продукта зеленым цветом, а все остальные атомы коричневым цветом.
c) Составьте таблицу экономии атомов для этого синтеза, аналогичную таблице 7.
d) Рассчитайте % атомной экономии этого синтеза.
.
1. Уильямсон, Кеннет Л., Макро- и микромасштабные органические эксперименты, 2-е изд., DC Heath and Co. , 1994, 247–252.
, 1994, 247–252.
2. Трост, Барри М., Атомная экономика – поиск синтетической эффективности. Наука 1991 , 254 , 1471-1477.
3. Канн, Майкл С.; Коннелли, Марк Э. Реальные случаи в зеленой химии ; ACS, Washington, 2000. Роджер Шелдон из Делфтского университета разработал очень похожую концепцию, называемую % использования атомов.Шелдон, Роджер А. Органический синтез — прошлое, настоящее и будущее. Хим. Ind. (Лондон) , 1992, (декабрь), 903-906.
4. Анастас, Пол Т. и Уорнер, Джон С. Грин. Химическая теория и практика, Oxford University Press, Нью-Йорк, 1998.
5. Предпринимаются значительные усилия по сокращению использования органических соединений в качестве растворителей для реакций. и замена их водой или, что еще лучше, вообще без растворителя.
6. Вестхаймер, Т. Премия достается BHC. Хим.Eng . 1993 , (декабрь), 84-95.
Вернуться к зеленому модулю органической химии на главную
.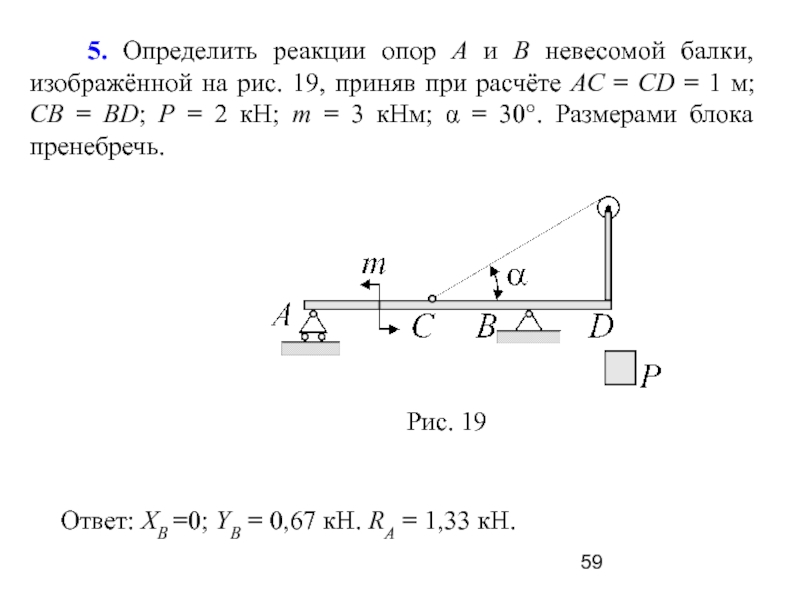
 099
099
 173
173
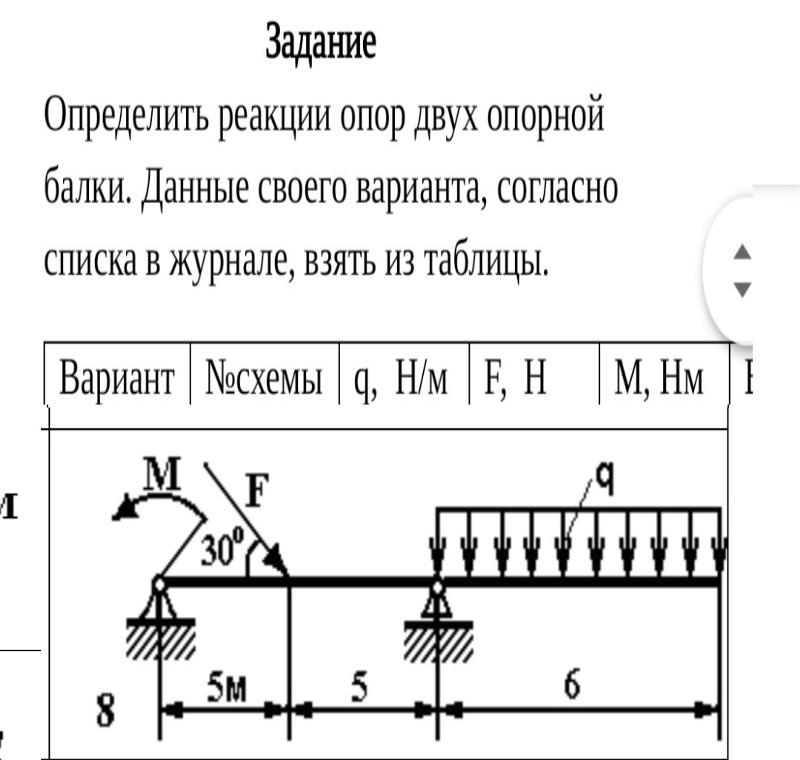 323
323
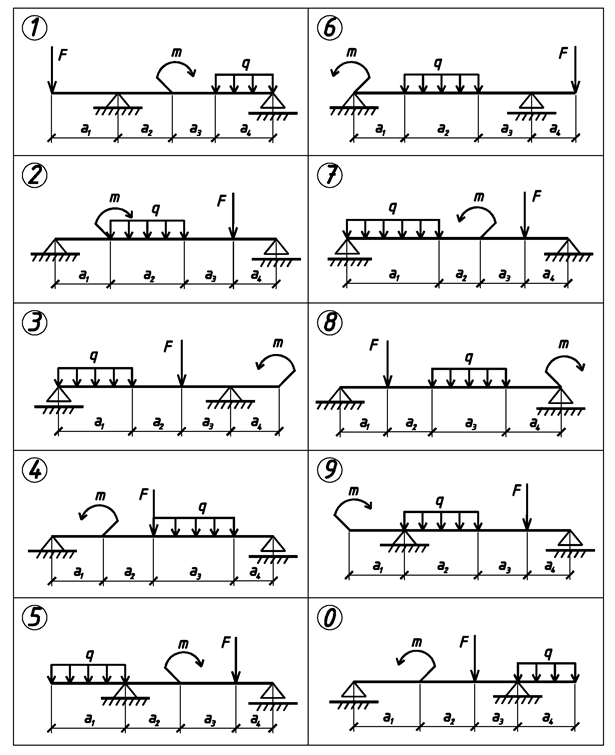 392e-004
392e-004