Сопротивление материалов
Сопротивление материалов
ОглавлениеПРЕДИСЛОВИЕГлава 1. ОСНОВНЫЕ ПОНЯТИЯ § 2.1. РАСЧЕТНАЯ СХЕМА. НАГРУЗКИ § 3.1. ВНУТРЕННИЕ СИЛЫ. МЕТОД СЕЧЕНИЙ § 4.1. НАПРЯЖЕНИЯ § 5.1. ДЕФОРМАЦИИ И ПЕРЕМЕЩЕНИЯ § 6.1. ОСНОВНЫЕ ПРЕДПОСЫЛКИ НАУКИ О СОПРОТИВЛЕНИИ МАТЕРИАЛОВ Вопросы для самопроверки Глава 2. РАСТЯЖЕНИЕ И СЖАТИЕ § 1.  § 2.2. НАПРЯЖЕНИЯ В ПОПЕРЕЧНЫХ И НАКЛОННЫХ СЕЧЕНИЯХ БРУСА § 3.2. ПРОДОЛЬНЫЕ И ПОПЕРЕЧНЫЕ ДЕФОРМАЦИИ § 4.2. ДИАГРАММЫ РАСТЯЖЕНИЯ И СЖАТИЯ § 5.2. ПЕРЕМЕЩЕНИЯ ПОПЕРЕЧНЫХ СЕЧЕНИЙ БРУСЬЕВ § 6.2. РАБОТА СИЛЫ ПРИ ЕЕ СТАТИЧЕСКОМ ДЕЙСТВИИ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ § 7.2. СОБСТВЕННЫЙ ВЕС БРУСА § 8.2. ДОПУСКАЕМЫЕ НАПРЯЖЕНИЯ. РАСЧЕТЫ НА ПРОЧНОСТЬ § 9.2. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ § 10.2. МЕСТНЫЕ НАПРЯЖЕНИЯ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 3. ТЕОРИЯ НАПРЯЖЕННОГО СОСТОЯНИЯ § 1.3. ВИДЫ НАПРЯЖЕННОГО СОСТОЯНИЯ § 2.3. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ § 3.3. ГЛАВНЫЕ НАПРЯЖЕНИЯ. ГЛАВНЫЕ ПЛОЩАДКИ § 4.3. ЭКСТРЕМАЛЬНЫЕ КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ § 5.3. ИССЛЕДОВАНИЕ ПЛОСКОГО НАПРЯЖЕННОГО СОСТОЯНИЯ С ПОМОЩЬЮ КРУГА МОРА § 6.3. ПОНЯТИЕ О ПРОСТРАНСТВЕННОМ НАПРЯЖЕННОМ СОСТОЯНИИ § 7.3. ОБОБЩЕННЫЙ ЗАКОН ГУКА § 8.3. ОБЪЕМНАЯ ДЕФОРМАЦИЯ § 9.3. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 4.  СДВИГ§ 1.4. ЧИСТЫЙ СДВИГ § 2.4. ДЕФОРМАЦИЯ ПРИ СДВИГЕ. ЗАКОН ГУКА ПРИ СДВИГЕ § 3.4. ОБЪЕМНАЯ ДЕФОРМАЦИЯ И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ПРИ ЧИСТОМ СДВИГЕ. ЗАВИСИМОСТЬ МЕЖДУ E, G и «мю» § 4.4. ПРАКТИЧЕСКИЕ РАСЧЕТЫ НЕКОТОРЫХ ПРОСТЕЙШИХ КОНСТРУКЦИЙ, РАБОТАЮЩИХ НА СДВИГ Расчет заклепочных соединений Расчет сварных соединений Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 5. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ § 2.5. СТАТИЧЕСКИЕ МОМЕНТЫ СЕЧЕНИЙ § 3.5. МОМЕНТЫ ИНЕРЦИИ СЕЧЕНИЙ § 4.5. ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ СЕЧЕНИЙ ПРОСТОЙ ФОРМЫ § 5.5. ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ ОСЕЙ § 6.5. ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ § 7.5. ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ. ГЛАВНЫЕ ОСИ ИНЕРЦИИ § 9.5. ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ СЛОЖНЫХ СЕЧЕНИЙ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 6.  КРУЧЕНИЕ§ 1.6. ОСНОВНЫЕ ПОНЯТИЯ. КРУТЯЩИЙ МОМЕНТ § 2.6. КРУЧЕНИЕ ПРЯМОГО БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ § 3.6. ГЛАВНЫЕ НАПРЯЖЕНИЯ И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ КРУЧЕНИИ БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ § 4.6. РАСЧЕТ БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ ПРИ КРУЧЕНИИ § 5.6. РАСЧЕТ ЦИЛИНДРИЧЕСКИХ ВИНТОВЫХ ПРУЖИН § 6.6. КРУЧЕНИЕ ПРЯМОГО БРУСА НЕКРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ § 7.6. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ ПРИ КРУЧЕНИИ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 7. ПРЯМОЙ ИЗГИБ § 1.7. ВНУТРЕННИЕ УСИЛИЯ § 3.7. ОПОРЫ И ОПОРНЫЕ РЕАКЦИИ § 4.7. ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ § 5.7. ДИФФЕРЕНЦИАЛЬНЫЕ ЗАВИСИМОСТИ МЕЖДУ ИЗГИБАЮЩИМ МОМЕНТОМ, ПОПЕРЕЧНОЙ СИЛОЙ И ИНТЕНСИВНОСТЬЮ РАСПРЕДЕЛЕННОЙ НАГРУЗКИ § 6.7. ПРИМЕРЫ ПОСТРОЕНИЯ ЭПЮР ВНУТРЕННИХ УСИЛИЙ § 7.7. ПРЯМОЙ ЧИСТЫЙ ИЗГИБ § 8.7. ПРЯМОЙ ПОПЕРЕЧНЫЙ ИЗГИБ § 9.7. ГЛАВНЫЕ НАПРЯЖЕНИЯ ПРИ ПРЯМОМ ПОПЕРЕЧНОМ ИЗГИБЕ § 10.  7. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ ИЗГИБЕ§ 11.7. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ § 12.7. ПОНЯТИЕ О ЦЕНТРЕ ИЗГИБА § 13.7. ПОНЯТИЕ О РАСЧЕТЕ СОСТАВНЫХ БАЛОК § 14.7. ПОНЯТИЕ О БАЛКАХ РАЗНОРОДНОЙ УПРУГОСТИ § 15.7. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПОСТОЯННОГО СЕЧЕНИЯ МЕТОДОМ НЕПОСРЕДСТВЕННОГО ИНТЕГРИРОВАНИЯ § 16.7. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПОСТОЯННОГО СЕЧЕНИЯ МЕТОДОМ НАЧАЛЬНЫХ ПАРАМЕТРОВ § 17.7. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ В БАЛКАХ ГРАФО-АНАЛИТИЧЕСКИМ МЕТОДОМ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 8. ТЕОРИИ ПРОЧНОСТИ § 1.8. КЛАССИЧЕСКИЕ И ЭНЕРГЕТИЧЕСКАЯ ТЕОРИИ ПРОЧНОСТИ § 2.8. ТЕОРИЯ ПРОЧНОСТИ МОРА § 3.8. ЕДИНАЯ ТЕОРИЯ ПРОЧНОСТИ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 9. СЛОЖНОЕ СОПРОТИВЛЕНИЕ § 1.9. КОСОЙ ИЗГИБ § 2.9. ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ И СЖАТИЕ БРУСЬЕВ БОЛЬШОЙ ЖЕСТКОСТИ § 3.  9. ЯДРО СЕЧЕНИЯ§ 4.9. ИЗГИБ С КРУЧЕНИЕМ БРУСЬЕВ КРУГЛОГО СЕЧЕНИЯ § 5.9. ОБЩИЙ СЛУЧАЙ ДЕЙСТВИЯ СИЛ НА БРУС КРУГЛОГО СЕЧЕНИЯ § 6.9. ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ УСИЛИЙ ДЛЯ ПРОСТРАНСТВЕННЫХ БРУСЬЕВ С ЛОМАНОЙ ОСЬЮ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 10. РАСЧЕТ КРИВЫХ БРУСЬЕВ § 2.10. ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ § 3.10. НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ В ПОПЕРЕЧНЫХ СЕЧЕНИЯХ БРУСА БОЛЬШОЙ КРИВИЗНЫ § 4.10. ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ НЕЙТРАЛЬНОЙ ОСИ ПРИ ЧИСТОМ ИЗГИБЕ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 11. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ В УПРУГИХ СИСТЕМАХ § 1.11. РАБОТА ВНЕШНИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ § 2.11. ТЕОРЕМА О ВЗАИМНОСТИ РАБОТ § 3.11. ТЕОРЕМА О ВЗАИМНОСТИ ПЕРЕМЕЩЕНИЯ 4.11. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ. ИНТЕГРАЛ МОРА § 5.11. ПРАВИЛО ВЕРЕЩАГИНА Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 12. РАСЧЕТ ПРОСТЕЙШИХ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СТЕРЖНЕВЫХ СИСТЕМ § 1.  12. СТАТИЧЕСКАЯ НЕОПРЕДЕЛИМОСТЬ§ 2.12. КАНОНИЧЕСКИЕ УРАВНЕНИЯ МЕТОДА СИЛ § 3.12. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ § 4.12. ИСПОЛЬЗОВАНИЕ СИММЕТРИИ § 5.12. ПОСТРОЕНИЕ ЭПЮР ПОПЕРЕЧНЫХ И ПРОДОЛЬНЫХ СИЛ § 7.12. НЕРАЗРЕЗНЫЕ БАЛКИ ПРИМЕРЫ РАСЧЕТА Вопросы для самопроверки Глава 13. ПРОДОЛЬНЫЙ ИЗГИБ ПРЯМОГО СТЕРЖНЯ § 1.13. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ УПРУГИХ ТЕЛ § 2.13. ПРОДОЛЬНЫЙ ИЗГИБ § 3.13. ПОТЕРЯ УСТОЙЧИВОСТИ ПРИ НАПРЯЖЕНИЯХ, ПРЕВЫШАЮЩИХ ПРЕДЕЛ ПРОПОРЦИОНАЛЬНОСТИ § 4.13. ПРАКТИЧЕСКИЕ РАСЧЕТЫ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ § 5.13. ПРОДОЛЬНО-ПОПЕРЕЧНЫЙ ИЗГИБ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 14. ДИНАМИЧЕСКАЯ НАГРУЗКА § 2.14. ДИНАМИЧЕСКИЕ ЗАДАЧИ, ПРИВОДИМЫЕ К ЗАДАЧАМ СТАТИЧЕСКОГО РАСЧЕТА СИСТЕМ § 3.14. УДАР § 4.14. ЧАСТНЫЕ СЛУЧАИ УДАРНОГО ДЕЙСТВИЯ НАГРУЗКИ § 5.14. КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 15.  НАПРЯЖЕНИЯ, ПЕРЕМЕННЫЕ ВО ВРЕМЕНИ§ 1.15. ПЕРЕМЕННЫЕ НАПРЯЖЕНИЯ. УСТАЛОСТЬ § 2.15. ПРЕДЕЛ ВЫНОСЛИВОСТИ § 3.15. ДИАГРАММЫ ПРЕДЕЛЬНЫХ АМПЛИТУД И ПРЕДЕЛЬНЫХ НАПРЯЖЕНИИ § 4.1. ОСНОВНЫЕ ФАКТОРЫ, ВЛИЯЮЩИЕ НА ВЕЛИЧИНУ ПРЕДЕЛА ВЫНОСЛИВОСТИ § 5.15. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ Примеры расчета Вопросы для самопроверки Глава 16. ТОНКОСТЕННЫЕ ОСЕСИММЕТРИЧНЫЕ ОБОЛОЧКИ И ТОЛСТОСТЕННЫЕ ЦИЛИНДРЫ § 1.16. РАСЧЕТ ТОНКОСТЕННЫХ ОСЕСИММЕТРИЧНЫХ ОБОЛОЧЕК § 2.16. РАСЧЕТ ТОЛСТОСТЕННЫХ ЦИЛИНДРОВ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 17. РАСЧЕТ КОНСТРУКЦИЙ ПО НЕСУЩЕЙ СПОСОБНОСТИ § 2.17. РАСТЯЖЕНИЕ И СЖАТИЕ § 3.17. КРУЧЕНИЕ ПРЯМОГО БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ § 4.17. ИЗГИБ БАЛОК § 5.17. МЕТОД РАСЧЕТА КОНСТРУКЦИЙ ПО РАСЧЕТНЫМ ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки ПРИЛОЖЕНИЯ |
Расчет кручения грунтовых балок | Dlubal Software
Долговечные клееные балки обычно опираются на железобетонную колонну с ограничениями на кручение.
Разветвленная балка с распределенной нагрузкой (Источник: [3])
В этих опорах вилки возникают крутящие моменты, которые необходимо проверять в соответствии с [2] , раздел 6.1.9:
Формула 1
τtor,dkshape · fv,d (τy,dfv,d)² (τz,dfv,d)²
Суперпозиция внутренних сил от сдвига и кручения должна предотвратить появление трещин на жесткой опоре.
Трещины на клееной балке (Источник: [4])
Крутящий момент на концевых опорах возникает из-за прогиба балки в случае синусоидальной нагрузки (см. Рисунок 03).
Согласно [1] , для прекамбера должно быть установлено значение l/400. Это основано на минимальных требованиях к усилению вторичной опорной системы. Более подробную информацию можно найти, например, в [3].
Однако современные методы расчета стержней не позволяют обнаружить кручение на опорах. Кроме того, многие программы расчета не учитывают деформацию сечения. Поскольку расчет часто выполняется в программах расчета двухмерных конструкций из каркаса, ограничивающий критерий приведен в [2], раздел NCI до 9.
2.5.3 (выражение 2):
Формула 2
λef = lef · hb² ≤ 225
Если коэффициент гибкости балки ниже этого значения, компонентами напряжения кручения можно пренебречь.
Расчет в клееной древесине RX-TIMBER
Следующий пример поясняет эту связь.
Конструкция:
Пролет = 25 м
Материал = GL24c
Сечение = 12 см/242 см (без конькового клина)
Балка подвергается равномерно распределенной нагрузке 13,5 кН/м. Собственный вес не учитывается.
Основным расчетом является расчет на кручение, указанный в Выражении 1. В этом случае длинапролета равна 2,46 м. Расстояние между опорами при продольном изгибе при кручении может применяться только в том случае, если горизонтальная жесткость вспомогательной опорной системы составляет <l/500 или l/1000. Здесь это не применяется.
Формула 3
λef = lef · hb² = 2.460 cm · 240 cm(12 cm)² = 4.100 > 225τtor,dkshape · fv,d τz,dfv,d2 = 0,11 kN/cm²1,3 · 0,16 kN/cm² 0,12 kN/cm²0,16 kN/cm²2 = 1,1
Внутренние силы и напряжения:
Формула 4
TM,d = Mmax,d80 = 102.
665 kNcm80 = 12,8 kNmWt = 11.520 cm³τtor,d = 1.280 kNcm11.520 cm³ = 0,11 kN/cm²τd = 1,5 · Vdkcr · b · h = 0,12 kN/cm²
Расчет с учетом кручения при деформации
RF-/FE-LTB позволяет приложить к балке эксцентрическую сжимающую силу. Таким образом, линейная нагрузка 13,5 кН/м может быть приложена не по центру балки.
Как показано на рисунке 05, эксцентриситет груза установлен на 6 см. Кроме того, применяется боковая деформация 6,15 см в соответствии с [2] (NA.5).
Формула 5
e = l400 · kl = 2.460 cm400 = 6,15 cm
Основываясь на теории изгиба Бернулли, RF‑/FE ‑ LTB может определить критическую нагрузку Fki и, следовательно, идеальный упругий критический момент Mki и нагрузку потери устойчивости Nki, phi .
Расчет основан на теории потери устойчивости второго порядка. Также учитывается перекос сечения (7-я степень свободы).
Чтобы учесть соответствующее покрытие крыши или усиление за счет вторичной опорной системы, определяется пружина вращения вокруг локальной оси x элемента.
Программа преобразует эту пружину в центр сдвига M.
Применяется только пружина кручения, чтобы получить величину деформации, показанную на рисунке 2. Поступательная пружина на верхнем фланце конструкции была бы ближе к реальности. Однако из-за кривизны балки невозможно создать требуемую форму несовершенства. Затем фигура несовершенства будет прорезана в середине, как показано на рисунке 7. Таким образом, крутящие моменты будут значительно уменьшены.
Режим отказа
При ограничении вращения 500 кНм/м на опорах возникает крутящий момент 9,8 кНм.
крутящие моменты
Используя этот крутящий момент, можно снова выполнить расчет по [1] на клееной балке RX-TIMBER. Для этого определенный крутящий момент определяется в RX-TIMBER Glued-Laminated Beam.
Момент кручения в клееной древесине RX-TIMBER
Формула 6
0,085 kN/cm²1,3 · 0,16 kN/cm² 0,12 kN/cm²0,16 kN/cm²2 = 0,97 < 1
Заключение
Конструкцию можно спроектировать гораздо более экономично, учитывая жесткость поперечного сечения на изгиб.
Отличие от общего подхода, описанного в разделе 9.2.5 в [2], становится еще более серьезным при замене виртуального ограничения вращения на поступательную жесткость пружины 915 Н/мм для продольной деформации обычного гвоздя в соединительном элементе, например .
| [1] | Eurocode 5: Design of timber structures — Part 1-1: General — Common rules and rules for buildings; EN 1995-1-1:2010-12 |
| [2] | National Annex — Eurocode 5: Design of timber structures — Part 1-1: General — Common rules and rules for buildings; DIN EN 1995-1-1/NA:2013-08 |
| [3] | Blass, H., Ehlbeck, J., Kreuzinger, H., & Steck, G. (2005). Erläuterungen zu DIN 1052: Entwurf, Berechnung und Bemessung von Holzbauwerken (2nd ed.). Karlsruhe: Bruderverlag. |
3.3 Распределенные нагрузки. Инженерная механика: статика
Глава 3. Основы твердого тела
Распределенные нагрузки — это способ представления силы на определенном расстоянии.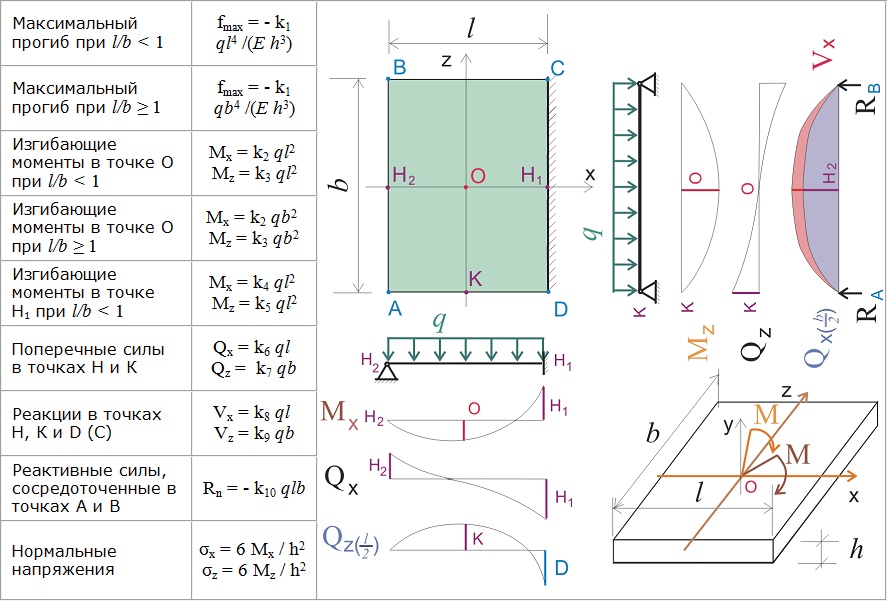
Иногда называется интенсивностью , учитывая переменную:
Интенсивность w = F / d [=] Н/м, фунт/фут
В то время как давление — это сила, действующая на площадь (для 3d-задач), интенсивность — это сила, действующая на расстояние (для 2d-задач). Это как куча матрасов на кузове грузовика. Вы можете смоделировать ее как 1 силу, действующую в центре (эквивалентная точечная нагрузка, как в 3.3.2), или вы можете смоделировать ее как интенсивность и разделить общую силу на ширину кузова грузовика (расстояние, которое не видно на этом изображении). [1] ).
Распределенная нагрузка — это любая сила, где точка приложения силы представляет собой площадь или объем . Это означает, что «точка приложения» на самом деле вовсе не точка. Хотя распределенные нагрузки сложнее анализировать, чем точечные силы, распределенные нагрузки довольно распространены в реальных системах, поэтому важно понимать, как их моделировать.
Распределенные нагрузки можно разделить на поверхностные силы и объемные силы . Поверхностные силы — это распределенные силы, точкой приложения которых является площадь (поверхность тела). Объемные силы — это силы, точкой приложения которых является объем (сила действует на все молекулы по всему телу). Ниже приведены некоторые примеры поверхностных и объемных сил.
Распределенные нагрузки представлены в виде поля векторов. Это нарисовано как ряд дискретных векторов вдоль линии, по поверхности или по объему, которые связаны с линией или поверхностью, как показано ниже.
Хотя эти представления показывают дискретное число отдельных векторов, на самом деле существует величина и направление во всех точках вдоль линии, поверхности или тела. Отдельные векторы представляют выборку этих величин и направлений.
Также важно понимать, что величины распределенных сил даны в силе на единицу расстояния, площади или объема.
Мы должны проинтегрировать распределенную нагрузку по всему ее диапазону, чтобы преобразовать силу в обычные единицы силы.
Анализ распределенной нагрузки:
Для целей анализа в статике и динамике мы обычно заменяем в одной точке силу, которая статически эквивалентна распределенной нагрузке в задаче. Эта одноточечная сила называется эквивалентной точечной нагрузкой , и она будет вызывать те же ускорения или силы реакции, что и распределенная нагрузка, при этом упрощая математику.
Источник: Engineering Mechanics, Джейкоб Мур и др., http://mechanicsmap.psu.edu/websites/4_statically_equivalent_systems/4-4_distributed_forces/distributedforces.html
Дополнительный пример:
Это более сложный пример распределенной нагрузки. Это мультяшный самолет с крылом, покрытым смесью снега и льда. В реальной ситуации грузы не вмещают людей для простоты расчета, вы получаете то, что получаете. В этом случае мы могли бы аппроксимировать эту форму двумя полуокружностями на каждом конце крыла с треугольником (∇» role=»presentation»>∇) в середине.
Для большей точности мы могли бы использовать систему, аналогичную правилу трапеций.
Источник: «Статика» от LibreTexts находится под лицензией CC BY-NC-SA. https://eng.libretexts.org/Bookshelves/Introduction_to_Engineering/EGR_1010%3A_Introduction_to_Engineering_for_Engineers_and_Scientists/14%3A_Fundamentals_of_Engineering/14.11%3A_Mechanics/14.11.01%3A_Statics
Распределенные нагрузки можно моделировать как одноточечную силу, расположенную в центре тела объекта. Вы можете использовать простую алгебру или использовать интеграцию для более сложных форм. Затем вы заменяете распределенную нагрузку одноточечной нагрузкой, действующей на расстоянии x. См. пример с грузовиком:
Есть два способа вычислить это: используя интегралы и используя площадь и центр тяжести.
Эквивалентная точечная нагрузка — это одноточечная сила , которая оказывает на тело такое же воздействие , что и исходное состояние нагрузки, которое обычно представляет собой распределенную нагрузку.
Эквивалентная точечная нагрузка всегда должна вызывать то же линейное ускорение и угловое ускорение, что и исходная нагрузка, которой она эквивалентна (или вызывать те же силы реакции, если тело ограничено). Нахождение эквивалентной точечной нагрузки для распределенной нагрузки часто помогает упростить анализ системы за счет удаления интегралов из уравнений равновесия или уравнений движения при последующем анализе.
Нахождение эквивалентной точечной нагрузки
При нахождении эквивалентной точечной нагрузки нам нужно найти величину, направление и точку приложения одиночной силы, которая эквивалентна заданной распределенной нагрузке. В этом курсе мы будем иметь дело только с распределенными нагрузками с однородным направлением, и в этом случае направление эквивалентной точечной нагрузки будет соответствовать равномерному направлению распределенной нагрузки. Остается определить величину и точку приложения. Доступны два варианта поиска этих значений:
- Мы можем найти величину и точку приложения эквивалентной точечной нагрузки путем интегрирования силовых функций.
- Мы можем использовать площадь/объем и центроид/центр объема площади или объема под функцией силы.
Первый метод является более гибким, позволяя нам найти эквивалентную точечную нагрузку для любой функции силы, для которой мы можем составить математическую формулу (при условии, что у нас есть навыки исчисления для интегрирования этой функции). Второй метод обычно быстрее, если предположить, что мы можем найти значения площади или объема под кривой силы и значения центроида или центра объема для площади под кривой.
Использование интегрирования в задачах 2D Surface Force:
Поиск эквивалентной точечной нагрузки с помощью интегрирования всегда начинается с определения математической формулы, которая представляет собой силовую функцию . Силовая функция математически связывает величину силы (F) с положением (x). В этом случае сила действует по одной линии, поэтому положение можно полностью определить, зная координату x, но в более поздних задачах нам также может понадобиться связать величину силы с координатами y и z.
В нашем примере слева мы можем связать величину силы с положением, заявив, что величина силы в любой точке в ньютонах на метр равна позиции x в метрах плюс один. 9{xmax}F(x)dx$$
Теперь, когда у нас есть величина эквивалентной точечной нагрузки, совпадающая с величиной исходной силы, нам нужно отрегулировать положение (x eq ) так, чтобы оно вызвать тот же момент , что и исходная распределенная сила. Момент распределенной силы будет интегралом силовой функции (F(x)) умноженной на плечо момента относительно начала координат (x). Момент эквивалентной точечной нагрузки будет равен величине только что найденной эквивалентной точечной нагрузки, умноженной на плечо момента для эквивалентной точечной нагрузки (x 9{xmax}(F(x)\ast x)dx}{F_{eq}}$$
Теперь, когда у нас есть величина, направление и положение эквивалентной точечной нагрузки, мы можем изобразить точечную нагрузку в исходном диаграмма. Эту точечную силу можно использовать вместо распределенной силы в дальнейшем анализе.
Использование площади и центроида в двухмерных поверхностных силовых задачах:
В качестве альтернативы использованию интегрирования мы можем использовать площадь под кривой силы и центр тяжести площади под кривой силы, чтобы найти эквивалентную величину точечной нагрузки. и точка приложения соответственно.
Величина (F eq ) эквивалентной точечной нагрузки будет равна площади под действием силовой функции . Мы можем найти эту площадь с помощью исчисления, но часто есть более простые способы, основанные на геометрии, для нахождения площади под функцией силы.
Эквивалентная точечная нагрузка также будет перемещаться через центр тяжести области под воздействием силовой функции . Это позволяет нам найти значение x eq . Центр тяжести для многих распространенных форм можно найти в таблицах, а теорему о параллельных осях можно использовать для определения центроида более сложных форм (более подробную информацию см.
На странице центроида).
Источник: Engineering Mechanics, Джейкоб Мур и др., http://mechanicsmap.psu.edu/websites/4_statically_equivalent_systems/4-5_equivalent_point_load/equivalentpointload.html
Вот уравнения для некоторых распространенных форм:
Пример 1: Эквивалентная сила и местоположение:
Чему равна результирующая сила и где она действует со стороны стены?
Источник: http://mechanicsmap.psu.edu/websites/4_statically_equivalent_systems/4-5_equivalent_point_load
См. здесь решение с использованием интеграции от Engineering Mechanics, Jacob Moore et al., http://mechanicsmap.psu.edu/websites/4_statically_equivalent_systems/4-5_equivalent_point_load/pdf/EquivalentPointLoad_WorkedExample1.pdf
Пример 2 (примечание: 1 кип = 1000 фунтов):
Пример 3:
Пример 4:
Источник: «Равновесные конструкции, опорные реакции, детерминированность и устойчивость балок и рам» LibreTexts находится под лицензией CC BY-NC-ND.
https://eng.libretexts.org/Bookshelves/Civil_Engineering/Book%3A_Structural_Analysis_(Udoeyo)/01%3A_Chapters/1.03%3A_Equilibrium_Structures_Support_Reactions_Determinacy_and_Stability_of_Beams_and_Frames
При наличии сложной формы может быть проще смоделировать ее как более одного типа распределенной нагрузки. Вы вычисляете каждую силу отдельно, а затем используете взвешенное уравнение, чтобы найти общее расстояние, на котором сила действует от выбранной точки.
[латекс]\quad\quad\quad\quad\text{Используя область: }\quad\quad\quad\quad\quad\quad\quad\quad\quad \text{Используя интегралы:}\\ \quad\quad \ quad \ quad \ bar {x} = \ frac {\ sum F_ {i} x_i} {\ sum F_i} \ quad \ quad \ quad \ quad \ quad \ quad \ quad \ quad \ quad \ quad \ bar {x }=\frac{\int x w(x) d x}{\int w(x) d x}[/latex]
Немного больше:
Для следующей сложной формы следующим образом можно найти составную эквивалентную точечную силу и положение ([латекс]\бар{х}[/латекс]):
В основном: Распределенные нагрузки — это способ моделирования сил в 2D.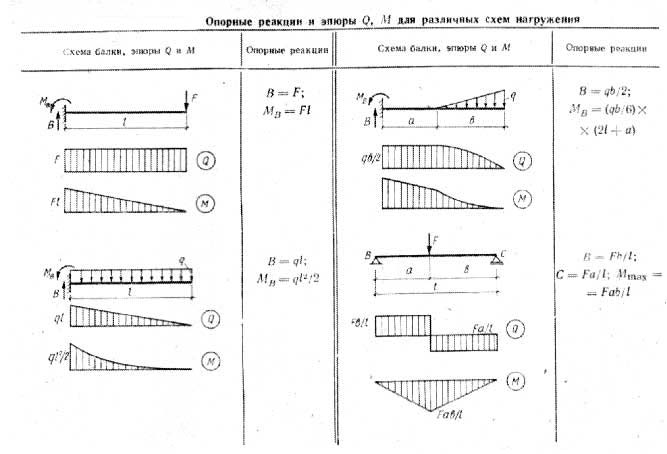
F = w d Распределенные нагрузки, иногда называемые интенсивностью, имеют единицы измерения силы на расстоянии: Н/м или фунт/фут.
Применение: Для грузовика, перевозящего тяжелый неравномерный груз, определите, где находится центр силы.
Забегая вперед: Распределенная нагрузка помогает моделировать неравномерные нагрузки. Мы еще увидим это, когда будем проводить анализ луча
- Изображение грузовика взято с: https://get.pxhere.com/photo/car-transport-truck-vehicle-market-mattress-full-load-small-business-rwanda-overload-pickup-truck-overfull- автомобиль-марка-612534.jpg ↵
Диаграмма изгибающего момента — форма и кривизна
Диаграмма изгибающего момента — форма и кривизна
Изгибающий момент требуется для расчета балки и
также для расчета
наклон и
отклонение луча. Следующие примеры будут
проиллюстрировать, как написать уравнение изгибающего момента для различных типов
нагрузки, а затем построить диаграммы изгибающих моментов.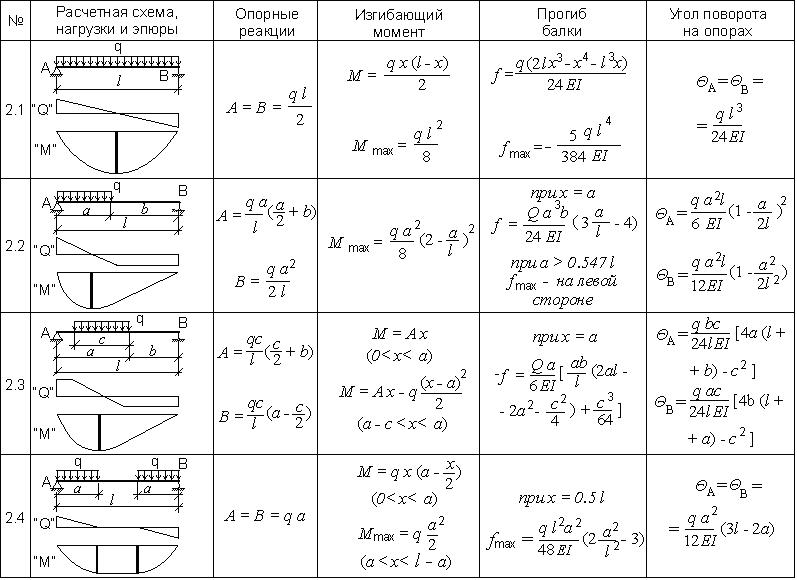
Случай I Изгибающий момент точечная нагрузка
Изгибающий момент от точки нагрузка является произведением нагрузки и ее перпендикулярного расстояния от суть момента. как показано ниже.
Рассмотрим кантилевер, подвергнутый точечная нагрузка на свободный конец.
Изгибающий момент на закрепленном конце = W х л = ВЛ
Изгибающий момент M x при расстояние x от свободного конца = W x х = Wx
Это уравнение прямой и построенная диаграмма изгибающего момента на приведенном выше рисунке показывает, что изменение изгибающий момент по пролету кантилевера представляет собой прямую.
Случай II Изгибающий момент равномерно распределенная нагрузка
Изгибающий момент от равномерно распределенная нагрузка (udl) составляет равна интенсивности нагрузки х длина груза Икс расстояние его центра от точки момента, как показано на следующие примеры.
Изгибающий момент на закрепленном конце = 10 х 2 х 1= 20 кНм
Изгибающий момент M x при расстояние «х» от свободного конца = 10 х (х) х (х/2)= 0,5 х 2
которая является функцией второй степени
«x» и, следовательно, параболический.
Случай III Изгибающий момент из-за равномерно изменяющаяся нагрузка
Изгибающий момент от переменной нагрузки равен равна площади диаграммы нагрузки x расстояние от его центра тяжести с точки зрения момента.
Форма диаграммы изгибающего момента, обусловленная к равномерно меняющейся нагрузке представляет собой кубическую параболу.
Случай IV Изгибающий момент от пара
Изгибающий момент в сечении из-за пара равна величине пары и в том же смысле как пара.
Следующие примеры будут очень полезны для объяснения того, как напишите уравнения для поперечной силы и расчет изгибающих моментов и построить диаграммы для консольные, свободно опертые и нависающие балки. Пример 5-1
Пример 5-2
Пример 5-3
Пример 5-4
Вы также можете использовать следующие калькуляторы для изгибающего момента и поперечной силы
Калькулятор изгибающего момента для консоли
Калькулятор изгибающего момента для свободно опертой балки
Калькулятор изгибающего момента для нависающей балки
Калькулятор изгибающего момента для неподвижной балки
Дополнительные примеры решений
регулярно обновляемые
Отличные калькуляторы
Калькулятор трансформации напряжения
Расчет главного напряжения, максимального напряжения сдвига и их плоскостей
Калькулятор для анализа подвижной нагрузки
Для определения абсолютного макс.