Помощь с учёбой студентам онлайн от Натальи Брильёновой

Обо мне

Здравствуйте, я, Брильёнова Наталья Валерьевна, бывший преподаватель кафедры информатики и электроники Екатеринбургского государственного института. С 2014 года занимаюсь онлайн образованием. У меня работает большая команда бывших преподавателей с огромным опытом и квалификацией.

Мы за этот месяц выполнили:заказов.

Мы помогаем с предметами любого уровня сложности из разных учебных заведений: средняя школа, колледж или университет. Независимо от темы, объёма, – задание в одну формулу или большая расчётная работа от 80 страниц, я и моя команда всегда выполняем высококачественно. Каждый день, я и моя команда преподавателей помогаем ученикам и студентам учиться лучше.

Мы всегда соблюдаем сроки. Наша цель – чтобы вы учились на хорошие оценки! Нет времени, но хотите хорошую оценку? Попросите меня вам помочь! Согласуем с вами требования и сроки и через 1-4 дня всё будет на «отлично».

Почему лучше заказать у меня? Потому что, кроме меня и моей команды преподавателей, ваше задание никто не увидит, так как WhatsApp и Gmail конфиденциальные системы. При размещении заказа в других сервисах и биржах, ваш заказ выкладывается в открытый доступ сети интернет, и поисковые системы yandex и google их индексируют. В результате история вашего заказа становится доступна всем. А это значит, что любой пользователь сможет найти историю вашего заказа и, следовательно, преподаватели также смогут всё узнать. Поэтому обращаясь ко мне, вы получаете лучшую конфиденциальность и безопасность.

Мои особенности

Любой срок — любой предмет:

• Я и моя профессиональная команда поможет с любым предметом, независимо от темы или сложности.

Whatsapp чат 24/7:

• Общайтесь со мной в любое время [контакты здесь], чтобы обсудить детали заказа, и т. д.

Оригинальность:

• У меня разработан эффективный алгоритм проверки на плагиат. Я проверяю каждую работу через различные инструменты обнаружения плагиата для получения оригинального текста. Оригинальность наших работ от 88%.

Доступные цены:

• Я предлагаю самую лучшую цену. У меня есть скидки от 20% для тех, кто сделает больше пяти заказов.

Как заказать?

Напишите мне в whatsapp [контакты здесь] и прикрепите своё задание и методические материалы (лекции) и укажите сроки выполнения.

Я изучу ваш заказ и рассчитаю стоимость.

Как только вы оплатите свой заказ, я и моя команда преподавателей его выполняем.

В указанную вами дату или, возможно, раньше получаете свой заказ!

Часто задаваемые вопросы

Сколько стоит помощь?

• Цена зависит от объёма, сложности и срочности. Присылайте любые задания по любым предметам — я изучу и оценю.

Какой срок выполнения?

• Нам под силу выполнить как срочный заказ, так и сложный заказ. Стандартный срок выполнения – от 1 до 3 дней. Мы всегда стараемся выполнять любые заказы раньше срока.

Если требуется доработка, это бесплатно?

• Доработка заказ бесплатна. Срок выполнения от 1 до 2 дней.

Могу ли я не платить, если меня не устроит стоимость?

• Оценка стоимости вашего задания бесплатна.

Каким способом можно оплатить?

• Можно оплатить любым способом: картой Visa / MasterCard, с баланса мобильного, google pay, apple pay, qiwi и т.д.

В какое время я вам могу написать и прислать задание на выполнение?

• Присылайте в любое время! [контакты здесь]

Книга отзывов

Пользовательское соглашение

Политика конфиденциальности

Помощь с учёбой студентам онлайн от Натальи Брильёновой

Обо мне

Здравствуйте, я, Брильёнова Наталья Валерьевна, бывший преподаватель кафедры информатики и электроники Екатеринбургского государственного института. С 2014 года занимаюсь онлайн образованием. У меня работает большая команда бывших преподавателей с огромным опытом и квалификацией.

Мы за этот месяц выполнили:заказов.

Мы помогаем с предметами любого уровня сложности из разных учебных заведений: средняя школа, колледж или университет. Независимо от темы, объёма, – задание в одну формулу или большая расчётная работа от 80 страниц, я и моя команда всегда выполняем высококачественно. Каждый день, я и моя команда преподавателей помогаем ученикам и студентам учиться лучше.

Мы всегда соблюдаем сроки. Наша цель – чтобы вы учились на хорошие оценки! Нет времени, но хотите хорошую оценку? Попросите меня вам помочь! Согласуем с вами требования и сроки и через 1-4 дня всё будет на «отлично».

Почему лучше заказать у меня? Потому что, кроме меня и моей команды преподавателей, ваше задание никто не увидит, так как WhatsApp и Gmail конфиденциальные системы. При размещении заказа в других сервисах и биржах, ваш заказ выкладывается в открытый доступ сети интернет, и поисковые системы yandex и google их индексируют. В результате история вашего заказа становится доступна всем. А это значит, что любой пользователь сможет найти историю вашего заказа и, следовательно, преподаватели также смогут всё узнать. Поэтому обращаясь ко мне, вы получаете лучшую конфиденциальность и безопасность.

Мои особенности

Любой срок — любой предмет:

• Я и моя профессиональная команда поможет с любым предметом, независимо от темы или сложности.

Whatsapp чат 24/7:

• Общайтесь со мной в любое время [контакты здесь], чтобы обсудить детали заказа, и т. д.

Оригинальность:

• У меня разработан эффективный алгоритм проверки на плагиат. Я проверяю каждую работу через различные инструменты обнаружения плагиата для получения оригинального текста. Оригинальность наших работ от 88%.

Доступные цены:

• Я предлагаю самую лучшую цену. У меня есть скидки от 20% для тех, кто сделает больше пяти заказов.

Как заказать?

Напишите мне в whatsapp [контакты здесь] и прикрепите своё задание и методические материалы (лекции) и укажите сроки выполнения.

Я изучу ваш заказ и рассчитаю стоимость.

Как только вы оплатите свой заказ, я и моя команда преподавателей его выполняем.

В указанную вами дату или, возможно, раньше получаете свой заказ!

Часто задаваемые вопросы

Сколько стоит помощь?

• Цена зависит от объёма, сложности и срочности. Присылайте любые задания по любым предметам — я изучу и оценю.

Какой срок выполнения?

• Нам под силу выполнить как срочный заказ, так и сложный заказ. Стандартный срок выполнения – от 1 до 3 дней. Мы всегда стараемся выполнять любые заказы раньше срока.

Если требуется доработка, это бесплатно?

• Доработка заказ бесплатна. Срок выполнения от 1 до 2 дней.

Могу ли я не платить, если меня не устроит стоимость?

• Оценка стоимости вашего задания бесплатна.

Каким способом можно оплатить?

• Можно оплатить любым способом: картой Visa / MasterCard, с баланса мобильного, google pay, apple pay, qiwi и т. д.

В какое время я вам могу написать и прислать задание на выполнение?

• Присылайте в любое время! [контакты здесь]

Книга отзывов

Пользовательское соглашение

Политика конфиденциальности

Примеры расчета статически неопределимой рамы методом

Перемещений

Пример 2.1. Построить эпюры внутренних усилий для рамы, показанной на рисунке 2,10, а.

Решение.

1 Проводим кинематический анализ стержневой системы. Степень статической неопределимости W = 3∙1 — 2∙0 – 7 = — 4, степень кинематической неопределимости n = n_у + n_л = 1 + 0 = 1.

2 Выбираем основную систему метода перемещений (рис. 2.10, б).

 

3 Записываем каноническое уравнение метода перемещений

Z₁r₁₁ + R_1p = 0.

4 Для определения единичной r₁₁ и грузовой R_1P реакций строим единичную (рисунок 2.11,а) и грузовую (рисунок 2.11,в) эпюры, пользуясь Таблицей реакции (Приложение В). На рисунках 2.10,в и 2.11,б показаны единичное и грузовое состояния.

 

5 Рассматривая равновесие узлов (рисунок 2.12), имея ввиду уравнение

∑m = 0, определяем значения реакций.

 

r₁₁ = 2EI + 2EI + EI = 5EI,

R_1p = 4P/8 = 5 кН.

 

6 Решаем каноническое уравнение и определяем значение неизвестного. Напомним, что это угол поворота жесткого узла.

 

7 Строим эпюру М₁, как: М₁ = ×Х₁ (рисунок 2.13, а)и, далее, строим результирующую эпюру М, в виде суммы М = М₁ + М_Р (рисунок 2.13, б). Проводим проверку равновесия жесткого узла.

 

Статическая проверка узла

 

8 Путем графического дифференцирования строим эпюру Q и, рассматривая равновесие узла, определяем и строим эпюру N (рисунок 2.15).

 

9 Выполняем статическую проверку рамы в целом (рисунок 2.16).

 

— 2,31 + 10 -2,31 – 5,375 = 10 – 9,995 ≈ 0,

Уравнения равновесия выполняются.

 

Пример 2.2Построить эпюры внутренних усилий для рамы, показанной на рисунок 2.17,а.

Решение.

Порядок расчета аналогичен предыдущему примеру 2.1.

1 Проводим кинематический анализ стержневой системы. Степень статической неопределимости W = 3∙1 — 2∙0 – 7 = — 4, степень кинематической неопределимости n = n_у + n_л = 0 + 1 = 1.

2 Выбираем основную систему метода перемещений (рис. 2.17, б).

3 Записываем каноническое уравнение метода перемещений

 

Z₁r₁₁ + R_1p = 0.

 

4 Для определения единичной r₁₁ и грузовой R_1P реакций строим единичную (рисунок 2.18,б) и грузовую (рисунок 2.19,б) эпюры, используя таблицы реакций.

5 Рассматривая равновесие ригеля рамы (рисунок 2.20), имея ввиду уравнение ∑х = 0, определяем значения реакций в наложенной связи.

 

 

6 Решаем каноническое уравнение и определяем значение неизвестного. В этой задаче неизвестным является горизонтальное смещение ригеля..

7 Строим эпюру М₁, как: М₁ = ×Х₁ (рисунок 2.21, а)и, далее, строим результирующую эпюру М, в виде суммы М = М₁ + М_Р (рисунок 2.21, б).

 

8 Путем графического дифференцирования строим эпюру Q и, рассматривая равновесие узлов, определяем продольные усилия и строим эпюру N (рисунок 2.22).

9 Выполняем статическую проверку рамы в целом (рисунок 2. 23).

 

q×2l – 13ql/8 – -3ql/8 = 0,

Уравнения равновесия выполняются.

 

 

Пример 2.3 Для заданной статически неопределимой рамы, показанной на рисунке 2.24, требуется построить эпюры внутренних усилий. Исходные данные: l = 4 м, h = 6 м, q = 2кН/м, Р = 10 кН, EI = const.

Решение.

1 Степень кинематической неопределимости рассматриваемой рамы составляет

n ₌ n_{у +} n_{л =} 1 + 1 = 2.

2 Система канонических уравнений в данном случае имеет вид

z₁∙r₁₁ + z₂∙r₁₂+ R_1Р = 0,

z₁∙r₂₁ + z₂∙r₂₂+ R_2Р = 0.

3 Используя таблицы (см. приложение В) строим единичные и грузовую эпюры. Для этого последовательно создаем единичные и грузовое состояния с показом ожидаемого деформированного вида, которые показаны на рисунках 2.25, 2.26, 2.27. Это помогает правильно воспользоваться таблицами реакций для построения эпюр изгибающих моментов. Необходимо помнить, что эпюры М строятся на растянутых волокнах.

 

 

 

 

 

4 Вычисляем единичные коэффициенты.

Для вычисления реакции r₁₁ вырежем узел с заделкой на эпюре (рисунок 2.25) и рассмотрим его равновесие под действием реактивных моментов, возникающих по концам стержней и реакции в заделке r₁₁, которую направляем по направлению единичного воздействия Z₁ = 1.

Во втором единичном состоянии при отклонении вправо в стержнях появляются реакции, направленные влево (рисунок 2. 26). Тогда

 

При определении побочных коэффициентов (т. е. реакций) воспользуемся правилом, что r₁₂ = r₂₁. Рассмотрим эпюру , где наглядно видно, что в первой наложенной связи при смещении Z₂ = 1 возникает момент 6EI/h², растягивающий правые волокна (рисунок 2.26) – направленный в сторону перемещения Z₁.

Реакция r₁₂ будет равна:

 

 

При определении знака поперечной реакции удобно пользоваться правилом знаков для поперечной силы – положительная поперечная сила вращает узел по часовой стрелке.

 

Грузовые коэффициенты определим по эпюре М_р. Вырежем узел с наложенной заделкой и рассмотрим действующие на нее моменты (рисунок 2. 31). Реакция R_1Р, возникающая в виде реактивного момента в заделке из условий равновесия будет

 

Минус у реакции R_1P означает, реакция направлена в сторону, обратную первому единичному воздействию.

Реакция R_2Р, возникающая в веденной опоре правого узла, равна верхней реакции в стойке от действия распределенной нагрузки (R_В).

Σх = 0. R_2Р = – R_В = – 6 кН_.

Знак минус означает, что реакция направлена в сторону, обратную линейному смещению z₂.

Запишем систему канонических уравнений с учетом полученных коэффициентов и свободных членов.

5 Решая записанную систему уравнений, получим

 

 

6 Построение окончательной эпюры изгибающих моментов для заданной системы производим на основании принципа независимости действия сил по формуле

M = Z₁ + Z₂ + M_p,

 

т.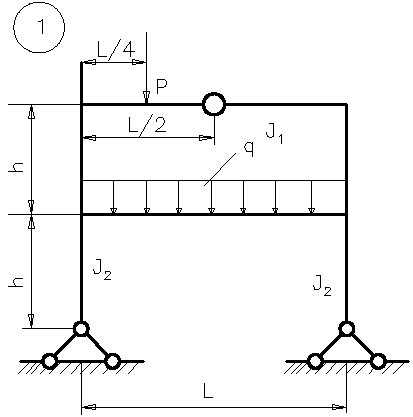 е. путем сложения эпюр от неизвестных (рисунок 2.32) и грузовой эпюры (рисунок 2.27). Эпюры от неизвестных получаются путем умножения единичных эпюр на значения соответствующих Z_i.

7 Для проверки правильности построения эпюры М производим статическую и деформационную проверки.

Для статической проверки, как и в методе сил, вырезаются незакрепленные жесткие узлы из эпюры М, прикладываются действующие в нем изгибающие моменты и проверяется выполнение уравнения Sm = 0. В нашем случае разность моментов в узле В равна 0,05 кНм, что составляет 1,2%.

Деформационная проверка проводится с применение метода сил и заключается в определении перемещений тех сечений, чье перемещение исключено. Так, если выбрать основную систему метода сил с использованием шарнирных узлов в опоре А и в узле В, то угол поворота сечения А должен быть равен нулю, поскольку в заданной системе в точке А жесткая опора.

Для его вычисления создадим единичное состояние метода сил (рисунок 2.33), построим единичную эпюру от единичного момента и перемножим результирующую эпюру на единичную.

8 Построение эпюр Q и N.

Как и в методе сил, эпюры поперечных сил строятся с использованием формулы графического дифференцирования эпюры моментов

а эпюра продольных сил строится путем рассмотрения равновесия узлов рамы.

В нашем примере:

Левая стойка.

Q_л = 10,28 кН, Q_пр = – 1,72 кН.

Поперечная сила меняет знак, следовательно, момент в пролете будет иметь экстремум.

Левая часть ригеля

Правая часть ригеля

Правая стойка

Строим эпюру Q (рисунок 2.34,а).

 

 

Вырезая левый и правый узлы рамы и рассматривая их равновесие (рисунок 2.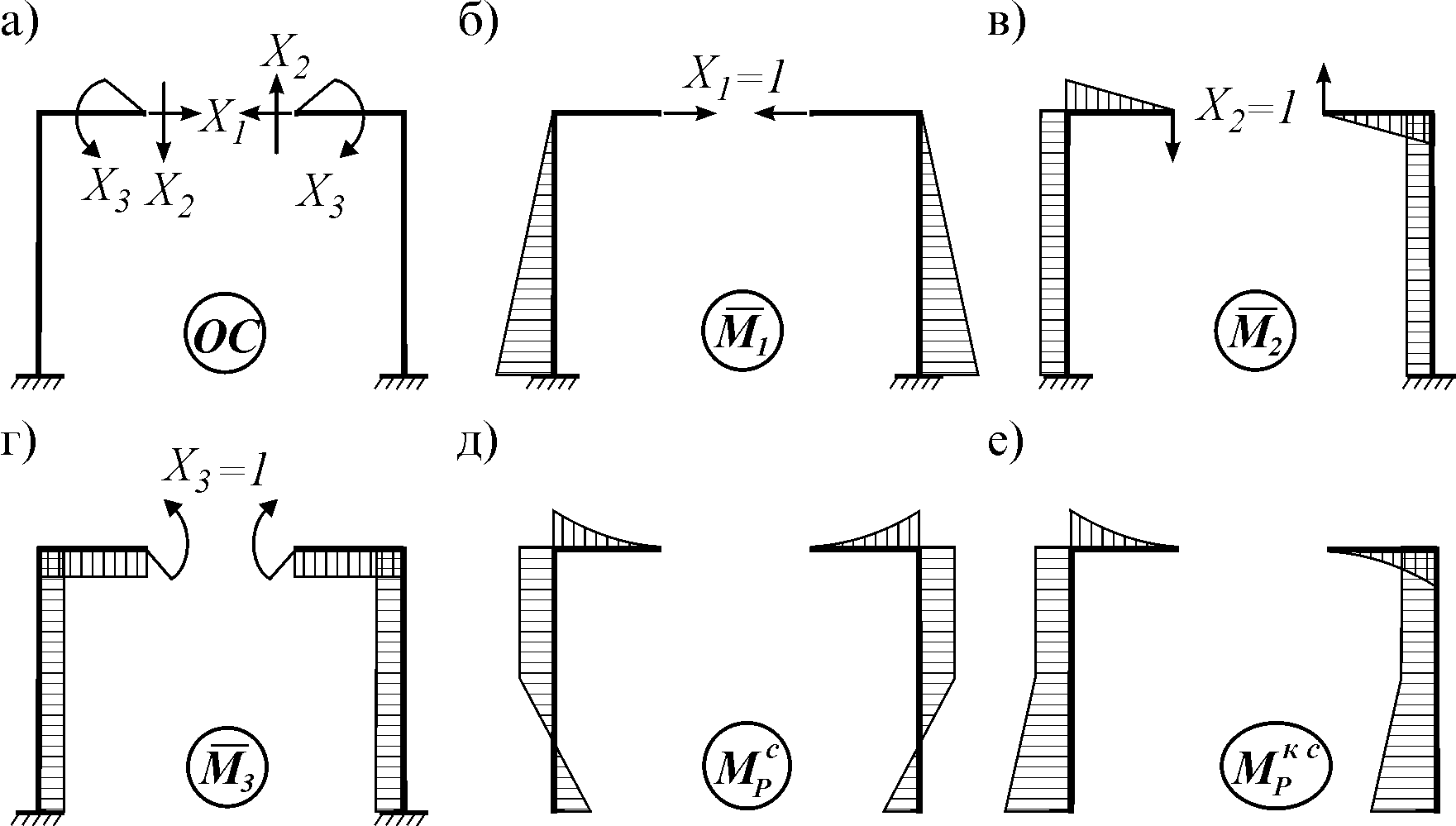 34,б), находим продольные усилия в стойках и ригеле и строим эпюру продольных сил N (рисунок 2.34,в).

9 В заключение, проводим статическую проверку по аналогии со статической проверкой в методе сил. Отсекаем раму от всех опор и прикладываем в местах отсечений силовые факторы (реакции) по эпюрам M, Q, N (рисунок 2.35).

Должны выполняться все три уравнения равновесия.

 

Sx = 0, q∙6 – 10.28 – 1.72 = 12 – 12 =0.

 

Sy = 0, — P + 3.925 + 6.05 = 10 – 9.975 = 0,025 ≈ 0.

Погрешность d = 0.025∙100/10 = 0.25%

Sm_A = 0, — P∙2 — q∙6∙3 + M_A + M_D+ N_D∙ 4 = — 20 – 36 + 21.45 + 10.32 +24.2 =

= 55.97 – 56 = 0.03 ≈ 0.

Погрешность d = 0,03∙100/56 = 0,05%. Т. е. равновесие рамы обеспечено с допустимой погрешностью.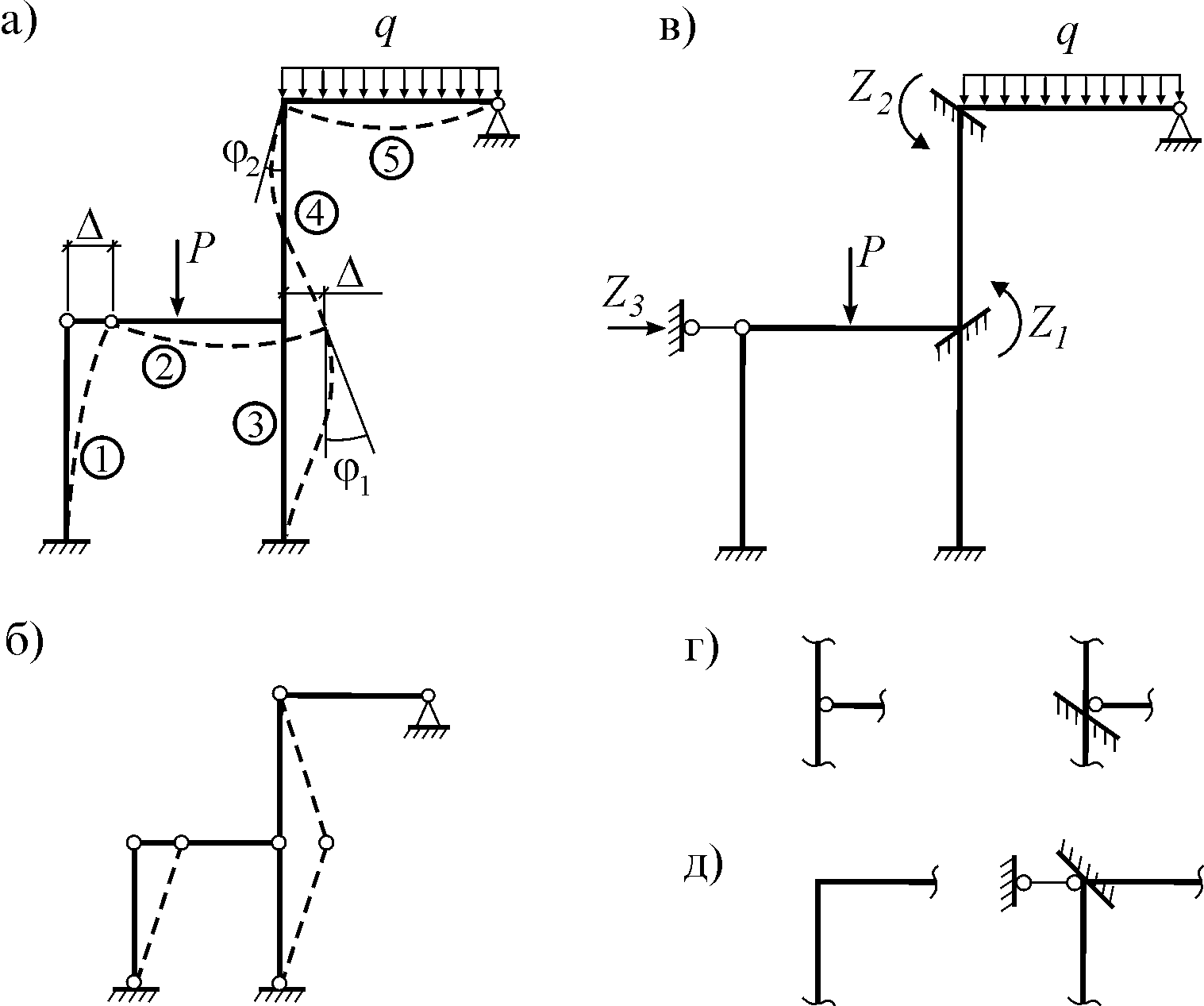

 

Ниже приводятся задачи по определению внутренних усилий в статически неопределимых системах методом перемещений.

 

 

 

 

 

 

 

Узнать еще:

Метод сил в сопромате

 

 

Заказать решение           Способ оплаты

 

При решении задач сопромата, статически неопределимой называется такая система, которая не может быть рассчитана при помощи одних только уравнений статики, так как имеет лишние связи. Для расчета таких систем составляются дополнительные уравнения, учитывающие деформации системы.

Оговоримся, что здесь и далее понятие “расчет” подразумевает только построение эпюр внутренних силовых факторов, возникающих в элементах системы, а не расчет на прочность, жесткость и т.д.

Статически неопределимые системы обладают рядом характерных особенностей:

1. Статически неопределимые конструкции являются более жесткими, чем соответствующие статически определимые, так как имеют дополнительные связи.
2. В статически неопределимых системах возникают меньшие внутренние усилия, что определяет их экономичность по сравнению со статически определимыми системами при одинаковых внешних нагрузках.
3. Нарушение лишних связей в статически неопределимой системе не всегда приводит к разрушению, в то время как потеря связи в статически определимой системе делает ее геометрически изменяемой.
4. Для расчета статически неопределимых систем необходимо предварительно задаваться геометрическими характеристиками поперечных сечений элементов, т.е. фактически их формой и размерами, так как их изменение приводит к изменению усилий в связях и новому распределению усилий во всех элементах системы.
5. При расчете статически неопределимых систем необходимо заранее выбрать материал конструкции, так как необходимо знать его модули упругости.
6. В статически неопределимых системах температурное воздействие, осадка опор, неточности изготовления и монтажа вызывают появление дополнительных усилий.

Основными методами расчетастатически неопределимых систем являются:

 

1. Метод сил. Здесь в качестве неизвестных рассматриваются усилия – силы и моменты.
2.Метод перемещений. Неизвестными являются деформационные факторы – углы поворотов и линейные смещения.
3.Смешанный метод. Здесь часть неизвестных представляет собой усилия, а другая часть – перемещения.
4. Комбинированный метод. Используется при расчете симметричных систем на несимметричные нагрузки. Оказывается, что на симметричную составляющую заданной нагрузки систему целесообразно рассчитывать методом перемещений, а на обратносимметричную составляющую – методом сил.
Помимо указанных аналитичеких методов при расчете особо сложных систем используются различные численные методы.

 

Канонические уравнения метода сил

 

Для получения дополнительных уравнений, о которых говорилось в предыдущем параграфе, нужно прежде всего превратить заданную, n раз статически неопределимую систему, в статически определимую, удалив из нее лишние связи. Полученная статически определимая система называется основной. Отметим, что преобразование заданной системы в статически определимую не является обязательным. Иногда используется модификация метода сил, в которой основная система может быть статически неопределимой, однако изложение этого вопроса выходит за рамки этого пособия. Устранение каких-либо связей не изменяет внутренние усилия и деформации системы, если к ней приложить дополнительные силы и моменты, представляющие собой реакции отброшенных связей. Значит, если к основной системе приложить заданную нагрузку и реакции удаленных связей, то основная и заданная системы станут эквивалентными.

В заданной системе по направлениям имеющихся жестких связей, в том числе и тех связей, которые отброшены при переходе к основной системе, перемещений быть не может, поэтому и в основной системе перемещения по направлениям отброшенных связей должны равняться нулю. А для этого реакции отброшенных связей должны иметь строго определенные значения.

Условие равенства нулю перемещения по направлению любой i-ой связи из n отброшенных на основании принципа независимости действия сил имеет вид:

 

 

где первый индекс означает направление перемещения и номер отброшенной связи, а второй указывает на причину, вызвавшую перемещение, т.е. — это перемещение по направлению i-ой связи, вызванное реакцией k-ой связи; — перемещение по направлению i-ой связи, вызванное одновременным действием всей внешней нагрузки.

В методе сил реакцию k-ой связи принято обозначать через Xk. С учетом этого обозначения и в силу справедливости закона Гука перемещения можно представить в виде:

 

 

где — единичное (или удельное) перемещение по направлению i-ой связи, вызванное реакцией т.е. реакцией, совпадающей по направлению с Xk, но равной единице.

Подставляя (2) в (1), получим:

 

 

Физический смысл уравнения (3): перемещение в основной системе по направлению i-ой отброшенной связи равно нулю.

Записывая выражения, аналогичные (3), для всей совокупности отброшенных связей, получим систему канонических уравнений метода сил:

 

 

Вид уравнения (4), т.е. количество слагаемых в каждом из них и их общее число, определяется только степенью статической неопределимости системы и не зависит от ее конкретных особенностей.

 

Коэффициенты системы канонических уравнений (4) определяются методом Мора-Верещагина путем перемножения соответствующих эпюр. Все эти коэффициенты, как указывалось выше, представляют собой перемещения; коэффициенты, стоящие при неизвестных – единичные перемещения, а свободные члены – грузовые. Единичные перемещения делятся на главные, расположенные по главной диагонали и имеющие одинаковые индексы и побочные (). Главные перемещения всегда положительные, в отличие от побочных. Симметрично расположенные перемещения в соответствии с теоремой о взаимности перемещений равны друг другу, т.е. .

 

Алгоритм расчета методом сил

 

Независимо от особенностей рассматриваемой конструкции, можно выделить следующую последовательность расчета статически неопределимых систем методом сил:

1. Определить степень статической неопределимости.
2. Выбрать основную систему.
3. Сформировать эквивалентную систему.
4. Записать систему канонических уравнений.
5. Построить единичные и грузовые эпюры внутренних силовых факторов, возникающих в элементах рассматриваемой конструкции.
6. Вычислить коэффициенты при неизвестных и свободные члены системы канонических уравнений.
7. Построить суммарную единичную эпюру.
8. Выполнить универсальную проверку коэффициентов при неизвестных и свободных членов.
9. Решить систему (4), т.е. определить реакции лишних связей.
10. Построить эпюры возникающих внутренних силовых факторов для заданной системы (иначе говоря, окончательные эпюры).
11. Выполнить статическую и кинематическую проверки.
Отметим, что пункты 7, 8, 11 приведенного алгоритма не являются безусловно необходимыми, хотя и позволяют контролировать правильность выполнения расчета. А для систем с одной лишней связью пункты 7 и 8 просто лишены смысла, так как в этом случае суммарная единичная эпюра совпадает с единичной.
Остановимся подробнее на некоторых из вышеперечисленных этапов расчета.

 

Выбор основной системы

 

Это важнейший этап расчета, так как рациональный выбор основной системы существенно упрощает вычислительную работу. Рассмотрим возможные способы удаления лишних связей, что и определяет вид основной системы.

1. Отбрасывание лишних связей осуществляется полным удалением некоторых опор или их заменой опорами с меньшим числом связей. Реакции, действующие в направлениях отброшенных связей, являются лишними неизвестными. На рис.1,б, в, г показаны различные варианты эквивалентной системы, полученные этим способом для рамы (рис.1,а).

2.Постановка шарниров в промежуточных сечениях стержней позволяет в каждом таком сечении установить связь, соответствующую изгибающему моменту. Эти моменты являются лишними неизвестными. Для рамы, имеющей степень статической неопределимости n=3 (рис.2,а), при выборе основной системы необходимо поставить три шарнира. Положение этих шарниров может быть произвольным, но удовлетворяющим требованию геометрической неизменяемости системы (рис.2,б).

3. Рассечение стержня устраняет три связи, соответствующие внутренним усилиям M, Q, N (рис.2,в). В частных случаях (рис.2,г) рассечение стержня по шарниру освобождает две связи (рис.2,д), а рассечение прямолинейного стержня с шарнирами по концам – одну связь (рис.2,е).

 

рис. 1

 

Среди связей статически неопределимой системы различают абсолютно необходимые и условно необходимые. К абсолютно необходимым относятся связи, при удалении которых система становится геометрически изменяемой. Для абсолютно необходимой связи характерна статическая определимость усилия в ней, т.е. реакция такой связи может быть вычислена из условия равновесия. При выборе основной системы абсолютно необходимые связи отбрасывать нельзя.

 

 

рис. 2

 

Связи, при удалении которых система продолжает оставаться геометрически неизменяемой, называются условно необходимыми. Система, у которой удалили такую связь, может являться основной системой метода сил.

 

Вычисление коэффициентов и свободных членов канонических уравнений

 

Этому этапу расчета предшествует построение единичных и грузовых эпюр внутренних силовых факторов (для балок и рам – эпюр изгибающих моментов). Единичные эпюры строятся от действия безразмерной единичной силы или безразмерного единичного момента, совпадающих по направлению с направлением соответствующей лишней неизвестной в эквивалентной системе, и обозначаются через , а единичная эпюра – через .

 

Грузовая эпюра строится от внешней нагрузки, приложенной к основной системе. При этом можно строить одну эпюру от одновременного действия всех внешних нагрузок или несколько эпюр, отдельно от каждой из приложенных нагрузок. Такое разбиение одной грузовой эпюры на несколько  более простых, как правило, целесообразно только тогда, когда среди действующих нагрузок есть равномерно распределенная, и эпюра моментов на соответствующем участке под ней является знакопеременной. При этом в каждом каноническом уравнении число свободных членов будет равно числу построенных грузовых эпюр.

Единичные и грузовые перемещения (коэффициенты и свободные члены канонических уравнений) в общем случае можно вычислить методом Мора. Для балок и рам это можно сделать при помощи правила Верещагина.

 

Универсальная проверка коэффициентов и свободных членов канонических уравнений

 

Для выполнения универсальной проверки необходимо построить суммарную единичную эпюру — эпюру моментов от одновременного действия всех единичных сил, приложенных к основной системе:

 

Перемножим суммарную единичную эпюру с эпюрой :

 

 

Таким образом результат перемножения суммарной и i-ой единичной эпюр — это перемещение по направлению i-ой связи от совместного действия единичных лишних неизвестных. Это перемещение равно сумме коэффициентов i-го канонического уравнения:

 

 

Такая проверка называется построчной и выполняется для каждого канонического уравнения.
Вместо n построчных проверок чаще всего выполняется одна – универсальная поверка, которая состоит в перемножении суммарной единичной эпюры самой на себя и проверке условия:

 

 

Если универсальная проверка выполняется, значит единичные перемещения вычислены правильно; если нет – необходимо выполнить построчные проверки, что позволит уточнить перемещение, при вычислении которого допущена ошибка.

Для выполнения проверки грузовых перемещений необходимо перемножить суммарную единичную и грузовую эпюры изгибающих моментов:

 

 

Таким образом, проверка свободных членов системы канонических уравнений (4) состоит в выполнении условия:

 

 

Построение окончательных эпюр внутренних силовых факторов

 

Окончательные эпюры можно построить двумя способами.

Так как при найденных значениях лишних неизвестных Xi выполняются условия совместности деформаций, то из расчета основной системы можно получить все искомые внутренние усилия заданной системы. На основании принципа независимости действия сил для изгибающих моментов получим:

 

или, учитывая, что

 

 

приходим к выражению:

 

 

Аналогично определяется продольные и поперечные силы:

 

Второй способ основан на том, что в результате вычисления реакций лишних связей Xi исходная статически неопределимая система приведена к статически определимой системе, загруженной внешними нагрузками и реакциями лишних связей. Поэтому окончательные эпюры внутренних силовых факторов можно построить для эквивалентной системы, вычислив предварительно (и то не всегда) из условий равновесия опорные реакции последней.

Недостатком первого способа является то обстоятельство, что для его реализации необходимо дополнительно построить эпюры Qi, Ni (i=1, 2, …,n), Qf, Nf, которые не используются в расчете методом сил и поэтому не были построены ранее.

В связи с этим для построения окончательных эпюр более рациональным представляется второй способ, а условие (8) можно использовать в качестве дополнительной проверки.

 

Проверка окончательной эпюры изгибающих моментов

 

Эта проверка выполняется в двух вариантах: статическая и кинематическая.

При статической проверке, выполняемой обычно для рам, вырезаются узлы и записываются условия их равновесия под действием узловых сосредоточенных моментов и изгибающих моментов на концах стержней. Эта проверка является вспомогательной и выполняется автоматически при правильных эпюрах изгибающих моментов в основной системе и при выполнении кинематической проверки.

Статическая проверка эпюр Q и N состоит в том, что для любой отсеченной части рамы сумма проекций на две оси всех действующих сил – внешних нагрузок и  внутренних усилий – должна быть равна нулю.

Основной проверкой окончательной эпюры моментов в методе сил является кинематическая проверка, которая может быть построчной или универсальной.<br /> При построчной проверке каждая единичная эпюра моментов перемножается с окончательной эпюрой моментов М:

 

 

Таким образом, в результате перемножения каждой единичной эпюры с окончательной эпюрой моментов получим ноль:

 

Вариантом построчной проверки является проверка по замкнутомуконтуру, состоящая в том, что сумма приведенных (т.е. деленных на жесткость соответствующего стержня или его участка) площадь эпюры М, находящихся внутри каждого замкнутого бесшарнирного контура, должна быть равна сумме приведенных площадей, находящихся снаружи этого контура.

Суммируя выражения типа (11) для всех n, получим выражение, служащее для универсальной кинематической проверки окончательной эпюры изгибающих моментов:

 

 

Формулу (12) можно интерпретировать следующим образом: условное перемещение эквивалентной, или, что то же самое, заданной системы по направлению всех неизвестных от действия всех неизвестных и внешних нагрузок, равно нулю.

 

Определение перемещений в статически неопределимых системах

 

Для определения перемещения в статически неопределимой системе используется тождественность заданной и эквивалентной систем в том смысле, что если условия совместности деформаций выполняются, т.е. справедливы уравнения (4), то перемещения в эквивалентной системе соответствуют перемещениям заданной системы. Тогда, построив для основной системы эпюру изгибающих моментов от единичной силы (или единичного момента) приложенной в направлении искомого перемещения, величину перемещения находим по формуле:

 

 

 

где М – эпюра изгибающих моментов от внешней нагрузки, построенная для статически неопределимой системы.

Отметим, что при вычислении перемещения можно поступить и наоборот: единичную эпюру моментов построить в статически неопределимой заданной системе, а эпюру моментов от внешних нагрузок М – в основной (статически определимой) системе.

 

Пример расчета

 

Построить эпюры продольных, поперечных сил и изгибающих моментов для плоской рамы (рис.3,а).

Степень статической неопределимости рамы:

n = r — s = 4 — 3 = 1

 

Выбираем основную систему, отбрасывая на правой опоре горизонтальный стержень (рис.3,б),  т.е. заменяем шарнирно-неподвижною опору на шарнирно-подвижную. На базе основной системы формируем эквивалентную систему (рис.3,в).

Заменяя реакцию лишней связи соответствующей единичной силой, (рис. 3,г) строим эпюру моментов M1 (рис.3,д).

Грузовая эпюра моментов (рис.3,ж), построенная от одновременного действия всех внешних нагрузок (рис.3,е), является знакопеременной на участке, где действует нагрузка q. Это создает определенные трудности (хотя и не непреодолимые!) при ее перемножении с единичной эпюрой M1. В связи с этим целесообразно построить две грузовых эпюры – отдельно от нагрузки q (эпюра Mq) и от совместного действия F и M (эпюра MF). Эти варианты нагружения и эпюры представлены на рис.3,з и рис.3,а,б,в.

При таком разбиении внешней нагрузки каноническое уравнение метода сил содержит два грузовых перемещения и имеет вид:

 

 

Вычислим коэффициенты канонического уравнения:

 

 

Реакция лишних связи:

 

Эпюры Nz, Qy, Mx для заданной системы, загруженной нагрузками F, M, q и X1 (рис.3,г) представлены на рис.3,д,е,ж.

Как уже говорилось, при построении эпюр Nz и Q в рамах ординаты можно откладывать в любую сторону, но обязательно указывать знаки; а при построении эпюр Mx знаки можно не указывать, но обязательно откладывать ординаты со стороны сжатых волокон соответствующих элементов.

В рассмотренном примере универсальная проверка правильности вычисления коэффициентов канонического уравнения и свободных членов не выполнялась, так как рама имеет степень статической неопределимости n = 1, а, значит, суммарная единичная эпюра (если ее построить) совпадет с единичной эпюрой M1. В этом случае можно (и желательно!) проверить правильность выполнения расчета при помощи универсальной кинематической проверки окончательной эпюры моментов Mx.

Выполним эту проверку для рамы, рассмотренной в последнем примере (рис.3,а). Должно выполняться условие:

 

Покажем отдельно фрагменты перемножаемых эпюр (рис.3,д и рис.4,ж) для ригеля (рис.5,а,б) и стойки (рис.5,в,г) с указанением всех характерных размеров и соответствующих им ординат. Причем стойка (на рис.5,в,г) показана в горизонтальном положении.

Точка пересечения кривой на ригеле эпюры  Mx с осью (рис.5,б) определяется следующим образом. Обозначим координату произвольного сечения, отсчитываемую от правого конца ригеля, через z, тогда момент Mx определяется в виде:

 

 

откуда z = 3,77 м (второй корень этого уравнения лишен физического смысла).

 

рис. 3

 

 

рис. 4

 

 

следовательно, расчет выполнен правильно.

 

 

 

Заказать решение

Контрольные и курсовые, решение задач по сопромату, теормеху…

На нашем сайте Вы можете скачать абсолютно бесплатно следующие материалы:

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Методичка с заданиями по сопромату и примерами решения задач:
1) Для рамы построить эпюры нормальных сил, поперечных сил и изгибающих моментов, подобрать размеры поперечного сечения и определить вертикальное и угловое перемещения сечения А при следующих данных: q = 20 кН/м, m = 40 кН м, l = R = 2 м, поперечное сечение ][—два швеллера.
2) Подобрать диаметр вала АВ зубчатой передачи, при следующих данных: N = 73кВт, n1=1050 об/мин, D1 = 28 см, D2 = 58 см, D3 = 26 см, D4 = 42 см, l1 = 18 см, l2 = 20 см, l3 = 20 см, b = 135°, g = 180°, a = 20°, n = 1,4…1,7, поверхность вала шлифованная, материал вала сталь 45.
плюс СПРАВОЧНЫЕ ДАННЫЕ К РАСЧЕТНО – ПРОЕКТИРОВОЧНЫМ И КУРСОВЫМ РАБОТАМ ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ Скачать>>>>>

Методичка с заданиями по сопромату с теорией и примерами решения задач:
1) расчет статически неопределимой стержневой системы с учетом изменения температуры. Абсолютно жесткий брус, нагруженный заданной нагрузкой, поддерживается шарнирно-неподвижной опорой и двумя деформируемыми стальными стержнями. Температура стержня в период эксплуатации может повышаться на величину дельта Т. Кроме того, стержень изготовлен на величину дельта длиннее проектного размера. Неточность изготовления дельта устраняется сжатием стержня при монтаже. Определить усилия в стержнях в период эксплуатации.
2) Подбор сечения балки. Для стальной балки построить эпюры и подобрать двутавровое сечение.
3) Применение метода начальных параметров к раскрытию статически неопределимой балки. Для балки постоянного сечения построить эпюры поперечных сил, изгибающих моментов и упругую линию балки. Скачать>>>>>

---

Чтобы заказать решение задач по сопромату, теормеху, материаловедению, присылайте свои условия задач на
e-mail: [email protected]

---

Расчетно-проектировочные работы по дисциплине «Сопротивление материалов» с примерами выполнения
1. Для стержня с прямой продольной осью определить на каждом участке стержня нормальные силы N, нормальные напряжения σ , относительные деформации ε и перемещение поперечных сечений вдоль оси стержня. После этого построить эпюры N,σ,ε,δ. 2. Для стержневой системы определить нормальные напряжения в поперечных сечениях стержней и перемещение точки К. Модуль упругости Е=2*1011 Па.
3. Стальной стержень, жёстко защемлённый левым концом и имеющий зазор Δ между правым торцом и неподатливой плоскостью, нагружен силами Р1 и Р2 и одновременно равномерно изменяется температура на Δ t° С левой части 1 длиной 13 или правой части 2 длиной l2+ l1. Построить эпюры N,σ,ε и перемещений поперечных сечений вдоль продольной оси стержня.
4. Для расчетной схемы балки написать выражения поперечных сил Q и изгибающих моментов М для каждого участка в общем виде и построить эпюры Q и М.
5. Для расчетной схемы балки написать выражения поперечных сил Q и изгибающих моментов М для каждого участка балки в общем виде и построить эпюры Q и М.
6. Для расчетной схемы балки написать выражения поперечных сил Q и изгибающих моментов М для каждого участка в общем виде и построить эпюры Q и М. Для опасного поперечного сечения определить максимальное нормальное напряжение σ по модулю и нормальное напряжение в точке К, координата которой Ук. Затем построить эпюру распределения нормальных напряжений по высоте сечения. Скачать>>>>>

РАСЧЕТ РАМ
пример решения задачи (краткое условие: построить эпюры M, Q, N в раме. Найти перемещения заданной точки рамы в определенном направлении). Скачать>>>>>

Программа для построения эпюр Скачать>>>>>

Кручение бруса с некруглым поперечным сечением Скачать>>>>>

Изгиб (теория, формулы) Скачать>>>>>

---

Чтобы заказать решение задач по сопромату, теормеху, материаловедению, присылайте свои условия задач на
e-mail: [email protected]

---

Методические указания к контрольным работам.
Примеры решения задач:
растяжение-сжатие и кручение стержней;
построение эпюр внутренних силовых факторов при изгибе;
расчет на прочность при изгибе.
Всего 9 задач. Скачать>>>>>

РГР-1: пример расчета плоской рамы методом сил. Скачать>>>>>

РГР-2: пример расчета плоской рамы методом сил. Скачать>>>>>

РГР-3: пример расчета плоской рамы методом перемещений. Скачать>>>>>

Лекция по сопромату — плоский изгиб. Решения задач. Скачать>>>>>

Примеры решения задач по сопромату:
1) Проверить прочность бруса.
2) Для промежуточного вала двухступенчатого редуктора требуется: а) построить эпюру крутящих моментов, эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях, эпюру продольных сил; б) определить требуемый диаметр вала. Расчет вести по гипотезе наибольших касательных напряжений.
3) Расчет на сопротивление усталости. Усталостное разрушение обычно происходит при напряжениях в несколько раз меньших, чем предельные. Причинами такого разрушения являются: динамический характер нагрузки (циклически изменяющаяся нагрузка) и реакция материала детали на такую нагрузку, наличие концентраторов напряжения (шпоночные канавки, проточки, сверления, резкий перепад размеров), упрочнение поверхности и др. Расчет выполняют в форме проверки коэффициента S запаса прочности. Скачать>>>>>

Сопромат, пример решения задачи
Для двухопорной балки постоянной жесткости EIx в общем виде определить методом Мора и способом Верещагина прогибы в точках «С», «D» и с помощью алгебры матриц — угол поворота на правой опоре. Используя вид эпюры Mx и вычисленные значения прогибов и углов поворота, показать для балки характер изогнутой оси балки. Скачать>>>>>

«Сопротивление материалов», Учебно-методическое пособие, Буланов В.Е.
Даны общие положения по изучению тем курса «Сопротивление материалов», вопросы для самопроверки, задания для контрольных работ, примеры их выполнения; предложены тесты по изучаемой дисциплине, список рекомендуемой литературы. Учебно-методическое пособие предназначено для студентов заочного отделения специальности 2903. Скачать>>>>>

---

Чтобы заказать решение задач по сопромату, теормеху, материаловедению, присылайте свои условия задач на
e-mail: [email protected]

---

---

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Примеры решения задач по теормеху (теоретической механике)
1. При пуске в ход электрической лебедки к барабану приложен вращающий момент, пропорциональный времени. Груз массы m поднимается при помощи каната, намотанного на барабан. Определить угловую скорость барабана. Барабан считать однородным сплошным цилиндром массы m1 и радиусом r. В начальный момент система находилась в покое.
2. Колесо массы m катится по горизонтальному прямолинейному рельсу. К колесу приложен вращающий момент… Какому условию должен удовлетворять вращающий момент, чтобы колесо катилось без проскальзывания?
3. Каток массы.. и радиуса.. катится без проскальзывания по горизонтальной поверхности под действием приложенного к нему постоянного вращающего момента. Трос, намотанный на боковую поверхность катка, сходит с него горизонтально и попадает на неподвижный блок массы.. и радиуса.. К свободному концу троса привязан груз массы.. Считая каток и блок сплошными однородными цилиндрами определить скорость оси катка, если в начальный момент система находилась в покое.
4. Колесо скатывается без проскальзывания по наклонной плоскости…. Определить скорость оси колеса, натяжение троса…
5. Определить зависимость скорости оси колеса от числа оборотов блока… Скачать>>>>>

---

МАТЕРИАЛОВЕДЕНИЕ
Курсовая работа по материалам
План:
1.Введение
2.Основные характеристики кристаллической решетки
3.Скорость охлаждения при закалке и факторы влияющие на выбор скорости охлаждения при закалке
4.Диаграмма состояния системы медь-серебро. Свойства сплавов в данной системе
5.Диаграмма состояния железо-углерод. Описание данной диаграммы.
6.Углеродистые стали У8 и 35
7.Расшифровки марок данных сталей и их свойства.
Скачать>>>>>

Технология термомеханической обработки в машиностроении (глава из книги Лахтина). Скачать>>>>>

Кривые охлаждения сплава железо-карбид железа(цементит) для сплавов с содержанием углерода 2,14-4,3%; 4,3%; 4,3-6,67%. Скачать>>>>>

---

Чтобы заказать решение задач по сопромату, теормеху, материаловедению, присылайте свои условия задач на
e-mail: [email protected]

---

Материаловедение, методичка с примерами выполнения заданий по анализу фазовых превращений в двухкомпонентных сплавах, построение кривой охлаждения.Скачать>>>>>

Лекции по материаловедению, автор Мальцев И.М. Скачать>>>>>

Металловедение, учебник
А.П.Гуляев
Книга представляет собой фундаментальный учебник по курсу металловедения для студентов металлургических, машиностроительных и политехнических вузов. В книге излагается общая теория сплавов, рассматриваются свойства и структуры углеродистых и легированных сталей, чугунов, жаропрочных, прецизионных и других сплавов, цветных металлов и их сплавов, а также теория и практика термической обработки металлов. В новое издание внесены изменения, вытекающие из развития металловедения за последние годы, и некоторые дополнения, содержащие справочные данные о составе и свойствах сплавов. Книга является не только учебником, но и монографией о металлах и их сплавах и в этом плане будет полезна инженерам и техникам промышленности.
Скачать часть 1>>>>>
Скачать часть 2>>>>>
Скачать часть 3>>>>>

---

ФИЗИКА

Методические указания к домашнему заданию по курсу общей физики, раздел: элементы квантовой механики. Примеры решения задач (всего 14 задач). Скачать>>>>>

Занятие по волновой природе микрочастиц. Краткая теория, примеры решения задач (всего 8 задач). Скачать>>>>>

Волновая теория высокоскоростных режимов обработки материалов резанием (статья). Скачать>>>>>

---

Чтобы заказать решение задач по сопромату, теормеху, материаловедению, присылайте свои условия задач на
e-mail: [email protected]

---

Физика, примеры решения задач:
Пример 1
Три точечных заряда по 1 нКл расположены в вершинах равностороннего треугольника. Какой заряд нужно поместить в центре треугольника, чтобы указанная система зарядов находилась в равновесии?

Пример 2
По тонкой нити, изогнутой по дуге окружности, равномерно распределен заряд с линейной плотностью τ = 10 нКл/м. Определить напряженность и потенциал электрического поля, создаваемого таким заряженным телом в точке, совпадающей с центром кривизны дуги. Длина нити составляет 1/3 длины окружности и равна 15 см.

Пример 1
Бесконечно длинный провод изогнут так, как показано на рисунке. Радиус R дуги окружности равен 10 см. Определить величину магнитной индукции поля, создаваемого в точке О током I = 80 А.

Пример 2
Электрон, пройдя ускоряющую разность потенциалов, стал двигаться в однородном магнитном поле с индукцией 50 мТл по винтовой линии с шагом 5 см и радиусом 1 см. Определить ускоряющую разность потенциалов, которую прошел электрон.

Пример 3
Ион, пройдя ускоряющую разность потенциалов 645 В, влетел в скрещенные под прямым углом однородные магнитное (В = 1,5 мТл) и электрическое (Е = 200 В/м) поля. Определить отношение заряда иона к его массе, если ион в указанных полях движется прямолинейно. Скачать>>>>>

---

ВЗАИМОЗАМЕНЯЕМОСТЬ И МЕТРОЛОГИЯ

Взаимозаменяемость, учебник

Основы взаимозаменяемости
Основные понятия и определения
Взаимозаменяемость гладких цилиндрических деталей
Общие положения
Неуказанные предельные отклонения размеров
Шероховатость поверхности
Точность формы и расположения
Суммарные отклонения и допуски формы и расположения поверхностей
Обозначение на чертежах допусков формы и расположения
Неуказанные допуски формы и расположения
Волнистость поверхности
Допуски на угловые размеры. Взаимозаменяемость конических соединений
Допуски угловых размеров
Взаимозаменяемость резьбовых соединений
Основные параметры метрической крепежной резьбы
Общие принципы взаимозаменяемости цилиндрических резьб
Допуски и посадки резьб с зазором
Допуски резьб с натягом и с переходными посадками
Стандартные резьбы общего и специального назначения
Допуски зубчатых и червячных передач
Плавность работы передачи
Контакт зубьев в передаче
Боковой зазор
Выбор степени точности и контролируемых параметров зубчатых передач
Допуски червячных цилиндрических передач
Допуски и посадки соединений с прямобочным профилем зубьев
Допуски и посадки шлицевых соединений с эвольвентным профилем зубьев
Контроль точности шлицевых соединений
Расчет допусков размеров, входящих в размерные цепи
Основные термины и определения, классификация размерных цепей
Теоретико-вероятностный метод расчета размерных цепей
Метод групповой взаимозаменяемости при селективной сборке
Метод регулирования и пригонки
Расчет плоских и пространственных размерных цепей
Скачать>>>>>

---

Чтобы заказать решение задач по сопромату, теормеху, материаловедению, присылайте свои условия задач на
e-mail: [email protected]

---

---

ХИМИЯ
Учебное пособие (Громов) Скачать>>>>>

Расчет рам. Жемочкин Б.Н. 1965 | Библиотека: книги по архитектуре и строительству

В книге изложены основные методы расчета плоских рам: сил, деформаций, моментных и угловых фокусов. Кратко излагается теория каждого метода и дается полное решение характерных числовых примеров инженерного расчета с построением эпюр внутренних сил. Помимо простых рам рассмотрены сложные многопролетные многоэтажные рамы с ломаными и криволинейными элементами. Кроме того, приводятся основные теоремы о деформациях упругих систем. Описаны некоторые из приближенных методов расчета. Книга предназначена для инженеров-проектировщиков, студентов вузов и аспирантов.

От издательства
Из предисловия автора к 1-му изданию
Введение. Понятие о рамах

Глава I. Общие сведения, основные теоремы о деформациях. Понятие о расчете рам
§ 1. Работа внешних сил
§ 2. Работа внутренних сил
§ 3. Зависимость между работой внешних и внутренних сил. Принцип Лагранжа. Теорема Мора
§ 4. Дополнительная и полная работа
§ 5. Перемещения. Определение перемещений аналитическим путем
§ 6. Теорема о взаимности перемещений
§ 7. Определение перемещений перемножением эпюр
§ 8. Потенциальная энергия
§ 9. Теорема о взаимности работ. Теорема Бетти
§ 10. Зависимость между потенциальной энергией, внешними силами и перемещениями. Теорема Кастилиано
§ 11. Различные способы расчета рам
§ 12. Применение на практике различных способов расчета

Глава II. Способ сил
§ 13. Общий порядок расчета рам способом сил
§ 14. Примеры расчета рам с одной лишней неизвестной
§ 15. Примеры расчета рам с двумя лишними неизвестными
§ 16. Примеры расчета рам с тремя лишними неизвестными
§ 17. Эпюры поперечных и продольных сил
§ 18. Объемлющие (огибающие) эпюры
§ 19. Упругий центр тяжести
§ 20. Примеры использования упругого центра тяжести
§ 21. Системы со многими неизвестными. Использование симметрии
§ 22. Групповые неизвестные
§ 23. Примеры расчета рам со многими неизвестными
§ 24. Поверка правильности построения эпюр
§ 25. Составление уравнений при помощи теорем Бетти, Мора и Кастилиано
§ 26. Решение уравнений
§ 27. Способ нулевых эпюр
§ 28. Пример расчета рамы способом нулевых эпюр
§ 29. Подбор нулевых вспомогательных эпюр
§ 30. Примеры расчета рам подбором нулевых вспомогательных эпюр
§ 31. Действие температуры
§ 32. Примеры расчета рам на действие температуры
§ 33. Линии влияния
§ 34. Примеры на построение линий влияния

Глава III. Способы трех и четырех моментов
§ 35. Уравнение трех моментов для неразрезной балки
§ 36. Расчет рам способом трех моментов
§ 37. Пример расчета рамы способом трех моментов
§ 38. Уравнение четырех моментов
§ 39. Общий порядок расчета рам способом четырех моментов
§ 40. Пример расчета рамы способом четырех моментов

Глава IV. Способ моментных фокусов
§ 41. Общий порядок расчета рам способом моментных фокусов
§ 42. Фокусные отношения. Коэффициенты распределения
§ 43. Моменты по концам загруженного элемента
§ 44. Моменты по концам повернувшегося элемента
§ 45. Примеры расчета рам способом моментных фокусов

Глава V. Способ деформаций
§ 46. Условные обозначения. Правило знаков
§ 47. Общий порядок расчета рам способом деформаций
§ 48. Моменты
§ 49. Поперечные силы
§ 50. Зависимость между линейными смещениями. Диаграммы
§ 51. Основные уравнения угловых деформаций
§ 52. Дополнительные уравнения
§ 53. Примеры расчета рам способом угловых деформаций
§ 54. Решение уравнений способом последовательных приближений
§ 55. Действие температуры
§ 56. Примеры расчета рам на действие температуры
§ 57. Расчет рам с криволинейными и ломаными элементами
§ 58. Пример расчета рамы с криволинейным элементом
§ 59, Линии влияния
§ 60. Примеры на построение линий влияния
§ 61. Применение общего приема для составления уравнений
§ 62. Пример расчета рамы при помощи групповых неизвестных деформаций
§ 63. Смешанные способы
§ 64. Пример расчета рамы смешанным способом

Глава VI. Способ угловых фокусов
§ 65. Общий порядок расчета рам способом угловых фокусов
§ 66. Фокусные отношения
§ 67. Углы поворота по концам загруженного элемента
§ 68. Углы поворота по концам повернувшегося элемента
§ 69. Примеры расчета рам способом угловых фокусов
§ 70. Расчет рам с непараллельными стойками
§ 71. Пример расчета рам с непараллельными стойками

Глава VII. Приближенные способы расчета
§ 72. Постановка вопроса. Случаи применения приближенных способов
§ 73. Простейшие способы расчета рам на вертикальную нагрузку
§ 74. Учет изгиба стоек в многоэтажных рамах при вертикальной нагрузке
§ 75. Примеры расчета рам простейшими способами
§ 76. Более точные способы расчета многоэтажных и многопролетных рам на вертикальную нагрузку
§ 77. Пример расчета рамы более точным способом
§ 78. Расчет рам на горизонтальную нагрузку
§ 79. Пример расчета рамы на горизонтальную нагрузку

От издательства

Предыдущее, первое издание книги профессора Бориса Николаевича Жемочкина (1887—1961 гг.) вышло в свет в 1933 г. в качестве учебного пособия для высших строительных учебных заведений. Эта работа нашла широкое применение не только в учебном процессе; она явилась наиболее полным специализированным пособием для инженеров-проектировщиков в их повседневной деятельности и оказала сильное влияние на дальнейшее развитие методов расчета статически неопределимых систем.

Необходимость нового издания книги «Расчет рам», пользующейся и до настоящего времени большой популярностью, подсказывается прежде всего тем, что здесь компактно изложен учебный курс предмета и дано достаточное число примеров, хорошо разъясняющих вопросы теории. Помимо так называемых классических, основных методов расчета (сил, деформаций, трех и четырех моментов, моментных и угловых фокусов — разработкой последнего мы обязаны Б.Н. Жемочкину), являющихся основой для приближенных методов, здесь изложены некоторые из приближенных методов, разработанных автором. Решение примеров доведено до окончательных результатов; объяснения к ним отличаются ясностью и сжатостью изложения. В состав книги входят и вопросы решения систем линейных уравнений — способом Гаусса и последовательными приближениями.

В новом издании книги почти полностью сохранен текст автора, сделаны лишь незначительные сокращения в нем, исключен параграф, касавшийся применения моментов высоких степеней, изъято четыре примера. В главу о способе угловых фокусов добавлен материал, вошедший в специальное пособие автора «Способ угловых фокусов», выпущенное Стройиздатом в 1932 г.

Из предисловия автора к 1-му изданию

В книге изложены различные применяющиеся на практике способы расчета рам. Знание их необходимо всем проектирующим рамные конструкции для того, чтобы из числа имеющихся способов они могли всегда выбрать тот, который в данных условиях позволяет наиболее просто и легко сделать необходимый расчет.

Книга построена таким образом, что в первой главе даны общие понятия и основные теоремы о деформациях упругих систем; каждому способу расчета в дальнейшем посвящена отдельная глава, наконец в последней главе излагаются приближенные способы расчета рам, которыми можно руководствоваться при проектировании как неответственных сооружений, так и ответственных в тех случаях, когда некоторыми факторами вследствие их малого влияния допустимо пренебречь.

Изложение каждого способа расчета сопровождается достаточным количеством практических примеров.

Новосибирский государственный архитектурно-строительный университет — Сибстрин

11 мая приглашаем на торжественный митинг, посвященный 76-ой годовщине Победы в Великой Отечественной войне! 11 мая 2021 года (вторник) в 13.40 на главной площади НГАСУ (Сибстрин) состоится торжественный митинг, посвященный 76-ой годовщине Победы в Великой Отечественной войне. По традиции, в рамках мероприятия пройдет возложение гирлянды и цветов к памятнику воинов-сибстриновцев. С торжественным словом к студентам, сотрудникам и преподавателям обратится ректор университета Ю.Л. Сколубович. Митинг завершится минутой молчания в память всех павших в годы войны. Перед началом торжественного митинга будет организована акция «Георгиевская ленточка», начало в 13.30.

Поздравление ректора Ю.Л. Сколубовича с Днем Победы Сердечно поздравляю ветеранов Великой Отечественной войны, преподавателей, сотрудников и студентов, весь коллектив университета с 76-летием Великой Победы! 9 Мая – священная дата в отечественной истории. Это день нашей общей Победы, день славы, доблести, силы духа. С каждым годом мы все дальше отдаляемся от мая 45-го года. Но память наша не имеет возрастных границ. НГАСУ (Сибстрин) внес достойный вклад в достижение Победы. Из стен нашего вуза на фронты войны было призвано 400 человек: 245 студентов, 36 преподавателей, 3 аспиранта, 116 других сотрудников и рабочих. Все они героически защищали Родину от фашизма, отдавая силы, здоровье и саму жизнь ради Победы. 106 имен высечены на памятнике воинам-сибстриновцам, погибшим в годы Великой Отечественной. В это же время самоотверженным трудом в тылу ученые Сибстрина внесли весомый вклад в развитие строительной…

Творческие коллективы НГАСУ (Сибстрин) поздравляют всех с праздником Великой Победы! Творческие коллективы Новосибирского государственного архитектурно-строительного университета (Сибстрин) поздравляют всех ветеранов, преподавателей, сотрудников и студентов с праздником Великой Победы! Желаем крепкого здоровья, счастья, благополучия и мирного неба над головой! В качестве подарка Центр по внеучебной и воспитательной работе НГАСУ (Сибстрин) подготовил записи музыкальных и литературных композиций на военную тему. Песни «Ты вернись, сынок», «В синем небе облака» и стихотворение «Баллада о матери» исполнили вокальная студия «Мегаполис» и победительница конкурса видеочтений Анастасия Боканева.

Поздравление ректора НГАСУ (Сибстрин) с 1 мая Дорогие сотрудники, преподаватели, студенты, выпускники и партнеры! Поздравляю вас с 1 мая – Праздником весны и труда! Первомай всегда был и остается символом весеннего обновления, единства, уважения и почета к труду. Весенний лозунг «Мир! Труд! Май!» вселяет в нас новые силы и светлые надежды, объединяет и наполняет оптимизмом. В этот день хотелось бы поблагодарить наших преподавателей и ученых, которые своей работой прославляют Сибстрин далеко за его стенами. Мы гордимся успехами наших талантливых студентов и молодых ученых, среди которых много победителей олимпиад, конкурсов и фестивалей различного уровня…

4.4 Детальный анализ кадра | Узнайте о структурах

>> Когда вы закончите читать этот раздел, проверьте свое понимание с помощью интерактивной викторины внизу страницы.

Каркасные конструкции сложнее балок, потому что они не обязательно лежат вдоль прямой линии, как балки. В рамах могут быть как вертикальные элементы, так и элементы, наклоненные под углом. В первой части этого раздела обсуждаются типы нагрузок на наклонные стержни и способы их устранения.Затем он объяснит метод, который используется для анализа определенных кадров (с использованием тех же методов, которые мы использовали ранее для определенных лучей).

Наклонные нагрузки

Для стержней, которые наклонены под углом, часто удобнее всего проанализировать их, сначала преобразовав все нагрузки на стержень в локальное направление оси стержня (перпендикулярно и параллельно наклонному стержню). Этот процесс показан на рисунке 4.7.

Рисунок 4.7: Разрешение нагрузок на наклонные стержни в направлениях локальной оси

Геометрия образца наклонного элемента показана в верхней части рисунка 4.7. На рисунке показаны четыре различных типа наклонных нагрузок.

Первый тип показывает преобразование точечных нагрузок на наклонный элемент в параллельные и перпендикулярные составляющие.

Второй тип («ветровой») типичен для распределенных нагрузок, вызываемых ветровыми или другими напорными нагрузками. Распределенная нагрузка прикладывается прямо перпендикулярно наклонному элементу и распределяется по диагональной длине элемента (в данном случае $ L / cos \ theta $). Поскольку нагрузка уже перпендикулярна стержню, преобразование не требуется.

Третий тип («неподвижный») — это распределенная нагрузка, которая не прикладывается перпендикулярно к стержню. В этом случае он совмещен с направлением глобальной вертикальной оси для имитации эффекта вертикальной гравитационной (или «мертвой») нагрузки. Этот тип нагрузки также распределяется по длине диагонали элемента, поскольку источник нагрузки (в данном случае собственный вес элемента) также распределяется по длине диагонали. В этом случае можно использовать прямое тригонометрическое преобразование, чтобы разделить вертикальную распределенную нагрузку на два разных компонента, один перпендикулярный элементу (что вызовет сдвиг и изгиб), а другой — параллельный элементу (что вызовет осевую нагрузку), как показано. на рисунке.

Четвертый и последний тип («снежный») представляет собой распределенную нагрузку, которая не перпендикулярна элементу и также распределяется не по длине элемента, а по его горизонтальной проекции (в данном случае расстояние $ L $). В случае снеговой нагрузки только определенное количество снега может упасть с определенной области неба, поэтому, чем больше наклон элемента, тем больше длина, на которую будет распространяться снег (таким образом, нагрузка на единицу длины стержня ниже).Общая вертикальная нагрузка здесь будет равна $ w_ {snow} L $, что меньше соответствующей общей вертикальной нагрузки от случая статической нагрузки, которая была равна $ w_ {dead} L / \ cos \ theta $. Прежде чем распределенная нагрузка снегового типа может быть разделена на перпендикулярные и параллельные компоненты, ее необходимо равномерно распределить по диагональной длине элемента (вместо того, чтобы равномерно распределяться по горизонтальной проекции элемента). Если мы разделим общую вертикальную нагрузку $ w_ {snow} L $ на общую длину диагонали $ L / \ cos \ theta $, то мы получим новую распределенную вертикальную нагрузку, равную $ w_ {snow} \ cos \ theta $, которая сейчас распределены по диагонали стержня.Отсюда нагрузка может быть разделена на перпендикулярные и параллельные компоненты, как это было сделано для статической нагрузки, в результате чего получаются компоненты, показанные на рисунке 4.7.

Метод анализа детерминированных кадров

Анализ определенных кадров очень похож на анализ определенных балок, за исключением того, что вам необходимо разделить каркас на отдельные элементы, чтобы каждый из них можно было анализировать отдельно как балки. Рамы также имеют дополнительную сложность из-за потенциально наклонных элементов, а также учет осевых сил в анализе, которым мы ранее пренебрегли при анализе балок.

Общие шаги для анализа детерминированного кадра:

1. Используйте равновесие, чтобы найти все силы реакции.
2. Разделите раму на отдельные элементы.

   Любая точечная нагрузка или момент, которые действуют непосредственно на соединение между двумя или более стержнями, должны быть приложены только к ОДНОМУ из стержней при их разделении. Неважно, какой элемент получает точечную нагрузку, если только на одном.

3. Найдите все силы на концах каждого элемента (на концах любого элемента или в местах разрезов между этим элементом и соседним элементом), используя равновесие на диаграммах свободного тела каждого элемента отдельно.
4. Разрешить все нагрузки на стержень (концевые нагрузки и моменты, а также нагрузки по длине стержня) в локальных направлениях оси стержня (т. Е. Перпендикулярно стержню и параллельно ему).
5. Теперь диаграммы осевого момента, поперечной силы и изгибающего момента можно найти, решив каждый элемент, как если бы это была отдельная балка (см. Раздел 4.3).
6. (При необходимости) Используйте результаты для каждого элемента, чтобы нарисовать диаграммы общей осевой силы, поперечной силы и изгибающего момента для всей конструкции рамы.

Пример

Анализ определенных кадров будет продемонстрирован на примере структуры, показанной на Рисунке 4.8. Нарисуйте диаграммы осевого усилия, сдвига и момента для всех элементов конструкции.

Рисунок 4.8: Пример структуры кадра определения

В качестве первого шага мы можем проверить, что структура устойчива и детерминирована, используя методы из главы 2. Используя уравнение \ eqref {eq: deg-indet}:

\ begin {уравнение} \ boxed {i_e = 3m + r — (3j + e_c)} \ label {eq: deg-indet} \ tag {1} \ end {уравнение} \ begin {align *} i_e & = 3m + r — (3j + e_c) \\ & = 3 (3) + 3 — (3 (4) + 0) \\ & = 0 \ end {align *}

Так как $ i_e = 0 $, то структура определена.Он также стабилен, поскольку отсутствуют механизмы разрушения.

Следующим шагом в анализе является определение сил реакции. В этой конструкции есть три силы реакции: $ A_x $ и $ A_y $ на левом штифте и $ D_y $ на правом ролике. Мы найдем реакции, используя равновесие на всей конструкции. Схема конструкции свободного тела представлена ​​на рис. 4.9.

Рисунок 4.9: Пример схемы свободного тела рамы

Начиная с момента равновесия относительно точки A, чтобы найти вертикальную реакцию в точке D ($ D_y $):

\ begin {align *} \ curvearrowleft \ sum M_A & = 0 \\ -75 (5) -25 (7) (3.5) + D_y (7) & = 0 \\ D_y & = +141.1 \ mathrm {\, kN} \ end {align *} \ begin {уравнение *} \ boxed {D_y = 141.1 \ mathrm {\, kN} \ uparrow} \ end {уравнение *}

Для горизонтального равновесия горизонтальная реакция в точке A ($ A_x $) изначально предполагается положительной (указывает вправо):

\ begin {align *} \ rightarrow \ sum F_x & = 0 \\ A_x + 75 & = 0 \\ A_x & = -75 \ mathrm {\, kN} \ end {align *}

Но отрицательное решение говорит нам, что $ A_x $ на самом деле указывает налево (как показано на рисунке 4.9):

\ begin {уравнение *} \ boxed {A_x = 75 \ mathrm {\, kN} \ leftarrow} \ end {уравнение *}

Вертикальное равновесие:

\ begin {align *} \ uparrow \ sum F_y & = 0 \\ A_y — 25 (7) + D_y & = 0 \\ A_y — 25 (7) + 141.1 & = 0 \\ A_y & = +33.9 \ mathrm {\, ​​kN} \ end {align *} \ begin {формула *} \ boxed {A_y = 33.9 \ mathrm {\, kN} \ uparrow} \ end {формула *}

Теперь конструкцию нужно разделить на отдельные элементы. Наша структура будет разделена на трех членов: AB, BC и CD.Мы рассмотрим каждый из них по очереди, решая все неизвестные концевые силы, осевую силу, поперечную силу и момент, прежде чем перейти к следующему элементу. Схема свободного тела и решение для элемента AB показаны на рисунке 4.10.

Рисунок 4.10: Пример элемента рамы AB

Диаграмма свободного тела (FBD) слева на рис. 4.10 показывает всю информацию, которая в настоящее время известна об элементе AB. Он содержит известные реакции в основании $ A_x $ и $ A_y $. Кроме того, также показаны неизвестные силы на разрезе в точке B.{AB} = 33.9 \ mathrm {\, kN} \ downarrow} \ end {уравнение *}

Результирующий решенный FBD показан на рисунке 4.10.

Теперь, когда мы знаем все силы, действующие на элемент AB, мы можем использовать методы анализа балки, чтобы найти диаграммы осевого, сдвигового и моментного моментов, которые показаны на рис. 4.10.

Конструкция диаграммы осевых сил аналогична диаграмме поперечных сил, начиная с одного конца, силы, параллельные элементу, вызывающие сжатие, перемещают диаграмму осевых сил в одну сторону, а силы, вызывающие растяжение, перемещают ее в другую. способ.Неважно, какой путь находится на диаграмме, если на диаграмме указаны стороны сжатия и растяжения. Сторона сжатия на диаграмме осевых сил обозначена на рисунке буквой «C». В этом случае мы можем начать с точки A, предполагая, что элемент закреплен на другом конце (точка B). Вертикальная сила реакции в точке A, равная $ 49,5 \ mathrm {\, kN} $, вызывает сжатие элемента, поэтому мы перемещаем диаграмму осевых сил вправо на ту же величину и указываем, что эта сторона находится в состоянии сжатия.Нет другой нагрузки, параллельной стержню до точки B, которая имеет силу $ 49,5 \ mathrm {\, kN} $, которая вызовет напряжение в элементе, если он оттолкнет его от B (предположим, что сила действует чуть ниже точки Б). Это сдвигает диаграмму осевых сил назад влево, встречаясь с осью стержня в точке 0.

Диаграммы сдвига и момента для этого элемента просты и построены снизу вверх. Диаграмма моментов «нарисована со стороны сжатия». Это означает, что для любой стороны элемента, которая показывает момент на диаграмме моментов, крайнее волокно на этой стороне балки будет сжиматься.Для этого участника AB весь момент находится слева от участника. Следовательно, левая сторона элемента находится в состоянии сжатия (а правая сторона в состоянии растяжения).

В месте разреза стрелки момента всегда указывают на сторону сжатия элемента.

Теперь, когда элемент AB полностью решен, мы можем перейти к следующему элементу, члену BC, который показан на рисунке 4.11.

Рисунок 4.11: Пример элемента рамы BC Равновесие и разрешение сил в направлении локальной оси

Часть (а) Рисунка 4.11 показана диаграмма свободного тела элемента BC со всей известной в настоящее время информацией. Поскольку элементы AB и BC находятся по обе стороны от разреза в точке B, силы и моменты должны передаваться в этой точке. Итак, мы можем взять силы в точке B от стержня AB и применить их к точке B на стержне BC; однако мы должны быть уверены, что изменили направление сил, поскольку силы и моменты должны быть равными и противоположными по обе стороны от разреза (как ранее обсуждалось в разделе 1.6). Горизонтальная сила в разрезе в точке B меняет направление справа налево, вертикальная сила изменяется с вниз на вверх, а момент изменяется с против часовой стрелки на по часовой стрелке.{BC} = 141.1 \ mathrm {\, kN} \ uparrow} \ end {уравнение *}

Полученная в результате диаграмма свободного тела показана в части (b) рисунка 4.11. Поскольку стержень BC является наклонным стержнем, нам необходимо разрешить все силы в локальных направлениях стержня (т. Е. Перпендикулярно и параллельно стержню), прежде чем мы сможем найти осевое усилие, сдвиг и момент на стержне. Этот процесс показан в частях (c) и (d) рисунка. В части (c) показано, как преобразовать горизонтальные и вертикальные силы в точке B в силы, перпендикулярные и параллельные стержню BC.\ circ} \\ P_ {para} & = 62.8 \ mathrm {\, kN} \ swarrow \ text {(параллельно BC)} \ end {align *}

Такой же процесс выполняется для точечных нагрузок в точке C.

В части (d) рисунка 4.11 показаны результирующие точечные нагрузки (параллельные и перпендикулярные) на любом конце элемента. Он также показывает распределенную нагрузку, разрешенную в направлениях локальной оси (стержня). Распределенная нагрузка снежного типа на балку разложена на перпендикулярное и параллельное направления с использованием выражений, ранее показанных на рисунке 4.2} = 7.28 \ mathrm {\, m} $) длиннее горизонтальной проекции ($ 7 \ mathrm {\, m} $).

Теперь, когда все нагрузки на элемент BC известны, диаграммы осей, сдвига и моментов могут быть построены с использованием методов расчета балок. Этот процесс показан на рисунке 4.12.

Рисунок 4.12: Пример элемента рамы BC Осевое, сдвиг и момент

Диаграмма осевых сил непостоянна для элемента BC, как показано на рисунке 4.12, потому что распределенная нагрузка снегового типа на элемент имеет параллельный компонент, который действует по длине элемента.Эту параллельную распределенную нагрузку можно назвать тяговым усилием по длине элемента. Двигаясь слева направо, стержень начинает с натяжения $ 62,8 \ mathrm {\, kN} $, которое затем постепенно увеличивается за счет тяги в том же направлении $ 6.59 \ mathrm {\, kN / m} $, которая перемещает диаграмма осевых сил дальше в сторону растяжения. В результате наклон на диаграмме осевых сил также равен $ 6.59 \ mathrm {\, kN / m} $. На правом конце элемента окончательное сжатие (в обратном направлении) 110 долларов.8 \ mathrm {\, kN} $ возвращает диаграмму осевых сил к нулю.

Диаграммы поперечной силы и изгибающего момента построены, как и раньше, с особым вниманием к тому, чтобы наклон диаграммы момента в любой точке был прямо равен значению диаграммы поперечной силы в той же точке. Моментная диаграмма, показанная на рисунке 4.12, начинается с прыжка вверх из-за момента по часовой стрелке в точке B, затем перемещается еще выше из-за сдвига между точками B и B ‘, прежде чем снова упасть между точками B’ и C.Важно определить максимальный момент и место его возникновения. Значение максимального момента легко найти, добавив момент в точке B ($ 600 \ mathrm {\, kNm} $) к площади под диаграммой поперечных сил между точками B и B ‘(треугольник высотой $ 53,2 \ mathrm {\, kN} $). Чтобы найти площадь этого треугольника, нам нужно знать длину основания. Это можно найти, используя аналогичные треугольники, как показано (общая длина элемента, умноженная на высоту маленького треугольника, деленная на общую высоту обоих треугольников).В этом случае длина меньшего треугольника составляет $ 2.303 \ mathrm {\, m} $, как показано. Это местоположение точки максимального момента, которую следует обозначить на диаграмме моментов. При такой длине площадь под диаграммой поперечных сил между точками B и B ‘равна $ 0,5 (53,2) (2.303) = 61,2 \ mathrm {\, kNm} $. Это дает максимальный момент $ 600 + 61.2 = 661.2 \ mathrm {\, kNm} $ в точке $ 2.303 \ mathrm {\, m} $ из точки B (как показано на рисунке 4.12).

Поскольку форма диаграммы поперечных сил является линейной, тогда форма диаграммы моментов должна быть параболической.Форму параболы можно легко определить, нарисовав наклон диаграммы моментов на обоих концах, как показано на рис. 4.12, и определив места с нулевым наклоном, то есть точки, в которых диаграмма поперечных сил равна нулю. Эта диаграмма моментов снова нарисована на стороне сжатия элемента, и можно видеть, что, как упоминалось ранее, моменты точки на концах элемента указывают на сторону сжатия балки на обоих концах.

Теперь, когда член BC полностью решен, мы можем перейти к последнему члену, члену CD, который показан на рисунке 4.13.

Рисунок 4.13: Пример элемента рамы CD

Схема свободного тела элемента CD, показанная на рис. 4.13, включает всю информацию, известную до этого момента (включая силы противоположного направления от элемента BC на другой стороне разреза в точке C). Как показано на этом рисунке, нет никаких неизвестных сил, которые необходимо найти для члена CD. Обычно это происходит с последним элементом при анализе рамы. Мы уже определили силы в точке D, когда нашли реакции, используя глобальное равновесие; однако мы можем использовать равновесие на члене CD как проверку правильности решения остальной части кадра.Если мы выполняем эту проверку и равновесие не достигается, значит, мы допустили ошибку на одном из предыдущих шагов. Итак, давайте проверим равновесие для участника CD:

\ begin {align *} \ curvearrowleft \ sum M_C & = 0 \\ -374,8 + 75 (5) & = 0 \; \ checkmark \ end {align *} \ begin {align *} \ rightarrow \ sum F_x & = 0 \\ 75 — 75 & = 0 \; \ checkmark \ end {align *} \ begin {align *} \ uparrow \ sum F_y & = 0 \\ 141.1 — 141.1 & = 0 \; \ checkmark \ end {align *}

Все уравнения равновесия удовлетворяются, поэтому мы можем быть уверены в правильности нашего решения.

Зная все силы на элементе CD, мы можем построить осевые диаграммы, диаграммы сдвига и моментов, используя методы расчета балок, как показано на рис. 4.13 (попробуйте сами!).

Теперь, когда все диаграммы осей, сдвигов и моментов построены для каждого элемента, последним необязательным шагом является объединение их в единую диаграмму, которая показывает осевое усилие, сдвиг и момент для всей конструкции. Эти сводные диаграммы показаны на Рисунке 4.14.

Рисунок 4.14: Пример краткого описания кадрового решения

Карта механики — Анализ рам и машин

Процесс, используемый для анализа рам и машин, включает разбиение конструкции на отдельные компоненты для определения сил, действующих на каждый компонент. Иногда конструкция в целом может быть проанализирована как твердое тело, и каждый компонент всегда может быть проанализирован как твердое тело.

Процесс, используемый для анализа рам и машин:

Процесс, используемый для анализа рам и машин, описан ниже:

1. Вначале обычно полезно маркировать элементы в вашей структуре. Это поможет вам сохранить все организованным и последовательным в последующем анализе. В этой книге мы все обозначим, присвоив каждому стыку буквы.
Первым шагом в анализе рам и машин является маркировка элементов.
2. Затем вам нужно будет определить, можем ли мы проанализировать всю конструкцию как твердое тело. Для этого конструкция должна быть жесткой независимо друг от друга. Это означает, что он будет жестким, даже если мы отделим его от опор. Если конструкция является независимо жесткой (нет машин, и только некоторые рамы будут независимо жесткими), проанализируйте конструкцию как единое твердое тело, чтобы определить силы реакции, действующие на конструкцию.Если конструкция не является жесткой по отдельности, пропустите этот шаг.
Если и только если конструкция является независимо жесткой, вам следует проанализировать всю конструкцию как единое твердое тело, чтобы найти силы реакции.
3. Затем вы нарисуете схему свободного тела для каждого из компонентов конструкции. Вам нужно будет включить все силы, действующие на каждый член, в том числе …
   • Сначала добавьте любую внешнюю реакцию или силы нагрузки, которые могут действовать на компоненты.
   • Второй идентифицирует любые два силовых элемента в конструкции. В своих точках соединения они вызовут силу неизвестной величины, но с известным направлением (силы будут действовать вдоль линии между двумя точками соединения на элементе).
   • Затем добавьте силы реакции (и, возможно, моменты) в точках соединения между не двумя силовыми элементами. Для сил с неизвестной величиной и направлением (например, в шарнирных соединениях) силы часто рисуются как имеющие неизвестные компоненты x и y (x, y и z для задач трехмерной фермы).
   • Помните, что силы в каждой из точек соединения будут парой Третьего закона Ньютона. Это означает, что если один элемент прилагает некоторую силу к другому элементу, тогда второй элемент будет оказывать равное и противоположное усилие обратно на первый. Когда мы вытягиваем неизвестные силы в точках соединения, мы должны убедиться, что силы, действующие на каждый элемент, на противоположны в направлении .
Разделите структуру на отдельные компоненты и нарисуйте схему свободного тела каждого компонента.Важно помнить, что силы в каждой точке соединения являются парой третьего закона Ньютона.
4. Запишите уравнения равновесия для каждого компонента, из которого вы нарисовали диаграмму свободного тела. Это будут вытянутые тела, поэтому вам нужно будет записать уравнения силы и момента.

Для двумерных задач у вас будет три возможных уравнения для каждого компонента, два уравнения силы и одно уравнение момента.

\ [\ sum \ vec {F} = 0 \]		\ [\ sum \ vec {M} = 0 \]
\ [\ сумма F_x = 0 \]	\ [\ сумма F_y = 0 \]	\ [\ сумма M_z = 0 \]

• Для трехмерных задач у вас будет шесть возможных уравнений для каждого компонента, три уравнения сил и три уравнения моментов.

\ [\ sum \ vec {F} = 0 \]
\ [\ сумма F_x = 0 \]	\ [\ сумма F_y = 0 \]	\ [\ sum F_z = 0 \]

\ [\ sum \ vec {M} = 0 \]
\ [\ сумма M_x = 0 \]	\ [\ сумма M_y = 0 \]	\ [\ сумма M_z = 0 \]

Наконец, решите уравнения равновесия для неизвестных.Вы можете делать это алгебраически, решая для одной переменной за раз, или вы можете использовать матричные уравнения, чтобы решить все сразу. Если какая-либо сила оказывается отрицательной, это означает, что сила на самом деле движется в направлении, противоположном тому, что указано на вашей исходной диаграмме свободного тела.

Вычисление реакций Проблемы и решения

Определите реакции на опорах для рамы, показанной на рис. 3.20 (а).

Solution
Схема свободного тела См. Рис.3.20 (б).
Статическая определенность Рама внутренне устойчива с r = 3. Следовательно, он статически определен.
Реакции опор

Определите реакции на опорах для балки, показанной на рис. 3.21 (a).

Solution
Схема свободного тела См. Рис. 3.21 (b).
Статическая определенность Балка внутренне нестабильна. Он состоит из трех жестких элементов AB, BE и EF, соединенных двумя внутренними шарнирами в точках B и E. Конструкция имеет r = 5 и ec = 2; поскольку r = 3 + ec, структура статически определена.

Остальные два уравнения равновесия теперь могут быть применены для определения двух оставшихся неизвестных,
Cy и Dy:

Важно понимать, что уравнения моментного равновесия включают моменты всех сил, действующих на всю поверхность. конструкции, тогда как моментные уравнения состояния включают только моменты тех сил, которые действуют на часть конструкции на одной стороне внутреннего шарнира.
Наконец, мы вычисляем Dy, используя уравнение равновесия,

Альтернативный метод Реакции балки можно определить альтернативно, применяя три уравнения равновесия к каждой из трех жестких частей AB, BE и EF балки. .Схемы свободного тела этих жестких частей показаны на рис. 3.21 (c). На этих диаграммах показаны внутренние силы, действующие через внутренние шарниры в точках B и E, в дополнение к приложенным нагрузкам и опорным реакциям. Обратите внимание, что внутренние силы, действующие на каждом конце B частей AB и BE и на каждом конце E частей BE и EF, имеют одинаковые величины, но противоположные значения, согласно закону действия и противодействия Ньютона.

Общее количество неизвестных (включая внутренние силы) — девять.Поскольку существует три уравнения равновесия для каждой из трех жестких частей, общее количество доступных уравнений также равно девяти (r + fi = 3nr = 9). Следовательно, все девять неизвестных (реакции плюс внутренние силы) могут быть определены из уравнений равновесия, а балка определена статически. Применяя три уравнения равновесия к части AB, получаем следующее:

Определите реакции на опорах для трехшарнирной арки, показанной на рис. 3.22 (а).

Solution
Схема свободного тела См. Рис. 3.22 (b).
Статическая определенность Дуга внутренне нестабильна; он состоит из двух жестких частей AB и BC, соединенных внутренним шарниром в точке B. Арка имеет r = 4 и ec = 1; поскольку r = 3 þ ec, он статически определен.
Реакции опор

Определите реакции на опорах для балки, показанной на рис. 3.23 (a).,

Solution
Диаграмма свободного тела Схема свободного тела всей конструкции изображенный на рис.3.23 (б).
Статическая определенность Балка внутренне нестабильна, с r 5 и ec ¼ 2. Так как r ¼ 3 þ ec, конструкция статически определена.
Опорные реакции Используя диаграмму свободного тела всей балки, показанную на рис. 3.23 (b), мы определяем реакции следующим образом:

Альтернативный метод Реакции балки также можно оценить, применив три уравнения равновесия для каждой из трех жестких частей AC, CD и DF балки.Схемы свободного тела этих жестких частей показаны на рис. 3.23 (c). Эти диаграммы показывают, помимо приложенных нагрузок и опорных реакций, внутренние силы, действующие через внутренние шарниры в точках C и D. Применяя три уравнения равновесия к части CD, мы получаем следующее:

Решение неопределенного покадровый метод распределения

Задача 8-2

Использовать Метод распределения моментов для нахождения результирующих конечных моментов для неподвижной рамы, показанной на рисунке 8-2 (a).Также нарисуйте диаграмму изгибающего момента. Возьмем EI как постоянный для все члены Рамка.

Рисунок 8-2 (а)

Решение:

Шаг 1 : Данная жесткая рама не раскачивается из-за боковой поддержки в D. Рассмотрим каждый пролет (AB, BC, CD и CE) с закрепленными обоими концами и рассчитать фиксированные моменты следующим образом;

M _AB = 0

M _{BA = 0}

M _BC = wL ² /12 = -6.67 кНм

M _CB = -wL ² /12 = +6,67 кНм

M _CD = PL / 8 = -10 кНм

M _DC = -PL / 8 = +10 кНм

M _CE = 0

M _{EC = 0}

Шаг 2: Коэффициенты жесткости

k _AB = 4EI / L = 4EI / 5 = 0,8EI

k _BA = 4EI / L = 4EI / 5 = 0,8EI

k _BC = 4EI / L = 4EI / 4 = EI

k _CB = 4EI / L = 4EI / 4 = EI

к _CD = 4EI / L = 4EI / 4 = EI

к _DC = 4EI / L = 4EI / 4 = EI

k _CE = 4EI / L = 4EI / 5 = 0.8EI

к _EC = 4EI / L = 4EI / 5 = 0,8EI

Шаг 3: Коэффициенты распределения

D _AB = 0 (фиксированная опора на конце)

D _BA = 0,8EI / (0,8EI + EI) = 0,44

D _BC = EI / (0,8EI + EI) = 0,56

D _CB = EI / (EI + EI + 0,8EI) = 0,36

D _CD = EI / (EI + EI + 0,8EI) = 0,36

D _CE = 0.8EI / (EI + EI + 0,8EI) = 0,28

D _DC = 0 (фиксированная опора на конце)

D _EC = 0 (фиксированная опора на конце)

Расчет для распределения моментов: показаны систематически в табличной форме. Каждый шарнир уравновешивается путем распределения неуравновешенного момента на связанных элементов пропорционально коэффициентам распределения. Эти этапы расчета балансировки стыков показаны серым цветом. цвет, чтобы показать иллюстрацию.Переходящие моменты (половина уравновешивающего момента около end) применяются на дальнем конце, например переходящая половина уравновешивающий момент от BA к AB, BC к CB, CB к BC, CD к DC и CE к EC и т. д.

(в случае мобильного устройства прокрутите по горизонтали, чтобы просмотреть всю ширину таблицы)

Стол для Распределение моментов
Соединения	А	В		К			D	E
Участники	AB	BA	BC	CB	CE	CD	постоянного тока	EC
Распределение Факторы	0	0.44	0,56	0,36	0,28	0,36	0	0
Первоначальный фиксированный конец Моменты	0	0	-6,67	+6,67	0	-10	+10	0
Балансировка		6.67×0,44 2,94	6,67×0,56 3,74	+ 3,33×0,36 1,2	+ 3,33×0,28 0,93	+ 3,33×0,36 1,2
Переходящий остаток	1,47		0,6	1,87			0.6	0,47
Балансировка		-0,6×0,44 -0,264	-0,6×0,56 -0,336	-1,87×0,36 -0,67	-1,87×0,28 -0,52	-1,87×0,36 -0,67
Переходящий остаток	-0.132		-0,33	-0,168			-0,33	-0,26
Балансировка		0,33×0,44 0,145	0,33×0,56 0,185	0,168×0,36 0,06	0.l68x0.28 0,048	0,168×0,36 0,06
Переходящий остаток	0,072		0,03	0,092			0,03	0,024
Балансировка		-0.03×0,44 -0,013	-0,03×0,56 -0,017	-0,092×0,36 -0,033	-0,092×0,28 -0,026	-0,092×0,36 -0,033
Переходящий остаток	-0,006		-0,016	-0.008			-0,016	-0,013
Финал Конечные моменты	1,41	2,83	-2,83	8,98	0,51	-9,49	10,26	0.26

Диаграмма результирующего изгибающего момента в рисунок 8-2 (b) построен путем наложения диаграммы момента пролета и диаграмма опорного момента.

Примечание: пожалуйста, используйте наш калькулятор изгибающего момента получить значения моментов пролета

(все значения в кНм)

(момент пролета в синий цвет, момент поддержки в красный цвет

Рисунок 8-2 (б)

Вы можете посетить следующие ссылки решенных примеров для неопределенных структур

Лучшее решение проблем с обрамлением

Когда вы хотите внедрить инновации, воспользоваться возможностью или решить проблему… одним из ваших первых шагов должно быть точное определение или «рамочная» возможность или проблема.Ваша рамка — это то, как вы сужаете и определяете то, что решаете. Лучшее обрамление ведет к лучшим решениям.

Думайте об этом как о рамке для картины, в центре которой есть то, что вы хотите показать.

Этот старый деревянный буксир требует много работы. Среди прочего… двигатель, новые окна, краска… Однако первоочередная задача — исправить огромную дыру в корпусе. Это наша рамка.

Это не означает, что вещи, выходящие за рамки кадра, не будут решены, однако эта большая дыра является приоритетом и нашей текущей областью внимания.

Но давайте будем честными. Не всегда так ясно, как правильно сфокусироваться, как дыра в этом рушащемся буксире.

Итак, как мы действительно можем узнать, какой должна быть рамка?

Один из способов определить правильную рамку — постоянно менять перспективу. Взгляните на ситуацию, используя разные типы кадров, и попробуйте, пока не найдете нужную зону фокусировки.

Вы видите, как кинорежиссеры делают это, формируя рамку с помощью большого пальца и указателя — обрамляя, чтобы увидеть, как сцена будет выглядеть на экране … Они продолжают менять перспективу, пока не найдут в сцене то, что им нужно.

Мы делаем то же самое с решением проблем. Однако вместо того, чтобы менять положение рук, мы меняем: время, людей, риск, ресурсы и нашу точку зрения.

Сдвиг во времени

Как бы это выглядело из будущего?

• Через x месяцев это решение сработало. Что бы мы сделали?
• Как бы мы это оформили x недель назад?

Людская смена

Посмотрите на это с чужой точки зрения.

• Как бы это сформулировали наши сотрудники?
• Как клиент определил бы проблему?
• Как насчет отрасли? Соревнование? Посторонние?

Сдвиг риска

Изучите его с консервативной до агрессивной точки зрения.

• Если бы мы не хотели рисковать, как бы мы определили проблему?
• Если бы мы были кучкой речных игроков, что бы мы сказали об этой возможности?

Смена ресурса

Как бы вы подумали об этом, если бы у вас был диапазон от отсутствия ресурсов до неограниченного.

• Если бы деньги не были объектом, как бы мы определили проблему?
• Если бы нам пришлось выяснить это на ограниченных средствах, как бы мы это сформулировали?

Перспективная смена

Подумайте: кирпич, стена или собор? Проверьте, правильно ли мы смотрим на это решение.

• Brick — должно ли это решение влиять только на небольшие, ограниченные процедурные шаги или изменения?
• Стена — должно ли это решение быть сосредоточено на ограниченной части общей или организационной проблемы?
• Собор — влияет ли это решение на организацию в целом?

В следующий раз, когда вы или ваша команда столкнетесь с проблемой — даже если проблема, стоящая за этой проблемой, может показаться довольно очевидной — попробуйте несколько разных кадров, прежде чем выбрать окончательный подход.

Вы можете заметить, что разные рамки меняют вид всего изображения.

Норма прибыли — Узнайте, как рассчитать норму прибыли (ROR)

Что такое норма прибыли?

Норма прибыли (ROR) — это прибыль или убыток от инвестиции за определенный период времени. Другими словами, норма доходности — это доходность прироста капитала. Доходность прироста капитала (CGY) — это повышение цены на инвестиции или ценные бумаги, выраженное в процентах. Поскольку расчет доходности от прироста капитала включает рыночную цену ценной бумаги с течением времени, его можно использовать для анализа колебаний рыночной цены ценной бумаги.См. Расчет и пример (или убыток) по сравнению со стоимостью первоначальных инвестиций, обычно выражаемой в форме процента. Когда ROR положительный, это считается прибылью, а когда ROR отрицательный, он отражает убыток от инвестиций.

Видео Объяснение нормы прибыли

Посмотрите это короткое видео, чтобы быстро понять основные концепции, рассматриваемые в этом руководстве, включая определение нормы прибыли, формулу для расчета ROR и ROR в годовом исчислении, а также примеры расчетов.

Формула нормы прибыли

Стандартная формула для расчета ROR выглядит следующим образом:

Имейте в виду, что любая прибыль, полученная в течение периода удержания инвестиций должны быть включены в формулу. Например, если акция стоит 10 долларов, а ее текущая цена составляет 15 долларов, а дивиденды в размере 1 доллара выплачиваются в течение периода, дивиденды должны быть включены в формулу ROR. Он будет рассчитан следующим образом:

((15 долларов США + 1 доллар — 10 долларов США) / 10 долларов США) x 100 = 60%

Пример расчета нормы прибыли

Адам является розничным инвестором и решает приобрести 10 акций компании. Компания А по цене 20 долларов за единицу.Адам владеет акциями компании А два года. За это время Компания А выплачивала годовые дивиденды в размере 1 доллар на акцию. После владения ими в течение двух лет Адам решает продать все 10 акций компании А по цене без выплаты дивидендов в 25 долларов. Адам хотел бы определить норму прибыли в течение двух лет, когда он владел акциями.

Для определения нормы прибыли сначала рассчитайте сумму дивидендов, полученных им за двухлетний период:

10 акций x (1 доллар годовых дивидендов x 2) = 20 долларов дивидендов от 10 акций

Затем подсчитайте, за сколько он продал акции:

10 акций x 25 долларов = 250 долларов (прибыль от продажи 10 акций)

Наконец, определите, во сколько Адам приобрел 10 акций компании A:

10 акций x 20 долларов = 200 долларов США (Стоимость покупки 10 акций)

Подставьте все числа в формулу нормы прибыли:

= ((250 долларов США + 20 долларов — 200 долларов США) / 200 долларов США) x 100 = 35%

Таким образом, Адам получил 35% прибыли на свои акции за двухлетний период.

Годовая норма прибыли

Обратите внимание, что обычная норма прибыли описывает прибыль или убыток, выраженный в процентах, от инвестиции за произвольный период времени. Годовая доходность, также известная как сложный годовой темп роста (CAGR) CAGRCAGR означает сложный годовой темп роста. Это показатель годового темпа роста инвестиций с течением времени с учетом эффекта начисления сложных процентов. Это доходность инвестиций за каждый год.

Формула годовой доходности

Формула годовой доходности следующая:

Аналогично простой норме доходности, любая прибыль, полученная в течение периода удержания этой инвестиции, должна быть включена в формула.

Пример годовой нормы прибыли

Давайте вернемся к приведенному выше примеру и определим годовую доходность. Напомним, что Адам купил 10 акций по цене 20 долларов за штуку, получал 1 доллар дивидендов на акцию каждый год и продал акции по цене 25 долларов через два года. Годовая доходность будет следующей:

((250 долларов + 20 долларов) / 200 долларов)

^1/2 — 1 = 16,1895%

Таким образом, Адам получил годовую прибыль в размере 16.1895% от его инвестиций.

Альтернативные меры возврата

Возвращение может означать разные вещи для разных людей, и важно знать контекст ситуации, чтобы понимать, что они означают. В дополнение к вышеупомянутым методам измерения доходности существует несколько других типов формул.

Общие альтернативные меры доходности включают:

• Внутренняя норма доходности (IRR) Внутренняя норма доходности (IRR) Внутренняя норма доходности (IRR) — это ставка дисконтирования, которая составляет чистую приведенную стоимость (NPV) проекта. нуль.Другими словами, это ожидаемая совокупная годовая норма прибыли, которая будет получена от проекта или инвестиций.
• Рентабельность капитала (ROE) Рентабельность капитала (ROE) Рентабельность собственного капитала (ROE) — это показатель прибыльности компании, который рассчитывается путем деления годовой прибыли (чистой прибыли) компании на стоимость ее общего акционерного капитала (т. Е. 12 %). ROE объединяет отчет о прибылях и убытках и баланс, поскольку чистая прибыль или прибыль сравнивается с собственным капиталом.
• Рентабельность активов (ROA) Формула рентабельности активов и ROA Формула ROA.Рентабельность активов (ROA) — это тип показателя рентабельности инвестиций (ROI), который измеряет прибыльность бизнеса по отношению к его общим активам. Этот коэффициент показывает, насколько хорошо компания работает, сравнивая прибыль (чистую прибыль), которую она генерирует, с капиталом, который она инвестирует в активы.
• Рентабельность инвестиций (ROI) Рентабельность инвестиций (ROI) Рентабельность инвестиций (ROI) — это показатель эффективности, используемый для оценки возврата инвестиций или сравнения эффективности различных инвестиций.
• Рентабельность инвестированного капитала (ROIC) Рентабельность инвестированного капитала (ROIC) Рентабельность инвестированного капитала (ROIC) — это рентабельность или показатель эффективности прибыли, полученной теми, кто предоставляет капитал, а именно держателями облигаций и акционерами фирмы. ROIC компании часто сравнивают с ее WACC, чтобы определить, создает ли компания ценность или разрушает ее.

Дополнительные ресурсы

CFI является официальным поставщиком услуг по анализу финансового моделирования и оценки (FMVA). Получите сертификат сертифицированного аналитика финансового моделирования и оценки (FMVA) ®, предназначенный для обучения финансовых аналитиков навыкам моделирования оценки.Для продолжения карьерного роста вам пригодятся следующие дополнительные ресурсы:

• Инвестирование: руководство для начинающих Инвестирование: руководство для начинающих Руководство CFI по инвестициям для начинающих научит вас основам инвестирования и научит их начинать. Узнайте о различных стратегиях и методах торговли, а также о различных финансовых рынках, на которые вы можете инвестировать.
• Бета без рычагов (бета-версия актива) Бета-версия без рычага / бета-версия актива (бета-версия актива) — это волатильность доходности для бизнеса без учета его финансовые рычаги.Он учитывает только свои активы.
• Базовые точки (bps) Базовые точки (BPS) Базовые точки (BPS) — это обычно используемая метрика для измерения изменений процентных ставок. Базисная точка — одна сотая процента. См. Примеры. Эта метрика
• Технический анализ: Руководство для начинающих Технический анализ — Руководство для начинающих Технический анализ — это форма оценки инвестиций, которая анализирует прошлые цены для прогнозирования будущих ценовых действий. Технические аналитики считают, что коллективные действия всех участников рынка точно отражают всю соответствующую информацию и, следовательно, постоянно определяют справедливую рыночную стоимость ценных бумаг.

Калькулятор размера выборки — уровень достоверности, доверительный интервал, размер выборки, размер совокупности, соответствующая совокупность

Этот калькулятор размера выборки представляет собой общедоступную услугу программного обеспечения для проведения опросов Creative Research Systems. Вы можете использовать его, чтобы определить, сколько людей вам нужно проинтервьюировать, чтобы получить результаты, отражающие целевую совокупность настолько точно, насколько это необходимо. Вы также можете найти уровень точности, который у вас есть в существующем образце.

Перед использованием калькулятора размера выборки вам необходимо знать два термина.Это: доверительный интервал и доверительный интервал . Если вы не знакомы с этими условиями, щелкните здесь. Чтобы узнать больше о факторах, влияющих на размер доверительных интервалов, щелкните здесь.

Введите свой выбор в калькулятор ниже, чтобы найти нужный размер выборки или доверительный интервал. у тебя есть. Оставьте поле Население пустым, если популяция очень большая или неизвестна.

Условия калькулятора размера выборки: доверительный интервал и доверительный уровень

Доверительный интервал (также называемый пределом погрешности) — это положительное или отрицательное значение, обычно указываемое в результатах газетных или телевизионных опросов.Например, если вы используете доверительный интервал 4 и 47% процентов вашей выборки выбирает ответ, вы можете быть «уверены», что если бы вы задали вопрос всей соответствующей совокупности, от 43% (47-4) до 51% (47 + 4) выбрали бы этот ответ.

Уровень достоверности говорит вам, насколько вы можете быть уверены. Он выражается в процентах и ​​показывает, как часто истинный процент населения, которое выберет ответ, находится в пределах доверительного интервала. Уровень достоверности 95% означает, что вы можете быть уверены на 95%; Уровень достоверности 99% означает, что вы можете быть уверены на 99%.Большинство исследователей используют уровень достоверности 95%.

Если сложить доверительный интервал и доверительный интервал вместе, можно сказать, что вы на 95% уверены, что истинный процент населения составляет от 43% до 51%. Чем шире доверительный интервал, который вы готовы принять, тем больше вы можете быть уверены в том, что ответы всего населения будут в пределах этого диапазона.

Например, если вы спросили у выборки из 1000 жителей города, какую марку колы они предпочитают, и 60% ответили маркой А, вы можете быть уверены, что от 40 до 80% всех жителей города действительно предпочитают этот бренд, но нельзя быть уверенным, что от 59 до 61% жителей города предпочитают этот бренд.

Факторы, влияющие на доверительные интервалы

Существует три фактора, которые определяют размер доверительного интервала для данного уровня достоверности:

• Объем выборки
• Процент
• Численность населения
чел.

Размер выборки

Чем больше размер вашей выборки, тем больше вы можете быть уверены в том, что их ответы действительно отражают население. Это означает, что для данного уровня достоверности, чем больше размер вашей выборки, тем меньше доверительный интервал.Однако связь не является линейной (, то есть , удвоение размера выборки не уменьшает вдвое доверительный интервал).

Процент

Ваша точность также зависит от процента вашей выборки, которая выбирает конкретный ответ. Если 99% вашей выборки ответили «Да», а 1% — «Нет», вероятность ошибки мала, независимо от размера выборки. Однако, если процентное соотношение составляет 51% и 49%, вероятность ошибки намного выше. Легче быть уверенным в крайних ответах, чем в промежуточных.

При определении размера выборки, необходимого для данного уровня точности, вы должны использовать процент наихудшего случая (50%). Вы также должны использовать этот процент, если хотите определить общий уровень точности для уже имеющейся пробы. Чтобы определить доверительный интервал для конкретного ответа, данного вашей выборкой, вы можете использовать процентное значение этого ответа и получить меньший интервал.

Численность населения

Сколько человек в группе, которую представляет ваша выборка? Это может быть количество людей в городе, который вы изучаете, количество людей, которые покупают новые машины и т. Д.Часто вы можете не знать точную численность населения. Это не является проблемой. Математика вероятности доказывает, что размер популяции не имеет значения, если размер выборки не превышает нескольких процентов от общей популяции, которую вы исследуете. Это означает, что выборка из 500 человек одинаково полезна при изучении мнений государства с населением 15000000 человек и города с населением 100000 человек. По этой причине Survey System игнорирует размер популяции, когда он «большой» или неизвестный. Размер населения может быть фактором, только если вы работаете с относительно небольшой и известной группой людей ( e.грамм. , члены ассоциации).

При расчетах доверительного интервала предполагается, что у вас есть подлинная случайная выборка из соответствующей генеральной совокупности. Если ваша выборка не является действительно случайной, вы не можете полагаться на интервалы. Неслучайные выборки обычно возникают в результате каких-либо недостатков или ограничений в процедуре отбора образцов.