Расчет рамы на устойчивость | ПроСопромат.ру

Для рамы требуется определить значение      и    . Дано:

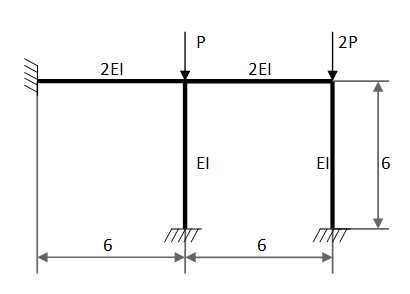
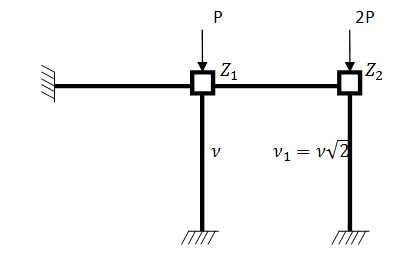
Выбираем основную систему:

Составляем канонические уравнения по методу перемещений:

Записываем уравнение устойчивости:

Определяем критические параметры: 

Строим единичные эпюры:

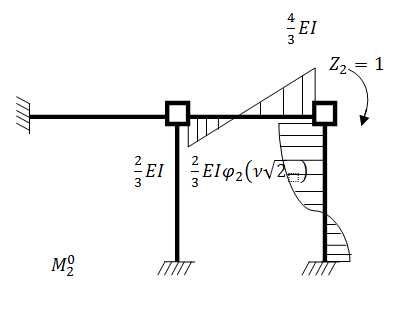
Определим коэффициенты при неизвестных:

Подставим коэффициенты в уравнение устойчивости:

Решаем уравнение устойчивости.

а) примем ν=3,98,  тогда:

б) примем ν=3,96, тогда:

Принимаем ν=3,97.

Определим 

Определим 

Для левой стойки: 

Для правой стойки: 

 

 

prosopromat.ru

Методическое указание к расчету рам на устойчивость

Для студентов заочного и очного обучения спец. «Строительство»

СОСТАВИТЕЛЬ: д.т.н. Достанова С.Х.

Казахская головная архитектурно-строительная академия

Дисциплина «Динамика и устойчивость сооружений»

Для бакалавров спец. «Строительство» ЗРПЗС

Ф.И.О. студента

Группа

Семестр

Задание выдано С.Х.Достанова

РГР №1

Расчет плоской рамы на устойчивость

Для заданной рамы (Рис.1) необходимо выполнить следующее:

1. Постановка задачи: Определить критические нагрузки и формы потери устойчивости.

2. Использовать метод перемещений к расчету рам на устойчивость. Записать уравнение устойчивости.

3. Использовать приближенный метод для нахождения корней трансцендентного уравнения.

4. Программа и алгоритм для решения трансцендентных уравнений.

5. Определить критические параметры и нагрузки, формы потери устойчивости.

Данные представлены в таблице1

Таблица 1

Данные к задаче устойчивости плоской рамы

L1	L2	h1	h2	P1/ P2	I1/I2	α
[м]	[м]	[м]	[м]			[град]

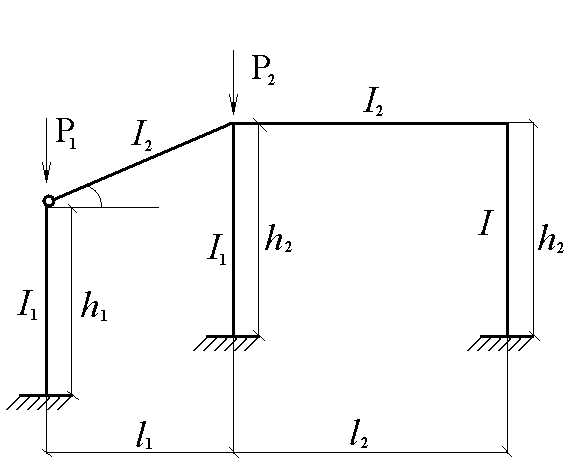
Рис.1 Расчетная схема плоской рамы

Пример расчета рамы на устойчивость

.

Полный расчет рамы на устойчивость включает следующее:

1. Постановку задачи.

2. Расчет рам на устойчивость. Метод перемещений к расчету рам на устойчивость. Уравнение устойчивости.

3. Приближенный метод для нахождения корней трансцендентного уравнения.

4. Программа для решения трансцендентных уравнений.

5. Критические нагрузки и формы потери устойчивости.

ПОСТАНОВКА ЗАДАЧИ

Рассматривается рама со сжатыми и в некоторых случаях со сжатыми и растянутыми элементами пр. узловой нагрузке Рi. Если пренебречь укорочением сжатых и уменьшениями растянутых элементов стоек и ригелей, то такая рама до потери устойчивости не будет иметь изгиба. /Рис.1/

Рис.2.1 Заданная система

Длина стоек и ригелей имеют следующие значения:

l₁=1,2 м; l₂=2 м; h₁=1 м; h₂=2 м.

Моменты инерции поперечных сечений стержней имеют следующие отношения: = 1,4 : 1,3. Отношения узловых сил:P₁: P₂=1,2: I,7. Угол α равен 45°. Расчетное сопротивление R = 2100 кгc/см², левая стойка имеет стандартный профиль I №16. Для заданной системы расчет на устойчивость заключается в выполнении следующих пунктов:

1. Используя метод перемещений, записать уравнение устойчивости.

2. Определить корни трансцендентного уравнения.

3. Найти критическую нагрузку и соответствующую ей форму потери устойчивости. Проверить условие устойчивости сжатого элемента.

РАСЧЕТ РАМ НА УСТОЙЧИВОСТЬ

Метод перемещений. Уравнение устойчивости.

Рассматриваем потерю устойчивости 1-го рода, т.е. полагаем, что до потери устойчивости нет изгиба стержней. Критическими зна­чениями внешней нагрузки считаем нагрузки, при которых происходит бифуркация, т.е. разветвление равновесных форм. В нашем случае бифуркации сопровождаются переходом системы из заданного прямолинейного состояния к изогнутому /деформированному/ состоянию. Исполь­зуем метод перемещений, выбираем основную систему путем наложения дополнительных связей препятствующих угловым и поступательным смещениям узлов. Для симметричных систем и нагрузок необходимо ис­пользовать симметричную основную систему, сгруппировав неизвестные, что позволит рассматривать отдельно симметричные и обратно-симметричные формы потери устойчивости и соответствующее им критические нагрузки. На рисунке 2 представлена основная система.

Неизвестные Z₁, Z₂ представляют углы поворота в связях 1 и 2, неизвестное Z₃ – поступательное перемещение по горизонтали, т. е. в направлении связи 3. запишем каноническое уравнение метода перемещений:

(2.1)

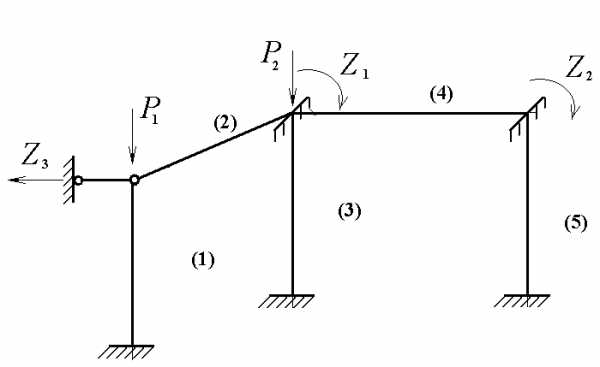
Рисунок 2. 2

Для случая осевой нагрузки свободные члены уравнений /I/ равны нулю, поэтому система /I/ годится к системе линейных одно­родных уравнений :

· = 0 (2.2)

В случае потери устойчивости 1-го родя стержни изгибаются» их деформаций должны быть отличны от нуля, поэтому неизвестные Z₁, Z₂, Z₃,

одновременно не могут быть равны нулю. Это выполнимо только тогда, когда дискриминант системы — (2.2)равен нулю, т.е.

=0 (2.3)

В уравнении (2.3) величина_iк представляет собой реакции по направлению « i» от единичных неизвестных Z₁, Z₂, Z₃. При наличии продоль­ных сил в стержнях _iк зависят от параметра нагрузки Р. И такуравнение (2.3) представляет собой уравнение устойчивости, из которо­го определяется параметр критической нагрузки.

Теперь распишем выражения коэффициентов iк через критические периметры. Для этого воспользуемся таблицами сжато-изогнутых стерж­ней при различных закреплениях. В таблице I представлены реакции стержней от единичных перемещений с учетом продольных сил. В таблице 2 представлены реакции стержней от единичных смещений без учета продольных сил. Критический параметр нагрузки равен , где — длина стержня,

N -продольная сила, EI — жесткость стержня на изгиб. В таблице I функции представ­ляют следующие зависимости от параметраV:

Значения этих специальных функций φ_{i ,} η₁ приведены в таблице 3 .

Для дальнейшего упрощения выразим силу Р₂ через Р₁ жесткость I₂ через I ₁, т.е. Р₂= I,42 Р₁ ;I₂ = 0.93 I₁ .На рис.2.1 указана нумерация стержней, поэтому погонные жесткости стержней имеют вид :

; ;;;

Критические параметры для 1-го и 3-го стержней выражаются через продольные силы следующим образом :

; .

РЕАКЦИИ СЖАТО – ИЗОГНУТЫХ СТЕРЖНЕЙ

Таблица 2. 1

studfiles.net

Расчет рамы на устойчивость методом перемещений

Задание 10
Расчет рамы на устойчивость методом перемещений
Задание:
Для заданного варианта № 48 (схема 48) при геометрических размерах, жесткостях элементов
и нагрузке по строке 15 таблицы (L = 4м, h = 6м, α = 2, EJриг = 2EJ, EJст = 3EJ) требуется:
Определить критическое значение параметрической нагрузки Ркр.
Решение:
1. Вычертим в масштабе расчетную схему рамы в соответствии с данными (Рис.1).

Рис.1
2. В доктрическом состоянии, из условия равновесия узлов 2 и 4, определим продольные силы
в сжатых элементах рамы, выражая их через заданную узловую нагрузку (Рис.2).

Рис.2
3. Определим значения коэффициентов влияния продольных сил νi для сжатых элементов
рамы, выражая их через единый коэффициент ν. В качестве ведущего параметра ν принимаем
наибольший из коэффициентов νi.

v1 = l 1 ⋅

N1
= 6⋅
EJ1

v2 = l2 ⋅

N2
= 6⋅
EJ 2

2P
= 4,9 ⋅
3E J

P
= ν,
EJ

P
= 3, 464 ⋅
3E J

P
= 0, 707ν.
EJ
1

4. Определим степень кинематической неопределимости рамы – К.
К = Ку + Кл = 1 + 1 = 2
5. Формируем основную системы метода перемещений (Рис.3).
⟶ Вводим плавающую заделку в жесткий узел 4 и задаем угол поворота жесткого узла Z1,
⟶ Вводим в узел 2 горизонтальный опорный стержень, препятствующий линейному смещению
узлов 2, 4, 6 по горизонтали, и придаем системе горизонтальное перемещение Z2.

Рис.3
6. Запишем систему канонических уравнений метода перемещений.
Так как заданная рама не имеет поступательных перемещений узлов и на неё действует только
узловая нагрузка, то все грузовые члены канонических уравнений равны нулю, т.к. при такой
нагрузке изгибающие моменты в основной системе повсюду равны нулю.
 r 11 ⋅ Z 1 + r 12 ⋅ Z 2 = 0

 r 21 ⋅ Z 1 + r 22 ⋅ Z 2 = 0
7. Определим значение параметра критической нагрузки, соответствующего местной потере
устойчивости сжатых стержней – Pкр∗ , для этого рассмотрим каждый сжатый стержень в
отдельности, изолированно от других (тривиальное решение: Z1 = Z2 = 0).
• Стержень 1:
∗
∗
N кр.1
= 2 Pкр.1
=

π 2 ⋅ EJ1

(µ

∗
1

⋅ l1

)

2

=

π 2 ⋅ 3E J

( 0, 7 ⋅ 6 )

2

∗
= 1, 679 E J ⇒ Pкр.1
= 0,84 E J

2

• Стержень 3:
∗
∗
= Pкр.2
=
N кр.2

π 2 ⋅ EJ 2

(

µ 2∗

⋅l2

)

2

=

π 2 ⋅ 3E J

( 0,5 ⋅ 6 )

2

∗
= 3, 29 E J ⇒ Pкр.2
= 3, 29 E J

8. Определим значение параметра критической нагрузки, соответствующего общей потере
устойчивости рамы – Pкр (нетривиальное решение Z1 ≠ 0 и Z2 ≠ 0).
⟶ Запишем уравнение устойчивости.
Условием получения отличного от нуля решения системы канонических уравнений метода,
является обращение в нуль определителя, составленного из коэффициентов при неизвестных.
Равенство определителя нулю – есть уравнение устойчивости, и выражает условие
существования изгибной (альтернативной по отношению к исходной) формы равновесия
системы.
D=

r 11 r 12
r 21 r 22

2
= r 11 ⋅ r 22 − r 12
=0

⟶ Определим значения коэффициентов r11 и r21 = r12.
Рассмотрим деформирование основной системы в результате поворота введенной в узел 5
связи на Z1 = 1 (Рис.4,а), построим эпюру изгибающих моментов M 1 с учетом влияния
сжимающих сил (Рис.4,б).

EJ 2
3E J
⋅ φ 2 (ν 2 ) = 4 ⋅
⋅ φ 2 (0, 707ν) = 2 E Jφ 2 (0, 707ν),
l2
6
EJ 2
3E J
m 54 = 2 ⋅
⋅ φ 3 (ν 2 ) = 2 ⋅
⋅ φ 3 (0, 707ν) = E Jφ 3 (0, 707ν),
6
l2
EJ 2
3E J
q 54 = 6 ⋅ 2 ⋅ φ 4 (ν 2 ) = 6 ⋅ 2 ⋅ φ 4 (0,707ν) = 0,5E Jφ 4 (0,707ν).
l2
6
m 45 = 4 ⋅

m 46 = 4 ⋅

EJ 5
2E J
EJ 5
2E J
= 4⋅
= 2 E J , m 64 = 2 ⋅
= 2⋅
= E J.
4
4
l5
l5

• Вырежем узел 4 (Рис.4,г) и из условия равновесия определим значение коэффициента r11:

Σ m 4 = r 11 − 2 E J − 2 E J φ 2 (0, 707ν) = 0 ⇒ r 11 = 2 E J + 2 E J φ 2 (0, 707ν).
• Вырежем ригель 2-4-6 (Рис.4,в) и из уравнения проекций всех сил на горизонтальную ось Х
определим значение коэффициента r21 = r12:

Σ X = r 21 + 0,5 E J φ 4 (0, 707ν) = 0 ⇒ r 21 = − 0,5E J φ 4 (0, 707ν) = r 12.

3

Рис.4
⟶ Определим значение коэффициента r22.
Рассмотрим деформирование основной системы в результате смещения введенной в узел 2
связи по горизонтали на Z2 = 1 (Рис.5,а).
4

q 12 = 3

EJ1
3E J
η1 (ν 1 ) = 3 3 η1 (ν) = 0, 0417 E J η1 (ν),
3
l1
6

q 54 = 12

EJ 2
3E J
EJ 3
3E J
η 2 (ν 2 ) = 12 3 η 2 (0, 707ν) = 0,1667 E J η 2 (0, 707ν), q 32 = 3 3 = 3 3 = 0, 0417 E J .
3
l2
6
l3
6

Рис.5
• Вырежем ригель 2-4-6 (Рис.5,б) и из уравнения проекций всех сил на горизонтальную ось Х
определим значение коэффициента r22:
Σ X = r 22 − 0,1667 E Jη 2 (0, 707ν ) − 0, 0417 E Jη1 (ν ) − 0, 0417 E J = 0,
r 22 = 0,1667 E Jη 2 (0, 707ν ) + 0, 0417 E Jη1 (ν ) + 0, 0417 E J .

⟶ Численно решаем уравнение устойчивости и определяем значение параметра Pкр .
2
D = r 11 ⋅ r 22 − r 12
= [2 E J + 2 E J φ 2 (0, 707ν)] ⋅ [0,1667 E Jη 2 (0, 707ν) + 0, 0417 E Jη1 (ν) + 0, 0417 E J ] −

− [− 0,5E J φ 4 (0, 707ν)] 2 = 2 E J ⋅ [1 + φ 2 (0, 707ν)] ⋅ 0, 0417 E J ⋅ [4η 2 (0, 707ν) + η1 (ν) + 1] −
− 0, 25E J 2 [φ 4 (0, 707ν)] 2 = 0.
Разделив полученное уравнение на 0,0834(EI)2, получаем:

D = [1 + φ 2 (0, 707ν)] ⋅ [4η 2 (0, 707ν) + η1 (ν) + 1] − 3 [φ 4 (0, 707ν)] 2 = 0.
5

• Определим интервал значений в котором лежит корень уравнения устойчивости методом
последовательных приближений, используя таблицу значений специальных функций метода
перемещений для сжато-изогнутых стержней:
v=0

D = [1 + φ 2 (0)] ⋅ [4η 2 (0) + η1 (0) + 1] − 3 [φ 4 (0)] 2 = [1 + 1] ⋅ [4 ⋅ 0,984 + 1 + 1] − 3 ⋅ 1 2 = 8,872.
v = 2,12

D = [1 + φ 2 (1,5)] ⋅ [4η 2 (1,5) + η1 (2,12) + 1] − 3 [φ 4 (1,5)] 2 = [1 + 0,92268] ⋅ [4 ⋅ 0,77438 + 0,08928 +
+1] − 3 ⋅ 0,96188 2 = 5, 274.
v = 2,7

D = [1 + φ 2 (1,9)] ⋅ [4η 2 (1,9) + η1 (2,7) + 1] − 3 [φ 4 (1,9)] 2 = [1 + 0,8735] ⋅ [4 ⋅ 0,63738 − 2,06794 +
+1] − 3 ⋅ 0,93822 2 = 0,13.
v = 2,76

D = [1 + φ 2 (1,95)] ⋅ [4η 2 (1,95) + η1 (2,76) + 1] − 3 [φ 4 (1,95)] 2 = [1 + 0,86627] ⋅ [4 ⋅ 0,6177 − 2, 2169 +
+1] − 3 ⋅ 0,93478 2 = −0, 28.
• Корень уравнения устойчивости – vкр определяем линейной интерполяцией в интервале от
2,7 до 2,76:

X
0,13
=
⇒ (0, 06 − X ) ⋅ 0,13 = X ⋅ 0, 28 ⇒ X = 0, 019 ⇒ ν кр = 2, 719.
0, 06 − X 0, 28
• Определим значение параметра критической нагрузки – Pкр :
4,9 ⋅

2
ν кр
⋅ E J 2, 719 2 ⋅ E J
P
= ν ⇒ Pкр =
=
= 0, 308 E J .
EJ
24, 01
4, 9 2

9. Определим истинное значение параметра Pкр.
Pкр = min ( Pкр∗ , Pкр ) = 0,308EJ – что соответствует общей потере устойчивости рамы.

6

freedocs.xyz

Расчет статически неопределимых рам на устойчивость методом перемещений

Рассмотрим раму, нагруженную силами, приложенными в узлах.

Р Р

Пренебрегая изменением длин стержней и их весом, можно считать, что при достаточно малых значениях сил все стержни остаются прямыми и в них возникают только продольные усилия. При достижении нагрузкой критического значения наряду с исходным появляется смежное, деформированное состояние равновесия.

Такой подход является идеализированным (как и при расчете центрально сжатых стержней), т.к реальные нагрузки имеют эксцентриситет приложения, а также имеется начальный прогиб элементов от их собственной массы.

Для расчета рам на устойчивость можно использовать те же методы, что и для расчета на прочность: метод сил, метод перемещений, смешанный метод и т.др.

Смысл расчета рам на устойчивость заключается в определении для всех сжатых элементов критических сил Р_кри их расчетных длин

Расчету на устойчивость предшествует расчет рамы на прочность любым из известных методов. Затем рама рассчитывается на устойчивость под действием только узловых сжимающих нагрузок, которые берут из эпюры Nрасчета на прочность.

Порядок расчета рам на устойчивость методом перемещений

Порядок расчета рам на устойчивость аналогичен расчету на прочность.

1. Определяют степень кинематической неопределимости рамы

,

где степень угловой подвижности рамы, равна числу жестких узлов;степень линейной подвижности, равна числу возможных независимых перемещений узлов рамы.

2. Выбирают основную систему метода перемещения, для чего в каждый жесткий узел вводят упругоподатливые защемления (связи 1^города), а по направлению возможных перемещений — дополнительные опорные стерженьки (связи 2^города).

Например:

P₁P₂P₁P₂

1 2 3

h

l₁l₂

Заданная система Основная система

3. Составляют систему канонических уравнений. В отличие от аналогичных уравнений расчета на прочность (поперечный изгиб) грузовые коэффициенты R_ipравны нулю, т.к. узловые нагрузки не вызывают реактивных усилий в дополнительных связях. Система канонических уравнений записывается :

Действие внешней нагрузки в данном случае учитывается при вычислении единичных коэффициентов r_ik=r_ki, т.к. при единичных смещениях дополнительных связей деформируемые элементы, в пределах которых действуют сжимающие усилия, находятся в условиях продольно-поперечного изгиба.

4. Порядок определения опорных реакций с учетом сжимающих сил покажем на примере балки, у которой один конец жестко защемлен, другой шарнирно оперт.

M_A _A=1 N

N

A R_A B

 R_B где

NN

M_A

R_AR_BДля того, чтобы основная система и

заданная были равноценны необходимо чтобы М_Аимел такую величину, при которой_А=1.

,

отсюда

.

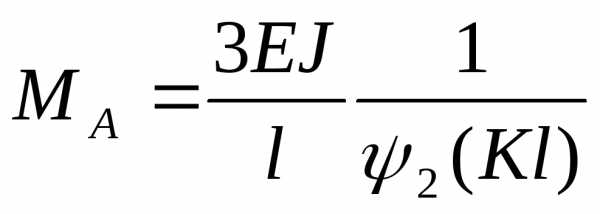Обозначим:

, где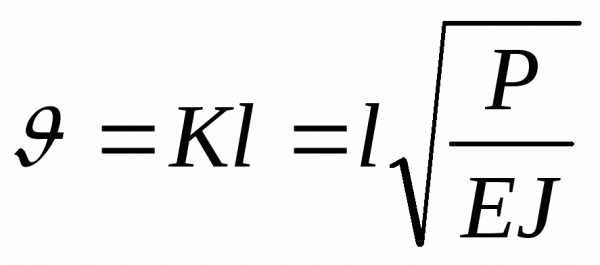

т.е.

Аналогично получают реакции опор и в других случаях.

Схемы и эпюры	Коэффициенты
Z=1 P  EI
P P l
P Z=1 l
Z=1 P P l
Z=1 P l

5. Строят эпюры от единичных смещений наложенных связей. В пределах элементов, которые сжаты внешней нагрузкой, эпюры криволинейны и строятся в соответствии с приведенной выше таблицей. В пределах элементов не подверженных сжатию, эпюры прямолинейны и строятся по таблицам обычного метода перемещений (как при расчете на прочность) .

P₁ P₂ P₁ P₂

1 2 3

AB C

Z₃=1

P₁P₂

6. Коэффициенты системы канонических уравнений определяют как и в обычном методе перемещений.

r₁₁

и т.д.

r₃₃

7. Для заданной системы уравнений (без свободных членов), возможны два решения: первое, когда все z_i= 0, такое решение нас не устраивает, т.е не соответствует условиям задачи; и второе решение, когда детерминант системы, составленный из единичных коэффициентов = 0.

Раскрывая этот определитель, получаем сложное трансцендентное уравнение, для решения которого необходимо вначале выразить все параметры v_iчерез один. Затем уравнение решается:

1) методом подстановки;

2) графическим методом.

Метод подстановки самый примитивный способ решения. Применяется для простейших характеристических уравнений.

Сущность графического способа заключается в следующем:

— выбираем произвольное значение параметра v_iи находимdet₁=f(v)

v₁ =>det₁

v₂ =>det₂

v₃ =>det₃

и т.д.

На основании полученных значений строим график функции det=f(v).

det

det = f (v)

v₁ v₂ v₃ v₄ v₅ v

v_кр

Наименьшее значение параметраv, при которомdet= 0 называетсяv_кр.

8. Для стойки, параметры которой мы принимаем за исходные определяем критическую силу:

и расчетную длину стержня:

, отсюда

где:l₀— расчетная длина стержня;

l— геометрическая длина стержня

или коэффициент приведения геометрической длины к расчетной:

9. Зная соотношение между параметрами остальных элементов и исходным элементом, определяют v_крдля всех остальных сжатых стержней.

10. Затем для всех сжатых стержней определяют Р_криl_0..

Лекция 8

studfiles.net

4.3 Статический расчет рамы

4.3.1 Расчет на постоянные нагрузки

Расчетная схема рамы на постоянную нагрузку приведена на рис. 4.3.

Из-за смещения осей нижней и верхней частей колонн в месте изменения сечения колонны появляется сосредоточенный момент

кНм.

По таблице 12.4 учебника находим параметры

,

.

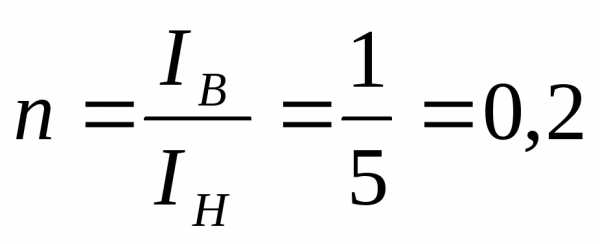
Каноническое уравнение имеет вид

На основании рисунка 4.8 составим следующую расчетную схему для расчета рамы на постоянную нагрузку

Рис. 4.8. Упрощенная расчетная схема рамы от постоянной нагрузки.

Моменты от поворота узлов на угол  = 1 равны:

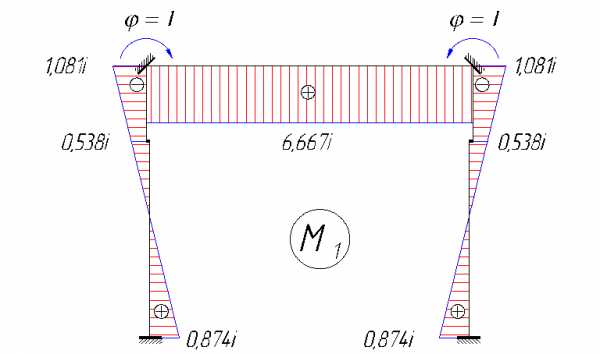
Моменты от нагрузок на стойки М_Р равны:

Моменты на опорах ригеля (защемленная балка постоянного сечения):

кНм.

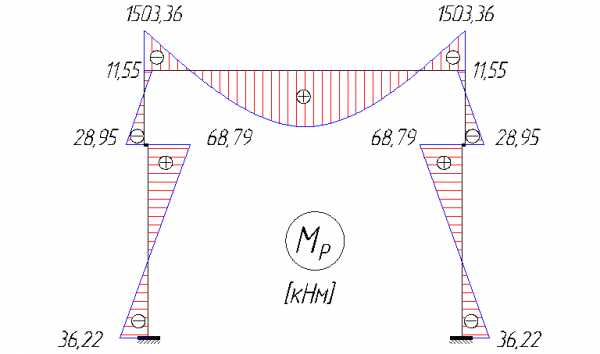
Определение r₁₁ и r_1Р:

— по эпюре М₁: ;

— по эпюре М_Р: .

Таким образом, из канонического уравнения метода перемещений получим угол поворота:

.

Моменты от фактического угла поворота (М₁·) равны:

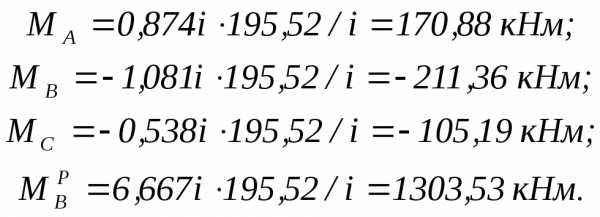
Эпюра моментов (М₁· + М_Р) от постоянной нагрузки

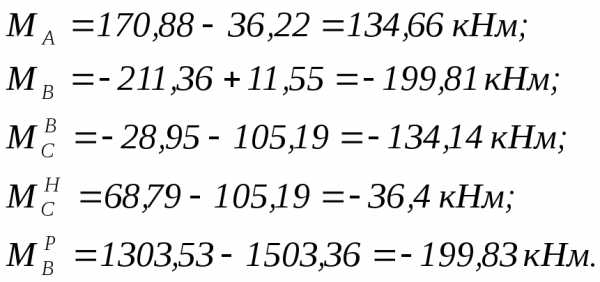
Эпюры изгибающих моментов, поперечных и продольных сил представлены на рисунке 4.9.

Рис. 4.9. Эпюры M, Q, N от постоянной нагрузки.

Проверкой служит:

— равенство моментов в узле В (199,81 = 199,83),

— равенство перепада эпюры моментов в точке С равной внешнему моменту: ,

— также равенство поперечных сил на верхней и нижней частях колонны: кН; кН.

4.3.2 Расчет на снеговую нагрузку

Расчетная схема рамы на снеговую нагрузку приведена на рис. 4.4.

Из-за смещения осей нижней и верхней частей колонн в месте изменения сечения колонны появляется сосредоточенный момент

кНм.

Эпюра единичных моментовМ₁, каноническое уравнение, параметры п и , значение коэффициента r₁₁ останутся теми же, что и при расчете рамы на постоянную нагрузку.

На рисунке 4.10 представлена расчетная схема для расчета рамы на снеговую нагрузку.

Рис. 4.10. Упрощенная расчетная схема рамы от снеговой нагрузки.

Моменты от нагрузок на стойки М_Р равны:

Моменты на опорах ригеля (защемленная балка постоянного сечения):

кНм.

Определяем r_1Р:

— по эпюре М_Р: .

Таким образом, из канонического уравнения метода перемещений получим угол поворота:

.

Моменты от фактического угла поворота (М₁·) равны:

Эпюра моментов (М₁· + М_Р) от постоянной нагрузки

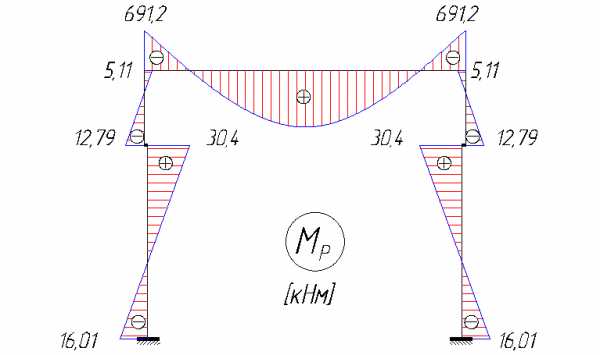
Эпюры изгибающих моментов, поперечных и продольных сил представлены на рисунке 4.11.

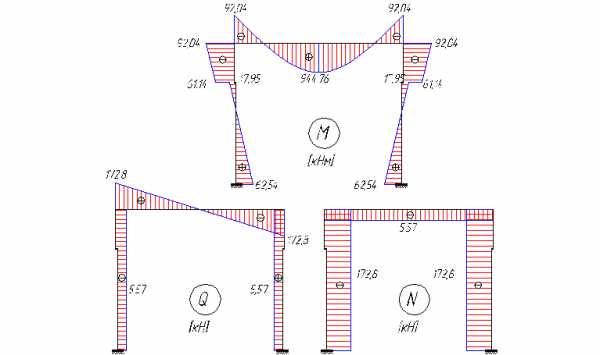
Рис. 4.11. Эпюры M, Q, N от снеговой нагрузки.

Проверкой служит:

— равенство моментов в узле В (92,04 = 92,04),

— равенство перепада эпюры моментов в точке С равной внешнему моменту: ,

— также равенство поперечных сил на верхней и нижней частях колонны: кН; кН.

4.3.3 Расчет на вертикальную нагрузку от мостовых кранов

Расчетная схема рамы на нагрузку от кранов приведена на рис. 4.6.

Проведем проверку возможности считать ригель абсолютно жестким:

,

где.

Каноническое уравнение для определения смещения плоской рамы имеет вид

.

На рисунке 4.12 представлена расчетная схема для определения усилий от вертикальных крановых нагрузок

Рис. 4.12. Упрощенная расчетная схема рамы от вертикальных крановых нагрузок.

Моменты от смещения верхних узлов стоек вдоль ригеля на  = 1 равны:

По вычисленным ранее п = 0,2 и  = 0,278 определим значения грузовой эпюры метода перемещений на левой стойке:

Усилия на правой стойке получим, умножая соответствующие усилия левой стойки на отношение

.

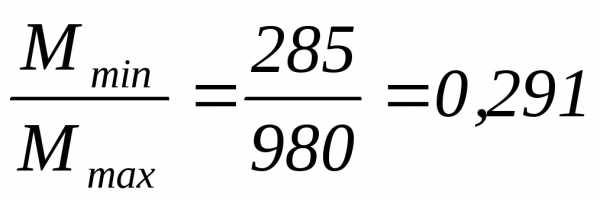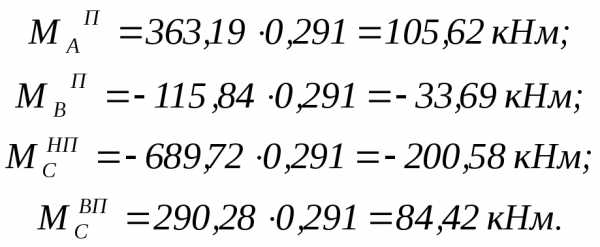
Единичная и грузовая эпюры изгибающих моментов от вертикальной крановой нагрузки представлены на рисунке 4.13.

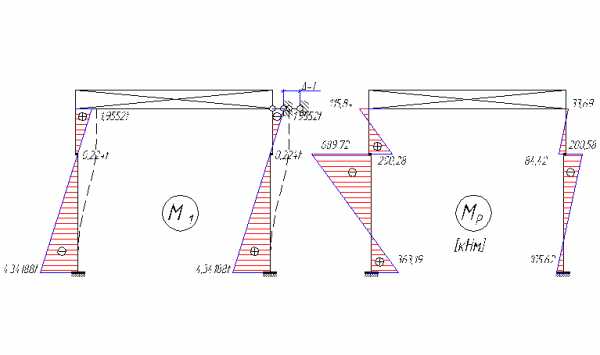
Рис. 4.13. Единичная и грузовая эпюры от вертикальной крановой нагрузки.

Найдем коэффициент и свободный член канонического уравнения:

,

кН.

Таким образом, из канонического уравнения получим смещение плоской рамы

.

В расчетной схеме я не учитывал работу упругоподатливой опоры в уровне подкрановых конструкций. В этом случае пространственную работу каркаса можно учесть, определив реакцию отпора на уровне ригеля или соответствующее смещение рамы в системе пространственного блока _пр. Оно меньше смещения плоской рамы , нагруженной той же силой.

Отношение _пр/ называют коэффициентом пространственной работы _пр, который определяется с учетом того, что смещение пропорционально силе, вызвавшей это смещение

,

где  = 0,713, ’ = – 0,2367 – коэффициенты зависящие от величины ;

п₀ =8 – число колес кранов на одной нитке подкрановых балок;

у – сумма ординат линии влияния реакции рассматриваемой рамы, по данным расчета в п. 4.2.3 равна 4,966.

Параметр  характеризует соотношение жесткостей поперечной рамы и покрытия и определяется по формуле

,

где I_н – сумма моментов инерции нижних частей колонн;

d – коэффициент привидения ступенчатой колонны к эквивалентной по смещению колонне постоянного сечения, равный при жестком сопряжении ригеля с колонной

;

С учетом крепления связей на сварке для кровли из панелей с профилированным настилом можно принять

.

.

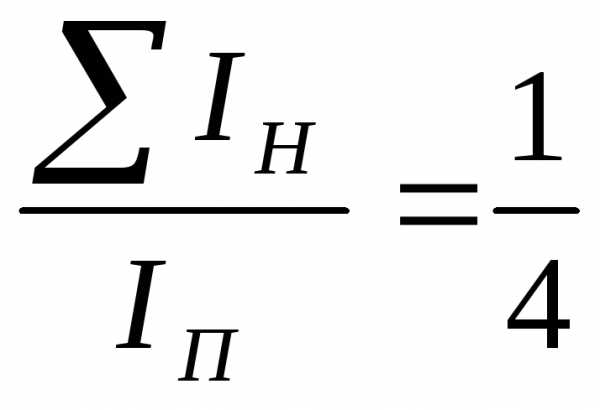С учетом найденного _пр пересчитаем эпюру М₁ и построим окончательную:

.

Моменты от фактического перемещения узлов (М₁ ·_пр) равны:

Эпюра моментов (М₁·_пр + М_Р) от крановой нагрузки для левой стойки:

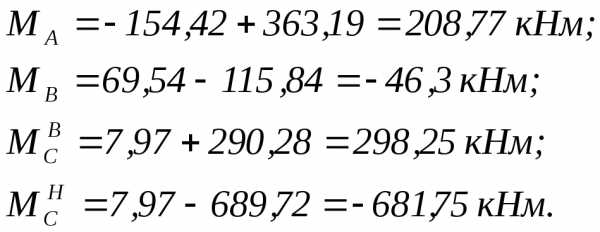
Эпюра М для правой стойки будет считать аналогично левой, только лишь единичные моменты будут браться с противоположным знаком:

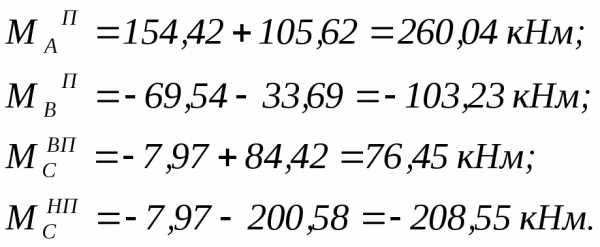
Единичная и грузовая эпюры изгибающих моментов от вертикальной крановой нагрузки с учетом пространственной работы каркаса представлены на рисунке 4.14.

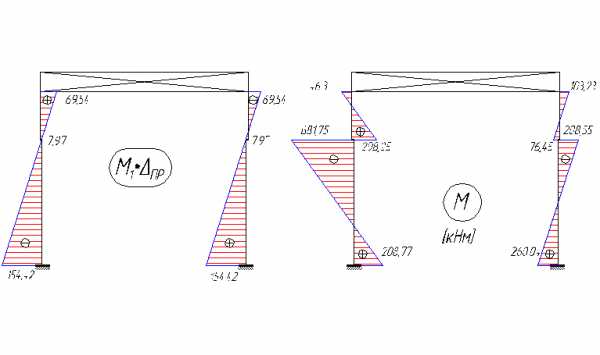
Рис. 4.14. Единичная и грузовая эпюры от вертикальной крановой нагрузки с учетом пространственной работы каркаса.

Эпюры поперечных и продольных сил представлены на рисунке 4.15.

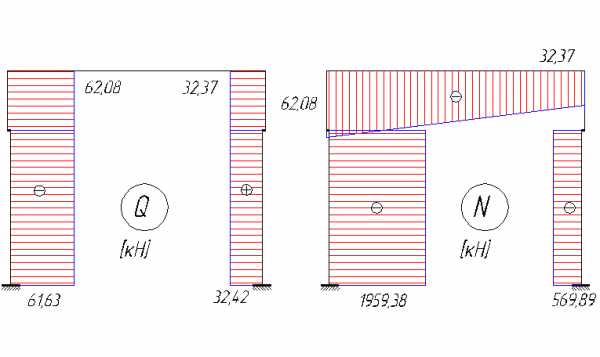Рис. 4.15. Эпюры Q, N от вертикальной крановой нагрузки с учетом пространственной работы каркаса.

Разница в значении нормальной силы у левого и правого концов ригеля получилась из-за передачи горизонтальных сил на соседние рамы вследствие учета пространственной работы каркаса.

Проверкой может служить значения перепада моментов в месте изменения жесткости стойки:

— на левой стойке;

— на правой стойке.

studfiles.net

Методическое указание к динамическому расчету рам Дл студентов заочного и очного обучения спец. «Строительство» Составитель: д.Т.Н. Достанова с.Х.

Казахская головная архитектурно-строительная академия

Дисциплина «Динамика и устойчивость сооружений»

Для бакалавров спец. «Строительство» ЗРПЗС

Ф.И.О. студента

Группа

Семестр

РГР №2

Динамический расчет плоской рамы

Для заданной рамы необходимо выполнить следующее:

Для динамического расчета необходимо выполнить следующее:

I. Определить динамическую степень свободы, указать направление

инерционных сил.

2. Записать вековое уравнение, определить спектр собственных частот

поперечных колебаний рамы

3. Определить формы главных или собственных колебаний ракш, построив

соответствующие эпюры изгибающих, моментов от инерционных сил.

4. Построить эпюры изгибающих моментов от амплитудных значений внешней вибрационной нагрузки.

5. Определить амплитудные значения инерционных сил,

6. Построить динамические эпюры изгибающих моментов и поперечных сил.

7. Определить динамический коэффициент .

Данные в таблице1

Таблица 1

Данные к задаче по динамическому расчету плоской рамы

L1	L2	h1	h2	P1	I4/I1	I2/I1	I3/I1	Q1	Q2	P2	q0
[м]	[м]	[м]	[м]	[кН]				[кН]	[кН]	[]кН	[град]

Динамический расчет плоских рам

1. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим плоскую статически неопределимую раму с располо­женными на ней сосредоточенными массами . Пренебрегаем собственным весом стержней по сравнению с весом присоединенного груза. На систему действуют вибрационные гармонические нагрузкиP_i , которые изменяются в одной фазе и с одинаковой частотой .

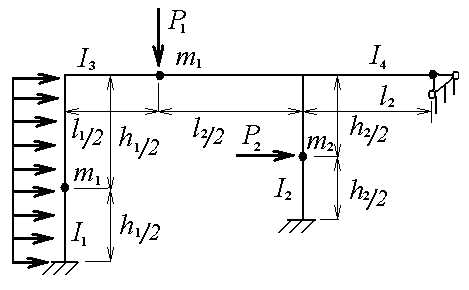
Рисунок 6.1 – Заданная система.

Длины стенок и ригелей имеют следующее величины:

h₁= 4 м; h₂= 3 м; l₁ = 4 м; l₂ = 5 м.

моменты инерции поперечных сечений стержней имеют следующие величины:

;;

Т.к. внешняя нагрузка – гармоническая, то ;;, амплитудные значения нагрузок имеют следующие значения:=30 кН,=30 кН,=40 кН,q⁰ = 5кН/м.

Вес масс m_i обозначим , где= 20кН,= 40 кН, массы определяют по формуле :, гдеg – ускорение свободно падающего тела, g = 9,81 м/сек². Круговая частота колебаний внешней нагрузки равна = 0,6, где- круговая частота собственных системы.

Для динамического расчета необходимо выполнить следующее:

I. Определить динамическую степень свободы, указать направление

инерционных сил.

2. Записать вековое уравнение, определить спектр собственных частот

поперечных колебаний рамы

3. Определить формы главных или собственных колебаний ракш, построив

соответствующие эпюры изгибающих, моментов от инерционных сил.

4. Построить эпюры изгибающих моментов от амплитудных значений внешней вибрационной нагрузки.

5. Определить амплитудные значения инерционных сил,

6. Построить динамические эпюры изгибающих моментов и поперечных сил.

7. Определить динамический коэффициент .

studfiles.net

Устойчивость рам — Строительная механика

 

Расчет на устойчивость деформируемых систем проводится в основном методом перемещений с помощью ЭВМ. В основе метода перемещений при расчете стержневых систем на устойчивость лежит дифференциальное уравнение изгиба сжатого прямолинейного стержня постоянного сечения.

 

 

Предварительно необходимо выполнить статический расчет сооружения, целью которого является определение перемещений узлов сооружения и внутренних сил в его элементах.

Внешние нагрузки исходного состояния, вызвавшие продольные силы, в дальнейшем расчете не участвуют.

 Основная система и основные неизвестные метода перемещений выбираются в обычном порядке. Т.к., дополнительные узловые нагрузки при исследовании устойчивости полагаются нулевыми, то канонические уравнения метода перемещений принимают вид:

 

R(N)∙Z=0

 

         где R – матрица мгновенной жесткости, элементы которой, реакции r_ik во введенных дополнительных связях, зависят от продольных сил в стержнях системы.

Расчет элементов матрицы мгновенной жесткости осуществляется как и в методе перемещений. Основная особенность метода перемещений в расчетах на устойчивость состоит в том, что в сжатых стержнях эпюры изгибающих моментов от единичных перемещений получаются криволинейными за счет дополнительного изгибающего действия продольных сил. А выражения для вычисления реакций в опорах сжатых стержней содержат поправочные множители в виде специальных функций от безразмерных параметров ν.

 

 

В несжатых стержнях построение единичных эпюр изгибающих моментов и вычисление реакций выполняется в обычном порядке.

Следовательно, коэффициенты канонических уравнений метода перемещений зависят от безразмерных параметров ν:

 

R(ν)∙Z=0

 

Т.е.:

 

 

Критическим состояниям равновесия отвечают ненулевые перемещения узлов деформируемой системы:

 

Z≠0

 

Это возможно, если определитель матрицы мгновенной жесткости равен нулю, что и соответствует моменту потери устойчивости:

 

 

Т.е.:

 

 

Раскрытие определителя приводит к уравнению, называемому уравнением устойчивости.

Дальнейшее решение задачи состоит в определении значений нагрузок на раму, удовлетворяющих уравнению устойчивости. Наименьшая из них является критической нагрузкой.

Критическое значение сжимающей силы определяется по формуле:

 

 

Критерием глобальной устойчивости сооружения является положительная определенность матрицы мгновенной жесткости деформированной системы:

 

R(ν)>0.

 

Примеры задач с решениями.

 

Таблица эпюр изгибающих моментов и реакций для прямых сжатых балок с разными условиями закрепления и значения специальных функций в зависимости от безразмерных параметров ν:

 

 

                   Таблица безразмерных параметров ν.

 

 

5stroymeh.ru