Расчет металлической балки
Двутавp колонный (К) по ГОСТ 26020-83
20К1
20К2
23К1
23К2
26К1
26К2
26К3
30К1
30К2
30К3
35К1
35К2
35К3
40К1
40К2
40К3
40К4
Двутавp с уклоном полок по ГОСТ 8239-89
10
12
14
16
18
20
22
24
27
30
33
36
40
45
50
55
60
Двутавp дополнительной серии (Д) по ГОСТ 26020-83
24ДБ1
27ДБ1
36ДБ1
35ДБ1
40ДБ1
45ДБ1
45ДБ2
30ДШ1
40ДШ1
50ДШ1
Двутавp нормальный (Б) по ГОСТ 26020-83
10Б1
12Б1
12Б2
14Б1
14Б2
16Б2
18Б1
18Б2
20Б1
23Б1
26Б1
26Б2
30Б1
30Б2
35Б1
35Б2
40Б1
40Б2
45Б1
45Б2
50Б1
50Б2
55Б1
- 55Б2
60Б1
60Б2
70Б1
70Б2
80Б1
80Б2
90Б1
90Б2
100Б1
100Б2
100Б3
100Б4
Двутавp широкополочный по ГОСТ 26020-83
20Ш1
23Ш1
26Ш1
26Ш2
30Ш2
30Ш3
35Ш1
35Ш2
35Ш3
40Ш1
40Ш2
40Ш3
50Ш1
50Ш2
50Ш3
50Ш4
60Ш1
60Ш2
60Ш3
60Ш4
70Ш1
70Ш2
70Ш3
70Ш4
70Ш5
Двутавp нормальный (Б) по СТО АСЧМ 20-93
10Б1
12Б1
12Б2
14Б1
14Б2
16Б1
16Б2
18Б1
18Б2
20Б1
25Б1
25Б2
30Б1
30Б2
35Б1
40Б1
40Б2
45Б1
45Б2
50Б1
50Б2
50Б3
55Б1
55Б2
60Б1
60Б2
70Б0
70Б1
70Б2
Двутавp широкополочный (Ш) по СТО АСЧМ 20-93
20Ш1
25Ш1
- 30Ш1
30Ш2
35Ш1
35Ш2
40Ш1
40Ш2
45Ш1
50Ш1
50Ш2
50Ш3
50Ш4
60Ш1
60Ш2
60Ш3
60Ш4
70Ш1
70Ш2
70Ш3
70Ш4
80Ш2
90Ш1
90Ш2
100Ш1
100Ш2
100Ш3
100Ш4
Двутавp колонный (К) по СТО АСЧМ 20-93
20К1
20К2
25К1
25К2
25К3
30К1
30К2
30К3
30К4
35К1
35К2
40К1
40К2
40К3
40К4
40К5
Строительная инженерия Калькулятор | Строительная инженерия Расчет
| Search | ||
| Дом | Инженерное дело ↺ | |
| Инженерное дело | Гражданская ↺ | |
| Гражданская | Строительная инженерия ↺ | |
| Строительная-Инженерия | Выберите предметБетонные конструкцииЖивые нагрузки на крышуПластический анализПредварительно напряженный бетонСтальные конструкцииСтруктурный анализ | |
| 6 Строительная инженерия Категории | ||
| Строительная инженерия Калькуляторы | ||
Строительная инженерия
- Область для поддержания напряжения как полностью сжимающего с учетом эксцентриситета
- Ширина балки с одинаковой прочностью для балок с простой опорой, когда нагрузка находится в центре
- Балка Глубина равномерной прочности для балки с простой опорой, когда нагрузка находится в центре
- Ширина прямоугольного сечения, позволяющая выдерживать напряжение как полностью сжимающее.

- Эксцентриситет для прямоугольного сечения для поддержания напряжения как полностью сжимающего
- Эксцентриситет для сплошного кругового сектора для поддержания напряжения как полностью сжимающего
- Эксцентриситет в колонне для полого круглого сечения, когда напряжение на крайнем волокне равно нулю
- Эксцентриситет для поддержания напряжения как полностью сжимающего
- Нагружение балки одинаковой прочности
- Модуль упругости сечения для поддержания напряжения как полностью сжимающего с учетом эксцентриситета
- Напряжение балки одинаковой прочности
Бетонные конструкции
Конструкция элементов сжатия
Оценка эффективной длины колонн
- Фактическая длина с учетом коэффициента гибкости
- Фактическая длина колонны с учетом эффективной длины, если оба конца колонны зафиксированы
- Фактическая длина колонны с учетом эффективной длины, если один конец закреплен, другой свободен.
- Фактическая длина колонны с учетом фактической длины, если один конец закреплен, а другой шарнирный.
- Площадь поперечного сечения колонны с учетом эффективной длины и радиуса инерции
- Площадь поперечного сечения колонны с учетом деформирующего напряжения
- Эффективная длина с учетом разрушающей нагрузки и радиуса инерции
- Эффективная длина столбца при заданной фактической длине, если оба конца столбца зафиксированы
- Эффективная длина колонны с учетом фактической длины, если один конец зафиксирован, другой свободен.
- Эффективная длина колонны с учетом фактической длины, если один конец закреплен, другой шарнирный.
- Эффективная длина колонны с учетом разрушающей нагрузки для любого типа конечного состояния
- Эффективная длина колонны с учетом деформирующего напряжения
- Наименьший радиус вращения с учетом коэффициента гибкости
- Модуль упругости с учетом разрушающей нагрузки для любого типа конечного состояния
- Модуль упругости при заданной эффективной длине и радиусе вращения
- Модуль упругости колонны при деформирующем напряжении
- Момент инерции при заданной разрушающей нагрузке для любого типа конечного состояния
- Радиус вращения с учетом калечащего напряжения
- Радиус вращения с учетом эффективной длины и разрушающей нагрузки
Структурный анализ
Разные темы
Эксцентричная нагрузка
- Критическая нагрузка потери устойчивости при прогибе при внецентренной нагрузке
- Площадь поперечного сечения с учетом радиуса инерции при внецентренной нагрузке
- Площадь поперечного сечения с учетом общего напряжения — это место, где нагрузка не лежит на плоскости.
- Площадь поперечного сечения при заданном суммарном единичном напряжении при внецентренной нагрузке
- Прогиб при эксцентрической нагрузке
- Расстояние от XX до самого дальнего волокна с учетом общего напряжения, когда нагрузка не лежит на плоскости
- Расстояние от YY до самого дальнего волокна с учетом общего напряжения, когда нагрузка не лежит на плоскости
- Эксцентриситет при заданном отклонении при внецентренной нагрузке
- Эксцентриситет относительно оси XX при заданном общем напряжении, где нагрузка не лежит на плоскости
- Эксцентриситет относительно оси YY при заданном общем напряжении, когда нагрузка не лежит на плоскости
- Нагрузка на прогиб при эксцентрической нагрузке
- Момент инерции около XX при общем напряжении, когда нагрузка не лежит на плоскости
- Момент инерции относительно YY при заданном общем напряжении, когда нагрузка не лежит на плоскости
- Момент инерции при заданном радиусе вращения при внецентренной нагрузке
- Момент инерции поперечного сечения при заданном суммарном единичном напряжении при внецентренной нагрузке
- Расстояние от нейтральной оси до самого внешнего волокна с учетом общего единичного напряжения при внецентренной нагрузке
- Радиус вращения при эксцентрической нагрузке
- Общее напряжение при эксцентрической нагрузке, когда нагрузка не лежит на плоскости
- Общее удельное напряжение при эксцентрической нагрузке
- Суммарное единичное напряжение при внецентренной нагрузке с учетом радиуса инерции
Share
Copied!Расчеты металлической балки перекрытия на прочность и прогиб, онлайн-калькулятор
Несмотря на бушующий в мире экономический кризис, который, к сожалению, затронул и нашу страну, строительство объектов различной важности продолжает производиться. При этом, в последнее время получило новый толчок развития именно промышленное строительство, однако, потребность жителей страны в жилых квадратных метрах не уменьшилось.
При этом, в последнее время получило новый толчок развития именно промышленное строительство, однако, потребность жителей страны в жилых квадратных метрах не уменьшилось.
- Описание ↓
- Область применения ↓
- Расчет ↓
- Онлайн ↓
- Пример расчета ↓
Сегодня в строительстве промышленных и гражданских объектов повсеместно применяются металлические балки перекрытия, которые повышают несущую способность всей конструкции.
Описание
Стальные балки перекрытия представляют собой металлический брус определённой длины и определённой формы поперечного сечения. Как правило, металлические балки исполняются из высокопрочной стали марки Ст 5 с формой поперечного сечения типа двутавр и швеллер.
Балки производятся именно в таких формах поперечного сечения, потому что расчёт показывает, что такая форма является более экономически выгодной по сравнению с другими геометрическими фигурами.
Кроме того, расчёты показывают, что балка именно двутаврогого сечения лучше всего воспринимает давление и такие нагрузки, как изгиб, кручение и их совместное действие.
Продолжая перечислять преимущества двутавровых балок, можно отметить немаловажный факт того, что такая форма сечения помогает уменьшить вес конструкции.
Это помогает снизить нагрузку, например, на стены и фундамент здания, если в межэтажном перекрытии использовать металлические балки перекрытия. Также, из преимуществ можно отметить простоту монтажа любой конструкции из балок, скорость выполнения работ.
Для большей экономии использования металла и для облегчения всей конструкции существует сортамент балок двутаврового и швеллерного поперечного сечения. Площадь сечения изменяется от минимальной равной 12 кв. см до максимальной 234 кв. см, соответственно, для номеров профиля 10 и 70б.
Все значения площадей и массы профиля представлены в таблицах ГОСТ 8239-72. Чтобы её произвести, необходимо произвести расчёт профиля по прочностным характеристикам и вычислить подходящую площадь. Точная методика представлена ниже.
Таким образом, видно, что в качестве бруса перекрытия стоит использовать именно стальные балки, так как они во многом выигрывают по сравнению с конкурирующими материалами.
Область применения
Чаще всего, двутавровые балки применяются в промышленном строительстве, а именно, в случае возведения зданий с большими пролётами между опорами.
Благодаря своим механическим характеристикам и стойкости к динамическим воздействиям, металлический брус используют при возведении дорог и мостов и в других случаях необходимости возведения конструкций, выдерживающих большие нагрузки подобного характера.
В последнее время, стальные двутавровые балки стали применять в качестве элемента декора в квартирах и офисах. После покраски, металлическая балка может выглядеть эстетично и иметь практическое применение в бытовом хозяйстве.
Расчет
Чтобы произвести выбор металлического бруса для той или иной конструкции, которая будет нести определённую нагрузку, необходимо произвести расчёт балки на прочность при изгибе. Это можно сделать, рассчитав все параметры самостоятельно по известной методике или воспользоваться онлайн-калькулятором.
Для выбора балки перекрытия, делают проверку из условия на прочность, где максимальная прочность стали должна быть больше суммы отношений максимального изгибающего момента в точке действия той или иной нагрузки к осевому моменту, и поперечных сил и площади поперечного сечения в максимально нагруженной точке.
Для определения всех неизвестных параметров этого условия, вычисления проводят поочерёдно.
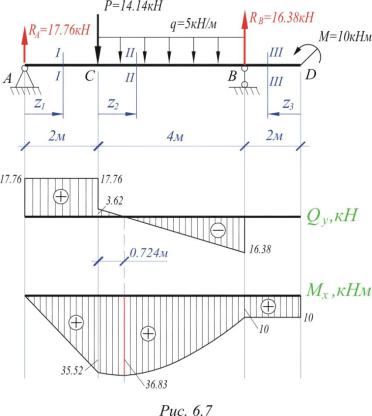
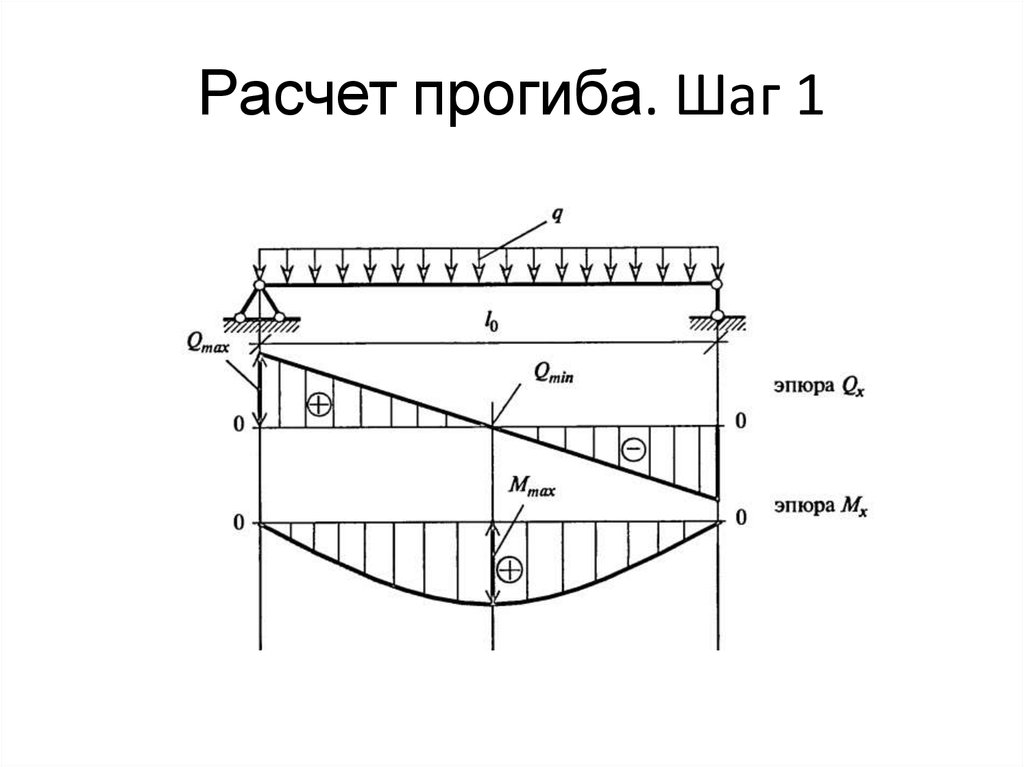
Сначала определяют максимально нагруженный участок балки. Для этого, строят эпюру поперечных сил и изгибающих моментов. Чтобы построить эпюру, необходимо вычислить все суммарные изгибающие моменты и поперечные силы, действующие на балку, по участкам.
Как правило, в случае металлического бруса перекрытия, расчётную схему заменяют балкой, лежащей на двух шарнирных опорах. В этих опорах возникают реакции сопротивления, у которых необходимо определить их условия:
Когда реакции определены, балку разбивают на участки по опорам. Первый участок находится от одного конца балки до опоры, второй участок располагается между опорами, третий за последней опорой и так далее. Необходимо знать, что если на одном участке имеется точка изменения нагрузки, то её нужно выделить в отдельный участок.
После того, как участки определены, строятся эпюры поперечных сил и изгибающий моментов, и определяется нагруженный участок. Далее, вычисляется осевой момент сопротивления сечения:
Далее, вычисляется осевой момент сопротивления сечения:
По вычисленному параметру производят выбор номера двутавра из сортамента. На этом расчёт балки считается оконченным.
Онлайн
Рассчитывать металлическую балку и производить её выбор вручную довольно трудоёмко и занимает время, которое не всегда можно выделить занятому человеку. Поэтому, стоит довериться расчётам профессионалов.
Но, если заказчик строительства сомневается в экономической целесообразности произведённого строителями расчёта, можно произвести быстрый автоматический расчёт при помощи сайтов, предлагающих данный товар.
Одним из примеров такого калькулятора может быть портал http://svoydomtoday.ru/building-onlayn-calculators/111-raschet-metallicheskoy-balki-perekritiya.html, который предлагает, находясь на сайте, рассчитать расход материала и выбрать балку из сортамента.
Данный калькулятор требует введения следующих исходных данных:
- Сначала нужно ввести условия эксплуатации металлической балки.

- После этого характеристики предварительно выбранной металлической балки.
- Указать нормативную и расчётную нагрузку на балку и произвести расчёт.
В результате, получается минимально возможный при заданных условиях момент сопротивления балки. Из полученного момента можно выбрать балку по таблице сортамента.
Так же определяется минимально допустимый момент инерции, по которому можно выбрать номер профиля из сортамента. Если для строительства в первую очередь важно не допустить прогиб балки, тогда стоит выбирать балку исходя из полученного момента инерции.
Пример расчета
Металлической балки перекрытия:
Расчет несущей способности:
- Чтобы рассчитать несущую способность одной балки нужно из таблицы сортамента выбрать момент осевого сопротивления и по формуле вычислить максимально допустимый изгибающий момент:
- Отсюда можно вычислить максимально допустимую равнораспределённую нагрузку на однопролётную балку.

Расчет сечения металлических балок:
- Для расчёта необходимого сечения металлической балки можно воспользоваться формулой расчёта момента сопротивления сечения.
- После вычисления результата, определить площадь сечения нужно по сортаменту фасонного профиля, выбрав при этом номер двутавра с ближайшим большим значением момента сопротивления.
При расчёте металлической балки пролёта необходимо отнестись ко всему ответственно и внимательно, потому что от расчёта зависит срок эксплуатации здания и его возможная нагрузка. Здания, построенные по ошибочным расчётам, могут разрушиться в любой момент, унеся за собой много жизней.
Статья была полезна?
0,00 (оценок: 0)
App Store: Прогиб
Описание
Прогиб — самое интерактивное, быстрое и точное приложение для анализа структурных балок. Проектируйте визуально и получайте инженерные результаты, графики и уравнения мгновенно!
Просто поместите грузы и опоры на балку и посмотрите, как она изгибается. Найдите сечение во встроенной библиотеке или определите пользовательскую форму. Прогиб, внутренние напряжения и другие полезные результаты автоматически обновляются.
Найдите сечение во встроенной библиотеке или определите пользовательскую форму. Прогиб, внутренние напряжения и другие полезные результаты автоматически обновляются.
Это программное обеспечение является результатом более чем шести лет непрерывного развития и инноваций, направленных на машиностроение, гражданское строительство и конструкцию. Этот инструмент поможет вам применить теорию упругости луча с 1-го дня, когда вы изучаете Механику материалов, и он будет вашим справочным материалом в любое время в будущем.
ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ
Получать результаты проектирования и диаграммы в режиме реального времени.
• Сдвигающая сила
• Изгибающий момент
• Прогиб
• Внутреннее изгибающее напряжение
• Внутреннее напряжение сдвига
КРОСС-СЕКЦИОННЫЕ БАЗЫ ДАННЫХ
Укажите значения напрямую или найдите общие формы и материалы, используя встроенные базы данных.
• Соединенные Штаты
• Европа
• Япония
• Индия
• Россия
• Великобритания
• Канада
• Австралия
• Китай
КРЕСТ СЕКТОР РЕДАКТОР
Редактировать встроенные сечения.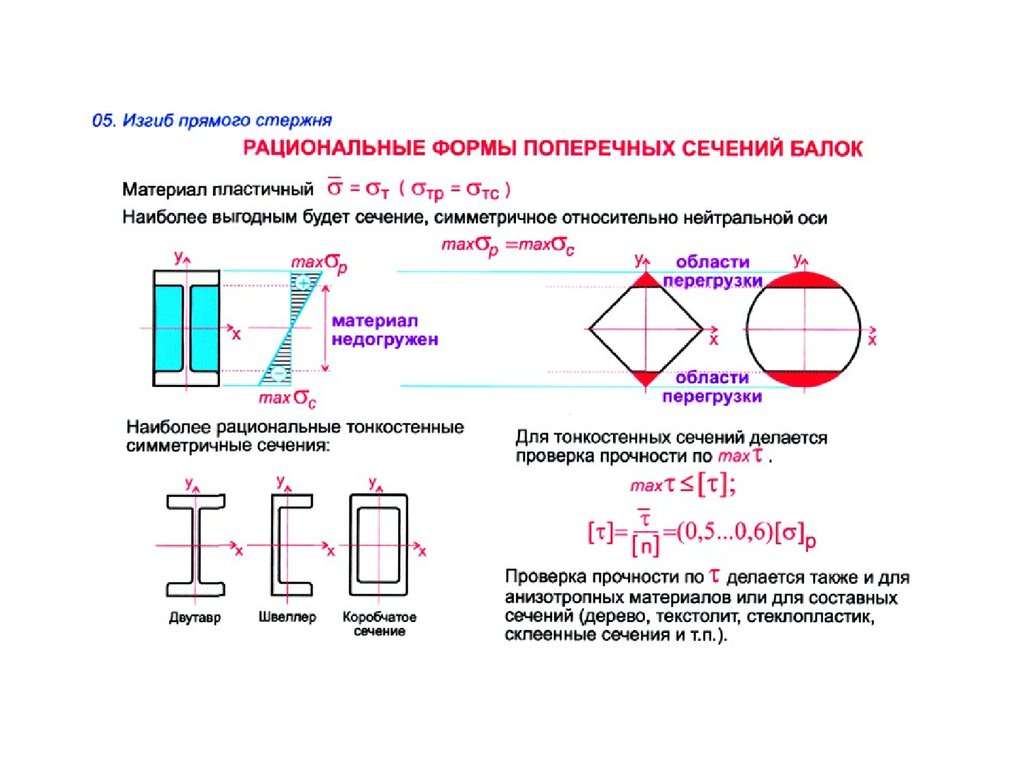 Свойства формы рассчитываются автоматически.
Свойства формы рассчитываются автоматически.
• Момент инерции
• Площадь
НЕОГРАНИЧЕННЫЕ НАГРУЗКИ И ОПОРЫ
Просто перетащите любой груз или опору на балку.
• Сосредоточенная нагрузок
• Распределенная нагрузок
• моменты
• неподвижные опоры
• Подвижные опоры
• неподвижные шарниры
• балка Гербера
ДРУГИЕ СВОЙСТВА
• Применить луч собственного веса по выбору
• Автоматическое определение локальных максимумов и минимумов на графиках
• Неограниченное количество файлов дизайна
• шаблоны быстрого запуска
• Метрические и стандартные единицы измерения
СВЯЗАТЬСЯ С НАМИ
Ждем вашего ответа! Проблемы, вопросы или запросы? Пожалуйста, отправьте отзыв или по электронной почте [email protected].
Версия 6.2.0
• NEW: South Africa steel shapes. Select the «ZA» database to enable.
Select the «ZA» database to enable.
• FIXED: For some European steel shapes, the «depth between fillets» was previously being incorrectly labeled as «detailing depth».
Оценки и отзывы
Оценок: 8
Почему невозможно выполнить…
Здравствуйте. После случайного обновления на iOS 11 была утрачена возможность использовать приложение ForceEffect от Autodesk. Ваше приложение пригодилось как дополнение к ForceEffect, так как последний не показывал перемещения. Теперь оно осталось основным.
В ForceEffect можно было создавать множество расчетов и всегда посмотреть чем отличались значения в разных расчётах. Была возможность сформировать отчёт и отправить кому-либо.
Было бы великолепно, если бы такие возможности появились и в этом приложении.
Почему невозможно выполнить расчёт для однопролётной балки с консолями на подвижной опоре и неподвижном шарнире?
На двух подвижных опорах расчёт выполняется.
support russian lang
russian lang add
Пожелание
Добавьте пожалуйста сплошные сечения.
Разработчик Blue Ketchep указал, что в соответствии с политикой конфиденциальности приложения данные могут обрабатываться так, как описано ниже. Подробные сведения доступны в политике конфиденциальности разработчика.
Не связанные с пользователем данные
Может вестись сбор следующих данных, которые не связаны с личностью пользователя:
- Пользовательский контент
- Идентификаторы
- Данные об использовании
- Диагностика
Конфиденциальные данные могут использоваться по-разному в зависимости от вашего возраста, задействованных функций или других факторов. Подробнее
Подробнее
Информация
- Провайдер
- Ketchep.com, LLC
- Размер
- 40,2 МБ
- Категория
- Производительность
- Возраст
- 4+
- Copyright
- © 2010-2022 Ketchep.com, LLC
- Цена
- 449,00 ₽
- Сайт разработчика
- Поддержка приложения
- Политика конфиденциальности
Поддерживается
Другие приложения этого разработчика
Вам может понравиться
Расчёт перекрытия с деревянным каркасом — О программе
Расчёт перекрытия с деревянным каркасом выполняется в соответствии с СП 20. 13333.2016 «Нагрузки и воздействия», СП 64.13330.2017 «Деревянные конструкции» и СП 31-105-2002 «Проектирование и строительство энергоэффективных одноквартирных жилых домов с деревянным каркасом» по следующим параметрам:
13333.2016 «Нагрузки и воздействия», СП 64.13330.2017 «Деревянные конструкции» и СП 31-105-2002 «Проектирование и строительство энергоэффективных одноквартирных жилых домов с деревянным каркасом» по следующим параметрам:
- прочность по нормативным напряжениям; предельное и расчётное значения определяются по СП 64.13330.2011, учёт нагрузок выполняется по СП 20.13330.2011;
- устойчивость плоской формы деформирования; расчёт производится в соответствии с СП 64.13330.2011, учёт нагрузок выполняется по СП 20.13330.2011;
- прогиб по конструктивным требованиям; предельное значение прогиба принимается СП 31-105-2002, учёт нагрузок выполняется по СП 20.13330.2016;
- прогиб по физиологическим требованиям; предельное и расчётное значения прогиба определяются и учёт нагрузок выполняется по СП 20.13330.2016.
Нормативная равномерно распределённая нагрузка (если не используется возможность самостоятельно указать её величину) выбирается по СП 20.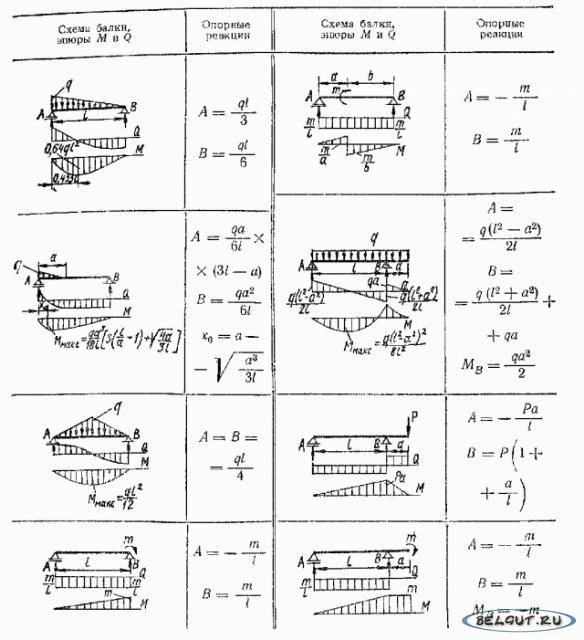 13330.2016.
13330.2016.
Указываемая нагрузка от конструкций должна включать вес перекрытия, и может учитывать нагрузки от других конструкций, в частности, ненесущих перегородок, приведённые к равномерно распределённой нагрузке по площади перекрытия.
При расчёте предполагается, что балки имеют опоры только на концах (промежуточные опоры отсутствуют).
Для использования программы требуется браузер с поддержкой HTML5 и WebGL.
Вернуться к расчёту
Расчёт перекрытия основывается на вычислении параметров единичной деревянной балки постоянного сечения под действием требуемых сочетаний нагрузок.
Геометрические характеристики балки прямоугольного сечения
Для выполнения расчёта требуется ряд геометрических характеристик досок перекрытия, являющихся балками прмоугольного сечения постоянной высоты.
Момент инерции поперечного сечения балки вычисляется по формуле:
I=bh412,
где b — ширина сечения балки;
h — высота сечения балки.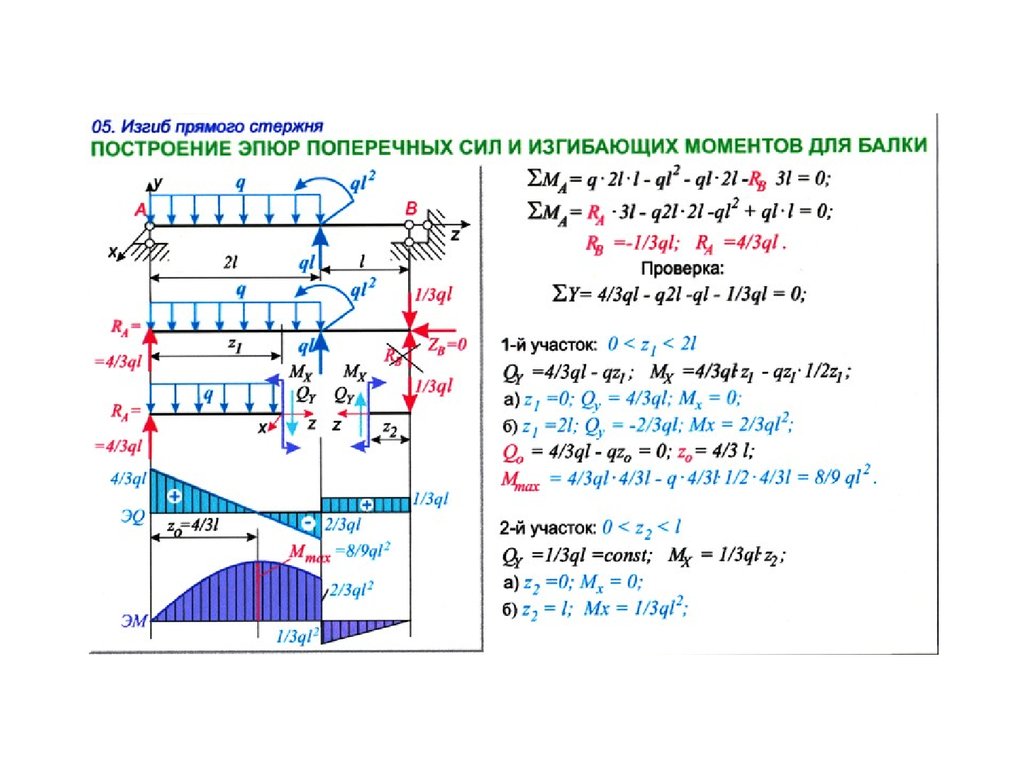
Характеристики материала балки
Выбранные характеристики балки соответствуют доске класса C24 (второй сорт) со следующими коэффициентами условий работы:
| Условие работы | Коэффициент | Значение коэффициента | |
|---|---|---|---|
| Режим нагружения | — | mдл,E | 1.0 |
| Условия эксплуатации конструкций | 2 (нормальные) | mв | 1.0 |
| Установившаяся температура эксплуатации | менее 35°C | mт | 1.0 |
| Срок службы | до 50 лет | mс.с | 1.0 |
Расчётные значения характеристик балки составляют:
| Описание | Обозначение | Базовое значение | Применяемые коэффициенты | Расчётное значение |
|---|---|---|---|---|
| EⅡ | Модуль упругости при расчёте по предельным состояниям 2-ой группы | Eср 13 МПа | mдл,Emвmтmс. с с | 11.7 МПа |
Расчёт прогиба балки
Наибольший прогиб шарнирно-опёртой изгибаемой балки постоянного сечения с учётом деформации сдвига производится по формуле, рекомендованной СП 64.13330.2017:
f=f0k1+chl2,
где f0 — прогиб балки постоянного сечения высотой h без учёта деформации сдвига;
k — коэффициент, учитывающий влияние переменности высоты сечения;
c — коэффициент, учитывающий влияние деформации сдвига от поперечной силы;
h — наибольшая высота сечения;
l — пролёт балки.
Коэффициенты k и c прининяты на основании данных СП 64.13330.2017 таблица Е.4 приложения Е для принятой расчётной схемы и равны:
k=1
c=19.2
Прогиб балки постоянного сечения под действием равномерно-распределённой нагрузки без учёта деформации сдвига выполняется по формуле теоретической механики:
f0=5ql4384EⅡI,
где q — величина равномерно-распределённой нагрузки;
l — пролёт балки;
EⅡ — расчётный модуль упругости древесины при расчёте по предельным состояниям 2-ой группы;
I — момент инерции поперечного сечения балки.
Значения нормативных нагрузок от людей, складируемых материалов могут быть приняты рекомендованными в СП 20.13330.2016 или указаны. Рекомендованые значения нагрузок зависят от назначения помещения и составляют:
Для вычисления расчётных и пониженных значений нагрузок применяются следующие коэффициенты по СП 20.13330.2016:
Кроме этого при расчёте балок для комнат и коридоров при грузовой площади одной балки применяется понижающий коэффициент для равномерно распределённой нагрузки:
где A — грузовая площадь с которой передаются нагрузки на балку. Для чердачных помещений этот коэффициент равен 1.0.
Расчет уголка на прогиб
Главная » Разное » Расчет уголка на прогиб
Расчет уголка на прогиб и изгиб
Данный онлайн-калькулятор предназначен для того, чтобы Вы могли легко и быстро подобрать размеры уголка в зависимости от приходящейся на него нагрузки. Особенность его в том, что на одной странице возможно сравнение равнополочных (ГОСТ 8509-93) и неравнополочных (ГОСТ 8510-86) уголков.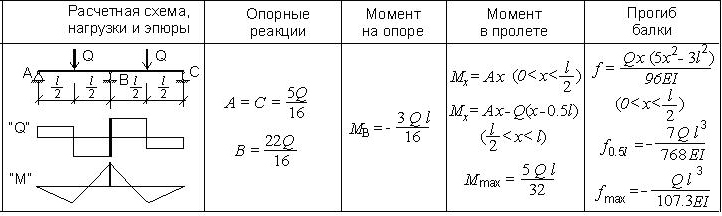 Последние, в свою очередь, можно подбирать в зависимости от расположения его в пространстве, т.е. в зависимости от того, как он будет ориентирован относительно нагрузки.
Последние, в свою очередь, можно подбирать в зависимости от расположения его в пространстве, т.е. в зависимости от того, как он будет ориентирован относительно нагрузки.
Содержание:
1. Калькулятор
2. Инструкция к калькулятору
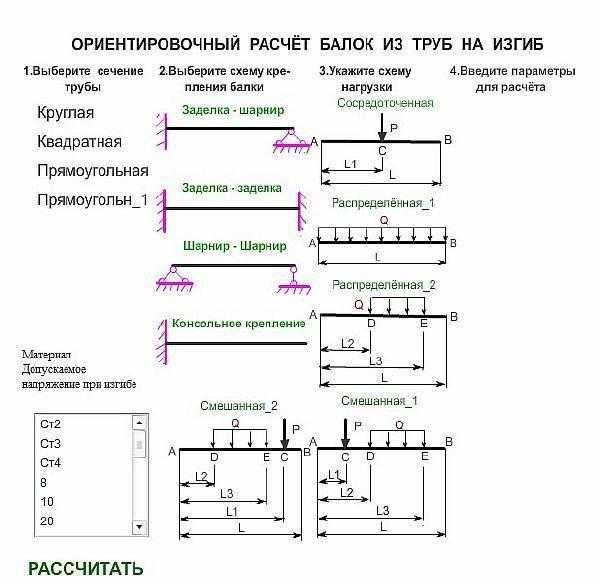
Расчет уголков производится на изгиб и прогиб (по прочности и по деформациям) для следующих расчетных схем:
- Тип 1 — однопролетная шарнирно-опертая балка с равномерно распределенной нагрузкой. Пример: перемычка из уголка, которая несет плиты перекрытия и небольшую высоту кладки. (Подробнее о расчете перемычек из уголка см. этот калькулятор).
- Тип 2 — консольная балка с жесткой заделкой с равномерно распределенной нагрузкой. Пример: железобетонный козырек, выполненный с применением уголка, который жестко (с применением ребер жесткости, ограничивающих любые повороты) приварен к железобетонной стене.

- Тип 3 — однопролетная шарнирно-опертая балка с консолью с равномерно распределенной нагрузкой. Пример: тот же козырек, что и в предыдущей схеме, только здесь уголок с одной стороны заводится в стену, а с другой опирается на раскос (на рисунке синий).
- Тип 4 — однопролетная шарнирно-опертая балка с одной сосредоточенной силой. Пример: перемычка, на которую опирается одна балка перекрытия.
- Тип 5 — однопролетная шарнирно-опертая балка с двумя сосредоточенными силами. Пример: перемычка, на которую опираются две сосредоточенные силы.
- Тип 6 — консольная балка с одной сосредоточенной силой. Пример: козырек дома с кирпичной стенкой на нем, построенного в африканской республике (где никогда не выпадает снег) по фантазии африканского архитектора. Уголки этого козырька жестко заделаны в стену, так как описано во второй схеме.
Примечание: рассчитываемый уголок на рисунках с примерами окрашен в красный цвет.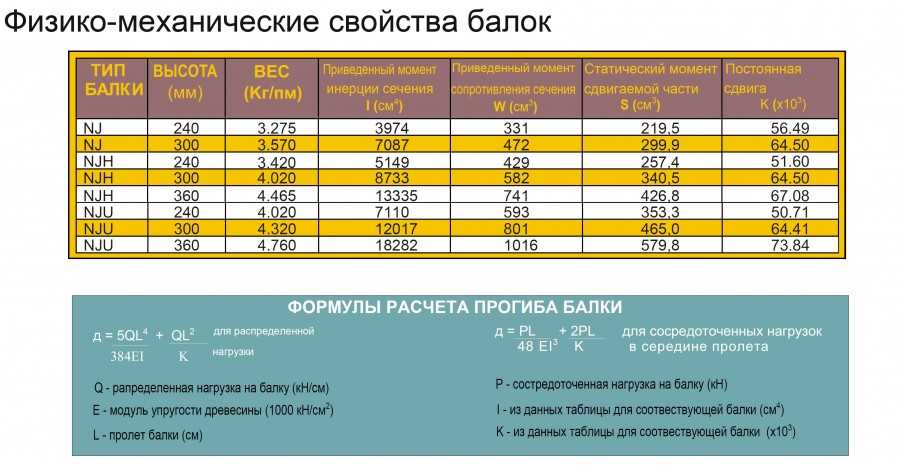
Расчет прогиба балки онлайн калькулятор. Площадь поперечного сечения профиля. Расчет на прочность.
Описание
При выборе схемы с распределенной нагрузкой, приложенная «Нагрузка Q» указывается как относительная «килограмм на метр». Определяется она по формуле Q = [общяя нагрузка, кг]/[общая длина, м].
Использование калькулятора «Расчет прогиба балки онлайн» значительно сократит время и послужит залогом надежных инженерных конструкций.
Калькулятор разработан исключительно по формулам Сопромата и справочным данным для каждого типа материала и сечения балки. Расчет прогиба сечения является теоретическим, следовательно практические значения могут быть отличными от расчетных и зависеть от множества условий.
Однако значения полученные в данном калькуляторе будут невероятно полезными и послужат основой для расчета необходимой конструкции.
Для быстрого доступа к расчетам необходимого профиля добавьте калькулятор в избранное (CTRL+D на ПК или значек «звездочка» справа вверху браузера)
Пример расчета уголка, швеллера и двутавра на прогиб и изгиб
На данной странице представлен пример расчета швеллера. Что касается расчетов уголка и двутавра, то они производится аналогичным образом. Другими словами, данный пример является полезным для следующих калькуляторов:
Что касается расчетов уголка и двутавра, то они производится аналогичным образом. Другими словами, данный пример является полезным для следующих калькуляторов:
В примере будут описаны несколько действий, которые должны выполняться последовательно.
Дано.
Район строительства — Нижний Новгород.
Расчетная схема — Тип 1.
Необходимо подобрать швеллер, который будет воспринимать нагрузку от снега.
Действие 1. Внесение исходных данных.
Расчетная нагрузка = 240 кг/м2 — так как город Н.Новгород находится в IV снеговом районе (в соответствии с табл. 10.1 и картой 1 СП 20.13330.2011 «Нагрузки и воздействия» [1]).
Fmax = 1/200 — так как пролет балки равен 5 м (пункт 2 табл. E1 [1]).
Расположение — по оси Х (швеллер воспринимает нагрузку вертикально).
Расчетное сопротивление Ry=210 МПа — берется как наихудший вариант для стали.
Действие 2. Выбор предполагающих номеров профилей.
Предположим, что мы рассматриваем два вида профилей: с параллельными гранями и с уклоном полок. Поэтому для первоначального расчета выбираются швеллеры размером 8П И 8У.
После произведенного расчета видно, что в графе «Запас» в том и другом случае стоят отрицательные значения. Это означает, что выбранные швеллеры не способны воспринимать приложенную на них нагрузку. Следовательно, необходимо выбирать профили большего размера.
Действие 3. Корректирующий расчет.
При увеличении профилей до 10П и 10У ситуация аналогичная. Но после того, как профили были увеличены до 12П и 12У в графах «Запас» появились положительные значения. Следовательно, в качестве балки перекрытия можно принять тот или иной профиль (имеется в виду 12П или 12У).
| Вид проката Уголок равнополочныйУголок неравнополочныйШвеллер с уклоном полокШвеллер с паралельными гранями полокДвутавр с уклоном полокДвутавр с паралел. | Вид и назначение стоек (колонн) Стойки и раскосы передаюшие реакции опорОсновные колонныВторостепенные колонны |
| Сталь С235 (Ст3кп2)Сталь С245 (Ст3пс5,Ст3сп5)Сталь С255 (СтГпс,Ст3Гсп)Сталь С285 (Ст3сп,Ст3Гпс,Ст3Гсп)Сталь С345 (12Г2С,09Г2С)Сталь С345К (10ХНДП)Сталь С375 (12Г2С)Сталь С390 (14Г2АФ)Сталь С390Д (14Г2АФД)Сталь С440 (16ГАФ)Сталь С590 (12Г2СМФ) |
| РАЗМЕРЫ ВЫБРАННОГО ПРОФИЛЯ: |
Размеры проката углового профиля оговариваются ГОСТ 8509-93 и ГОСТ 8510-86; швеллеров ГОСТ 8240-97; двутавров ГОСТ 26020-83; тавров – ТУ 14-2-685-86; (получаемых продольной разрезкой пополам горячекатаных двутавров с параллельными гранями полок по ГОСТ 26020-83).
При проектировании строительных конструкций необходимо принимать схемы, обеспечивающие прочность, устойчивость и пространственную неизменяемость сооружения в целом, а также его отдельных элементов при монтаже и эксплуатации.
Поэтому стойку,находящуюся под действием сжимающей её нагрузки необходимо проверять:
- на прочность;
- устойчивость;
- допустимую гибкость.
Согласно Актуализированной редакция СНиП II-23-81 (CП16.13330, 2011) расчет на прочность элементов из стали при центральном растяжении или сжатии силой P следует выполнять по формуле:
P/Fp*Ry*Yc <= 1, где
- P – действующая нагрузка,
- Fp – плошадь поперечного сечения стойки,
- Ry – расчётное сопротивление материала (стали стойки), выбирается по таблице В5 Приложения “В” того же СНиПа;
- Yc – коэффициент условий работы по таблице 1 СНиПа (0.9-1.1). В соответствии с примечанием к этой таблице (пункт 5) в калькуляторе принято Yc=1.

Проверку на устойчивость элементов сплошного сечения при центральном сжатии силой P следует выполнять по формуле:
P / Fi*Fp*Ry*Yc <= 1, где
Fi – коэффициент продольного изгиба центрально-сжатых элементов.
Коэффициент Fi введён в расчёт в качестве компенсации возможности некоторой не прямолинейности стойки, недостаточной жесткости её крепления и неточности в приложении нагрузки относительно оси стойки. Значение Fi зависит от марки стали и гибкости колонны и часто берётся из таблицы 72 СНиП II-23-81 1990г. исходя из гибкости стойки и расчётного сопротивления выбранной стали сжатию, растяжению и изгибу.
Это несколько упрощает и огрубляет расчёт, так как СНиП II-23-81* предусматривает специальные формулы для определения Fi. Гибкость (Lambda) – некоторая величина, характеризующая свойства рассматриваемого стержня в зависимости от его длины и параметров поперечного сечения, в частности радиуса инерции:
Lambda = Lr / i; здесь
- Lr – расчётная длина стержня;
- i – радиус инерции поперечного сечения стержня (стойки,колонны).
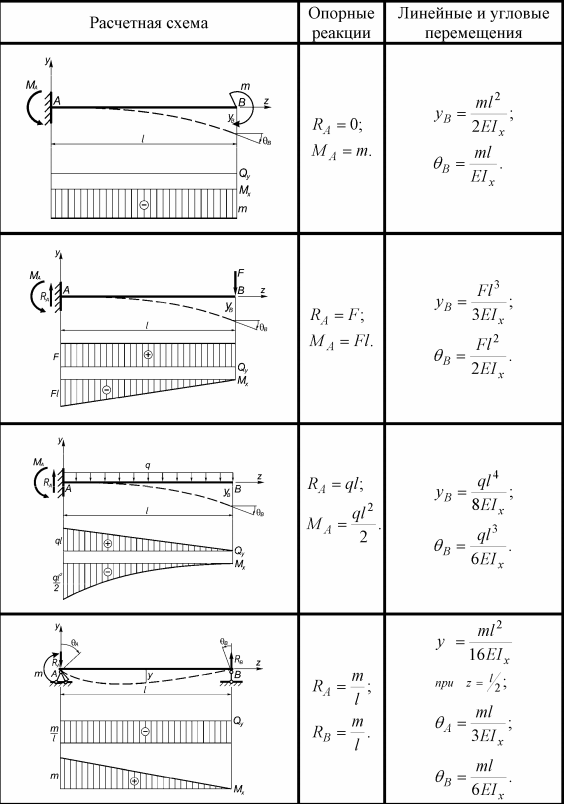
Радиус инерции сечения i равен корню квадратному из выражения I / Fp, где
- I – момент инерции сечения,
- Fp – его площадь.
Lr (расчётная длина) определяется как MuL;
здесь L- длина стойки,а Mu – коэфф., зависящий от схемы её крепления:
- “заделка-консоль”(свободный конец) – Mu = 2;
- “заделка-заделка”-Mu = 0.5;
- “заделка-шарнир” -Mu = 0.7;
- “шарнир-шарнир”-Mu=1.
Следует иметь ввиду,что при наличии у формы поперечного сечения 2-ух радиусов инерции (например, у швеллера, двутавра, тавра – относительно осей x-x и y-y), при расчёте Lambda используется меньший.
Уголки (как равнополочные так, и неравнополочные) имеют минимальный радиус инерции относительно оси z-z, который и используется в расчётах. Кроме того,сама Lambda (гибкость стойки), рассчитанная по формуле Lambda=Lr/i не должна превышать 220-ти в соответствии с табл. 19.СНиП II-23-81*; там же содержатся ограничения на предельную гибкость центрально-сжатых стержней.
Для их использования необходимо сделать выбор в таблице калькулятора “Вид, назначение стоек…”. Предельная гибкость стоек, кроме их геометрических параметров, зависит также от коэфф. продольного изгиба (Fi), действующей нагрузки(P), расчётного сопротивления материала стойки (Ry) и условий её работы (Yc).
ПРИМЕЧАНИЕ. Размеры выбранного швеллера, двутавра и тавра указываются в строке “РАЗМЕРЫ ВЫБРАННОГО ПРОФИЛЯ”; размеры полок уголков-в их таблицах; толщина уголков выбирается отдельно после появления возможных толщин выбранного номера уголка в вышеуказанной строке.
Расчет металлической балки на прогиб: учимся составлять формулы
Приветствую тебя, читатель экспресс-курса — «сопромат для чайников» на сайте – SoproMats.ru. Меня зовут Константин Вавилов, я являюсь автором статей по сопромату и других материалов данного ресурса. В этой статье, будем рассматривать универсальную методику расчета прогибов балки — метод начальных параметров. Как и любая другая статья для чайников, на нашем проекте, этот материал будет изложен максимально просто, лаконично и без лишних заумных терминов.
Как и любая другая статья для чайников, на нашем проекте, этот материал будет изложен максимально просто, лаконично и без лишних заумных терминов.
В качестве примера, возьмем металлическую балку на двух опорах. Запишем для нее формулу для вычисления прогиба, посчитаем его численное значение. И также в конце этой статьи дам ссылки на другие полезные статьи с примерами определения прогибов для различных расчетных схем.
Что такое прогиб балки?
Под действием внешней нагрузки, поперечные сечения балки перемещаются вертикально (вверх или вниз), эти перемещения называются прогибами. Сопромат позволяет нам определить прогиб балки, зная ее геометрические параметры: длину, размеры поперечного сечения. И также нужно знать материал, из которого изготовлена балка (модуль упругости).
Кстати! Помимо вертикальных перемещений, поперечные сечения балки, поворачиваются на определенный угол. И эти величины также можно определить методом начальных параметров.
ν-прогиб сечения C; θ-угол поворота сечения C.
Прогибы балки необходимо рассчитывать, при расчете на жесткость. Расчётные значения прогибов не должны превышать допустимых значений. Если расчетное значение меньше, чем допустимое, то считают, что условие жесткости элемента конструкции соблюдается. Если же нет, то принимаются меры по повышению жесткости. Например, задаются другим материалом, у которого модуль упругости БОЛЬШЕ. Либо же меняют геометрические параметры балки, чаще всего, поперечное сечение. Например, если балка двутаврового профиля №12, не подходит по жесткости, принимают двутавр №14 и делают перерасчет. Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.
Метод начальных параметров
Метод начальных параметров, является довольно универсальным и простым методом. Используя этот метод можно записывать формулу для вычисления прогиба и угла поворота любого сечения балки постоянной жесткости (с одинаковым поперечным сечением по длине.)
Под начальными параметрами понимаются уже известные перемещения:
- в опорах прогибы равны нулю;
- в жесткой заделке прогиб и угол поворота сечения равен нулю.
Учитывая эти хитрости, их называют еще граничными условиями, определяются перемещения в других частях балки.
Расчет прогибов балки
Посмотрим, как пользоваться методом начальных параметров на примере простой балки, которая загружена всевозможными типами нагрузок, чтобы максимально охватить все тонкости этого метода:
Реакции опор
Для расчета нужно знать все внешние нагрузки, действующие на балку, в том числе и реакции, возникающие в опорах.
Если ты не знаешь, как определять реакции, то рекомендую изучить данный материал, где я как раз рассказываю, как они определяются на примере этой балки:
Система координат
Далее вводим систему координат, с началом в левой части балки (точка А):
Распределенная нагрузка
Метод начальных параметров, который будем использовать чуть позднее, работает только в том случае, когда распределенная нагрузка доходит до крайнего правого сечения, наиболее удаленного от начала системы координат. Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.
Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.
Если бы нагрузка была приложена вот таким способом:
То можно было бы сразу приступать к расчету перемещений. Нам же потребуется использовать один хитрый прием – ввести дополнительные нагрузки, одна из которых будет продолжать действующую нагрузку q, другая будет компенсировать это искусственное продолжение. Таким образом, получим эквивалентную расчетную схему, которую уже можно использовать в расчете методом начальных параметров:
Вот, собственно, и все подготовительные этапы, которые нужно сделать перед расчетом.
Приступим непосредственно к самому расчету прогиба балки. Рассмотрим наиболее интересное сечение в середине пролета, очевидно, что это сечение прогнется больше всех и при расчете на жесткость такой балки, рассчитывалось бы именно это сечение. Обзовем его буквой – C:
Относительно системы координат записываем граничные условия. Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:
Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:
\[ { V }_{ A }=0\quad при\quad x=0 \]
\[ { V }_{ B }=0\quad при\quad x=8м \]
Записываем уравнение метода начальных параметров для сечения C:
\[ E{ I }_{ z }{ V }_{ C }=… \]
Произведение жесткости балки EI и прогиба сечения C будет складываться из произведения EI и прогиба сечения в начале системы координат, то есть сечения A:
\[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+ … \]
Напомню, E – это модуль упругости первого рода, зависящий от материала из которого изготовлена балка, I – это момент инерции, который зависит от формы и размеров поперечного сечения балки. Также учитывается угол поворота поперечного сечения в начале системы координат, причем угол поворота дополнительно умножается на расстояние от рассматриваемого сечения до начала координат:
\[ E{ I }_{ z }{ V }_{C }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ \theta }_{ A }\cdot 4+… \]
Учет внешней нагрузки
И, наконец, нужно учесть внешнюю нагрузку, но только ту, которая находится левее рассматриваемого сечения C. { 4 } } =-2см \]
{ 4 } } =-2см \]
Таким образом, такая балка прогнется максимально на 2 см. Знак «минус» указывает на то, что сечение переместится вниз.
На этом, пожалуй, закончу данный урок. Если у вас возникли какие-либо вопросы по представленным материалам, задавайте вопросы в комментариях к этой статье. А также рекомендую вам посмотреть другие примеры определение прогибов этим методом. Там вы найдете более сложные задачи, определение углов поворотов, примеры расчета консольных балок (с жесткой заделкой).
Расчёт балки, рамы бесплатно онлайн
Лимит расчётов:
|
Добро пожаловать! Данный онлайн-калькулятор предназначен для расчёта балки или рамы и
позволит построить эпюры внутренних силовых факторов (изгибающих моментов, поперечных и
осевых или продольных сил), рассчитать реакции в опорах. В итоге формируется отчёт с
готовым решением. |
|
| КАЛЬКУЛЯТОРЫ КОМПРЕССИОННЫХ ЧЛЕНОВ | |
| Калькулятор | Определение |
| Расчет элементов сжатия (продольного изгиба) | |
| ПРОСТО ОПОРНАЯ БАЛКА КАЛЬКУЛЯТОРЫ ПРОГИБА | |
| Балка с простой опорой и множественными точечными / распределенными нагрузками и моментами | |
| Балка с простой опорой и сосредоточенной нагрузкой в любой точке | |
| Просто поддерживаемая балка с двумя Точечные нагрузки | |
| Балка с простой опорой и частично распределенной промежуточной нагрузкой | |
| Балка с простой опорой и двумя частично распределенными промежуточными нагрузками | |
| Балка с простой опорой и моментом | |
| Балка с простой опорой и двумя моментами | |
| КАНТИЛЬНАЯ БАЛКА КАЛЬКУЛЯТОРЫ ПРОГИБА | |
| Консольная балка с множественными точечными / распределенными нагрузками и моментами | |
| Консольная балка с одинарной нагрузкой | |
| Распределенная нагрузка консольной балки | |
.
% PDF-1.6 % 104 0 объект > endobj xref 104 52 0000000016 00000 н. 0000002216 00000 н. 0000002377 00000 н. 0000002421 00000 н. 0000002547 00000 н. 0000002902 00000 н. 0000003045 00000 н. 0000003182 00000 п. 0000003324 00000 н. 0000003351 00000 п. 0000003418 00000 н. 0000003955 00000 н. 0000004444 00000 н. 0000004471 00000 н. 0000005149 00000 п. 0000005176 00000 п. 0000005771 00000 п. 0000006307 00000 н. 0000006764 00000 н. 0000007200 00000 н. 0000007333 00000 н. 0000007360 00000 п. 0000007733 00000 н. 0000008258 00000 н. 0000008758 00000 н. 0000009241 00000 п. 0000009643 00000 п. 0000009713 00000 н. 0000009908 00000 н. 0000046337 00000 п. 0000046548 00000 п. 0000046941 00000 п. 0000047011 00000 п. 0000047272 00000 п. 0000106092 00000 н. 0000106298 00000 п. 0000106421 00000 н. 0000117145 00000 н. 0000117340 00000 н. 0000117547 00000 н. 0000117617 00000 н. 0000117799 00000 н. 0000156281 00000 н. 0000156483 00000 н. 0000156859 00000 н. 0000156929 00000 н. 0000157517 00000 н.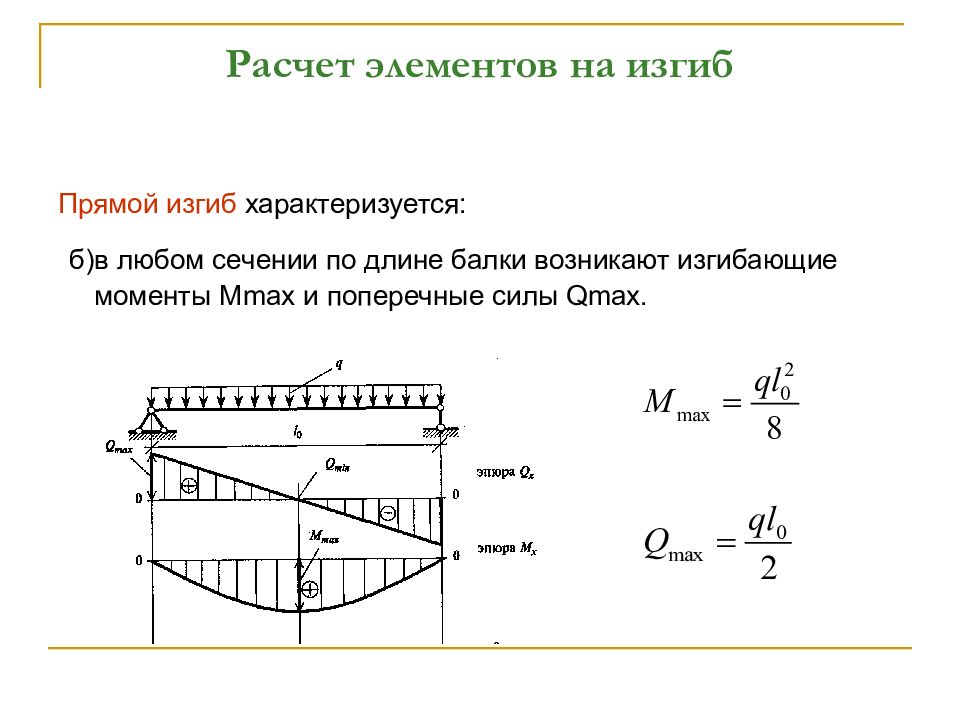 0000157588 00000 н. 0000157704 00000 н. 0000157824 00000 н. 0000157913 00000 н. 0000001336 00000 н. трейлер ] / Назад 1604346 >> startxref 0 %% EOF 155 0 объект > поток hb«`b«ce`c«`f @
0000157588 00000 н. 0000157704 00000 н. 0000157824 00000 н. 0000157913 00000 н. 0000001336 00000 н. трейлер ] / Назад 1604346 >> startxref 0 %% EOF 155 0 объект > поток hb«`b«ce`c«`f @
.
Калькулятор для инженеров — момент инерции площади, центр тяжести, модуль упругости углового сечения
Дополнительные ссылки
Викторина по гражданскому строительству
Проверьте свои знания по различным темам гражданского строительства
Статически неопределенные структуры
Определение и методы решения
Решенных примеров
Расчет сил стержня фермы
методом соединений и методом секций
Сила сдвига и изгибающий момент
Иллюстрированные решенные примеры для построения диаграмм силы сдвига и изгибающего момента
Наклон и прогиб балки и фермы
Иллюстрированные решенные примеры для определения наклона и прогиба балки и фермы
Решение неопределенных конструкций
Отклонение откоса, распределение момента и т. Д.
Д.
Балка железобетонная
Решенные примеры для определения прочности и других параметров
Другие полезные ссылки
Небоскребы мира
Высокие здания мира
Профиль инженеров-строителей
Познакомьтесь с выдающимися инженерами-строителями
Профессиональные общества
Международные профессиональные общества инженеров-строителей
Расскажите о нас друзьям
Поищите на нашем сайте больше…
.
Что такое прогиб? | Программное обеспечение SkyCiv Cloud для структурного анализа
перейти к содержанию
Искать:
- Программное обеспечение
- SkyCiv Structural 3D: Программное обеспечение для структурного анализа
- SkyCiv Beam
- SkyCiv Section Builder
- SkyCiv Connection Design
- SkyCiv RC Design
- SkyCiv Foundation Design
- SkyCiv8 Модуль нагрузки на ветер SkyCiv8 Интеграции и надстройки
.
Угол возвышения Солнца (на год) Калькулятор
- Цель использования
- различные солнечные приложения, конечно, но в основном просто для того, чтобы быть проинформированным о моем физическом окружении.
- Комментарий / запрос
- Я мог бы быть более поучительным, если бы время наблюдения имело вариант местного кажущегося полудня, когда солнце находится на самом высоком уровне. Поскольку вы запрашиваете долготу наблюдателя, это должно быть просто.
[1] 2020/12/20 04:17 Мужчина / 60 лет и старше / Пенсионер / Полезно /
- Цель использования
- Расчет максимальной высоты дерева относительно расположения солнечных панелей.
- Комментарий / запрос
- Вычисление корректировки времени от GMT с использованием долготы было бы полезным и простым.
[2] 2020/12/07 03:31 Мужчина / 60 лет и старше / Инженер / Очень /
- Цель использования
- Размещение солнечных панелей
- Комментарий / запрос
- Arigatou gozaimasu!
[3] 2020/12/07 03:25 Мужской / 40-летний уровень / Средняя школа / Университет / аспирант / Очень /
- Цель использования
- Я хочу построить пассивную теплицу на севере ( Северный Квебек), и я хотел знать, под каким углом поставить стену, чтобы максимально эффективно использовать солнце в зимние месяцы
[4] 2020/12/01 22:20 Мужчина / Уровень 50 лет / Офисный работник / Государственный служащий / Полезный /
- Цель использования
- Определение того, в какое время года, в какое время суток и в каком направлении можно видеть радугу в моем местоположении (солнце должно быть ниже 42 градусов над горизонтом).

- Комментарий / запрос
- Я знаю, как узнать мою широту и долготу, поэтому мог бы использовать этот сайт, но если бы была возможность печатать в ближайшем городе, даже если это было бы менее точно, гораздо больше людей уметь его использовать.
[5] 2020/11/16 15:41 Женщина / 60 лет или старше / Пенсионер / Полезно /
- Цель использования
- Анализ выходной мощности солнечной батареи в зависимости от высоты Солнца
- Комментарий / Запрос
- Отличный калькулятор
[6] 2020/11/05 00:16 Мужчина / 60 лет и старше / Учитель / Исследователь / Очень /
- Цель использования
- Проверка тени на крыше для установка PV
- Отчет об ошибке
- По сравнению с диаграммой, углы которой указаны в таблице, азимут и углы возвышения не имеют никакого смысла.Как может полуденное солнце находиться только по азимуту (азимуту) между 39 и 67 градусами? Я мог бы понять эти углы, если бы они были даны от восточной оси.
 Тогда азимут будет в районе 129–157 градусов, то есть примерно в юго-восточном направлении. Кроме того, как солнце может быть выше в зимнее время, чем в летние месяцы? Возможно, если бы эти углы были измерены от вертикальной оси (Зинет), они имели бы больше смысла. Извините, но, на мой взгляд, приведенная здесь информация неверна.
Тогда азимут будет в районе 129–157 градусов, то есть примерно в юго-восточном направлении. Кроме того, как солнце может быть выше в зимнее время, чем в летние месяцы? Возможно, если бы эти углы были измерены от вертикальной оси (Зинет), они имели бы больше смысла. Извините, но, на мой взгляд, приведенная здесь информация неверна.
[7] 2020/11/04 20:42 Мужчина / 60 лет и старше / Инженер / Совсем нет /
- Цель использования
- Я фотограф, выясняю положение солнца в определенные дни в месяц, чтобы я мог делать красивые фотографии в «контролируемой» обстановке.
- Комментарий / запрос
- Спасибо. Продолжайте в том же духе!
[8] 2020/11/04 18:11 Женский / 50-летний уровень / Самозанятые / Полезные /
- Цель использования
- ИСПОЛЬЗОВАНИЕ СОЛНЕЧНОЙ ЭНЕРГИИ
- Комментарий / запрос
- ДУМАЯ О СОЛНЦЕ ПАНЕЛИ
[9] 2020/10/20 04:13 Мужчина / 60 лет и старше / Пенсионер / Очень /
- Цель использования
- Самообразование
[10] 2020/10/19 18:32 Мужчина / 60 лет и старше / Пенсионер / Очень /
.
Самодельные роботы Дейла — Калькуляторы отклонения пяти балок (сплошная/полая, круглая, прямоугольная, треугольная)
Я в основном использую эти калькуляторы для проектирования листовых рессор.
Ограничения:
- Отношение длины балки к высоте должно быть больше 10.
- Отклонения, превышающие 10 % длины балки, могут быть менее точными.
- Если напряжение при изгибе превышает предел текучести материалов, результаты будут недействительными.
Для справки внизу этой страницы есть удобная диаграмма предела текучести.
| Вычислитель прогиба для сплошных прямоугольных балок | |
|---|---|
| Вход | Выход |
Длина (дюймы) Ширина (дюймы) Высота (дюймы) Сила (фунты) | Прогиб (дюймы) Напряжение при изгибе (psi) Энергия (джоули) |
Это Javascript-калькулятор для расчета отклонения простых прямоугольных балок. Предполагается, что балка поддерживается на одном конце, а сила приложена к другому концу перпендикулярно ширине. (Как трамплин). 93) / 12 . Напряжение изгиба вычисляется по формуле: (сила*длина)/(I/(0,5*высота)) | |
Продукт компании Dales Homemade Robots, Copyright 2007 Dale A. Heatherington Heatherington | |
| Вычислитель прогиба для сплошных треугольных балок | |
|---|---|
| Вход | Выход |
Длина (дюймы) Ширина (дюймы) Высота (дюймы) Сила (фунты) | Прогиб (дюймы) Напряжение при изгибе (psi) Энергия (джоули) |
Это Javascript-калькулятор для расчета деформации сплошных треугольных балок. Предполагается, что балка поддерживается на одном конце, а сила приложена к другому концу перпендикулярно ширине. (Как треугольная доска для прыжков с заостренным концом над водой). Также рассчитывается напряжение изгиба. Если напряжение при изгибе превышает предел текучести материала, он будет безвозвратно деформирован и не вернется к своей первоначальной форме. | |
| Продукт компании Dales Homemade Robots, Copyright 2012 Dale A. Heatherington | |
| Вычислитель прогиба для полых прямоугольных балок | |
|---|---|
| Вход | Выход |
Длина (дюймы) Ширина (дюймы) Высота (дюймы) Толщина стенки (дюймы) Сила (фунты) | Прогиб (дюймы) Напряжение при изгибе (psi) Энергия (джоули) |
Это Javascript-калькулятор для расчета деформации полых прямоугольных балок. Предполагается, что балка поддерживается на одном конце, а сила приложена к другому концу перпендикулярно ширине. (как доска для прыжков в воду) Также рассчитывается напряжение на изгиб. Напряжение изгиба вычисляется по формуле: (сила*длина)/(I/(0,5*высота)) | |
| Продукт компании Dales Homemade Robots, Copyright 2007 Dale A. Heatherington | |
| Вычислитель прогиба для сплошных круглых балок | |
|---|---|
| Вход | Выход |
Длина (дюймы) Диаметр (дюймы) Сила (фунты) | Прогиб (дюймы) Напряжение при изгибе (psi) Энергия (джоули) |
Это Javascript-калькулятор для расчета отклонения простых круглых балок. Также рассчитывается напряжение изгиба. Если напряжение при изгибе превышает предел текучести материала, он будет безвозвратно деформирован и не вернется к своей первоначальной форме. Введите длину и диаметр, затем выберите материал из выпадающего меню. Нажмите ВЫЧИСЛИТЬ и прочтите значение отклонения на панели вывода. 94) / 64 . Напряжение изгиба рассчитывается по формуле: (сила*длина)/(I/(0,5*диаметр)) | |
| Продукт компании Dales Homemade Robots, Copyright 2007 Dale A. Heatherington | |
| Вычислитель прогиба для круглых трубчатых балок | |
|---|---|
| Вход | Выход |
Длина (дюймы) Диаметр (дюймы) Толщина стенки (дюймы) Сила (фунты) | Прогиб (дюймы) Напряжение при изгибе (psi) Энергия (джоули) |
Это Javascript-калькулятор для расчета деформации простых круглых трубчатых балок. Также рассчитывается напряжение изгиба. Если напряжение при изгибе превышает предел текучести материала, он будет безвозвратно деформирован и не вернется к своей первоначальной форме. 94)) / 64 . Напряжение изгиба рассчитывается по формуле: (сила*длина)/(I/(0,5*наружный диаметр)) | |
| Продукт компании Dales Homemade Robots, Copyright 2007 Dale A. Heatherington | |
| Таблица прочности на растяжение материалов | |
|---|---|
| 1020 Сталь | 65 000 |
| 1040 Сталь | 90 000 |
| 1080 Сталь | 140 000 |
| 12L14 Сталь | 60 000 |
| 4130 Сталь | 97 000 |
| 4140 Отожженная сталь | 98 000 |
| 4140 Закаленная сталь | 156 000 |
| Титан 6AL4V | 130 000 |
| Нержавеющая сталь 303 | 90 000 |
| 5052-х42 Алюминий | 33 000 |
| 6061-T6 Алюминий | 45 000 |
| 2024-T361 Алюминий | 72 000 |
| 7075-T6 Алюминий | 76 000 |
| Желтая латунь | 71 000 |
| Поликарбонат | 10 500 |
| Делрин | 10 000 |
| Нейлон | 11 500 |
| ПВХ | 7000 |
| сверхвысокой молекулярной массы | 4000 |
Отказ от ответственности: Информация и программы на этом сайте предоставляются «как есть», без каких-либо явных или подразумеваемых гарантий. |
Предыдущая страница: Калькулятор траектории
Следующая страница: Звездочка и цепь
Калькулятор прогиба консольной балки
Калькулятор консольной балки
Прочие калькуляторы
Что такое консольная балка
Балка, которая на одном конце ограничена от линейного перемещения и вращения во всех направлениях, а другой конец свободен, называется консольной балкой.
Консольную балку на практике можно увидеть под балконом, надстроенным над зданием.
Конструкция консольной балки может быть такой, что глубина балки на фиксированном конце максимальна, а затем над свободным концом она может постепенно уменьшаться.
Как пользоваться калькулятором
Этот калькулятор прогиба консольной балки запрограммирован для расчета профиля прогиба, уклона, диаграммы поперечной силы (sfd), диаграммы изгибающего момента (bmd) и концевых реакций.
Требуются: модуль Юнга (E) материала, длина (L) балки, момент инерции площади (I), интенсивность нагрузки (w1), расстояние, на котором действует w1 ‘a’, интенсивность нагрузки w2 и расстояние при который w2 действует как ‘b’.
Консоль с трапециевидной нагрузкой может быть преобразована в udl при сохранении интенсивности нагрузки w1=w2. Та же самая нагрузка может быть преобразована в udl, если оставить любой из них равным нулю.
Консольная балка с трапециевидной нагрузкой
Для консольной балки с трапециевидной нагрузкой используйте калькулятор 1 и выберите трапециевидный тип нагрузки.
Трапециевидная нагрузка может быть преобразована в удл, увл, а также комбинацию удл и увл. В следующем примере трапециевидная нагрузка была преобразована в UDL + UVL путем сохранения расстояния «a» = расстояния «b» = 0 и расстояния «c» = расстояния «d» = L.
Консольная балка с трапециевидной нагрузкойПараметр 9{4}}{24 * L}
Консольная балка с udl
Консольная балка с udl можно рассчитать с помощью «Калькулятора 1» и выбора типа нагрузки как UDL.
Консольная балка, несущая половину udl, будет иметь расстояние «a» = 0, расстояние «b» = L/2 или расстояние «a» = L/2 и расстояние «b» = L.
Для консольной балки с равномерно распределенная нагрузка по всей длине будет иметь расстояние ‘a’ = 0, а расстояние ‘b’ = L.
Все единицы измерения могут быть изменены пользователем. 9{3}}{6}
Консольная балка с треугольной нагрузкой
Для консольной балки с треугольной нагрузкой используйте «Калькулятор 1» и выберите треугольный тип нагрузки.
Консольная балка с треугольной нагрузкой может быть преобразована в консольную балку с увл (левосторонняя) или увл (правосторонняя). Равномерно изменяющаяся нагрузка может быть достигнута путем сохранения либо расстояния «a» = расстоянию «b», либо расстояния «b» = расстоянию «c».
Консольная балка с треугольной формулой нагрузки 9{4}}{24 * L}
Консольная балка с точечной нагрузкой
Для консольной балки с точечной нагрузкой используйте «Калькулятор 2» и выберите тип нагрузки «Точечная нагрузка».
Ниже представлен случай консольной балки с точечной нагрузкой, действующей в центре или в середине пролета. Для этого расстояние «а» = L/2.
Для консольной балки с точечной нагрузкой на свободном конце введите расстояние «a» = L.
Консольная балка с точечной нагрузкой формула
Консольная балка с точечной нагрузкой 9{2}}{2}Консольная балка с моментной нагрузкой
Для консольной балки с моментной нагрузкой используйте «Калькулятор 2» и выберите тип нагрузки как «Момент».
Консольная балка с моментом в середине пролета рассчитывается по формуле расстояния ‘a’ = L/2.
Консольная балка с формулой момента в середине пролета
Калькулятор прогиба консольной балки сосредоточенный момент 9{2}}{2} -M_{A} * x-M(x-a)Прогиб балки — FlexBeam Pro
Основные характеристики FlexBeam
Существует две версии из FlexBeam для расчета прогиба и потери устойчивости балки: FlexBeam Pro и FlexBeam Lite . FlexBeam Pro имеет полную функциональность. Наиболее важные функции FlexBeam Pro и Lite:
FlexBeam Pro имеет полную функциональность. Наиболее важные функции FlexBeam Pro и Lite:
| Функции | Lite | Pro |
|---|---|---|
| Рассчитать Отражение луча | ||
| Рассчитайте Buckling (New In Release 2,0) | ||
| четырех типов. площади для различных сечений балки | 4 | 23 |
| различных стандартных профилей (IPE, HEA, HEB, HEM, UBP, UB, ASTM, UC, PFC, UPN (UNP), UPE , HD и квадратные, прямоугольные и круглые полые профили) | 17 | |
| entering a known second moment of area | ||
| managing a materials selection list | ||
| simultaneous loads | 1 | 3 |
| метрические единицы единицы и британские единицы единицы | ||
| расчет максимальной балки прогиб, напряжение и уклон | ||
| calculation of the beam deflection, stress and slope at any desired position | ||
| calculation reaction forces | ||
| buckling calculation around X- and Y -ось с центральной нагрузкой и с внецентренной нагрузкой | ||
| схема прогиба и slope | ||
| diagram of the stress and shear force | ||
| copying all entered data and calculation results to the Windows clipboard | ||
| saving последний расчет | ||
| распечатка загружения и результатов, включая диаграммы | ||
| help function | ||
| languages English and Dutch | ||
| Free | € 9. 50* 50* |
* There is a discount for multiple users:
- 5 пользователей; скидка 2,50 евро;
- 10 пользователей; скидка 10,00 €;
- 20 пользователей; скидка € 25,00;
- 50 и более пользователей; € 65,00 скидка.
FlexBeam самый последний выпуск версия 2.6.0 . См. примечания к выпуску.
Скриншот из расчеты Flexbeam Pro Buckling :
Скриншот изгиба Flexbeam Pro Отражение с примером диаграммы отклонения:
Заказ. Pro
с его обширным функционалом стоит 9,50 евро на пользователя, все будущие обновления бесплатны. Есть динамика скидка (5% .. 15%) для 5, 10, 20 и 50 пользователей. FlexBeam Lite предоставляется бесплатно. Вы можете безопасно и надежно оплатить с помощью кредитной карты через PayPal или через iDeal, MrCash и SOFORT Banking . После оплаты вы получите электронное письмо со ссылкой для скачивания .
После оплаты вы получите электронное письмо со ссылкой для скачивания .Системные требования
Системные требования можно найти здесь.
Антивирус
Некоторые антивирусные программы блокируют установку FlexBeam и отмечают ее как подозрительную. Это так называемый «ложноположительный результат». FlexBeam на 100% без вирусов .
FlexBeam Lite
Хотите сначала попробовать FlexBeam или вам не нужны функциональные возможности версии Pro? Затем скачать бесплатную версию FlexBeam Lite . Вы можете скачать и использовать FlexBeam Lite для бесплатно после регистрации . Через регистрацию мы будем держать вас в курсе обновлений программы и новых разработок.
Функциональность FlexBeam Lite больше ограничено , чем у версии Pro, см. таблицу выше. Версия FlexBeam Lite , как и программы HertzWin и FlexHinge, всегда будет оставаться бесплатной и будет постоянно обновляться.
FlexBeam Lite Скачать после регистрации
Вы можете скачать и пользоваться калькулятором прогиба FlexBeam Lite бесплатно после регистрации . Вы получите электронное письмо со ссылкой для скачивания программного обеспечения.
Пожалуйста проверьте программы, о которых вы хотите получать новости . Вы будете проинформированы об обновлениях программы и новых разработках.
Вы всегда можете изменить настройки и личные данные или удалить все личные данные. Ознакомьтесь с политикой конфиденциальности.
Имя
Электронная почта
HertzWin
FlexHinge
FlexBeam Lite
Нет уведомлений об обновлении программного обеспечения / Geen updatemeldingen
Комментарии
Мне интересно узнать о вашем опыте использования FlexBeam . Поделитесь ими в комментарии или отправьте электронное письмо.
Бесплатный онлайн-калькулятор луча | Civils.ai
Расчет изгибающего момента, поперечной силы, силы прогиба и реакции для консольных или свободно опертых балок.
Этот инструмент оптимизирован для настольного использования
Длина балки: 10,0 м
Второй момент площади: 473,0 см 4 909:25
Модуль Юнга: 210,0 ГПа
Загрузка…
Условия крепления неудовлетворительны, добавьте еще одну опору.
Загрузка…
Макс. БМ: Мин. BM:
Макс. SF: Мин. SF:
Макс. отклонение:
Мин. отклонение:
Как работает этот анализ?
Введение
Балки бывают самых разных форм и размеров, поэтому понимание того, как рассчитать силы, действующие на конструкционную балку, может быть затруднено. Но здесь мы дадим вам краткое введение в теорию того, как они устроены. Начиная с теории напряжение балки .
Когда мы прикладываем силу где-то вдоль пролета балки, мы создаем внутренние напряжения. Существует два типа напряжений, которые создаются:
- Нормальное напряжение: Возникает из-за сил, действующих по длине балки при сжатии или растяжении.
- Касательное напряжение: Возникает из-за сил, действующих параллельно направлению нагрузки.
Происхождение этих двух компонентов напряжения можно разделить на два компонента силы, которые мы называем Изгибающий момент и Перерезывающая сила .
Типы внешней нагрузкиПростейшие нагрузки, прикладываемые к балке, можно разделить на три категории:
- Точечные нагрузки: Это сила, приложенная к одной точке балки.

- Распределенные нагрузки: Эта сила распределяется по определенной длине и действует как форма давления.
- Сосредоточенный момент: Это чистый момент, действующий на балку в заданном положении.
Простейшие опоры балки можно разделить на три категории:
- Шарнирная опора: Удерживает балку как в горизонтальном, так и в вертикальном направлениях, не ограничивая ее вращение.
- Роликовая опора: Опора, обеспечиваемая балке только в одном направлении, без ограничения изгиба или вращения.
- Фиксированная опора: Эти опоры обеспечивают фиксацию балки во всех направлениях и препятствуют вращению.
Диаграмма сил свободного тела
Чтобы найти силы, действующие на балку, мы должны следовать процессу создания диаграммы сил свободного тела.
Как рассчитать силы реакции опор на пролет балки? Сначала мы рисуем балку в масштабе с указанием силовых составляющих приложенных нагрузок, а затем рассчитываем силы реакции опоры.
Для расчета реакций необходимо использовать уравнения равновесия для разрешения внешних сил:
- Σ Приложенные вертикальные силы = 0 кН
- Σ Приложенные горизонтальные силы = 0 кН
- Σ Прикладываемые моменты = 0 кНм
Существует два типа случаев при разрешении внешних условий балки:
- Статически определяемые: Когда количество уравнений равно количеству неизвестных, и расчеты могут быть решены с помощью ручных вычислений в закрытой форме.
- Статически неопределимое: Когда количество неизвестных превышает количество уравнений и необходимо использовать более продвинутые методы, такие как теория сопротивления момента.
Чтобы создать диаграмму поперечной силы, вы работаете слева направо поперек балки, суммируя приложенные силы и реакции в каждой точке приложения. Консоли являются наиболее простым примером этого с единственной реакцией на одном конце пролета балки с нулевой силой сдвига на неподдерживаемом конце.
Консоли являются наиболее простым примером этого с единственной реакцией на одном конце пролета балки с нулевой силой сдвига на неподдерживаемом конце.
Чтобы создать диаграмму изгибающего момента, вы снова должны работать слева направо поперек балки и вычислять момент слева от каждой интересующей вас точки. наш расчет стальной балки для расчета в соответствии с Еврокодом 3.
Проектировщик стальных профилей
Расчет бетонной балки
Результаты этого анализа затем можно использовать в нашем расчете бетонной балки для расчета в соответствии с Еврокодом 2.
Конструктор бетонных секций
Для чего нужен этот калькулятор?
Этот бесплатный калькулятор может использоваться инженерами-конструкторами для проектирования балок. Этот инструмент можно использовать для создания диаграмм изгибающих моментов, диаграмм поперечной силы и измерения прогиба для неопределенного пролета балки. Максимальный изгибающий момент можно рассчитать вместе с поперечными силами, силами реакции и прогибом, используя реальные свойства стального сечения. Укажите геометрию балки и точечные или распределенные нагрузки, чтобы приступить к анализу балки.
Максимальный изгибающий момент можно рассчитать вместе с поперечными силами, силами реакции и прогибом, используя реальные свойства стального сечения. Укажите геометрию балки и точечные или распределенные нагрузки, чтобы приступить к анализу балки.
Внесите свой вклад в этот код
Этот код является открытым исходным кодом, и вы можете внести свой вклад в его разработку.
Вы можете найти исходный код на GitHub здесь:
IndeterminateBeamСпециальные кредиты: Джесси Бонанно
Обновление длины балки
м
Категория стального профиля:
Универсальный
Балки
Универсальный
Колонны
Европейский
Балки
Европейский
Колонны
Американский
Балки
ШС
(Квадратный)
Правая сторона
(Прямоугольная)
CHS
(Круг)
Универсальная балка (UB)Универсальная колонна (UC)
Выберите классификацию стальных профилей:
Раздел:
Столы открытого сечения
Момент инерции
см 4
Модуль Юнга
ГПа
Проверить входные данные >0
Ручная перезапись значений E и I
Учитывать собственный вес балки
Вес балки кг/м
Контрольный вес > 0
Номер поддержки:
Позиция мм
Жесткость кН/мм
Острие ножа
Весна
Убедитесь, что штифт находится в пределах балки
Номер точечной нагрузки:
Положение
мм
Величина
кН
Проверить, что нагрузка находится в пределах балки и величина >0 кН
Номер распределенной нагрузки:
Из
мм
Убедитесь, что нагрузка не перекрывает другую нагрузку и не находится внутри балки
Распределенные нагрузки
Расчет прогиба.
 Когда мы должны сделать этот тип расчета? SINADRIVES Перейти к содержимому
Когда мы должны сделать этот тип расчета? SINADRIVES Перейти к содержимомуПредыдущий Следующий
Привет любителям мехатроники!
Добро пожаловать в последний пост в блоге Sinadrives.
Июнь 2022
В этом посте мы рассмотрим некоторые расчеты, которые инженеры и проектировщики промышленного оборудования должны производить для повышения производительности машин. В частности, мы собираемся обсудить расчеты отклонения.
Расчет прогиба требуется в случае балок, поддерживаемых с обоих концов, и балок, поддерживаемых только с одного конца. Давайте рассмотрим оба случая, чтобы увидеть, как они рассчитываются.
Изображение 1
Расчет прогиба требуется в случае балок, поддерживаемых с обоих концов, и балок, поддерживаемых только с одного конца. Давайте рассмотрим оба случая, чтобы увидеть, как они рассчитываются.
Прежде чем обсуждать математическую формулу расчета, мы должны рассмотреть, как эта балка крепится. Есть две возможности: жесткое (встроенное) крепление или нежесткое (поддерживаемое) крепление. В случае мостового крана или козлового крана, такого как показанный на рисунке 1, крепление не является жестким, поскольку происходит движение в направлении X.
Есть две возможности: жесткое (встроенное) крепление или нежесткое (поддерживаемое) крепление. В случае мостового крана или козлового крана, такого как показанный на рисунке 1, крепление не является жестким, поскольку происходит движение в направлении X.
На изображении 2 показана поддерживаемая балка, а на изображении 3 — встроенная балка.
Рисунок 2
Рисунок 3
где:
f – прогиб, мм
F – точечная нагрузка, действующая в центре балки, Н
m – общий вес балки (распределенный по всей ее длине), кг
g – ускорение свободного падения (9,81 м/с2)
l – расстояние между точками опоры, мм
E – модуль упругости, Н/мм² *
I – геометрический момент инерции мм4
Первый член соответствует точечной нагрузке, действующей на балку ; второй член соответствует весу самой балки.
* Модуль упругости стали составляет 205 000 Н/мм², а алюминия — 70 000 Н/мм².
где:
f – прогиб, мм
F – точечная нагрузка, действующая в центре балки, Н
m – общий вес балки (распределенный по всей ее длине), кг
г – ускорение свободного падения (9,81м/ s2)
l – расстояние между опорными точками, мм
E – модуль упругости, Н/мм2
I – геометрический момент инерции, мм4 встроенный пучок.
На рисунке 4 показана балка, поддерживаемая с одного конца.
Рисунок 4
В этом случае балка может иметь только жесткое (закладное) крепление:
f – прогиб, мм
F – сосредоточенная нагрузка, действующая на свободный конец балки, Н
м – общий вес балка (по всей длине), кг
г – ускорение свободного падения (9,81 м/с2)
l – расстояние между точками опоры, мм
E – модуль упругости, Н/мм2
I – геометрический момент инерции мм4
Важно:
В дополнение к точечной нагрузке, действующей на балку, мы также должны учитывать влияние собственного веса балки. В большинстве случаев собственный вес вызывает больший прогиб, чем нагрузка, которую он должен нести.
На этот вопрос нет однозначного ответа; это зависит от приложения. Например, в случае 15-метрового мостового крана отклонение в 100 мм может быть приемлемым, но в случае динамического козлового крана такое отклонение будет иметь катастрофические последствия. Как правило, мы должны учитывать следующие моменты:
Прежде всего, мы должны проанализировать применение и оценить, как потеря высоты, вызванная отклонением, может повлиять на процесс. Например, при лазерной резке отклонение в 3 мм может быть критическим из-за потери точности лазера. При гидроабразивной резке этот изгиб не так критичен.
Например, при лазерной резке отклонение в 3 мм может быть критическим из-за потери точности лазера. При гидроабразивной резке этот изгиб не так критичен.
В этом случае важно проанализировать, есть ли какие-либо вертикальные движения (цилиндр или линейный привод) на мосту (или балке). Чем больше прогиб, тем более упругой становится балка и в результате теряет жесткость. Если движение линейного привода является динамическим и, прежде всего, влечет за собой постоянные изменения направления, это может привести к тому, что луч войдет в состояние резонанса. Как правило, для динамических приложений отклонение не должно превышать 1 мм, а для медленных приложений оно не должно превышать 3 мм. Эти цифры не следует принимать за правило; каждое приложение требует детального изучения.
В некоторых случаях чрезмерное отклонение может создать ряд проблем и трудностей для приложения. Потеря жесткости, потеря точности, резонансы или собственные частоты, которые могут поставить под угрозу работу оборудования.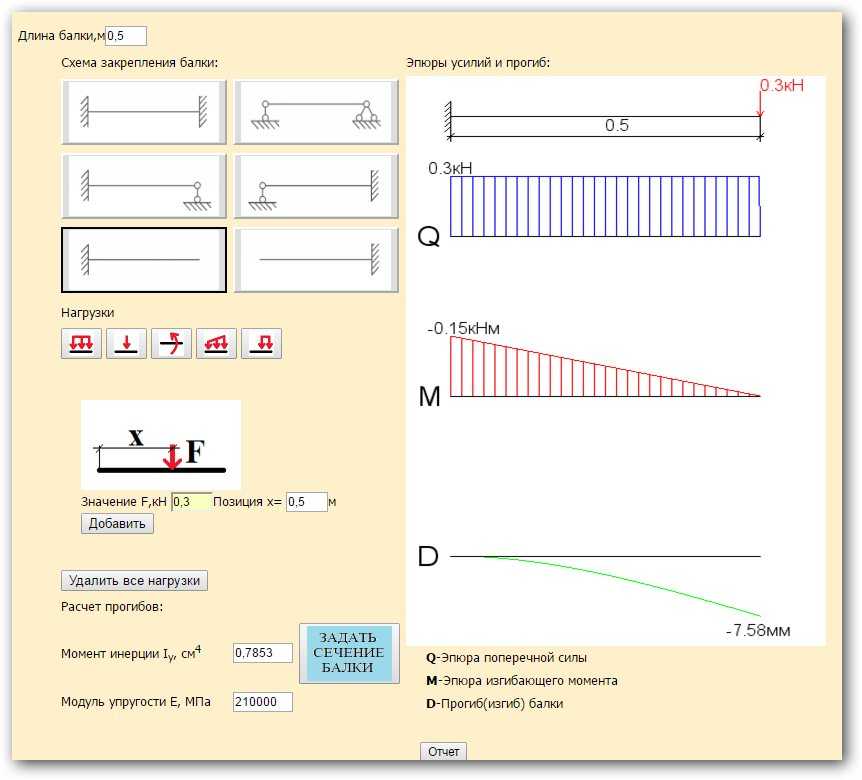 Чтобы уменьшить прогиб, можно предпринять следующие шаги:
Чтобы уменьшить прогиб, можно предпринять следующие шаги:
Мы можем увеличить момент инерции, используя балку, состоящую из раскосов и угловой арматуры (в стиле строительного крана), вместо сплошной балки. Существует множество стандартных стальных или алюминиевых профилей с высокими значениями инерции.
Уменьшение веса балки также может быть хорошим решением. Изгиб можно уменьшить, облегчив балку, сделав в ней пустоту или используя альтернативные материалы и т. д.
Эластичность стали в три раза выше, чем у алюминия. Прогиб можно уменьшить, используя сталь. Не будем забывать, что в этом случае будет увеличиваться и вес, а значит, цель состоит в том, чтобы увеличить модуль упругости в большей пропорции, чем вес.
Если у вас есть приложение, в котором вы хотите улучшить производительность своей машины, будь то скорость, динамика, точность или просто сокращение потребностей в обслуживании, свяжитесь с нами.
Наши специалисты по технологии прямого привода и линейным модулям с технологией линейного двигателя будут рады бесплатно проконсультировать вас.
Делайте выводы сами. Решите, какие инновации вы хотите внедрить в свою машину, чтобы быть конкурентоспособными. Мы можем помочь тебе.
Ваша команда SINADRIVES.
Подпишитесь на наш блог
Область ползунка переключения
Поиск
Поиск:
Общение
Ссылка для загрузки страницыПерейти к началу
13 Формулы прогиба балки
Внутренние силы
АвторLaurin Dominik Обновлено
Последнее обновление: 13 января 2023 г.
Расчет сил реакции, внутренних сил и прогибов балок для различных сценариев нагрузки — это одна из задач проектирования конструкций, которой мы занимаемся на протяжении всего обучения, а также в дальнейшей карьере.
Хотя очень важно уметь рассчитывать реакции и внутренние силы, гораздо сложнее рассчитать прогиб балок из-за различных нагрузок.

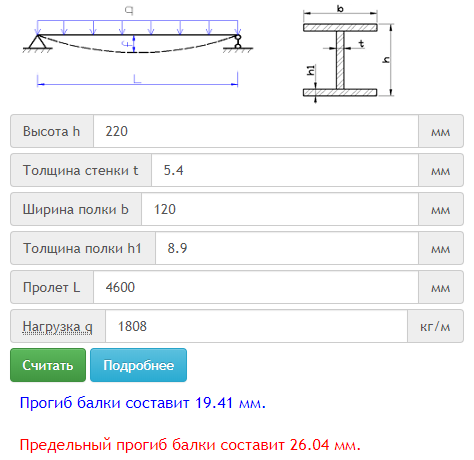 гранями полок нормальныйДвутавр с паралел. гранями полок широкопол.Двутавр с паралел. гранями полок колнныйДвутавр с паралел. гранями полок доп.сери(Д)Тавр с паралелными гранями полок нормальныйТавр с паралел. гранями полок широкополочныйТавр с паралелными гранями полок колнный
гранями полок нормальныйДвутавр с паралел. гранями полок широкопол.Двутавр с паралел. гранями полок колнныйДвутавр с паралел. гранями полок доп.сери(Д)Тавр с паралелными гранями полок нормальныйТавр с паралел. гранями полок широкополочныйТавр с паралелными гранями полок колнный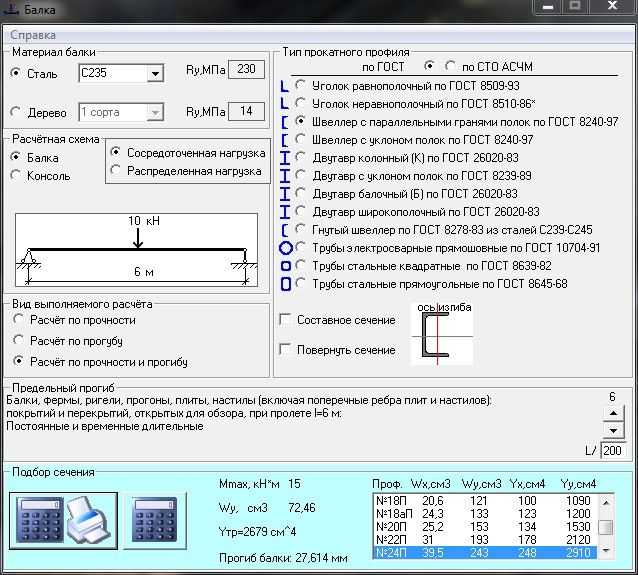 Удачи!
Удачи! 92)
92) Если напряжение при изгибе превышает предел текучести материала, он будет безвозвратно деформирован и не вернется к своей первоначальной форме. 93)) / 12 .
Если напряжение при изгибе превышает предел текучести материала, он будет безвозвратно деформирован и не вернется к своей первоначальной форме. 93)) / 12 . Предполагается, что балка поддерживается на одном конце, а сила приложена к другому концу.
Предполагается, что балка поддерживается на одном конце, а сила приложена к другому концу. Предполагается, что балка поддерживается на одном конце, а сила приложена к другому концу.
Предполагается, что балка поддерживается на одном конце, а сила приложена к другому концу. Ни при каких обстоятельствах Дейл А. Хизерингтон не несет ответственности за любой ущерб, возникший в результате использования информации или программ на этом веб-сайте.
Ни при каких обстоятельствах Дейл А. Хизерингтон не несет ответственности за любой ущерб, возникший в результате использования информации или программ на этом веб-сайте.