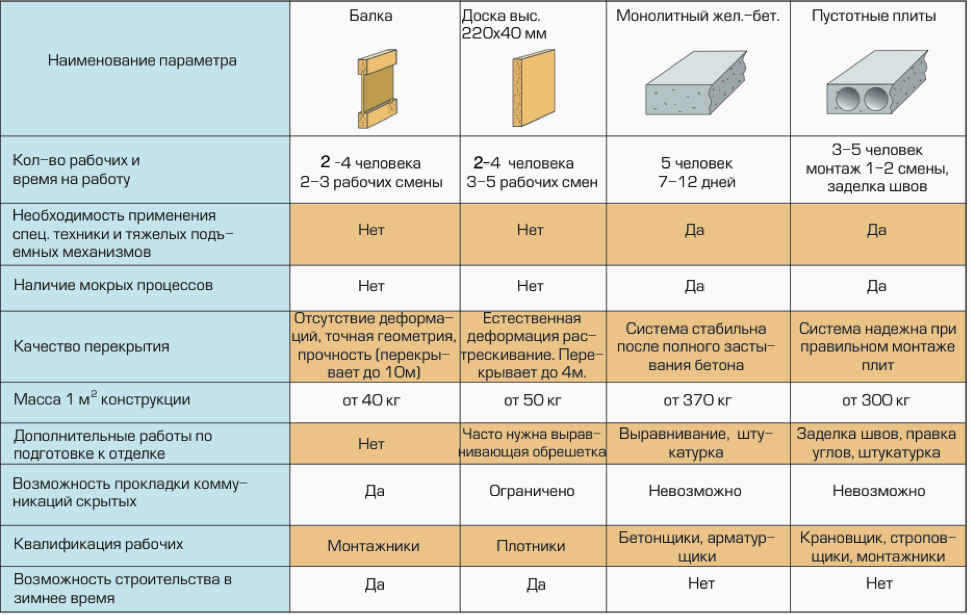
По каким нормам и как рассчитывают прочность двутавровой балки

Двутавровая стальная балка является одним из самых востребованных типов металлического проката. Помимо хозяйственной деятельности этот вид продукции широко применяется в частном домостроении, как правило, в качестве элемента каркаса для межэтажных перекрытий.

От правильного выбора двутавровой балки могут зависеть надежность и долговечность возводимого строения. Если речь идет о капитальном строительстве или в качестве застройщика выступает специализированная организация, то при расчетах необходимо учитывать все тонкости и нюансы материала.

Из легких и устойчивых к изгибу двутавровых балок часто возводят кровельные конструкции для заводских цехов. Источник unsplash.com

Совсем другая картина может быть в ситуации, когда в роли застройщика выступает сам владелец будущего дома, не слишком разбирающийся в вопросе. В этом случае, решив купить двутавровую балку для строительства дома, покупатель в стремлении сэкономить может заказать продукцию недостаточной прочности. Такие балки могут впоследствии деформироваться под весом, на который они не рассчитаны. Возможен и противоположный вариант, когда покупатель исходит из принципа «чем мощнее, тем лучше». Такое решение может стать причиной сильного удорожания проекта, а также привести к чрезмерной нагрузке на фундамент или конструкции здания.

Чтобы правильно выбрать подходящую разновидность двутавровой балки, требуется знание ее параметров, одним из которых является прочность. При правильных расчетах прочности закупаемого проката можно гарантированно избежать прогиба балок или обрушения, снизить нагрузку на элементы здания и сократить финансовые затраты при строительстве.

Особенности и основные параметры двутавровой балки

Основным отличием двутавровой балки от других видов металлопроката, применяемых в строительной отрасли, является форма профиля поперечного сечения, которая выглядит как лежащая на боку буква «Н». Параллельные «ножки» у этой буквы принято называть полками, а перемычку между ними – стенкой.

Такое решение позволило обеспечить высокую жесткость изделия при значительно уменьшенном его весе по сравнению, например, с цельной стальной балкой квадратного профиля. За счет этих качеств двутавровой балки удается сократить расходы материалов при строительных работах, снизить требования к другим несущим элементам, повысить рентабельность строительных работ.

Современные производители металлопроката предлагают большой выбор двутавровых балок, которые отличаются весом, длиной или по ряду других параметров. Так, для разных отраслей и условий строительства существуют балки из различных марок низкоуглеродистой стали, такие изделия могут иметь параллельные или наклонные грани полок. В соответствии с требованиями ГОСТ 823989, такой металлопрокат может выпускаться длиной от 3 до 12 метров.

Также производятся специализированные двутавровые балки, которые могут быть колонными, балочными, монорельсовыми, широкополочными. Назначение и тип балки имеют буквенное обозначение в маркировке изделия.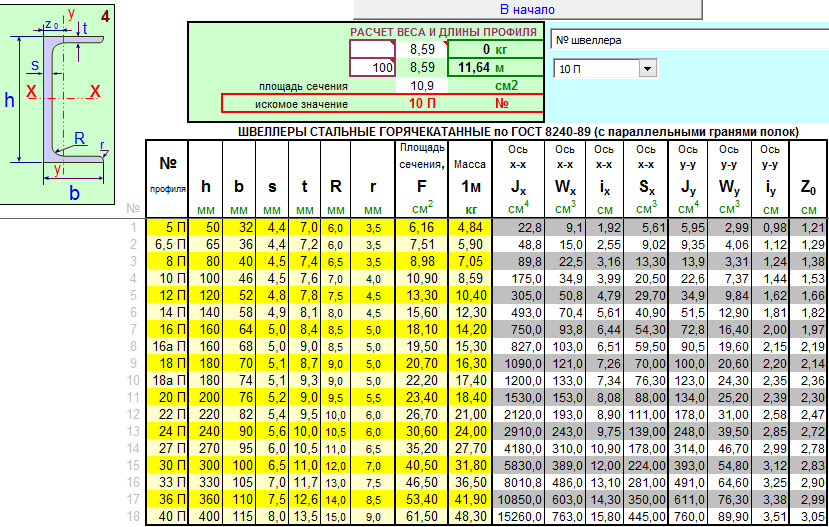

Что требуется учитывать при расчете прочностных характеристик

Прочность, которая должна быть у двутавровой балки, применяемой при сооружении каркаса перекрытий, зависит от максимальной и минимальной нагрузки на изгиб и деформацию – с учетом этих параметров выбирают подходящую для строительства разновидность.

При расчетах учитываются следующие характеристики металлического профиля:

• Расстояние между полками балки с учетом их толщины.
• Максимальная расчетная нагрузка на перекрытие.
• Конфигурация конструкции перекрытия, способ крепления балок.
• Площадь поперечного сечения балки.

В отдельных случаях может учитываться и расстояние (шаг), через которое балки монтируются параллельно друг другу. Также имеет значение технология производства балки – методом проката или с применением сварки. Параметры прочности для сварного профиля могут быть до 30% выше.

Как рассчитывают прочность двутавровой балки

Высокая прочность и жесткость позволяют применять двутавровые балки при сооружении высоконагруженных перекрытий.

Источник unsplash.com

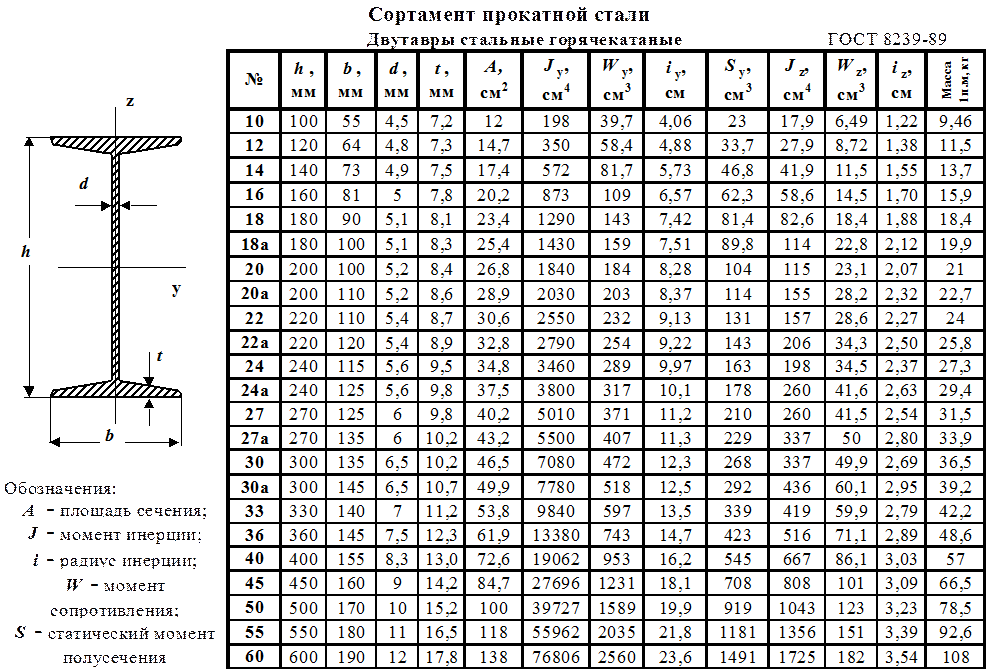
Используемые в металлургической промышленности таблицы сортамента и регламентирующий производство двутавра ГОСТ содержат ряд важных параметров продукции, на основании которых производится расчет.

В таблицах сортамента всем разновидностям стальных двутавровых балок присвоены номера, которые выражают высоту профиля в сантиметрах, а выбор требуемого номера выполняется с учетом расчетной нагрузки, длины пролета и веса изделия.

Расчет нагрузки, которую выдерживает балка, выполняется по следующему алгоритму:

• На основе величины общей нагрузки на перекрытие (с учетом веса самих балок) рассчитываем максимальную нагрузку на один погонный метр двутаврового профиля.
• Полученную величину умножаем на указанный в ГОСТ 823989 показатель коэффициента надежности и упругости стали.
• С применением таблицы расчетных значений (указана в ГОСТе) определяем величину момента сопротивления.
• На основе полученного значения подбираем подходящий номер профиля балки из таблицы сортамента.

Специалисты в строительной отрасли рекомендуют выбирать разновидность профиля балки на 1–2 номера выше, чем полученный при вычислении. Такая мера позволит предусмотреть некоторый запас прочности, не перегружая слишком сильно конструктивные элементы строения.

Чтобы гарантированно не допустить ошибок при расчетах, имеет смысл воспользоваться квалифицированной помощью. Например, вы можете обратиться для этого к сотрудникам нашей компании, которые учтут все важные аспекты предстоящего строительства и предложат оптимальное решение.

Двутавровые балки — виды и расчет нагрузки металлической балки

Двутавровая балка (двутавр) является одним из главных профилей проката, который получил широкое использование в строительной сфере. Выдерживаемая таким профилем нагрузка намного превышает нагрузку квадратного профиля, имеющего аналогичную площадь сечения, чем и объясняется популярность двутавровой балки.

Широкое использование двутавров Н-образной формы связано со строительством объектов промышленности, военной сферы и др. Кроме того, такая балка используется в местах необходимости высокой прочности и сопротивляемости металлоконструкций, в частности в горнорудной промышленной сфере в процессе строительства шахт, а также железнодорожных мостов, опор и иных инженерных конструкций. Для покупки двутавровых балок рекомендуем обращаться к производителям. Вы сможете купить металлическую балку нужного размера, которую изготовят по вашим чертежам.

Виды двутавровых балок

Имеются определенные параметры, по которым все двутавровые балки классифицируются на виды. Классификация двутавров на виды производится по размерам, назначению, технологическим особенностям изготовления, толщине стеновой поверхности, составу материала, расположению планок и иным параметрам.

Промышленники выпускают стандартные двутавры, угол наклона в которых составляет до 12°, а также балки серий М и С, классифицирующихся ценой и параметрами.

Использование серии М связано с монорельсами, визуально определяющимся по углу наклона внутренних граней, не превышающему 12°.

Для армирования стволов шахт применяется серия С, имеющая угол наклона до 16°.

Маркировка балок иного назначения также осуществляется следующими буквами следующих:

Б — стандартный, обыкновенный тип двутавры;

Ш — широкополочный тип балки, применяющийся в процессе строительства ненагруженных колонн;

К — балки, применение которых связано с возведением тяжелых колонн.

По изготовлению двутавры бывают горячекатаного и сварного типа. Выпуск горячекатаных балок цельного типа, в соответствии со строительными стандартами, осуществляется 4-12 метровой длиной и 100-500 миллиметровой высотой. Однако размеры балок зависят от производителя, и при составлении с заказчиком проката договора длина двутавров даже может превышать установленные стандартом.

Изготовление сварных балок характеризуется определенными особенностями, поэтому их высота может превышать 500 миллиметров, а в некоторых случаях даже превышать 1000 мм. Выбор двутавров должен осуществляться при учете не только их габаритов, но и толщины полки. Для определения данного параметра у балок с наклонными гранями берется общее среднее значение.

Вес одного погонного метра двутавра тоже является важным параметром. Вследствие использования качественной легированной стали с низким содержанием углерода в таких балках они обладают солидным весом, которые необходимо учитывать в проектировании с применением двутавров.

Как рассчитать нагрузку на двутавровую балку

Для расчета веса двутавров берутся параметры профиля из ГОСТ 8239—89. Данным стандартом приводятся параметры всех стандартных профилей, которые выпускаются в промышленной сфере. Расчет нагрузки и выбор из сортамента подходящего профиля осуществляется на основании произведения расчета несущей способности двутавров и последующего добавления запаса прочности. Обязательным является запас прочности в 20-30 процентов для конструкций сварного типа. С учетом прогиба нужно выбирать более крепкий профиль, который превышает по свойствам профиль, подходящий по нагрузке.

Как правило, на двутавре указывается допустимый уровень нагрузки и размер. Необходимо помнить, что для двутавров, применяемых в качестве перекрытий, требуется определенный запас для сварных швов. Особенную актуальность это имеет для колонных балок, для размещения которых необходимо наличие подушки из железобетона, к которой производится приварка балки. Допуск, который необходимо оставлять в данном случае, должен составлять 40 мм для приваривания двутавров.

Точность прокатки

В соответствии со стандартом, выпуск двутавровых балок осуществляется с обычной и повышенной точностью.

Имеется целый ряд отклонений от эталона, по которым замеряется качество профиля. В ГОСТ 8239—89 указаны не только все характеристики, но и требования к качеству изготовления профиля, вне зависимости от серии. Кроме того, там можно ознакомиться со существующими методами замера показателей двутавров. Двутавровые балки представляют собой незаменимый тип металлоконструкций в строительной отрасли и являются широко применимыми в строительстве долговечных конструкций.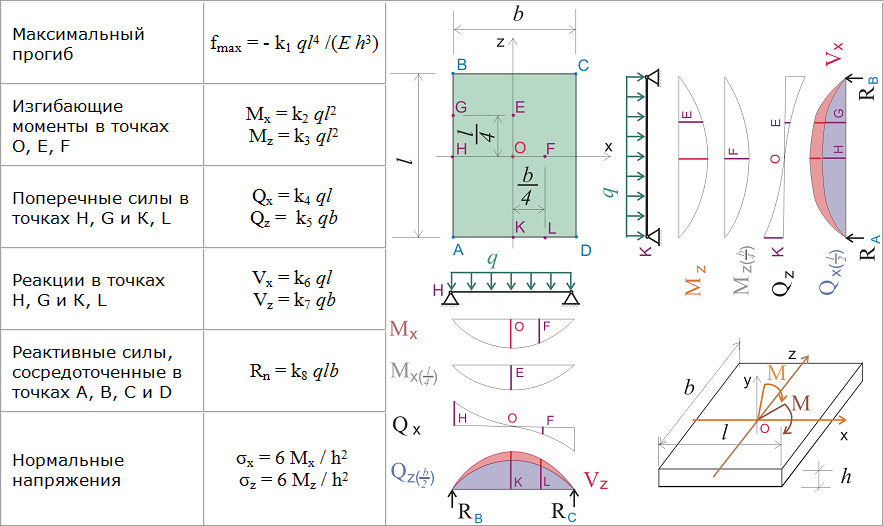

Статья подготовлена совместно с компаний «СтройМеталл» http://stroimetall.ru/.

Конспект лекций

Мы будем рассматривать здесь только балки, которые имеют ось симметрии в плоскости нагружения (обычно вертикально). Размер в плоскости загрузки будет называться глубиной. Кроме того, для Для достижения наилучших результатов длина должна быть в десять раз больше глубины балки.

При изучении прогибов балки обычно принимаются следующие условия:

1. линейная теория упругости,
2. гомогенный изотропный материал,
3. небольшие деформации,
4. чистый изгиб.

Хотя условие чистого изгиба (изгибающий момент без сопутствующего сдвига) редко выполняется когда-либо встречавшихся на практике, при разработке теории предполагается чистый изгиб. На практике сдвиг вклад, как правило, достаточно мал, чтобы не ограничивать серьезно использование отклонения уравнения, полученные из чистой теории изгиба. Для балок длиной более чем в десять раз глубина вклад сдвига в прогиб обычно не превышает двух-трех процентов. от полного прогиба.

Предположение о малых деформациях требует уточнения, т. к. малые, очевидно, относительны. В вывод дифференциального уравнения, связывающего прогиб y с изгибающим моментом M (и, таким образом, нагрузки) мы используем выражение для кривизны. В любой хорошей книге по математическому анализу вы найдете выражение для кривизны (обратное радиусу кривизны):

Небольшие прогибы определяются как прогибы, для которых наклон кривой dy/dx < 0,1. Под это ограничение, знаменатель приведенного выше выражения кривизны приблизительно равен единице, а кривизна определяется

Погрешность этого приближения очень мала и составляет всего около 1,5% в худшем случае, где dy/dx = 0,1.

При изучении изгибающих напряжений в балках мы обнаружили, что кривизна связана с изгибом момент отношения

где E — модуль упругости, а I — момент инерции относительно нейтрали.

ось изгиба. Таким образом, дифференциальное уравнение для отклонения балки имеет вид

Для относительно простых ситуаций нагрузки на балку изгибающий момент M легко записать как функция х. Если EI постоянна, мы просто дважды интегрируем, чтобы получить отклонение y. константы интегрирования оцениваются с использованием граничных условий. В большинстве балочных задач EI постоянно.

 

Эксперимент

Целью этого эксперимента является сравнение экспериментальных отклонений балки для две простые ситуации нагружения балки с отклонениями, предсказанными теорией.

Загрузите две балки следующим образом:

1. Просто поддержите балку и нагрузите ее по центру (рис. 1). Измерьте и запишите отклонения в двух местах, назначенных вашим инструктором. Рекомендуется проводить измерения на четверти точки и в месте, близком к центру луча. Используйте примерно десять равных нагрузок приращения.
   Обязательно запишите все соответствующие размеры, включая места измерения.

2. Установите балку на консоль и нагрузите ее ближе к концу (рис. 2). Измерьте и запишите отклонение в двух местах, как указано вашим инструктором. Предлагается чтобы измерения проводились в средней точке и вблизи точки загрузки для каждого десять приращений нагрузки.

Инкременты нагрузки и упругие константы будут предоставлены вашим лаборант. Обязательно запишите размеры балки, нагрузку точка, длина опоры и константы упругости в вашем листе данных. Этот информация должна быть показана вместе с эскизом балки и геометрией нагрузки.

 

Отчет

1. Постройте график зависимости прогиба от нагрузки P для каждой балки (используйте отдельный график для каждого луча) (рис. 3).
2. Получить наклоны кривых (прогиб на единицу нагрузки) с помощью метод наименьших квадратов.
   
3. Получите теоретические отклонения на единицу нагрузки из уравнений.
4. Сравните теоретический и экспериментальный прогиб на единицу нагрузки и определите процент, на который экспериментальные значения отклоняются от теоретических значений.

Опция

Использовать данные одного из испытаний (по выбору инструктора) для определения модуля упругости для члена. Вы должны рассчитать значение E для каждого набора данных об отклонении, а затем сравните два результата.

Предлагается использовать деревянную балку, чтобы показать, что а) древесина действует как линейная упругая материала (но заметьте, что он не изотропен) и б) чтобы показать, что E древесины примерно порядка величина меньше, чем у алюминия и стали.

 

Формат сводки результатов

ПРОСТО ПОДДЕРЖИВАЕМАЯ БАЛКА

	Эксперимент	Теория	% Отклонение от теории
dy(a)/dP
dy(b)/dP

КОНСОЛЬНАЯ БАЛКА

	Эксперимент	Теория	% Отклонение от теории
dy(a)/dP
dy(b)/dP

ОПЦИЯ
(заменяет один из вышеуказанных наборов значений)

	Экспериментальный	Арт. Значение (если известно)
E из данных dy(a)/dP
E из данных dy(b)/dP

 

Ссылки

«Механика материалов», Хигдон и др., 4-е изд., Wiley, 1985, глава 7.
«Механика материалов» Хиббелера, Macmillan, 1991, стр. 557–562.
«Механика материалов» Хиббелера, Macmilian, 2 ^и Ed, 1994, стр. 581–589.

Прогиб балки

Обзор упражнения

В этом упражнении учащиеся строят ряд точечных балок с различными граничными условиями и наблюдают за результирующими отклонениями. Сопровождающие электронные таблицы позволяют им изучить, как нагрузка, отклонение, наклон, момент и сдвиг связаны друг с другом.

Это была наша самая дорогая и технически сложная ученическая модель, и мы используем ее в нашем первом курсе «Механика деформируемых твердых тел» (МОД), который мы преподаем на втором году нашей программы.

К модели прилагается таблица, и, если в таблице указаны граничные условия и внешние нагрузки на балку, будут рассчитаны результирующие отклонения. Если вместо этого в электронной таблице указаны отклонения балки (предположительно, измеренные от физического устройства), в электронной таблице будут рассчитаны нагрузки, необходимые для создания этих отклонений (и эти рассчитанные нагрузки должны по существу соответствовать тем, которые фактически действуют на физическое устройство). Если отклонения измеряются с достаточной тщательностью, значения, рассчитанные с помощью электронной таблицы, часто находятся в пределах от 10 до 20% нагрузок, фактически действующих на физическое устройство.

Цели обучения

К концу занятия учащиеся должны уметь:

1. Читать показания циферблата
2. Обсудите экспериментальные ошибки, связанные с использованием индикаторов часового типа
3. Объясните разницу между просто поддерживаемыми и зажатыми условиями поддержки
4. Продемонстрировать, как различные граничные условия влияют на отклоненную форму балки
5. Показать и объяснить, как точечные нагрузки в различных местах влияют на отклоненную форму балки
6. Продемонстрируйте зарождающуюся интуицию о том, как луч отклоняется

И, если они использовали электронные таблицы,

7. Продемонстрировать элементарное понимание взаимосвязи между нагрузкой на балку, прогибом, уклоном, моментом и сдвигом.

Загружаемые материалы

Советы по использованию занятия

Учащихся следует поощрять к получению удовольствия от занятия.

Они не должны торопиться или находиться под давлением, чтобы получить «правильный ответ» или высокую оценку.

Вместо этого им следует предложить подумать о том, как прогибаются балки и как граничные условия и нагрузки влияют на прогиб балки.

Если учащиеся используют электронные таблицы, им следует предоставить достаточно времени для рассмотрения взаимосвязей между отклонением, наклоном, моментом (кривизной) и сдвигом.

В любом случае учащимся может быть предложено провести дополнительные наблюдения или измерения. Например, они могут поместить короткую линейку, касательную к балке, в различных местах для измерения уклона или использовать линейку для определения степени и направления локальной кривизны в различных точках.

Продвинутые учащиеся могут наблюдать изменения кривизны консольной балки, на которую действует точечная нагрузка посередине ее длины, и они могут связать эти изменения со сдвигом балки. Изменения кривизны (и сдвиг) происходят только на участке балки между опорой и точечной нагрузкой. Никаких изменений кривизны или сдвига на участке балки от точечной нагрузки до ее свободного конца (за исключением собственного веса балки) нет.

Проектирование оборудования

При разработке этого задания возникло множество проблем, особенно при измерении отклонения точек по длине балки. Циферблатные датчики обычно содержат пружины, предназначенные для обеспечения плотного контакта их наконечников с объектами, положение которых они измеряют. Хотя эта контактная сила пренебрежимо мала в большинстве настроек измерения, она вызывала достаточное возрастание отклонений в наших очень гибких пластиковых балках, поэтому показания не имели большого значения. Снятие пружин в манометрах помогло, но трения плунжера (даже при использовании графитовой смазки) все же было достаточно, чтобы при опоре на балку сверху показания манометра менялись в зависимости от того, давит балка на манометр или нет.