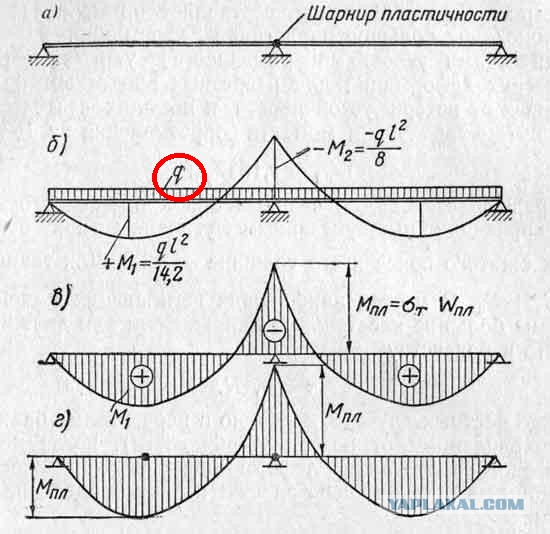
Тема 8. Неразрезные балки

Понятие неразрезной балки. Уравнение трех моментов как частный случай системы канонических уравнений метода сил. Основная система метода сил. Построение эпюр моментов, поперечных сил и их проверка.

Моментные фокусы и моментальные фокусные отношения. Формулы опорных моментов загруженного пролета.

Формулы зависимостей левых фокусных отношений, правых фокусных отношений. Расчет неразрезной балки методом фокусных отношений.

Методические указания

Уравнения трех моментов для расчета неразрезных балок получены благодаря рациональному выбору основной системы. При этом надо знать, как применяются уравнения трех моментов в случае заделки на крайней опоре и в случае консоли.

Эпюра моментов для неразрезной балки строится сложением грузовой эпюры с эпюрой опорных моментов, которая является «исправленной» суммарной эпюрой от неизвестных.

Проверка эпюры моментов выполняется обычным для метода сил путем. Эпюра поперечных сил, как и прежде, строится по эпюре моментов.

При расчете неразрезных балок на временную нагрузку большое значение имеет метод фокусных отношений. Здесь важно уметь определять фокусные отношения для крайних пролетов.

Вопросы для самопроверки

1. Почему за неизвестные в неразрезной балке удобнее принимать опорные моменты, а не реакции?

2. Сколько уравнений трех моментов требуется решить для расчета двухпролетной балки с заделками на обоих концах?

3. Что такое приведенные длины пролетов?

4. Что такое левое фокусное отношение?

5. Каков смысл фиктивных реакций?

6. Постройте эпюры М и Q данной балки:

Список рекомендуемой литературы

1. Дарков А. В. Строительная механика : учеб. / А.В. Дарков, Н.Н. Шапошников. – 11-е изд., стер. – СПб.: Лань, 2008. – 655 с.

2. Анохин Н.Н. Строительная механика в примерах и задачах : учеб. пособие для вузов : в 2 ч. / Н.Н. Анохин. – 2-е изд., доп. и перераб. – М. : Изд-во АСВ, 2007. Ч. 1: Статически определимые системы. – 334 с. Ч. 2: Статически неопределимые системы. – 464 с.

3. Леонтьев Н.Н. Основы строительной механики стержневых систем : учеб. для вузов / Н.Н. Леонтьев, Д.Н. Соболев, А.А. Амосов. – М. : Изд-во АСВ, 1996. – 541 с.

4. Саргсян А.Е. Строительная механика. Механика инженерных конструкций : учеб. для вузов / А.Е. Саргсян.– М. : Высш. шк., 2004. – 462 с.

5. Строительная механика. Стержневые системы : учеб. для вузов / А.Ф. Смирнов [и др.]; под ред. А. Ф. Смирнова. – М. : Стройиздат, 1981. – 512 с.

6. Руководство к практическим занятиям по курсу строительной механики (статика стержневых систем) : учеб. пособие для вузов / Г.К. Клейн [и др.]; под ред. Г.К. Клейна. – 4-е изд., перераб. и доп. – М. : Высш. шк., 1980. – 384 с.

7. Розин Л.А. Расчет статически неопределимых стержневых систем : учеб. пособие / Л.А. Розин, И.А. Константинов, В.А. Смелов; Ленингр. политехн. ин-т им. М.И. Калинина. – Л. : Изд-во Ленингр. ун-та, 1988. – 328 с.

Задания к расчетно-проектировочным работам

В соответствии с учебным планом студенты-заочники специальности «Промышленное и гражданское строительство» должны выполнить шесть заданий (четыре из них включены в курсовую работу и два в контрольные работы):

1. Расчет статически определимой многопролетной балки на неподвижную и подвижную нагрузки.

2. Расчет плоской статически определимой фермы на неподвижную и подвижную нагрузки.

3. Расчет трехшарнирной арки.

4. Расчет статически неопределимой рамы методом сил.

5. Расчет статически неопределимой рамы методом перемещений.

6. Расчет неразрезной балки.

Каждое задание выполняется по схеме и исходным данным в зависимости от шифра из соответствующих таблиц. Номер схемы и шифр выдаются преподавателем.

Контрольные задания выполняются на листах формата А4. Титульный лист оформляется в соответствии с образцом (прил. 1).

Расчетную схему сооружения следует показывать в масштабе. На схеме проставляются выбранные числовые значения размеров и нагрузок.

Выполненная расчетно-проектировочная работа должна содержать вычисления и необходимые чертежи. Вся пояснительная записка выполняется ручкой (не использовать красный цвет).

Расчет неразрезных балок

Строительство и архитектура \ Строительная механика

Страницы работы

29 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

М-10. РАСЧЕТ НЕРАЗРЕЗНЫХ БАЛОК

10.0. Введение в модуль

Основными целями модуля являются:

—  рассмотрение  особенностей  применения  метода  сил  для  расчета неразрезных балок на действие нагрузки и осадки опор;

—  преобразование  канонических  уравнений  метода  сил  в  уравнения трех моментов;

—  определение внутренних усилий в неразрезной балке от действия неподвижной нагрузки и осадки опор;

—  изучение особенностей изменения изгибающих моментов   в незагруженных пролетах неразрезных балок от действия неподвижной нагрузки;

—  введение понятия объемлющей эпюры и рассмотрение способов ее построения.

Структура  изучаемого  модуля  включает  следующие  учебные  элементы:

1. Общие сведения о неразрезной балке.

2. Применение метода сил для расчета неразрезных балок на действие неподвижной нагрузки и осадки опор.

3. Расчет  неразрезных  балок  на  действие  неподвижной  нагрузки  с использованием фокальных свойств

4. Расчет неразрезных балок на действие временной нагрузки.

При изучении учебных элементов рекомендуется использование следующей литературы – [4, c.258 – 291]; [5, c.288 – 328].

10.1. Общие сведения о неразрезной балке

10.1.1. Понятие о неразрезной балке

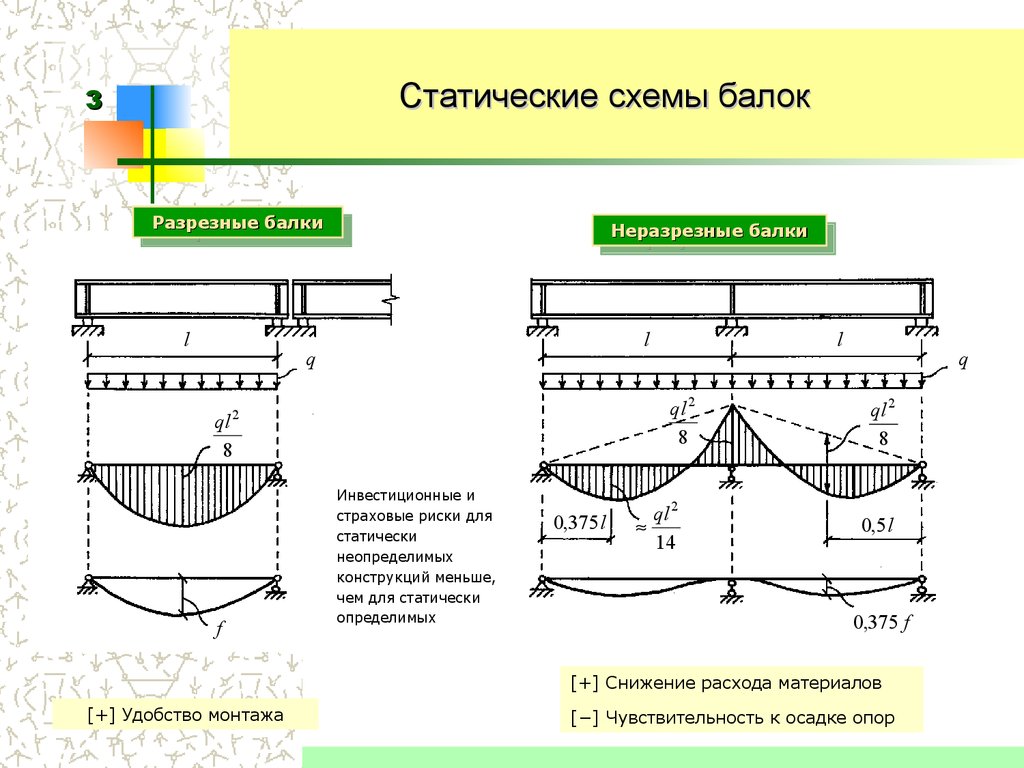
Среди  конструкций,  применяемых  для  перекрытия  пролетов  в  со- оружениях различного назначения, важное место занимают балочные кон- струкции. К их числу относятся простые балки, многопролетные шарнир- ные балки и неразрезные балки. Но если первые два типа балочных конст- рукций  относятся  к  статически  определимым  конструкциям,  то  неразрез- ная балка является внешне статически неопределимой конструкцией.

Неразрезнойбалкойназывается балка, имеющая не менее двух пролетов и не прерываемая на всем своем протяжении сквозными разрезами и

шарнирами.  Пример  простейшей  двухпролетной  неразрезной  балки  показан на рис.10.1

Рис.

10.1

Неразрезные балки могут быть железобетонными, металлическими и деревянными.  По  сравнению  с  аналогичными  простыми  и  многопролет- ными шарнирными балками они имеют определенные преимущества и по- этому широко применяются при возведении различных сооружений.

Примерами применения неразрезных балок в реальной строительной практике являются мостовые конструкции, подкрановые балки, ребристые железобетонные перекрытия, металлические балочные клетки, деревянные и металлические прогоны покрытий.

10.1.2. Разновидности неразрезных балок

Принято различать следующие разновидности неразрезных балок:

—   простые неразрезные балки (рис.10.2)

Рис.10.2

—   неразрезные балки с консолями (рис.10.3)

Рис.10.3

—   неразрезные балки с защемляющими опорами (рис.10.4)

Рис.10.4

В устройстве опорных закреплений неразрезных балок имеются две особенности.

Перваяособенность. Все опоры, кроме одной, допускают продольные  перемещения  тела  балки  вследствие  деформаций  конструкционного материала. Это позволяет исключить температурные напряжения при рав- номерном нагреве или охлаждении неразрезной балки.

Втораяособенность. Свободная укладка неразрезной балки на опоры  не разрешается.  Все  опоры  должны  быть двусторонними  связями,  исключающими отрыв балки от опор. При отрыве балки от опор произойдет изменение  расчетной  схемы  балки  и,  как  следствие  этого,  возможно  исчерпание несущей способности балки.

10.1.3. Система нумерации опор и пролетов

При расчете неразрезных балок любой разновидности принята взаи- мосвязанная единая система обозначения опор и пролетов. Согласно этой системе счет опор и пролетов производится слева направо. Счет опор на- чинается с нуля, а счет пролетов – с единицы. В этом случае номер пролета всегда совпадает с номером правой опоры этого пролета.

Наиболее  естественно  данная  система  реализуется  при  нумерации опор и пролетов простой неразрезной балки. Пример обозначения показан на рис.10.5

Рис.10.5

В случае неразрезной балки с консолями последние не включаются в единую  систему  нумерации  пролетов,  так  как  являются  статически  опре- делимыми  участками  неразрезной  балки.  Длины  консолей  обозначаются независимо,  а  все  остальное  обозначается,  как  и  в  случае  простой  нераз- резной балки. Пример обозначения показан на рис.10.6

Рис.10.6

В  случае  неразрезной  балки  с  защемляющими  опорами  последние заменяются  эквивалентным  шарнирно-стержневым  изображением.  В  ре- зультате получается простая неразрезная балка с одним или двумя фиктив-

ными пролетами нулевой длины, для которой и производится обозначение опор и пролетов. Пример обозначения показан на рис.10.7

Рис.10.7

При принятой системе нумерации опор и пролетов степеньстатиче- скойнеопределимостинеразрезнойбалкилюбой разновидности опреде- ляется по формуле

Л = n -1

и совпадает с числом промежуточных опор.

(10.1)

10.2. Применение метода сил для расчета неразрезных балок на дейст-

вие неподвижной нагрузки и осадки опор

10.2.1. Выбор расчетного варианта основной системы

Рассмотрим простую неразрезную балку, имеющую n пролетов. Изгибная жесткость считается постоянной в каждом пролете, но переменной

в различных пролетах. Балка подвержена   действию произвольной непод- вижной  нагрузки  и  осадки  опор.  Исходная  система  называется  заданной система  и  она,  как  и  ранее,  считается  линейно  деформируемой  системой (рис.10.8)

Рис.10.8

Внешние  воздействия  показаны  на  рис.10.8  условными  буквенными  обозначениями: P – нагрузка,  c – осадка опор.

При  расчете  рассматриваемой  неразрезной  балки  методом  сил  воз- можно  использование  различных  вариантов  основной  системы  и  все  они позволяют получить следующую систему канонических уравнений

Похожие материалы

Информация о работе

Скачать файл

Выбери свой ВУЗ

• АлтГТУ 419
• АлтГУ 113
• АмПГУ 296
• АГТУ 267
• БИТТУ 794
• БГТУ «Военмех» 1191
• БГМУ 172
• БГТУ 603
• БГУ 155
• БГУИР 391
• БелГУТ 4908
• БГЭУ 963
• БНТУ 1070
• БТЭУ ПК 689
• БрГУ 179
• ВНТУ 120
• ВГУЭС 426
• ВлГУ 645
• ВМедА 611
• ВолгГТУ 235
• ВНУ им. Даля 166
• ВЗФЭИ 245
• ВятГСХА 101
• ВятГГУ 139
• ВятГУ 559
• ГГДСК 171
• ГомГМК 501
• ГГМУ 1966
• ГГТУ им. Сухого 4467
• ГГУ им. Скорины 1590
• ГМА им. Макарова 299
• ДГПУ 159
• ДальГАУ 279
• ДВГГУ 134
• ДВГМУ 408
• ДВГТУ 936
• ДВГУПС 305
• ДВФУ 949
• ДонГТУ 498
• ДИТМ МНТУ 109
• ИвГМА 488
• ИГХТУ 131
• ИжГТУ 145
• КемГППК 171
• КемГУ 508
• КГМТУ 270
• КировАТ 147
• КГКСЭП 407
• КГТА им. Дегтярева 174
• КнАГТУ 2910
• КрасГАУ 345
• КрасГМУ 629
• КГПУ им. Астафьева 133
• КГТУ (СФУ) 567
• КГТЭИ (СФУ) 112
• КПК №2 177
• КубГТУ 138
• КубГУ 109
• КузГПА 182
• КузГТУ 789
• МГТУ им. Носова 369
• МГЭУ им. Сахарова 232
• МГЭК 249
• МГПУ 165
• МАИ 144
• МАДИ 151
• МГИУ 1179
• МГОУ 121
• МГСУ 331
• МГУ 273
• МГУКИ 101
• МГУПИ 225
• МГУПС (МИИТ) 637
• МГУТУ 122
• МТУСИ 179
• ХАИ 656
• ТПУ 455
• НИУ МЭИ 640
• НМСУ «Горный» 1701
• ХПИ 1534
• НТУУ «КПИ» 213
• НУК им. Макарова 543
• НВ 1001
• НГАВТ 362
• НГАУ 411
• НГАСУ 817
• НГМУ 665
• НГПУ 214
• НГТУ 4610
• НГУ 1993
• НГУЭУ 499
• НИИ 201
• ОмГТУ 302
• ОмГУПС 230
• СПбПК №4 115
• ПГУПС 2489
• ПГПУ им. Короленко 296
• ПНТУ им. Кондратюка 120
• РАНХиГС 190
• РОАТ МИИТ 608
• РТА 245
• РГГМУ 117
• РГПУ им. Герцена 123
• РГППУ 142
• РГСУ 162
• «МАТИ» — РГТУ 121
• РГУНиГ 260
• РЭУ им. Плеханова 123
• РГАТУ им. Соловьёва 219
• РязГМУ 125
• РГРТУ 666
• СамГТУ 131
• СПбГАСУ 315
• ИНЖЭКОН 328
• СПбГИПСР 136
• СПбГЛТУ им. Кирова 227
• СПбГМТУ 143
• СПбГПМУ 146
• СПбГПУ 1599
• СПбГТИ (ТУ) 293
• СПбГТУРП 236
• СПбГУ 578
• ГУАП 524
• СПбГУНиПТ 291
• СПбГУПТД 438
• СПбГУСЭ 226
• СПбГУТ 194
• СПГУТД 151
• СПбГУЭФ 145
• СПбГЭТУ «ЛЭТИ» 379
• ПИМаш 247
• НИУ ИТМО 531
• СГТУ им. Гагарина 114
• СахГУ 278
• СЗТУ 484
• СибАГС 249
• СибГАУ 462
• СибГИУ 1654
• СибГТУ 946
• СГУПС 1473
• СибГУТИ 2083
• СибУПК 377
• СФУ 2424
• СНАУ 567
• СумГУ 768
• ТРТУ 149
• ТОГУ 551
• ТГЭУ 325
• ТГУ (Томск) 276
• ТГПУ 181
• ТулГУ 553
• УкрГАЖТ 234
• УлГТУ 536
• УИПКПРО 123
• УрГПУ 195
• УГТУ-УПИ 758
• УГНТУ 570
• УГТУ 134
• ХГАЭП 138
• ХГАФК 110
• ХНАГХ 407
• ХНУВД 512
• ХНУ им. Каразина 305
• ХНУРЭ 325
• ХНЭУ 495
• ЦПУ 157
• ЧитГУ 220
• ЮУрГУ 309

Полный список ВУЗов Пример расчета консольной балки

 – Google. thestructuralengineer.info

www.thestructuralengineer.info › образование › расчет…

Найдите схемы стержней для треугольной нагрузки. РЕШЕНИЕ Рассчитаем реакции на закрепленном конце A.

Ähnliche Fragen

Как рассчитать консольные балки?

Какова формула изгиба консольной балки?

Как рассчитать консольную нагрузку?

Какова формула эффективной длины консольной балки?

Консольные балки – Моменты и прогибы

www.engineeringtoolbox.com › консольные балки-d…

Максимальный прогиб. на конце консольной балки можно выразить как. δB = F L3 / (3 E I) (1в). где. δB = максимальное отклонение в B (м, мм, дюйм).

Полное руководство по консольной балке | Прогибы и моменты

skyciv.com › Учебные пособия по балкам › Учебные пособия

16.02.2023 · Взято из нашей формулы отклонения балки и страницы уравнений. Уравнения консольной балки можно рассчитать по следующей формуле, где:.

Рабочий пример консольной балки — услуги по анализу конечных элементов

www.valuedes.co.uk › консольная балка, обработанная-exa…

Учебное пособие по консольной балке с анализом конечных элементов и ручными расчетами. Пример стержня при изгибе, сдвиге и прямом растягивающем напряжении по сравнению с МКЭ.

Как рассчитать реакции консольной балки с равномерным …

www.youtube.com › смотреть

21.05.2018 · Краткое руководство с численным рабочим примером, показывающее, как определить реакции при . ..
Dauer: 4:36
Прислан: 21.05.2018

Как рассчитать опорные реакции консольной балки с .