Расчет балки на прочность — онлайн-калькулятор —
Расчет балки на устойчивость онлайн: Расчет балки на прочность — онлайн-калькулятор
Содержание
Расчет двутавровой балки на устойчивость
Двутавровую балку при расчете на изгиб необходимо рассчитывать не только по несущей способности и деформациям, но и на устойчивость. Ведь бывают случаи, когда балка удовлетворяет первым двум условиям и не удовлетворяет третьему. Это в свою очередь приводит к тому, что двутавр несет все вышележащие конструкции (обрушения нет), но в то же время потерял свое проектное положение — завалился на бок.
На данной странице представлен калькулятор, который позволяет определить будет ли заваливаться двутавр или нет. Расчет реализован согласно п. 8.4.1 СП 16.13330.2017 «Стальные конструкции».
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Обращаю ваше внимание, что в нецелых числах необходимо ставить точку, а не запятую, то есть, например, 5.Исходные данные7 м, а не 5,7. Также, если что-то не понятно, задавайте свои вопросы через форму комментариев, расположенную в самом низу.
Длина пролета (L) — расстояние между крайними опорами.
Расчетная нагрузка — сумма всех нагрузок (например, от конструкций перекрытия, покрытия пола, перегородок, снега и т.д.), приложенных на балку, помноженных на коэффициенты надежности по нагрузке.
Расчетное сопротивление Ry — сопротивление проката на растяжение, сжатие и изгиб по пределу текучести. Подбирается из нижеследующей таблицы:
Расчетная длина Lef — расстояние между опорами, которые расположены сбоку. Если опор (закреплений) нет, то данная величина равна длине пролета, т.е. Lef = L. Для балок типов 2 и 6 в случае, если нет других закреплений Lef = 2L.
Количество закреплений — количество точек закрепления сжатого (верхнего) пояса двутавра от поперечных смещений. То есть сколько опор препятствует наклону балки. Такими опорами можно считать балки сопоставимой жесткости (деревянные балки не считаются), приходящиеся в стык к рассчитываемой балке или лежащие сверху ее, которые соединены с последней посредством сварки или болтов и которые ограничены от горизонтального смещения. Также такой опорой считается место присоединения горизонтальной связи.
То есть сколько опор препятствует наклону балки. Такими опорами можно считать балки сопоставимой жесткости (деревянные балки не считаются), приходящиеся в стык к рассчитываемой балке или лежащие сверху ее, которые соединены с последней посредством сварки или болтов и которые ограничены от горизонтального смещения. Также такой опорой считается место присоединения горизонтальной связи.
Коэффициент условий работы — подбирается по таблице 1 п. 4.3.3 СП 16.13330.2017 «Стальные конструкции», находится в пределах от 0,75 до 1,2.
РезультатРазмер (h x b) — высота и ширина двутавра.
Вес балки — вес двутавра на один погонный метр. Чтобы получить общую массу балки, необходимо эту величину умножить на длину балки.
Wx— момент сопротивления сечения относительно оси Х.
Ix и Iy— моменты инерции сечения относительно оси Х и Y, соответственно.
It— момент инерции при свободном кручении.
Коэф. A, P, G1, Gb — коэффициенты необходимые для расчета.
Коэф. использования (К) — если он меньше 1, то балка по устойчивости не проходит и требуется либо увеличить сечение балки, либо добавить опор, препятствующие опрокидыванию.
Добавить комментарий
Расчет прочности и жесткости сварной балки двутаврового сечения
а – схема изменения сечения по длине балки; б – сечение балки и эпюры напряжений.
Цель: Проверка режима расчета сопротивления сечений в постпроцессоре «Сталь» вычислительного комплекса SCAD
Задача: Проверить расчетное сечение сварного двутаврового профиля для главных балок пролетом 18 м в балочной клетке нормального типа. Верхний пояс главных балок раскреплен балками настила, расположенными с шагом 1,125 м.
Источник: Металлические конструкции : учебник для студ. Учреждений высш. проф. Образования / [Ю. И. Кудишин, Е. И. Беленя, В. С. Игнатьева и др.] ; под. Ред. Ю. И. Кудишина. — 13-е изд., испр. — М. : Издательский центр «Академия», 2011. С 195.
Учреждений высш. проф. Образования / [Ю. И. Кудишин, Е. И. Беленя, В. С. Игнатьева и др.] ; под. Ред. Ю. И. Кудишина. — 13-е изд., испр. — М. : Издательский центр «Академия», 2011. С 195.
Соответствие нормативным документам: СНиП II-23-81*, СП 16.13330, ДБН В.2.6-163:2010.
Имя файла с исходными данными:
4.1 SectionResistance_Example_4.1.spr;
отчет — 4.1 SectionResistance_Example_4.1.doc
Исходные данные:
Параметры SCAD Постпроцессор СТАЛЬ:
[Элемент № 1] Усилия
N Макс. 0 Т Макс. 0 Т | My Макс. 0 Т*м Макс. 353,65 Т*м | Mz Макс. 0 Т*м Макс. 0 Т*м |
Mk Макс. Макс. 0 Т*м | Qz Макс. 94,31 Т
| Qy Макс. 0 Т Макс. 0 Т |
Длина стержня 3,75 м |
Расчет выполнен по СНиП II-23-81*
Конструктивный элемент Section
Сталь: C255
Длина элемента 3,75 м
Предельная гибкость для сжатых элементов: 220
Предельная гибкость для растянутых элементов: 300
Коэффициент условий работы 1
Коэффициент надежности по ответственности 1
Расчетная длина в плоскости XoY 1,125 м
Расчетная длина в плоскости XoZ 18 м
Расстояние между точками раскрепления на плоскости 1,125 м
Сечение
Результаты расчета | Проверка | Коэффициент использования | ||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
п. | Прочность при действии изгибающего момента My | 0,99 | ||||||||||||||||||||||||||||||||||||||
пп.5.12,5.18 | Прочность при действии поперечной силы Qz | 0,41 | ||||||||||||||||||||||||||||||||||||||
пп.5.24,5.25 | Прочность при совместном действии продольной силы и изгибающих моментов без учета пластики | 0,99 | ||||||||||||||||||||||||||||||||||||||
п. 5.14* | Прочность по приведенным напряжениям при одновременном действии изгибающего момента и поперечной силы | 0,86 | ||||||||||||||||||||||||||||||||||||||
п.5.15 | Устойчивость плоской формы изгиба | 0,99 | ||||||||||||||||||||||||||||||||||||||
пп.6.15,6.16 | Предельная гибкость в плоскости XoY | 0,09 | ||||||||||||||||||||||||||||||||||||||
пп. {2} \] 4. Гибкость элемента в плоскости действия момента: \[ \lambda_{y} =\frac{\mu l}{i_{y} }=\frac{18\cdot 100}{63,715}=28,2508. 5. Гибкость элемента из плоскости действия момента: \[ \lambda_{y} =\frac{\mu l}{i_{y} }=\frac{1,125\cdot 100}{4,265}=26,3775. \] Сравнение решений
Ярлык при проектировании деревянных конструкций — коэффициент устойчивости балки (и коэффициент устойчивости колонны)Введение Если вы изучали или занимались проектированием деревянных конструкций, вы наверняка сталкивались с «коэффициентом устойчивости балки». Это выглядит примерно так ((Уравнение NDS 3.3–6): Сейчас я не буду вдаваться в подробности обо всех переменных; я просто хотел поговорить о конечном факторе C L . Как вы уже знаете, получив F bE и F b * , вычисление C L выполняется просто по принципу «подключи и пей». Это очень просто, но утомительно… Я не могу вспомнить, сколько раз я случайно вставлял неправильные числа или совершал глупые ошибки при вводе чисел в калькулятор. Результат, как вы уже догадались, обычно некрасивый (в зависимости от того, насколько рано я узнаю об ошибке). Поэтому я придумал более простой способ избежать всех этих утомительных «подключи и пыхни». Знакомство с табличной таблицей для коэффициента устойчивости луча: Эта таблица не только помогла мне избежать арифметических ошибок, но и несколько раз спасла меня во время экзамена SE (который, как вы знаете, на счету каждая секунда!) и до того, как я знал это, жизнь снова стала хорошей (хорошо, это может быть немного преувеличением, но вы поняли идею). Как пользоваться табличной таблицей коэффициента устойчивости балкиПоскольку C L зависит только от [F bE / F b * ], я подумал, что если у меня есть таблица, в которой перечислены все возможные [F bE / F b * ] и соответствующий C L , мне никогда не придется используйте калькулятор, чтобы снова «подключи и пыхти». Таким образом, способ его использования очень прост:
Пример 5.3 (SERM)Давайте проверим это на примере 5.3 Справочного руководства по проектированию конструкций (SERM).
Вычислить C L Используя табличную таблицу (пример 5.3) Готово! (Хотя реальный C L равен 0,974, разница в 0,004 не будет иметь большого значения для вашего дизайна в 99 % случаев.) Пример 5.4 (SERM)Давайте сделаем еще один, используя пример 5.4.
Рассчитать C L Использование табличной таблицы (пример 5.4) Представьте, что вы выполняете этот простой двухэтапный процесс с использованием таблицы, а не вручную вычисляете следующее с помощью неграфического калькулятора… Видите разницу? Я надеюсь на это, потому что это действительно помогло мне совсем немного. Далее: Табулированная таблица для коэффициента устойчивости колонны Подобно коэффициенту устойчивости балки, коэффициент устойчивости колонны также требует от вас выполнения тех же действий – утомительного «подключи и пыхни» (уравнение NDS 3. В этом случае, кроме [F cE / F c * ], есть еще одна переменная, c, которая может принимать значения 0,8, 0,85 или 0,9 в зависимости от типа пиломатериала. Нет проблем, я просто создам еще 3 таблицы. Если вы считаете таблицу коэффициента устойчивости балки полезной, нажмите кнопку ниже, чтобы получить доступ к «Таблированной таблице коэффициента устойчивости колонны», а также ко ВСЕМ другим полезным ресурсам , которыми я делюсь только с нашими подписчиками. Щелкните здесь, чтобы получить бесплатные ресурсы. Пример 5.7 (SERM)Мы еще раз проверим это на примере из SERM. Из примера 5.7:
Рассчитать C P Использование табличной таблицы (пример 5.4) Опять же, используя таблицу, вы избежали необходимости делать это во время экзамена: Мысли? Пока все. Спасибо за прочтение и удачи в изучении! Программное обеспечение для расчета конструкций RSTAB 9 | РасчетДом Товары Программное обеспечение для анализа кадров Расчет Линейный и нелинейный структурный анализРСТАБ 9 | Программное обеспечение для расчета несущей конструкции и фермы Модели расчета конструкций для загрузки Выберите многочисленные структурные модели, чтобы использовать их в целях обучения или для ваших проектов.
Модель рассчитывается линейно, согласно линейному статическому анализу, или нелинейно, согласно анализу второго порядка или больших деформаций. Для определения внутренних сил результаты могут быть объединены в комбинации. 1 Индивидуальная настройка параметров расчета Расчет может выполняться для всех типов стержней в соответствии с линейным статическим анализом, анализом второго порядка или анализом больших деформаций. 2 Опциональное приложение инкрементной нагрузкиНагрузку можно применять постепенно. Этот вариант особенно удобен для расчетов по анализу больших деформаций. Кроме того, RFEM позволяет выполнять посткритический анализ. 3 Вычислительное ядро с многоядерной процессорной технологией Расчет теперь оптимизирован с использованием многоядерной процессорной технологии. Это позволяет выполнять параллельные расчеты вариантов линейной нагрузки и сочетаний нагрузок с использованием нескольких процессоров без дополнительных требований к оперативной памяти: матрицу жесткости необходимо создать только один раз. Таким образом, даже большие системы могут быть рассчитаны с помощью быстрого прямого решателя. You may also likeUpdated on Анкер клиновой для чего используется: АНКЕР КЛИНОВОЙUpdated on Как правильно клеить обои в коридоре: в комнате, коридоре, от окна, и откуда надо приступать, правильно ли делать это из угла, какие есть нюансы при использовании флизелиновых?Updated on Схема проводки выключателя двухклавишного: Как подключить двухклавишный выключатель: схема подключения, инструкцияUpdated on Как зашить трубы в туалете: Как закрыть трубы в туалете |
Задание 3 расчет балки на прочность и жесткость
Целью задания является расчет балки на прочность при плоском изгибе и исследование влияния формы поперечного сечения на ее металлоемкость.
Для заданной балки (рис. 18):
1) определить реакции опор;
2) записать уравнения поперечной силы и изгибающего момента для всех участков и построить эпюры поперечной силы и изгибающего момента;
3) подобрать балку двутаврового поперечного сечения из условия прочности по нормальным напряжениям и проверить балку на прочность по касательным напряжениям;
4) произвести анализ изменения веса балки в зависимости от формы ее поперечного сечения (рис. 17), приняв за единицу вес двутавровой балки;
5) построить эпюры распределения нормальных и касательных напряжений по высоте двутавровой балки в произвольном ее сечении, в котором ни поперечная сила, ни изгибающий момент не равны нулю;
6) записать уравнения углов поворота и прогибов сечений балки для всех участков и построить эпюры углов поворота и прогибов;
7) графическая
часть задания должна содержать чертеж
балки в стандартном масштабе с указанием
размеров балки и нагрузки (под чертежом
балки расположить эпюры поперечных
сил, изгибающих моментов, углов поворота
и прогибов сечений балки), эпюры
распределения нормальных и касательных
напряжений по высоте сечения балки.
Материал балки – сталь Ст.3. При расчетах принять: допускаемые напряжения adm = 160 МПа, adm = 100 МПа, модуль упругости Е = = 2105 МПа.
Для построения эпюр углов поворота и прогибов сечений балки необходимо подсчитать соответствующие величины в 4-6 сечениях на каждом участке.
Разрешается ординаты эпюр углов поворота и прогибов сечений балки увеличить в EI раз.
Исходные данные взять из табл. 3.
Таблица 3
Номер строки | l, м | l1, м | l2, м | F, кН | M, кНм | q, кН/м |
а | б | в | г | а | б | |
1 | 2,0 | 4,0 | 3,0 | 50 | 10 | 40 |
2 | 2,5 | 5,0 | 3,5 | 45 | 20 | 30 |
3 | 3,0 | 6,0 | 4,5 | 40 | 30 | 20 |
4 | 3,5 | 7,0 | 1,5 | 35 | 40 | 10 |
5 | 4,0 | 6,0 | 2,0 | 30 | 50 | 15 |
6 | 1,5 | 5,0 | 2,5 | 25 | 15 | 25 |
7 | 2,0 | 4,0 | 3,0 | 20 | 25 | 35 |
8 | 3,0 | 3,0 | 3,5 | 15 | 35 | 45 |
9 | 4,0 | 2,0 | 4,0 | 10 | 45 | 20 |
0 | 2,5 | 7,0 | 2,0 | 60 | 55 | 30 |
Рассчитать балку
(рис.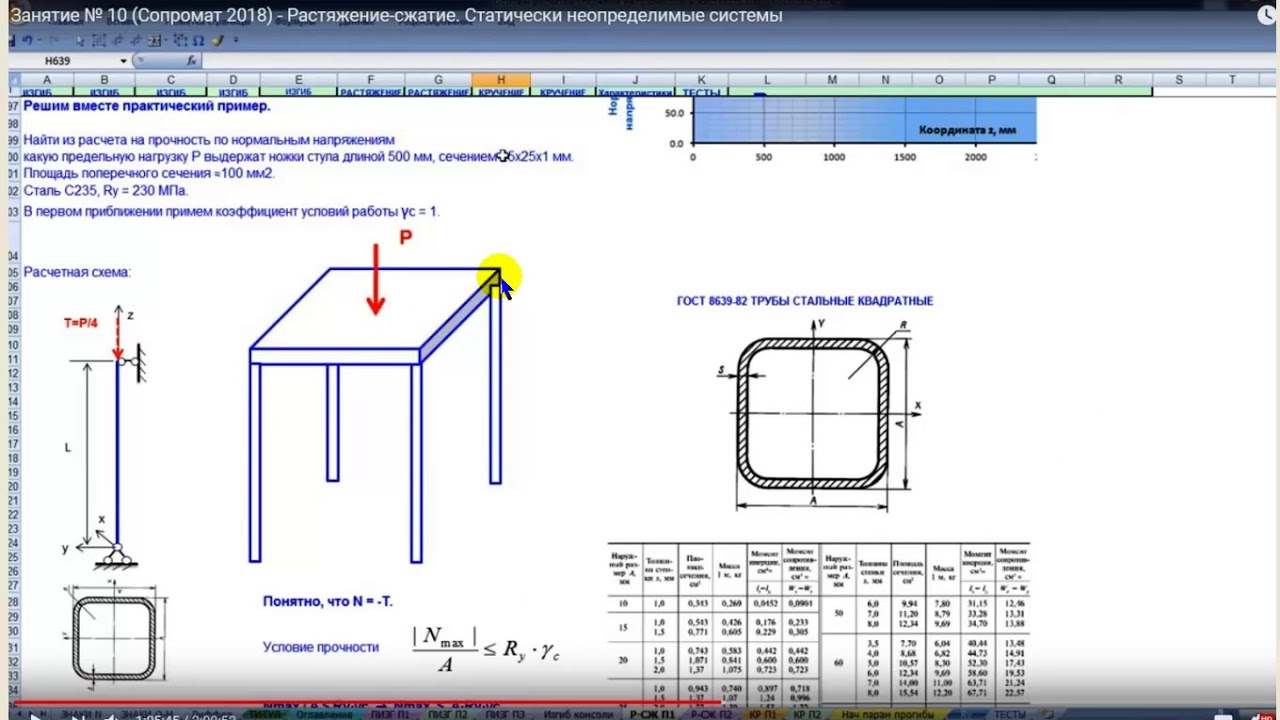 19) постоянного поперечного сечения
на прочность при плоском поперечном
изгибе и исследовать влияние формы
поперечного сечения на ее весовые
характеристики.
19) постоянного поперечного сечения
на прочность при плоском поперечном
изгибе и исследовать влияние формы
поперечного сечения на ее весовые
характеристики.
Исходные данные: l = 2 м, l1 = 5 м, l2 = 2 м, F = 30 кН, М = 30 кНм, q = 20 кН/м, adm = 160 МПа; adm = 100 МПа.
Решение
1. Определим опорные реакции из условия равновесия балки:
, НА =0;
, ;
= = -57,14 кН.
, ;
== 27,14 кН.
Проверка правильности определения реакций опор:
, ;
27,14 — 57,14 — 20·2 + 30 + 202 = 0;
0 = 0.
2.
Запишем выражения поперечной силы Q и изгибающего момента Mz по участкам, используя
метод сечений.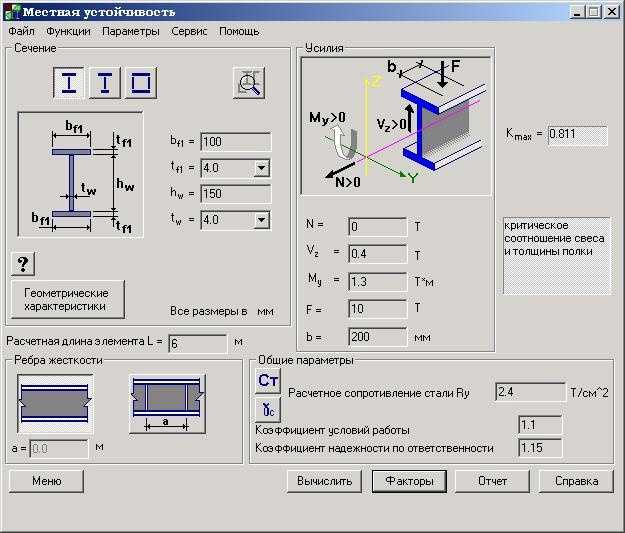 Определим значения
поперечных
сил Q и изгибающих моментов Мz в характерных точках по длине балки
и построим эпюры Q и Mz.
Определим значения
поперечных
сил Q и изгибающих моментов Мz в характерных точках по длине балки
и построим эпюры Q и Mz.
1-й участок: 0 ≤х1≤ 2 м (рис. 20)
;
= = 10.
При х1 = 0 Q = 0, Mz = 0; при х1 = 3 м Q = -40 кН, -40 кНм.
2-й участок: 2 м ≤ х2 ≤ 7 м
= 27,14 — 202 = -12,86 кН;
.
При х2 = 2 м -10 кНм, при х2 = 7 м -74,3 кНм.
3-й участок: 7 м ≤ х3 ≤ 9 м
При х3 = 7 мQy = 17,14 кН, = -74,3 кНм,
при х3 = 13 м 0, Qy =57,14 кН.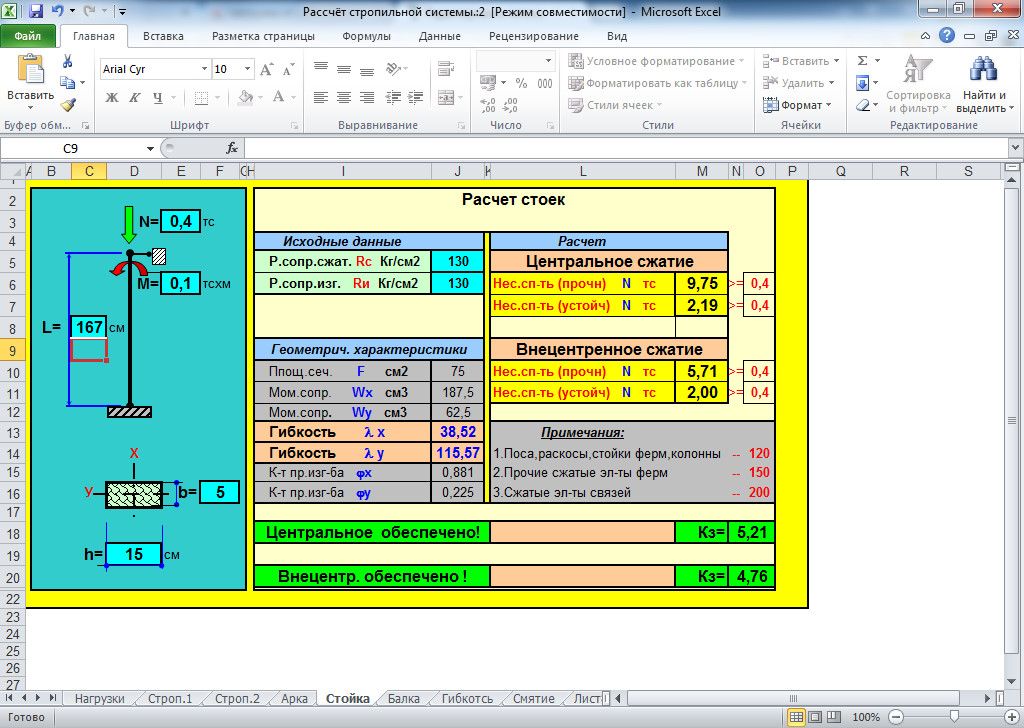
По результатам расчета построим эпюры поперечных сил Q и изгибающих моментов Mz (рис. 19).
3. Определим опасное сечение: из эпюр поперечных сил и изгибающих моментов = 57,14 кН,74,3 кНм.
4. Подбираем двутавровую балку из условия прочности по нормальным напряжениям
,
Откуда
см3.
По величине осевого момента сопротивления выбираем двутавр №30 по ГОСТ 8239-72, у которого Wzтабл = 472 см3. Вычисляем фактическое максимальное напряжение
фmax = == 157,4 МПа.
Вычисляем недонапряжение по нормальным напряжениям
=100%=100 = 1,6 % < 5 %.
При расчетах
допускается недонапряжение и
перенапряжение до 5 %.
Выбранный двутавр № 40 удовлетворяет
условию прочности по нормальным
напряжениям. Из таблицы балок двутавровых
выписываем геометрические характеристики: Wz = 472 см3, h = 30 см, b = 13,5 см, А1 = =46,5 см2;
7080
см4,
=
268 см3, s = 0,65 см, t =1,02 см.
Из таблицы балок двутавровых
выписываем геометрические характеристики: Wz = 472 см3, h = 30 см, b = 13,5 см, А1 = =46,5 см2;
7080
см4,
=
268 см3, s = 0,65 см, t =1,02 см.
Проверяем балку на прочность по касательным напряжениям
max = = МПа аdm = 100 МПа.
Таким образом, выбранная двутавровая балка удовлетворяет условию прочности по касательным напряжениям.
5. Определим размеры поперечных сечений балки различной формы:
а) коробчатое сечение (рис. 23)
;
= 10,6 см, 0,7210,62 = 80,9 см2;
б) прямоугольное сечение (рис. 24)
= 464,4, = 8,9 см,
28,92 = 158,4 см2;
в) квадратное
сечение (рис. 25)
25)
464,4, а = = 14,1 см,198,8 см2;
г) круглое сечение (рис. 26)
= 464,4, см,
= 221,6 см2;
д) трубчатое сечение (рис. 27)
, ;
ymax = d/2, =464,4,см,
= 113 см2;
е) квадратное сечение с углами по осям координат (рис. 28)
, 0,707 a, (для квадратного сечения моменты инерции относительно любых центральных осей одинаковы),
464,4, а = = 15,8 см,
= 249,6 см2.
6. Производим анализ изменения веса балки в зависимости от формы ее сечения, приняв за единицу вес двутавровой балки. Вес балки определим по формуле .
Обозначим отношение веса балки различной формы сечения к весу двутавровой балки:
Таким образом,
сечения балки в порядке возрастания ее
веса выстроятся в ряд: двутавр, коробчатое
сечение, трубчатое сечение, прямоугольное
сечение, квадратное сечение, круглое
сечение, квадратное сечение с углами
по осям координат.
7. Строим эпюры распределения нормальных и касательных напряжений по высоте двутавровой балки для сечения, где приложена сила F. В этом сечении Q = 17,14 кН, Мz = 74,3 кНм.
Нормальные напряжения определяются по формуле
= .
Подсчитаем нормальные напряжения в характерных точках сечения:
y1 = h / 2, 1 = = 157,4 МПа;
y4 = 0, 4 = 0.
Эпюра нормальных напряжений показана на рис. 29.
Касательные напряжения определяются по формуле Журавского
= .
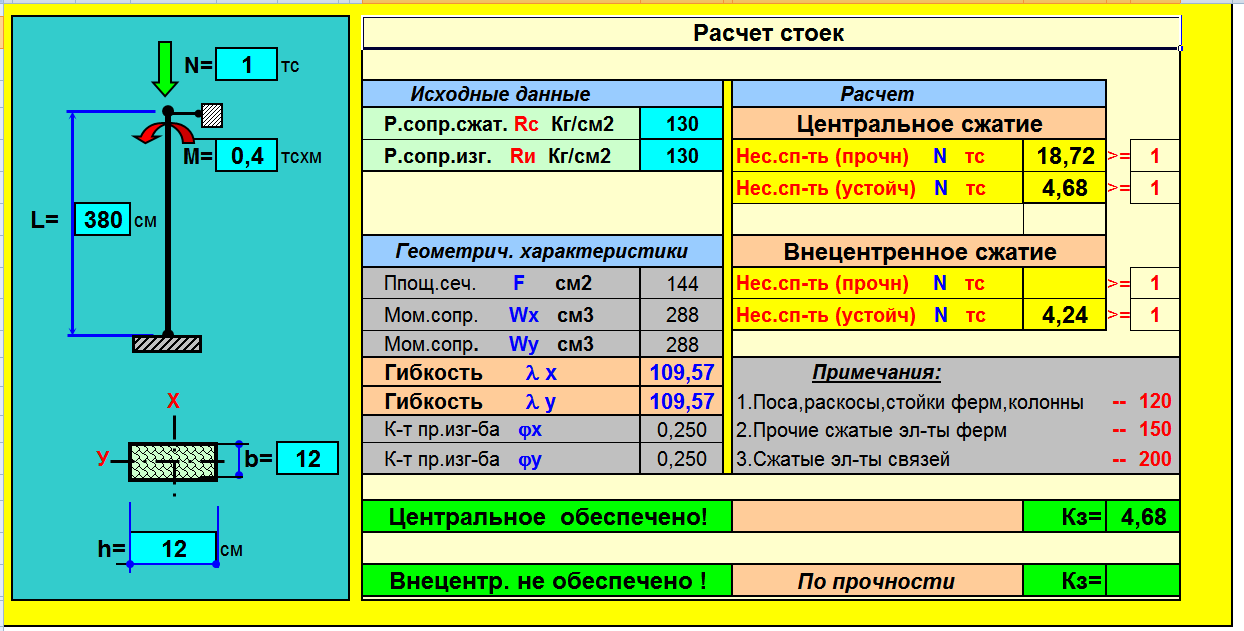
У двутаврового сечения ширина b сечения и статический момент отсеченной части сечения меняются по высоте, поэтому вычисляем касательные напряжения в характерных точках сечения:
Точка 1:
;.
Точка 2: 199,5 см3.
В точке 2 ширина волокон равна ширине полки b, поэтому
0,35 МПа.
Точка 3: = 199,5 см3, ширина волокон равна толщине стенки s, поэтому
7,4 МПа.
Точка 4: 268 см3, ширина волокон равна толщине стенки s, поэтому
10 МПа.
Эпюра касательных напряжений показана на рис. 29.
8. Определим углы поворота и прогибы сечений балки методом начальных параметров. Уравнения углов поворота и прогибов сечений пометоду начальных параметровимеют вид:
;
,
где ,- угол поворота и прогиб сечения балки в начале координат (на левом конце балки).
Запишем уравнения углов поворота и прогибов сечений балки для различных участков:
1-й участок: 0 ≤ х1 ≤ 2 м
,
.
2-й участок: 2 м ≤ х2 ≤ 7 м
,
.
3-й участок: 7 м ≤ х3 ≤ 9 м
Постоянные интегрирования C и D определяем из граничных условий — прогибы на опорах равны нулю:
при x = l = 2 м yA= y1 = y2 = 0;
при x2 = l + l1 + l2 = L = 9 м yB = y3 = 0.
Получаем систему уравнений
или
Решая систему
уравнений, получаем С = 159,1 кНм2, D = -304,8 кНм3.
Вычислим значения углов поворота и прогибов сечений балки в 3-4 точках на каждом участке. Результаты расчета приведены в табл. 4.
Таблица 4
№ участка, i | 1 | 2 | ||||
xi, м | 0 | 1 | 2 | 2 | 3 | 5 |
, кНм2 | 159,1 | 155,8 | 132,4 | 132,4 | 101,0 | 44,6 |
EIzyi, кНм3 | -304,8 | -146,5 | 0 | 0 | 125,4 | 294,5 |
Продолжение
табл. 4
4
№ участка, i | 2 | 3 | |||
xi, м | 6 | 7 | 7 | 8 | 9 |
,кНм2 | -10,4 | -78,3 | -78,3 | -140,7 | -166,0 |
EIzyi, кНм3 | 312,6 | 269,3 | 269,3 | 157,5 | 0 |
Определим экстремальное (максимальное) значение прогиба на 2-м участке:
Решая уравнение
методом последовательных приближений,
получим х2 = 5,827 м,
313,5 кН· м3.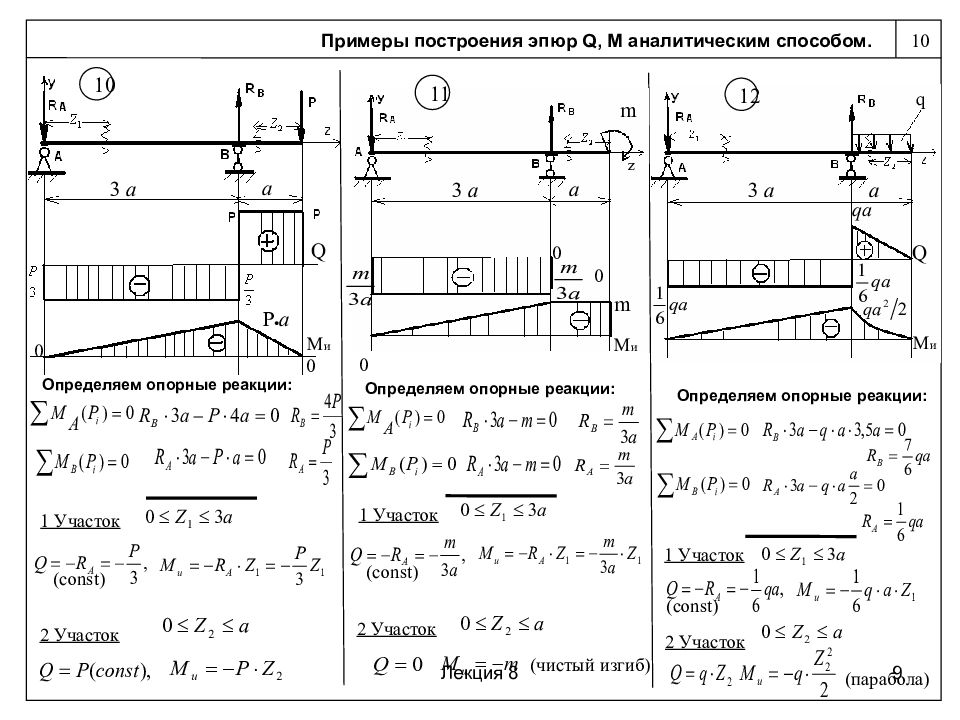
На основе полученных результатов строим эпюры углов поворота и прогибов сечений балки (рис. 21).
Луч | Fine
Эта программа обеспечивает расчет опирающихся фундаментных балок
на упругом основании (грунте).
Подписка Вечный
625 € Местная лицензия
94 € Ежегодное обслуживание
- Пакеты со скидкой:
250 € Ежегодно
Преимущества подписки
- Пакеты со скидкой:
Дополнительные функции
Подписка Вечный
625 € Местная лицензия
94 € Ежегодное обслуживание
- Пакеты со скидкой:
250 € Ежегодно
Преимущества подписки
- Пакеты со скидкой:
Учебные материалы
Образец выходного отчета «Луч»
Основные преимущества
- Настраиваемая структура отчета
- Персонализация заголовка отчета
- Добавляйте и редактируйте неограниченное количество изображений из анализа
- Изображения автоматически обновляются для отображения результатов на основе текущих настроек
Новые функции в GEO5 2023
Поддерживаемые типы конструкций
Программа GEO5 Beam может использоваться для проектирования ленточного фундамента под колонны.
GEO5 экономит ваше время!
Интуитивно понятный интерфейс Рабочий процесс сверху вниз
ПрограммыGEO5 имеют унифицированную среду и интуитивно понятный рабочий процесс сверху вниз.
От исследования к передовому дизайну
GEO5 объединяет моделирование геологических данных с расширенными геотехническими задачами.
Аналитические методы и МКЭ
GEO5 позволяет сравнить два независимых решения.
Мобильное приложение для каротажа скважин
Соберите геологические данные в полевых условиях и отправьте их в программу Стратиграфия.
Поддержка BIM
GEO5 экспортирует данные в распространенные форматы BIM и передает их сторонним программам.
Многие стандарты и методы
GEO5 — универсальный инструмент для инженеров всего мира.
Комплексные результаты
Выходные отчетыGEO5 можно легко редактировать или экспортировать в форматы PDF или MS Word.
Программы, связанные вместе
GEO5 позволяет передавать данные между отдельными программами.
Языки выходных отчетов
GEO5 генерирует выходные отчеты на разных языках, что полезно для зарубежных проектов.
Удобное для пользователя программное обеспечение GEO5 ускоряет время проектирования и обеспечивает надежные результаты во многих отношениях. С тех пор, как мы начали его использовать, у нас появилась возможность легко представить проекты с множеством различных геометрических форм и в соответствии с различными требуемыми стандартами.
Кроме того, очень приятно работать со службой технической поддержки программы, и мы можем получить быстрый ответ в случае возникновения какой-либо проблемы.
Sefa Apaydın, компания Viacon
Несколько вещей делают GEO5 уникальным программным обеспечением. Во-первых, все модули просты в использовании, а распечатка очень аналитическая. Программное обеспечение также сопровождается обширными вспомогательными руководствами и дополнительной документацией. Мы настоятельно рекомендуем это!
Мы настоятельно рекомендуем это!
Яннис Периклеус, инженер-строитель, A. J. Pericleous LLC
Благодаря интуитивно понятному пользовательскому интерфейсу для начала работы не требуется специальной подготовки. Программные модули хорошо взаимодействуют друг с другом и с программным обеспечением AutoCAD, что экономит много времени.
В.Н. Марьенко, главный инженер филиала Московский проектно-изыскательский институт «Мосжелдорпроект» — филиала Акционерного общества «Росжелдорпроект»
Больше отзывовЛуч
Попробуйте работать с ПО GEO5
Скачать демо-версию
Бесплатно активируйте 14-дневную пробную версию без ограничений анализа.
Комплект программного обеспечения GEO5
- Абатмент
- Противоскользящая свая
- Луч
- Консольная стена
- Сборщик данных (приложение)
- Давление Земли
- МКЭ
- ФЭМ – Консолидация
- МКЭ — Землетрясение
- МКЭ — туннель
- МКЭ – расход воды
- Габион
- Гравитационная стена
- Потеря земли
- Кирпичная стена
- Микросвая
- Стена МСЭ
- Прибитый склон
- Куча
- Свая СРТ
- Группа свай
- Облако точек
- Сборная стена
- Стена Реди-Рок
- Стабильность горных пород
- Урегулирование
- Вал
- Проверка защитного покрытия
- Дизайн листов
- плита
- Устойчивость склона
- Устойчивость склона – поток воды
- Распространение фундамента
- Распространение Фундамент CPT
- Стратиграфия
- Стратиграфия — разрезы
- Стратиграфия — Земляные работы
- Стратиграфия — журналы
Программный луч | Индивидуальные программы | ГЕО5
Программа:Все программы Абатмент Противоскользящая свая Луч Консольная стена Давление Земли МКЭ Габион Гравитационная стена Потеря земли Кирпичная стена Микросвая Стена МСЭ Прибитый склон Куча Свая СРТ Группа свай Облако точек Сборная стена Стена Реди-Рок Стабильность горных пород Урегулирование Вал Проверка защитного покрытия Дизайн листов плита Устойчивость склона Распространение фундамента Распространение Фундамент CPT Стратиграфия Местность
Язык:Чешский Английский испанский польский Русский Немецкий португальский французский
Программа Луч | Индивидуальные программы | ГЕО5 | Онлайн помощьПрограммный луч
class=»h2″> Эта программа обеспечивает расчет фундаментных балок, опирающихся на упругое основание.
Справка по программе « Балка » включает следующие разделы :
- Ввод данных в отдельные кадры:
Проект | Настройки | Геометрия | Грунт 9 Почва 04 | Вода | Опоры | Варианты нагрузки | Нагрузка | Комбинация ULS | Комбинированный SLS | |
Анализ | 903 21 |
- Стандарты и методы анализа
- Теория для анализа в программе « Луч «:
Геостатическое напряжение (подъемное давление) | Анализ с использованием одометрического модуля | Определение глубины зоны влияния |
- Выходы
- Общая информация о работе в Пользовательской среде программ GEO5
- 90 012 Общий вход для всех программ
Попробуйте программное обеспечение GEO5 бесплатно.
 А
А использования (K)
использования (K) А
А использования (K)
использования (K) 0 Т*м
0 Т*м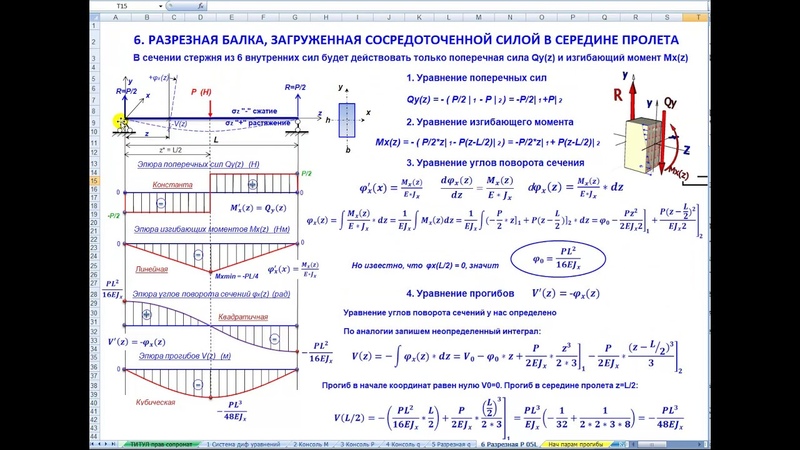 5.12
5.12 \]
\]
 7-1):
7-1): Считаете ли вы это полезным? Позвольте мне знать в комментариях ниже.
Считаете ли вы это полезным? Позвольте мне знать в комментариях ниже. Этот вариант выбора доступен для загружений и сочетаний нагрузок. Дополнительные параметры расчета индивидуально настраиваются для загружений, сочетаний нагрузок и результирующих сочетаний. Это обеспечивает высокую степень гибкости в отношении метода расчета и подробных спецификаций.
Этот вариант выбора доступен для загружений и сочетаний нагрузок. Дополнительные параметры расчета индивидуально настраиваются для загружений, сочетаний нагрузок и результирующих сочетаний. Это обеспечивает высокую степень гибкости в отношении метода расчета и подробных спецификаций.