Расчет деформации стержня при растяжении-сжатии
Задача
Рассчитать деформации участков и общее изменение длины прямого стержня постоянного сечения.
Модуль продольной упругости стали E=200ГПа.
Пример решения
Предыдущие пункты решения задачи
- Определение опорных реакций,
- Построение эпюр внутренних продольных сил,
- Подбор размеров поперечного сечения стержня,
- Построение эпюр нормальных напряжений.
Стержень имеет три силовых участка, на которых площадь сечения одинакова, но внутренние силы и нормальные напряжения отличаются, поэтому определим абсолютные деформации всех участков в отдельности, после чего сложив их, получим изменение длины всего стержня в целом.
Изменение длины участков стержня при растяжении-сжатии рассчитывается по формуле:
где N – величина внутренней продольной силы,
l – длина рассматриваемого участка,
A – площадь его поперечного сечения,
E – модуль Юнга (продольной упругости) для материала стержня,
Значения внутренних сил и напряжений принимаются с построенных эпюр N (σ).

По эпюрам видно, что первый участок сжимается, а участки II и III растягиваются, следовательно, деформации Δl второго и третьего участков будут положительны (их длина увеличивается), а первого отрицательны (продольный размер уменьшается).
Рассчитаем их:
Деформация I участка (KM)
II участок (CK)
Удлинение третьего участка BC
Сложив (с учетом их знака) деформации всех участков получим величину изменения длины всего стержня в целом:
В результате деформации общая длина стержня увеличится на 0,51мм.
Расчет и построение эпюры перемещения сечений >
Другие примеры решения задач >
isopromat.ru
Расчет стержня на прочность
Задача
Для прямого стержня постоянного сечения подобрать размер стороны a квадратного сечения по условию прочности. Материал стержня – сталь. Допустимые напряжения [σ]=160 МПа.
Полученные размеры принять согласно ГОСТ 6636.
Пример решения
Предыдущие пункты решения задачи
- Определение опорных реакций.
- Построение эпюр внутренних продольных сил.
Рассматриваемый стержень нагружен исключительно продольными силами, поэтому для подбора размеров его поперечного сечения воспользуемся условием прочности при растяжении-сжатии.
где N – внутренние продольные силы (найдены ранее),
A — площадь поперечного сечения стержня.
Чтобы найти размеры поперечного сечения стержня рассчитаем площадь A. Для этого запишем условие прочности относительно площади:
Площадь сечения в данном случае постоянна по всей длине стержня и должна обеспечивать прочность на всех его силовых участках. Поэтому расчет будем вести по самому нагруженному из них, т.е. где внутренняя сила максимальна (N

По построенной эпюре внутренних сил видно, что наиболее нагруженным является II участок, где N=Nmax=70кН.
Тогда расчетная площадь сечения стержня:
Таким образом для обеспечения необходимой прочности стержня площадь его поперечного сечения должна быть не менее 437,5 мм2.
Теперь, зная площадь квадрата, рассчитаем его сторону
Это соответственно минимальный размер поперечного сечения стержня, обеспечивающий его прочность.
В случаях, когда в задании не ставится дополнительных условий полученный размер можно округлить до целого миллиметра, но только в большую сторону.
По ГОСТ 6636 окончательно принимаем ближайший в сторону увеличения линейный размер а=22мм.
Все дальнейшие расчеты стержня будем вести по этому размеру.
Расчет и построение эпюры нормальных напряжений >
Другие примеры решения задач >
isopromat.ru
2.4. Расчеты на прочность при растяжении



2.4. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ РАСТЯЖЕНИИ Основной задачей расчета конструкции на растяжение является обеспечение ее прочности в условиях эксплуатации. Условие прочности – оценка прочности элемента конструкции, сводящаяся к сравнению расчетных напряжений с допускаемыми: σ≤рσ[р ]; σ с ≤[ с],σ (2.9) где σр и σс – наибольшие расчетные растягивающие и сжимающие напряжения; [σр] и [σс] – допускаемые напряжения при растяжении и сжатии. Допускаемое напряжение – наибольшее напряжение, которое можно допустить в элементе конструкции при условии его безопасной, долговечной и надежной работы: Здесь σпред – предельное напряжение (состояние), при котором конструкция перестает удовлетворять эксплуатационным требованиям; им мо- гут быть предел текучести, предел прочности, предел выносливости, пре- дел ползучести и др. Для конструкций из пластичных материалов при определении допускаемых напряжений используют предел текучести σт (рис. 2.4, а). Это связано с тем, что в случае его превышения деформации резко возрастают при незначительном увеличении нагрузки и конструкция перестает удовлетворять условиям эксплуатации. Допускаемое напряжение в этом случае определяют как Для хрупких материалов (чугун, бетон, керамика) где σвр и σвс – пределы прочности при растяжении и сжатии (рис. 2.4, б). Здесь [n] – нормативный коэффициент запаса прочности. В зависимости от той предельной характеристики, с которой сравнивают расчетное напряжение σ, различают [nт] – нормативный коэффициент запаса прочности по отношению к пределу текучести σт и [nв] – нормативный коэффициент запаса прочности по отношению к пределу прочности σв. Запас прочности – отношение предельно допустимой теоретической нагрузки к той нагрузке, при которой возможна безопасная работа конструкции с учетом случайных перегрузок, непредвиденных дефектов и недостоверности исходных данных для теоретических расчетов. Нормативные коэффициенты запаса прочности зависят: − от класса конструкции (капитальная, временная), − намечаемого срока эксплуатации, − условий эксплуатации (радиация, коррозия, загнивание), − вида нагружения (статическое, циклическое, ударные нагрузки) − неточности задания величины внешних нагрузок, − неточности расчетных схем и приближенности методов расчета − и других факторов. Нормативный коэффициент запаса прочности не может быть единым на все случаи жизни. В каждой отрасли машиностроения сложились свои подходы, методы проектирования и приемы технологии. В изделиях общего машиностроения принимают [nт] = 1,3 – 2,2; [nв] = 3 – 5. Вероятность выхода из строя приближенно можно оценить с помощью коэффициента запаса в условии прочности: n = 1 соответствует вероятности невыхода из строя 50 %; n = 1,2 соответствует вероятности невыхода из строя 90 %; n = 1,5 соответствует вероятности невыхода из строя 99 %; n = 2 соответствует вероятности невыхода из строя 99,9 %. Для неответственных деталей n = 2 много. Для ответственных – мало. Так для каната подъемного лифта это означает на 1000 подъемов одно падение. При расчете конструкций на прочность встречаются три вида задач, которые вытекают из условия прочности а) поверочный расчет (проверка прочности). Известны усилие N и площадь A. Вычисляют σ = N/A и, сравнивая его с предельным σт или σв (для пластичного и хрупкого материалов соответственно), находят фактический коэффициент запаса прочности который затем сопоставляют с нормативным [n]; б) проектный расчет (подбор сечения). Известны внутреннее усилие N и допускаемое напряжение [σ]. Определяют требуемую площадь поперечного сечения стержня в) определение грузоподъемности (несущей способности). Известны площадь А и допускаемое напряжение [σ]. Вычисляют внутреннее усилие N≤N[ ] = ⋅[σ]A, (2.15) а затем в соответствие со схемой нагружения – величину внешней нагрузки F ≤ [F].
dx-dy.ru
Сопротивление материалов Задача 1. Расчет стержней при центральном растяжении ( сжатии).
Стальной
стержень (модуль Юнга кН/см2)
с размерами см;см,см
и площадью поперечного сечения нижнего
участкасм2,
а верхнего – см2 нагружен
внешними осевыми силами кН
икН
(см. рис.). Построить эпюры продольных
сили
нормальных напряжений.
Оценить прочность стержня, если предельное
напряжение (предел текучести)кН/см
№ вар. | а | b | c | Fн | Fв | P1 | P2 |
1 | 100 | 100 | 300 | 10 | 40 | 100 | 500 |
2 | 110 | 110 | 290 | 18 | 42 | 110 | 490 |
3 | 120 | 120 | 280 | 12 | 44 | 120 | 480 |
4 | 130 | 130 | 270 | 14 | 46 | 130 | 470 |
5 | 140 | 140 | 260 | 16 | 48 | 140 | 460 |
6 | 150 | 150 | 250 | 18 | 50 | 150 | 450 |
7 | 160 | 160 | 240 | 20 | 51 | 160 | 440 |
8 | 170 | 170 | 230 | 22 | 52 | 170 | 430 |
9 | 180 | 180 | 220 | 24 | 52 | 180 | 420 |
10 | 190 | 190 | 210 | 26 | 54 | 190 | 410 |
11 | 200 | 200 | 400 | 28 | 55 | 200 | 400 |
12 | 210 | 210 | 300 | 30 | 56 | 210 | 390 |
13 | 220 | 230 | 290 | 29 | 56 | 220 | 380 |
14 | 230 | 220 | 270 | 28 | 57 | 230 | 370 |
15 | 240 | 250 | 270 | 27 | 58 | 240 | 360 |
16 | 250 | 240 | 260 | 26 | 59 | 250 | 350 |
17 | 260 | 270 | 300 | 25 | 60 | 260 | 340 |
18 | 270 | 260 | 310 | 24 | 61 | 270 | 330 |
19 | 280 | 290 | 320 | 23 | 62 | 280 | 320 |
20 | 290 | 300 | 330 | 22 | 63 | 290 | 310 |

Решение.
1.Определяем значение опорной реакции , возникающей в заделке.
Учитывая, что , направим опорную реакциювниз. Тогда из уравнения равновесиянаходим:
кН.
2.Строим эпюру продольных сил .
Разбиваем длину стержня на три участка (рис. а). Границами участков являются те сечения, в которых приложены внешние силы и (или) изменяется размер поперечного сечения стержня.
Воспользуемся методом сечений (РОЗУ). Делаем по одному сечению в произвольном месте каждого из трех участков стержня.
Начнем с сечения 1 – 1. Отбросим (или закроем листком бумаги) верхнюю часть стержня (рис. б). Само сечение 1 – 1 мысленно считаем неподвижным. Мы видим, что внешняя сила растягиваетрассматриваемую нижнюю часть стержня. Отброшенная нами верхняя часть стержня противодействует этому растяжению. Это противодействие мы заменим внутренней продольной силой , направленной от сечения и соответствующей растяжению. Разрушения стержня не произойдет только в том случае, если возникающая в сечении1 – 1 внутренняя продольная сила уравновесит внешнюю силу . Поэтому очевидно, что
кН.
Переходим к сечению 2 – 2 (рис. в). Внешняя сила растягивает рассматриваемую нами нижнюю часть стержня, а силаее сжимает (напомним, что2 – 2 мы мысленно считаем неподвижным). Причем, согласно условию задачи, . Чтобы уравновесить эти две силы, в сечении2 – 2 должна возникнуть внутренняя сила , противодействующаясжатию, то есть направленная к сечению. Она равна:
кН.
Делаем сечение 3 – 3 (рис. г). Отбросим теперь часть стержня, расположенную ниже этого сечения. Внутренняя продольная сила должна уравновесить внешнюю (реактивную)сжимающую силу R. Поэтому она направлена к сечению и равна:
кН.
Легко убедиться в том, что полученный результат не изменится, если мы отбросим не нижнюю, а верхнюю часть стержня. В этом случае продольная сила также противодействуетсжатию. Она равна:
кН.
При построении эпюры продольных сил будем пользоваться следующим правилом знаков:внутренняя продольная сила, возникающая в поперечном сечении стержня, считается положительной, если она противодействует растяжению стержня, и отрицательной, если она противодействует его сжатию.
Это правило знаков вводится для того, чтобы можно было наглядно видеть, какая часть стержня испытывает деформацию растяжения, а какая часть – деформацию сжатия. Это обстоятельство может оказаться крайне важным, в частности для стержней из хрупкого материала, которые имеют разные допускаемые напряжения на растяжение и на сжатие.
Таким образом, мы установили, что в любом сечении нижнего участка стержня внутренняя продольная сила противодействует растяжению и равна кН. В любом сечении среднего и верхнего участков стержня имеет место деформациясжатия, поэтому кН.
Для построения эпюры продольных сил проводимтонкой линией ось, параллельную оси стержня z (рис. д). Вычисленные значения продольных сил в выбранном масштабе и с учетом их знака откладываем от этой вертикальной оси. В пределах каждого из участков стержня продольная сила остается постоянной, поэтому мы как бы «заштриховываем» горизонтальными линиями соответствующий участок.
Отметим, что каждая линия «штриховки» (то есть ордината эпюры) в принятом масштабе дает значение продольной силы в соответствующем поперечном сечении стержня.
Полученную эпюру обводим жирной линией.
Анализируя полученную эпюру, мы видим, что в местах приложения внешних сил на эпюре имеет место скачкообразное изменение продольной силы на величину, равную значению соответствующей внешней силы. Причем изменение поперечного размера стержня, как это видно из рис.д, никак не сказывается на характере эпюры .
3. Строим эпюру нормальных напряжений .
Нормальное напряжение, возникающее в k–м поперечном сечении стержня при растяжении (сжатии), вычисляется по следующей формуле
,
где и– продольная сила и площадьk–го поперечного сечения стержня соответственно.
В первом поперечном сечении стержня нормальное напряжение равно
кН/см2,
во втором –
кН/см2,
в третьем –
кН/см2.
Строим по вычисленным значениям эпюру (рис.е). В пределах каждого из участков стержня напряжения постоянны, то есть эпюра напряжений параллельна оси. Заметим, что в отличие от эпюры N, на эпюре«скачок» имеет место не только в местах приложения внешних сил, но и там, где происходит изменение размеров поперечного сечения стержня.
4. Оцениваем прочность стержня.
Сопоставляем наибольшее (по модулю) нормальное напряжение , которое в нашем примере возникает во втором сечении стержня, сдопускаемым напряжением . Напомним, что допускаемое напряжение представляет собой долю от предельного напряжения , то есть от напряжения, при котором начинается разрушение материала. Разрушение стали, какпластичного материала, начинается при появлении значительных остаточных деформаций. Поэтому для стали предельное напряжение равно пределу текучести: . Тогда
кН/см2.
Условие прочности имеет вид . В нашем случае
кН/см2 > кН/см2,
следовательно, прочность стержня на втором участке не обеспечена.
Таким образом, площадь поперечного сечения стержня на втором участке, равную см2, нам необходимо увеличить.
Несложный анализ показывает, что на других участках стержня условие прочности выполняется.
Из условия прочности определяем требуемую площадь поперечного сечения стержня на втором участке:
см2.
Принимаем на втором участке см2.
5. Вычисляем удлинение всего стержня .
При переменных по длине стержня значениях продольной силы и площади поперечного сечения удлинение вычисляется по формуле
,
где E – модуль Юнга, а – длина соответствующего участка стержня.
Тогда
см.
Таким образом, длина стержня уменьшается на 1,7 мм.
Вопросы для защиты.
1.Что такое прочность, жесткость, устойчивость?
2.В чем сущность метода сечений?
3.Что такое напряжение и в каких единицах измеряется?
4.Какие известны виды деформаций?
5.Какая деформация называется центральным растяжением (сжатием)?
6.Какие формулы, выражающие закон Гука, Вы знаете?
Задача 2. Расчет вала на прочность при кручении
К стальному валу (см.рис.5.10) приложены скручивающие моменты: М1, M2, M3, M4. Требуется:
1) построить эпюру крутящих моментов;
2) при заданном значении определить диаметр вала из расчета на прочность и округлить его величину до ближайшей большей, соответственно равной:30, 35, 40, 45, 50, 60, 70, 80, 90, 100 мм;
3) построить эпюру углов закручивания;
4) найти наибольший относительный угол закручивания.
Дано: М1 = М3 = 2 кНм, М2 = М4 = 1,6 кНм, а = b = с = 1,2 м, = 80 МПа.
№ вар. | M1 | M2 | M3 | M4 | a | b | c |
1 | 2 | 1 | 4 | 6 | 1,0 | 2,9 | 2,0 |
2 | 3 | 2 | 5 | 7 | 1,1 | 2,8 | 2,1 |
3 | 4 | 3 | 6 | 8 | 1,2 | 2,7 | 2,2 |
4 | 5 | 4 | 7 | 9 | 1,3 | 2,6 | 2,3 |
5 | 6 | 5 | 8 | 10 | 1,4 | 2,5 | 2,4 |
6 | 7 | 6 | 9 | 11 | 1,5 | 2,4 | 2,5 |
7 | 8 | 7 | 10 | 12 | 1,6 | 2,3 | 2,6 |
8 | 9 | 8 | 11 | 13 | 1,7 | 2,2 | 2,7 |
9 | 10 | 9 | 12 | 14 | 1,8 | 2,1 | 2,8 |
10 | 11 | 10 | 13 | 15 | 1,9 | 2,0 | 2,9 |
11 | 12 | 11 | 14 | 16 | 2,0 | 1,9 | 3,1 |
12 | 13 | 12 | 15 | 17 | 2,1 | 1,8 | 3,2 |
13 | 14 | 13 | 16 | 18 | 2,2 | 1,7 | 3,3 |
14 | 15 | 14 | 17 | 19 | 2,3 | 1,6 | 3,4 |
15 | 16 | 15 | 18 | 20 | 2,4 | 1,5 | 3,5 |
16 | 17 | 16 | 19 | 21 | 2,5 | 1,4 | 3,6 |
17 | 18 | 17 | 20 | 22 | 2,6 | 1,3 | 3,7 |
18 | 19 | 18 | 2` | 23 | 2,7 | 1,2 | 3,8 |
19 | 20 | 19 | 22 | 24 | 2,8 | 1,1 | 3,9 |
20 | 21 | 20 | 23 | 25 | 2,9 | 1,0 | 4,0 |
Решение.
1. Построить эпюру крутящих моментов.
При построений эпюр Мкр примем следующее правило знаков: крутящий момент считается положительным, если при взгляде в торец отсеченной части бруса действующий на него момент представляется направленным по движению часовой стрелки.
Крутящие моменты, возникающие в поперечных сечениях брусьев, определяются по внешним окручивающим моментам с помощью метода сечений. На основании метода сечения крутящий момент в произвольном поперечном сечении бруса численно равен алгебраической сумме внешних скручивающих моментов, приложенных к брусу по одну сторону от рассматриваемого сечения.
Для брусьев, имеющих один неподвижно закрепленный (заделанный) и один свободный конец, крутящие моменты всех поперечных сечений удобно выражать через внешние моменты, приложенные с той стороны от рассматриваемого сечения, с которой расположен свободный конец. Это позволяет определять крутящие моменты, не вычисляя реактивного момента, возникающего в заделке.
Для построения эпюры крутящих моментов необходимо найти величины крутящих моментов на каждом участке вала.
I участок (КД):
кНм,
II участок (СД):
кНм,
III участок (СВ):
кНм,
IV участок (ВА):
кНм.
По значению этих моментов строим эпюру Мкр в выбранном масштабе. Положительные значения Мкр откладываем вверх, отрицательные — вниз от нулевой линии эпюры.
2. При заданном значении определим диаметр вала из расчета на прочность.
Условие прочности при кручении имеет вид
.
— максимальный крутящий момент, взятый по абсолютной величине. Определяется из эпюры Мкр .
кНм;
— полярный момент сопротивления для сплошного круглого вала.
Диаметр вала определяется по формуле
.
Принимаем d = 50 мм = 0,05 м.
3. Построим эпюру углов закручивания.
Угол закручивания участка вала длиной l постоянного поперечного сечения определяется по формуле
.
где — жесткость сечения вала при кручении.
Н/м2;
— полярный момент инерции круглого вала
м4.
Вычислим углы закручивания сечений В, С, D и К относительно закрепленного конца вала (сечения А)
рад,
рад,
рад,
рад.
Строим эпюру углов закручивания.
4. Найдем наибольший относительный угол закручивания
рад/м.
Вопросы для защиты.
1.Какие напряжения возникают в поперечных сечениях при кручении?
2.Что такое полярный момент сопротивления?
3.Напишите условие прочности при кручении.
4.Какая деформация возникает при кручении?
5.При какомнагружении возникает кручение?
Задача 3. Расчет балки на прочность при изгибе.
№ вар. | F,кН | M,кНм | q,кН/м | a1,м | a2,м | l,м |
1 | 2 | 20 | 2 | 1,0 | 2 | 5 |
2 | 3 | 21 | 2 | 1,1 | 2 | 5 |
3 | 4 | 22 | 2 | 1,2 | 3 | 5 |
4 | 5 | 23 | 3 | 1,3 | 3 | 5 |
5 | 6 | 24 | 3 | 1,4 | 4 | 5 |
6 | 7 | 25 | 3 | 1,5 | 4 | 5 |
7 | 8 | 25 | 4 | 1,6 | 2 | 5 |
8 | 9 | 27 | 4 | 1,7 | 2 | 5 |
9 | 10 | 28 | 4 | 1,8 | 2 | 5 |
10 | 11 | 29 | 5 | 1,9 | 2 | 5 |
11 | 12 | 30 | 5 | 2,0 | 3 | 6 |
12 | 13 | 31 | 5 | 2,1 | 3 | 6 |
13 | 14 | 32 | 2 | 2,2 | 1 | 6 |
14 | 15 | 33 | 2 | 2,3 | 1 | 6 |
15 | 16 | 34 | 2 | 2,4 | 1 | 6 |
16 | 17 | 35 | 3 | 2,5 | 2 | 6 |
17 | 18 | 36 | 3 | 2,6 | 2 | 6 |
18 | 19 | 37 | 3 | 2,7 | 2 | 6 |
19 | 20 | 38 | 1 | 2,8 | 1 | 6 |
20 | 21 | 39 | 2 | 2,9 | 1 | 6 |
studfiles.net
Расчет напряжений в стержне при растяжении-сжатии
Задача
Рассчитать величину напряжений в стержне заданной формы, нагруженном продольными силами и построить их эпюру.
Поперечное сечение стержня — квадрат со сторонами a=22мм.
Допустимые напряжения [σ]=160МПа
Пример решения
Предыдущие пункты решения задачи:
- Расчет опорной реакции стержня,
- Построение эпюры внутренних продольных сил,
- Подбор размеров квадратного сечения стержня по условию прочности.
Как известно, расчет нормальных напряжений при растяжении-сжатии производится по формуле:
т.е. напряжения определяются отношением соответствующей величины внутренней силы к площади поперечного сечения на рассматриваемом участке стержня.
Площади поперечного сечения стержня:
В пределах участка стержня, где внутренняя сила и площадь постоянны, напряжения тоже будут одинаковы, при этом положительные (растягивающие) внутренние силы в сечениях вызывают действие положительных напряжений, и наоборот.
Величину и знаки внутренних сил примем с построенной эпюры N.

Расчет напряжений
Напряжения на I силовом участке (KM)
На II участке (CK)
На III участке (BC)
По этим данным строим эпюру нормальных напряжений σ.

По эпюре видно, что все напряжения лежат в пределах допустимых значений, следовательно, поперечные размеры стержня были рассчитаны правильно и необходимая прочность обеспечена.
Другие примеры решения задач >
isopromat.ru
Условие прочности при растяжении-сжатии
При продольном осевом нагружении (растяжении-сжатии) в поперечных сечениях бруса имеют место только нормальные напряжения σ. Поэтому для обеспечения прочности стержней и стержневых систем достаточно выполнение условия:

Здесь
σmax – максимальные расчетные нормальные напряжения в стержне,
N – внутренние продольные силы (принимаются с построенных эпюр),
А – соответствующая площадь поперечного сечения бруса,
[σ] – допустимые напряжения (расчетное сопротивление) для материала стержня, определяемое как:
n – коэффициент запаса прочности, устанавливаемый нормативными документами.
Данное условие означает что для того чтобы стержень при растяжении-сжатии оставался прочным, напряжения σ в его сечениях не должны превышать допустимых значений [σ].
В случаях, когда для материала стержней допустимые напряжения на растяжение [σ]р и на сжатие [σ]сж отличаются, при сравнении необходимо учитывать знак напряжений σ, который зависит только от знака соответствующих внутренних сил N.
Так, положительные значения напряжений σ сравниваются с [σ]р, отрицательные напряжения по модулю не должны превышать значения [σ]сж.
Три задачи расчета на прочность
Данное условие прочности позволяет решать три основных задачи сопротивления материалов и технической механики:
Проверка на прочность.
В случае, когда известны внешние нагрузки, а также размеры и материал стержня можно выполнить проверку его прочности. Для этого по каждому участку рассчитывается величина нормальных напряжений σ, после чего максимальная из них сравнивается с заданным допустимым значением [σ].
Ответ в данной задаче дается в виде заключения:
- если σmax ≤ [σ] стержень прочный,
- если σmax > [σ] стержень непрочный.
Подбор размеров сечения (проектировочный расчет)
Эта задача является основной в технической механике. Здесь, по известным схеме нагружения и материалу стержня определяется минимально необходимая площадь поперечного сечения A обеспечивающая его прочность.
Для этого условие прочности записывается относительно искомой величины.

Полученные размеры в случае необходимости можно только увеличивать. Уменьшение размеров приведет к превышению напряжениями допустимых значений.
Определение грузоподъемности стержня.
Данная формула позволяет по известным размерам и материалу рассчитать величину допустимой внутренней силы, которую может выдержать стержень, оставаясь прочным.
В данном случае условие прочности записано относительно внутренней силы N.
Напряжения при растяжении-сжатии >
Расчеты на прочность при растяжении-сжатии >
isopromat.ru
2.5. Расчеты на жесткость при растяжении
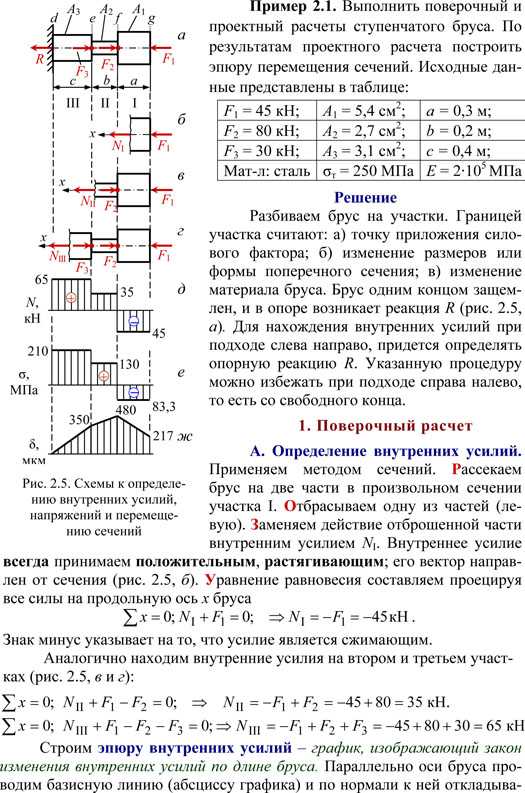





2.5. РАСЧЕТЫ НА ЖЕСТКОСТЬ ПРИ РАСТЯЖЕНИИ Иногда наряду с условиями прочности добавляют ограничения на перемещение некоторых элементов конструкции, то есть вводят условие жесткости δmax ≤ [δ], где [δ] – величина допускаемого перемещения (изменение положения в пространстве) некоторого контролируемого сечения. Деформацию растягиваемого или сжимаемого элемента вычисляют по формуле (2. 4) закона Гука. Пример 2.1. Выполнить поверочный и проектный расчеты ступенчатого бруса. По результатам проектного расчета построить эпюру перемещения сечений. Исходные данные представлены в таблице: Решение Разбиваем брус на участки. Границей участка считают: а) точку приложения силового фактора; б) изменение размеров или формы поперечного сечения; в) изменение материала бруса. Брус одним концом защемлен, и в опоре возникает реакция R (рис. 2.5, а). Для нахождения внутренних усилий при подходе слева направо, придется определять опорную реакцию R. Указанную процедуру можно избежать при подходе справа налево, то есть со свободного конца. 1. Поверочный расчет А. Определение внутренних усилий. Применяем метод сечений. Рассекаем брус на две части в произвольном сечении участка I. Отбрасываем одну из частей (левую). Заменяем действие отброшенной части внутренним усилием NI. Внутреннее усилие всегда принимаем положительным, растягивающим; его вектор направлен от сечения (рис. 2.5, б). Уравнение равновесия составляем проецируя все силы на продольную ось x бруса Знак минус указывает на то, что усилие является сжимающим. Аналогично находим внутренние усилия на втором и третьем участках (рис. 2.5, в и г): Строим эпюру внутренних усилий – график, изображающий закон изменения внутренних усилий по длине бруса. Параллельно оси бруса проводим базисную линию (абсциссу графика) и по нормали к ней откладываем найденные выше значения внутренних усилий (ординаты графика) в выбранном масштабе с учетом знака. Положительные значения откладываем выше базисной линии, отрицательные – ниже (рис. 2.5, д). Поскольку в пределах каждого из участков внутренние усилия неизменны, высоты ординат графика – постоянны и огибающие линии (жирные) – горизонтальны. Б. Определение напряжений на каждом из участков: Строим эпюру напряжений. В. Коэффициенты запаса прочности по отношению к пределу текучести: Вывод: недогружен участок I, перегружен участок III. Для этих участков выполняем проектный расчет. 2. Проектный расчет Из условия прочности при растяжении σ = ≤ [σ] выполняем подбор размеров поперечных сечений I и III участков, предварительно назначив допускаемое напряжение Нормативный коэффициент запаса прочности выбрали из рекомендуемого диапазона значений [nт] = 1,3–2,2. 3. Определение перемещений сечений А. Удлинения каждого из участков Б. Перемещения сечений. За начало отсчета принимаем сечение d. Оно защемлено, его перемещение равно нулю δd = 0. Строим эпюру перемещений. Выводы 1. Выполнен поверочный расчет ступенчатого бруса. Прочность одного из элементов обеспечена; другого – избыточна; третьего – не- достаточна. 2. Из условия прочности при растяжении подобраны площади попе- речных сечений двух элементов конструкции. 3. По результатам проектного расчета вычислены деформации каждого элемента конструкции. Крайнее сечение переместится относительно защемления на 217 мкм в сторону от защемления. Пример 2.2. К стальному брусу постоянного сечения вдоль его оси приложены две силы. По условиям эксплуатации введено ограничение на величину перемещения [δ] концевого сечения С. Из условий прочности и жесткости подобрать размер поперечного сечения. Решение 1. Определение внутренних усилий Покажем возникающую в опоре реакцию R; определение внутренних усилий методом сечений начнем вести со свободного конца. Ось х – про- дольная ось бруса (на рисунке не показана). I участок: ∑ x = 0; − NI + F1 = 0; ⇒ NI = F1 = 40кН. II участок: ∑ x = 0; − NII + F1 − F2 = 0; ⇒ NII = F1 − F2 = 40 − 60 = −20кН . F1 = 40 кН; F2 = 60 кН; a = 0,5 м; [σ] = 180 МПа; [δ] = 1 мм. Строим эпюру внутренних усилий. Опасным является участок I, на котором действует Nmax = – 40 кН (пластичные материалы одинаково сопротивляются деформации растяжения и сжатия). 2. Проектный расчет из условия прочности Из условия прочности при растяжении находим требуемую площадь поперечного сечения стержня 3. Проектный расчет из условия жесткости Перемещение сечения С является суммой двух слагаемых: откуда требуемая площадь поперечного сечения стержня Сравнивая результаты проектных расчетов из условия прочности и жесткости, назначаем большее из двух значений площади поперечного сечения: 2,22 и 1,5 см2, удовлетворяющее обоим условиям: А ≥ 2,22 см2. Пример 2.3. Жесткая балка (ее деформацией пренебречь) подперта стальным стержнем (подкосом). Проверить прочность стержня. Определить допускаемую нагрузку F для заданного размера поперечного сечения стержня. Выполнить проектный расчет из условия прочности и жесткости ([δF] – допускаемая величина перемещения балки в точке приложения силы). Решение 1. Поверочный расчет А. Определение внутреннего усилия в стержне Рассекаем стержень на две части (рис. а). Отбрасываем одну из частей и показываем внешнюю нагрузку F, внутреннее усилие N и две составляющих опорной реакции R (рис. б). Составляем такое уравнение равновесия, в которое не вошли бы опорные реакции. Усилие в стержне сжимающее. Б. Определение напряжения В. Коэффициент запаса прочности Фактический коэффициент запаса 1,06 не входит в рекомендуемый (нормативный) диапазон значений [nт]=1,3−2,3. Вывод: прочность недостаточна. 2. Определение допускаемой нагрузки на конструкцию для заданного размера поперечного сечения стержня Из условия прочности при растяжении σ = ≤ [σ] находим допускаемую нагрузку на стержень [N]≤ A⋅[σ]= 15⋅10−4 ⋅170⋅106 = 255 кН. Здесь допускаемое Нормативный коэффициент запаса по текучести назначили из рекомендуемого диапазона n[ т]=1,3−2,3. Из условия равновесия (см. этап 1) находим связь между допускаемой внешней нагрузкой [F] на конструкцию и внутренним усилием [N] в стержне: 3. Проектный расчет из условия прочности Требуемое значение площади поперечного сечения из условия прочности при растяжении: 4. Проектный расчет из условия жесткости Под действием внешней нагрузки стержень деформируется; сечения балки изменяют свое положение в пространстве. Установим связь между внутренним усилием, деформацией стержня и перемещением заданного сечения конструкции. Покажем схему в исходном и деформированном (пунктирные линии) состояниях (рис. в). Контролируемое перемещение сечения балки в точке D приложения силы δF связано с перемещением узла С точки прикрепления стержня к балке соотношением: Вследствие перемещения узла С стержень укорачивается на Δ = CC′⋅sinα. Деформацию стержня определяем по закону Гука: Здесь ℓ – длина стержня, определяется из схемы нагружения (рис. а). Тогда из условия жесткости конструкции: Сравнивая результаты проектных расчетов из условия прочности и жесткости, назначаем большее из двух значений: 28,2 и 33,3 см2, удовлетворяющее обоим условиям, то есть А ≥ 33,3 см2. Выводы 1. Выполнен поверочный расчет стержня. Прочность элемента конструкции недостаточна. 2. Для заданного размера поперечного сечения нагрузка F, приложенная к конструкции, не должна превышать 42,5 кН. 3. Из условий прочности и жесткости при растяжении найдено значение площади поперечного сечения элемента конструкции, удовлетворяющее обоим условиям: 33,3 см2.
dx-dy.ru