Открытое занятие. По технической механике
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ ДОНЕЦКОЙ НАРОДНОЙ РЕСПУБЛИКИ
ГПОУ «ДОНЕЦКИЙ ЭЛЕКТРОМЕТАЛЛУРГИЧСКИЙ ТЕХНИКУМ»
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
открытого занятия
На тему «Растяжение и сжатие»
по дисциплине ОП. 03 Техническая механика
по специальности 15.02.01. Монтаж и техническая эксплуатация промышленного оборудования (по отраслям)
2017
Министерство образования и науки Донецкой Народной Республики
ГПОУ «Донецкий электрометаллургический техникум»
ЦК Механических дисциплин
СОГЛАСОВАНО УТВЕРЖДАЮ
зам. директора директор ГПОУ Донецкий
поучебной работе ГПОУ электрометаллургический
Донецкий электрометаллургический техникум
техникум
_____________Р. Н. Михненко _____________И.А. Караван
Н. Михненко _____________И.А. Караван
« »___________ 2017 г. « »___________2017 г.
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
открытого занятия
на тему: «Растяжение и сжатие»
по дисциплине ОП. 03 Техническая механика
по специальности 15.02.01. Монтаж и техническая эксплуатация промышленного оборудования (по отраслям)
Составитель — Ковалева Ольга Александровна, преподаватель технической механики, квалификационной категории «специалист»ГПОУ «Донецкий электрометаллургический техникум».
Рецензенты:
1. Вахитова Любовь Васильевна, преподаватель специальных дисциплин, специалист высшей категории, председатель цикловой комиссии механических дисциплин ГПОУ «Донецкий электрометаллургический техникум».
В данной методической разработке на тему «Растяжение и сжатие» дана методика проведения практического занятия на основе педагогических инновационных технологий.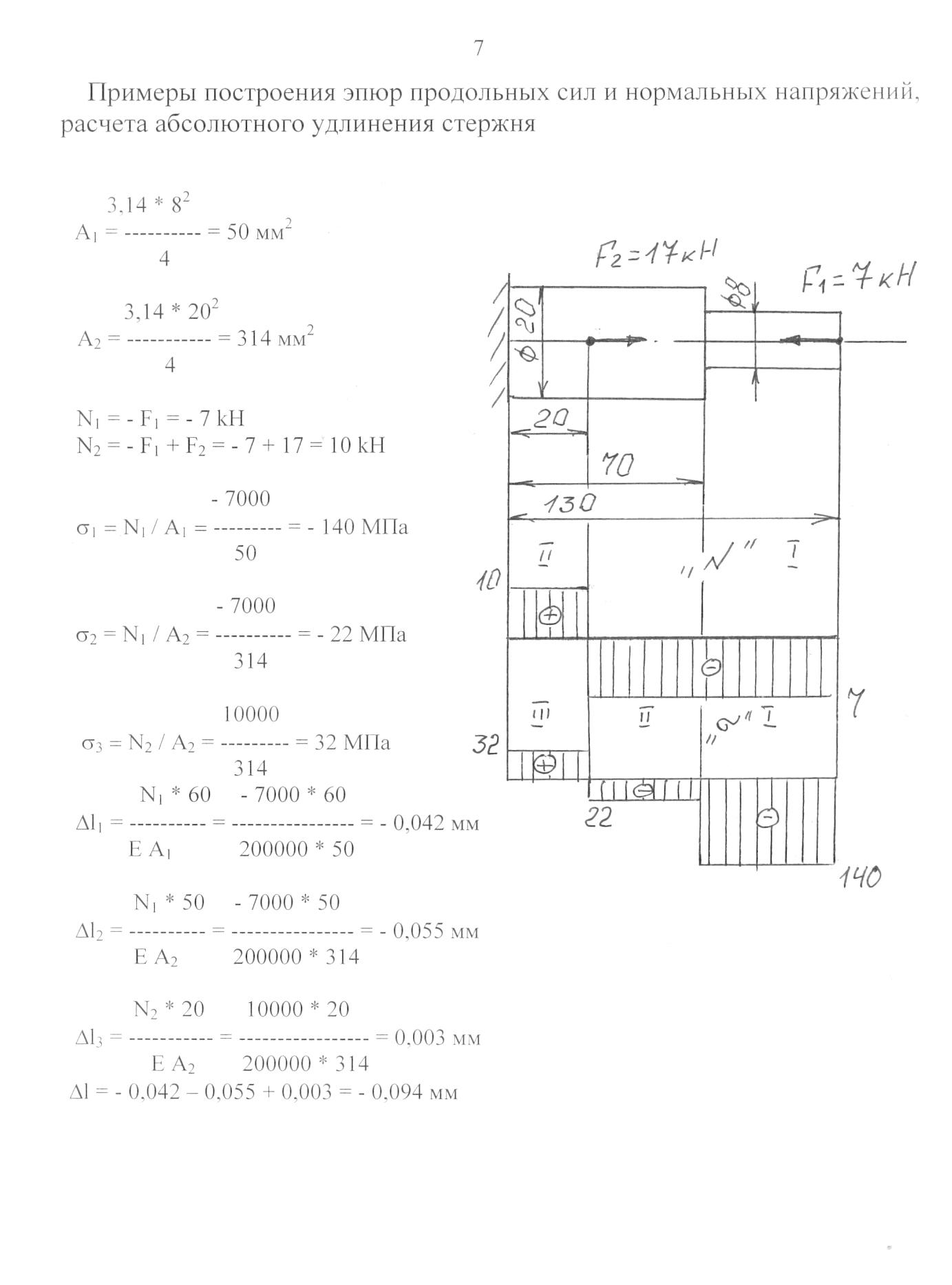
Разработка занятия направлена на обобщение и систематизацию знаний студентов, на творческую самостоятельную поисково-аналитическую работу студентов, самореализацию личности студента путем применения форм и методов критического мышления, проблемной, акмеологической технологий обучения.
Методическая разработка рекомендована преподавателям технической механики для внедрения в учебно-воспитательный процесс.
Методическая разработка на тему «Растяжение и сжатие»
ЦК механических дисциплин
ПЦК___________________Л. В. Вахитова
Протокол № от «9» января 2017 г.
Рецензия
на методическую разработку открытого занятия преподавателя Государственного профессионального образовательного учреждения «Донецкий электрометаллургический техникум»
Ковалевой Ольги Александровны
Методическая разработка открытого занятия на тему «Растяжение и сжатие» по дисциплине ОП. 03 Техническая механика15.02.01 Монтаж и техническая эксплуатация промышленного оборудования (по отраслям) составлена в соответствии с рекомендациями Государственной инспекции образования Донецкой народной республики для определения уровня педагогического мастерства преподавателя.
03 Техническая механика15.02.01 Монтаж и техническая эксплуатация промышленного оборудования (по отраслям) составлена в соответствии с рекомендациями Государственной инспекции образования Донецкой народной республики для определения уровня педагогического мастерства преподавателя.
В данной разработке изложена методика преподавания открытого занятия – практическое занятие с использованием проблемного и поискового (эвристического) методов обучения. Цель методической разработки — повысить активную мыслительную деятельность студентов, их творческий поиск; сформировать навыки исследовательской работы; развить умение анализировать, сравнивать, делать выводы и самостоятельно принимать решения.
Разработка занятия содержит необходимое методическое обеспечение для проведения занятия.
Актуальность темы определяется тем, что теоретические знания и практические навыки, полученные студентами, нужны будут при изучении специальных дисциплин и в будущей профессии.
Преподаватель Ковалева О.А. проводит практическое занятие как проблемное, которое является методом активного обучения, позволяет приблизить процесс обучения к реальным условиям практической деятельности.
Материалы данной методической разработки отражают современный подход преподавателя к организации учебного процесса, тесную связь обучения с производством. Использование преподавателем нетрадиционных методов обучения – инновационных, интерактивных педагогических технологий делает более эффективной подготовку младших специалистов в соответствии с требованиями Государственных стандартов Донецкой народной республики.
Методическая разработка преподавателя ГПОУ ДЭМТ Ковалевой О.А. рекомендована для преподавателей дисциплин общепрофессионального цикла среднего профессионального образования по дисциплине ОП.03 Техническая механика для специальности 15.02.01 Монтаж и техническая эксплуатация промышленного оборудования (по отраслям)
Преподаватель Ковалева О.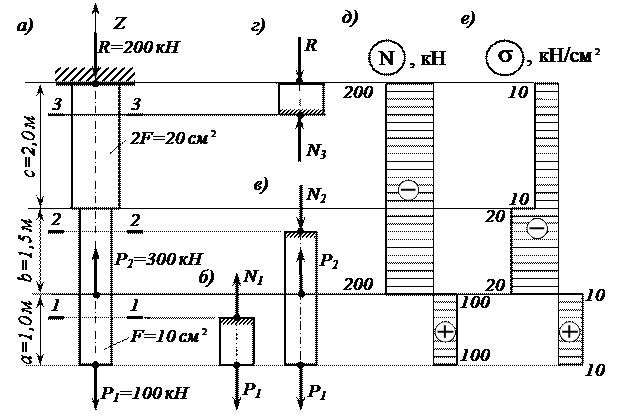
Рецензент: Л.В. Вахитова, преподаватель специальных дисциплин, специалист высшей категории, председатель цикловой комиссии механических дисциплин, ГПОУ «Донецкий электрометаллургический техникум»
ПЦК механических дисциплин___________________ Л.В. Вахитова
Введение
Современный уровень развития требует создания новых машин, наиболее рациональных, экономически выгодных при изготовлении и эксплуатации, долговечных, надежных, высокопроизводительных, удобных в обслуживании.
«Техническая механика» является важным предметом цикла освоения общепрофессиональных дисциплин, состоящим из трех разделов: теоретической механики, сопротивления материалов и деталей машин. Изученный материал по технической механике, необходим студентам, он обеспечивает приобретенные навыки при решениях многих инженерных задач, которые будут встречаться в их практической деятельности.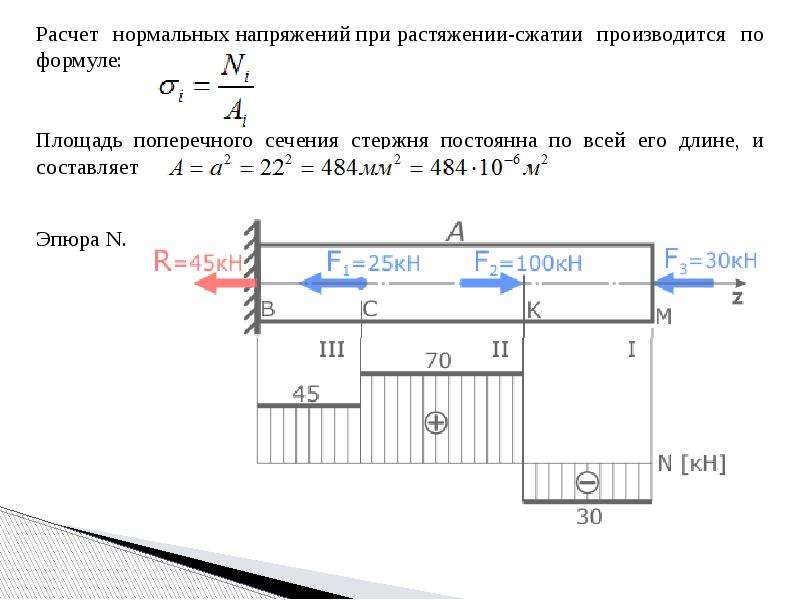
При решении задач сопротивления материалов используются как опыт, так и теория, которые в этой науке неразрывно связаны между собой. На практике опытные исследования дают возможность изучить механические свойства и поведение материала как в самых простых, так и в более сложных условиях его работы. Теория же позволяет применить и обобщить результаты опытных исследований для построения метода расчета конструкции, находящейся в любых условиях работы. Соответствие теории с опытом устанавливается широкой практикой, на которой проверяются как теоретические выводы, так и опытные исследования. Выводы, полученные в сопротивлении материалов, широко используются во многих специальных, технических дисциплинах.
На занятиях по технической механике преподаватель уделяет особое внимание на развитие самостоятельного творческого мышления, которое характеризуется тем, что человек не только получает знания в готовом виде, а самостоятельно применяет их к решению познавательных и практических задач.
Тема «Расчеты на прочность при растяжении – сжатии» одна из важнейших в курсе «Техническая механика». Она имеет большое значение с точки зрения практического применения. Многие детали конструкций испытывают деформацию растяжения – сжатия. Очень важно знать и какие факторы приводят к их разрушению, к невозможности дальнейшей эксплуатации.
Технологическая карта
практического занятия
Дата 10.02.2017Специальность —
Дисциплина —
Преподаватель —
Тема:
Группа МО-15-1/д Курс 2
15.02.01 Монтаж и техническая эксплуатация промышленного оборудования (по отраслям)
ОП.03 Техническая механика
Ковалева Ольга Александровна
«Растяжение и сжатие»
Цели:
методическая –
усовершенствовать уровень проведения практического занятия с применением инновационных педагогических технологий (акмеологической, интерактивной, проблемной, развития критического мышления), что обеспечивает творческий уровень освоения содержания учебного материала;
дидактическая –
создать оптимальные условия для развития самореализации студентов;
закрепить знания предыдущего материала лекции;
рассмотреть и основы практического расчета тел на прочность при растяжении – сжатии;
решение проблемы;
прокомментировать и оценить работу студентов на занятии, их знания и умения с помощью дифференцированного подхода;
развивающая –
формировать навыки и умения логического и инженерного мышления при решении задач;
развивать навыки коллективной работы, самообразования;
повысить образовательный уровень личности студента, его профессиональную компетентность;
способствовать формированию информационной и технической культуры студента;
воспитательная –
воспитывать моральные качества студентов и способствовать повышению его культурного уровня;
стимулировать интерес к усовершенствованию знаний и самореализации, стремление к исследовательской работ.
прививать студентам аккуратность и четкость при выполнении схем и эпюр, добиваться активности и высокой работоспособности студентов на занятии.
Вид занятия –
практическое занятие
Тип занятия —
практическое занятие с проблемным направлением обучения.
Методы:
проблемно-поисковый, наглядно-демонстрационный (интерактивный).
Формы:
индивидуальная, коллективно-групповая.
Междисциплинарные связи:
обеспечивающие-
обеспечиваемые –
математика, физика, материаловедение, инженерная графика
«Технологическое оборудование», «Процессы формообразования и инструменты», «Технология отрасли», «Организация и проведение монтажа и ремонта промышленного оборудования», «Эксплуатация промышленного оборудования».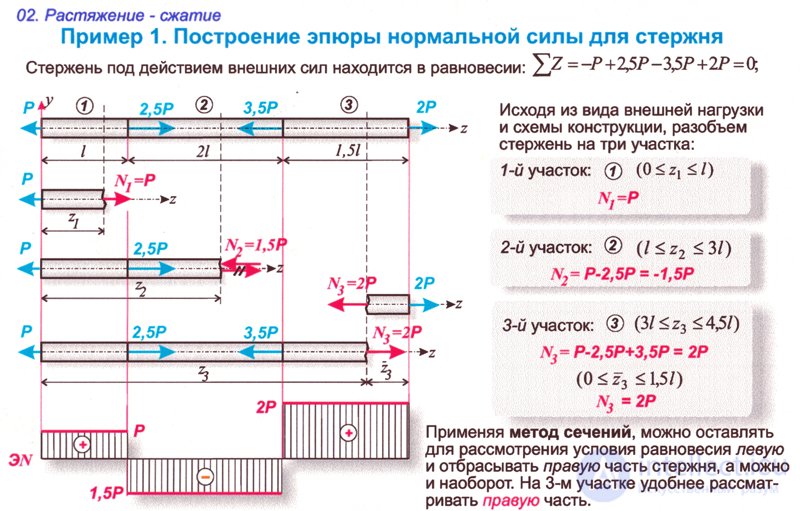
Методическое обеспечение занятия –
1. Рабочая программа дисциплины.
2. Методическая разработка открытого занятия.
3. Опорный конспект лекции для студентов.
4. Тесты для самопроверки знаний,
6. Типовая задача по теме Растяжение и сжатие
7. Презентация практического занятия №6 Расчеты на растяжение-сжатие. Определение напряжения в конструкционных элементах
ТСО–мультимедийное проекционное оборудование, ноутбук.
Литература:
Основные источники:
1. Вереина Л. И., Краснов М. М. Техническая механика: учебник для студ. учреждений сред. проф. образования — М:. Издательский центр «Академия», 2004 -288 с.
2. Сетков В. И. сборник задач по технической механике: учеб. пособие для студ. учреждений сред. проф. образования — М:. Издательский центр «Академия», 2010 -224 с.
учреждений сред. проф. образования — М:. Издательский центр «Академия», 2010 -224 с.
3. Олофинская В.П. Техническая механика (курс лекций с вариантами практических и тестовых заданий) – Москва, Форум, 2009.
4. Олофинская В.П. Детали машин – Москва, Форум, 2008.
5. Аркуша А.И. Теоретическая механика и сопротивление материалов. – Москва, Высшая школа, 2002.
6. Олофинская В.П. Техническая механика. Сборник тестовых заданий. – Москва, Форум, Инфра М, 2002.
7. Аркуша А.И. . Техническая механика. Теоретическая механика и сопротивление материалов. – Москва, Высшая школа, 2003.
8. Эрдеди А.А. Эрдеди Н. А. Теоретическая механика. Сопротивление материалов. – Москва, Высшая школа, 2010
Дополнительные источники:
1. Аркуша А.И. Руководство к решению задач по теоретической механике. — М.: Высшая школа, 2002.
2.Ицкович Г.М. Минин М.С., Винокуров А.И. Руководство к решению задач по сопротивлению материалов. – М.: Высшая школа, 2001.
Ход занятия
Номер элементаЭлементы занятия, учебные вопросы
Продолжи-тельность в минутах (80 минут)
1
2
3
1.
Организационная часть
-2 мин
1.1
Взаимное приветствие преподавателя и студентов.
1.2
Проверка присутствия студентов и их готовности к занятию.
2.
Актуализация опорных знаний (связь с предыдущими темами)
— 20 мин
2.1
Вопросы для текущего контроля знаний: разгадывание кроссворда. (Приложение Б)
(Приложение Б)
3.
Мотивация учебной деятельности.
«Расчеты на прочность при растяжении – сжатии» одна из важнейших тем в курсе «Техническая механика». Она имеет большое значение с точки зрения практического применения. Многие детали конструкций испытывают деформацию растяжения – сжатия. Очень важно знать, какие факторы приводят к их разрушению к невозможности дальнейшей эксплуатации Любые создаваемые конструкции должны быть не только прочными и надежными, но и недорогими, простыми в изготовлении и обслуживании, с минимальным расходом материалов, труда и энергии. Знания данной темы пригодятся вам, студентам при работе над курсовым и дипломным проектами.
— 3 мин
4.
Основная часть.
-48 мин
Тема: Растяжение и сжатие
Проблема:
Что необходимо знать при расчетах на растяжение и сжатие, чтобы уменьшить себестоимость конструкции?
4. 1
1
План:
1. Для стального ступенчатого стержня необходимо построить эпюры продольных сил и нормальных напряжений.
2. Определить абсолютное удлинений (укорочение) стержня.
3. Определить размеры поперечного сечения круга и квадрата.
— 23 мин
4.2
Самостоятельная работа студентов на закрепление полученных знаний, решение типовых задач (Приложение Г). Выполнение тестовых заданий (Приложение Д)
— 25 мин
4.3
Решение проблемы
Знание расчетов при растяжении-сжатии позволяет уменьшить себестоимость конструкций и продлить срок их эксплуатации.
2- мин
5.
Заключительная часть. Подведение итогов занятия, комментирование и оценивание работы студентов с помощью дифференцированного подхода.
Рефлексия: самоанализ работы на занятии (Приложение Ж).
— 3 мин
6.
Домашнее задание (преподаватель подробно указывает объем домашнего задания, конкретно ставит цели и задачи, форму и способы выполнения).
Для стального ступенчатого стержня необходимо построить эпюры продольных сил и нормальных напряжений, определить абсолютное удлинение (укорочение) стержня. Приложение Е
— 2 мин
Приложение
Приложение А-Лекция Тема: Растяжение и сжатие.
Приложение Б – Кроссворд
Приложение В – Практическая работа №7 Расчеты на растяжение-сжатие. Определение напряжения в конструкционных элементах
Приложение Г – Закрепление материала в форме решения типовых задач.
Приложение Д –Тестовые задания
Приложение Е — Домашнее задание
Приложение Ж — Рефлексия: самоанализ работы на занятии
Приложение А
Лекция
Тема: Растяжение и сжатие.
План
1. Растяжение и сжатие
2. Примеры построения эпюры продольных сил
3 Напряжения при растяжении и сжатии
4. Деформации при растяжении и сжатии
5. Выводы
6. Примеры решения задач
Иметь представление о продольных силах, о нормальных напряжениях в поперечных сечениях.
Знать правила построения эпюр продольных сил и нормальных напряжений, закон распределения нормальных напряжений в поперечном сечении бруса.
Уметь строить эпюры продольных сил и нормальных напряжений.
1. Растяжение и сжатие
Растяжением или сжатием называют вид нагружения, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор — продольная сила.
Продольные силы меняются по длине бруса. При расчетах после определения величин продольных сил по сечениям строится график — эпюра продольных сил.
Условно назначают знак продольной силы.
Если продольная сила направлена от сечения, то брус растянут. Растяжение считают положительной деформацией (рис. 20.1а).
Если продольная сила направлена к сечению, то брус сжат. Сжатие считают отрицательной деформацией (рис. 20.1б).
2. Примеры построения эпюры продольных сил
Рассмотрим брус, нагруженный внешними силами вдоль оси. Брус закреплен в стене (закрепление «заделка») (рис. 20.2а). Делим брус на участки нагружения.
Участком нагружения считают часть бруса между внешними силами.
На представленном рисунке 3 участка нагружения.
Воспользуемся методом сечений и определим внутренние силовые факторы внутри каждого участка.
Расчет начинаем со свободного конца бруса, чтобы не определять величины реакций в опорах.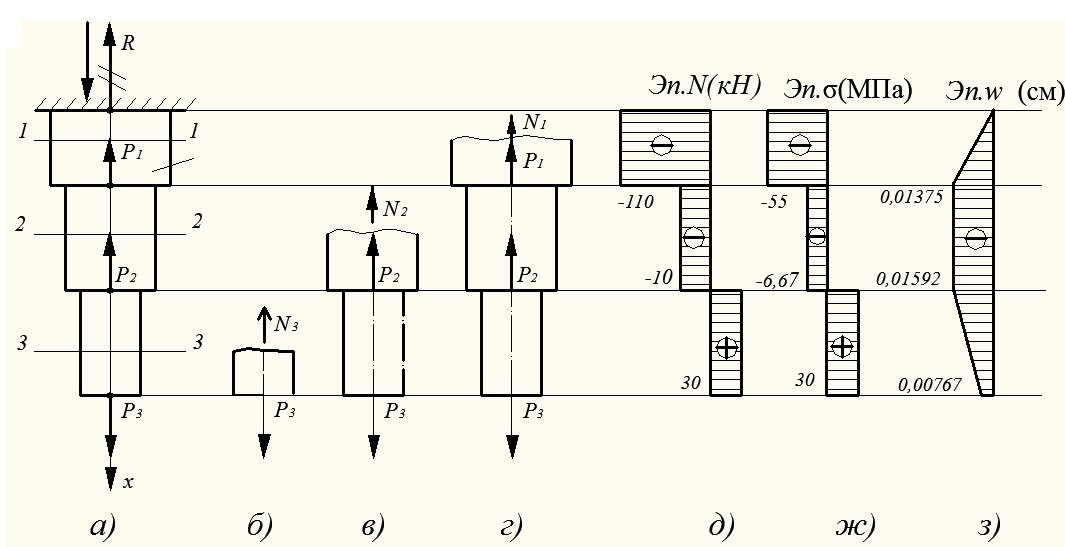
Продольная сила положительна, участок 1 растянут.
Продольная сила положительна, участок 2 растянут.
Продольная сила отрицательна, участок 3 сжат.
Полученное значение N3 равно реакции в заделке.
Под схемой бруса строим эпюру продольной силы (рис. 20.2, б).
Эпюрой продольной силы называется график распределения продольной силы вдоль оси бруса.
Ось эпюры параллельна продольной оси.
Нулевая линия проводится тонкой линией. Значения сил откладывают от оси, положительные — вверх, отрицательные — вниз.
В пределах одного участка значение силы не меняется, поэтому эпюра очерчивается отрезками прямых линий, параллельными оси Oz.
Правило контроля: в месте приложения внешней силы на эпюре должен быть скачок на величину приложенной силы.
На эпюре проставляются значенияNz. Величины продольных сил откладывают в заранее выбранном масштабе.
Эпюра по контуру обводится толстой линией и заштриховывается поперек оси.
Изучая деформации при растяжении и сжатии, обнаруживаем, что выполняются гипотеза плоских сечений и принцип смягчения граничных условий.
Гипотеза плоских сечений заключается в том, что поперечное сечение бруса, плоское и перпендикулярное продольной оси, после деформации остается плоским и перпендикулярным продольной оси.
Следовательно, продольные внутренние волокна удлиняются одинаково, а внутренние силы упругости распределены по сечению равномерно.
Принцип смягчения граничных условий гласит: в точках тела, удаленных от мест приложения нагрузки, модуль внутренних сил мало зависит от способа закрепления.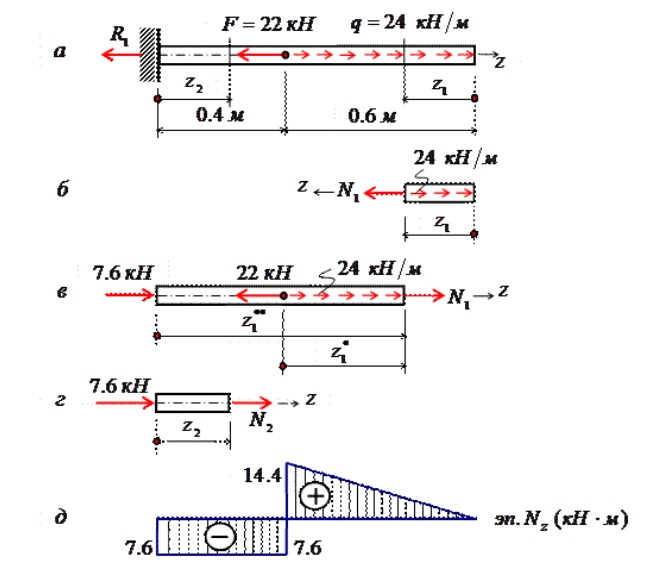 Поэтому при решении задач не уточняют способ закрепления.
Поэтому при решении задач не уточняют способ закрепления.
3. Напряжения при растяжении и сжатии
При растяжении и сжатии в сечении действует только нормальное напряжение.
Напряжения в поперечных сечениях могут рассматриваться как силы, приходящиеся на единицу площади.
Таким образом, направление и знак напряжения в сечении совпадают с направлением и знаком силы в сечении (рис. 20.3).
Исходя из гипотезы плоских сечений, можно предположить, что напряжения при растяжении и сжатии в пределах каждого сечения не меняются. Поэтому напряжение можно рассчитать по формуле
гдеNz — продольная сила в сечении; А — площадь поперечного сечения.
Величина напряжения прямо пропорциональна продольной силе и обратно пропорциональна площади поперечного сечения.
Нормальные напряжения действуют при растяжении от сечения (рис. 20.4а), а при сжатии к сечению (рис. 20.4б).
Размерность (единица измерения) напряжений — Н/м2 (Па), однако это слишком малая единица, и практически напряжения рассчитывают в Н/мм2 (МПа):
1 МПа = 106 Па =1 Н/мм2.
При определении напряжений брус разбивают на участки нагружений, в пределах которых продольные силы не изменяются, и учитывают места изменений площади поперечных сечений.
Рассчитывают напряжения по сечениям, и расчет оформляют в виде эпюры нормальных напряжений.
Строится и оформляется такая эпюра так же, как и эпюра продольных сил.
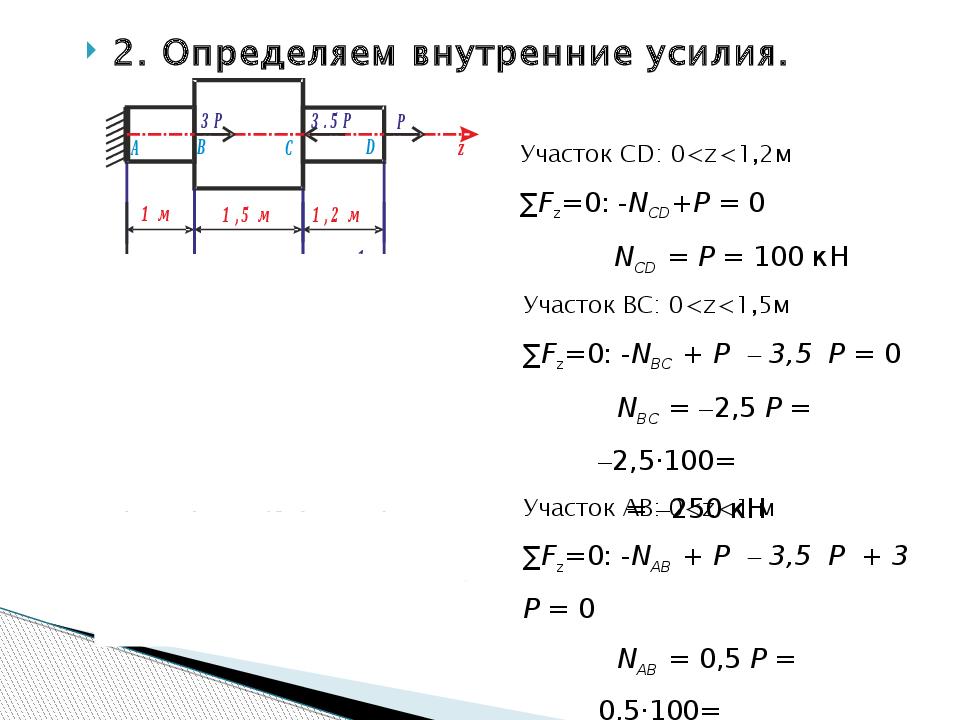
Рассмотрим брус, нагруженный внешними силами вдоль оси (рис. 20.5).
Обнаруживаем три участка нагружения и определяем величины продольных сил.
Участок 1: N1 = 0. Внутренние продольные силы равны нулю.
Участок 2:N2 = 2F. Продольная сила на участке положительна.
Участок 3: N3 =2F–3F =-F. Продольная сила на участке отрицательна.
Брус – ступенчатый.
С учетом изменений величин площади поперечного сечения участков напряжений больше.
Строим эпюры продольных сил и нормальных напряжений.
Масштабы эпюр могут быть разными и выбираются исходя из удобства построения.
4. Деформации при растяжении и сжатии
Рассмотрим деформацию бруса под действием продольной силы F(рис. 21.1).
В сопротивлении материалов принято рассчитывать деформации в относительных единицах:
Между продольной и поперечной деформациями существует зависимость
где μ— коэффициент поперечной деформации, или коэффициент Пуассона, —характеристика пластичности материала.
Закон Гука
В пределах упругих деформаций деформации прямо пропорциональны нагрузке:
гдеF — действующая нагрузка;к — коэффициент. В современной форме:
Получим зависимость
гдеЕ — модуль упругости, характеризует жесткость материала.
В пределах упругости нормальные напряжения пропорциональны относительному удлинению.
ЗначениеЕ для сталей в пределах (2 – 2,1) • 105МПа. При прочих равных условиях, чем жестче материал, тем меньше он деформируется:
Формулы для расчета перемещений поперечных сечений бруса при растяжении и сжатии
Используем известные формулы.
Относительное удлинение
В результате получим зависимость между нагрузкой, размерами бруса и возникающей деформацией:
где
Δl — абсолютное удлинение, мм;
σ — нормальное напряжение, МПа;
l — начальная длина, мм;
Е — модуль упругости материала, МПа;
N — продольная сила, Н;
А — площадь поперечного сечения, мм2;
Произведение АЕ называют жесткостью сечения.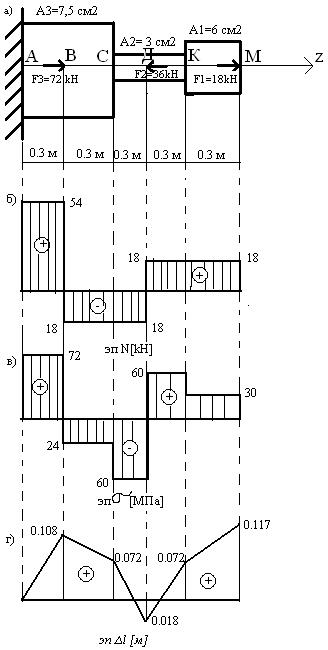
5. Выводы
Абсолютное удлинение бруса прямо пропорционально величине продольной силы в сечении, длине бруса и обратно пропорционально площади поперечного сечения и модулю упругости.
Связь между продольной и поперечной деформациями зависит от свойств материала, связь определяется коэффициентом Пуассона,называемом коэффициентом поперечной деформации.
Коэффициент Пуассона: у стали μ от 0,25 до 0,3; у пробки μ = 0; у резины μ = 0,5.
Поперечные деформации меньше продольных и редко влияют на работоспособность детали; при необходимости поперечная деформация рассчитывается через продольную.
где Δа — поперечное сужение, мм;
ао — начальный поперечный размер, мм.
Закон Гука выполняется в зоне упругих деформаций, которая определяется при испытаниях на растяжение по диаграмме растяжения (рис.
 21.2).
21.2).
При работе пластические деформации не должны возникать, упругие деформации малы по сравнению с геометрическими размерами тела. Основные расчеты в сопротивлении материалов проводятся в зоне упругих деформаций, где действует закон Гука.
На диаграмме (рис. 21.2) закон Гука действует от точки 0 до точки 1.
Определение деформации бруса под нагрузкой и сравнение ее с допускаемой (не нарушающей работоспособности бруса) называют расчетом на жесткость.
6. Примеры решения задач
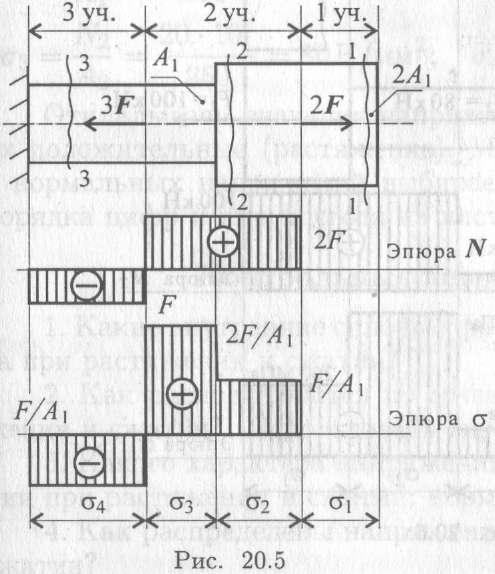
Пример 1. Ступенчатый брус нагружен вдоль оси двумя силами. Брус защемлен с левой стороны (рис. 20.6). Пренебрегая весом бруса, построить эпюры продольных сил и нормальных напряжений.
Решение
Определяем участки нагружения, их два.
Определяем продольную силу в сечениях 1 и 2.
Строим эпюру.
Рассчитываем величины нормальных напряжений и строим эпюру нормальных напряжений в собственном произвольном масштабе.
Определяем продольные силы.
В обоих сечениях продольные силы положительны.
Определяем нормальные напряжения
Сопоставляя участки нагружения с границами изменения площади, видим, что образуется 4 участка напряжений.
Нормальные напряжения в сечениях по участкам:
Откладываем значения напряжений вверх от оси, т. к. значения их положительные (растяжение). Масштаб эпюр продольной силы и нормальных напряжений выбирается отдельно в зависимости от порядка цифр и имеющегося на листе места.
Пример 2. Стальной стержень круглого сечения диаметром d = 20 мм растягивается силой Р = 65 кН.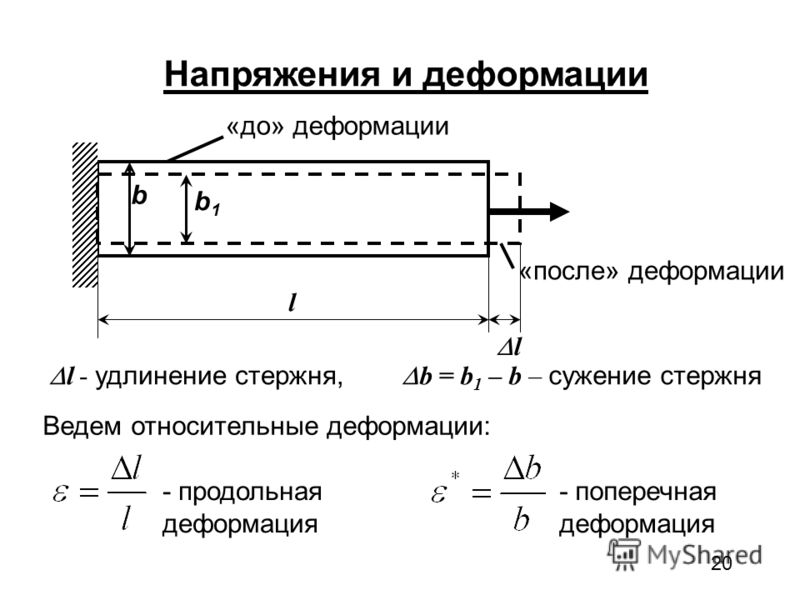 Проверить прочность стержня, если его предел текучести σ = σт = 300 Н/мм2 и требуемый коэффициент запаса [n] = 1,5.
Проверить прочность стержня, если его предел текучести σ = σт = 300 Н/мм2 и требуемый коэффициент запаса [n] = 1,5.
Решение
Напряжения, возникающие в поперечном сечении стержня,
Расчетный коэффициент запаса
Следовательно, можно считать, что прочность стержня достаточна, так как расчетный коэффициент запаса незначительно (на 3%) меньше требуемого.
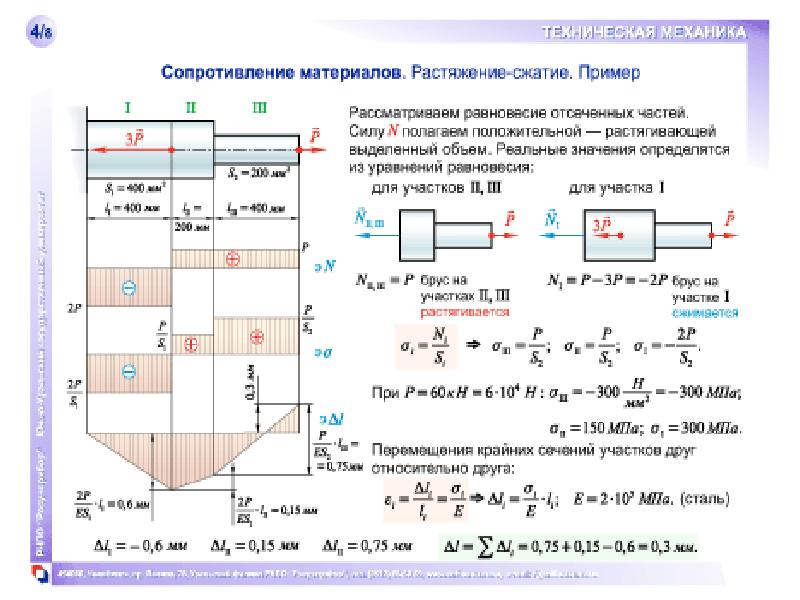
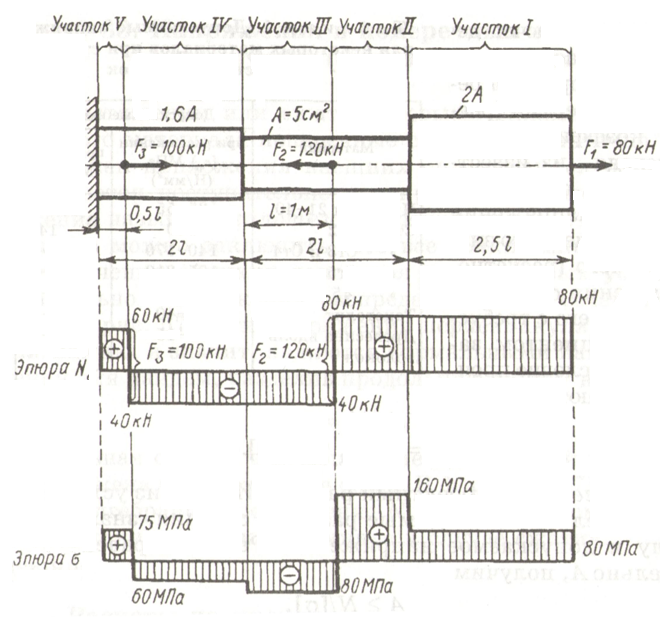
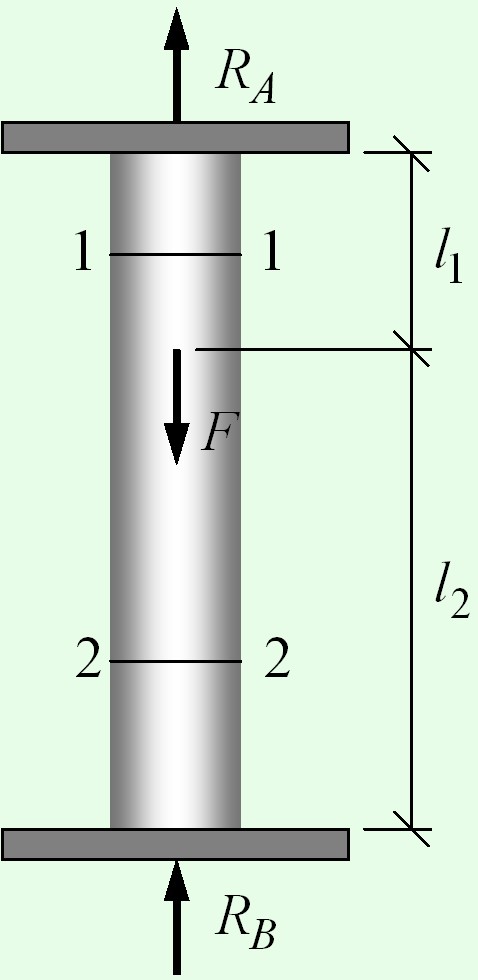
Пример 3. Дана схема нагружения и размеры бруса до деформации (рис. 21.3). Брус защемлен, определить перемещение свободного конца.
Решение
Брус ступенчатый, поэтому следует построить эпюры продольных сил и нормальных напряжений.
Делим брус на участки нагружения, определяем продольные силы, строим эпюру продольных сил.
Определяем величины нормальных напряжений по сечениям с учетом изменений площади поперечного сечения.

Строим эпюру нормальных напряжений.
На каждом участке определяем абсолютное удлинение. Результаты алгебраически суммируем.
Примечание. Балка защемлена, в заделке возникает неизвестная реакция в опоре, поэтому расчет начинаем со свободного конца (справа).
Два участка нагружения:
участок 1:
растянут;
участок 2:
Три участка по напряжениям:
Приложение Б
Кроссворд
По горизонтали:
1. Способ решения задачи (ответ: расчет).
2. Метод сечения (ответ:РОЗУ).
3. Изменение формы и размеров тел под действием нагрузки (ответ: деформация).
Изменение формы и размеров тел под действием нагрузки (ответ: деформация).
4. Единица измерения напряжения (ответ:Паскаль).
5. Ученый, именем которого назван модуль упругости (ответ:Юнг).
6. Свойство материала сопротивляться проникновению одного тела в поверхность другого (ответ: твердость).
7. Внутренний силовой фактор, деленный на геометрическую характеристику сечения (ответ: напряжение).
8. Как называется напряжение, действующее перпендикулярно площади поперечного сечения (ответ: нормальное).
9. Величина, определяемая проектным расчетом (ответ: размер).
10. Способность материала сопротивляться действию нагрузок не разрушаясь (ответ: прочность).
11. Как называется напряжение, действующее по площади поперечного сечения (ответ: касательное).
12. Как называется момент, являющийся внутренним силовым фактором (ответ: крутящий).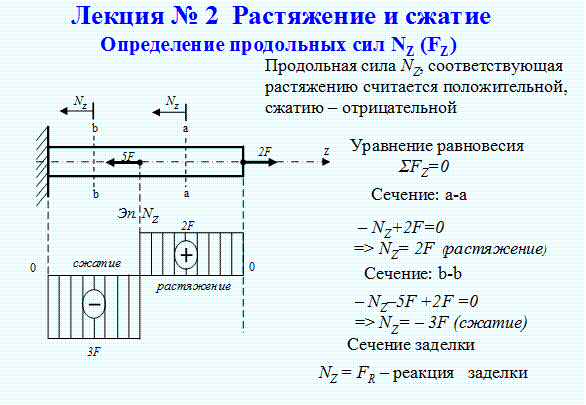
13. Деформация, при которой внутренним силовым фактором является поперечная сила (ответ: сдвиг)
14. Ученый, именем которого назван закон сопромата (ответ:Гук).
По вертикали:
Характер деформации (ответ: срез).
Знак внешней силы, если она сжимает участок бруса (ответ: минус).
Величина, определяемая проектным расчетом вала (ответ: диаметр).
Знак внешней силы, если она растягивает участок бруса (ответ: плюс).
Диаграмма или график изменения внутреннего силового фактора по длине бруса (ответ: эпюра).
Способность материала давать большие остаточные деформации (ответ: пластичность).
Способность материала восстанавливать свою форму и размеры после снятия нагрузки (ответ: упругость).
Деформация, внутренним силовым фактором которой является момент (ответ: кручение).
Способность тела не давать больших деформаций (ответ: жесткость).
10. Деформация, внутренним силовым фактором которой является продольная сила (ответ: растяжение).
11. Величина, равная произведению силы на плечо (ответ: момент).
12. Ученый, показавший зависимость между продольной и поперечной деформациями (ответ:Пуассон).
13. Что вызывает деформацию (ответ: нагрузка).
Деформация, внутренними соловыми факторами которой являются Мх, Мy (ответ: изгиб).
1р
а
1с
ч
е
т
2р
о
з
у
3д
е
ф
о
р
2м
а
ц
и
я
и
з
и
5э
а
н
п
м
у
6п
ю
е
4п
а
с
к
а
л
ь
6т
в
е
р
д
о
с
т
ь
л
а
8к
а
р
5ю
н
г
с
9р
а
з
м
е
р
с
т
у
и
ч
ч
7у
е
7н
а
п
р
я
9ж
е
н
и
е
о
р
е
и
с
у
с
е
т
г
т
8н
о
12р
м
а
л
ь
н
о
е
к
а
с
о
с
11м
т
с
т
о
ь
т
я
м
ь
ж
е
е
н
10п
р
о
ч
н
о
с
т
ь
11к
р
у
т
я
щ
и
й
а
е
с
12к
а
с
а
т
е
л
ь
13н
о
е
о
а
н
13с
д
в
14и
г
з
р
14г
у
к
и
з
б
к
а
Приложение В
Приложение Г
Закрепление материала в форме решения типовых задач.
Задача 1. Ступенчатый брус нагружен вдоль оси двумя силами. Брус защемлен с левой стороны (рис. 20.6). Пренебрегая весом бруса, построить эпюры продольных сил и нормальных напряжений.
Решение
Определяем участки нагружения, их два.
Определяем продольную силу в сечениях 1 и 2.
Строим эпюру.
Рассчитываем величины нормальных напряжений и строим эпюру нормальных напряжений в собственном произвольном масштабе.
Определяем продольные силы.
В обоих сечениях продольные силы положительны.
Определяем нормальные напряжения
Сопоставляя участки нагружения с границами изменения площади, видим, что образуется 4 участка напряжений.
Нормальные напряжения в сечениях по участкам:
Откладываем значения напряжений вверх от оси, т. к. значения их положительные (растяжение). Масштаб эпюр продольной силы и нормальных напряжений выбирается отдельно в зависимости от порядка цифр и имеющегося на листе места.
Задача 2. Определить диаметры стержней, если [s] = 160 МПа
Решение:
Определим сосредоточенную силу
Q = q ∙ 5 = 20 ∙ 5 =100 кН
Составим уравнения равновесия
Fy=0; Nz1 — F — Q+ Nz2 =0;
mc = 0; F∙3 – Nz2 ∙ 5 + Q∙ 2,5= 0.
Из полученных уравнений выразим Nz1 и Nz2
Nz1 = F + Q- Nz2 Nz1 = 100 +100 – 110 = 90 кН.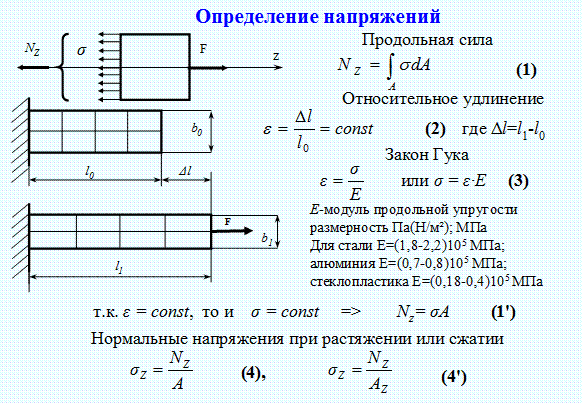
Определим диаметры поперечного сечения стержней
Приложение Д
Тестовые задания
№1
вопросаВопрос
№ ответа
Ответ
1.
Какая эпюра сил будет верна для данного бруса?
1.
2.
3.
4.
5.
2.
Какая эпюра напряжений будет верна для данного бруса?
1.
2.
3.
4.
5.
3.
Какая эпюра перемещений верна для данного бруса?
1.
2.
3.
4.
5.
4.
Расчет на прочность при растяжении-сжатии.
1.
2.
3.
4.
5.
σ = Nz/A ≤ [σ]
σ = εE
ε = Δl / l
Δl = Fl / EA
σ = F/A ≥ [σ]
5.
Зависимость, выведенная Пуансоном
1.
2.
3.
4.
5.
ε =Δа/а
σ = εE
ε = Δl / l
ε = με
Δl = Fl / EA
№ 2
вопросаВопрос
№ ответа
Ответ
1.
Какая эпюра сил будет верна для данного бруса?
1.
2.
3.
4.
5.
2.
Какая эпюра напряжений будет верна для данного бруса?
1.
2.
3.
4.
5.
3.
Какая эпюра верна для данного бруса?
1.
2.
3.
4.
5.
4.
Какое напряжение возникает при одноосном растяжении в плоскости, перпендикулярной оси тела?
1.
2.
3.
4.
5.
Нормальное, касательное
Никакое.
Касательное.
Нормальное.
Максимальное касательное.
5.
Закон Гука для растяжения-сжатия.
1.
2.
3.
4.
5.
Δl = Fl / EA
σ = εE
ε = με
Δl = l1 – l0
σ = F/A
№ 3
вопросаВопрос
№ ответа
Ответ
1.
Какая из эпюр сил верна для данного бруса?
1.
2.
3.
4.
5.
2.
Какая из эпюр напряжений верна для данного бруса?
1.
2.
3.
4.
5.
3.
Какая эпюра перемещений верна для данного бруса?
1.
2.
3.
4.
5.
4.
Какое напряжение возникает при одноосном растяжении в плоскости, перпендикулярной оси тела?
1.
2.
3.
4.
5.
Касательное и нормальное.
Максимальное касательное.
Нормальное.
Касательное.
Никаких.
5.
Следствие из закона Гука.
1.
2.
3.
4.
5
Δl = Nzl / EA
σ = εE
ε = με
Δl = l1 – l0
σ = Nz/A
№ 4
ВопросаВопрос
№ ответа
Ответ
1.
Какая из эпюр сил верна для данного бруса?
1.
2.
3.
4.
5.
2.
Какая из эпюр напряжений верна для данного бруса?
1.
2.
3.
4.
5.
3.
Какая из эпюр перемещений верна для данного бруса?
1.
2.
3.
4.
5.
4.
Относительная деформация бруса это:
1
2.
3.
4.
5.
Разность между конечной и начальной длиной.
Отношение абсолютной деформации к первоначальной длине
Δl = Nzl / EA
σ = F/A
.
Отношение продольной силы к площади поперечного сечения.
5.
Закон Гука выражает зависимость между:
1.
2.
3.
4.
5.
Δl =Nzl / EA
ε = με
σ = εE
Δl = l1 – l0
σ = Nz/A
№5
вопросаВопрос
№ответа
Ответ
1.
Какая из эпюр сил верна для данного бруса?
1.
2.
3.
4.
5.
2.
Какая из эпюр напряжений верна для данного бруса?
1.
2.
3.
4.
5.
3.
Какая из эпюр перемещений верна для данного бруса?
1.
2.
3.
4.
5.
4.
Какое сечение является опасным для бруса переменного сечения?
1.
2.
3.
4.
5.
Где нормальные напряжения максимальны.
Где изменяется размер сечения.
Где приложена максимальная внешняя сила.
Где продольная сила максимальна.
Где приложены внешние силы.
5.
Какие напряжения называются предельными для пластичного материала?
1.
2.
3.
4.
5.
Предел пропорциональности.
Предел прочности.
Допускаемые напряжения.
Предел упругости.
Предел текучести.
№6
вопросаВопрос
№ ответа
Ответ
1.
Какая из эпюр сил верна для данного бруса?
1.
2.
3.
4.
5.
2.
Какая из эпюр напряжений верна для данного бруса?
1.
2.
3.
4.
5.
3.
Какая из эпюр перемещений верна для данного бруса?
1.
2.
3.
4.
5.
4.
Предел упругости это:
1.
2.
3.
4.
5.
Напряжение, при котором остаточные деформации очень малы.
Напряжение, при котором соблюдается закон Гука.
Напряжение, при котором возникают остаточные деформации.
Напряжение, при котором в образце появляются линии Чернова.
Напряжение, соответствующее допускаемым напряжениям.
5.
Размерность модуля упругости первого рода в системе единиц СИ
1.
2.
3.
4.
5.
Нет размерности.
кг
кг/см2
н/мм2 (МПА)
см2
№7
вопросаВопрос
№ ответа
Ответ
1.
Какая эпюра сил будет верна для данного бруса?
1.
2.
3.
4.
5.
2.
Какая эпюра напряжений будет верна для данного бруса?
1.
2.
3.
4.
5.
3.
Какая эпюра перемещений будет верна для данного бруса?
1.
2.
3.
4.
5.
4.
Размерность коэффициента Пуассона.
1
2.
3.
4.
5.
Н/мм2
кг/см2
мм
нет
Н
5.
Нормальное напряжение при растяжении – сжатии это:
1.
2.
3.
4.
5.
Произведение площади сечения на модуль упругости.
Внутренняя продольная сила, деленная на площадь поперечного сечения.
Внешняя сила, деленная на площадь поперечного сечения.
Внутренняя поперечная сила, деленная на площадь сечения.
Алгебраическая сумма всех внешний сил, приложенных по одну сторону от поперечного сечения.
№ 8
вопросаВопрос
№ ответа
Ответ
1.
Какая из эпюр сил верна для данного бруса?
1.
2.
3.
4.
5.
2.
Какая из эпюр напряжений верна для данного бруса?
1.
2.
3.
4.
5.
3.
Какая из эпюр перемещений верна для данного бруса?
1.
2.
3.
4.
5.
4.
В каких сечениях бруса на эпюре продольных сил имеются скачки?
1
2.
3.
4.
5.
Эпюра не имеет скачков.
В сечениях, где изменяются размеры бруса.
В сечениях, где приложены наибольшие по величине силы.
В сечениях, где приложены внешние силы и изменяются размеры бруса.
В сечениях, где приложены внешние силы.
5.
Какое сечение является опасным для ступенчатого бруса?
1.
2.
3.
4.
5.
Где нормальные напряжения максимальны.
Где изменяется размер сечения.
Где приложена максимальная внешняя сила.
Где продольная сила максимальна.
Где приложены внешние силы.
№ 9
вопросаВопрос
№ ответа
Ответ
1.
Какая из эпюр сил верна для данного бруса?
1.
2.
3.
4.
5.
2.
Какая из эпюр напряжений верна для данного бруса?
1.
2.
3.
4.
5.
3.
Какая из эпюр перемещений верна для данного бруса?
1.
2.
3.
4.
5.
4.
Размерность модуля упругости первого рода в технической системе единиц.
1.
2.
3.
4.
5.
Нет размерности.
Кг
Кг/см2
Н/мм2
см2
5.
Расчет на прочность при растяжении – сжатии.
1.
2.
3.
4.
5.
σ = Nz/A ≤ [σ]
σ = εE
ε = Δl / l
Δl = Fl / EA
σ = Nz/A ≥ [σ]
№ 10
вопросаВопрос
№ ответа
Ответ
1.
Какая из эпюр сил верна для данного бруса?
1.
2.
3.
4.
5.
2.
Какая из эпюр напряжений верна для данного бруса?
1.
2.
3.
4.
5.
3.
Какая из эпюр перемещений верна для данного бруса?
1.
2.
3.
4.
5.
4.
Чему равен скачок на эпюре продольных сил?
1
2.
3.
4.
5.
Алгебраической сумме сил.
Алгебраической сумме сил, действующих по одну сторону от сечения.
Геометрической сумме сил.
Сумме всех внешних сил
Величине силы в данном сечении.
5.
Как определить реакцию заделки?
1.
2.
3.
4.
5.
Величиной скачка.
Величиной продольной силы в месте закрепления бруса.
Величиной максимальной продольной силы.
Суммой внешних сил.
Алгебраической суммой внутренних сил.
№11
вопросаВопрос
№ ответа
Ответ
1.
Какая из эпюр продольных сил верна для данного бруса?
1.
2.
3.
4.
5.
2.
Какая эпюра напряжений верна для данного бруса?
1.
2.
3.
4.
5.
3.
Определить реакцию заделки.
1.
2.
3.
4.
5.
F = 5 кН
F = 16 кН
F = 21 кН
F = 18 кН
F = 41 кН
4.
Какое сечение является опасным для бруса переменного сечения?
1.
2.
3.
4.
5.
Где приложены внешние силы.
Где изменяется размер сечения.
Где продольная сила максимальна.
где максимальна внешняя сила.
Где нормальные напряжения максимальны.
5.
Как определяется нормальное напряжение при растяжении-сжатии?
1
2.
3.
4.
5.
σ = F/A
σ = εE
ε = Δl / l
Δl = Fl / EA
σ =Nz /A
№12
вопросаВопрос
№ ответа
Ответ
1.
Какая эпюра сил будет верна для данного бруса?
1.
2.
3.
4.
5.
2.
Какая эпюра напряжений будет верна для данного бруса?
1.
2.
3.
4.
5.
3.
Какая эпюра перемещений верна для данного бруса?
1.
2.
3.
4.
5.
4.
Какое напряжение возникает при одноосном растяжении в плоскости, перпендикулярной оси тела?
1.
2.
3.
4.
5.
Нормальное, касательное
Никакое.
Касательное.
Нормальное.
Максимальное касательное.
5.
Какие напряжения называются предельными для пластичного материала?
1.
2.
3.
4.
5.
Предел пропорциональности.
Предел прочности.
Допускаемые напряжения.
Предел упругости.
Предел текучести.
Ключ ответа на тесты
- карточки
1
2
3
4
5
1
2
5
3
1
4
2
3
2
4
4
2
3
2
4
3
3
1
4
1
5
4
2
3
5
3
1
2
1
5
6
4
4
1
1
4
7
3
1 (3)
3
4
2
8
5
4
2
5
1
9
2
3
4
3
1
10
4
2
2
5
2
11
1
3
3
5
5
12
3
2
5
3
5
Приложение Е
Приложение Ж.
Самоанализ работы на занятии.
- 1. На занятии я работал
2. Своей работой на занятии я
3. Занятие для меня показалось
4. На занятии я
5. Мое настроение
6. Материал занятия мне был
7. Домашнее задание мне кажетсяактивно / пассивно
доволен / не доволен
коротким / длинным
не устал / устал
стало лучше / стало хуже
понятен / не понятен
полезен / бесполезен
интересен / скучен
легким / трудным
интересно / не интересно
Как определить удлинение (укорочение) стержня (бруса) ?
В данной статье будем разбираться, как определить удлинение или укорочение стержня (бруса) под действием внешней нагрузки. Будем разбираться сразу на примерах.
Пример расчета удлинения бруса
Возьмем брус круглого и постоянного поперечного сечения, который нагружен растягивающей силой.При таком раскладе, очевидно, что брус удлинится на какую-то величину дельта.Как ее найти? Вычислить удлинение можно по формуле:В формуле есть уже знакомая вам буква N – продольная сила, l – длина недеформированного бруса, то есть до действия внешней нагрузки, E – модуль упругости и A – площадь поперечного сечения. Если проанализировать формулу, то можно сделать вывод, что, по сути, по ней площадь эпюры продольных сил делится на произведение модуля упругости и площади поперечного сечения.
Вернемся к нашему примеру. Слегка модифицируем формулу, подставив исходные данные и площадь поперечного сечения – круга. Вот что получим:Вот так просто можно найти удлинение или укорочения брусьев.
А что делать, если, например брус ступенчатый или на него действуют несколько внешних сил? В этом случае обязательно строится эпюра продольных сил, разбивается на кусочки, так чтобы на этих кусочках внутренняя сила была одна, вычисляются уже относительные удлинения (укорочения) по вышеприведенной формуле для этих кусочков и результат складывают.
Посмотрим эту технику на примере двухступенчатого бруса загруженного парой сил. Найдем перемещение свободного торца бруса. Как и обговаривалось ранее, сначала строим эпюру внутренних усилий:Дальше эпюру бьем на два участка и вычисляем относительные перемещения с учетом знака продольной силы. Потом складываем эти два значения.Так как в итоге получили положительное значение, то значит, что брус удлинился, если бы получили отрицательное значение, то соответственно это значило, что он укоротился.
На практике на стержни помимо сосредоточенных сил могут действовать и распределенные нагрузки. Как быть в таком случае? Ответ нам даст эпюра продольной силы. Рассмотрим стержень, загруженный только распределенной нагрузкой, построим для него эпюру. Как видно, эпюрой продольных сил от распределенной нагрузки является прямоугольной треугольник. Что есть равно половина от прямоугольника. Тогда вычисляя перемещение, выражение нужно дополнительно помножить на ½. Вот и все, постарался рассмотреть все возможные случаи, спасибо, что прочел эту статью.
Подбор сечений с учётом собственного веса (при растяжении и сжатии)
Содержание:
Подбор сечений с учётом собственного веса (при растяжении и сжатии)
- Подбор секций с учетом собственного веса (при растяжении и сжатии). Установление внешних сил и удлинение или сжатие конструктивных элементов, которые до сих пор игнорируются в их собственном весе. Возникает вопрос, не слишком ли сильно это упрощение расчетов Фигура. 60. B(х) TR. б) Допустимая погрешность?
В связи с этим величины напряжений и деформаций рассчитываются с учетом влияния мертвого веса растянутого или сжатого стержня. Вертикальный стержень(рис. Длина стержня/, площадь поперечного сечения F, удельный вес и модуль упругости материала 7 E. Рассчитаем напряжение участка AB, который расположен на расстоянии x от свободного конца стержня.
Отрежьте верхнюю часть стержня и выберите нижнюю часть длины x с помощью Людмила Фирмаль
внешней силы(рис. 60, б) — нагрузка P и собственный вес yFx. Эти две силы уравновешиваются напряжением, действующим на область AB от отброшенной части. Эти напряжения являются нормальными, равномерно распределенными в поперечном сечении и направленными наружу от рассматриваемой части стержня. — F—x — = — PP+, IX ’ (6.1)§ 29]
подраздел 103 с учетом веса пространства Поэтому, учитывая его собственный вес, обычные напряжения не равны во всех сечениях. Наиболее интенсивным и опасным будет участок выше, где x достигает наибольшего значения Z. Следовательно, требуемая площадь стержня равна ч——р-н °т(6.2) Сила условия должна соответствовать этому разделу: Шах-4 ″ yzj[a]. (6.3)) (6.4) От формулы
- определения площади вытянутого стержня без учета влияния его собственного веса эта формула отличается только тем, что значение yZ вычитается из допустимого напряжения. Чтобы оценить величину этой поправки, рассчитаем ее для двух случаев. Возьмите для него стержень из мягкой стали длиной 10 м[а]=1400кг] см \ значение yZ=7,85 • 10’3 • 103 = 7,85 кг / см*. Так, для стержней из мягкой стали коррекция составит 7 85 pIqq, т. е. около 0,6%. Теперь высоту
кирпичного столба также возьмем 10W; для него[a] = 12kg) cm\value yZ= 1,8 • 10″3 • 103 = = 1,8 кг! см * таким образом, для кирпичных столбов, исправлено 1. Восемь Это будет уже 15%. Если вы имеете дело не с длинными стержнями или стержнями из материала с достаточным весом и относительно небольшой прочностью (камень, кирпич), то необходимо рассчитать длину каната, различные типы длинных стержней и высокие каменные конструкции (башни маяков, фермы мостов), расчет конструкции и ввод в нее собственного веса.
В таких случаях возникает вопрос Людмила Фирмаль
о правильной форме стержня. При выборе поперечного сечения стержня(рис. 60) согласно формуле (6.4), дающей одинаковую площадь поперечного сечения по всей длине, материал стержня используется реже. Поэтому желательно спроектировать размеры стержня так, чтобы при всем его поперечном сечении (перпендикулярном оси) вертикальное напряжение было постоянным.104 фискальная [глава] для собственного веса растяжения и сжатия. ВИ Такой стержень называется стержнем сопротивления, равного растяжению или сжатию. Если при этом напряжение равно допустимому напряжению, то берем и берем Г Ф(Х)\ф(х)+ДФ(х) Фигура.5 Стержень получает криволинейный контур(рис. 61), что усложняет и удорожает работу. Поэтому обычно такой конструкции придается лишь приблизительная форма равных по сопротивлению стержней, например, в виде усеченной пирамиды с плоской поверхностью. Приведенные выше расчеты являются приблизительными. Предполагается, что только нормальное напряжение передается по всему поперечному сечению стержней изосориса. В случае длинного каната или растянутого стержня форма стержня равного сопротивления также выполняется приблизительно путем деления стержня по длине на несколько секций. 62) — получается так называемый ступенчатый стержень. FIF подходит для решения области.. . В выбранной длине он становится следующим. Поперечное сечение первого нижнего сечения соответствует формуле (6.4),
которая равна F-P 1-1 ’-74 1′ Для того чтобы получить площадь поперечного сечения второй секции, необходимо нагрузить ее внешней силой Р и весом первой секции fa n_P+lF. х Н-Т4′ В третьей секции веса первой и второй секций добавляются к внешним силам. Для других сайтов, которые прибыли таким же образом. Рассмотрим численные примеры для сравнения рентабельности использования стержней одинакового сопротивления, ступенчатого и фиксированного сечения. Пример 15. Высота опоры L=42 ндриложенной силой Р=400 г I подвергается сжатию в центре; кладка 2,2 т / м \ допустимо принять насыпной вес при напряжении сжатия 12 кг! Опора
постоянного сечения, опора из трех призматических частей одинаковой длины, опора одинакового сопротивления сжатию.106 учет собственного веса натяжения и сжатия[гл. ВИ Расчет производится в тоннах и метрах. В первом случае площадь поперечного сечения Громкость есть Р400 B1-Lu120-42-2,2 14.5 м \ V=F h=]£• 4 2 6 1 0 м. В последнем случае площадь поперечного сечения верхней части составляет 400 120-14-2, 2 =4,48 м. Площадь поперечного сечения второго поперечного сечения равна p+1F1. 4 0 0 + 2,2 • 4,48 • 14.. ч~120-14. 2, 2 и 3-7 =6,04 м». Площадь поперечного сечения в третьем сечении составляет±3+l F»-3^400-f-2,2•4,48.4 0 0 — S_120 =3,33 м*. Площадь нижней секции Т_Л2, 2. Сорок два Fh=Foe1 ″ =3. 33e120=3. 33E0-77=7,15 м». Вес опоры с равным сопротивлением G определяется из условий И так оно и есть. Р+Г=нет. С=[а]ГЛ-Р= 1 2 0 • 7,15 — 400 = 460 г Объем поддержки выглядит следующим образом =209M8, Она меньше объема ступенчатой опоры на 20% и примерно в три раза меньше опоры неподвижного сечения.
Смотрите также:
Основные типы расчетов на прочность — КиберПедия
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Методические указания для самостоятельной
работы студентов
Красноярск 2011
ОГЛАВЛЕНИЕ
Введение……………………………………………………………………………..4
1. Растяжение-сжатие……………………………………………………………….5
Задача 1. Расчёт статически определимой стержневой системы
при растяжение (сжатии)…………………………………………….…6
Задача 2. Расчёт статически определимого ступенчатого бруса
при растяжение (сжатие)………………………………………………14
Задача 3. Расчёт статически неопределимого ступенчатого бруса
при растяжение (сжатие)…………………………….…………………20
2. Плоский изгиб…………………………………………………………………27
Задача 4. Плоский изгиб балки………………………………………………….28
3. Кручение вала ………………………………………………………………….34
Задача 5. Кручение вала……………………………………………………….…34
Введение
Современная действительность требует ускорения научно-технического прогресса, повышения конкурентоспособности выпускаемой продукции, снижения материалоемкости конструкции, повышения производительности, долговечности, надежности машин. Исключительная роль в обеспечении этого процесса принадлежит инженерам, конструкторам, машиностроителям. Значительная роль в формировании облика инженеров широкого профиля отводится дисциплинам общеинженерного цикла и, в частности, дисциплине «Сопротивление материалов». Создавая новую конструкцию, инженер назначает первоначальные размеры ее элементов, проводя прочностные расчеты методами сопротивления материалов. Дальнейший расчет конструкций, как правило, производится с помощью ЭВМ численными методами с использованием пакетов прикладных программ. Однако для анализа достоверности получаемых результатов используется сравнение с результатами расчетов по упрощенным моделям методами сопротивления материалов.
В решении задачи по ускорению развития агропромышленного комплекса страны важная роль принадлежит науке о прочности материалов и конструкций, назначение которой – повысить качество расчета и проектирования, дать теоретическую основу для разработки новых эффективных материалов и конструкций и тем самым способствовать повышению эффективности качества, надежности и экономичности сооружений конструкций машин и приборов.
Цель курса «Сопротивление материалов» — выработка у студента умения производить расчеты на прочность, жесткость и устойчивость элементов инженерных конструкций, применяемых в агропромышленном комплексе, подготовить его к правильному выбору методов расчета и проектирования, с целью обеспечения надежности, экономичности и снижения материалоемкости этих конструкций.
У студентов, изучающих курс «Сопротивление материалов», наибольшие трудности обычно возникают при решении задач. Настоящее методическое указание призвано облегчить процесс изучения данного курса, а главное помочь овладеть методикой решения задач и получить необходимый навык в их решении.
Методическое указание содержит материал, относящийся к разделам: растяжение-сжатие, плоский поперечный изгиб, кручение вала.
В данное методическое указание включены задания для самостоятельной работы студента (30 вариантов задач на каждую тему) и примеры решения типовых задач.
Номер схемы определяется по сумме двух последних цифр шифра зачётной книжки, а номер варианта – по последней цифре шифра.
Растяжение-сжатие
Осевым растяжением бруса называется вид нагружения, при котором равнодействующая внешних сил прикладывается в центре тяжести поперечного сечения и действует вдоль продольной оси. В этом случае в поперечных сечениях стержня из шести внутренних силовых факторов возникает только один – продольная осевая сила N.
Для определения внутренних усилий используется метод сечений.
Сущность метода заключается в следующем:
1. Рассекают (мысленно) тело на две части плоскостью, перпендикулярной продольной оси тела (поперечным сечением).
2.Отбрасывают правую или левую часть тела. Чтобы оставшаяся часть находилась в равновесии, по плоскости сечения должны действовать внутренние силы.
3.Заменяют действие одной части на другую внутренними силами. Так как отсеченная часть тела находится в равновесии, то для определения внутренних усилий, в общем случае нагружения, составляют шесть уравнений статического равновесия:
При растяжении в поперечных сечениях стержня возникает только один внутренний силовой фактор — нормальная сила N.
Нормальная сила считается положительной, если она растягивает отсеченную часть стержня, (направлена по внешней нормали), при сжимающем действии нормальная сила считается отрицательной, что можно изобразить графически, как показано на рис.1.1.
Нормальная сила в сечении бруса является равнодействующей нормальных напряжений, действующих в плоскости поперечного сечения
Закон распределения напряжений может быть определен из эксперимента. Установлено, что если на стержень нанести прямоугольную сетку, то после приложения продольной нагрузки вид сетки не изменится, она по-прежнему останется прямоугольной, а все линии прямыми. Поэтому можно сделать вывод о равномерном по сечению распределении продольных деформаций, а на основании закона Гука () и нормальных напряжений s = const. Тогда N = s F , откуда получим формулу для определения нормальных напряжений в поперечном сечении при растяжении
.
Подставляя напряжение в закон Гука получим
От сюда .
Эта формула выражает закон Гука для абсолютных удлинений. Произведение EF называется жёсткостью поперечного сечения при растяжении и сжатии.
Полное удлинение участка длиной l получим, суммируя удлинения всех бесконечно малых участков.
При растяжение (сжатии)
Для статически определимой стержневой системы (см. схемы к задаче 1), загруженной силой Р (см. таблица 1.1) необходимо:
1. Определить продольную силу в каждом из стержней, поддерживающих жёсткий брус.
2. Подобрать размеры поперечного сечения стержней.
Стержень 1 стальной, круглого поперечного сечения. Допускаемое напряжение .
Стержень 2 деревянный, квадратного поперечного сечения. Допускаемое напряжение .
Стержень 3 дюралюминиевый, трубчатого поперечного сечения. Допускаемое напряжение . Отношение наружного и внутреннего диаметра составляет . Высоту жёсткого бруса считать малой по сравнению с размерами конструкции и в расчётах её не учитывать.
Схемы к задаче 1
Схемы к задаче 1
Схемы к задаче 1
Схемы к задаче 1
Таблица 1.1
| № варианта | Р, кН | а, м | в, м | с, м | α, град |
| 0,9 | 0,3 | ||||
| 1,5 | 0,6 | ||||
| 12,5 | 0,9 | 1,8 | 0,4 | ||
| 1,1 | 1,7 | 0,5 | |||
| 1,3 | 1,6 | 0,7 | |||
| 22,3 | 1,5 | 0,5 | |||
| 25,6 | 1,2 | 1,7 | 0,6 | ||
| 17,8 | 0,8 | 1,6 | 0,2 | ||
| 11,5 | 0,7 | 1,5 | 0,3 | ||
| 16,2 | 1,3 | 2,1 | 0,6 |
Пример решения задачи 1
Для статически определимой стержневой системы (см рис. 1.2), загруженной силой Р необходимо:
1. Определить продольную силу в каждом из стержней, поддерживающих жёсткий брус.
2. Подобрать размеры поперечного сечения стержней.
Рис. 1.2 Схема к примеру решения задачи 1
Стержень 1 стальной, круглого поперечного сечения. Допускаемое напряжение .
Стержень 2 деревянный, квадратного поперечного сечения. Допускаемое напряжение .
Стержень 3 дюралюминиевый, трубчатого поперечного сечения. Допускаемое напряжение . Отношение наружного и внутреннего диаметра составляет .
Высоту жёсткого бруса считать малой по сравнению с размерами конструкции и в расчётах её не учитывать.
Р=2кН; а=2м; в=2,5; с=0,5м; α=300.
Решение
Рассмотрим равновесие жёсткого бруса (рис.1.2). Для освобождения бруса от связей мысленно рассечем стержни и заменим связи их реакциями , и . Внутренние усилия, возникающие в стержнях, определим, составив уравнения равновесия.
Из рис.1.2 не трудно заметить, что угол наклона стержня 1 и стержня 3 к оси х одинаков. Обозначим этот угол через α.
Уравнение проекций всех сил на ось х:
. (1.1)
Рис. 1.3 Расчётная схемак примеру решения задачи 1
Уравнение проекций всех сил на ось у:
. (1.2)
Сумма моментов всех сил относительно точки О:
. (1.3)
Определим cosα и sinα.
Решая систему трёх уравнений найдём усилия в стержнях.
Из уравнения (1.3) определяем усилие в первом стержне N1:
.
Из уравнения (1.1) определяем усилие в третьем стержне N3:
.
Из уравнения (1.2) определяем усилие во втором стержне N2:
Получили усилия в стержнях одинаковые. Что бы убедиться в правильности наших вычислений сделаем проверку. Составим проверочное уравнения – сумма моментов от всех сил относительно точки А:
Размеры поперечных сечений определяют из условия прочности при растяжении-сжатии:
.
Несмотря на то, что усилия в стержнях получились одинаковые, размеры поперечных сечений будут отличаться, так как они выполнены из различных материалов, с разными допускаемыми напряжениями.
1 стержень стальной круглого поперечного сечения. Определим из условия прочности диаметр поперечного сечения стержня:
.
2 стержень деревянный квадратного поперечного сечения. Определим сторону квадрата поперечного сечения:
.
3 стержень дюралюминиевый трубчатого поперечного сечения. Определим внешний и внутренний диаметры поперечного сечения:
D=1,2d=86,9мм
При растяжение (сжатие)
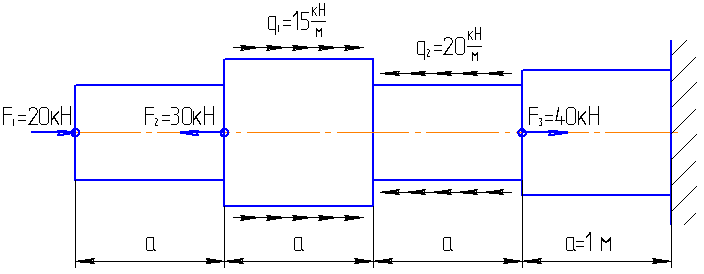
Для статически определимого ступенчатого бруса с жёстко защемлённым концом (см. схемы к задаче 2), нагруженного продольными усилиями Р1 ,Р2 , q1и q2 (см. таб. 1.2), необходимо:
1. Построить эпюры продольных сил N, нормальных напряжений s и перемещений .
2. Подобрать величину площади поперечных сечений для всех участков бруса из условия прочности по допускаемым нормальным напряжениям при растяжении и сжатии.
Таблица 1.2
| № | Р1, кН | Р2, кН | q1, кН/м | q2, кН/м |
| 10 | 80 | 10 | 70 | |
| 20 | 70 | 15 | 80 | |
| 30 | 60 | 20 | 90 | |
| 40 | 50 | 25 | 60 | |
| 50 | 40 | 30 | 50 | |
| 60 | 30 | 35 | 40 | |
| 70 | 10 | 40 | 30 | |
| 80 | 20 | 45 | 20 | |
| 10 | 50 | 55 | 50 | |
| 20 | 70 | 65 | 20 |
Принять для всех вариантов следующие соотношения: , , Е=105МПа, а=1м.
Схемы к задаче 2
Схемы к задаче 2
Схемы к задаче 2
Пример решения задачи 2
Для ступенчатого бруса (см. рис.1.4,а) с жёстко защемлённым концом необходимо:
1. Построить эпюры продольных сил N, нормальных напряжений s и перемещений .
2. Подобрать величину площади поперечных сечений всех участков бруса из условия прочности по нормальным напряжениям, используя следующие числовые значения:
Р1=30 кН; Р2=20 кН; q2=20 кН/м; а=1м; ; ; Е=1,8×105МПа; F1=F; F2=2F; F3=3F.
Решение
1. Брус состоит из трёх участков. Границами участков являются сечения, к которым приложены внешние силы, или сечения, где изменяются размеры поперечных сечений.
Величину внутренних продольных усилий определим, используя метод сечений. При этом рассматриваем всё время правую отсечённую часть бруса.
Продольную силу N считаем положительной, если нагрузка, её создающая, вызывает растяжение рассматриваемого участка, т.е. направлена от рассматриваемого сечения. Нагрузка, вызывающая сжатие рассматриваемой части бруса, т.е. направленная к сечению, создаёт отрицательную продольную силу. В соответствии с расчётной схемой (рис. 2.1,а) аналитические зависимости для N будут иметь следующий вид:
тогда
.
После подстановки численных значений, получим:
.
На основании полученных значений строим эпюру продольных сил (рис.2.1,б).
Рис. 1.4 Схема нагружения и эпюры N, σ и Δl для ступенчатого
статически определимого бруса
2. Эпюру нормальных напряжений s получим, разделив значения продольной силы N на соответствующие площади поперечных сечений бруса (рис. 1.4,в). Знак продольной силы N определяет и знак соответствующего нормального напряжения s.
, подставляя 2 крайних значения х2 будем иметь:
3. Из условия прочности по нормальным наибольшим напряжениям растяжения и сжатия определим параметр F, а затем площади поперечных сечений каждого участка бруса.
Из условия прочности по растягивающим нормальным напряжениям находим:
,
отсюда .
Из условия прочности по сжимающим нормальным напряжениям находим:
,
отсюда .
Окончательно выбираем параметр F=250мм2.
Определим площади поперечных сечений каждого участка:
F1=F=250мм2, F2=2F=500мм2, F3=3F=750мм2.
3. Зная площади поперечных сечений можно построить эпюру перемещений (рис.1.4, г). Проще расчёт перемещений вести от заделки, т.е. за точку отсчёта брать сечение, перемещение которого равно 0.
Т.к. уравнение для перемещения на втором участке содержит квадратичную функцию, то графиком функции перемещения на втором участке будет являться парабола, причём в сечении, где парабола будет иметь экстремум. Приравняв уравнение для продольной силы к 0, получим расстояние до этого сечения.
где — расстояние до сечения, в котором .
Подставляя, полученное значение для , получим значение экстремума на параболе:
По найденным значениям строим эпюру перемещений (рис.1.4, г).
При растяжение (сжатие)
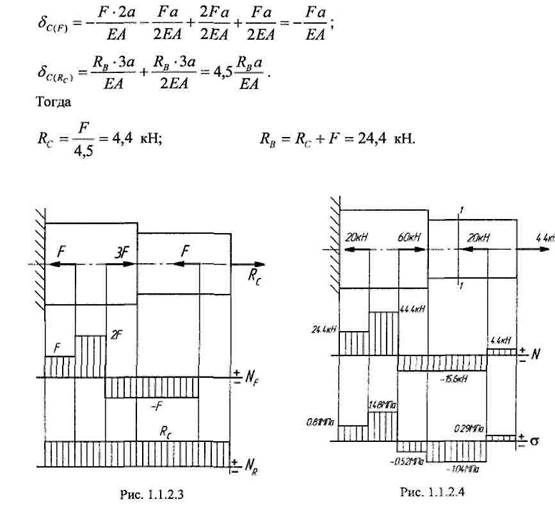
Для статически неопределимого бруса с жёстко защемлёнными концами, нагруженного продольной нагрузкой как показано на схеме к задаче 3 необходимо:
1. Построить эпюры продольных сил N, нормальных напряжений и перемещений ;
2. Подобрать величину площади поперечных сечений всех участков бруса методом допускаемых нагрузок,
Необходимые данные для решения задачи взять из таблицы 1.3.
Схемы к задаче 3
Схемы к задаче 3
Схемы к задаче 3
Таблица 1.3
| Вариант | Усилия | Длины участков | |||
| Р, кН | q,кН/м | l1, м | l2, м | l3, м | |
| 27 | 12 | 2 | 0,5 | ||
| 35 | 24 | 1,2 | 1,9 | 0,8 | |
| 53 | 46 | 1,3 | 1,8 | 1 | |
| 29 | 10 | 1,4 | 1,7 | 1,1 | |
| 37 | 22 | 1,5 | 1,2 | 1,2 | |
| 45 | 32 | 1,6 | 1,4 | 2 | |
| 10 | 30 | 1,7 | 1 | 1,8 | |
| 15 | 18 | 1,8 | 1,1 | 1,5 | |
| 25 | 20 | 1,9 | 1,2 | 1,2 | |
| 50 | 44 | 2 | 0,8 | 1 |
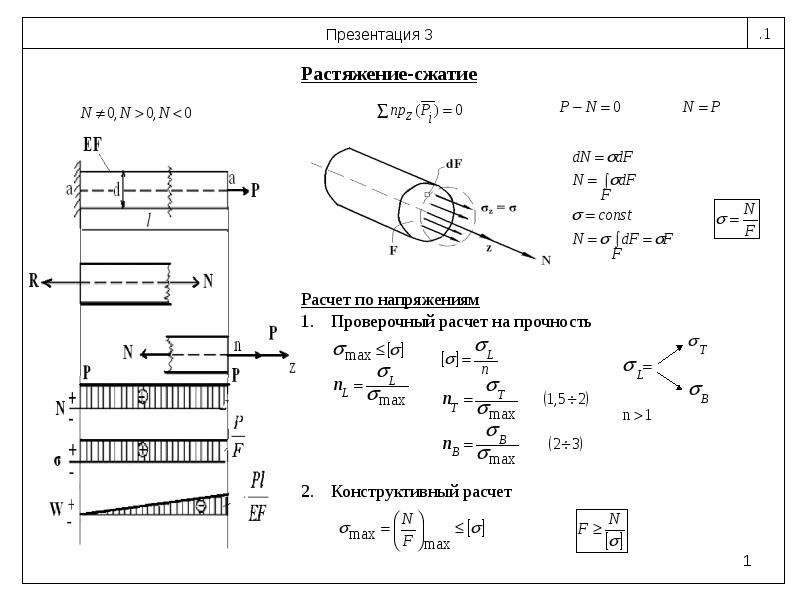
Пример решения задачи 3
Для ступенчатого бруса (см. рис. 1.5а) построить эпюры продольных сил N, нормальных напряжений и перемещений ; подобрать величину площади поперечных сечений всех участков бруса методом допускаемых нагрузок если Р1=3Р; Р2=2Р.
Решение
Задача один раз статически неопределима в силу плоской системы сил, действующих по одной прямой, для которой как известно можно составить только одно уравнение равновесия:
,
в котором два неизвестных: и .
Отбросим правую опору, заменив её действие на брус реакцией .
Перемещение сечения в точке В равно нулю, т.к. это сечение жёстко заделано. Используя принцип независимости действия сил, получим уравнение совместности деформаций:
Распишем эти деформации по закону Гука:
,
отсюда, после сокращения на а и EF, кН.
Рис. 1.5 Расчётная схема и эпюры для примера решения задачи 3
В соответствии с расчётной схемой рис. 1.5б аналитические зависимости N, и будут следующими:
Участок 1
кН ; ; .
Подставим в уравнение для перемещения два крайних значения , после подстановки будем иметь:
.
Участок 2
кН; ; .
Подставляя пределы получим:
.
Участок 3
кН; ; .
Подставляя пределы получим:
.
На основании данных аналитических зависимостей строим эпюры N, и (рис. 1.5 в, г,д).
Построение эпюры перемещений может служить проверкой правильности решения задачи. Перемещение на участке 1 при z1=0 равно нулю, перемещение на участке 3 при z=a также должно равняться нулю, т.к. эти два сечения соответствуют жёсткому закреплению бруса, перемещения которых невозможны.
2. На эпюре нормальных напряжений найдём максимальное напряжение: .
Для определения площади поперечного сечения воспользуемся условием прочности по нормальным напряжениям:
.
Приравняв максимальное нормальное напряжение к допускаемому, определим площадь поперечного сечения F:
.
Таким образом, на участке 1 площадь поперечного сечения должна быть , а на участке 2 в два раза больше, т.е. .
Плоский изгиб
Изгиб называется плоским, если плоскость действия изгибающей нагрузки проходит через главную центральную ось инерции сечения.
Если изгибающий момент Mx является единственным внутренним силовым фактором, то такой изгиб называется чистым. При наличии поперечной силы изгиб называется поперечным.
Брус, работающий при изгибе, называется балкой.
Построение эпюр поперечной силы Qyи изгибающего момента Mx является одним из основных этапов при расчете конструкций на изгиб. По эпюрам Qy и Mx определяется опасное сечение, т.е. сечение в котором может произойти разрушение.
Опасным сечением называется сечение, в котором изгибающий момент достигает наибольшего по модулю значения .
В некоторых случаях опасным сечением может быть также сечение, где наибольшего значения достигает поперечная сила .
Между поперечной силой и изгибающим моментом существует следующая зависимость:
,
то есть первая производная от изгибающего момента по длине участка равна поперечной силе.
Это соотношение в общем виде было получено Журавским и носит название теоремы Журавского.
На основании теоремы Журавского могу быть сформулированы правила проверки эпюр:
1. В точке приложения сосредоточенной силы на эпюре Qy должен быть скачок, равный по величине и знаку приложенной силе.
2. В точке приложения сосредоточенного момента на эпюре Mxдолжен быть скачок, равный по величине и по знаку приложенному моменту.
3. На участке, где приложена распределенная нагрузка, эпюра Qy является наклонной прямой (наклон по направлению действия нагрузки), а эпюра Mx — параболой, выпуклость которой направлена навстречу распределенной нагрузке.
4. На участках, где Qy > 0, Mx возрастает, на участках, где Qy< 0, Mx убывает, если Qy = 0 (эпюра пересекает нулевую линию), то эпюра Мx имеет экстремум.
5. В тех точках, где на эпюре Qy имеется скачок, на эпюре Мx будет излом.
6. Чем больше по модулю величина Qy , тем круче изменяется эпюра Мx.
7. На свободных концах балки изгибающий момент равен нулю.
Максимальное нормальное напряжение в балке возникает в сечении, где изгибающий момент достигает наибольшей по модулю величины, то есть в опасном сечении
.
Условие прочности при изгибе формулируется следующим образом: Балка будет прочной, если максимальные нормальные напряжения не превысят допускаемых напряжений
Схемы к задаче 4
Схемы к задаче 4
Пример решения задачи 4
Для балки работающей на изгиб (рис. 2.1,а) необходимо:
1. Определить значение поперечной силы Q и изгибающего момента М, построить соответствующие эпюры.
2. Подобрать размеры поперечного сечения балки из условия прочности по допускаемым напряжениям на изгиб для 3-ёх вариантов:
а) двутавра;
б) прямоугольного поперечного сечения со сторонами b и h при соотношении h/b=2;
в) круглого поперечного сечения.
Дано: М=10 кН×м; Р=10 кН; q1=50кН/м; а=1м; в=1м; с=1м; .
Решение
1. Опорные реакции и (рис. 2.1,б) направим вверх. На балку не действуют горизонтальные силы, поэтому на опоре А будет только вертикальная реакция. Для определения реакций опор составим 2 уравнения равновесия:
Рис. 2.1 Схема и эпюры внутренних усилий к примеру решения задачи4
;
.
Из этих уравнений определим реакции и :
; .
После подстановки численных значений получим: кН; кН.
Дополнительное уравнение можно использовать для проверки полученного результата:
;
12,5+27,5-50+10=0;
2. В поперечных сечениях балки возникают изгибающие моменты М и поперечные силы Q.
При решении задачи используем правило знаков внутренних усилий: поперечная сила Q в сечении положительна, если равнодействующая внешних сил стремится повернуть рассматриваемую часть по часовой стрелке относительно центра тяжести сечения.
Изгибающий момент М в сечении будем считать положительным, если балка изгибается таким образом, что растянутые волокна находятся в нижней части балки, а сжатые – в верней части.
Разобьём балку на 3 силовых участка. Границами участков являются сечения, к которым приложены сосредоточенные моменты и силы, а также конец и начало распределённой нагрузки.
Первый участок: .
Составим аналитические выражения для определения величины поперечной силы и момента, используя метод сечений и учитывая правило знаков.
;
Второй участок: .
Эпюрой изгибающего момента на 2-ом участке является квадратная парабола (рис.2.1,г). Поэтому для её построения надо знать координаты трёх точек: в начале, в конце участка и в точке, где эпюра имеет экстремум. Экстремум на параболе будет в том же сечении балки, в котором поперечная сила Q равна нулю. Расстояние до сечения, в котором на эпюре момента будет экстремум, обозначим через z0. Значение z0 найдём из следующего уравнения:
.
Подставим значение z0 в уравнение для и найдём экстремум на параболе.
.
Третий участок: .
По найденным значениям Q и М строим эпюры поперечной силы (рис.4,в) и изгибающего момента (рис.2.1,г).
3. Из условия прочности балки по нормальным напряжениям подберём размеры поперечного сечения балки для 3-ёх вариантов.
Опасным сечением является сечение балки, проходящее через экстремум на параболе, т.к. в этом сечении будет наибольший изгибающий момент по абсолютной величине . Из условия прочности:
для стальной балки определим :
.
а) По найденному значению подберём номер двутавра по ГОСТ 8239-72. Ближайшая величина момента сопротивления , что соответствует двутавру № 18а .
б) Для прямоугольного поперечного сечения момент сопротивления сечения имеет следующую зависимость: , при отношении h/b=2 будем иметь: , откуда высота сечения , а ширина сечения b=h/2=6,08 см .
в) Для круглого поперечного сечения момент сопротивления сечения следующий: .
Из этого выражения определим диаметр: .
Кручение вала
Кручением называется вид нагружения, при котором к брусу прикладываются внешние скручивающие моменты, а в поперечных сечениях возникает единственный внутренний силовой фактор — крутящий момент Mк.
Брусья, передающие крутящий момент называются валами.
Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала. В местах приложения внешних моментов ординаты эпюры скачкообразно изменяются на величину приложенного внешнего момента.
Условие прочности при кручении формулируется следующим образом: максимальные касательные напряжения, возникающие в опасном сечении вала, не должны превышать допускаемых напряжений и записывается в виде
.
Величина называется моментом сопротивления сечения при кручении или полярным моментом сопротивления сечения
Для сплошного круглого сечения
.
Для кольцевого сечения
, где .
Из условия прочности можно определить диаметр вала:
— для сплошного сечения
,
— для кольцевого сечения
,
Задача 5. Кручение вала
К стальному валу круглого поперечного сечения (см. схемы к задаче 5) приложены сосредоточенный момент М и распределённый момент m необходимо:
1. Составить аналитические выражения для определения внутреннего крутящего;
2. По полученным выражениям построить эпюру крутящего момента;
3. Из условия прочности по касательным напряжениям определить диаметр поперечного сечения;
4. Построить эпюру углов закручивания.
Численные значения приведены в таблице 3.1.
Схемы к задаче 5
Схемы к задаче 5
Растяжение (сжатие) — Энциклопедия по машиностроению XXL
Чему равны нормальные напряжения в поперечных сечениях бруса ппи растяжении-сжатии [c.13]Какие типы задач позволят решать условие прочности ппи осевом растяжении-сжатии бруса [c.13]
S чем заключается расчет конструкций на жесткость при осевом растяжении-сжатии [c.13]
Порядок расчета статически неопределимых систем растяжения-сжатия по допускаемым напр яжениям. [c.88]
Валы с поперечным отверстием при растяжении-сжатии [c.64]
Для определения прочности при статических нагрузках образцы испытывают на растяжение, сжатие, изгиб и кручение. Испытания на растяжение — обязательны. Прочность при статических нагрузках оценивается временным сопротивлением а и пределом текучести СГ — о — это условное напряжение, соответствующее наибольшей нагрузке, предшествующей разрушению образца — напряжение, при котором начинается пластическое течение металла. На рис, 1.4 представлен типовой образец прямоугольного сечепия для испытаний на растяжение. [c.9]
Пружина растяжения-сжатия Стальная углеродистая пружинная проволока (по ГСХ Т 9389—75) 3.2.. .3,6 4 4.5.. .5,0 5.6.. .6,0 6.3.. .8.0 Класс проволоки [c.282]
Площадь сечения при расчете на растяжение (сжатие) Л = я (8 —й о)/4. [c.167]
Кривые усталости материала по контактным напряжениям подобны кривым усталости по напряжениям изгиба, растяжения — сжатия и другим (см. курс Сопротивление материалов и рис. 8.39). Здесь так же, как и при других напряжениях, имеется точка перелома кривой усталости при числе циклов N но и соответствующий предел вы- [c.104]
Как правило, на рабочем чертеже помещают диаграмму испытаний, показывающую зависимость деформации (растяжения, сжатия) от силы F — при предварительной деформации в Н (кгс), р2, обеспечивающей предусмотренные рабочие деформации, и Ез, вызывающей максимальную деформацию (рис. 8.114). Деформации указывают или изменение высоты пружины (рис. 8.115, где I—высота пружины при предварительной деформации, 2 — то же, при рабочей и /з — при максимальной деформации ф — высота пружины в свободном состоянии), или [c.281]
Наиболее выгоден случаи растяжения-сжатия, когда все точки сечения работают при одинаково.м напряжении и материал используется наиболее полно. [c.124]
Где только возможно, следует заменять изгиб растяжением-сжатием, как это делается, например, в стержневых и ферменных системах. [c.124]
Наибольший выигрыш достигается при растяжении-сжатии, когда масса обратно пропорциональна напряжению [c.160]
Основной особенностью железобетона как конструкционного материала являются пониженные по сравнению с металлическими материалами прочность и жесткость. Допустимые напряжения растяжения и сжатия у железобетона примерно в 3 раза меньше, чем у серых чугунов. Для создания конструкций, равнопрочных чугунным, необходимо увеличение сечений п моментов сопротивления, согласно которо.му сечения железобетонных конструкций должны быть больше сечений соответствующих чугунных конструкций не менее чем в 3 раза. Так как модуль упругости железобетона примерно в 3 раза ниже модуля упругости чугуна, то увеличение сечений в том же отношении доводит жесткость железобетонных конструкций при растяжении-сжатии до жесткости чугунных конструкций. [c.194]
Растяжение-сжатие. Масса деталей, испытывающих растяжение, йлй сжатие, при прочих равных условиях (одинаковая длина деталей , оди- наковая нагрузка) [c.197]
Ввиду того чго оценка выгодности ио массе является приближенной, обычно для сравнения всех видов нагружения пользуются наиболее простыми по структуре факторами, соответствующи.ми случаю растяжения-сжатия. [c.198]
Для случая растяжения-сжатия бруса постоянного сечения в пределах упругой деформации, коэффициент жесткости согласно закону Гука [c.203]
При аппроксимации неразвертывающих-ся поверхностей следует учитывать, что аппроксимирующие поверхности этих поверхностей нельзя получить так, как для торсов — только путем последовательного ряда изгибов разверток. В этих случаях материал развертки после превращения ее в одежду модели должен иметь соответствующие остаточные деформации (растяжение, сжатие и др.). [c.297]
Еозникают ли при осевом растяжении-сжатии в поперечных сечениях бруса касательные напряжения [c.13]
Для расчета статически неопределимых систем растяжения-сжатия по допускаемым напряжениям обычно используют способ сравнения деформаций. Систему изображают в предполягпемом дг -формированном состоянии и непосредственно из чертежа геометрически) устанавливают зависимости между деформациями различных частей (стержней) системы, то ость составляют уравнения совместности деформаций (перемещений) в количестве, равном степени статической неопределимости системы. [c.66]
При расчете статически неопределимых систем растяжения-сжатия обязательно выполнение следующего условия деформированное состояние системы всегда должно соответствовать направлению внутренних продольных усилий в стержнях, в противном случае возможны ошибки. Способ сравнения деформаций лучше начинать с ыбора возможного деформированного состояния, а затем по нему изобразить направление соответствующих внутренних усилий. [c.67]
В первом разделе рассмотрены эпюры внутренних силовых факторов и растяжение-сжатие пряиолинейного стержня, во -втором — теория напряженного состояния, включая гипотезы прочности, кручение круглых ваюв. геометрические характеристики поперечных сечений в третьем — плоский прямой изгиб в четвертом -статически неопределимые системы и сложное сопротивление в пятом — устойчивость деформируемых систем, динамическое нагру-Ж ение, тонкостенные сосуды в шестом — плоские кривые стержни, толстостенные трубы и переменные напряжения. [c.39]
Испытание на усталость чаще всего осуществляют на вращающемся об разце (гладком или с надрезом) с приложенной постоянной изгибающей нагрузкой, На поверхности образца, а затем и в глубине, по мере развития трещины, нагрузка (растяжение — сжатие) изменяется по синусоиде или другому закону. Определив при данном напряжении время (число циклов) до разрушения, наносят точку на график и испытывают при другом напряжении. В результате получают кривую усталости (сплошная линия) (рис. 63). На этой кривой мы видим, что существует напряжение, которое не вызовет усталостного разрушения, это так называемый r ). При напряжениях ниже ст деталь может работать сколь угодно долго. Но это может быть не всегда необходимо и даже нецелесообразно, так как слишком малы допустимые напряжения (apa6o4ограниченной выносливости. При таких напряжениях работают, например, железнодорожные рельсы. Существенно важно вовремя снять рельс с пути, чтобы избе- кать поломки и крушения поезда. [c.83]
Режущие инструменты работают в условиях больших силовых нагрузок, высоких температур и трения. Поэтому инструментальные материалы должны удовлетворять ряду особых эксплуатационных требований. Материал рабочей части инструмента должен иметь большуро твердость и высокие допустимые напряжения на изгиб, растяжение, сжатие, кручение. Твердость материала рабочей части инструмента должна значительно превышать твердость материала заготовки. [c.276]
В машиностроении наиболее часто для витых цилиндрических пружин растяжения — сжатия используют стальную углеродистую холоднокатаную п1юво-локу круглого сечения диаметром от 0,2 до 8 мм по ГОСТ 9389— 75. [c.306]
Равномерная коррозия представляет собой один из наименее опасных видов коррозии при условии, что скорость растворения металла не превышает норм, определяемых шкалой коррозионной стойкос гн металлов. При достаточной толщине металла гнлошная коррозия мало сказывается на механической прочности конструкции при равномерно распределеншчх напряжениях (растяжение, сжатие) по сечению конструкции. Равномерная коррозия опасна при работе деталей на изгиб и кручение, так как разрушаются наиболее нагруженные слои металла. [c.160]
Материал которых испытьгоает напряжения растяжения-сжатия [c.98]
В система.х, работающих иа растяжение-сжатие, изгиб нередко возникает в результате асимметрии сечений, виецентрениого приложения нагрузки или крнволпнейностн формы детали. [c.124]
При одноосном напряженном состоянии (растяжение, сжатие) достаточно уетановрть один датчик с базой, расположенной по направлении) действия- рапряхеепия, Величина напря жения определяется по закону Гука (а еЕ, где е относительное удлинение проволоки датчика). [c.155]
В случае растяжения-сжатия способов борьбы с уменьшением жесткости нет, так как при данных а п Е величина деформации определяется только площадью сечения и не зависит от его формы. Вследствие этого ферменные и стержневые системы, вын лненные из сверхпрочных сталей, неизбежно будут обладать пониженной жесткостью. [c.179]
Подставляя это выражение в формулу (39), получаем G г= onst у/ств.. Фактор ajy, называемый удельной прочностью, характеризует выгодность по массе материала при растяжении-сжатии. [c.197]
На жесткость сильно влияют размеры и форма сечеций. В случае растяжения-сжатия жесткость, пропорциональна квадрату, а при изгибе — четвертой степени размеров сечения (в направлении действия изгибающего момента). [c.205]
Задачи для самостоятельного решения — Студопедия
Расчет статически неопределимых стержней при растяжении-сжатии
Статически неопределимыми системами называются системы, для которых реакции связей и внутренние усилия не могут быть определены только из уравнений равновесия. Поэтому при их расчете необходимо составлять дополнительные уравнения перемещений, учитывающие характер деформации системы. Число дополнительных уравнений, необходимых для расчета системы, характеризует степень ее статической неопределимости. Способы составления уравнений перемещений будут рассмотрены на примерах решения различных задач.
Пример 1.
Статически неопределимыми называются такие конструкции, в элементах которых при помощи только одних уравнений статики определить усилия невозможно. Например, на рис.1 показан ступенчатый стержень, жестко закрепленный в точках и . На стержень действуют силы и . Модуль продольной упругости материала стержня . Площади поперечных сечений участков: ; ; . Длина участка . Необходимо раскрыть статическую неопределимость, определить продольные усилия, возникающие в различных частях стержня, нормальные напряжения и перемещения различных точек стержня при заданной нагрузке.
Решение.
Заменим действие опор на стержень реакциями ( и ) и составим уравнение проекций сил на ось стержня (ось ):
; , (1)
Рис. 1
Остальные уравнения статики дадут нам такое же выражение (1). В одно уравнение входят два неизвестных усилия ( и ), следовательно, задача один раз статически неопределима.
Для расчета таких систем необходимо использовать уравнения, содержащие деформации элементов конструкций. Так как концы стержня жестко закреплены, то общая длина не изменяется:
.
Общая деформация стержня будет складываться из деформаций его элементов:
, (2)
где – продольное усилие на -том участке; – длина — того участка; – модуль продольной упругости материала; – площадь поперечного сечения — того участка.
Выразим продольные усилия в поперечных сечениях стержня через одну из неизвестных реакций .
Разделим стержень на участки по местам приложения сосредоточенных нагрузок и местам изменения поперечного сечения стержня. Для приведенной схемы получаем три участка (рис. 1).
Мысленно рассечем первый участок произвольно взятым поперечным сечением и отбросим нижнюю часть балки, заменяя ее действие на верхнюю часть продольной силой , которую первоначально направляем в сторону растяжения рассматриваемого элемента первого участка (рис. 2).
Рис. 2
Из условия равновесия:
; (3)
Рис. 3
Мысленно рассечем второй участок произвольно взятым поперечным сечением и отбросим нижнюю часть балки, заменяя ее действие на верхнюю часть продольной силой которую первоначально направляем в сторону растяжения рассматриваемого элемента первого участка (рис. 3).
Из условия равновесия:
;
(4)
Для третьего участка (рис. 3):
;
(5)
Рис. 4
Деформация участков согласно формуле (2):
(6)
(7)
(8)
Общая деформация должна равняться нулю:
Умножив обе части уравнения на получим:
,
или:
.
Из выражения (1):
(9)
Знак «-» указывает на обратное направление реакции .
Определяем значения осевых усилий для каждого участка по найденным ранее выражениям (3) – (5):
;
;
.
По полученным значениям строим эпюру осевых усилий. Для этого проводим нулевую (базовую) линию параллельно оси стержня, перпендикулярно которой будем в масштабе откладывать значения осевых усилий (рис. 1). В одну сторону откладываем положительные значения, в другую — отрицательные. Эпюра заштриховывается перпендикулярно нулевой линии, а внутри эпюры ставится знак откладываемой величины. Рядом указываются значения откладываемых величин. Рядом с эпюрой в кавычках указывается название эпюры («») и через запятую — единицы измерения (кН).
Нормальные напряжения в поперечных сечениях:
(10)
;
;
.
По полученным значениям нормальных напряжений строим эпюру нормальных напряжений («») (рис. 1).
Определим деформацию каждого участка:
;
;
.
Эпюру перемещений строим по перемещениям точек, , , .
Сечение в точке возьмем как базовое, перемещение которого . Тогда перемещение точки будет равно удлинению первого участка:
Перемещение точки будет складываться из перемещения точки и удлинения второго участка:
Перемещение точки будет складываться из перемещения точки и удлинения второго участка:
Перемещение является своего рода проверкой правильности решения данной задачи, так как точка принадлежит неподвижной опоре.
По полученным значениям строим эпюру перемещений («») (рис. 1).
Так как внутри участков перемещения поперечных сечений имеют пропорциональную зависимость от координаты сечения , значения, отложенные в точках , , , , соединяются между собой прямыми линиями.
Пример 2.
Задан стальной стержень, заделанный обоими концами и нагруженный силой F = 1000 Н (рис. а). Удельный вес материала стержня = 78,5 кН/м3, модуль упругости – .
Требуется построить эпюры нормальных сил и напряжений, а также определить перемещение сечения I – I.
Решение.
Выбираем основную систему, которая должна представлять собой статически определимую неизменяемую систему. Основная система получается из заданной системы путем отбрасывания лишних связей и замены их действия неизвестными реакциями. Принятая основная система показана на рис. б.
Строим эпюру нормальных сил для основной системы, для чего определяем нормальные силы в соответствующих сечениях (рис. б):
Определяем перемещение нижнего конца стального стержня основной системы:
Таким образом, если в статически неопределимом брусе (рис. а) убрать одну нижнюю опору, то нижнее опорное сечение переместится вниз на величину , но этого в реальном брусе не может быть, следовательно, на опореВ должна действовать опорная реакция RB, от которой будет возникать линейная деформация , равная по величине , но противоположная по знаку:
Уравнение перемещений будет иметь вид:
или откуда находим RB= 857,16 Н.
Опорная реакция RB вызывает в брусе сжатие, следовательно, эпюра нормальных сил от действия только опорной реакции RB будет иметь вид прямоугольника (рис. в).
Для получения эпюры нормальных сил для статически неопределимого бруса (рис. а) следует сложить две эпюры: эпюру нормальных сил в основной системе (рис. б) и эпюру нормальных сил от действия опорной реакции RB(рис. в). Сложение эпюр проводим, складывая значения нормальных сил двух эпюр в соответствующих точках (рис. г). После чего строится эпюра нормальных напряжений по формуле
Эпюра нормальных напряжений показывает, что самое большое сжимающее нормальное напряжение будет в нижнем опорном сечении ( КПа), а самое большое растягивающее напряжение – в верхнем опорном сечении ( = 154,2 КПа). По эпюре нормальных сил находим опорную реакцию в верхней заделке – RС = 770,84 Н.
Критерием правильности вычислений является равенство нулю площади эпюры нормальных напряжений, т.е. или , где – площадь части эпюры нормальных напряжений со знаком «плюс» (рис. д):
– площадь части эпюры нормальных напряжений со знаком «минус»:
В нашем случае == 191,6, следовательно, расчет выполнен правильно.
Определим перемещение сечения I – I (рис. а), для чего применим метод сечений. Проведем сечение I – I на эпюре нормальных сил (рис. г) и отбросим нижнюю часть эпюры, тогда по оставшейся части эпюры определяем
Перемещение можно вычислить, если отбросить верхнюю часть эпюры нормальных сил:
Получили одно и то же значение перемещений, но с разными знаками, что естественно, так как сечение I – I переместилось вниз, следовательно, верхняя часть бруса увеличила линейные размеры вдоль оси, а нижняя, наоборот уменьшила.
Пример 3.
Определить нормальное напряжение в бетоне и арматуре железобетонной колонны, квадратное поперечное сечение которой показано на рисунке, причем h = 30 см, модуль продольной упругости стали , а бетона тяжелого класса В 30 –
Решение.
В поперечном сечении колонны установлены четыре стержня диаметром 20 мм, следовательно, по справочнику принимаем, что общая их расчетная площадь поперечного сечения Аа = 12,56 см2. Площадь поперечного сечения, занимаемого бетоном, определяется как
Пусть в поперечном сечении колонны действует сжимающая сила N, тогда уравнение равновесия примет вид:
.
Для определения усилий в арматуре Na и в бетоне Nb одного записанного выше уравнения равновесия недостаточно, так как задача один раз статически неопределима. Составим дополнительное уравнение возможных перемещений (уравнение совместности деформаций). Очевидно, что между арматурой и бетоном существует сцепление, так что абсолютное и относительное удлинения арматуры и бетона равны
или .
Учитывая, что , получаем равенство относительных удлинений:
или , или, что то же самое откуда находим
Подставляя полученное соотношение в уравнение равновесия при учете, что , , и полагая, что внешняя сосредоточенная сжимающая сила N = 600 , имеем
откуда находим
Напряжения имеют знак «минус», так как колонна работает на сжатие.
Пример 4.
Задан стальной стержень, защемленный одним концом и загруженный силой F = 1000 Н (рис. а). Удельный вес стали стержня модуль продольной упругости стали .
Требуется построить эпюры нормальных сил и нормальных напряжений, учитывая, что до приложения нагрузок имелся зазор между нижним торцом бруса и нижней опорой равный
Решение.
Если нижнюю опору не принимать во внимание и вычислить перемещение нижнего торца стержня при учете сосредоточенной силы F и собственного веса стержня, то будем иметь . Полученное значение показывает, что нижний торец бруса в этом случае должен был бы опуститься ниже уровня нижней опоры на величину (рис. а)
Но этого быть не может, так как имеется абсолютно жесткая нижняя опора. Следовательно, будет возникать опорная реакция RB, которая будет препятствовать возникновению перемещения нижнего торца стержня, равного :
Приравняем два значения : 82870/Е = RB680/Е, откуда найдем значение опорной реакции RB = 121,87 Н.
Эпюра нормальных сил от действия только опорной реакции RB будет иметь вид, показанный на рис. б. Для построения окончательной эпюры нормальных сил для статически неопределимого бруса, показанного на рис. а, следует сложить две эпюры: эпюру нормальных сил в основной системе (рис. б) и эпюру нормальных сил от действия опорной реакции RB (рис. б). Проведя сложение двух эпюр, получим окончательную эпюру N, показанную на рис. в, а затем можно переходить к построению эпюры нормальных напряжений (рис. г).
Пример 5.
Стержень переменного сечения с заданным соотношением площадей поперечного сечения , выполненный из разного материала, загружен силой F (см. рис. 1). Между правым концом стержня и стенкой существует зазор .
Требуется:
1) определить продольные силы, напряжения на каждом участке и проверить прочность стержня от действия заданной нагрузки F.
2) найти дополнительные напряжения, возникающие в стержне при его нагревании на температуру и проверить прочность стержня от температурного воздействия.
Рис.1
Решение.
I. Определение напряжений от заданной нагрузки
Прежде всего надо убедиться, что заданная система является статически неопределимой. Найдем абсолютную деформацию стержня, показанного на рисунке, предполагая сначала, что правая стенка отсутствует. Тогда, используя метод сечений, определим продольные силы на трех участках стержня:
— на первом участке длиной ;
— на втором и третьем участках .
Полное удлинение стержня, равное в общем случае , в данной задаче равно удлинению первого участка и, следовательно, по
.
Если под действием нагрузки абсолютная деформация стержня будет больше заданного зазора , то стержень упрется правым концом в стенку и возникнут опорные реакции как в левом защемлении (), так и в правом опорном закреплении () (рис. 2, а). Для заданной системы можно составить только одно независимое уравнение статики . Таким образом, две неизвестные опорные реакции нельзя найти из одного уравнения, и система в процессе деформации становится один раз статически неопределимой.
Рис.2
Для раскрытия статической неопределимости используем расчет по упругой стадии деформаций и запишем три группы уравнений:
1) уравнения равновесия. Из них получим:
— для всего стержня ;
— для отсеченных частей стержня Заметим, что при составлении уравнений равновесия отсеченных частей стержня сделано предположение, что первая и вторая части стержня растянуты, а третья часть – сжата;
2) уравнение совместности деформаций, смысл которого в данной задаче очень простой: полная деформация стержня равна заданному зазору. При составлении уравнения совместности деформаций важно, чтобы знаки абсолютных деформаций соответствовали сделанным предположениям о направлении усилий. В нашем примере ;
3) физические уравнения
.
Решив полученную систему уравнений, найдем продольные силы, а затем напряжения в разных частях стержня и построим эпюры их распределения по длине стержня (рис. 2, б). Если знак усилия после решения системы уравнений получился отрицательным, это означает, что сделанное предположение о направлении продольной силы не подтвердилось. В рассмотренной задаче отрицательным должно получиться усилие , т. е. второй участок длинойb не растянут, а сжат. Знаки N и s на эпюрах ставим в соответствии с правилом знаков для продольной силы.
После определения напряжений производим проверку прочности по формулам или так же, как в статически определимой системе. Если условие прочности на каком-нибудь участке стержня не будет выполняться, измените значение F так, чтобы условие прочности соблюдалось.
II. Определение температурных напряжений
Найдем удлинение стержня от температурного воздействия и убедимся в том, что это удлинение больше заданного зазора .
.
Если , то система является один раз статически неопределимой и раскрытие статической неопределимости производим по той же схеме, что и в предыдущей части задачи:
Из уравнений равновесия следует, что и . Здесь в соответствии с рис. 3, а предполагаем, что стержень всюду сжат. (Силу F при определении температурных напряжений считаем равной нулю.)
Рис.3
Уравнение совместности деформации показывает, что абсолютная деформация стержня, равная разности удлинения стержня от температурного воздействия и укорочения от действия сжимающих продольных сил не может быть больше заданного зазора :
,
где .
Укорочение стержня от действия продольных сил найдем, используя физические уравнения (закон Гука):
и .
После решения полученной системы уравнений найдем усилия в обеих частях стержня. Полученный положительный знак должен подтвердить предположение о том, что стержень сжат. Строим эпюры продольной силы и напряжений (рис. 3, б) от температурного воздействия.
Проверяем прочность стержня и в случае невыполнения условия прочности на каком-нибудь участке находим новое значение , при котором условие прочности будет соблюдаться на всех участках.
Пример 6.
На рис.1,а изображен стальной ступенчатый брус (E = 2×105 МПа), жестко закрепленный с одной стороны. С другой стороны между стержнем и заделкой имеется зазор = 0,01 мм. Данный стержень нагружен осевыми силами, выраженными через кратную нагрузку F = 2 кН, длина участков l = 0,4 м, Е = 2×105МПа, а площади поперечных сечений, выражены через А = 4×10-4м2.
Требуется:
1. Установить, закроется ли зазор для заданной расчетной схемы.
2. Раскрыть статическую неопределимость.
3. Построить эпюру продольных сил и нормальных напряжений.
4. Проверить прочность бруса, если допускаемое напряжение = 160 МПа.
а) б) в)
Рис.1
Решение.
1. Устанавливаем закроется ли зазор между стержнем и заделкой от приложенных внешних нагрузок.
Получили, что полная деформация бруса от действия внешних сил больше, чем зазор = 0,01 мм, т.е. зазор перекрывается и возникает опорная реакция RB.
2. Определение степени статической неопределимости. В результате перекрытия зазора возникает вторая опорная реакция RB. Для заданной линейной системы сил составим уравнение статического равновесия:
; — RB + 6F – F + RL = 0.
В результате имеем два неизвестных RBи RLи одно уравнение статического равновесия. Следовательно задача один раз статически неопределима и требуется составить еще одно уравнение – условие совместности перемещений.
3. Раскрытие статической неопределимости.
Для определения опорных реакций составим условие совместности перемещений для сечения В: от действия внешних нагрузок и от силы реакции RB; или ;
Согласно результатов расчета п.1 выше: .
Перемещение сечения В только от реакции :
;
Тогда исходное уравнение примет вид: ;
Умножаем обе части уравнения на ЕА и делим на l:
.
Отсюда находим RВ :
.
Из уравнения равновесия (см. п.2) находим вторую реакцию RL:
; кН.
Полученный знак минус перед реакцией RL показывает, что действительное ее направление, в противоположную сторону от выбранного.
4. Построение эпюры продольных сил и нормальных напряжений.
Далее, используя метод сечения (рис. 2), определяем величины продольных сил на участках стержня и строим эпюру N (рис. 2, б)
а) б) в)
Рис.2
Участок ВС: ; N1 — RВ = 0; N1 = RВ = 8,67 кН.
Участок СК: ; N2 + 6F — RВ = 0; N2 = 6F — RВ = 6 ×2 –8,67 = 3,33 кН.
Участок KL: ; — RВ + 6F — F + N3 = 0; N3 = RВ –5F = 8,67 – 5 × 10 = — 1,33 кН.
Так как продольная сила N3 = — 1,33 кН, то меняем на схеме рисунка 2,в направление вектора на противоположный.
Определяем величину нормальных напряжений по участкам бруса, строим эпюру (рис.2,в) и сравниваем эти величины с допускаемым нормальным напряжением = 160 МПа.
Участок ВС:
Сравнение выполняем по модулю. Условие прочности выполняется.
Участок CD:
Условие прочности выполняется.
Участок DK:
Условие прочности выполняется.
Участок КL:
Условие прочности выполняется.
Пример 7.
Определить усилия и нормальные напряжения в стержне с зазором , изображенном на рисунке, при действии силы P и нагревании на .
Принять зазор =0,1 мм, а=0,5 м, F=100 см2, P=1500 кН, =300 С.
Решение.
В результате сборки конструкции (ликвидации зазора ), действии силы P и температуры в опорах возникнут реакции . Уравнение равновесия имеет вид
.
Задача один раз статически неопределима. Решаем задачу методом сил. Для эквивалентной системы составляем дополнительное уравнение совместности деформаций. Перемещение сечения ограничено, поэтому
.
Используя принцип независимости действия сил и закон Гука для эквивалентной системы получаем
,
или
,
откуда
.
Тогда:
.
Методом сечения находим усилия на каждом из участков стержня:
Напряжения
Таким образом, каждое из слагаемых в выражениях для напряжений содержит три вида слагаемых. Первые возникают за счет действия силы , вторые – за счет изменения температуры (температурные напряжения), третьи − за счет устранения зазора (монтажные напряжения).
В первом случае, когда (), силовые напряжения
, , ,
т.е. первый участок стержня растягивается, а второй сжимается.
Во втором случае, когда действует только температура ()
, , ,
т.е. напряжения во всем стержне сжимающие.
В третьем случае ()
, ,
оба участка растянуты. В этом случае стержень был растянут для ликвидации зазора и закреплен.
Пример 8.
Сила передаётся через абсолютно жёсткую плиту А на сплошной стальной цилиндр 1 площадью поперечного сечения 15 см2 и полый медный цилиндр 2 площадью 20 см2. Сила действует по оси обоих цилиндров (рис. 1).
Принять: Р = 45 кН; F1 = 15 см2; F2 = 20 см2; E1 = 2∙105 МПа; E2 = 1∙105 МПа; коэффициент линейного расширения для стали = 1,2∙10 -5 1/град, для меди = 1,6∙10 -5 1/град.
Требуется:
1. найти усилия в стальном N1 и медном цилиндрах N2; изменить температуру конструкции, чтобы усилия в стальном и медном цилиндрах были одинаковы N1=N2;
2. изменить температуру конструкции, чтобы напряжения в стальном и медном цилиндрах были одинаковы .
Рис. 1
Решение.
1. Определение усилий и
Сделаем сечение и рассмотрим равновесие верхней отсечённой части, действие отброшенной части заменим усилиями и (рис. 2).
Для данной системы сил можно составить одно уравнение статики. (У=1). Число неизвестных равно двум (R=2). Таким образом, система один раз статически неопределима:
.
Рис. 2
Составим уравнение равновесия
Рассмотрим систему в деформированном состоянии (рис. 3) и составим уравнение совместности перемещений.
Рис. 3
Очевидно, что
.
Выразим деформацию цилиндров 1 и 2 через усилия
где учтено .
Тогда:
Следовательно:
Подставляя полученное выражение , получим
откуда
Тогда
Знак «минус» в выражениях говорит о том, что усилия в цилиндрах будут сжимающими.
2. Изменение температуры конструкции , чтобы усилия в цилиндрах стали одинаковыми ()
Следовательно:
.
В выражениях для деформаций цилиндров нужно учесть влияние изменения температуры DТ. Тогда
Отсюда:
или
откуда
.
Таким образом, чтобы усилия в цилиндрах стали одинаковыми, конструкцию нужно нагреть на 9,4 °С.
3. Изменение температуры конструкции (), чтобы напряжения в цилиндрах стали одинаковыми ()
Напряжения в цилиндрах равны
Тогда с учетом получаем
или
Тогда:
откуда
Выражения для деформаций каждого из цилиндров
Тогда:
Таким образом, чтобы напряжения в стальном и медном цилиндрах стали одинаковыми, конструкцию нужно нагреть на 16 °С.
Задачи для самостоятельного решения
Задача № 1
Стержень, жестко защемленный двумя концами (см. рисунок), имеет площадь поперечного сечения верхней части 10 см2 и нижней части 40 см2. Определить напряжения в каждой части стержня.
Ответ: = 50 МПа, = —100 МПа.
Задача № 2
Стальной болт пропущен сквозь медную трубку, как показано на рисунке. Шаг нарезки болта равен 3 мм. Какие напряжения возникают в болте и трубке при завинчивании гайки на 1/4 оборота?
Ответ:=127,4 МПа;=- 36,4 МПа.
Задача № 3
Стержень с площадью поперечного сечения A =100 см2защемлен верхним концом и нагружен, как показано на рисунке. Между нижним его концом и неподатливой плоскостью до нагружения имеется зазор = 0,02 мм.Найти по способу допускаемых нагрузок наибольшее безопасное значение силы F при [] = 100 МПа.
Ответ: 2000 кН.
Задача № 4
Определить допускаемую нагрузку [F] для стального стержня, если допускаемое напряжение [] =120 МПа как для растяжения, так и для сжатия. Найти перемещение сечения I—I, если ℓ1 = ℓ3 =2ℓ2, а ℓ2 =0,4 м, S1 = S3 = 1,5S2,S2 = 10 см2 (см. рис.).
Ответ.Нагрузка [Р]=110 кН, I—I = 0, 44 мм.
Задача № 5
Сравнить температурные напряжения, возникающие в трех стержнях, заделанных в абсолютно неподатливые стенки, при одинаковом перепаде температур.
Задача № 6
Определить, при каком значении размера а обеспечивается равнопрочность бруса, если предел текучести материала при растяжении составляет две трети предела текучести при сжатии.
Задача № 7
Брус, жестко закрепленный по концам, нагрет по всей длине на 0С и нагружен силой F. Считая заданными размеры бруса, F и A, определить, при каком значении силы F сечение mn остается неподвижным. выполнить количественную оценку при следующих данных: А = 8 см2, =12,5.10-6, =10 оС, Е=200 ГПа.
Задача № 8
Дан прямой стержень кусочно-постоянного сечения, защемленный обеими концами и нагруженный силами F1=1 кН, F2=0,5 кН (см. рис.), а также собственным весом с =78,5 кН/м3. Построить эпюры нормальных сил и нормальных напряжений. Определить перемещение сечения, находящегося на расстоянии 30 см от верхней опоры, если модуль упругости материала стержня .
Ответ: RA= 327,2 Н; .
Задача № 9
Стержень с постоянной площадью поперечного сечения А нагружен сосредоточенными силами (см. рис.). Определить перемещения сечений I – I и II – II. Собственный вес стержня в расчете не учитывать.
Ответ:
Задача № 10
Определить нормальные напряжения в каждом участке стального стержня квадратного поперечного сечения, находящегося под воздействием сосредоточенных сил, направленных вдоль оси стержня. Размеры сторон квадратного поперечного сечения и величины сосредоточенных сил показаны на рисунке. Собственный вес стержня не учитывать, а модуль продольной упругости принять .
Ответ: = 22,07 МПа; = 58,57 МПа; = –12,65 МПа; = –68,22 МПа.
Задача № 11
Определить нормальные напряжения в опорных сечениях стержня постоянного поперечного сечения площадью А, заделанного обоими концами и находящегося под действием собственного веса, направленного вдоль оси стержня, – удельный вес материала стержня. Длина стержня – l.
Ответ:
Задача № 12
Стержень постоянного поперечного сечения заделан одним концом. После установки стержня в проектное положение был произведен замер величины зазора между нижним сечением бруса и нижней опорой, который оказался равен = 0,5 мм, длина стержня l = 2 м, объемный вес материала бруса = 78,5 кН/м3, (см. рис.). После этого стержень был загружен сосредоточенной силой F = 200 кН. Определить опорные реакции RB, RC и построить эпюры нормальных сил и напряжений.
Ответ: RB = –48,503 кН; RC = 151,654 кН.
Задача № 13
Стержень постоянного поперечного сечения заделан одним концом. Между нижним концом стержня и нижней жесткой опорой имеется зазор, равный = 0,5 мм (см. рис.). После измерения зазора стержень был загружен своим собственным весом с = 78,5 кН/м3 и сосредоточенной силой F = 200 кН. Длина стержня l = 2 м, модуль продольной упругости . Определить опорные реакции RB, RC и построить эпюры нормальных сил и напряжений.
Ответ: RB= –48,581 кН; RC= 151,576 кН.
Задача № 14
Дан стальной прямой стержень кусочно-постоянного сечения, защемленный двумя концами и нагруженный силой F = 10 т (рис. а). Один из участков стержня выполнен из двутавра № 16. Материал всей конструкции – сталь с . Построить эпюры нормальных сил и напряжений. Собственный вес элементов конструкции в расчете не учитывать.
Ответ: эпюры нормальных сил и нормальных напряжений представлены на рис. б.
Задача № 15
Стержень постоянного поперечного сечения А и длиной l заделан двумя концами. В процессе эксплуатации он нагрелся на величину . Определить возникшие внутренние усилия и напряжения.
Ответ: ;
Задача № 16
Медный стержень с постоянной площадью поперечного сечения А = 10 см2 загружен сосредоточенными силами F = 1000 кг (см. рис.) и нагрет на = 20о. Определить опорные реакции нижней опоры R1 и верхней опоры R2. Собственный вес стержня не учитывать. Принять модуль Юнга
| MechaniCalc
На этой странице представлен набор интерактивных графиков для общих факторов концентрации напряжений. См. Справочный раздел для получения более подробной информации.
Прямоугольный стержень с центральным отверстием, осевое усилие
На этой вкладке определяется коэффициент концентрации напряжений для стержня с прямоугольным поперечным сечением и центральным круглым отверстием. К стержню прилагается осевая сила (растягивающая или сжимающая).
- w = ширина стержня
- d = диаметр отверстия
- t = толщина прутка
- F = приложенная сила (растягивающая или сжимающая)
Невозможно отобразить сюжет — браузер устарел.
Максимальное напряжение рассчитывается как σ max = K t σ nom , где K t — коэффициент концентрации напряжений, определенный на графике ниже, а σ nom рассчитывается как:
Невозможно отобразить сюжет — браузер устарел.
Значение коэффициента концентрации напряжений рассчитывается по формуле:
Источники:
Прямоугольный стержень с центральным отверстием, изгиб вне плоскости
На этой вкладке определяется коэффициент концентрации напряжений для стержня с прямоугольным поперечным сечением и центральным круглым отверстием.К стержню прилагается изгибающий момент вне плоскости.
- w = ширина стержня
- d = диаметр отверстия
- t = толщина прутка
- M = приложенный изгибающий момент
Невозможно отобразить сюжет — браузер устарел.
Максимальное напряжение рассчитывается как σ max = K t σ nom , где K t — коэффициент концентрации напряжений, определенный на графике ниже, а σ nom рассчитывается как:
Невозможно отобразить сюжет — браузер устарел.
Значение коэффициента концентрации напряжений рассчитывается по формуле:
Источники:
Прямоугольный стержень с U-образными пазами, осевое усилие
На этой вкладке определяется коэффициент концентрации напряжений для стержня с прямоугольным поперечным сечением и двумя U-образными пазами. К стержню прилагается осевая сила (растягивающая или сжимающая).
- w = ширина стержня
- h = высота надреза
- r = радиус надреза
- t = толщина прутка
- F = приложенная сила (растягивающая или сжимающая)
Невозможно отобразить сюжет — браузер устарел.
Максимальное напряжение рассчитывается как σ max = K t σ nom , где K t — коэффициент концентрации напряжений, определенный на графике ниже, а σ nom рассчитывается как:
Невозможно отобразить сюжет — браузер устарел.
Значение коэффициента концентрации напряжений рассчитывается по формуле:
где коэффициенты в приведенном выше уравнении рассчитываются на основе «коэффициентов концентрации напряжений Петерсона»:
| 0.1 ≤ ч / р ≤ 2,0 | 2,0 ≤ ч / об ≤ 50,0 | |
|---|---|---|
| С 1 | 0,955 и выше; 2,169 & Sqrt; ч / р — 0,081 (ч / р) | 1.037 и плюс; 1.991 & Sqrt; h / r & plus; 0,002 (ч / об) |
| С 2 | −1,557 — 4,046 & Sqrt; h / r & plus; 1.032 (ч / р) | −1,886 — 2,181 & Sqrt; h / r — 0,048 (h / r) |
| С 3 | 4.013 и выше; 0,424 & Sqrt; h / r — 0.748 (ч / р) | 0,649 и больше; 1.086 & Sqrt; h / r & plus; 0,142 (час / об) |
| С 4 | -2,461 & плюс; 1,538 & Sqrt; ч / р — 0,236 (ч / р) | 1,218 — 0,922 & Sqrt; ч / р — 0,086 (ч / р) |
Источники:
Прямоугольный стержень с U-образными пазами, изгиб
На этой вкладке определяется коэффициент концентрации напряжений для стержня с прямоугольным поперечным сечением и двумя U-образными пазами. К стержню прилагается изгибающий момент в плоскости.
- w = ширина стержня
- h = высота надреза
- r = радиус надреза
- t = толщина прутка
- M = приложенный изгибающий момент
Невозможно отобразить сюжет — браузер устарел.
Максимальное напряжение рассчитывается как σ max = K t σ nom , где K t — коэффициент концентрации напряжений, определенный на графике ниже, а σ nom рассчитывается как:
Невозможно отобразить сюжет — браузер устарел.
Значение коэффициента концентрации напряжений рассчитывается по формуле:
где коэффициенты в приведенном выше уравнении рассчитываются на основе «коэффициентов концентрации напряжений Петерсона»:
| 0,1 ≤ ч / об ≤ 2,0 | 2,0 ≤ ч / об ≤ 50,0 | |
|---|---|---|
| С 1 | 1.024 и выше; 2,092 & Sqrt; h / r — 0,051 (h / r) | 1.113 и выше; 1.957 & Sqrt; h / r |
| С 2 | −0.630 — 7.194 & Sqrt; ч / р & плюс; 1,288 (ч / р) | −2,579 — 4,017 & Sqrt; h / r — 0,013 (h / r) |
| С 3 | 2.117 и выше; 8,574 & Sqrt; h / r — 2,160 (h / r) | 4.100 и выше; 3.922 & Sqrt; h / r & plus; 0,083 (час / об) |
| С 4 | -1,420 — 3,494 & Sqrt; h / r & plus; 0,932 (ч / р) | −1,528 — 1,893 & Sqrt; h / r — 0,066 (h / r) |
Источники:
Прямоугольный стержень с галтелем, осевое усилие
На этой вкладке определяется коэффициент концентрации напряжений для стержня с прямоугольным поперечным сечением и скруглением.К стержню прилагается осевая сила (растягивающая или сжимающая).
- D = ширина большей секции
- d = ширина меньшей секции
- r = радиус скругления
- t = толщина прутка
- F = приложенная сила (растягивающая или сжимающая)
Невозможно отобразить сюжет — браузер устарел.
Максимальное напряжение рассчитывается как σ max = K t σ nom , где K t — коэффициент концентрации напряжений, определенный на графике ниже, а σ nom рассчитывается как:
Невозможно отобразить сюжет — браузер устарел.
Значение коэффициента концентрации напряжений рассчитывается по формуле:
где коэффициенты в приведенном выше уравнении рассчитываются по «формулам Рорка для напряжений и деформаций»:
| 0,1 ≤ ч / об ≤ 2,0 | 2,0 ≤ ч / об ≤ 20,0 | |
|---|---|---|
| С 1 | 1.007 и выше; 1.000 & Sqrt; ч / р — 0,031 (ч / р) | 1.042 и выше; 0,982 & Sqrt; ч / р — 0,036 (ч / р) |
| С 2 | −0.114 — 0,585 & Sqrt; h / r & plus; 0,314 (час / об) | −0,074 — 0,156 & Sqrt; h / r — 0,010 (h / r) |
| С 3 | 0,241 — 0,992 & Sqrt; h / r — 0,271 (h / r) | -3,418 и больше; 1,220 & Sqrt; ч / р — 0,005 (ч / р) |
| С 4 | -0,134 и плюс; 0,577 & Sqrt; ч / р — 0,012 (ч / р) | 3,450 — 2,046 & Sqrt; h / r & plus; 0,051 (ч / об) |
Источники:
Пруток прямоугольный с закруглением, изгиб
На этой вкладке определяется коэффициент концентрации напряжений для стержня с прямоугольным поперечным сечением и скруглением.К стержню прилагается изгибающий момент в плоскости.
- D = ширина большей секции
- d = ширина меньшей секции
- r = радиус скругления
- t = толщина прутка
- M = приложенный изгибающий момент
Невозможно отобразить сюжет — браузер устарел.
Максимальное напряжение рассчитывается как σ max = K t σ nom , где K t — коэффициент концентрации напряжений, определенный на графике ниже, а σ nom рассчитывается как:
Невозможно отобразить сюжет — браузер устарел.
Значение коэффициента концентрации напряжений рассчитывается по формуле:
где коэффициенты в приведенном выше уравнении рассчитываются по «формулам Рорка для напряжений и деформаций»:
| 0,1 ≤ ч / об ≤ 2,0 | 2,0 ≤ ч / об ≤ 20,0 | |
|---|---|---|
| С 1 | 1.007 и выше; 1.000 & Sqrt; ч / р — 0,031 (ч / р) | 1.042 и выше; 0,982 & Sqrt; ч / р — 0,036 (ч / р) |
| С 2 | −0.270 — 2.404 & Sqrt; h / r & plus; 0,749 (ч / р) | −3,599 и больше; 1,619 & Sqrt; ч / р — 0,431 (ч / р) |
| С 3 | 0,677 и выше; 1,133 & Sqrt; ч / р — 0,904 (ч / р) | 6.084 — 5.607 & Sqrt; h / r & plus; 1,158 (ч / р) |
| С 4 | -0,414 и плюс; 0,271 & Sqrt; ч / р & плюс; 0,186 (час / об) | −2,527 & плюс; 3,006 & Sqrt; ч / р — 0,691 (ч / р) |
Источники:
Калькулятор напряжений
Этот калькулятор напряжений поможет вам решить задачи механики, связанные с напряжением, деформацией и модулем Юнга.За несколько простых шагов вы узнаете зависимость напряжения от деформации для любого материала, который остается эластичным. Мы также научим вас рассчитывать деформацию и применять уравнение напряжения.
Как рассчитать деформацию и напряжение
Деформация определяется как мера деформации — пропорция между изменением длины и исходной длиной объекта. Например, если взять резинку и растянуть ее так, чтобы она была вдвое длиннее, чем изначально, то деформация будет равна 1 (100%).
Формула деформации:
ε = ΔL / L₁ = (L₂ - L₁) / L₁ L₁ обозначает начальную длину, L₂ — конечную длину, а ΔL — изменение длины. Обратите внимание, что деформация безразмерна.
Напряжение, с другой стороны, является мерой давления, которое частицы материала оказывают друг на друга. Он определяется как сила, действующая на объект на единицу площади. Однако это отличается от давления; при расчете напряжения рассматриваемая площадь должна быть настолько маленькой, чтобы анализируемые частицы считались однородными.Если принять во внимание большую площадь, расчетное напряжение обычно является средним значением.
Уравнение напряжения:
σ = F / A F обозначает силу, действующую на тело, а A обозначает площадь. Единицы напряжения такие же, как единицы давления — Паскали (символ: Па) или Ньютоны на квадратный метр.
Положительное напряжение означает, что объект находится в напряжении — он «хочет» удлиниться. Отрицательное напряжение означает, что оно находится в состоянии сжатия и «хочет» стать короче.
Модуль Юнга (напряжение по отношению к деформации)
Если материал линейно упругий , то напряжение и деформация напрямую связаны следующей формулой:
E = σ / ε E — это модуль упругости или модуль Юнга . Это материальная константа, разная для каждого вещества.
Что такое линейно-упругое поведение материала? Если мы прикладываем напряжение к материалу, деформация увеличивается пропорционально.Это может быть верно только для некоторого диапазона напряжений — после достижения определенного значения материал может сломаться или деформироваться. Под текучестью понимается увеличение деформации при постоянном напряженном состоянии.
Пример расчетов
Предположим, мы хотим найти модуль Юнга стали. Для этого мы подготовили стальной стержень, который тянули с большим усилием.
- Мы решаем, что сила тяги штанги будет равна 30 кН (
30 * 10³ Н). - Определяем размеры стержня.Предположим, что длина составляет 2 м (2000 мм), а площадь поперечного сечения — 1 см² (
1 * 10⁻⁴ м²). - Мы заметили удлинение стержня на 3 мм.
- Рассчитываем деформацию стержня по формуле:
ε = ΔL / L₁ = 3/2000 = 0,0015. - Рассчитываем напряжение по формуле напряжения:
σ = F / A = 30 * 10³ / (1 * 10⁻⁴) = 300 * 10⁶ = 300 МПа. - Наконец, разделим напряжение на деформацию, чтобы найти модуль Юнга стали:
E = σ / ε = 300 * 10⁶ / 0.0015 = 200 * 10⁹ = 200 ГПа.
Модуль упругости
Единицы модуля Юнга такие же, как единицы давления и напряжения: Паскали или ньютоны на квадратный метр. В единицах СИ
1 Па = 1 Н / 1 м² = 1 кг · м / с² / м² = 1 кг / (м · с²)
Если вас интересует механика, попробуйте калькулятор крутящего момента.
Силы сжатия и растяжения в бетонных столешницах
Балка — это горизонтальный элемент конструкции, который охватывает некоторое открытое пространство и поддерживается рядом с концами.Балка может поддерживать некоторый вес, помещенный на нее где-то между концевыми опорами. Балка перекрытия — это балка. Бетонные столешницы — это тоже балки.
Когда на балку помещен груз, этот вес заставляет балку отклоняться (изгибаться). Небольшой вес на жестких балках почти не вызывает прогиба, в то время как большой вес на гибких балках вызывает значительный прогиб. Отклонение балки вызывает две вещи: верхняя поверхность балки сжимается и пытается стать короче, а нижняя поверхность находится в напряжении и пытается удлиниться.
Между ними происходит что-то важное. Сжатие противоположно растяжению, поэтому по мере продвижения вниз по балке от верхней поверхности к нижней, напряжение сжатия постепенно уменьшается до нуля, а затем напряжения меняются, переходя в растяжение и постепенно увеличиваясь по направлению к нижней части балки. Если неармированная балка имеет симметричное поперечное сечение (например, прямоугольник), переключение напряжения происходит в средней точке между верхней и нижней гранями.
Это важно, потому что, учитывая отсутствие напряжения растяжения или сжатия в средней части столешницы, размещение арматуры там абсолютно бесполезно.Точка, в которой происходит это переключение, называется нейтральной осью, и ее можно рассматривать как воображаемую линию, проходящую параллельно длине луча.
Если столешница сделана из традиционного сборного железобетона (без армирования), любой значительный вес, помещенный на нее, приведет к ее разрушению в нижней части столешницы, потому что напряжения растяжения в нижней части столешницы будут превышать растяжение прочность бетона. На дне образуется трещина, которая продвигается вверх буквально со скоростью звука.
Обратите внимание, что в случае столешниц из бетона GFRC структурное армирование обеспечивается не сталью, а смешанными стекловолокнами AR. Буквально это «бетон, армированный стекловолокном». Пожалуйста, ознакомьтесь с обширными бесплатными статьями GFRC на этом сайте, чтобы понять, как работает GFRC.
Некоторые утверждают, что, поскольку бетонные столешницы обычно охватывают только ширину шкафа (обычно максимум 36 дюймов), они представляют собой довольно короткие балки, и поэтому возникающие напряжения не так велики.Это правда, но как насчет случая, когда сборная плита длиной 8 футов берется в магазине и загружается на грузовик для транспортировки? В цехе возникают самые большие нагрузки и самый большой риск растрескивания. После того, как плиты будут установлены, только установка шкафов или здания создаст большую нагрузку.
В этом видео гораздо более подробно рассматривается вопрос о силах сжатия и растяжения в бетонных столешницах.
Расчет дважды армированных бетонных прямоугольных балок на примере
🕑 Время чтения: 1 минута
Конструкция балки из дважды армированного бетона может потребоваться, когда поперечное сечение балки ограничено по архитектурным или другим соображениям.В результате бетон не может развивать силу сжатия, необходимую для сопротивления заданному изгибающему моменту. В этом случае стальные стержни добавляются в зону сжатия балки, чтобы улучшить ее при сжатии.
Таким образом, балка, армированная стальным растяжением и компрессионной сталью, называется балкой из дважды армированного бетона. Момент сопротивления дважды армированной бетонной балки больше, чем у одноармированной бетонной балки для того же поперечного сечения, марки стали и бетона.
Использование компрессионной арматуры значительно сократилось из-за использования метода расчета прочности, который учитывает полный потенциал прочности бетона в зоне сжатия. Тем не менее, компрессионная арматура может использоваться по причинам, отличным от прочности, например, для уменьшения длительного прогиба балки, учета нагрузки с минимальным моментом и удержания хомутов на своих местах.
Почему в балке используется арматура сжатия?- Для повышения прочности бетонной балки.
- Для уменьшения длительных прогибов стержней.
- Для минимальной моментной нагрузки.
- Для установки хомутов (привязав их к прижимным стержням) и удержания их на месте во время укладки бетона и вибрации.
Когда сжатая арматура добавляется для целей, отличных от прочности, наличие сжатых стержней не учитывается в расчетах на изгиб.
Рекомендации по проектированию
1. Геометрия балки
Разработчик может не иметь большого контроля над размером балки из-за архитектурных или любых других соображений, которые ограничивают геометрию балки.
Размеры балки устанавливаются инженерами-архитекторами, поэтому инженер-строитель знает размер балки, и единственное, что неизвестно, — это площадь армирования.
2.
Арматура стальнаяACI 318-19 определяет максимальный коэффициент усиления при растяжении ( p max ), который может быть помещен в одноармированную бетонную балку. ( p max ) можно рассчитать с помощью следующего выражения:
Если расчетный коэффициент армирования ( p ) рассматриваемой балки больше, чем ( p max ), она должна быть спроектирована как балка из дважды армированного бетона.
ACI 318-19 также определил максимальный коэффициент армирования ( p max ), который может быть помещен в дважды армированную бетонную балку для обеспечения текучести стальных стержней в зоне растяжения балки. Следовательно, ( p max ) гарантирует, что балка разрушится из-за текучести стали при растяжении вместо дробления бетона, что является внезапным и нежелательным.
Где:
B 1 : равно 0,85, если (fc ‘= <28 МПа), в противном случае используйте уравнение 3 для его вычисления.
fc ‘: прочность бетона на сжатие, МПа
фу: предел текучести стального проката, МПа
Epsilon, cu: предельная деформация сжатия бетона, равная 0,003 согласно ACI 318-19
.p ‘: степень армирования при сжатии, которая рассчитывается согласно уравнению 4
3.
Размеры стального пруткаОбычно рекомендуется избегать использования стержней больших размеров для балок. Это связано с тем, что такие стержни вызывают растрескивание при изгибе и требуют большей длины для развития их прочности.Однако стоимость размещения бруса большого размера ниже, чем стоимость установки большого количества бруса малых размеров.
Кроме того, стандартные размеры стержней для балок варьируются от № 10 до № 36 (единица СИ) или от № 3 до № 10 (обычная единица США), а два стержня большего диаметра № 43 (№ 14) и № 57 (№ 18) используются для столбцов.
Кроме того, можно комбинировать прутки разных диаметров для более точного соответствия требованиям к площади стали. Наконец, максимальное количество стержней, установленных в балке заданной ширины, определяется диаметром стержня, минимальным расстоянием, максимальным размером заполнителя, диаметром хомута и требованиями к бетонному покрытию.
Рисунок-1: Различные размеры стержней4.
Расстояние между стержнямиACI 318-19 определяет минимальное расстояние между стержнями, равное диаметру стержня или 25 мм. Это минимальное расстояние должно поддерживаться, чтобы гарантировать правильное размещение бетона вокруг стальных стержней и предотвратить образование воздушных карманов под арматурой, которые, следовательно, обеспечивают хорошее сцепление между стальными опорами и бетоном. Если в балку уложены два слоя стальных стержней, то расстояние между ними должно быть не менее 25 мм.
5.
Защита бетона для арматурыПроектировщик должен поддерживать минимальную толщину бетонного покрытия за пределами самой внешней стали, чтобы обеспечить достаточную защиту бетона от огня и коррозии.
В соответствии с Кодексом ACI рекомендуется бетонное покрытие толщиной 40 мм для монтируемых балок, не подвергающихся непосредственному воздействию земли или погодных условий, и не менее 50 мм покрытия, если бетонная поверхность должна подвергаться воздействию погодных условий или контакта.
Для упрощения конструкции и снижения затрат габаритные размеры балок b и h почти округлены до ближайших 25 мм.
Рисунок-2: Бетонное покрытие Расчет дважды железобетонных балокОбычно балки проектируются как отдельно армированные бетонные балки, но неспособность бетона развивать адекватную силу сжатия потребует добавления стальных стержней в зону сжатия бетона.
Распределение напряжений и деформаций в дважды армированной бетонной балке показано на Рисунке 1.Когда арматура добавляется в зону сжатия балки, такое же количество добавляется в зону растяжения балки, чтобы противостоять силе сжатия стального стержня, как показано на рисунке 1, напряжение-деформация (B).
Рисунок-3: Диаграмма напряжения-деформации дважды армированной бетонной балкиВозможны два варианта расчета двояковыпуклой бетонной балки по режимам разрушения балки:
Случай 1: сталь для растяжения и сжатия при напряжении текучестиПредположим, что и компрессионная сталь (A’s), и растяжимая сталь (As) подвергаются напряжению до разрушения (предел текучести (fy)):
fs = fs ‘ = fy
Полный момент сопротивления балки можно разделить на две части.Первая часть (Mn 1 ) обеспечивается парой, состоящей из силы сжатия стали (A ‘s) и силы в зоне равного растяжения стали; см. Рисунок 1, диаграмма напряжений (B):
Вторая часть (Mn 2 ) представляет собой вклад оставшейся растянутой стали (As-A), действующей на сжатый бетон; см. Рисунок 1, диаграмма напряжений (A):
Где:
А: компрессионная сталь, мм 2
фу: предел текучести стального проката, МПа
d: эффективная глубина, измеренная от поверхности сжатия до центра стального стержня в зоне растяжения, мм
d ‘: расстояние от поверхности сжатия до центра сжатых стальных стержней, мм
As: общая площадь стали в растянутой зоне балки, мм 2
a: глубина прямоугольного блока напряжений, мм, может быть вычислена по уравнению 3
Где:
fc ‘: прочность бетона на сжатие, МПа
b: ширина бетонной балки, мм
Полный момент сопротивления дважды армированной бетонной балки можно рассчитать по следующей формуле:
Случай 2: Сталь для сжатия ниже предела текучестиАрматура сжатия может не достигать предела текучести, если:
- Балка широкая или мелкая.
- Имеет необычное бетонное покрытие над сжатой арматурой.
- Коэффициент усиления балки при растяжении низкий.
- Или балка армирована сталью с высоким пределом текучести.
Когда компрессионные стали ниже предела текучести при разрушении балки, предположение ( fs = fs ‘ ) больше не действует, поэтому следует разработать новые уравнения для учета сжимающего напряжения стали, которое ниже предел текучести.
Используйте минимальный коэффициент усиления при растяжении ( p — cy ), чтобы определить, поддается ли компрессионная сталь или нет:
Если коэффициент усиления при растяжении ( p ) меньше минимального коэффициента усиления при растяжении ( p — cy ), нейтральная ось достаточно высока, чтобы сжатие стали меньше предела текучести.
Итак, новые уравнения для напряжения при сжатии стали (f ‘ s ) и прочности на изгиб будут следующими:
Где:
E s : модуль упругости стали 200000 МПа
c: глубина нейтральной оси, мм, см. Рисунок-1.
Краткое описание методики проектирования дважды железобетонной балки
Шаг 1: Рассчитайте максимальный момент или момент сопротивления (M n ), которому может противостоять недостаточно армированная секция с ρ = ρ max .Соответствующая площадь растяжения стали As = ρ max bd,
Вычислите (a) из уравнения 7 и вычислите (d), используя следующее уравнение:
d = высота балки-крышка-диаметр хомута-0,5 * диаметр продольного стержня Уравнение 14
Шаг 2: Найдите избыточный момент (M 1 ), если он есть, который должен выдерживаться, и установите M 2 = M n , как рассчитано на шаге 1:
Где применяется M и или предельный момент рассчитывается исходя из приложенных нагрузок.
Шаг 3: Определите (As), которое рассчитывается на шаге 1, как As2, т. Е. Ту часть растянутой стальной площади в дважды армированной балке, которая работает с силой сжатия в бетоне, в (As-A’s = Как 2 ).
Шаг 4: Предварительно предположим, что fs ′ = fy, затем вычислите площадь сжатой стали (A), используя уравнение 5.
Шаг 5: Добавьте дополнительное количество растяжимой стали (As 1 = A ‘s), тогда общая площадь растянутой стали (As) в растянутой зоне балки будет (As 2 ) из шага 2. плюс (As 1 ).
Шаг 6: Проанализируйте дважды армированную бетонную балку, чтобы убедиться, что fs ′ = fy, то есть проверьте коэффициент армирования при растяжении ( p ) относительно ρ — cy . Вычислите ( p ) с помощью уравнения 4 и используйте (As) из (, шаг 5, ).
Шаг 7: Если ρ> ρ — cy , напряжение стали сжатия равно (fy), и расчет завершен. Однако при ρ <ρ — cy напряжение стали при сжатии меньше (fy), и площадь стали при сжатии должна быть увеличена, чтобы обеспечить необходимое усилие.
Шаг 8: Рассчитайте глубину нейтральной оси, которая равна прямоугольному блоку напряжений, деленному на B 1 , т.е. либо 0,85, либо значение из уравнения 3.
Шаг 9: Рассчитайте напряжение в стали при сжатии с помощью уравнения 10 и, наконец, оцените измененную площадь армирования при сжатии с помощью уравнения 5, в котором значение пробки (fs ‘) вместо (fy).
Шаг 10: Определите количество стержней и нарисуйте детали конструкции.
Пример:
Спроектируйте прямоугольную балку, которая должна выдерживать рабочую временную нагрузку 45 кН / м и расчетную статическую нагрузку 20 кН / м (включая собственный вес) на 5.Пролет 5 м ограничен в поперечном сечении по архитектурным причинам шириной 250 мм и общей глубиной 500 мм. Если fy = 420 МПа и fc ′ = 28 МПа.
Решение:
1- Сначала вычислите предельную распределенную нагрузку (w u ), используя подходящую комбинацию нагрузок, предоставленную ACI 318-19:
w u = 1,2DL + 1,6LL = 1,2 (15,5) +1,6 (38) = 79,4 кН / м
2- Рассчитайте приложенный или предельный момент, используя уравнение максимального момента для балки без опоры:
M u = (w u l 2 ) / 8 = (79.4 * 5,5 2 ) / 8 = 300,23 кН.м
Используйте уравнение 13, чтобы оценить максимальный момент сопротивления (M n ), который может обеспечить балка из монолитного железобетона:
Определите неизвестные параметры уравнения 13:
Используйте уравнение 14, чтобы определить эффективную глубину (d), принимая диаметр стержня 29 мм, два слоя стержней и размер стержня 10 мм для хомутов.
d = 500-40-10-29- (25/2) = 408,5 мм
Примечание:
Если уравнение 1 используется для вычисления ( p max ) , то значение коэффициента уменьшения прочности для балки равно 0.9, следует проверить. Вот почему ACI 318-19 рекомендует использовать деформацию растяжения 0,005 в уравнении 1 вместо 0,004, чтобы избежать этой проверки и обеспечить коэффициент снижения прочности 0,9:
.p макс = 0,85 * 0,85 * (28/420) * (0,003 / (0,003 + 0,005)) = 0,01806
As = p bd = 0,01806 * 250 * 412,5 = 1862,695 мм 2 , это значение будет определено как As2 (обсуждается в шаге 3 процедуры проектирования), если балка спроектирована как балка из дважды армированного бетона
а = (1862.695 * 420) / (0,85 * 28 * 250) = 131,484 мм
M n = 1862,695 * 420 * (408,5- (131,484 / 2)) = 268150517,4 Н · мм = 268,150 кН · м
M d = коэффициент снижения прочности * M n = 0,9 * 268,150 = 241,335 кН.м
Так как M d < M u , балка должна быть спроектирована как дважды армированная бетонная балка.
3- Рассчитайте избыточный момент (M 1 ) по уравнению 15:
M 1 = (300.23 / 0,9) -241,335 = 92,253 кН.м
4- Предположим, что напряжение сжатия стали достигает предела текучести fs ‘= fy, затем вычислите площадь сжатой стали (A) с помощью уравнения 5. Для вычисления (d’) предположите, что диаметр стержня сжатия составляет 22 мм.
d ‘= диаметр крышки стержня хомутов + 0,5 * диаметр продольного стержня
d ‘= 40 + 10 + 11 = 61 мм
A = ( 92,253 * 10 6 ) / (420 * ( 408,5 -61)) = 632,086 мм 2 = As1
5- Расчет общей площади растягиваемой арматуры, проверка, если (fs ′ = fy):
As = As1 + As2 = 1862.695+ 632,086 = 2494,78 мм 2
p = As / bd = 2494,78 / (250 * 408,5) = 0,02442
p ‘= A’s / bd = 632,086 / (250 * 408,5) = 6,189 * 10 -3
p — cy = 0,85 * 0,85 * (28/420) * (61 / 408,5) * (0,003 / (0,003-0,0021)) + 6,189 * 10 -3 = 0,03016
Так как p — cy > p , компрессионная сталь не поддается деформации, и площадь компрессионной стали следует пересмотреть.
6- Вычислить глубину нейтральной оси (c):
c = a / B 1 = 131,484 / 0,85 = 154,687 мм
7- Используйте уравнение 7 для расчета напряжения в стали на сжатие:
fs ‘ = 0,003 * 200000 * ((154,687-61) / 154,687) = 363,393 МПа
As ‘= (92,253 * 10 6 ) / (363,393 * (408,5-61)) = 730,548 мм 2
8- Определите количество стержней для арматуры на сжатие и растяжение:
№стержней для зоны растяжения = Общая площадь армирования / площадь одиночного стержня
Кол-во стержней = 2494,78 / (PI / 4 * 29 2 ) = 3,7 = 4
Количество стержней для зоны сжатия = Общая площадь армирования / площадь одиночного стержня
Кол-во стержней = 730,548 / (PI / 4 * 22 2 ) = 1,92 = 2
Следовательно, имеется четыре стержня в двух слоях на стороне растяжения балки и два стержня в одном слое на стороне сжатия балки.
Следует знать, что количество стержней было округлено, поэтому площадь армирования как в зоне сжатия, так и в зоне растяжения увеличивается.Новые стальные площадки следующие:
As = 4 * (PI / 4 * 29 2 ) = 2642,079 мм 2
As ‘= 2 * (PI / 4 * 22 2 ) = 760,265 мм 2
Поскольку площадь армирования увеличивается, мы должны проверить, достигает ли компрессионная сталь 363,393 МПа или нет:
As-As ‘= 2642.079-632.086 = 2009.993 мм 2
a = (2009,993 * 420) / (0,85 * 28 * 250) = 141,881 мм
с = 141,881 / 0.85 = 166,919 мм
fs ‘ = 0,003 * 200000 * ((166,919-61) /166,919) = 380,733 МПа> 363,393 МПа
Для получения более подробной информации о проверке и оценке коэффициента снижения прочности щелкните здесь.
dt = 500-40-10- (29/2) = 435,5 мм
c / dt = 166,919 / 435,5 = 0,383> 0,375, поэтому коэффициент снижения прочности равен 0,9.
Наконец, используйте уравнение для оценки момента сопротивления (M d ) балки, и оно должно быть больше приложенного момента ( M u = 300.23 ):
Наконец, используйте уравнение 12 для оценки проектного сопротивления моменту (M d ) балки, и оно должно быть больше приложенного момента ( M u = 300,23 ):
M n = 2009,993 * 420 * (408,5- (141,881 / 2)) + 380,733 * 760,265 (408,5-61) = 385553383,5 Н · мм = 385,553 кН · м
M d = 0,9 * 385,553 = 346,998 кН.м > 300,23 , поэтому конструкция безопасна.
Рисунок-4: Деталь конструкции балкиЧасто задаваемые вопросы
Что такое двояковыпуклая бетонная балка?Балка из железобетона со стальной арматурой как в зоне растяжения, так и в зоне сжатия называется балкой двойного армирования.
Почему в бетонных балках предусмотрено армирование на сжатие? Для увеличения несущей способности балок предусмотрена компрессионная арматура. Увеличить несущую способность балки можно за счет увеличения ее размеров.
Однако не всегда возможно изменить размеры по архитектурным соображениям. Следовательно, дважды армированная бетонная балка будет единственным вариантом, который следует рассмотреть.
Балка, армированная только в зоне растяжения, называется балкой из однокомпонентного железобетона, тогда как балка из дважды армированного бетона армируется как на растянутой, так и на сжатой поверхности.
Каковы преимущества компрессионной арматуры помимо повышения прочности? 1- Уменьшение долговременного прогиба балки.
2- Удерживает хомуты в их положении во время заливки и уплотнения бетона.
3. Для минимального нагружающего момента
1- Балка неглубокая или широкая.
2- Низкий коэффициент усиления при растяжении балки.
3. Марка арматуры высокая.
4- Поверх сжатой арматуры используется необычное бетонное покрытие.
Подробнее
Расчет прямоугольной железобетонной балки
Как рассчитать несущую способность существующей балки для ремонта?
Общие сведения о передаче нагрузок с плиты на балки
Калькулятор концентрации напряжения — Филе уступа в плоском стержне
Противоположные лопатки на ступенчатой планке. Калькулятор коэффициентов концентрации напряжений (K t ) для растягивающих, изгибающих и скручивающих нагрузок.
Примечание. Используйте точку «.» как десятичный разделитель.
| РЕЗУЛЬТАТЫ | ||
| ТИП НАГРУЗКИ — НАПРЯЖЕНИЕ | ||
| Параметр | Стоимость | |
| Коэффициент концентрации напряжений [K t ] * | — | — |
| Номинальное напряжение растяжения на полосе [σ номинал ] o | — | МПапсикси |
| Максимальное напряжение растяжения от растягивающей нагрузки [σ макс ] | — | |
| ВИД НАГРУЗКИ — ГИБКА | ||
| Параметр | Стоимость | |
| Коэффициент концентрации напряжений [K t ] * | — | — |
| Номинальное напряжение растяжения на полосе [σ ном ] + | — | МПапсикси |
| Максимальное напряжение растяжения из-за изгиба [σ макс ] | — | |
Примечание 1: * Геометрия увеличивается на σ nom в K t .(K т = σ макс / σ ном )
Коэффициент концентрации напряжений: Изменения размеров и неоднородности элемента в нагруженной конструкции вызывают колебания напряжения, и высокие напряжения концентрируются около этих изменений размеров. Эта ситуация высоких напряжений вблизи изменений размеров и разрывов элемента (отверстия, острые углы, трещины и т. Д.) Называется концентрацией напряжений. Отношение пикового напряжения около места возникновения напряжений к среднему напряжению по стержню называется коэффициентом концентрации напряжений.
% PDF-1.6 % 2 0 obj > эндобдж 43 0 объект > поток 2010-03-17T14: 58: 59-04: 002010-03-17T14: 58: 59-04: 002010-03-17T14: 58: 59-04: 00application / pdfuuid: 94ef03ab-bef3-4dc0-9c7f-4dc0525e526euuid: b057a40d-2a15-44c7-8c8f-84bfc57d44f5 конечный поток эндобдж 38 0 объект > / Кодировка >>>>> эндобдж 1 0 объект > эндобдж 3 0 obj > эндобдж 8 0 объект > эндобдж 13 0 объект > эндобдж 18 0 объект > эндобдж 23 0 объект > эндобдж 28 0 объект > эндобдж 30 0 объект > поток 1006 0 0612 0 0 см / Img6 Do конечный поток эндобдж 29 0 объект > / ProcSet [/ PDF / ImageB] >> эндобдж 31 0 объект > / Высота 2551 / Тип / XObject >> stream ‘^ YJ / غ ;? TO? OM_ _ M’4_ ߪ n `j% / R | װ M! | A7 / o] _m l ~ / |` P97u # k @ hnAnAA = W D] ^ Av [/ A ږ T > км.zT0t6 / # Vmcî_f: E] f $ zkBMO: N? 7ѻVO] 0 ~ 0߱ ꓆ Ot: ߿_ I, mekh0a «X: SDU1ȹ.2B9A@d» CX2 {C (hXmWԄV ޗ2 Y ~ YA ݦ Ǽ ״ pBe! $ B% Fu pDDDDD @: aug ڤ> xa ICMwm0Rm \ 0gc
Принцип суперпозиции континуума —Принцип суперпозиции континуума —
при равномерном сжатии стержня
Общие уравнения для трех деформаций: $$ \ epsilon_x = \ frac {\ sigma_x- \ nu (\ sigma_y + \ sigma_z)} {E} $$ $$ \ epsilon_y = \ frac {\ sigma_y- \ nu (\ sigma_x + \ sigma_z)} {E} $$ $$ \ epsilon_z = \ frac {\ sigma_z- \ nu (\ sigma_x + \ sigma_y)} {E} $$ Для случая одноосного нагружения $ \ sigma_x = \ sigma $ в направлении x, в то время как напряжения в направлениях y и z равны нулю ($ \ sigma_y = \ sigma_z = 0 $), мы получаем из трех приведенных выше уравнений: $$ \ epsilon_x = \ frac {\ sigma} {E} $$ $$ \ epsilon_y = — \ nu \ frac {\ sigma} {E} = — \ nu \ epsilon_x $$ $$ \ epsilon_z = — \ nu \ frac {\ sigma} {E} = — \ nu \ epsilon_x $$
Теперь давайте рассмотрим другой вид нагрузки, где вместо нагрузки только в направлении x существуют также равные напряжения в направлениях y и z, так что $$ \ sigma_x = \ sigma_y = \ sigma_z = \ sigma $ $ Если мы подставим их в три общих уравнения для деформаций через напряжения, мы получим: $$ \ epsilon_x = \ epsilon_y = \ epsilon_z = (1-2 \ nu) \ frac {\ sigma} {E} $ $ Это уравнение также можно получить, начав с одноосного напряжения в направлении x, затем наложив одинаковое напряжение в направлении y, а затем наложив такое же напряжение в направлении z.
Если $ \ sigma = -p $, линейные деформации в трех направлениях равны $$ \ epsilon = — (1-2 \ nu) \ frac {p} {E} $$ Объемная деформация $ \ epsilon_v $ равна трем. умноженное на линейную деформацию, поэтому $$ \ epsilon_v = -3 (1-2 \ nu) \ frac {p} {E} $$ Поскольку исходный объем равен $ L_xL_yL_z $, изменение объема равно $$ \ Delta V = -3 (1-2 \ nu) \ frac {p} {E} L_xL_yL_z $$ ПРИЛОЖЕНИЕ
Вот еще один способ взглянуть на это. Предположим, вы начали с одноосного напряжения $ \ sigma_x $ на теле. Тогда деформации в трех направлениях равны $$ \ epsilon_x = \ frac {\ sigma_x} {E} $$ $$ \ epsilon_y = — \ nu \ epsilon_x = — \ nu \ frac {\ sigma_x} {E} $$ и $$ \ epsilon_z = — \ nu \ epsilon_x = — \ nu \ frac {\ sigma_x} {E} $$ Если вместо этого вы начнете с единственного напряжения $ \ sigma_y $ на теле, тогда напряжения в трех направлениях будут $$ \ epsilon_y = \ frac {\ sigma_y} {E} $$ $$ \ epsilon_x = — \ nu \ epsilon_y = — \ nu \ frac {\ sigma_y} {E} $$ и $$ \ epsilon_z = — \ nu \ epsilon_y = — \ nu \ frac {\ sigma_y} {E} $$
Если вместо этого вы начнете с единственного напряжения $ \ sigma_z $ на теле, тогда напряжения в трех направлениях будут $$ \ epsilon_z = \ frac {\ sigma_z} {E} $$ $$ \ epsilon_x = — \ nu \ epsilon_z = — \ nu \ frac {\ sigma_z} {E} $$ и $$ \ epsilon_y = — \ nu \ epsilon_z = — \ nu \ frac {\ sigma_z} {E} $$
Если вместо этого вы приложите к телу все три этих напряжения одновременно, полученные вами деформации будут получены путем линейного наложения (т.