Расчет балки онлайн
Автор admin На чтение 3 мин Просмотров 5.7к. Опубликовано
Для расчета балок первым делом необходимо определить усилия, возникающие в конструкциях. В данном разделе показано, как находить усилия, опорные реакции, прогибы и углы поворота в различных изгибаемых конструкциях. Для самых распространенных из них вы можете воспользоваться онлайн расчетом. Для редких — приведены все формулы определения необходимых значений.
Содержание
- Онлайн расчет балки на двух опорах (калькулятор).
- >>> Перейти к расчету балки на двух опорах <<<
- Онлайн расчет консольной балки (калькулятор).
- >>> Перейти к расчету консольной балки <<<
- Расчет однопролетной балки на двух шарнирных опорах.
- Расчет балок с жестким защемлением на двух опорах
- Расчет консольных балок
- Расчет двухпролетных балок
Онлайн расчет балки на двух опорах (калькулятор).
Приведен расчет на момент, прогиб и опорные реакции от сосредоточенной и распределнной силы.
Синие ячейки — ввод данных. (Белые ячейки — ввод координаты для определения промежуточного итога).
Зеленые ячейки — расчетные, промежуточный итог.
Оранжевые ячейки — максимальные значения.
>>> Перейти к расчету балки на двух опорах <<<Онлайн расчет консольной балки (калькулятор).
Приведен расчет на момент, прогиб и опорные реакции от сосредоточенной и распределнной силы.
Синие ячейки — ввод данных. (Белые ячейки — ввод координаты для определения промежуточного итога).
Зеленые ячейки — расчетные, промежуточный итог.
Оранжевые ячейки — максимальные значения.
>>> Перейти к расчету консольной балки <<<Расчет однопролетной балки на двух шарнирных опорах.
Рис.1 Расчет балки на двух шарнирных опорах при одной сосредоточенной нагрузке
Рис.2 Расчет балки на двух шарнирных опорах при двух сосредоточенных нагрузках
Рис.3 Расчет балки на двух шарнирных опорах при одной равномерно-распределенной нагрузке
Рис4. Расчет балки на двух шарнирных опорах при одной неравномерно-распределенной нагрузке
Рис5. Расчет балки на двух шарнирных опорах при действии изгибающего момента
Расчет балок с жестким защемлением на двух опорах
Рис6. Расчет балки с жестким защемлением на опорах при одной сосредоточенной нагрузке
Рис7. Расчет балки с жестким защемлением на опорах при двух сосредоточенных нагрузках
Рис8. Расчет балки с жестким защемлением на опорах при одной равномерно-распределенной нагрузке
Рис9. Расчет балки с жестким защемлением на опорах при одной неравномерно-распределенной нагрузке
Рис10.
Расчет балки с жестким защемлением на опорах при действии изгибающего момента
Расчет консольных балок
Рис11. Расчет однопролетной балки с жестким защемлением на одной опоре при одной сосредоточенной нагрузке
Рис12. Расчет однопролетной балки с жестким защемлением на одной опоре при одной равномерно-распределенной нагрузке
Рис13. Расчет однопролетной балки с жестким защемлением на одной опоре при одной неравномерно-распределенной нагрузке
Рис14. Расчет однопролетной балки с жестким защемлением на одной опоре при действии изгибающего момента
Расчет двухпролетных балок
Рис15. Расчет двухпролетной балки с шарнирными опорами при одной сосредоточенной нагрузке
Рис16. Расчет двухпролетной балки с шарнирными опорами при одной равномерно-распределенной нагрузке
Рис17. Расчет двухпролетной балки с шарнирными опорами при одной неравномерно-распределенной нагрузке
|
Random converter |
Калькуляторы рычагаНажать для просмотра увеличенного изображения Калькулятор выигрыша в силе и усилия нагрузки рычагаКалькулятор определяет усилие нагрузки и выигрыш в силе для рычага любого порядка. Пример: Рассчитать выигрыш в силе и усилие нагрузки для рычага первого рода, если его плечо приложения силы равно 50 см, плечо приложения нагрузки равно 20 см и приложенное усилие равно 10 Н. Входные данные Род рычага 1 2, AE > AL 3, AEL Плечо приложения силы (входное плечо) AEсантиметр (см)метр (м)дюймфут Плечо приложения нагрузки (выходное плечо) ALсантиметр (см)метр (м)дюймфут Приложенное усилие FEньютон (Н)джоуль на метр (Дж/м)грамм-сила (гс)килограмм-сила (кгс)фунт-сила Для расчета введите значения и нажмите кнопку Рассчитать. Для расчета выигрыша нужно ввести только величины плеч рычага. Если нужно рассчитать усилие нагрузки, введите приложенное усилие. Поделиться Поделиться ссылкой на этот калькулятор, включая входные параметры Twitter Facebook Google+ VK Закрыть Выходные данные Выигрыш в силе MA Усилие нагрузки FL Н Калькулятор положения опоры рычага I родаКалькулятор определяет положение опоры и размер плеча приложения силы рычага первого рода, в котором опора расположена между точками приложения сил. Пример: Рассчитать положение опоры рычага первого рода, если его длина равна 60 см, приложенное усилие равно 10 Н и усилие нагрузки равно 20 Н. Входные данные Общая длина рычага L=AE+ALсантиметр (см)метр (м)дюймфут Приложенное усилие FEньютон (Н)джоуль на метр (Дж/м)грамм-сила (гс)килограмм-сила (кгс)фунт-сила Усилие нагрузки FLньютон (Н)джоуль на метр (Дж/м)грамм-сила (гс)килограмм-сила (кгс)фунт-сила Поделиться Поделиться ссылкой на этот калькулятор, включая входные параметры Twitter Facebook Google+ VK Закрыть Выходные данные Положение опоры (плечо нагрузки) AL м Плечо приложения силы AE м Калькулятор положения нагрузки для рычага II родаВ рычаге II рода точка опоры и точка приложения силы находятся на противоположных концах рычага. Пример: рассчитать положение нагрузки для рычага II рода, если его полная длина равна 40 см, приложенное усилие равно 10 Н и усилие нагрузки равно 20 Н. Входные данные Общая длина рычага L=AEсантиметр (см)метр (м)дюймфут Приложенное усилие FEньютон (Н)джоуль на метр (Дж/м)грамм-сила (гс)килограмм-сила (кгс)фунт-сила Усилие нагрузки FLньютон (Н)джоуль на метр (Дж/м)грамм-сила (гс)килограмм-сила (кгс)фунт-сила Поделиться Поделиться ссылкой на этот калькулятор, включая входные параметры Twitter Facebook Google+ VK Закрыть Выходные данные Положение нагрузки (плечо нагрузки) AL м Плечо приложения силы AE=L м Калькулятор положения приложенного усилия для рычага III родаВ рычаге III рода точка опоры и нагрузка находятся на противоположных концах рычага. Пример: Рассчитать положение точки приложения нагрузки рычага III рода, если его полная длина равна 50 см, приложенное усилие равно 20 Н и усилие нагрузки равно 10 Н. Входные данные Общая длина рычага L=ALсантиметр (см)метр (м)дюймфут Приложенное усилие FEньютон (Н)джоуль на метр (Дж/м)грамм-сила (гс)килограмм-сила (кгс)фунт-сила Усилие нагрузки FLньютон (Н)джоуль на метр (Дж/м)грамм-сила (гс)килограмм-сила (кгс)фунт-сила Поделиться Поделиться ссылкой на этот калькулятор, включая входные параметры Twitter Facebook Google+ VK Закрыть Выходные данные Точка приложения усилия (плечо усилия) AE м Плечо нагрузки AL=L м Определения и формулыРычаги и их типыРычаг представляет собой простейший механизм, состоящий из твердого тела, которое может вращаться вокруг неподвижной опоры. Для идеального рычага, в котором не теряется энергия и который является абсолютно жестким, отношение плеч рычага определяет отношение приложенного усилия и нагрузки. Эта взаимосвязь называется правилом рычага: Выигрыш в силе, даваемый рычагом, определяется как отношение выходной силы (нагрузки) FL к входной силе (приложенному усилию) FE: Отсюда можно определить приложенное усилие: Существует три типа рычагов, которые отличаются взаимным расположением точки опоры и плеч рычага, причем правило рычага одинаково для всех трех типов рычагов. Рычаги I рода: В этих рычагах опора находится между точками приложения сил, которые находятся на противоположных концах рычага. Примерами рычагов I рода являются качели (перекладина) и плоскогубцы. В рычагах I рода плечо нагрузки может быть больше или меньше плеча приложения силы, а выигрыш в силе может быть больше, меньше или равен единице. В рычагах I рода полная длина рычага L равна сумме длин плеча нагрузки AL и плеча усилия AE: Формулу для определения плеча нагрузки (и, соответственно, положения точки опоры) можно вывести из приведенного выше правила рычага: Рычаги II рода: В этих рычагах точка опоры и точка приложения силы расположены на противоположных концах рычага. Нагрузка приложена между опорой и усилием. Примеры рычагов II рода — тачка, щипцы для орехов и открывалка для бутылок. В рычаге второго рода плечо приложения силы всегда больше плеча приложения нагрузки и выигрыш в силе всегда больше единицы. В рычаге II рода полная длина рычага равна плечу приложения нагрузки: Плечо приложения нагрузки (или точка приложения нагрузки) рассчитывается по формуле, которая выводится из приведенного выше правила рычага: Рычаги III рода: В этих рычагах точка опоры и нагрузка расположены на противоположных концах рычага. Усилие приложено между нагрузкой и точкой опоры. Примеры рычагов III рода — метла, предплечье человека и удочка. В рычагах III рода выигрыш в силе всегда меньше единицы и плечо приложения силы всегда меньше плеча приложения нагрузки. В рычагах III рода полная длина рычага равна длине плеча приложения нагрузки: Длины плеча приложения силы (точка приложения силы) рассчитывается по формуле, выведенной из правила рычага: В экскаваторе для перемещения стрелы (рычаг III рода слева), рукояти (рычаг I рода в центре) и ковша (еще один рычаг I рода справа) используются гидравлические цилиндры Автор статьи: Анатолий Золотков Другие калькуляторы простейших механизмов:
Калькуляторы Механика |
Обычно рычаги используют для перемещения тяжелых грузов (обычно говорят об усилии нагрузки или просто грузе FL) путем приложения меньшей силы FE. Часть рычага между его концом и точкой опоры, к которой приложена нагрузка, называется плечом нагрузки AL. Вторая часть рычага, к которой приложено усилие, называется плечом приложения усилия AE. Рычаг — один из шести простейших механизмов, определенных учеными эпохи Возрождения.
(БЕСПЛАТНЫЙ онлайн-инструмент)
30 января 2023 г.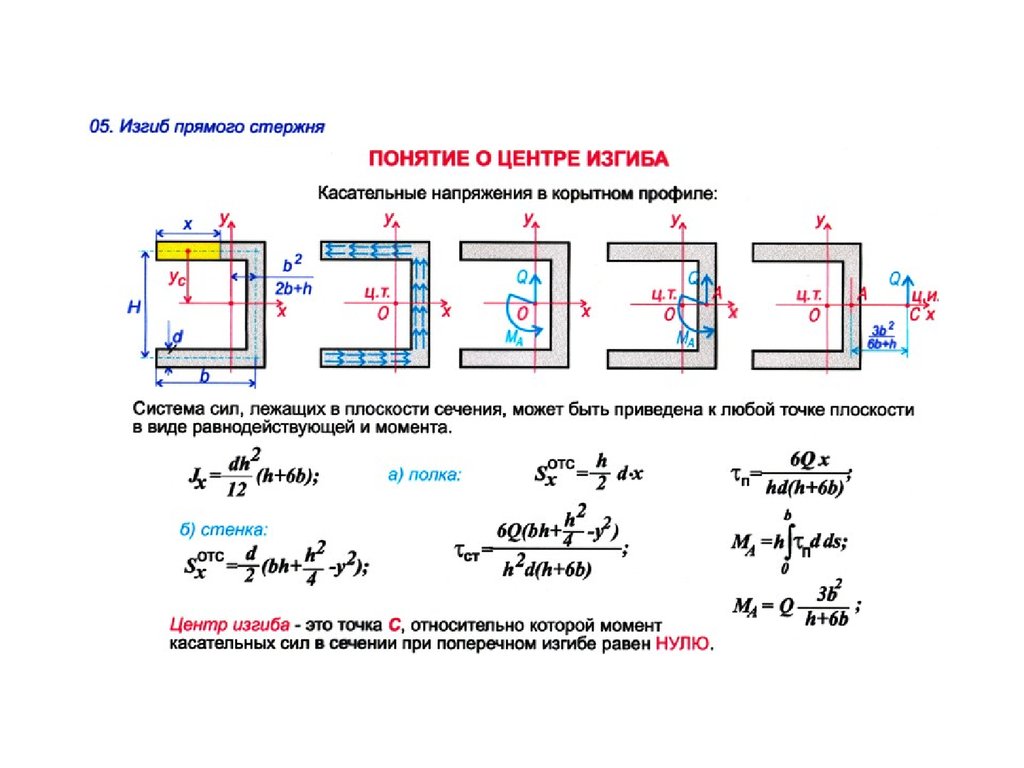
Припуск на изгиб – это значение, используемое для определения длины листового металла после гибки. Она зависит от материала, толщины листа и типа используемой гибочной матрицы. Припуск на изгиб представляет собой статистическую величину, полученную на основе многолетнего опыта и многократных проверок опытных конструкторов пресс-форм.
Разработчики пресс-форм могут использовать расчетную формулу непосредственно для получения размера развернутой пластины изогнутой конструкции, который основан на данных допуска на изгиб.
Метод расчета припуска на изгиб
Расчет припуска на изгиб и вычета при изгибе — это методы, которые можно использовать для определения длины исходных материалов из листового металла в плоской форме, чтобы получить желаемый размер изгибаемой части.
Метод расчета припуска на изгиб:
При использовании значения припуска на изгиб для определения общей длины правки используется следующее уравнение:
L t = A + B + BA
Где:
·L t – общая длина плоской детали
·A и B показаны на рисунке
·BA – величина припуска на изгиб
Метод расчета вычета изгиба: определить общую длину правки при использовании величины вычета изгиба:
L t = A + B – BD
Где:
·L t – общая длина плоского проката
·A и B показаны на цифра
·BD – значение вычета при изгибе.
Другие методы расчета для определения плоской длины исходного листового металла включают использование таблицы допусков на изгиб, К-фактор и расчеты на изгиб.
Для новых операторов листогибочных прессов, которые могут не знать, как рассчитать допуск на изгиб, был создан калькулятор допуска на изгиб, облегчающий их повседневную работу.
Чтобы узнать больше о допусках на изгиб, вы также можете посмотреть видео на эту тему.
- Калькулятор К-фактора
- Калькулятор Y-фактора
- Калькулятор вычета изгиба
Дополнительная литература:
- Как рассчитать допуск на изгиб, вычет изгиба и К?
Bend allowance chart
Bend allowance chart for SPCC (mild steel)
| Material | Thickness | Bending angle | V opening | Inner radius | Bends Allowance |
|---|---|---|---|---|---|
| SPCC | 0. 5 | 90 | V4 | 0.5 | 0.95 |
| 100 | 0.73 | ||||
| 135 | 0.3 | ||||
| 175 | 0.03 | ||||
| SPCC | 0.5 | 90 | V5 | 0.5 | 1.03 |
| 100 | 0.79 | ||||
| 135 | 0.33 | ||||
| 175 | 0.03 | ||||
| SPCC | 0.5 | 90 | V6 | 0.5 | 1.1 |
| 100 | 0.85 | ||||
| 135 | 0.35 | ||||
| 175 | 0.03 | ||||
| SPCC | 0. 6 | 90 | V4 | 0.5 | 1.08 |
| 100 | 0.83 | ||||
| 135 | 0.35 | ||||
| 175 | 0.03 | ||||
| SPCC | 0.6 | 90 | V5 | 0.5 | 1.15 |
| 100 | 0.89 | ||||
| 135 | 0.37 | ||||
| 175 | 0.03 | ||||
| SPCC | 0.6 | 90 | V6 | 0.5 | 1.23 |
| 100 | 0.95 | ||||
| 135 | 0.39 | ||||
| 175 | 0.03 | ||||
| SPCC | 0. 8 | 90 | V6 | 0.5 | 1.49 |
| 120 | 0.73 | ||||
| 135 | 0.47 | ||||
| 150 | 0.25 | ||||
| SPCC | 0.8 | 90 | V8 | 0 | 1.64 |
| 120 | 0.81 | ||||
| 135 | 0.52 | ||||
| 150 | 0.27 | ||||
| SPCC | 0.8 | 90 | V10 | 0 | 1.79 |
| 120 | 0.88 | ||||
| 135 | 0.57 | ||||
| 150 | 0.3 | ||||
| SPCC | 1 | 90 | V10 | 0 | 2. 05 |
| 100 | 1.58 | ||||
| 120 | 1.01 | ||||
| 135 | 0.62 | ||||
| 175 | 0.06 | ||||
| SPCC | 1 | 90 | V8 | 0 | 1.9 |
| 100 | 1.47 | ||||
| 120 | 0.93 | ||||
| 135 | 0.6 | ||||
| 175 | 0.05 | ||||
| SPCC | 1 | 90 | V6 | 0 | 1.74 |
| 100 | 1.35 | ||||
| 120 | 0.86 | ||||
| 135 | 0.56 | ||||
| 175 | 0.05 | ||||
| SPCC | 1.2 | 90 | V10 | 1. 4 | 2.31 |
| 100 | 1.78 | ||||
| 120 | 1.13 | ||||
| 135 | 0.73 | ||||
| 175 | 0.06 | ||||
| SPCC | 1.2 | 90 | V8 | 1.4 | 2.15 |
| 100 | 1.66 | ||||
| 120 | 1.06 | ||||
| 135 | 0.69 | ||||
| 175 | 0.06 | ||||
| SPCC | 1.2 | 90 | V6 | 1.4 | 2 |
| 100 | 1.55 | ||||
| 120 | 0.98 | ||||
| 135 | 0.64 | ||||
| 175 | 0.05 | ||||
| SPCC | 1.5 | 90 | V6 | 1. 7 | 2.36 |
| 100 | 1.82 | ||||
| 120 | 1.16 | ||||
| 135 | 0.75 | ||||
| 175 | 0.06 | ||||
| SPCC | 1.5 | 90 | V12 | 1.7 | 2.8 |
| 100 | 2.17 | ||||
| 120 | 1.38 | ||||
| 135 | 0.89 | ||||
| 175 | 0.08 | ||||
| SPCC | 1.5 | 90 | V10 | 1.7 | 2.65 |
| 100 | 2.05 | ||||
| 120 | 1.31 | ||||
| 135 | 0.85 | ||||
| 175 | 0.07 | ||||
| SPCC | 1.5 | 90 | V8 | 1. 7 | 2.5 |
| 100 | 1.94 | ||||
| 120 | 1.23 | ||||
| 135 | 0.8 | ||||
| 175 | 0.07 | ||||
| SPCC | 2 | 90 | V10 | 2 | 3.29 |
| 100 | 2.54 | ||||
| 120 | 1.62 | ||||
| 135 | 1.05 | ||||
| 175 | 0.09 | ||||
| SPCC | 2 | 90 | V12 | 2 | 3.44 |
| 100 | 2.66 | ||||
| 120 | 1.69 | ||||
| 135 | 1.1 | ||||
| 175 | 0.09 | ||||
| SPCC | 2.5 | 90 | V18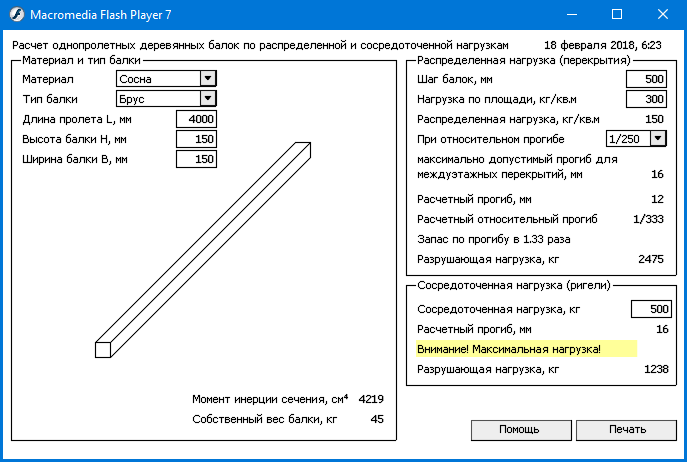 | 3. 03 | 4.6 |
| 100 | 3.56 | ||||
| 120 | 2.26 | ||||
| 135 | 1.47 | ||||
| 175 | 0.12 | ||||
| SPCC | 2.5 | 90 | V12 | 3.03 | 4.15 |
| 100 | 3.21 | ||||
| 120 | 2.04 | ||||
| 135 | 1.32 | ||||
| 175 | 0.11 | ||||
| SPCC | 2.5 | 90 | V10 | 3.03 | 4 |
| 100 | 3.09 | ||||
| 120 | 1.97 | ||||
| 135 | 1.28 | ||||
| 175 | 0.11 | ||||
| SPCC | 3 | 90 | V18 | 3. 133.13 | 5.22 |
| 100 | 4.03 | ||||
| 120 | 2.57 | ||||
| 135 | 1.66 | ||||
| 175 | 0.14 | ||||
| SPCC | 3 | 90 | V12 | 3.13 | 4.78 |
| 100 | 3.69 | ||||
| 120 | 2.35 | ||||
| 135 | 1.52 | ||||
| 175 | 0.13 | ||||
| SPCC | 3 | 90 | V10 | 3.13 | 4.63 |
| 100 | 3.58 | ||||
| 120 | 2.28 | ||||
| 135 | 1,48 | ||||
| 175 | 0,13 | ||||
Таблица допусков на изгиб для SUS (нержавеющая сталь)
| Bending angle | V opening | Inner radius | Bends Allowance | ||
|---|---|---|---|---|---|
| SUS | 0.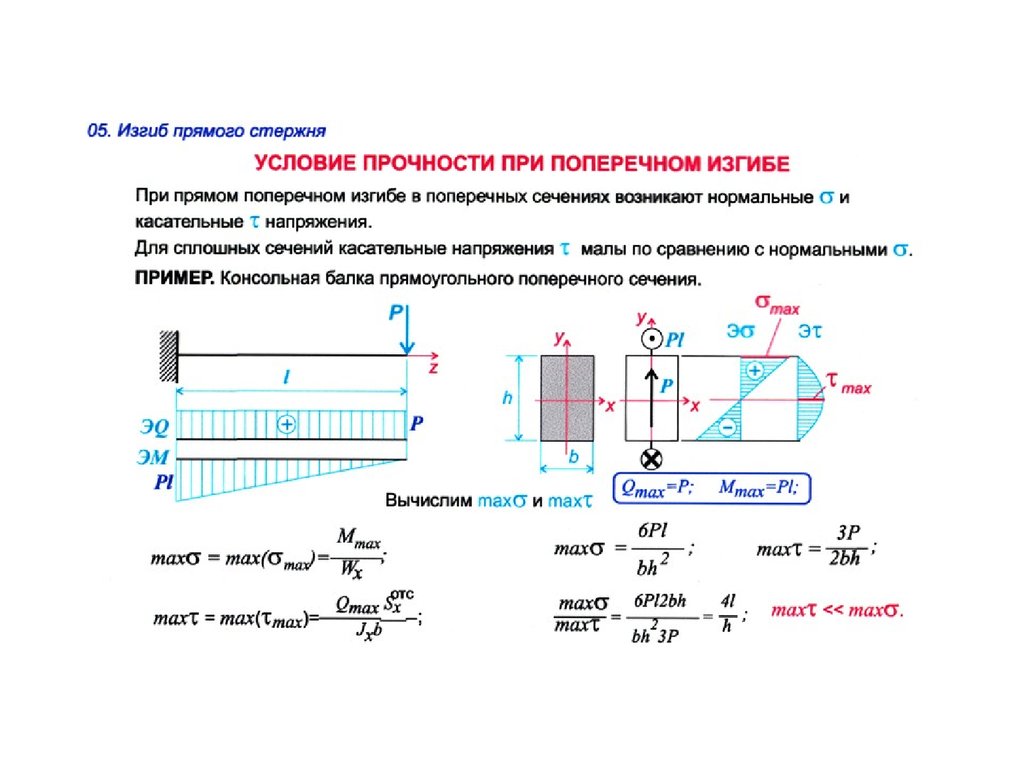 5 | 90 | 4 | 0.6 | 1.04 |
| 100 | 0.79 | ||||
| 120 | 0.48 | ||||
| 135 | 0.3 | ||||
| 175 | 0.04 | ||||
| SUS | 0.5 | 90 | 5 | 0.6 | 1.15 |
| 100 | 0.88 | ||||
| 120 | 0.54 | ||||
| 135 | 0.33 | ||||
| 175 | 0.04 | ||||
| SUS | 0.5 | 90 | 6 | 0.6 | 1.27 |
| 100 | 1.13 | ||||
| 120 | 0.59 | ||||
| 135 | 0.37 | ||||
| 175 | 0.04 | ||||
| SUS | 0. 6 | 90 | 4 | 0.6 | 1.16 |
| 100 | 0.88 | ||||
| 120 | 0.54 | ||||
| 135 | 0.34 | ||||
| 175 | 0.04 | ||||
| SUS | 0.6 | 90 | 5 | 0.6 | 1.27 |
| 100 | 0.97 | ||||
| 120 | 0.59 | ||||
| 135 | 0.37 | ||||
| 175 | 0.04 | ||||
| SUS | 0.6 | 90 | 6 | 0.6 | 1.38 |
| 100 | 1.05 | ||||
| 120 | 0.64 | ||||
| 135 | 0.4 | ||||
| 175 | 0.05 | ||||
| SUS | 0. 8 | 90 | 4 | 1.1 | 1.4 |
| 100 | 1.06 | ||||
| 120 | 0.65 | ||||
| 135 | 0.4 | ||||
| 175 | 0.05 | ||||
| SUS | 0.8 | 90 | 5 | 1.1 | 1.51 |
| 100 | 1.15 | ||||
| 120 | 0.7 | ||||
| 135 | 0.44 | ||||
| 175 | 0.05 | ||||
| SUS | 0.8 | 90 | 6 | 1.1 | 1.62 |
| 100 | 1.23 | ||||
| 120 | 0.75 | ||||
| 135 | 0.47 | ||||
| 175 | 0.06 | ||||
| SUS | 1 | 90 | 6 | 1. 9 | 1.87 |
| 100 | 1.42 | ||||
| 120 | 0.87 | ||||
| 135 | 0.54 | ||||
| 175 | 0.07 | ||||
| SUS | 1 | 90 | 8 | 1.9 | 2.1 |
| 100 | 1.6 | ||||
| 120 | 0.98 | ||||
| 135 | 0.61 | ||||
| 175 | 0.07 | ||||
| SUS | 1.2 | 90 | 6 | 1.6 | 2.1 |
| 100 | 1.59 | ||||
| 120 | 0.97 | ||||
| 135 | 0.61 | ||||
| 175 | 0.07 | ||||
| SUS | 1.2 | 90 | 8 | 1. 6 | 2.32 |
| 100 | 1.76 | ||||
| 120 | 1.08 | ||||
| 135 | 0.67 | ||||
| 175 | 0.08 | ||||
| SUS | 1.2 | 90 | 10 | 1.6 | 2.54 |
| 100 | 1.93 | ||||
| 120 | 1.18 | ||||
| 135 | 0.74 | ||||
| 175 | 0.09 | ||||
| SUS | 1.5 | 90 | 8 | 2.1 | 2.68 |
| 100 | 2.03 | ||||
| 120 | 1.24 | ||||
| 135 | 0.77 | ||||
| 175 | 0.09 | ||||
| SUS | 1.5 | 90 | 10 | 2. 1 | 2.9 |
| 100 | 2.2 | ||||
| 120 | 1.35 | ||||
| 135 | 0.84 | ||||
| 175 | 0.1 | ||||
| SUS | 2 | 90 | 10 | 3.49 | |
| 100 | 2.65 | ||||
| 120 | 1.62 | ||||
| 135 | 1.01 | ||||
| 175 | 0.12 | ||||
| SUS | 2 | 90 | 12 | 3.7 | |
| 100 | 2.82 | ||||
| 120 | 1.72 | ||||
| 135 | 1.07 | ||||
| 175 | 0.13 | ||||
Bend allowance chart for SPHC (stainless steel)
| Material | Thickness | Угол изгиба | V-отверстие | Внутренний радиус | Припуск на изгиб |
|---|---|---|---|---|---|
| SPHC | 1 | 7 90 9009 | 1. 86 | 2.05 | |
| 100 | 1.58 | ||||
| 120 | 1.01 | ||||
| 135 | 0.62 | ||||
| 175 | 0.06 | ||||
| SPHC | 1 | 90 | V8 | 1.86 | 1.9 |
| 100 | 1.47 | ||||
| 120 | 0.93 | ||||
| 135 | 0.6 | ||||
| 175 | 0.05 | ||||
| SPHC | 1 | 90 | V6 | 1.86 | 1.74 |
| 100 | 1.35 | ||||
| 120 | 0.86 | ||||
| 135 | 0.56 | ||||
| 175 | 0.05 | ||||
| SPHC | 1.2 | 90 | V10 | 1. 44 | 2.31 |
| 100 | 1.78 | ||||
| 120 | 1.13 | ||||
| 135 | 0.73 | ||||
| 175 | 0.06 | ||||
| SPHC | 1.2 | 90 | V8 | 1.44 | 2.15 |
| 100 | 1.66 | ||||
| 120 | 1.06 | ||||
| 135 | 0.69 | ||||
| 175 | 0.06 | ||||
| SPHC | 1.2 | 90 | V6 | 1.44 | 2 |
| 100 | 1.55 | ||||
| 120 | 0.98 | ||||
| 135 | 0.64 | ||||
| 175 | 0.05 | ||||
| SPHC | 1.5 | 90 | V12 | 1. 74 | 2.8 |
| 100 | 2.17 | ||||
| 120 | 1.38 | ||||
| 135 | 0.89 | ||||
| 175 | 0.08 | ||||
| SPHC | 1.5 | 90 | V10 | 1.74 | 2.65 |
| 100 | 2.05 | ||||
| 120 | 1.31 | ||||
| 135 | 0.85 | ||||
| 175 | 0.07 | ||||
| SPHC | 1.5 | 90 | V8 | 1.74 | 2.5 |
| 100 | 1.94 | ||||
| 120 | 1.23 | ||||
| 135 | 0.8 | ||||
| 175 | 0.07 | ||||
| SPHC | 2 | 90 | V12 | 2. 01 | 3.44 |
| 100 | 2.66 | ||||
| 120 | 1.69 | ||||
| 135 | 1.1 | ||||
| 175 | 0.09 | ||||
| SPHC | 2 | 90 | V10 | 2.01 | 3.29 |
| 100 | 2.54 | ||||
| 120 | 1.62 | ||||
| 135 | 1.05 | ||||
| 175 | 0.09 | ||||
| SPHC | 2.5 | 90 | V18 | 3 | 4.6 |
| 100 | 3.25 | ||||
| 120 | 2.26 | ||||
| 135 | 1.47 | ||||
| 175 | 0.12 | ||||
| SPHC | 2.5 | 90 | V12 | 3 | 4. 15 |
| 100 | 3.21 | ||||
| 120 | 2.04 | ||||
| 135 | 1.32 | ||||
| 175 | 0.11 | ||||
| SPHC | 2.5 | 90 | V10 | 3 | 4 |
| 100 | 3.09 | ||||
| 120 | 1.97 | ||||
| 135 | 1.28 | ||||
| 175 | 0.11 | ||||
| SPHC | 3 | 90 | V18 | 3.1 | 5.22 |
| 100 | 4.03 | ||||
| 120 | 2.57 | ||||
| 135 | 1.66 | ||||
| 175 | 0.14 | ||||
| SPHC | 3 | 90 | V12 | 3.1 | 4. 78 |
| 100 | 3.69 | ||||
| 120 | 2.35 | ||||
| 135 | 1.52 | ||||
| 175 | 0.13 | ||||
| SPHC | 3 | 90 | V10 | 3.1 | 4.63 |
| 100 | 3.58 | ||||
| 120 | 2.28 | ||||
| 135 | 1.48 | ||||
| 175 | 0.13 | ||||
Bend allowance chart for SECC (galvanized steel sheet)
| Материал | Толщина | Угол изгиба | V-образное отверстие | Внутренний радиус | Припуск на изгиб |
|---|---|---|---|---|---|
| SECC0097 | 1 | 90 | V10 | 1.9 | 2.05 |
| 100 | 1. 58 | ||||
| 120 | 1.01 | ||||
| 135 | 0.62 | ||||
| 175 | 0.06 | ||||
| SECC | 1 | 90 | V8 | 1.9 | 1.9 |
| 100 | 1.47 | ||||
| 120 | 0.93 | ||||
| 135 | 0.6 | ||||
| 175 | 0.05 | ||||
| SECC | 1 | 90 | V6 | 1.9 | 1.74 |
| 100 | 1.35 | ||||
| 120 | 0.86 | ||||
| 135 | 0.56 | ||||
| 175 | 0.05 | ||||
| SECC | 1.2 | 90 | V10 | 1.4 | 2.31 |
| 100 | 1. 78 | ||||
| 120 | 1.13 | ||||
| 135 | 0.73 | ||||
| 175 | 0.06 | ||||
| SECC | 1.2 | 90 | V8 | 1.4 | 2.15 |
| 100 | 1.66 | ||||
| 120 | 1.06 | ||||
| 135 | 0.69 | ||||
| 175 | 0.06 | ||||
| SECC | 1.2 | 90 | V6 | 1.4 | 2 |
| 100 | 1.55 | ||||
| 120 | 0.98 | ||||
| 135 | 0.64 | ||||
| 175 | 0.05 | ||||
| SECC | 1.5 | 90 | V12 | 1.7 | 2.8 |
| 100 | 2. 17 | ||||
| 120 | 1.38 | ||||
| 135 | 0.89 | ||||
| 175 | 0.08 | ||||
| SECC | 1.5 | 90 | V10 | 1.7 | 2.65 |
| 100 | 2.05 | ||||
| 120 | 1.31 | ||||
| 135 | 0.85 | ||||
| 175 | 0.07 | ||||
| SECC | 1.5 | 90 | V8 | 1.7 | 2.5 |
| 100 | 1.94 | ||||
| 120 | 1.23 | ||||
| 135 | 0.8 | ||||
| 175 | 0.07 | ||||
| SECC | 2 | 90 | V12 | 2 | 3.44 |
| 100 | 2. 66 | ||||
| 120 | 1.69 | ||||
| 135 | 1.1 | ||||
| 175 | 0.09 | ||||
| SECC | 2 | 90 | V10 | 2 | 3.29 |
| 100 | 2.54 | ||||
| 120 | 1.62 | ||||
| 135 | 1.05 | ||||
| 175 | 0.09 | ||||
| SECC | 2.5 | 90 | V18 | 3.03 | 4.6 |
| 100 | 3.56 | ||||
| 120 | 2.26 | ||||
| 135 | 1.47 | ||||
| 175 | 0.12 | ||||
| SECC | 2.5 | 90 | V12 | 3.03 | 4. 15 |
| 100 | 3.21 | ||||
| 120 | 2.01 | ||||
| 135 | 1.32 | ||||
| 175 | 0.11 | ||||
| SECC | 2.5 | 90 | V10 | 3.03 | 4 |
| 100 | 3.09 | ||||
| 120 | 1.97 | ||||
| 135 | 1.28 | ||||
| 175 | 0,11 | ||||
| SECC | 3 | 90 | V18 | 3,13 | 5,22 |
| 100 | 4,03 | 99999999999999999999999999999999999999999999999999999999999999999999н 999999999999999999999999999999999999999теля 9999999999999999999999999999999999999999999999999999999999999999009н72.57 | |||
| 135 | 1.66 | ||||
| 175 | 0. 14 | ||||
| SECC | 3 | 90 | V12 | 3.13 | 1.78 |
| 100 | 3.69 | ||||
| 120 | 2.35 | ||||
| 135 | 1.52 | ||||
| 175 | 0.13 | ||||
| SECC | 3 | 90 | V10 | 3.13 | 4.63 |
| 100 | 3.58 | ||||
| 120 | 2.28 | ||||
| 135 | 1.48 | ||||
| 175 | 0.13 | ||||
Bend allowance chart for aluminum plate
| Материал | Толщина | Угол изгиба | V-образное отверстие | Внутренний радиус | Припуск на изгиб |
|---|---|---|---|---|---|
| AL | 0. | 90 | 4 | 0.6 | 1.15 |
| 100 | 0.81 | ||||
| 120 | 0.5 | ||||
| 135 | 0.36 | ||||
| 175 | 0.03 | ||||
| AL | 0.8 | 90 | 5 | 0.6 | 1.2 |
| 100 | 0.85 | ||||
| 120 | 0.52 | ||||
| 135 | 0.37 | ||||
| 175 | 0.03 | ||||
| AL | 0.8 | 90 | 6 | 0.6 | 1.25 |
| 100 | 0.88 | ||||
| 120 | 0.54 | ||||
| 135 | 0.39 | ||||
| 175 | 0.03 | ||||
| AL | 1 | 90 | 6 | 0. 6 | 1.49 |
| 100 | 1.05 | ||||
| 120 | 6.5 | ||||
| 135 | 0.46 | ||||
| 175 | 0.04 | ||||
| AL | 1 | 90 | 8 | 0.6 | 1.59 |
| 100 | 1.13 | ||||
| 120 | 0.69 | ||||
| 135 | 0.5 | ||||
| 175 | 0.04 | ||||
| AL | 1.2 | 90 | 6 | 0.9 | 1.73 |
| 100 | 1.22 | ||||
| 120 | 0.75 | ||||
| 135 | 0.54 | ||||
| 175 | 0.04 | ||||
| AL | 1.2 | 90 | 8 | 0. 9 | 1.82 |
| 100 | 1.29 | ||||
| 120 | 0.79 | ||||
| 135 | 0.57 | ||||
| 175 | 0.05 | ||||
| AL | 1.5 | 90 | 8 | 1.2 | 2.18 |
| 100 | 1.54 | ||||
| 120 | 0.95 | ||||
| 135 | 0.68 | ||||
| 175 | 0.06 | ||||
| AL | 1.5 | 90 | 10 | 1.2 | 2.28 |
| 100 | 1.61 | ||||
| 120 | 0.99 | ||||
| 135 | 0.71 | ||||
| 175 | 0.06 | ||||
| AL | 1.5 | 90 | 12 | 1. 2 | 2.38 |
| 100 | 1.68 | ||||
| 120 | 1.03 | ||||
| 135 | 0.74 | ||||
| 175 | 0.06 | ||||
| AL | 2 | 90 | 14 | 1.6 | 3.07 |
| 100 | 2.17 | ||||
| 120 | 1.3 | ||||
| 135 | 0.93 | ||||
| 175 | 0.08 | ||||
| AL | 2 | 90 | 12 | 1.6 | 2.98 |
| 100 | 2.11 | ||||
| 120 | 1.34 | ||||
| 135 | 0.95 | ||||
| 175 | 0.08 | ||||
| AL | 2 | 90 | 18 | 1. 6 | 3.25 |
| 100 | 2.3 | ||||
| 120 | 1.42 | ||||
| 135 | 1.01 | ||||
| 175 | 0.08 | ||||
| AL | 2.5 | 90 | 18 | 2.4 | 3.89 |
| 100 | 2.75 | ||||
| 120 | 1.7 | ||||
| 135 | 1.21 | ||||
| 175 | 0.1 | ||||
| AL | 3 | 90 | 18 | 2.5 | 4.5 |
| 100 | 3.18 | ||||
| 120 | 1.96 | ||||
| 135 | 1.4 | ||||
| 175 | 0.1 | ||||
| AL | 3.2 | 90 | 18 | 2. 5 | 4.74 |
| 3.35 | |||||
| 120 | 2.06 | ||||
| 135 | 1.47 | ||||
| 175 | 0.12 | ||||
| AL | 4 | 90 | 40 | 4.6 | 6.77 |
| 100 | 4.79 | ||||
| 120 | 2.95 | ||||
| 135 | 2.11 | ||||
| 175 | 0.17 | ||||
| AL | 6.8 | 90 | 800 | 9.4 | 12.09 |
| 100 | 8.55 | ||||
| 120 | 5.27 | ||||
| 135 | 3.76 | ||||
| 175 | 0,31 | ||||
0 Акции
Листовый металл K-фактор, разрешение на изгиб и расчеты плоской длины
K Фактор в листовом металлокодел.
шаблон. Математически значение коэффициента k равно отношению положения нейтральной оси к толщине листа. В этой статье мы обсудим вычет изгиба листового металла , допуск на изгиб , K-фактор , Y-фактор и расчет развертки листового металла.
Чтобы понять, что такое К-фактор? во-первых, нам нужно понять, зачем нам нужен К-фактор? что такое припуск на изгиб и вычет изгиба в деталях из листового металла?
Зачем нужен коэффициент К при гибке листового металла
Оператор, гибящий деталь из листового металла с помощью гибочного прессаГибка листового металла — это операция формования, при которой листы пластически деформируются для изменения их формы. Во время гибки листового металла материал подвергается напряжению, превышающему его предел текучести, но ниже предела прочности при растяжении.
После гибки детали из листового металла общая длина листового металла превышает длину плоскости.
Это изменение длины может быть представлено как вычет изгиба или допуск изгиба. Этот допуск на изгиб и уменьшение изгиба рассчитываются с использованием константы, известной как коэффициент K или коэффициент Y.
Что такое уменьшение изгиба листового металла?
При гибке листового металла внутренняя поверхность гиба сжимается, а внешняя растягивается. Что увеличивает общую площадь внешней поверхности. Другими словами, после гибки общая длина детали из листового металла (A + B) будет больше, чем длина листового металла в плоском виде.
Математически Вычет за изгиб равен разнице между общей длиной листового металла после гибки и плоской длиной.
Вычет изгиба = общая длина изгиба листового металла (A+B) – длина изгиба
Вычет изгиба листового металлаРасчет размеров заготовки из листового металла.
Расчет уменьшения изгиба в деталях из листового металла
Суммарный вычет изгиба деталей из листового металла можно рассчитать по следующей формуле:
Длина листового металла в плоском виде = длина A + длина B – вычет изгиба
Вычет изгиба = длина A + длина B – листовой металл Плоская длина
Что такое допуск на изгиб листового металла?
Прибавка на изгиб служит той же цели, что и вычет изгиба.
Но по сравнению с вычетом изгиба, прибавка на изгиб листового металла рассчитывает материал, который необходимо добавить к длине полки (A1 и B1) для расчета длины листового металла в плоском виде.
Формула расчета припуска на изгиб листового металла
Как показано на рисунке выше:
Длина листового металла в плоском виде = длина A1 + длина B1 + припуск на изгиб
Припуск на изгиб = длина листового металла в плоском виде – (Длина A1 + Длина B1 )
Взаимосвязь между допуском на изгиб листового металла и вычетом изгиба
Припуск на изгиб листового металла и вычетом изгиба напрямую связаны друг с другом. Математически сумма припуска на изгиб и вычета изгиба равна удвоенному внешнему отступу.
Допуск на изгиб + Вычет изгиба = 2 × OSSB
Из приведенного выше уравнения, если известно значение внешнего отступа, допуск изгиба можно рассчитать из вычета изгиба и наоборот.
Математически внешний отступ равен произведению суммы толщины листа, внутреннего радиуса изгиба и тангенса половины угла изгиба.
Внешний отступ ( OSSB ) = Tan (A / 2) × (T + R)
Где:
A = угол изгиба; T = толщина листа, R = внутренний радиус изгиба
Что такое К-фактор в листовом металле?
K Коэффициент изгиба листового металла — это константа, которая используется для расчета длины плоского листа листового металла. Его значение является константой для данного материала, толщины и станка. Значение К-фактора также может варьироваться от машины к машине.
Если известно значение коэффициента k для данной толщины материала и гибочной машины. Плоскую длину листового металла можно рассчитать по 3D-модели детали с помощью программного обеспечения САПР. Таким образом, k-фактор устраняет необходимость расчета длины листового металла вручную. Но рекомендуется всегда проверять развертки из листового металла, рассчитанные программным обеспечением САПР, также вручную.
Расчет К-фактора
К-фактор для гибки листового металла можно рассчитать либо путем расчета положения нейтральной оси, либо путем расчета допуска на изгиб или уменьшения изгиба. Вот более подробная информация о том, как рассчитать значение К-фактора для гибки листового металла?
Вариант-1: Расчет нейтральной оси и К-фактора
Чтобы понять взаимосвязь между К-фактором и нейтральной осью, сначала нам нужно понять что такое нейтральная ось при гибке листового металла?
Представление нейтральной осиПри гибке листового металла внутренняя поверхность гиба сжимается, а внешняя поверхность гиба растягивается. Где-то между толщиной материала лежит нейтральная ось, где материал не сжимается и не растягивается.
Положение нейтральной оси зависит от материала, направления волокон, инструмента и условий окружающей среды. Математически К-фактор представляет собой отношение положения нейтральной оси к толщине листа.
Коэффициент К = Положение нейтральной оси / Толщина материала
Опция 2: Расчет припуска на изгиб и коэффициента К
Существует прямая зависимость между припуском на изгиб листового металла и коэффициентом К. Математически припуск на изгиб при гибке листового металла можно рассчитать по следующей формуле.
Допуск на изгиб (BA) = (Π/180) × (R + K × T) × A
Где
R = внутренний радиус изгиба; А = угол изгиба; T = толщина листа; K = значение К-фактора
В приведенной выше формуле допуска на изгиб, за исключением коэффициента k листового металла и значений допуска на изгиб, все остальные значения известны. Поэтому, чтобы рассчитать значение k-фактора, сначала нам нужно рассчитать значение допуска на изгиб.
Значение припуска на изгиб для материала можно рассчитать с помощью эксперимента, выполнив следующие шаги.
Этап-1
Вырежьте образец листа и измерьте его общую длину в плоском виде и толщину листа в мм.
Ширина полосы не очень критична.
Этап-2
Согните лист на 90 градусов и измерьте длины A и B.
(Обратите внимание, что гибка образца детали выполняется так же, как мы планируем производство. Потому что разные машины и гибочные инструменты укажите различные значения коэффициента k.)
Шаг-3
Значение внутреннего радиуса изгиба зависит от гибочного инструмента и штампа. Обычно он считается равным толщине листа.
Мы предлагаем вам посетить эту страницу для пошагового руководства по расчету К-фактора листового металла с использованием практичного и более точного подхода.
Факты о К-факторе
- К-фактор является безразмерной величиной.
- Внутреннее сжатие листового металла не может превышать внешнее растяжение. Поэтому значение k-фактора не может превышать «0,5».
- Нейтральная ось не может выходить за середину толщины листа.
- Коэффициент К Значение обратно пропорционально толщине листа.
Увеличение толщины уменьшает значение k-фактора. - Значение К-фактора обратно пропорционально твердости материала. Поэтому с увеличением твердости значение К-фактора уменьшается.
Взаимосвязь между К-фактором и Y-фактором
Подобно коэффициенту К, коэффициент Y также является константой, используемой для расчета развернутой длины детали из листового металла. Y-фактор и k-фактор напрямую связаны друг с другом по следующей формуле.
Расчет длины плоского листового металла
Длина плоского листового металла Если известно значение коэффициента К листового металла и длина изгибаемой полки. Плоскую длину листового металла можно рассчитать, выполнив следующие три шага.Шаг 1: Рассчитайте значение допуска на изгиб для требуемого изгиба листового металла, используя приведенную ниже формулу.
Допуск на изгиб (BA) = (Π/180) × (R + K×T) × A
Шаг 2: Рассчитайте значение вычета из значений допуска на изгиб и внешнего отступа.