Расчет многопролетной шарнирной балки онлайн: СОПРОМАТ ГУРУ. Расчет балки онлайн. Построение эпюр

Содержание

реакции опор и построение эпюр

Пример решения задачи по расчёту многопролетной балки: выполним её кинематический анализ, определим реакции опор и построим эпюры внутренних поперечных сил и изгибающих моментов.

Многопролетной (шарнирной) балкой называется статически определимая система, состоящая из ряда однопролетных и консольных балок, соединенных между собой шарнирами.

В большинстве случаев на практике возведение многопролетных балок выгодно с точки зрения снижения расхода материалов.

Рассмотрим типовой пример расчета многопролетной статически определимой балки (рисунок 3.17):

W = 3×6 – 3×3 – 2×2 −5 = 0, следовательно система может быть неизменяемой;
Структурный анализ: диск АВ вместе с диском «земля» образует единый диск, который соединен с диском СDЕGН с помощью трех непараллельных и непересекающихся в одной точке стержней.
Система в целом неизменяема.

После кинематического анализа выполняется определение опорных реакций и реакций связей.

Для этого: заменим внутренние (шарниры В,С) и внешние (заделка А, шарнирно-подвижные опоры D,G) связи их реакциями, которые будут представлять собой неизвестные пока сосредоточенные воздействия.

После этого расчленим заданную систему на элементы.

Рассматривая каждый элемент с учетом их совместной работы, определим опорные реакции и реакции связей.

Рисунок 3.17 – Пример расчета многопролетной балки

Построение эпюры изгибающих моментов

Для решения задачи методом сечений имеем шесть (AB, ВС, СD, DЕ, ЕG, GН) силовых участков.

Участок АВ:

Начало силового участка примем в сечении «А»:

Рисунок 3.18 – Построение эпюры М на участке АВ

Если же за начало силового участка принять сечение «В» (это приводится здесь для доказательства того, что выбор начала участка не влияет на окончательную эпюру):

Рисунок 3. 19 — Построение эпюры М на участке ВА

Участок ВС:
Начало консоли примем в точке «В».

Рисунок 3.20 — Построение эпюры М на участке ВС

Участок СD:
Начало участка в сечении «С» (очевидно, что сечение «D» пока началом участка быть не может).

Рисунок 3.21 — Построение эпюры М на участке СD

Участок DЕ:

Начало силового участка примем в сечении «D».

Рисунок 3.22 — Построение эпюры М на участке DE

Участок GH:
Начало силового участка примем в сечении «H».

Рисунок 3.23 — Построение эпюры М на участке GH

Участок ЕG:
Начало силового участка примем в сечении «G».

Рисунок 3.24 — Построение эпюры М на участке ЕG

Окончательно получим эпюру моментов, изображенную на рисунке 3.17.

Построение эпюры поперечных сил

Первоначально рассмотрим силовые участки с линейной эпюрой моментов.

Участок GН:

Эпюра моментов параллельна базису (оси участка), поэтому тангенс угла наклона эпюры моментов, а значит и поперечная сила на этом участке равны нулю.

Участок ЕG: Участок DЕ:

Участок АВ: Участок ВС:

Участок СD:

Рисунок 3.25 – Построение Эпюр Q на участках EG, DE, AB, BC, CD

Окончательная эпюра Q изображена на рисунке 3.17.

Построение эпюры продольных сил

Отсутствие горизонтальных составляющих всех реакций позволяет сделать вывод о том, что продольные усилия на всех силовых участках отсутствуют.

Общая статическая проверка.

Рисунок 3.26 – Статическая проверка

Трехшарнирные системы >
Примеры решения задач >

1.2 Расчет статически определимых многопролетных балок на неподвижную и подвижную нагрузки

Многопролетные статически определимые балки представляют собой протяженные балочные конструкции, перекрывающие несколько пролетов и состоящие из простых балок, соединенных между собой шарнирами (рис. 1.14).

Особенность расчета подобных стержневых конструкций заключается в расчленении многопролетной балки в шарнирных соединениях на отдельные простые балки, расчет которых осуществляется по методам сопротивления материалов.

В этом случае составляется поэтажная схема балки, в которой определяются основная (несущая) и вспомогательные балки, опирающиеся на несущую балку, имеющую три связи с землей.

На рис. 1.15, а показана поэтажная схема многопролетной балки, приведенной на рис. 1.14, а. Несущей балкой здесь является балка АС, которая остается неподвижной при удалении других вспомогательных балок СЕ и ЕF.

Статический расчет (расчет на неподвижную нагрузку) начинается с верхней балки. Следующая вспомогательная балка рассматривается под воздействием своей внешней нагрузки и реакции в опорном шарнире и т. д.

Верхняя балка ЕF нагружена активной силой Р, следующая балка СЕ нагружена только реакцией R_е, возникающей в шарнире Е. Аналогично, балка АС будет нагружена только реакцией R_с.

При расчете на подвижную нагрузку наиболее удобным способом построения линий влияния в многопролетных балках является кинематический способ. В качестве иллюстрации на рис. 1.16 приведены линии влияния реакции R_А, поперечных сил и моментов в сечении «n» справа от опоры D.

Пример 1. 2. Для заданной статически определимой многопролетной балки (рис. 1.17, а) необходимо, используя поэтажную схему балки, построить эпюры внутренних усилий. Построить линии влияния реакций R_A и R_B, линии влияния М и Q в сечениях n (слева от опоры

В) и в сечении m.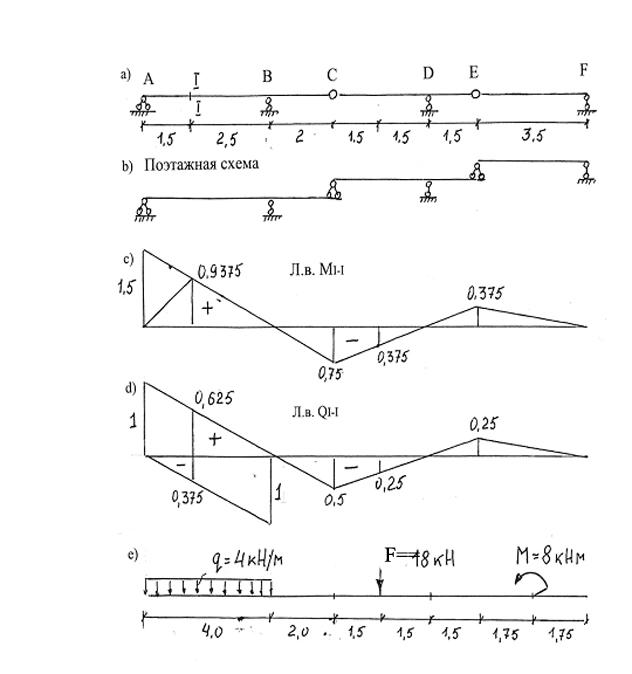

Вычислить по ним внутренние усилия и сравнить со значениями, полученными при построении эпюр.

Решение. 1. Для построения поэтажной схемы многопролетной балки проводим анализ заданной стержневой системы., которая состоит их двух простых балок АС и СD. Балка АС, имеющая три связи с землей, является основной (несущей), а балки СD  вспомогательная. В соответствии с этим и строим поэтажную схему (рис. 1.17, б).

2. Для статического расчета  построения эпюр внутренних усилий  рассмотрим каждую балку. Начинаем расчет с верхней вспомогательной балки СD (рис. 1.18). Определяем опорные реакции.

m_D= 0, q∙4∙1

— R_c∙3 = 0,

R_C= 40/3 кН.

m_C= 0, R_d∙3 — q∙4∙2 = 0.

R_D= 80/3 кН.

Проверка: y = 0.

R_D q∙4 + R_C= 80/3  40 + 40/3 = 0.

Вычисляем по участкам внутренние усилия.

1й участок. 0 < x₁< 1 м.

Q₁= q∙x₁Q_x₌₀= 0, Q

x₌₁= 10 кН.

M₁= — q∙x₁²/2, M_x₌₀= 0, M_x₌₁= 5 кНм,

M_x_=0.5= 1.25 кНм

2-й участок. 0<x₂<3 м.

Q₂= R_C — q∙x₂, Q_x₌₀= 13. 3 кН, Q_x₌₃= — 16,7 кН, Q_m= Q_x₌₁= 3.33 кН;

M₂= R∙_сx₂— q∙x₂²/2, М_х

=0 = 0, М_х₌₃= — 5 кНм.

На участке CD поперечная сила Q меняет знак. Q₂= R_c — q∙x₀= 0,

х₀ = R_c/q = 1.33 м и

М_х_=1,33= 13,3∙1,33 — 10∙1,33∙0,67 = 8,89 кНм.

М_m= М_х₌₁= 13,3∙1 — 10∙1∙0,5 = 8,3 кНм

По полученным значениям строим эпюры М и Q для балки DЕ (рис. 1.18).

Рассмотрим теперь балку AC (рис. 1.19), которая находится под воздействием реакции со стороны балки CDR_С

. Реакция R_С должна быть направлена в сторону, обратную направлению этой же реакции, приложенной к балке CD, поскольку при совмещении балок в шарнире C эти реакции должны быть взаимно уравновешены. Проводим статический расчет балки AC.

Определяем опорные реакции.

m_A= 0. R_В∙2 – R_С∙4 = 0.

R_В= 80/3 = 26.7 кН.

m_B= 0. – R_С∙2 + R_А∙2 = 0.

R_А= 13. 3 кН.

Проверка реакций. y=0.



R_А+ R_В R_С=  13.3 + 26,7  13.3 = 0.

Вычисляем по участкам внутренние усилия.

3-й участок. 0 < x₃< 2 м.

Q₃= R_c 13.3 кН.

M₃=  R_cx₃. М_х₌₀= 0, М_х₌₂=  26,7 кНм.

4-й участок. 0 < x₄< 2 м.

Q₄=  R_А = — 13.3 кН.

M₄=  R_Аx₄, М_х₌₀= 0, М_х₌₂=  26,7 кНм.

По полученным значениям строим эпюры Q и М в простой балке (рис. 1.19).

Совместим все построенные эпюры внутренних усилий вдоль многопролетной балки в едином масштабе (рис. 1.17, в, г) и проведем окончательную проверку на соответствие их заданной нагрузке.

3. Строим линии влияния двух реакций R_А и R_С и поперечной силы и изгибающего момента для сечений m и n. Построение линий влияния будем проводить кинематическим способом.

Так, при построении линии влияния реакции R_А убираем связь, препятствующую вертикальному смещению опоры и даем единичное смещение этой опоры по направлению R_А. Это единичное перемещение приведет к повороту консольной балки АС вокруг опоры В. Шарнир С опустится вниз и повернет балку

СD вокруг опоры D Полученная в результате схема перемещений и дает вид линии влияния этой реакции.

Аналогично получена линия влияния R_С путем вертикального смещения опоры С вверх на единицу.

При построении линий влияния Q и М необходимо убрать связи, воспринимающие поперечную силу и изгибающий момент. То есть, для построения линии влияния Q в сечении n нам необходимо в этом сечении дать торцам взаимное вертикальное смещение на единицу. Отметим, что если торцы стержней параллельны, то параллельны друг другу левый и правый стержни целиком. Аналогично поступаем и с сечением m при построении линии влияния Q_m.

Врезав поочередно в сечениях n и m шарниры и задав единичное угловое смещение получаем эпюры возможных перемещений, дающих вид линий влияния М_m и М_n (рис. 1.20).

4. Подсчитаем значения внутренних усилий в заданных сечениях по линиям влияния. Для этого нам необходимо интенсивность распределенной нагрузки q умножить на площадь, очерченную линией влияния под нагрузкой. При перемножении используем следующие правила знаков: нагрузки, направленные вниз и ординаты линий влияния и площади, расположенные выше осевой линии  положительны.

Q_m= q∙(- 0,5∙1∙1/3 + 0,5∙2∙2/3) = 10∙(-1/6 + 2/3)= 3.33 кН,

М_n= q∙( — 0,523 + 0.512/3) = 10∙(-3 + 1/3)=  26.7 кНм.

Q_n= q∙(- 0,5∙1∙3 + 0,5∙1∙1/3) = 10∙(-3/2 + 1/6)= — 13.3 кН,

M_m= q∙(0,52/3∙3 — 0.511/3) = 10∙(1 — 1/6)= 8.3 кНм.

Значения внутренних усилий, полученные по линиям влияния, совпадают со значениями расчета на постоянную нагрузку.

Пример 1. 3. Для заданной статически определимой многопролетной балки (рис. 1.21, а) необходимо, используя поэтажную схему балки, построить эпюры внутренних усилий. Построить линии влияния двух опорных реакций и линии влияния М и Q в сечениях m и n. Вычислить по ним внутренние усилия и сравнить со значениями, полученными при построении эпюр. В расчетах принять d = 1,5 м, Р = 45 кН, q = 6 кН/м.

Решение. 1. Для построения поэтажной схемы многопролетной балки проводим анализ заданной стержневой системы, которая состоит их трех простых балок АВ, ВD и DЕ . При этом видно, что консольная балка АВ, имеющая три связи с землей, является основной (несущей), а балки ВD и DЕ  вспомогательными. В соответствии с этим и строим поэтажную схему, представив балку АВ как опорную (рис. 1.8, б).

2. Для статического расчета  построения эпюр внутренних усилий  рассмотрим каждую балку отдельно. Начинаем расчет с верхней вспомогательной балки DЕ (рис. 1.22). Определяем опорные реакции.

m_D= 0,  P∙2d+R_E∙3d = 0, R_E= 30 кН.

m_E=0, — R_D∙3d + P∙d = 0. R_D= 15 кН.

Проверка:

y = 0. R_D P + R_E=15  45 + 30 = 0.

Вычисляем по участкам внутренние усилия.

1й участок. 0 < x₁< 1,5 м.

Q₁=  R_е, Q_x₌₀= Q_x_=1,5=  30 кН.

M₁= R_ex₁, M_x₌₀= 0, M_x_=1,5= 45 кНм.

2-й участок. 0 <x₂<3 м.

Q₂= R_D, Q_x₌₀= Q_x₌₃= 15 кН;

M₂= R_dx₂, М_х₌₀= 0, М_х₌₃= 45 кНм.

По полученным значениям строим эпюры М и Q для балки DЕ (рис. 1.22).

Рассмотрим теперь балку ВD (рис. 1.23), которая находится под воздействием реакции со стороны балки DE R_D. Реакция R_D должна быть направлена в сторону, обратную направлению этой же реакции, приложенной к балке DЕ, поскольку при совмещении балок в шарнире D эти реакции должны быть взаимно уравновешены. Проводим статический расчет балки ВD.

m_B= 0. R_C∙2d – R_D∙3d = 0.

R_C= 22,5 кН.

m_С= 0. – R_B∙2d – R_D∙d = 0.

R_B=  7,5 кН.

Знак минус у реакции R_Bозначает, что она направлена в обратную сторону. Направим ее вниз, зачеркнув первоначально выбранное направление и в дальнейших расчетах значение реакции R_Bбудем принимать положительным.

Проверка реакций. y=0.

 R_B+ R_C R_D=  7,5 + 22,5  15 = 0.

Вычисляем по участкам внутренние усилия.

3-й участок. 0<x₃<1,5 м.

Q₃= R_D, Q_x₌₀= Q_x_=1,5= 15 кН.

M₃=  R_Dx₃. М_х₌₀= 0, М_х₌₃=  22,5 кНм.

4-й участок. 0 < x₄< 3 м.

Q₄=  R_B, Q_x₌₀=Q_x₌₃=  21,5 кН.

M₄=  R_Bx₄, М_х₌₀= 0, М_х₌₃=  22,5 кНм.

По полученным значениям строим эпюры Q и М во второй простой балке (рис. 1.23).

Консольная балка АВ нагружена распределенной нагрузкой и реакцией R_Bсо стороны балки ВD, направленной вверх (рис. 1.24). В данном случае при вычислении внутренних усилий можно обойтись без определения реакций, рассматривая правую часть балки.

5-й участок. 0 < x₅< 6 м.

Q₅= q∙x₅ R_B,

Q_x₌₀=  7, ∙5 кН, Q_x₌₆= 28,5 кН,

M₅= R_B∙x₅ q∙x²/2,

М_х₌₀=0, М_х₌₃=4,5 кНм,

М_х₌₆=63 кНм.

Поскольку Q на 5-м участке меняет знак, найдем координату х₀, при которой:

Q₅= q∙x₀ R_B= 0,

тогда х₀= 7,5/6 = 1,25 м.

М_х_=1,25= 4,7 кНм.

Эпюры М и Q для основной балки показаны на рис. 1.24.

Совместим все построенные эпюры внутренних усилий вдоль многопролетной балки в едином масштабе (рис. 1.21, в, г) и проведем окончательную проверку на соответствие их заданной нагрузке.

3. Строим линии влияния двух реакций R_A и R_C и поперечной силы и изгибающего момента для сечений m и n (рис. 1 25). Построение линий влияния будем проводить кинематическим способом.

Так, при построении линии влияния реакции вертикальной R_А убираем связь, препятствующую вертикальному смещению опоры, и даем единичное смещение этой опоры по направлению R_А. Поскольку опора А – заделка, которая при воздействии малой поперечной силы не перемещается, то единичное перемещение приведет к перемещению консольной балки АВ параллельно самой себе. Полученная в результате схема перемещений и дает вид линии влияния этой реакции R_А. Аналогично получена линия влияния R_С путем вертикального смещения опоры С на единицу (рис. 1.25,в).

При построении линий влияния Q и М необходимо убрать связи, воспринимающие поперечную силу и изгибающий момент. То есть для построения линии влияния Q в сечении m нам необходимо в этом сечении дать торцам взаимное вертикальное смещение на единицу (рис. 1.25, г). Отметим, что если торцы стержней параллельны, то параллельны друг другу левый и правый стержни целиком. Аналогично поступаем и с сечением n при построении линии влияния Q_n(рис. 1.25, е)

Врезав поочередно в сечениях m и n шарниры и задав единичное угловое смещение получаем эпюры возможных перемещений, дающих вид линий влияния М_m и М_n (рис. 1.25, д, ж).

. Подсчитаем значения внутренних усилий в заданных сечениях по линиям влияния. Для этого нам необходимо силу Р умножать на ординаты соответствующих линий влияния, а интенсивность распределенной нагрузки q на площадь, очерченную линией влияния под нагрузкой q. При перемножении используем следующие правила знаков: нагрузки, направленные вниз, ординаты линий влияния и площади, расположенные выше осевой линии  положительны.

Q_m=  P∙0,167 + q∙12d =  7,5 + 18 = 10,5 кН,

М_m= Р∙d/3  q(0,52d2d) = 22,5  27 =  4,5 кНм.

Q_n=  P∙2/3 =  30 кН (Сила Р находится слева от сечения n, поэтому умножили ее на левую ординату л.в. Q_n).

M_n= P∙2d/3 = 45 кНм.

Пример расчета — балка с внутренним шарниром (часть A). Найти реакции

Дом
Образование
Подготовка к профессиональным экзаменам
Примеры расчета
Пример расчета – Балка с внутренним шарниром (Часть A). Найдите отзывы

Премия Bentley «Год в инфраструктуре и цифровизации» (YII 2022) начинается с 15 ноября 2022

Подробнее

Содержание [скрыть]

Описание
Выбранные темы

Выбранные темы

Пример расчета. для поперечной панели Пример расчета: расчет изменения длины стержня, загруженного в удлинении Пример расчета — расчет осевых усилий на стержнях фермы Пример расчета — расчет схем стержней Пример расчета — расчет диаграмм стержней для балки Пример расчета — балка с внутренним шарниром (часть B) ). Расчет диаграмм стержней. Пример расчета — анализ рамы. Пример расчета — анализ рамы — равномерная нагрузка. Пример расчета — поиск центра тяжести (поверхности). Пример расчета — расчетное болтовое соединение натяжных пластин (EC3). , Изменение температуры. Пример расчета — незатухающая свободная вибрация (часть A). Пример расчета — незатухающая свободная вибрация (часть B). Пример расчета — оценка матриц структурных свойств. Пример расчета — угловое ускорение, угловая скорость. Пример расчета — соединение срезным болтом EC3. Пример расчета — потеря устойчивости колонны (EC3). Пример расчета — расчет диаграмм стержней. Пример расчета — расчет диаграмм стержней. Пример расчета — расчет уравнения упругой кривой. Пример расчета — расчет положения опоры. Пример расчета — плоскость Напряжение. Пример расчета — кольцевое поперечное сечение, Экзамен на определение напряжения. ple – Допустимая сила сдвига для балки. Пример расчета – Расчет прогиба. Теорема Кастильяно. Пример расчета — определение поперечной силы и момента. Пример расчета — определение величин F1, F2. Пример расчета — внутренние силы. Пример расчета — расчет осевых сил элементов фермы. Пример расчета — расчет моментов инерции Ix и Iy. Пример расчета — расчет напряжения сдвига для температурной нагрузки. Пример расчета — расчет силы растяжения с использованием виртуальной работы. Пример расчета — крутящий момент — напряжение. Пример расчета — железобетонная колонна при напряжении. Пример расчета — консольная балка с равномерной нагрузкой. Пример расчета — консольная балка с точечными нагрузками. Пример расчета — нагрузка на стержень Пример расчета — максимальный прогиб Пример расчета — схема стержня. Пример расчета — минимально допустимый диаметр. Пример расчета — критическая нагрузка. Пример — FrictionCalculatio n Пример — модуль упругости сечения S. Пример расчета — пластическая нейтральная ось. Пример расчета — потеря устойчивости колонны (EC3). Пример расчета — соединение срезным болтом EC3. Пример расчета — схема стержня. Треугольная нагрузка. Пример расчета — крутящий момент-напряжение. Пример расчета — угловое ускорение, угловая скорость. угловое ускорениеИзменение температурыСреднее напряжение сдвига в сосуде под давлениемДопустимая сила сдвига балкиПримеры расчетаРасчет изменения длины стержняПружинные сборки в серии/параллельно: Две пружины в серииФерма против тросаРасчет вертикального отклонения балкиИзгибная трещина в бетонной балкеМаксимальный коэффициент вертикального сдвигаКолонна в изгибеБалки: максимум момент

См. Также

Читать Статья
Диафрагмы
сентябрь, 16, 2022
Введение в диафрагмы при диафрагме
.
.
.
.
.
.
.
.
.
.
.
Усталость является инициированием и распространением трещин…
Новости отрасли
События отрасли
Инженер-конструктор (thestructuralengineer.info) использует сторонние файлы cookie для улучшения нашего веб-сайта и вашего удобства при его использовании.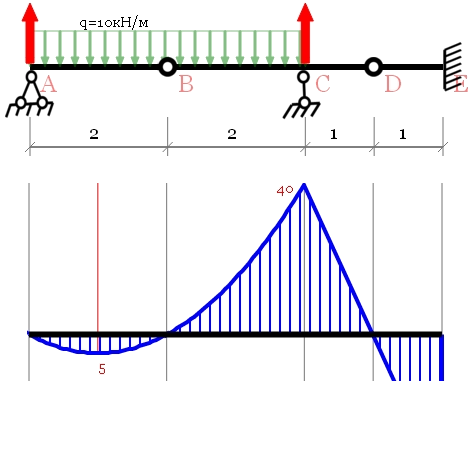
Чтобы узнать больше о файлах cookie, которые мы используем, и о том, как их удалить, посетите нашу страницу о файлах cookie. Разрешить куки-файлы
Полномасштабный анализ многопролетных сегментных мостов из предварительно напряженного бетона Академическая исследовательская статья по «Гражданскому строительству»
Доступно на сайте www.sciencedirect.com
Procedia Engineering
www.elsevier.conc’locate/procedia
Двенадцатый Восточно-Азиатско-Тихоокеанский центр проектирования и строительства
FuSS-Range Анализ многопролетного бетона PrrstrrssrO
Сегментные мосты
Francis T.K. AUa and Cliff C.Y. LEUNG
Факультет гражданского строительства, Гонконгский университет, Китай
Abstract
9 Бетонные швы
9 сегментного моста из предварительно напряженного бетона являются местами потенциальной слабости всего настила моста, но в этой области было выполнено относительно мало работ. Влияние выполнения швов на месте на общее поведение настила моста изучено недостаточно.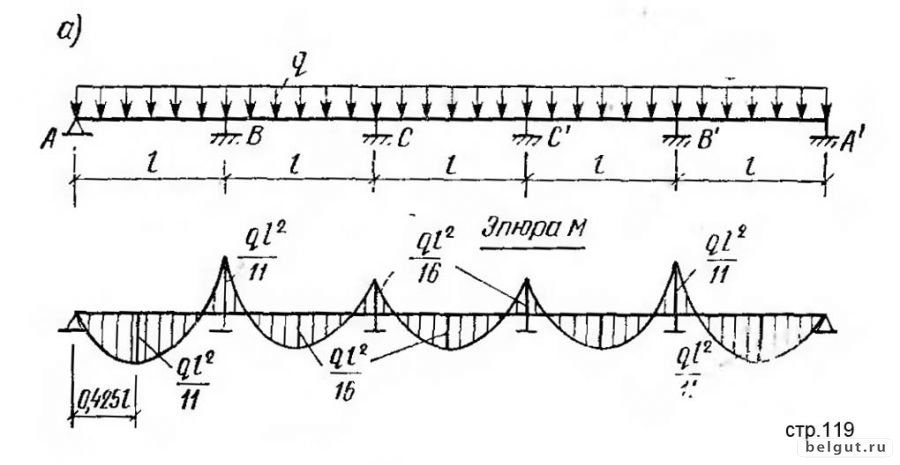 Поскольку большинство существующих методов не могут справиться с таким полнодиапазонным анализом, был разработан численный метод для проведения полнодиапазонного анализа неразрезных мостов из предварительно напряженного железобетона при возрастающих нагрузках или смещениях. Мост моделируется как ряд балочных элементов, каждый из которых определяется соответствующим соотношением момент-кривизна репрезентативной секции внутри него. В то время как большинство существующих методов способны анализировать поведение неразрезных предварительно напряженных железобетонных балок только до пиковой несущей способности, настоящая методика может распространяться и на послепиковый диапазон, который имеет решающее значение для исследования пластичности или деформируемости. . Разработка и проверка методики представлены в данной статье.
Ключевые слова: Полнодиапазонный анализ, нелинейный анализ, постпиковое поведение, предварительно напряженный бетон, сегментные мосты.
1. ВВЕДЕНИЕ
Метод уравновешенной консоли для строительства сегментных мостов из сборного железобетона включает в себя последовательное удлинение сборных сегментов наружу от каждой опоры приблизительно уравновешенным образом.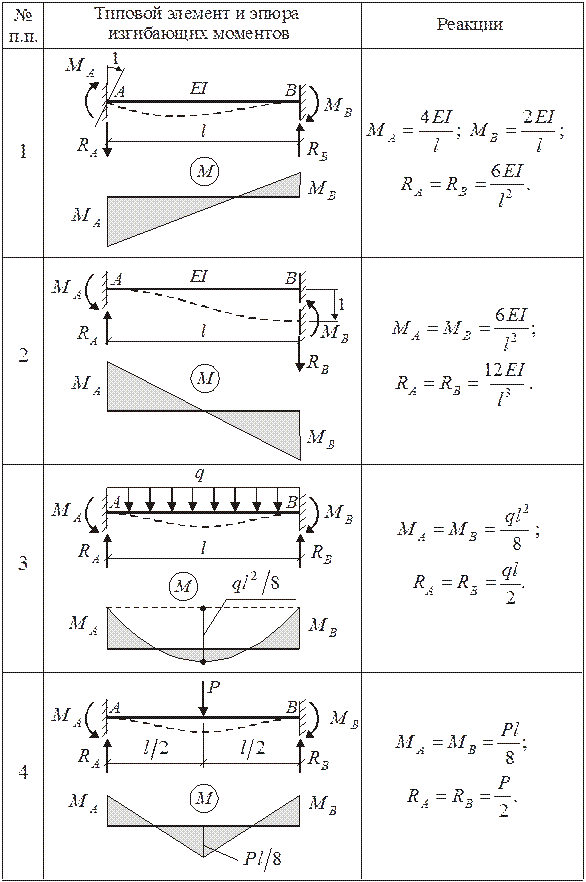 Вокруг середины пролета между двумя последними подходящими сегментами обычно делают зазор шириной от 100 до 200 мм для облегчения монтажа. Затем заливается бетон на месте, чтобы «сшить» сегменты вместе, что делает настил моста непрерывным. Шов на месте обычно рассчитан на то, чтобы выдерживать значительный момент провисания, но только номинальный момент заклинивания. Если разрыв шва in situ произошел, когда момент заклинивания стал высоким в исключительных обстоятельствах, это потенциально могло бы
a Ответственный автор и ведущий: Электронная почта: [email protected]
1877-7058 © 2011 Опубликовано Elsevier Ltd. Таким образом, монолитные бетонные швы являются местами потенциальной слабости всего настила моста, но в этой области было проведено относительно мало исследований. Влияние выполнения швов на месте на глобальное поведение всего настила моста, а именно перераспределение момента и механизм разрушения, изучены недостаточно.
Величина перераспределения момента, которому может подвергнуться настил моста, сильно зависит от постпиковой неупругой деформации конструкции в местах расположения пластичных шарниров. Более того, от того, как перераспределяются внутренние моменты, будет ли настил моста страдать только от локальных повреждений или будет происходить прогрессирующее обрушение в экстремальных условиях. Другими словами, послепиковое поведение структурного элемента оказывает заметное влияние на его способность перераспределять моменты и, что более важно, влияет на надежность конструкции.
Однако большинство существующих численных методов были разработаны для расчета предварительно напряженных железобетонных элементов только до максимальной несущей способности. Чтобы изучить влияние производительности стежков на месте на перераспределение моментов и надежность, необходим соответствующий метод с необходимой численной стабильностью для полнодиапазонного нелинейного анализа предварительно напряженных железобетонных конструкций. Это привело к разработке специального численного метода для настоящего исследования. Техника была проверена путем сравнения расчетной реакции нагрузки на прогиб различных предварительно напряженных бетонных балок с теми, которые были получены экспериментально предыдущими исследователями. Предыстория разработки методики и проверка представлены в этой статье.
2. МЕТОД АНАЛИЗА
2.1. Общая схема
Непрерывное сегментное настил моста идеализируется как ряд балочных элементов, определяющее поведение которых определяется соответствующим соотношением момент-кривизна репрезентативного сечения внутри элемента. Затем к конструкции применяется дополнительная нагрузка или смещение, после чего выполняется серия итераций для получения допустимых узловых смещений, которые удовлетворяют определяющему поведению каждого элемента. Таким образом, метод по существу включает три этапа, а именно (i) дискретизацию настила моста с помощью ряда балочных элементов; (ii) выполнение анализа сечения репрезентативного сечения в каждом элементе для получения соотношения момент-кривизна; и (iii) выполнение итераций для получения допустимых узловых сил и перемещений для каждого приращения приложенной нагрузки или смещения. Они будут более подробно описаны ниже.
Настоящая методика в определенной степени аналогична методике, предложенной Уорнером и Йео (1986), в которой предварительно напряженная бетонная балка идеализируется как ряд балочных элементов с предварительно сгенерированными кривыми момент-кривизна, управляющими изгибным поведением элементов. Методика Уорнера и Йео (1986) была позже принята Кэмпбеллом и Кодуром (1990) при проведении нелинейного анализа предварительно напряженных железобетонных неразрезных балок. Однако, по сути, есть два основных различия между настоящей техникой и той, что была разработана Уорнером и Йео (19).86), а именно (i) принятая схема итераций; и (ii) конститутивное моделирование секций разгрузки, когда конструкция входит в постпиковый диапазон.
Схема итераций, использованная Уорнером и Йео (1986), в основном основана на обновлении секущей жесткости каждого элемента при каждом приращении нагрузки для получения набора перемещений и внутренних сил, удовлетворяющих равновесию. Однако этот метод часто приводит к затруднениям в достижении сходимости для участков, имеющих крутую послепиковую ветвь на кривой моментной кривизны, а также для участков разгрузки, у которых путь разгрузки пересекается с секущей под чрезвычайно малым углом. В предлагаемой методике, обеспечивающей лучшую сходимость, используется метод начальной жесткости.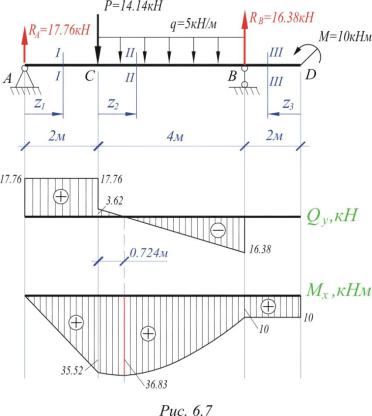 Вместо итераций по секущим жесткостям элементов будут выполняться итерации по остаточным кривизнам 9) (1)
где M — момент, приложенный к сечению, EI — жесткость на изгиб, выраженная через начальный модуль Юнга E и второй момент площади I, а j и jr — кривизна сечения и остаточная кривизна сечения соответственно . Составная модель графически проиллюстрирована на рисунке 1, где жесткость на изгиб EI упругой области используется для определения других параметров.
Рис. 1: Конструктивная модель используемого балочного элемента.
Последующий вывод с использованием подхода потенциальной энергии, основанного на конститутивной модели, показанной в уравнении (1), дает соотношение сила-перемещение для каждого элемента
f = K 5 -J BT (EI )jrdx (2)
где матрица жесткости K и матрица деформации B заданы как
K = J BT (EI )B dx (3)
6 12x 4 6x 6 12x 2 6x L L L L L L L L
x — координата в осевом направлении элемента, а L — длина элемента. В уравнении (2) за остаточную кривизну jr принимается кривизна в середине элемента.
Сетка конечных элементов модели конструкции должна быть достаточно мелкой, чтобы жесткость на изгиб можно было считать постоянной по длине каждого элемента. Поэтому длину элемента выбирают так, чтобы она не превышала общей глубины сечения. Элементы, расположенные внутри потенциальных пластических шарниров, идентифицируются и группируются во время дискретизации. Предполагается, что все элементы, лежащие в пределах потенциального пластического шарнира, имеют ту же кривизну, что и элемент, который первым достигает максимальной допустимой нагрузки по моменту в соответствующей группе. Центр потенциального пластического шарнира находится в точке, где на диаграмме изгибающего момента имеется локальный пик. Длина пластического шарнира приблизительно оценивается по формуле Маттока (1967), который был принят такими исследователями, как Du et al. (2008) при анализе пластичности предварительно напряженных железобетонных балок с несвязанными напрягающими элементами. Формула для оценки длины пластического шарнира lp:
lp = 0,5dp + 0,05Z (5)
, где dp — глубина центра тяжести напрягаемой арматуры; Z — пролет сдвига или расстояние между точкой максимального момента и точкой противоизгиба. Считается, что длина пластикового шарнира может иметь заметное влияние на результаты. Поэтому формулы для длины пластического шарнира, предложенные различными исследователями, также будут рассмотрены. В ближайшем будущем будет проведено параметрическое исследование для изучения влияния длины пластического шарнира на перераспределение момента настила моста.
2.3. Анализ сечения
Каждому элементу в модели неразрезной балки назначается предварительно созданная кривая момент-кривизна, которая определяет его поведение при изгибе. Чтобы получить кривую момент-кривизна, как показано на рисунке 1, анализ сечения выполняется для репрезентативного сечения, выбранного в середине элемента. Такой анализ выполняется численно с помощью компьютерной программы, разработанной на основе подхода Ho et al. (2003), который предназначен для анализа железобетонных сечений. Были внесены изменения, позволяющие анализировать полностью и частично предварительно напряженные секции.
В компьютерной программе для анализа сечения предполагается, что как ненапрягаемая сталь, так и предварительно напряженная сталь идеально связаны с бетоном. Принимается итерационный процесс с постепенно применяемой заданной кривизной. На каждом шаге итерации определяется изменение деформации, предполагая, что плоские сечения остаются плоскими после изгиба, а напряжения в бетоне и стали оцениваются по их соответствующим конститутивным моделям. Осевое равновесие используется для определения положения нейтральной оси, после чего рассчитывается момент сопротивления. Этот итерационный процесс повторяется до тех пор, пока не будет получена достаточная длина кривой момент-кривизна полного диапазона. Кривые момент-кривизна, полученные в результате анализа сечения, затем вводятся в компьютерную программу для глобального структурного анализа для присвоения каждому элементу.
2.4. Итерационный процесс
Анализ начинается с формирования матрицы элементов и общей жесткости K и Kg соответственно. Как упоминалось выше, схема итераций настоящей методики принимает начальные жесткости, и, следовательно, глобальная матрица жесткости остается неизменной на протяжении всего анализа. Значение изгибной жесткости EI, необходимое для расчета матрицы жесткости элемента K, принимается как наклон упругой области кривой момент-кривизна, соответствующей каждому элементу, как показано на рисунке 1. Кумулятивная дополнительная нагрузка или перемещение прикладывается при заданное место, по которому выполняются итерации и обновляется остаточная кривизна каждого элемента до набора допустимых перемещений
и сил на всех узлах получается. Процедура итерации на любом шаге нагрузки i поясняется следующим образом.
Шаг 1. Набор узловых перемещений и усилий определяется путем решения уравнения (2). Кривизну (ßi в репрезентативном сечении каждого элемента можно рассчитать по вектору узлового смещения ô этого элемента по формуле
= B ôn (6)
, где индексы i и n относятся к i-му шагу нагрузки и n-му шагу итерации соответственно. Момент mi, соответствующий кривизне (i), затем рассчитывается с использованием уравнения (1). Остаточная кривизна (r в уравнении (1) принимается как остаточная кривизна, определенная из предыдущего шага нагрузки или шага итерации. Шаг 2. Для каждого элемент, максимально допустимый момент Mi, соответствующий расчетной кривизне, получается из кривой момент-кривизна.Кривая момент-кривизна фактически рассматривается как огибающая в том смысле, что расчетный момент не может превышать момент, заданный кривой в определенный Другими словами, Mn есть момент на кривой момент-кривизна при расчетной кривизне 9.0019
Шаг 3. Расчетный момент mi сверяется с максимально допустимым моментом M » . Если mi больше M n на определенный допуск, принимается максимальный момент M «, соответствующий расчетной кривизне, и соответствующим образом обновляется остаточная кривизна , а именно
{(r ))» = ( — Mr o
, которое получается в результате преобразования уравнения (1) и (r fi» является обновленной остаточной кривизной, используемой на следующем шаге итерации.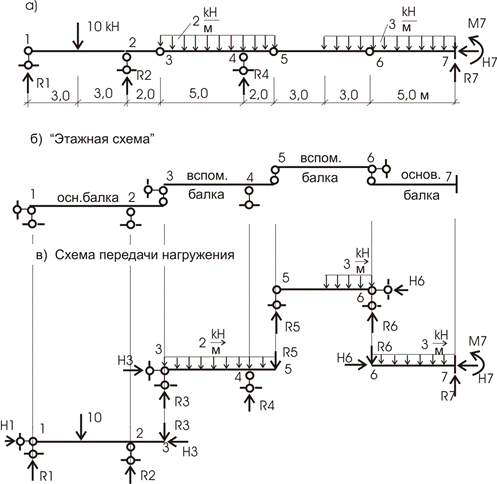 наоборот, если m меньше, чем M r , то m будет считаться моментом, которому подвергается сечение, и остаточная кривизна не будет обновляться. 3 повторяются до тех пор, пока расчетные моменты и кривизна всех элементов не будут достаточно близки к кривой момент-кривизна соответствующего элемента Процесс итерации также можно продемонстрировать графически, используя рисунок 2. Рисунок 2 (а) показывает момент и кривизну типичный элемент ent увеличивается от точки I к точке J. Увеличенный вид кривой момент-кривизна между точками I и точками J показан на рисунке 2 (b), чтобы проиллюстрировать процесс итерации. Предположим, что начальный момент и кривизна элемента в начале шага нагрузки i лежат в точке I, а элемент имеет остаточную кривизну {(r f. На рис. 2(b) расчетные момент и кривизна после первой итерации шагом являются m1 и (1 соответственно, что дает точку 1 с моментом, превышающим максимально допустимый момент M1, обозначенный точкой 2. Таким образом, остаточная кривизна обновляется новым значением (r f ). Затем компьютерная программа переходит ко второму этапу итерации, который дает момент и кривизну, соответствующие точке 3. Так как момент точки 3 не выходит за пределы кривой момент-кривизна, остаточная кривизна сохраняется неизменной. Последующие итерации дают точку 4 и т. д. Циклы итераций завершатся, когда значения момента и кривизны сходятся к значениям в точке J.
Предположим, что при достижении точки J сечение в этом элементе испытывает разгрузку (рис. 2(а)), так как некоторые другие элементы конструкции достигли своих пиковых моментов и перешли в постпиковый диапазон. Момент и кривизна разгружающего элемента будут следовать по пути разгрузки кривой момент-кривизна от точки J, которая предполагается параллельной упругому наклону. Ни Уорнер и Йео (1986), ни Кэмпбелл и Кодур (1990) не объяснили четко свою трактовку соотношения момент-кривизна при разгрузке секции.
Рисунок 2: Процесс итерации. (а) Момент и кривизна типичного элемента увеличиваются от точки I до точки J; (b) итерации момента и кривизны от точки I до точки J.
Рисунок 4: Реакция на нагрузку-перемещение свободно опертой предварительно напряженной бетонной балки.
3. ПРОВЕРКА
Группа предварительно напряженных железобетонных балок была испытана Mitchell et al. (1993) для изучения влияния прочности бетона на длину передачи предварительно натянутых прядей. Свободно опертая балка, выбранная для проверки, имеет пролет 3730 мм с точечной нагрузкой, действующей в середине пролета. Сечение балки было прямоугольным, глубиной 250 мм и шириной 200 мм. Балка имела прямое сухожилие с крестом
сечением 146,4 мм2, расположенным на 75 мм ниже центральной оси, нагруженное до 1286 МПа. Прочность бетона в цилиндре составила 31,0 МПа, а предел прочности на растяжение – 1793 МПа. Реакция нагрузка-смещение в загруженной точке, как показано на рисунке 4, указывает на хорошее соответствие между численными и экспериментальными результатами. Обратите внимание, что настоящий метод может генерировать зависимость нагрузки-перемещения в послепиковой ветви, в то время как большинство существующих численных методов останавливаются после прогнозирования пиковой несущей способности.
Пристли и Парк (1972) провели экспериментальное исследование перераспределения моментов в неразрезных предварительно напряженных железобетонных балках. Соотношение нагрузки и смещения одной из испытанных балок было проанализировано численно с помощью настоящего метода. Балка имела два равных пролета по 3015 мм каждый и была симметрично нагружена точечной нагрузкой на каждый пролет на расстоянии 1489 мм от конца. Сечение балки прямоугольное, глубиной 203 мм и шириной 99 мм. Был обеспечен один слой изогнутых напрягающих элементов, состоящих из двух проволок диаметром 7 мм, нагруженных до 750 МПа, где эксцентриситет был равен нулю с каждого конца до ближайшей точки нагрузки, а напрягающие элементы находились на высоте 63,5 мм над центральной осью на центральной опоре. Кубическая прочность бетона составила 48,0 МПа, а предел прочности арматуры принят равным 1860 МПа. Реакция нагрузка-перемещение в загруженной точке показана на рис. 5, что свидетельствует о хорошем согласии между численными и экспериментальными результатами.
4. ВЫВОДЫ
Представлена разработка численной методики полнодиапазонного нелинейного анализа предварительно напряженного железобетона сегментного моста. Этот метод идеализирует настил моста как серию элементов балки, поведение которых определяется соотношением момент-кривизна репрезентативного сечения в каждом элементе. Затем выполняются итерации с использованием метода начальной жесткости для получения набора допустимых узловых перемещений и внутренних сил, удовлетворяющих определяющему поведению каждого элемента. Экспериментальные результаты двух предварительно напряженных бетонных балок, ранее испытанных различными исследователями, были использованы для проверки настоящего метода. Реакции нагрузки-перемещения, полученные с помощью настоящего метода, сравниваются с доступными экспериментальными результатами, и наблюдается хорошее совпадение.
Перемещение в нагруженной точке (мм)
Рис. 5: Реакция двухпролетной неразрезной предварительно напряженной бетонной балки на нагрузку-перемещение.
БЛАГОДАРНОСТЬ
Исследование проведено при поддержке Совета по исследовательским грантам Специального административного района Гонконг, Китай (проект RGC № HKU 710207E).
ССЫЛКИ
[1] Campbell TI и Kodur VKR (1990). Нелинейный расчет контролируемых деформаций предварительно напряженных железобетонных неразрезных балок. Журнал PCI. 35(5), стр. 42-55.
[2] Du JS, Au FTK, Cheung YK и Kwan AKH (2008). Анализ пластичности предварительно напряженных железобетонных балок с несвязанными напрягающими элементами. Инженерные сооружения. 30, стр. 13-21
[3] Ho JCM, Kwan AKH и Pam HJ (2003). Теоретический анализ послепикового изгиба нормальных и высокопрочных железобетонных балок. Конструктивное проектирование высотных и специальных зданий. 12, стр. 109-125.
[4] Матток А.Х. (1967). Обсуждение «вращательной способности бетонных балок» Корли, В. Журнал структурного подразделения ASCE. 93(2), стр. 519-522.
[5] Митчелл Д., Кук В.Д., Хан А.