5.3.2. Сбор нагрузок
Расчетные нагрузки собираем на 1 м длины второстепенной балки:
1. Постоянная:
— от веса плиты и пола: 2,470*2,4=5,928 кН/м;
— от веса балки сечением 0,2*0,34 м: 0,2*0,34*25*1,1= 1,87 кН/м;
2. Временная: v=6*2,4=14,4 кН/м.
С учётом коэффициента надёжности по назначению здания нагрузка на 1 м будет.
5.3.3.Компьютерный расчет усилий от расчетных нагрузок
Погонная масса балки:т/м.
Момент инерции сечения: м4.
Изгибная жесткость: т*м2.
ППП/Статический расчет/Статический расчет неразрезных балок/ Задание исходных данных/ Расчет / Записка.
Исходные данные:
1. Конструктивное решение:
— количество пролетов: 3;
— изгибная жесткость: 1507 т*м2;
—
погонная масса: 0.
187 т/м.
2. Параметры: балка постоянного сечения – поставить «галочку».
3. Информация об опорах: установить шарнирные опоры с линейной жесткостью 10000 т/м на крайних опорах и 0 т/м на средних опорах.
4. Информация об нагрузках: назначаем равномерно-распределенную нагрузку по всей длине пролета без учета собственного веса балки .
Рис. 5.3.
Изгибающие моменты:
в первом пролёте (в нижней зоне):
на первой промежуточной опоре (в верхней зоне):
в среднем пролете (в нижней зоне):
Поперечные силы:
На первой опоре (в верхней зоне):
На первой промежуточной слева (в нижней зоне):
На первой промежуточной справа (в верхней зоне):
На второй промежуточной слева (в нижней зоне):
5.3.4.Ручной расчет усилий от расчетных нагрузок
Изгибающие
моменты определяем как для равнопролетных
неразрезных балок (табл.
в первом пролёте (в нижней зоне):
на первой промежуточной опоре (в верхней зоне):
в среднем пролете (в нижней зоне):
отрицательные моменты в средних пролетах (в верхней зоне) определяются от отношения временной нагрузки к постоянной . В расчетном сечении в месте теоретического обрыва надопорной арматуры отрицательные моменты можно принять 40% от промежуточных опор.
Поперечные силы также определяем как для равнопролетных неразрезных балок (табл. 5.3 методических указаний):
На первой опоре (в верхней зоне):
На первой промежуточной слева (в нижней зоне):
На первой промежуточной справа (в верхней зоне):
На второй промежуточной слева (в нижней зоне):
Расхождение
между компьютерным и ручным расчетом
незначительные.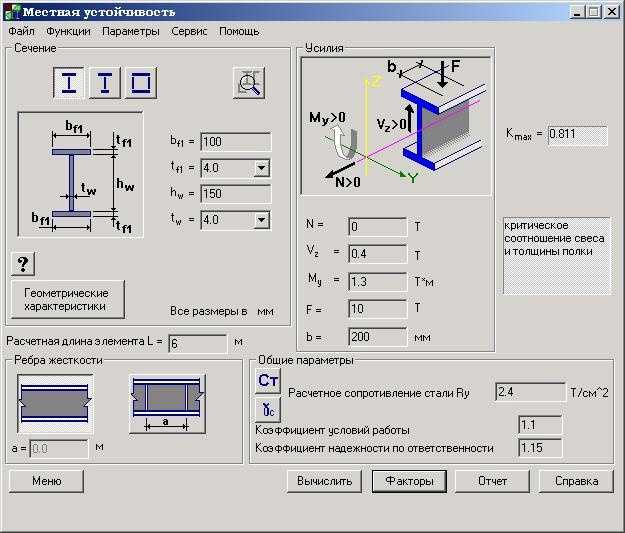
Результаты расчета
достоверны.
5.3.5. Компьютерный расчет армирования монолитной второстепенной балки
Бетон тяжёлый класса В15 имеет призменную прочность , прочность при осевом растяжении. Коэффициент условий работы бетона. Арматура продольная класса А500С с, поперечная — класса Вр-I диаметром 5 мм с .
В пролетах сечение тавровое – полка в сжатой зоне. Расчетная ширина полки назначается из условий:
при принимается меньшее из расстояния между балками и .
при ,.
В данном случае , следовательнои. Принимаем.
На опорах и зоне действия отрицательного изгибающего момента сечение работает как прямоугольное.
ППП/ Железобетонные конструкции/ Расчет сечений Ж.Б. элементов по СНиП/ Данные/ Исходные данные и расчет/ Тип сечения – балка/ Ввод исходных данных/ ОК/ Отчет
Расчет выполняется отдельно для таврового и для прямоугольного сечения.
Продольная арматура:
—
в первом пролёте (в
нижней зоне): .
— в среднем пролёте (в нижней зоне):
— в среднем пролёте (в верхней зоне):
— на первой промежуточной опоре (в верхней зоне):
Поперечная арматура:
— на первой опоре (в верхней зоне):
-на первой промежуточной слева (в нижней зоне):
— на первой промежуточной справа (в верхней зоне):
— на второй промежуточной слева (в нижней зоне):
Linear — optiCutter
Ищете калькулятор раскроя листов ?
Попробуйте наш оптимизатор резки 1d, чтобы узнать, как резать линейные материалы, такие как пиломатериалы, трубы, прутки или балки, с минимальными отходами материала. Просто укажите длину материала, пропил (при необходимости) и введите необходимую длину и количество деталей. Наш калькулятор линейного разреза найдет наилучшее возможное решение.
Пропил / Толщина лезвия
Этикетки на деталях
Используйте складские группы
Обрезать края
Накладка левая
Накладка правая
Доступные запасы
| # | Длина | Количество | Группа | Действия |
|---|---|---|---|---|
| 1 | ||||
Примечание. Количество запасов не требуется, если у вас много запасов такой длины. | ||||
Необходимые детали
| # | Длина | Количество | Этикетка | Группа | Действия |
|---|---|---|---|---|---|
| 1 | |||||
Если вам нужен более сложный план резки, рассмотрите один из наших планов подписки Premium .
Об этом оптимизаторе резки 1d
Этот калькулятор длины реза предназначен для решения задач по резке линейных или длинных заготовок, таких как пиломатериалы, балки, прутки, бумажные рулоны или трубы, на куски заданной длины с минимальными отходами материала, что называется проблемой раскроя.
В общем, это своего рода программное обеспечение для оптимизации длины резки, другими словами, это оптимизатор длины резки или калькулятор линейной резки.
Для простых задач найти оптимальное решение не составляет большого труда, но когда вам нужно разрезать материал на большее количество частей или требуется больше деталей разной длины, все становится сложнее. Базовые и наиболее распространенные алгоритмы оптимизации длины, такие как «First Fit» или «Best Fit», не являются хорошим выбором. Здесь начинается сила нашего линейного калькулятора списков раскроя.
Этот оптимизатор длины очень популярен в столярном деле. Его можно использовать в качестве мощного калькулятора распила пиломатериалов, который выдает оптимальные решения о том, как распилить пиломатериал или древесину с минимальными отходами.
Как видите, этот линейный калькулятор списков раскроя не требует каких-либо надстроек или плагинов Excel. Если вы хотите просмотреть историю планов раскроя в одном месте, попробуйте один из наших планов.
Калькулятор площади поверхности
Используйте приведенные ниже калькуляторы для расчета площади поверхности некоторых распространенных форм.
Площадь поверхности шара
Площадь поверхности конуса
Площадь поверхности куба
Площадь поверхности цилиндрического резервуара
Площадь поверхности прямоугольного резервуара
| |||||||||
Площадь поверхности капсулы
Площадь поверхности крышки
Для расчета укажите любые два значения ниже.
| |||||||||
Площадь конической усеченной поверхности
| |||||||||
Площадь поверхности эллипсоида
| |||||||||
Площадь поверхности квадратной пирамиды
Калькулятор связанного объема | Калькулятор площади | Калькулятор площади поверхности тела
Площадь поверхности твердого тела является мерой общей площади, занимаемой поверхностью объекта.
Сфера
Площадь поверхности (SA) сферы можно рассчитать с помощью уравнения:
SA = 4πr 2
где r радиус
Ксаэль не любит ни с кем делиться своими шоколадными трюфелями. Когда она получает коробку трюфелей Lindt, она начинает вычислять площадь поверхности каждого трюфеля, чтобы определить общую площадь поверхности, которую ей нужно облизать, чтобы уменьшить вероятность того, что кто-нибудь попытается съесть ее трюфели. Учитывая, что каждый трюфель имеет радиус 0,325 дюйма:
SA = 4 × π × 0,325 2 = 1,327 дюйма 2
Конус
Площадь поверхности круглого конуса можно рассчитать, суммируя площади поверхности каждого из его отдельных компонентов.
«Основной SA» относится к кругу, который содержит основание в замкнутом круглом конусе, в то время как боковой SA относится к остальной части конуса между основанием и его вершиной. Уравнения для расчета каждого, а также общего SA замкнутого круглого конуса показаны ниже:
основание SA = πr 2
боковой SA = πr√r 2 + h 2
общая SA = πr(r + √r 2 + h 2 )
где r — радиус, а h — высота. в ряде стран Юго-Восточной Азии. Она решает сшить свое собственное и, будучи очень практичным человеком, не погрязшим в сентиментальности, достает свадебное платье своей матери из темных ниш шкафа, в котором оно находится. Она определяет площадь поверхности материала, которая ей нужна для создания шляпы радиусом 1 фут и высотой 0,5 фута, следующим образом:
поперечная SA = π × 0,4√0,4 2 + 0,5 2 = 0,805 фута 2
Куб
Площадь поверхности куба можно рассчитать суммированием общая площадь его шести квадратных граней:
СА = 6а 2
где a — длина ребра
Анна хочет подарить своему младшему брату кубик Рубика на день рождения, но знает, что у ее брата короткая продолжительность концентрации внимания и он легко расстраивается.
Она заказывает кубик Рубика, в котором все грани черные, и должна заплатить за настройку в зависимости от площади поверхности кубика с длиной ребра 4 дюйма.
SA = 6 × 4 2 = 96 дюймов 2
Цилиндрический бак
Площадь поверхности закрытого цилиндра можно рассчитать, суммируя площади его основания и боковой поверхности:
основание SA = 2πr 2
боковой SA = 2πrh
общая СА = 2πr(r + h)
где r — радиус, а h — высота
У Джереми есть большой цилиндрический аквариум, в котором он купается, потому что он не любит душ или ванну. Ему любопытно, остывает ли его нагретая вода быстрее, чем в ванне, и ему нужно рассчитать площадь поверхности его цилиндрического резервуара высотой 5,5 фута и радиусом 3,5 фута.
общая SA = 2π × 3,5(3,5 + 5,5) = 197,920 футов 2
Прямоугольный резервуар
Площадь поверхности прямоугольного резервуара равна сумме площадей каждой из его сторон:
SA = 2лв + 2лв + 2вч
где l — длина, w — ширина, h — высота
Банана, старшая дочь в длинной череде банановых фермеров, хочет научить свою избалованную гнилую младшую сестру, Банан-Хлеб, урок о надежде и ожиданиях.
Banana-Bread всю неделю требовала новый набор ящиков для своих новых фигурок Бэтмена. Таким образом, Банана покупает ей большой кукольный дом Барби с кухонной утварью ограниченного выпуска, духовкой, фартуком и реалистичными гниющими бананами для Бэтмена. Она упаковывает их в прямоугольную коробку тех же размеров, что и ящик, который хочет Banana-Bread, и ей нужно определить количество оберточной бумаги, которое ей нужно, чтобы завершить презентацию подарка в виде сюрприза 3 фута × 4 фута × 5 футов:
SA = (2 × 3 × 4) + (2 × 4 × 5) + (2 × 3 × 5) = 94 фута 2
Капсула
Площадь поверхности капсулы можно определить путем объединения уравнения площади поверхности шара и площади боковой поверхности цилиндра. Обратите внимание, что площадь поверхности оснований цилиндра не включена, поскольку она не составляет часть площади поверхности капсулы. Общая площадь поверхности рассчитывается следующим образом:
СА = 4πr 2 + 2πrh
где r радиус и h высота
Горацио производит плацебо, предназначенное для оттачивания индивидуальности, критического мышления и способности объективно и логически подходить к различным ситуациям.
Он уже протестировал рынок и обнаружил, что подавляющее большинство выборочной совокупности не обладает ни одним из этих качеств и очень готово купить его продукт, еще больше укоренившись в чертах, от которых они так отчаянно стремятся избавиться. Горацио нужно определить площадь поверхности каждой капсулы, чтобы он мог покрыть их чрезмерным слоем сахара и обратиться к предрасположенным к сахару языкам населения, готовясь к своему следующему плацебо, которое «излечивает» все формы сахарного диабета. Учитывая, что в каждой капсуле r размером 0,05 дюйма и h размером 0,5 дюйма:
SA = 4π × 0,05 2 + 2π × 0,05 × 0,5 = 0,188 дюйма 2
Сферический колпачок
Площадь поверхности сферического колпачка составляет в зависимости от высоты рассматриваемого сегмента. Предоставленный калькулятор предполагает твердую сферу и включает основание колпачка в расчет площади поверхности, где общая площадь поверхности представляет собой сумму площади основания и площади боковой поверхности сферического колпачка.
Если вы используете этот калькулятор для вычисления площади поверхности полой сферы, вычтите площадь поверхности основания. Имея два значения высоты, радиуса крышки или радиуса основания, третье значение можно рассчитать с помощью уравнений, приведенных в калькуляторе объема. Уравнения площади поверхности следующие:
сферическая крышка SA = 2πRh
основание SA = πr 2
Общая твердая сфера SA = 2πRh + πr 2
где R — радиус сферической крышки, r — радиус основания, h — высота
Дженнифер завидует глобусу, который ее старший брат Лоуренс получил на день рождения. Поскольку Дженнифер на две трети младше своего брата, она решает, что заслуживает одну треть земного шара своего брата. Вернув ручную пилу отца в сарай для инструментов, она вычисляет площадь поверхности своей полой части земного шара с помощью R 0,80 фута и h 0,53 фута, как показано ниже:
SA = 2π × 0,80 × 0,53 = 2,664 фута 2
Коническая форма усеченного конуса
900 02 Площадь поверхности сплошного прямоконического усеченного конуса равна сумме площадей его двух круглых концов и площади его боковой поверхности: круглый конец SA = π(R 2 + r 2 )
боковой SA = π(R+r)√(R-r) 2 + h 2
общая SA = π(R 2 + r 2 ) + π(R+r)√(R-r) 2 + ч 2
где R и r — радиусы концов, h — высота
Пол делает вулкан в форме усеченного конуса для своего проекта научной ярмарки.
Пол рассматривает извержения вулканов как насильственное явление и, выступая против всех форм насилия, решает сделать свой вулкан в виде замкнутого конического усеченного конуса, который не извергается. Хотя его вулкан вряд ли произведет впечатление на судей научной выставки, Пол все же должен определить площадь поверхности материала, который ему нужен, чтобы покрыть внешнюю стену своего вулкана R в 1 фут, r в 0,3 фута и h в 1,5 фута:
всего SA = π(1 2 + 0,3 2 ) + π(1 + 0. 3) √(1 — 0,3) 2 + 1,5 2 = 10,185 футов 2
Эллипсоид
Вычисление площади поверхности эллипсоида не имеет простой и точной формулы, такой как куб или другая более простая форма. Калькулятор выше использует приблизительную формулу, которая предполагает почти сферический эллипсоид:
SA ≈ 4π 1,6 √(a 1,6 b 1,6 + a 1,6 c 1,6 + b 1,6 c 1,6 )/3
где a , b и c — оси эллипса
Колтейн всегда любила готовить и недавно выиграла на конкурсе керамический нож.
К несчастью для его семьи, которая питается почти исключительно мясом, Колтейн практиковал свою технику нарезки на чрезмерном количестве овощей. Вместо того, чтобы есть овощи, отец Колтейна уныло смотрит на свою тарелку и оценивает площадь поверхности эллиптических надрезов кабачка с осями 0,1, 0,2 и 0,35 дюйма:
SA ≈ 4π 1,6 √(0,1 1,6 0,2 1,6 + 0,1 1,6 0,35 1,6 + 0,2 1,6 0,35 1,6 )/3 = 0,562 дюйма 2
Квадратная пирамида
Площадь поверхности квадратной пирамиды состоит из площади ее квадратного основания и площади каждой из четырех треугольных граней. Учитывая высоту h и длину ребра a , площадь поверхности можно рассчитать с помощью следующих уравнений:
база SA = 2
боковой SA = 2a√(a/2) 2 + h 2
всего SA = a 2 + 2a√(a/2) 2 + h 2
В классе Вонкуайлы недавно завершилось строительство модели Великой пирамиды Гизы.