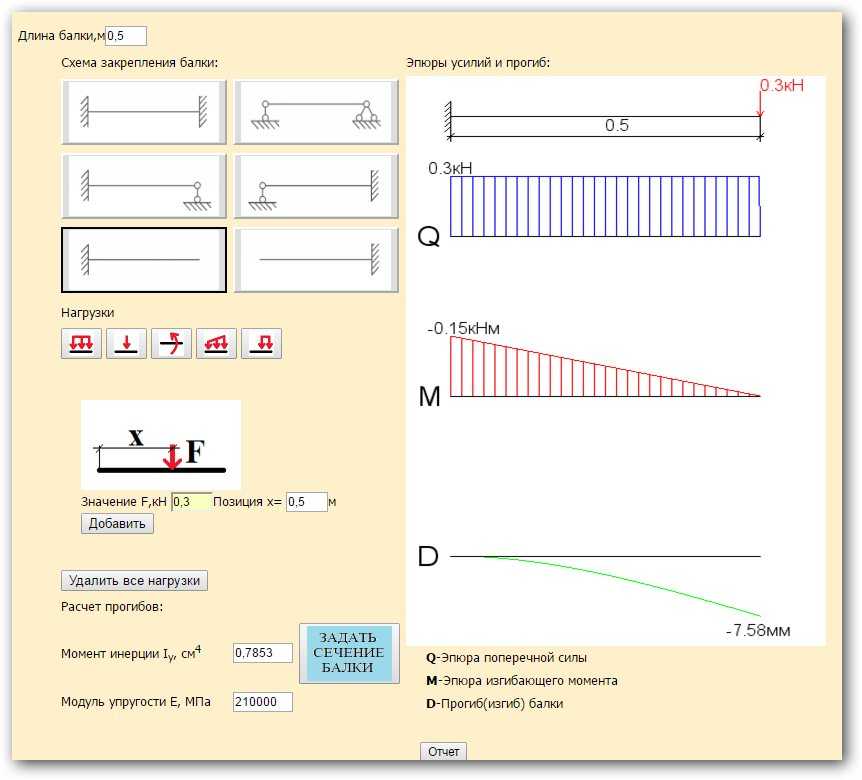
Расчет прочности и жесткости балок настила для нормального типа балочной клетки
Цель: Проверка режима расчета и подбора балок
1 – балка настила
Задача: Подобрать прокатный двутавровый профиль для балок настила пролетом 6 м в балочной клетке нормального типа. Верхний пояс балок настила непрерывно раскреплен по всей длине настилом.
Ссылки: Металлические конструкции: учебник для студ. Учреждений высш. проф. Образования / [Ю. И. Кудишин, Е. И. Беленя, В. С. Игнатьева и др.]; под ред. Ю. И. Кудишина. — 13-е изд., испр. — М.: Издательский центр «Академия», 2011. С 183.
Соответствие нормативным документам: СНиП II-23-81*, СП 16.13330, ДБН В.2.6-163:2010.
Имя файла с исходными данными:
3.1.sav;
Kristall3.1.doc — отчет.
Исходные данные:
| а = 1,125 м | Шаг балок настила |
| qн = (0,77 + 20) кН/м2 ×1,125 м = 23,37 кН/м | Суммарная нормативная нагрузка; |
| q1 = 1,05×0,77 кН/м2 ×1,125 м = 0,91 кН/м | Расчетная постоянная нагрузка; |
| q2 = 1,2×20 кН/м2 ×1,125 м = 27 кН/м | Расчетная временная нагрузка; |
| Ry = 23 кН/cм2, | Сталь марки C235; |
| l = 6 м | Пролет балки; |
| [ f ] = 1/250×6,0 м = 24 мм | Предельный прогиб; |
| γc = 1 | Коэффициент условий работы; |
| Wx = 596,364 см3 | Принятый двутавр №33 по ГОСТ 8239-89; |
Ix = 9840 см4, Sx= 339 см3, tw = 7 мм. |
Параметры КРИСТАЛЛ:
Сталь: C235
Группа конструкций по таблице 50* СНиП II-23-81* 4
Коэффициент надежности по ответственности γn = 1
Коэффициент надежности по ответственности (2-е предельное состояние) = 1
Коэффициент условий работы 1
Закрепления от поперечных смещений и поворотов
| Слева | Справа |
|---|---|---|
Смещение вдоль Y | Закреплено | Закреплено |
Смещение вдоль Z | Закреплено | Закреплено |
Поворот вокруг Y |
|
|
Поворот вокруг Z |
|
|
Сплошное закрепление сжатого пояса из плоскости изгиба
Сечение
Профиль: Двутавp с уклоном полок по ГОСТ 8239-89 33
Ручной расчет:
1. {2}. \]
{2}. \]
Сравнение решений:
Фактор | Прочность при действии поперечной силы | Прочность при действии изгибающего момента | Устойчивость плоской формы изгиба при действии момента | Максимальный прогиб |
|---|---|---|---|---|
Ручной счет | 4,126/13,34 = 0,309 | 546,06/596,36 = 0,916 | – | 19,46/24 = 0,81 |
КРИСТАЛЛ | 0,309 | 0,916 | 0,916 | 19,451/24 = 0,81 |
Отклонение от ручного счета, % | 0,0 | 0,0 | 0,0 | 0,0 |
Источник | – | 0,83 | – | 0,81 |
Комментарии:
- Проверка общей устойчивости балки при ручном счете не выполнялась, поскольку сжатый пояс балки раскреплен от поперечных смещений из плоскости изгиба приваренным настилом.

- Проверка прочности при действии изгибающего момента в источнике выполнялась с учетом развития ограниченных пластических деформаций.
- Проверка прочности балки с учетом развития ограниченных пластических деформаций не выполнялась, поскольку согласно норм такой расчет возможен только при соответствующем оребрении стенки балки. В исходных данных примера балка настила задавалась без промежуточных ребер жесткости.
Сопротивление материалов
Сопротивление материалов
ОглавлениеПРЕДИСЛОВИЕГлава 1. ОСНОВНЫЕ ПОНЯТИЯ § 2.1. РАСЧЕТНАЯ СХЕМА. НАГРУЗКИ § 3.1. ВНУТРЕННИЕ СИЛЫ. МЕТОД СЕЧЕНИЙ § 4.1. НАПРЯЖЕНИЯ § 5.1. ДЕФОРМАЦИИ И ПЕРЕМЕЩЕНИЯ § 6.1. ОСНОВНЫЕ ПРЕДПОСЫЛКИ НАУКИ О СОПРОТИВЛЕНИИ МАТЕРИАЛОВ Вопросы для самопроверки Глава 2. РАСТЯЖЕНИЕ И СЖАТИЕ § 1.2. ПРОДОЛЬНАЯ СИЛА § 2.2. НАПРЯЖЕНИЯ В ПОПЕРЕЧНЫХ И НАКЛОННЫХ СЕЧЕНИЯХ БРУСА § 3.2. ПРОДОЛЬНЫЕ И ПОПЕРЕЧНЫЕ ДЕФОРМАЦИИ § 4.2. ДИАГРАММЫ РАСТЯЖЕНИЯ И СЖАТИЯ § 5.2. ПЕРЕМЕЩЕНИЯ ПОПЕРЕЧНЫХ СЕЧЕНИЙ БРУСЬЕВ § 6.2. РАБОТА СИЛЫ ПРИ ЕЕ СТАТИЧЕСКОМ ДЕЙСТВИИ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ § 7.2. СОБСТВЕННЫЙ ВЕС БРУСА § 9.2. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ § 10.2. МЕСТНЫЕ НАПРЯЖЕНИЯ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 3. ТЕОРИЯ НАПРЯЖЕННОГО СОСТОЯНИЯ § 1.  3. ВИДЫ НАПРЯЖЕННОГО СОСТОЯНИЯ 3. ВИДЫ НАПРЯЖЕННОГО СОСТОЯНИЯ§ 2.3. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ § 3.3. ГЛАВНЫЕ НАПРЯЖЕНИЯ. ГЛАВНЫЕ ПЛОЩАДКИ § 4.3. ЭКСТРЕМАЛЬНЫЕ КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ § 5.3. ИССЛЕДОВАНИЕ ПЛОСКОГО НАПРЯЖЕННОГО СОСТОЯНИЯ С ПОМОЩЬЮ КРУГА МОРА § 6.3. ПОНЯТИЕ О ПРОСТРАНСТВЕННОМ НАПРЯЖЕННОМ СОСТОЯНИИ § 7.3. ОБОБЩЕННЫЙ ЗАКОН ГУКА § 8.3. ОБЪЕМНАЯ ДЕФОРМАЦИЯ § 9.3. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 4. СДВИГ § 1.4. ЧИСТЫЙ СДВИГ § 2.4. ДЕФОРМАЦИЯ ПРИ СДВИГЕ. ЗАКОН ГУКА ПРИ СДВИГЕ § 3.4. ОБЪЕМНАЯ ДЕФОРМАЦИЯ И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ПРИ ЧИСТОМ СДВИГЕ. ЗАВИСИМОСТЬ МЕЖДУ E, G и «мю» § 4.4. ПРАКТИЧЕСКИЕ РАСЧЕТЫ НЕКОТОРЫХ ПРОСТЕЙШИХ КОНСТРУКЦИЙ, РАБОТАЮЩИХ НА СДВИГ Расчет заклепочных соединений Расчет сварных соединений Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 5. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ § 2.  5. СТАТИЧЕСКИЕ МОМЕНТЫ СЕЧЕНИЙ 5. СТАТИЧЕСКИЕ МОМЕНТЫ СЕЧЕНИЙ§ 3.5. МОМЕНТЫ ИНЕРЦИИ СЕЧЕНИЙ § 4.5. ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ СЕЧЕНИЙ ПРОСТОЙ ФОРМЫ § 5.5. ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ ОСЕЙ § 6.5. ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ § 7.5. ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ. ГЛАВНЫЕ ОСИ ИНЕРЦИИ § 8.5. ИССЛЕДОВАНИЕ МОМЕНТОВ ИНЕРЦИИ ПЛОСКИХ СЕЧЕНИЙ С ПОМОЩЬЮ КРУГА МОРА § 9.5. ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ СЛОЖНЫХ СЕЧЕНИЙ Примеры расчета Вопросы для самопроверки Глава 6. КРУЧЕНИЕ § 1.6. ОСНОВНЫЕ ПОНЯТИЯ. КРУТЯЩИЙ МОМЕНТ § 2.6. КРУЧЕНИЕ ПРЯМОГО БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ § 3.6. ГЛАВНЫЕ НАПРЯЖЕНИЯ И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ КРУЧЕНИИ БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ § 4.6. РАСЧЕТ БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ ПРИ КРУЧЕНИИ § 5.6. РАСЧЕТ ЦИЛИНДРИЧЕСКИХ ВИНТОВЫХ ПРУЖИН § 6.6. КРУЧЕНИЕ ПРЯМОГО БРУСА НЕКРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ § 7.6. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ ПРИ КРУЧЕНИИ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 7.  ПРЯМОЙ ИЗГИБ ПРЯМОЙ ИЗГИБ§ 1.7. ВНУТРЕННИЕ УСИЛИЯ § 3.7. ОПОРЫ И ОПОРНЫЕ РЕАКЦИИ § 4.7. ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ § 5.7. ДИФФЕРЕНЦИАЛЬНЫЕ ЗАВИСИМОСТИ МЕЖДУ ИЗГИБАЮЩИМ МОМЕНТОМ, ПОПЕРЕЧНОЙ СИЛОЙ И ИНТЕНСИВНОСТЬЮ РАСПРЕДЕЛЕННОЙ НАГРУЗКИ § 6.7. ПРИМЕРЫ ПОСТРОЕНИЯ ЭПЮР ВНУТРЕННИХ УСИЛИЙ § 7.7. ПРЯМОЙ ЧИСТЫЙ ИЗГИБ § 8.7. ПРЯМОЙ ПОПЕРЕЧНЫЙ ИЗГИБ § 9.7. ГЛАВНЫЕ НАПРЯЖЕНИЯ ПРИ ПРЯМОМ ПОПЕРЕЧНОМ ИЗГИБЕ § 10.7. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ ИЗГИБЕ § 11.7. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ § 12.7. ПОНЯТИЕ О ЦЕНТРЕ ИЗГИБА § 13.7. ПОНЯТИЕ О РАСЧЕТЕ СОСТАВНЫХ БАЛОК § 14.7. ПОНЯТИЕ О БАЛКАХ РАЗНОРОДНОЙ УПРУГОСТИ § 15.7. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПОСТОЯННОГО СЕЧЕНИЯ МЕТОДОМ НЕПОСРЕДСТВЕННОГО ИНТЕГРИРОВАНИЯ § 16.7. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПОСТОЯННОГО СЕЧЕНИЯ МЕТОДОМ НАЧАЛЬНЫХ ПАРАМЕТРОВ § 17.7. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ В БАЛКАХ ГРАФО-АНАЛИТИЧЕСКИМ МЕТОДОМ § 18.7. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ БАЛОК Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 8.  ТЕОРИИ ПРОЧНОСТИ ТЕОРИИ ПРОЧНОСТИ§ 2.8. ТЕОРИЯ ПРОЧНОСТИ МОРА § 3.8. ЕДИНАЯ ТЕОРИЯ ПРОЧНОСТИ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 9. СЛОЖНОЕ СОПРОТИВЛЕНИЕ § 1.9. КОСОЙ ИЗГИБ § 2.9. ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ И СЖАТИЕ БРУСЬЕВ БОЛЬШОЙ ЖЕСТКОСТИ § 3.9. ЯДРО СЕЧЕНИЯ § 4.9. ИЗГИБ С КРУЧЕНИЕМ БРУСЬЕВ КРУГЛОГО СЕЧЕНИЯ § 5.9. ОБЩИЙ СЛУЧАЙ ДЕЙСТВИЯ СИЛ НА БРУС КРУГЛОГО СЕЧЕНИЯ § 6.9. ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ УСИЛИЙ ДЛЯ ПРОСТРАНСТВЕННЫХ БРУСЬЕВ С ЛОМАНОЙ ОСЬЮ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 10. РАСЧЕТ КРИВЫХ БРУСЬЕВ § 2.10. ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ § 3.10. НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ В ПОПЕРЕЧНЫХ СЕЧЕНИЯХ БРУСА БОЛЬШОЙ КРИВИЗНЫ § 4.10. ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ НЕЙТРАЛЬНОЙ ОСИ ПРИ ЧИСТОМ ИЗГИБЕ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 11.  ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ В УПРУГИХ СИСТЕМАХ ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ В УПРУГИХ СИСТЕМАХ§ 1.11. РАБОТА ВНЕШНИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ § 2.11. ТЕОРЕМА О ВЗАИМНОСТИ РАБОТ § 3.11. ТЕОРЕМА О ВЗАИМНОСТИ ПЕРЕМЕЩЕНИЯ 4.11. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ. ИНТЕГРАЛ МОРА § 5.11. ПРАВИЛО ВЕРЕЩАГИНА Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 12. РАСЧЕТ ПРОСТЕЙШИХ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СТЕРЖНЕВЫХ СИСТЕМ § 1.12. СТАТИЧЕСКАЯ НЕОПРЕДЕЛИМОСТЬ § 2.12. КАНОНИЧЕСКИЕ УРАВНЕНИЯ МЕТОДА СИЛ § 3.12. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ § 4.12. ИСПОЛЬЗОВАНИЕ СИММЕТРИИ § 5.12. ПОСТРОЕНИЕ ЭПЮР ПОПЕРЕЧНЫХ И ПРОДОЛЬНЫХ СИЛ § 6.12. ПРОВЕРКА ПРАВИЛЬНОСТИ ЭПЮР М, Q И N § 7.12. НЕРАЗРЕЗНЫЕ БАЛКИ ПРИМЕРЫ РАСЧЕТА Вопросы для самопроверки Глава 13. ПРОДОЛЬНЫЙ ИЗГИБ ПРЯМОГО СТЕРЖНЯ § 1.13. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ УПРУГИХ ТЕЛ § 2.13. ПРОДОЛЬНЫЙ ИЗГИБ § 3.13. ПОТЕРЯ УСТОЙЧИВОСТИ ПРИ НАПРЯЖЕНИЯХ, ПРЕВЫШАЮЩИХ ПРЕДЕЛ ПРОПОРЦИОНАЛЬНОСТИ § 4.  13. ПРАКТИЧЕСКИЕ РАСЧЕТЫ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ 13. ПРАКТИЧЕСКИЕ РАСЧЕТЫ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ§ 5.13. ПРОДОЛЬНО-ПОПЕРЕЧНЫЙ ИЗГИБ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 14. ДИНАМИЧЕСКАЯ НАГРУЗКА § 2.14. ДИНАМИЧЕСКИЕ ЗАДАЧИ, ПРИВОДИМЫЕ К ЗАДАЧАМ СТАТИЧЕСКОГО РАСЧЕТА СИСТЕМ § 3.14. УДАР § 4.14. ЧАСТНЫЕ СЛУЧАИ УДАРНОГО ДЕЙСТВИЯ НАГРУЗКИ § 5.14. КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 15. НАПРЯЖЕНИЯ, ПЕРЕМЕННЫЕ ВО ВРЕМЕНИ § 1.15. ПЕРЕМЕННЫЕ НАПРЯЖЕНИЯ. УСТАЛОСТЬ § 2.15. ПРЕДЕЛ ВЫНОСЛИВОСТИ § 3.15. ДИАГРАММЫ ПРЕДЕЛЬНЫХ АМПЛИТУД И ПРЕДЕЛЬНЫХ НАПРЯЖЕНИИ § 4.1. ОСНОВНЫЕ ФАКТОРЫ, ВЛИЯЮЩИЕ НА ВЕЛИЧИНУ ПРЕДЕЛА ВЫНОСЛИВОСТИ § 5.15. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ Примеры расчета Вопросы для самопроверки Глава 16. ТОНКОСТЕННЫЕ ОСЕСИММЕТРИЧНЫЕ ОБОЛОЧКИ И ТОЛСТОСТЕННЫЕ ЦИЛИНДРЫ § 1.16. РАСЧЕТ ТОНКОСТЕННЫХ ОСЕСИММЕТРИЧНЫХ ОБОЛОЧЕК § 2.  16. РАСЧЕТ ТОЛСТОСТЕННЫХ ЦИЛИНДРОВ 16. РАСЧЕТ ТОЛСТОСТЕННЫХ ЦИЛИНДРОВПримеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 17. РАСЧЕТ КОНСТРУКЦИЙ ПО НЕСУЩЕЙ СПОСОБНОСТИ § 2.17. РАСТЯЖЕНИЕ И СЖАТИЕ § 3.17. КРУЧЕНИЕ ПРЯМОГО БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ § 4.17. ИЗГИБ БАЛОК § 5.17. МЕТОД РАСЧЕТА КОНСТРУКЦИЙ ПО РАСЧЕТНЫМ ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки ПРИЛОЖЕНИЯ |
Лучшее руководство по определению прогиба в балках переменного сечения
Таблицы балок дают информацию и предполагают, что прогиб Расчет основан на постоянном поперечном сечении. Итак, что мы делаем, если наш луч имеет крест сечение, изменяющееся по длине балки?
Калькулятор гибки древесины
Включите JavaScript
Калькулятор гибки древесины
Чтобы определить величину прогиба в
балка переменного сечения, необходимо интегрировать формулу прогиба балки
с моментом инерции, являющимся переменной по отношению к длине и
применять граничные условия. Луч
формула отклонения: v’’ = M(x)/[E*I(x)].
Луч
формула отклонения: v’’ = M(x)/[E*I(x)].
Непрерывная или дискретная – Существует два типа секций балки: непрерывная и дискретная. Большинство балок представляют собой непрерывных балок и имеют либо постоянное сечение, либо сечение, которое постепенно изменяется по длине балки. Балки крыши в больших стальных зданиях являются отличным примером непрерывной переменной балки. Балка относительно короткая по высоте на концах и очень высокая в середине.
Дискретные лучи являются лучами которые имеют внезапные разрывы в разрезе. Хотите верьте, хотите нет, иногда это проще для расчета, потому что дискретные сечения обычно постоянны, что приводит к более легкий расчет.
Формула отклонения балки является универсальной
формула, которая позволяет настраивать несколько нагрузок и балок
разделы. Я предупрежу вас, что чем больше
точным должен быть ваш расчет, тем сложнее будет сделать математику. Упрощение здесь сэкономит много времени
и усилие. Как упоминалось перед
формула:
Упрощение здесь сэкономит много времени
и усилие. Как упоминалось перед
формула:
v’’ = M(x)/[E*I(x)]
ускорение отклонения), M — момент, который обычно является функцией положение по длине балки, х. E — модуль упругости, I — момент инерции площади. луч. Все табличные лучи будут считать это константой, и поэтому ни одна из формул отклонения может быть использован.
Теперь, когда мы проинтегрируем приведенное выше уравнение, мы получим выполнение неопределенного интеграла, что означает, что мы должны добавить константу, C n, к многочлену каждый раз, когда мы интегрируем. Поскольку мы будем интегрировать уравнение два раза, мы получим две константы. Если у нас есть дискретный случае у нас будет два или более уравнений.
Граничные условия требования, которым должна соответствовать формула отклонения луча, когда она
находится в окончательном виде. Окончательная форма
приходит только тогда, когда мы используем граничные условия для решения констант
образован неопределенным интегралом.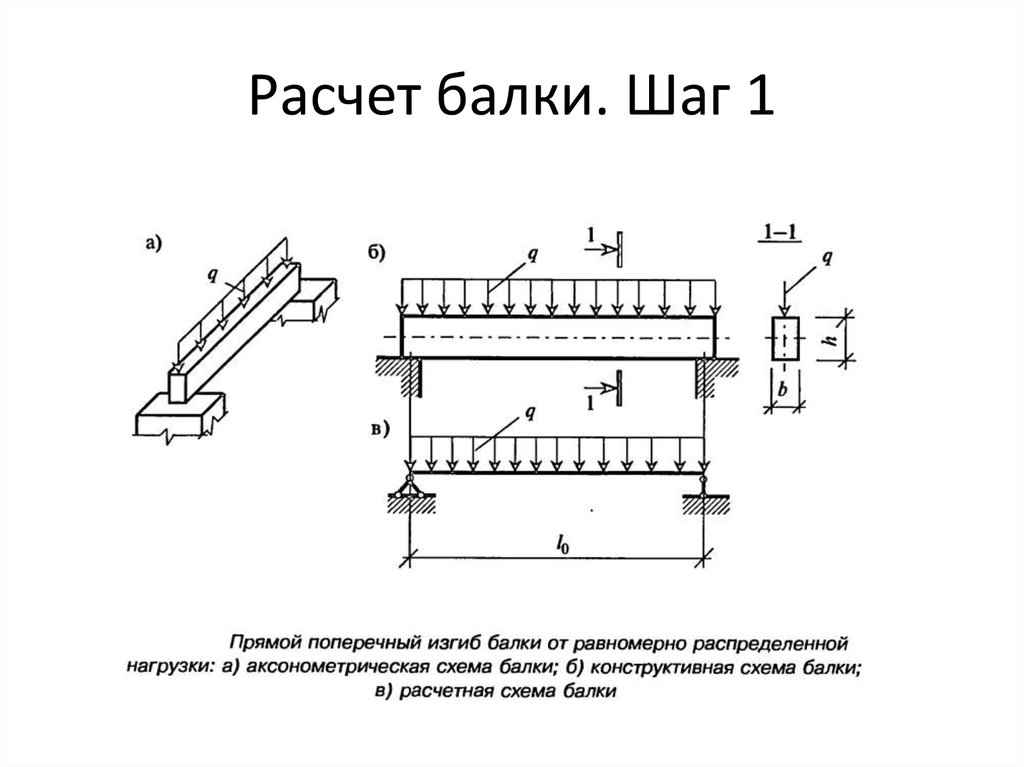 Общий
случаи, когда концы свободно опертой балки должны быть 0 (дюймы, мм и т. д.) или
наклон консольной балки должен быть 0 радиан.
Общий
случаи, когда концы свободно опертой балки должны быть 0 (дюймы, мм и т. д.) или
наклон консольной балки должен быть 0 радиан.
В этой статье мы рассмотрим три примера обычных балок переменного сечения.
- Двухсекционная консольная балка с точечной нагрузкой на конце.
- Двухсекционная свободно опертая балка под собственным весом.
- Постоянно меняющаяся неразрезная свободно опертая балка с постоянной распределенной нагрузкой.
https://mentoredengineer.com/the-best-guide-to-solving-statically-indeterminate-beams/
Пример 1: Двухсекционная консольная балка с точечной нагрузкой на конце. 94. Теперь определим момент и дважды проинтегрируем уравнение прогиба балки, каждый раз добавляя переменную для неопределенного интеграла. Я выбрал, чтобы моя система координат (переменная x) начиналась с основания. Это немного усложняет интегрирование, но переменные C 1 и C 2 взаимно компенсируются из-за граничных условий 1 и 2. Через секунду вы увидите.
Через секунду вы увидите.
Мне нужно только сделать интеграцию для одного из разделов, а затем изменить I 1 до I 2 в уравнениях. Я также сохранил переменную «v» как отклонение балки, но изменил первую производную отклонения на переменную «s», чтобы указать наклон. Я также указал переменные.
Теперь, когда проблема определена, давайте настроим граничные условия. Нам нужно, чтобы положение и наклон на фиксированном конце балки были равны 0 дюймов и 0 радиан. Также нам потребуются еще два граничных условия на стыке отрезков. Наклон и положение в этом положении должны быть одинаковыми.
Найдем граничные условия 1 и 2
Как упоминалось выше, я предвидел, что переменные C1 и C2 будет равно 0, если я решу, чтобы система координат начиналась с база.
Далее мы рассмотрим граничные условия 3 и 4. Они немного сложнее.
Обратите внимание на галочку, которую я поставил в блоке «Найти», чтобы
чтобы мы могли убедиться, что v 1 = v 2 и s 1 =
s 2 на 50 дюймов. Это подтверждает
что положение и наклон будут непрерывными в этой точке.
Это подтверждает
что положение и наклон будут непрерывными в этой точке.
Следующим шагом является проверка результатов. Это делается в два этапа. Во-первых, построить каждый сегмент по всей длине. Мы ищем четыре граничных условия, которые должны быть выполнены. Как видите, линии пересекаются и касаются друг друга на расстоянии 50 дюймов. Кроме того, v 1 не имеет отклонения или наклона в основании.
Наконец, мы объединим два графика вместе, сформировав окончательное уравнение для отклонения нашей консольной балки.
Как вы можете видеть, отклонение быстро увеличивается после 50 дюймов от основания. Это ясно видно на обоих графиках. 94.
Теперь определим момент и проинтегрируем уравнение отклонения луча дважды каждый раз добавляя переменную. Я выбрал две системы координат. Координата x идет слева направо и координата y идет справа налево. Они связаны:
г = L-x
Я выбрал эту систему координат так, что C 2 и C 4 сократятся, когда мы найдем граничные условия 1 и 2.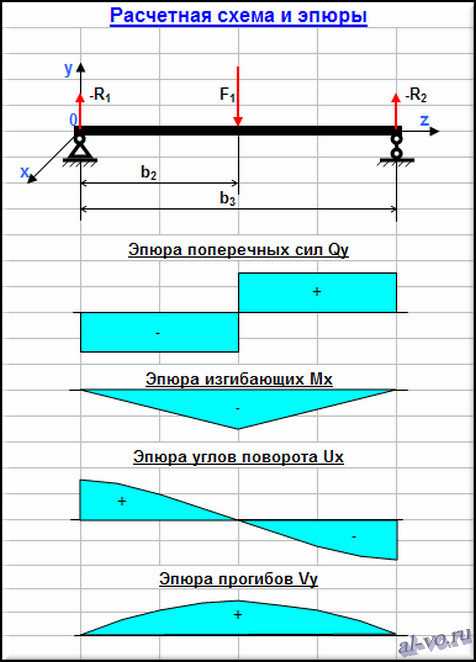 Это также упрощает математику.
чрезвычайно. Вы увидите через секунду.
Это также упрощает математику.
чрезвычайно. Вы увидите через секунду.
Мне нужно выполнить интегрирование только для одного из разделов, а затем изменить I 1 на I 2 и w 1 на w 2 в уравнениях. В уравнениях правого сечения я также заменю «у» на «х». Я также сохранил переменную «v» как отклонение балки, но изменил первую производную отклонения на переменную «s», чтобы указать наклон. Я также указал переменные.
Теперь, когда проблема определена, давайте настроим граничные условия. Нам нужно, чтобы концы балки имели отклонение 0 дюймов (BC 1 и 2). Также нам потребуются еще два граничных условия на стыке отрезков. Наклон и положение в этом месте должны быть одинаковыми в месте соединения сегментов.
Найдем граничные условия 1 и 2
Как упоминалось выше, я предвидел, что переменные C 2 и C 4 будет равно 0, когда я выберу координату запуск системы на базе.
Далее мы рассмотрим граничные условия 3 и 4. Они немного сложнее.
Они немного сложнее.
Обратите внимание на галочку, которую я поставил в блоке «Найти», чтобы чтобы мы могли убедиться, что v 1 = v 2 и s 1 = с 2 на высоте 200 дюймов. Это подтверждает что положение и наклон будут непрерывными в этой точке.
Следующим шагом является проверка результатов. Это делается в два этапа. Во-первых, построить каждый сегмент по всей длине. Мы ищем четыре граничных условия, которые должны быть выполнены.
О-о, что случилось!?
Линии определенно пересекаются на расстоянии 200 дюймов, и каждый конец имеет 0 дюймов
отклонение, но они не касаются в месте пересечения. Я не только иллюстрирую силу
построение графика решения для точности, а также демонстрация того, что использование двух
различные системы координат представляли собой проблему.
Согласно уравнениям, склоны приближаются к месту
узел на нисходящем склоне равный по величине. Однако сделать эту работу одним из склонов
на самом деле должен подойти. Мы можем
устраните эту проблему, внеся одно небольшое изменение.
Мы можем
устраните эту проблему, внеся одно небольшое изменение.
с 1 = -s 2
Давайте внесем это изменение и приступим к решению.
Да, намного лучше! Наконец, мы объединим два графика вместе, сформировав окончательное уравнение для отклонения нашей консольной балки.
Как и ожидалось, более длинная жесткая секция меньше прогибается.
Как рассчитать данные балки, если вашего случая нет в таблице
Пример 3: постоянно меняющаяся, непрерывная, свободно опертая балка с постоянной распределенной нагрузкой.Эта задача состоит из свободно опертой стальной балки длиной 300 дюймов с распределенной нагрузкой 1000 фунтов/дюйм поперек балки. Секция начинается с высоты 10 дюймов и линейно увеличивается к центру, где достигает высоты 24 дюймов. Затем он сужается до 10 дюймов.
Чтобы определить, как изменяется момент инерции относительно x, мы будем моделировать в Solidworks и брать сечения через каждые 30 дюймов. Мы сведем эти данные в таблицу и подгоним к ним строку.
Мы сведем эти данные в таблицу и подгоним к ним строку.
Вы, наверное, заметили, что я составил таблицу только для значений от 0 до 150 дюймов. Это потому, что я собираюсь использовать симметрию, чтобы упростить эту сложную задачу. Мы можем использовать симметрию, потому что и нагрузка, и сечение балки симметричны относительно середины балки. Из-за симметрии нам нужно, чтобы конечная точка имела отклонение 0 дюймов, а наклон в середине луча был 0 градусов. Затем мы можем отразить это, чтобы получить непрерывное отклонение луча. В этом случае у нас будет координата x слева направо.
Здесь можно увидеть, что рассчитанные значения I(x) близко соответствуют значениям, указанным в таблице выше. Я назвал вторую производную от положения «а1» (ускорение). Как видите, с верхней и нижней частью, имеющей переменную «x», будет очень весело интегрировать это. Итак, есть одна вещь, которую вам нужно знать обо мне. У меня есть ограничения в том, что я не буду делать. Интеграция — одна из таких вещей.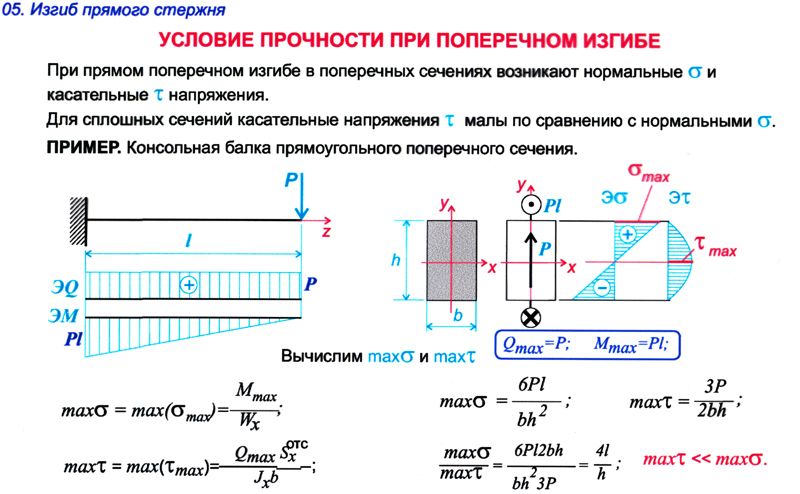 Вот почему у нас есть MathCAD!
Вот почему у нас есть MathCAD!
Как видите, очень кропотливая работа по интеграции был замазан, и мы смогли напрямую решить для нашей границы условия. В уравнениях s(x) и v(x), на самом деле были натуральные бревна и каким-то образом появился арктангенс (не показано). я до сих пор не жалею позволяя MathCAD делать всю работу.
Следующим шагом является проверка результатов. Это делается в два этапа. Во-первых, построить каждый сегмент по всей длине. Мы ищем, чтобы наши граничные условия были выполнены. Как видите, отклонение при x = 0 дюймов составляет 0 дюймов, а наклон кажется плоским при x = 150 дюймов.
Наконец, мы зеркально отразим графики вместе, сформировав окончательное уравнение для отклонения нашей консольной балки.
Как видите, отклонение составляет 0 дюймов в конечных точках и имеет максимальное отклонение в центре.
Лучшее руководство по расчету статически неопределимых балок
Заключение В этой статье рассматриваются три популярных варианта нагружения, в которых балка имеет переменное поперечное сечение. Хотя это требует исчисления, часто это очень легко сделать вручную, потому что это многочлены. Если нет, будьте благодарны надежным программам, таким как MathCAD, которые сделают это за вас. Эта статья должна дать вам хорошее представление о процедуре, используемой для анализа таких лучей. Если ваша балка не загружена именно так, вы всегда можете найти расчет момента в таблице и интегрировать свое сердце.
Хотя это требует исчисления, часто это очень легко сделать вручную, потому что это многочлены. Если нет, будьте благодарны надежным программам, таким как MathCAD, которые сделают это за вас. Эта статья должна дать вам хорошее представление о процедуре, используемой для анализа таких лучей. Если ваша балка не загружена именно так, вы всегда можете найти расчет момента в таблице и интегрировать свое сердце.
Использование интегрирования для получения прогиба балки
Примечание редактора. Эта статья блога изначально была написана в виде рабочего листа PTC Mathcad Prime. Чтобы получить наилучшие впечатления от чтения, загрузите рабочий лист Mathcad Prime 8 здесь. Если вам нужна программа для просмотра листов Mathcad Prime, загрузите Mathcad Prime бесплатно здесь.
В предыдущих блогах мы узнали, как создавать диаграммы сдвига и изгибающего момента с помощью диаграмм свободного тела. Я также объяснил, как можно использовать Mathcad для расчета максимального изгибающего момента для трех условий нагрузки.
В этом блоге я выведу функции для сдвига, момента, наклона и прогиба для равномерно нагруженной свободно опертой балки, начиная только с условия нагружения и используя интегрирование. Затем процесс повторяется для треугольной нагрузки.
При интегрировании Mathcad не включает константу интегрирования C. Это необходимо решить с использованием известных ограничений.
Поскольку равномерная нагрузка действует вниз, я буду использовать отрицательное значение для w (сила/длина).
Я также буду использовать некоторые числовые данные для проверки расчетных функций:
- Длина балки: Длина = 20 футов
- Равномерная нагрузка: W=2,0 тысячи фунтов/фут
- Модуль упругости: E1=29000 ksi
- Момент инерции: I1=448 в 4
РАВНОМЕРНАЯ НАГРУЗКА
НАГРУЗКА
Рассчитайте левую реакцию путем суммирования моментов относительно точки B. С1.
Найдите постоянную интегрирования C1. Мы знаем, что при x=0 сдвиг равен левой реакции R A .
Мы знаем, что при x=0 сдвиг равен левой реакции R A .
C1 равно Span*w/2. Теперь его можно ввести в функцию сдвига, а функцию сдвига можно переопределить без необходимости использования C1 в качестве входной переменной.
МОМЕНТ
Рассчитайте функцию момента, интегрируя функцию сдвига и включая константу интегрирования C2.
Найдите постоянную интегрирования C2. Мы знаем, что при x=0 момент равен 0.
C2 равно 0. Теперь его можно ввести в функцию для момента, а функцию для момента можно переопределить без необходимости использования С2 в качестве входных данных. переменная.
НАКЛОН
Соотношение радиуса кривизны p балки определяется из механики материалов как 1/p = M/(E*I), а отношение момента к наклону θ определяется как M = E * I * d/dx(θ). Рассчитайте наклон, интегрируя M/(E*I).
Есть два способа найти C3 для равномерно нагруженной балки.
Во-первых, мы знаем, что для равномерно нагруженной балки наклон балки равен нулю в точке максимального момента, и мы знаем, что максимальный момент возникает в месте, где сдвиг равен нулю.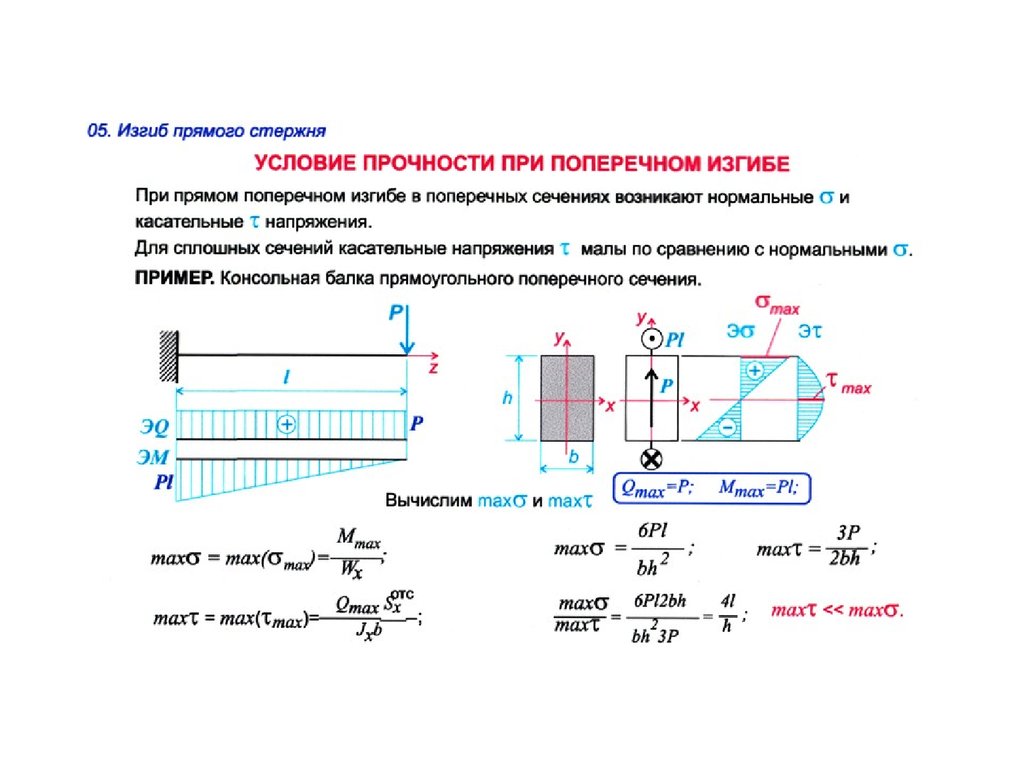 Первый способ решения для C3 состоит в том, чтобы вычислить местоположение нулевого сдвига и использовать ограничение наклона = 0 в месте нулевого сдвига.
Первый способ решения для C3 состоит в том, чтобы вычислить местоположение нулевого сдвига и использовать ограничение наклона = 0 в месте нулевого сдвига.
Второй способ расчета C3 состоит в том, чтобы дождаться, пока будет получена функция отклонения, и использовать два места, где отклонение равно нулю. Затем используйте два уравнения для решения двух неизвестных C3 и C4.
ПРОГИБ
Рассчитайте прогиб путем интегрирования функции наклона. Обратите внимание, что есть две константы интегрирования, которые необходимо решить.
C3 и C4 неизвестны. Прогиб при x=0 равен 0, а прогиб при x=Span равен 0. Используйте эти два значения для решения C3 и C4.
C3 равно -((span 3 * w) / (24 * E * I)). Теперь его можно ввести в функцию наклона, а функцию наклона можно переопределить без необходимости использовать C3 в качестве входной переменной. C4 равен нулю, а C4 можно исключить.
На приведенном ниже графике представлены графики сдвига, момента, наклона балки и прогиба. Значения наклона и отклонения умножаются на 100, чтобы их можно было отобразить в нужном масштабе. Вертикальный маркер, расположенный в середине пролета, находится в месте нулевого сдвига, максимального момента, нулевого наклона и максимального прогиба.
Значения наклона и отклонения умножаются на 100, чтобы их можно было отобразить в нужном масштабе. Вертикальный маркер, расположенный в середине пролета, находится в месте нулевого сдвига, максимального момента, нулевого наклона и максимального прогиба.
Выведите функцию для расчета максимального прогиба равномерно нагруженной балки. Максимальный прогиб происходит там, где наклон балки равен 0, где момент наибольший и где сдвиг равен 0. Это значение, VZero, было рассчитано ранее.
ТРЕУГОЛЬНАЯ НАГРУЗКА
В следующем примере повторяется процесс, использованный выше для получения функций для расчета сдвига, момента, наклона и прогиба для треугольной нагруженной балки, начиная с функции треугольной нагрузки.
НАГРУЗКА
Рассчитайте левую реакцию, суммируя моменты относительно точки B.
СДВИГ
Рассчитайте функцию сдвига, интегрируя функцию нагрузки и включая постоянную интегрирования CT1.
Найдите константу интегрирования CT1.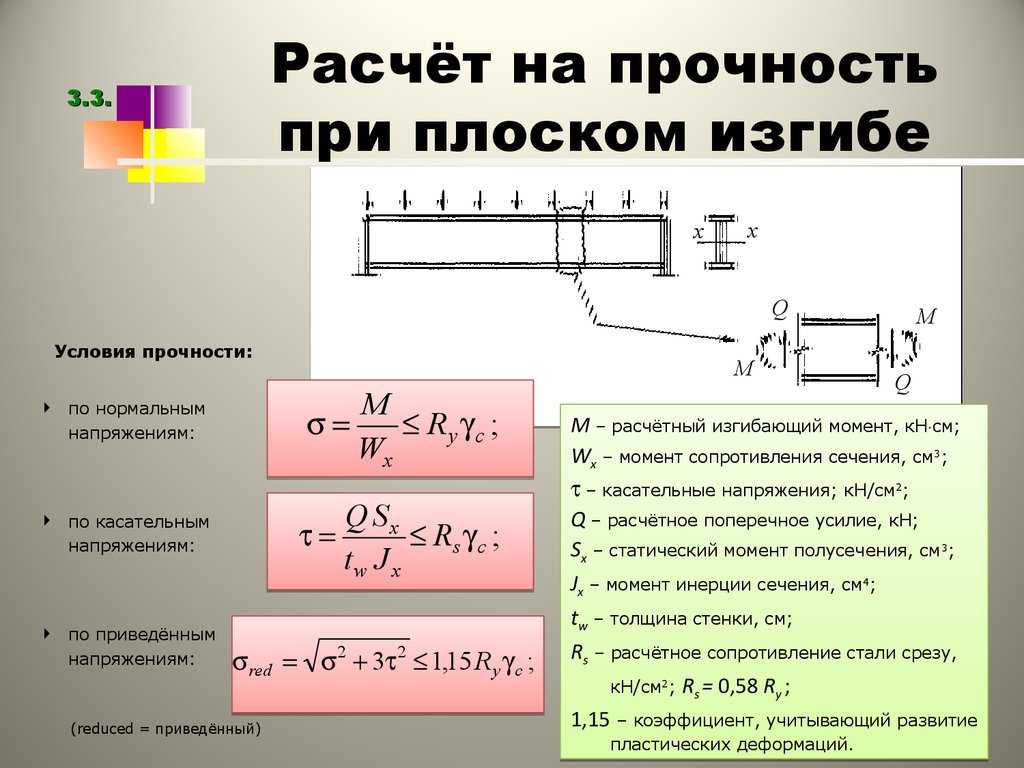 Мы знаем, что при x=0 сдвиг равен левой реакции R A .
Мы знаем, что при x=0 сдвиг равен левой реакции R A .
CT1 равно Span*w/6. Теперь его можно ввести в функцию сдвига, а функцию сдвига можно переопределить без необходимости использования CT1 в качестве входной переменной.
МОМЕНТ
Рассчитайте функцию момента путем интегрирования функции сдвига и включения константы интегрирования CT2.
Найдите константу интегрирования CT2. Момент при x=0 равен 0.
CT2 равен 0. Теперь его можно ввести в функцию для момента, а функцию для момента можно переопределить без необходимости использования CT2 в качестве входной переменной.
НАКЛОН
Соотношение радиуса кривизны p балки определяется из механики материалов как 1/p = M/E * I, а отношение момента к наклону θ определяется как M = E * I * d/dx(θ). Рассчитайте наклон путем интегрирования M/E * I.
В случае треугольной нагрузки максимальное отклонение не происходит в месте нулевого сдвига и максимального момента. Из-за этого мы не знаем никаких ограничений, которые нужно решить для CT3.
Из-за этого мы не знаем никаких ограничений, которые нужно решить для CT3.
В этом случае единственный способ найти CT3 — дождаться получения функции отклонения, а затем использовать два местоположения, где отклонение равно нулю, для решения двух неизвестных CT3 и CT4.
ПРОГИБ
Рассчитать прогиб путем интегрирования функции наклона. Обратите внимание, что есть две константы интегрирования, которые необходимо решить.
CT3 и CT4 неизвестны. Прогиб при x=0 равен 0, а прогиб при x=Span равен 0. Используйте эти два значения для решения для CT3 и CT4.
Теперь, когда известны CT3 и CT4, можно переопределить функцию наклона и отклонения.
Получите функцию для расчета максимального прогиба для треугольной нагрузки, которая возникает, когда уклон балки равен нулю. Решение для x имеет четыре решения.
Проверьте численные результаты и выберите 3-е решение для местоположения нулевого наклона луча. Примечание: нижний индекс 3 получается с помощью левой скобки [.
Примечание: нижний индекс 3 получается с помощью левой скобки [.
На приведенном ниже графике представлены графики сдвига, момента, наклона балки и прогиба. Значения наклона и отклонения умножаются на 100, чтобы их можно было отобразить в нужном масштабе. Левый вертикальный маркер находится в месте нулевого наклона балки и в месте максимального прогиба. Правый вертикальный маркер находится в месте нулевого сдвига и максимального момента.
В этом блоге я использовал интеграцию для получения функций для отклонения, начиная только с функции загрузки. Попутно я вывел функции для сдвига, изгибающего момента и наклона балки. Эти функции были проверены с использованием известных уравнений из AISC Руководство по стальным конструкциям .
Интеграция — мощный инструмент в наборе инструментов Mathcad. Я продемонстрировал, как найти константы интегрирования, используя известные ограничения, и как использовать ключевое слово решить с оператором символьного вычисления вместе с другими ключевыми словами, чтобы получить нужные функции.
В этом блоге я использовал нагрузку на балки для иллюстрации концепций, но эти же концепции можно использовать во многих других областях науки и техники. Примеры в этом блоге иллюстрируют использование:
- Функции
- Символьная оценка для получения функций, особенно когда числовые значения неизвестны
- Графики XY с несколькими кривыми
- Вертикальные маркеры для обозначения местоположений на участке
- Переменные диапазона
- Интегрирование и решение констант интегрирования
Попробуйте Mathcad Prime
Загрузите бесплатную 30-дневную пробную версию Mathcad Prime, чтобы лично увидеть лучшие возможности Mathcad.
Получить мою пробную версиюОб авторе
Брент Максфилд из Солт-Лейк-Сити, штат Юта.