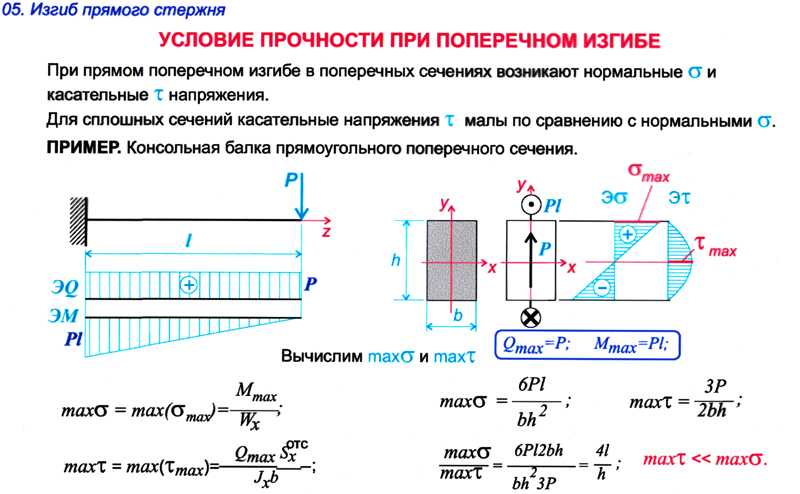
Расчет консольной балки, подбор прямоугольного сечения, эпюры онлайн
Назад к примерам
Начать расчет балки
Определение опорных реакций
1. Согласно схеме решения задач статики определяем, что для нахождения неизвестных реакций необходимо рассмотреть равновесие балки.
2. На балку наложена связь в точке A (справа) типа жесткая заделка, поэтому освобождаем балку, заменив действие связи реакциями (HA, RA, MA).
3. Определим реакции опор в соответствии с уравнениями равновесия балки: ΣFx = 0, ΣFy = 0, ΣMA = 0.
ΣFx = 0: HA = 0
ΣFy = 0: - q1*1 + P1 + RA = 0;
ΣMA = 0: q1*1*(1.1+1/2) - 1.1*P1 - M1 + MA = 0;
4. Решаем полученную систему уравнений, находим неизвестные :
HA = 0 (кН)
RA = q1*1 - P1 = 90*1 - 70 = 20.00 (кН)
MA = - q1*1*(1.1+1/2) + 1.1*P1 + M1 = - 90*1*(1.1+1/2) + 1.1*70 + 18 = -49.00 (кН*м), так как момент отрицателен, на расчетной схеме направим его в противоположную сторону.
5. Сделаем проверку, составив дополнительное моментное уравнение отоносительно свободного конца балки:
- q1*1*(1/2) + 1*P1 - M1 + 2.1*RA - MA = - 90*1*(1/2) + 1*70 - 18.00 + 2.1*20.00 - 49.00 = 0
00 (кН)Построение эпюр
Рассмотрим 1-й участок 0 ≤ x1 < 1
Поперечная сила Q:
Q(x1) = - q1*(x1 - 0)
Значения Q на краях участка:
Q1(0) = - 90*(0 - 0) = 0 (кН)
Q1(1) = - 90*1 = -90 (кН)
Изгибающий момент M:
M(x1) = - q1*(x1)2/2
Значения M на краях участка:
M1(0) = - 90*(0 - 0)2/2 = 0 (кН*м)
M1(1) = - 90*12/2 = -45 (кН*м)
Рассмотрим 2-й участок 1 ≤ x2 < 1.
5
Поперечная сила Q:
Q(x2) = - q1*1 + P1
Значения Q на краях участка:
Q2(1) = - 90*1 + 70 = -20 (кН)
Q2(1.50) = - 90*1 + 70 = -20 (кН)
Изгибающий момент M:
M(x2) = - q1*1*[(x2 - 1) + 1/2] + P1*(x2 - 1)
Значения M на краях участка:
M2(1) = - 90*1*(0 + 0.50) + 70*(1 - 1) = -45 (кН*м)
M2(1.50) = - 90*1*(0.50 + 0.50) + 70*(1.50 - 1) = -55 (кН*м)
Рассмотрим 3-й участок 1.5 ≤ x3 < 2.1
Поперечная сила Q:
Q(x3) = - q1*1 + P1
Значения Q на краях участка:
Q3(1.50) = - 90*1 + 70 = -20 (кН)
Q3(2.10) = - 90*1 + 70 = -20 (кН)
Изгибающий момент M:
M(x3) = - q1*1*[(x3 - 1) + 1/2] + P1*(x3 - 1) + M1
Значения M на краях участка:
M3(1.
M3(2.10) = - 90*1*(1.10 + 0.50) + 70*(2.10 - 1) + 18 = -49 (кН*м)
50) = - 90*1*(0.50 + 0.50) + 70*(1.50 - 1) + 18 = -37 (кН*м)Подбор сечения
Прямоугольное сечение балки подбираем из условия прочности при допускаемом напряжении: = 160 (МПа)
, где:
— нормальные напряжения, МПа;
— наибольшее по абсолютной величине значение изгибающего момента, определяемое по эпюре моментов Mx, кН*м;
— момент сопротивления, см3;
— допустимое значение нормального напряжения (расчетное сопротивление), МПа;
Момент сопротивления прямоугольного сечения определим по формуле:
Требуемый момент сопротивления определяем по формуле:
Поскольку дано соотношение сторон
Отметим, что полученные размеры являются минимально необходимыми для обеспечения прочности заданной балки. Следовательно, за окончательные размеры прямоугольного сечения балки принимаем: h=165 (мм), b=85 (мм)
Расчет произведен при помощи онлайн-сервиса SOPROMATGURU.
Назад к примерам
Начать расчет балки
видео-инструкция по монтажу своими руками, как подобрать, рассчитать нагрузки, прочность, максимальный пролет, размеры, цена, фото
Статьи
Если вы самостоятельно решили сделать в строящемся или уже построенном доме деревянное перекрытие, то вам обязательно следует разобраться, как подобрать деревянные балки в соответствии с их сечением и длиной пролёта.
Кроме того, такой профиль, даже если у него одинаковое сечение, не обязательно идентичен по прочности, ведь это может быть, е примеру, цельный массив или клееный брус, что, вполне естественно, сказывается на его характеристиках. Мы предлагаем вам научиться считать самостоятельно, а ещё хотим предложить вам к просмотру видео в этой статье по нашей теме.
Перекрытие — конструкция пола по деревянным балкам с утеплением и вентзазором
Деревянные балки
Нагрузка на деревянную балку осуществляется сверху вниз
Примечание.
На практике представляет собой горизонтальный профиль, несущий на себе определённую степень тяжести различных элементов конструкции.
Слово «балка», которое широко применяется в русской строительной терминологии, означает несущий конструктивный элемент, который, главным образом, работает на изгиб.Каким может быть профиль
Виды бруса (слева направо): из цельного массива дерева, клееный
- Как мы уже сказали, расчет нагрузки на деревянную балку будет зависеть не только от её сечения, но и от прочности, что можно привести на примере цельного и клееного бруса одинаковой величины. Так, если цельный профиль представляет собой обычное обрезанное со всех сторон бревно, то второй вариант, это обработанные различными составами и склеенные между собой доски (ламели), которые для этого случая располагаются вертикально. Такая клеевая сборка несколько увеличивает прочность материала на изгиб, а также продлевает срок его эксплуатации.
- Кроме того, в современном строительстве инструкция позволяет использовать комбинированные деревянные профили, например, это может быть ориентировано-стружечная плита с цельным массивом дерева или пространственные балки, элементы которых скрепляются зубчатыми пластинами. Конечно, на прочность они более слабые, нежели сталь или бетон, поэтому приходится прибегать к большему поперечному сечению. Но, как бы там ни было, но у пиломатериалов всегда есть преимущество – это экологическая чистота и малый вес конструкции по сравнению с другими материалами.
Конечно, на прочность они более слабые, нежели сталь или бетон, поэтому приходится прибегать к большему поперечному сечению. Но, как бы там ни было, но у пиломатериалов всегда есть преимущество – это экологическая чистота и малый вес конструкции по сравнению с другими материалами.Примечание. Если при строительстве дома вы хотите обустроить балкон из дерева, то подберите соответствующие размеры деревянных балок по длине.
Их выступающие концы будут служить опорой для основания конструкции.
Но расчет деревянной консольной балки вам здесь не нужен – будет вполне достаточно сечения для прочности перекрытия.
Традиционные балки
Монтаж перекрытия
Предел прочности деревянных балок зависит не только от их сечения, но и от их длины, так, максимальный пролет деревянной балки в оптимальном режиме не должен превышать 4м, но, тем не менее, существуют и допуски на определённых условиях.
А вот оптимальное сечение профиля не квадратное, как многие считают, а прямоугольное, где соотношение высоты к ширине составляет 1,4:1.
Если балка заделывается в стену, то её следует закрыть по кругу гидроизоляцией, не трогая при этом торец, но в любом случае конец, который туда заводится, должен быть не менее 12 см, кроме того, его желательно закрепить анкерным болтом для жёсткости.
Если вы производите расчёты поперечного сечения своими руками, вам следует учитывать, что здесь идёт в учёт нагрузка от собственной массы, которая обычно составляет 190-220 кг/м2, а эксплуатационная нагрузка берётся за 200 кг/м 2. Направление установки определяется по более короткому расстоянию пролёта, а шаг определяется наличием стояков в каркасе (одна горизонталь на одну вертикаль).
| Длина пролёта (м) | 2,5 | 3,0 | 3,5 | 4,0 | 4,5 | 5,0 | 6,0 |
| Шаг монтажа (м) ↓ | Поперечное сечение (мм) | ||||||
| 0,6 | 75х100 | 75х150 | 75х200 | 100х200 | 100х200 | 125х200 | 150х225 |
| 1,0 | 75х150 | 100х150 | 100х175 | 125х200 | 150х200 | 150х225 | 175х250 |
Таблица под нагрузку 400 кг/м2
Нагрузка (кг/м пог. | 3,0 | 3,5 | 4,0 | 4,5 | 5,0 | 5,5 | 6,0 |
| Поперечное сечение (мм) | |||||||
| 150 | 50х140 | 50х160 | 60х180 | 80х180 | 80х200 | 100х200 | 100х220 |
| 200 | 50х160 | 50х180 | 70х180 | 70х200 | 100х200 | 120х220 | 140х220 |
| 250 | 60х160 | 60х180 | 70х200 | 100х200 | 120х200 | 140х220 | 160х220 |
Более слабые нагрузки
Примечание. Как видите, деревянная балка с пролетом 6 метров может использоваться при нагрузках от 250 до 400 кг/м2.
Но это крайний случай – гораздо надёжнее, если есть предположение возникновения больших нагрузок, использовать центральные опоры.
Монтаж подпоры
| Ширина пролёта (м) | Шаг (м) | Сечение бревна (см) |
| 2 | 1 | 13 |
| 0,6 | 11 | |
| 2,5 | 1 | 15 |
| 0,6 | 13 | |
| 3 | 1 | 17 |
| 0,6 | 14 | |
| 3,5 | 1 | 19 |
| 0,6 | 16 | |
| 4 | 1 | 21 |
| 0,6 | 17 | |
| 4,5 | 1 | 22 |
| 0,6 | 19 | |
| 5 | 1 | 24 |
| 0,6 | 20 | |
| 5,5 | 1 | 25 |
| 0,6 | 21 | |
| 6 | 1 | 27 |
| 0,6 | 23 | |
| 6,5 | 1 | 29 |
| 0,6 | 25 | |
| 7 | 1 | 31 |
| 0,6 | 27 |
Параметры для круглого бревна при расчетной нагрузке 400 кг/м2
| Порода дерева | Сорт | Диаметр поперечного сечения (мм) | Максимальный пролёт (м) | ||||||||
| Есть горизонтальные связи у стояков | Есть перекрёстные связи у стояков | Есть горизонтальные и перекрёстные связи у стояков | |||||||||
| Хвойные | 2 | Расстояние между балками (мм) | |||||||||
| 300 | 400 | 600 | 300 | 400 | 600 | 300 | 400 | 600 | |||
| 38х89 | 1,86 | 1,72 | 1,58 | 1,99 | 1,81 | 1,58 | 1,99 | 1,81 | 1,58 | ||
| 38х140 | 2,92 | 2,71 | 2,49 | 3,14 | 2,85 | 2,49 | 3,14 | 2,85 | 2,49 | ||
| 38х184 | 3,54 | 3,36 | 3,20 | 3,81 | 3,58 | 3,27 | 3,99 | 3,72 | 3,27 | ||
| 38х235 | 4,17 | 3,96 | 3,77 | 4,44 | 4,17 | 3,92 | 4,60 | 4,29 | 4,00 | ||
| 38х286 | 4,75 | 4,52 | 4,30 | 5,01 | 4,71 | 4,42 | 5,17 | 4,82 | 4,49 | ||
Общие параметры для пролётов перекрытий
Пояснение.
Настоящая таблица актуальна для тех случаев, когда распределённая равномерно временная нагрузка составляет не более 2,4 кПа=0,0024мПа=244,73 кгс/м2Монтаж перекрытий
Несмотря на различные современные технологии конструктивных особенностей деревянных балок, всё-таки в России отдают предпочтение цельному массиву дерева, и основной причиной такого предпочтения является низкая цена, по которой в РФ можно приобрести пиломатериалы для населения.
Да и какой смысл строить дом из цельномассивного бруса или бревна и при этом перекрытия монтировать из клееного профиля или с добавками стальных укрепляющих ламелей.
Декоративные деревянные балки
Таблицы, которые вы видели выше, не распространяются на декоративные балки, которые просто держат потолок, но при этом со стороны чердака нет абсолютно никаких нагрузок, а в некоторых случаях чердак отсутствует вообще.
Поэтому, здесь поперечное сечение начинается от размера 100×50 мм и регулируется исключительно фантазией дизайнера и особенностями освещения.
На верхнем фото вы видите именно такую конструкцию, где балки имеют 100×50 мм с ячейкой каркаса 100 см.
Заключение
Для крепежа деревянных балок используется металлическая фурнитура. Среди этих элементов основными являются стальные скобы, анкерные болты, металлические перфорированные полосы, простые и усиленные уголки. Весь этот крепёж для усиления жёсткости потолочной конструкции фиксируется при помощи саморезов разного сечения, в зависимости от потребности.
Расчет консолей | Новости Timber Trader
Консоли становятся все более распространенными, но требуют продуманных проектных решений. Джордж Долезал, главный инженер Meyer Timber.
Каждый, кто занимается проектированием и проработкой деталей современного двухэтажного семейного дома, знает, что это не так просто, как раньше. Прошли времена красивой прямоугольной коробки с шатровой или двускатной крышей. Теперь нам предстоит иметь дело со сложной формой крыши, кирпичной кладкой внизу и облицовкой наверху, смещенными стенами первого этажа с несколькими ступенями в них и, в довершение всего, цокольным этажом открытой планировки с несколькими внутренними стенами.
Как будто нам нужен старый добрый скайхук, чтобы повесить первый этаж.
Эта сложность приводит к тому, что в систему перекрытий добавляется гораздо больше консолей. Консоль — это конструктивный элемент, выступающий горизонтально без опоры на конце балки. В строительстве жилых домов консольная балка почти всегда будет иметь «пролет», как показано на рисунке 1 (ниже), что обеспечивает устойчивость элемента. Для несущих и балочных перекрытий, указанных с помощью таблиц пролетов AS 1684, требуется задний пролет, по крайней мере, в два раза превышающий консольный, чтобы предотвратить подъем на опору (на основе равномерно распределенных нагрузок). Чтобы еще больше усложнить ситуацию, может быть более одного заднего пролета, неравномерная нагрузка или могут быть консоли на обоих концах.
Рисунок 1
Крейг Кей затронул кантилеверы в своей статье «Нет серебряной пули» в апреле 2021 года в TTN , и я немного углублюсь в эту тему. Проницательному дизайнеру важно понять, как устроен пол и чего можно добиться с помощью консоли в различных сценариях.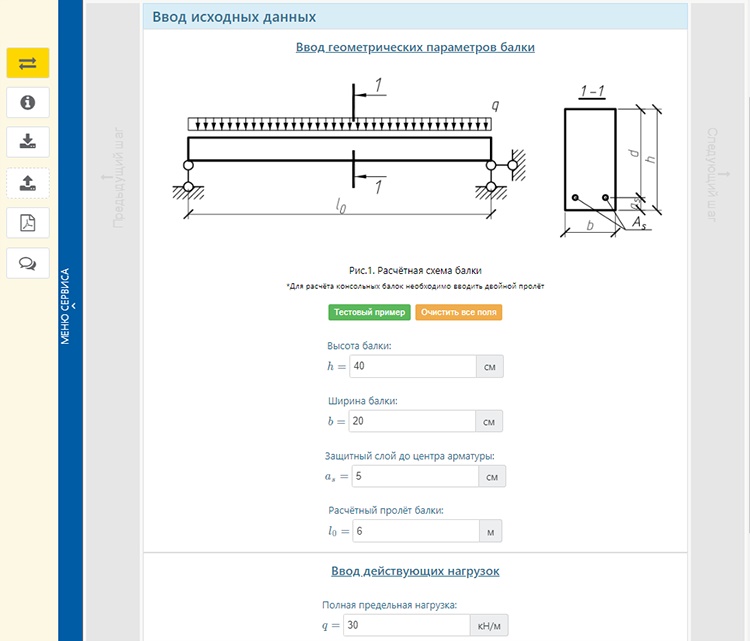
Что произойдет, если задний пролет станет меньше?
Ограничения в AS1684 могут быть уменьшены, но необходимо учитывать последствия. Чем меньше пролет, тем больше подъем на конце балки. Эти значения реакции поддержки включены (с предупреждениями) в распространенные программные пакеты EWP, такие как designIT. Если эта опора врезана в стальную балку, то балка будет обеспечивать сопротивление подъему. Если рассматриваемый элемент представляет собой двутавровую балку, упирающуюся в балку, необходимо рассмотреть вопрос о соединении, поскольку стандартные подвески двутавровой балки с торцевым креплением имеют минимальное сопротивление подъему. Возможно, вам придется использовать элементы жесткости стенки с подвеской частичной глубины.
Скрытая консоль
Недавно меня спросили о конструкции балки А, показанной на рис. 2 (ниже). Полая балка лестницы с пролетом 6 м не будет работать в LVL. Но более пристальный взгляд на это показывает, что балки имеют пролет 4,2 м и 0,9 м, если LVL является опорой; ИЛИ они охватывают 4,2 м с консолью 0,9 м.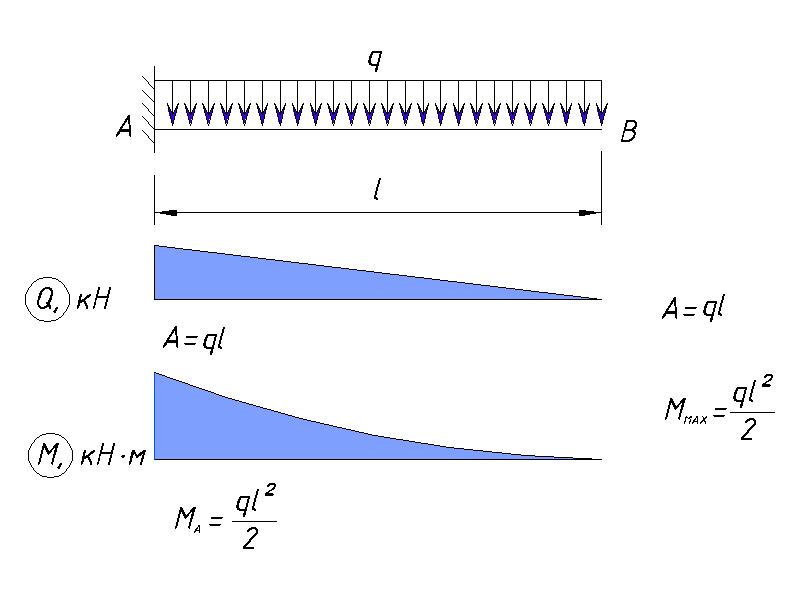
Это работает в программном обеспечении для проектирования, а это означает, что LVL затем становится концевым триммером, распределяющим нагрузку на балки и укрепляющим их, решая проблему.
В действительности относительная жесткость между балкой и консолью балки будет определять, будет ли балка поддерживать балку или нет.
Рисунок 2: различные сценарии использования консолей
Консоли с выступом из кирпича
В этих случаях используется консоль 150 мм, чтобы внешняя часть верхней рамы совпадала с кирпичной кладкой нижнего этажа (см. Рисунок 2). Концевые триммеры не требуются для коротких консолей на перекрытиях с двутавровыми балками, но могут потребоваться для крепления или поддержки точечных нагрузок. Короткие балки, идущие перпендикулярно основному пролету, также потребуются там, где консоль параллельна прогону балок.
Работа с углами на двусторонней консоли
Если у вас есть консоль на обеих перпендикулярных внешних стенах, угол требует особого внимания.
Проще всего иметь элемент под углом 45° (например, плоское бедро), в который втыкаются балки. Но с двутавровыми балками это сложнее, и установщикам трудно сделать это правильно. Одно из решений состоит в том, чтобы спроектировать концевой триммер с одной стороны, чтобы удерживать противоположный концевой триммер вверх, что упрощает все соединения (см. консольный угол на рис. 2). Это то, с чем лучше всего справится инженер, поэтому обсудите это с вашим предприятием F&T или поставщиком EWP. Стандартные детали могут быть сделаны для более распространенных сценариев.
Окна могут помочь (или помешать)
Если большая консоль поддерживает внешнюю стену с проемами в ней, балки под проемом не несут никакой нагрузки на крышу, но в местах расположения стоек косяков будут точечные нагрузки . Часто бывает проще спроектировать балки LVL в этих точках с высокой нагрузкой, а затем вы можете убрать нагрузку на крышу между ними, чтобы облегчить расчет.
Прогибы
Консольная балка является неразрезным элементом, то есть любое отклонение консоли будет способствовать прогибу заднего пролета и наоборот.
Если на задний пролет приходится нагрузка крыши, например, консольная балка балкона под внешней стеной, это следует учитывать, так как это поможет с жесткостью. Кроме того, если вы упретесь в балку, она будет немного прогибаться, поэтому опора заднего пролета не будет полностью жесткой. Эффект от этого нелегко определить количественно, но отклонение вниз опорной балки заднего пролета также уменьшит отклонение на конце кантилевера. Точно так же любое перемещение балки в подвеске заднего пролета повлияет на прогибы, поэтому установщик должен закрепить подвесы с помощью креплений во всех доступных отверстиях.
Таким образом, имея возможность определить, какие элементы действуют как консоли и как управлять соединениями, вы часто можете упростить компоновку сложных проектов домов. При этом вы должны включить правильную документацию, чтобы убедиться, что она будет установлена так, как вы предполагали.
Мы все можем шутить о скайхуках, но пока они не будут изобретены, древний инженерный принцип гравитации будет действовать.
Структурные консоли, которые должным образом детализированы и построены, будут стоять на протяжении всего срока службы дома. И последнее постоянное напоминание — если вы сомневаетесь, проконсультируйтесь с инженером, прежде чем продолжить.
Для получения дополнительной информации по этой теме свяжитесь с Джорджем Долезалом по электронной почте [email protected]
Консольная балка – моменты и силы (ручной расчет)
Поскольку мы использовали программы КЭ для расчета изгибающих моментов, силы и прогибы конструкций в последних уроках, мы делаем шаг назад к самым основам проектирования конструкций и выполняем ручные расчеты: Мы начинаем с одной из наиболее часто используемых статических систем — консольной балки.
В этом посте мы шаг за шагом рассмотрим, как рассчитать силы и моменты консолей для различных ситуаций нагрузки.
Не будем долго говорить, давайте углубимся в это.
🙋♀️ Что такое консоль или консольная балка?
Консоль — это статическая система, действующая как балка при изгибе и сдвиге.
Поэтому ее также называют консольной балкой. Он характеризуется наличием только одной опоры — фиксированной — на одном из двух концов.В повседневной жизни мы окружены консолями. Вероятно, наиболее часто встречающимся примером консолей являются балконы.
Here are 10 examples of cantilevers
- Traffic light posts and systems cantilevering over the street
- Overhangs of roofs
- Construction of bridges with the balanced cantilever method
- Balconies
- Aeroplane wings
- Side mirrors on a автомобиль
- Высотные здания (вертикальные консоли)
- Книжные полки, прикрепленные к стене
- Краны
- Лопасти ветряных турбин
Консоль в большинстве случаев представляет собой горизонтальную балку, имеющую фиксированную опору на одном конце и не имеющую опоры на другом конце. Консоль может воспринимать как изгибающие моменты, так и поперечные усилия.
Давайте посмотрим на статическую систему.
Статическая система консольной балкиИз рисунка видно, что неподвижная опора (а) воспринимает
- реакцию момента M
- вертикальную силу реакции V и
- силу горизонтальной реакции H
Понимание Статическая система конструкции, вероятно, является одной из самых сложных частей статики и проектирования конструкций в начале.
Судя по моему опыту, этому также плохо учат в университете, и в Интернете очень мало информации о нем, не так ли?
Итак, давайте рассмотрим несколько прикладных примеров.
- Высотные монолитные стержни в качестве вертикальных консолей для придания жесткости зданию при воздействии горизонтальных нагрузок (ветер, землетрясения)
- Свес стропил скатных крыш также можно рассматривать как консольную балку. Однако чаще говорят, что стропила представляют собой неразрезную балку с консольным свесом.
- Столбы наружного освещения и светофора представляют собой вертикальные консольные балки.
- Балконы часто делают консольными. Когда мы говорим о балконах, мы говорим о консольных плитах, однако в большинстве случаев трехмерная конструкция преобразуется в двухмерную систему, как мы увидим далее.
⬇️ 2 примера ситуаций загрузки
Мы хотим, чтобы в этом блоге было немного радостно и реалистично, верно? Итак, давайте посмотрим на сценарии загрузки, к которым мы все можем относиться.
🧍 Я стою на балконе — Точечная нагрузка
Давайте рассмотрим пример, где человек — в данном случае я😊 — стоит на балконе и предположим, что я вешу 75 кг.
Я на балконе. Этот вес 75 кг можно напрямую перевести в 0,74 кН. Теперь, когда я стою двумя ногами в определенной точке, нагрузка сосредоточена, и, следовательно, 0,74 кН равняется точечной нагрузке на консольную плиту.
Как мы видели в предыдущем разделе, плита равна балке, и поэтому мы можем применить точечную нагрузку к консольной балке. 92 * 3м = 14,1 кН/м$
Линейная нагрузка на консольную балку🧮 Ручной расчет изгибающего момента и поперечных сил – консоль
Теперь для расчета толщины и свойств материала балкона – или любого другого (консольного) конструкции необходимо рассчитать силы и моменты, действующие в балке.
Как правило, статически определяемые конструкции, такие как консольные или свободно опертые балки, должны удовлетворять трем условиям равновесия:
- Горизонтальное равновесие $\sum H = 0$: Сумма всех горизонтальных нагрузок и реакций равна 0.
- Вертикальное равновесие $\sum V = 0$: Сумма всех вертикальных нагрузок и реакций равна 0.
- Момент равновесия $ \sum M = 0$: Сумма всех моментов равна 0.
Давайте продолжим с двумя ситуациями нагружения, с которыми мы уже знакомы – точечной и линейной нагрузкой.
🔎 Изгибающий момент и поперечные силы от точечной нагрузки
1.
Первое, что мы всегда рассчитываем в детерминированных конструкциях, это силы реакции/момент . В нашем случае это $V_a, H_a$ и $M_a$ на опоре A из-за условий равновесия.
$\sum H = 0: H_a = 0$
$\sum V = 0: V_a – 0,74 кН = 0$ -> $V_a = 0,74 кН$
$\sum M = 0: M_a + 0,74 кН \ cdot 0,75m = 0$ -> $M_a = -0,56 кНм$
2. На основе сил реакции можно рассчитать сдвиг и распределение момента вдоль балки. Это также можно сделать без учета сил реакции для консольной балки. Параметр x вводится как длина между точкой a и любой точкой на балке.
Параметр x 3. Перерезывающие силы и изгибающие моменты можно рассчитать в зависимости от x. Сделаем первый разрез в точке между опорой и точечной нагрузкой 0 Как и при расчете силы реакции, условия равновесия используются для расчета момента и поперечной силы в точке x $\sum H = 0: H_a = 0$ $ \sum V = 0: 0,74 кН – V_x = 0$ -> $V_x = 0,74 кН$ $\sum M = 0: M_x – (-0,56 кНм) – 0,74 кН \cdot x = 0$ -> $M_x = -0,56 кНм + 0,74 кН \cdot x$ Как мы видим, сила сдвига постоянна и не зависит от параметра x. $M_{0,5м} = -0,56 кНм + 0,74 кН \cdot 0,5м = -0,19 кНм$ 4. Разрезать в точке между точечной нагрузкой и конечной точкой 0 Условия равновесия приводят к $\sum H = 0: H_a = 0$ $\sum V = 0: 0,74 кН – V_x – 0,74 кН = 0$ -> $V_x = 0 кН$ $\sum M = 0: M_x – (-0,56 кНм) – 0,74 кН \cdot x + 0,74 кН \cdot (x-0,75м) = 0$ $M_x = -0,56 кНм + 0,74 кН \cdot x – 0,74 кН \cdot x + 0,74 кН \cdot 0,75м = 0$ .. и на этом рисунке очень быстро видно, что изгибающий момент и поперечная сила равны 0. 5. Диаграммы изгибающего момента и силы сдвига Диаграммы могут быть построены с помощью инструмента, такого как Excel, с использованием приведенных выше формул или нарисованы вручную, если известна геометрическая форма распределения. Диаграмма поперечной силы – консоль Диаграмма изгибающего момента – консольная 1.Что касается точечной нагрузки, мы сначала вычисляем силы реакции $V_a, H_a$ и момент $M_a$ в детерминированной конструкции – консольная балка – из-за условий равновесия. $\sum H = 0: H_a = 0$ $\sum V = 0: V_a – 14,1 кН/м \cdot 1,0m = 0$ -> $V_a = 14,1 кН$ $\sum M = 0 : M_a + 14,1 кН/м \cdot 1,0м \cdot 0,5м = 0$ -> $M_a = -7,05 кНм$ 2. Расчет распределения сдвига и момента вдоль балки от сил реакции. Это также можно сделать без учета сил реакции консольной балки. Параметр x вводится как длина между точкой a и любой точкой на балке. 3. Перерезывающие силы и изгибающие моменты можно рассчитать в зависимости от x. Сделаем разрез в точке между опорой и концом консоли 0 Как и при расчете силы реакции, условия равновесия используются для расчета момента и поперечной силы в точке x. $\sum H = 0: H_a = 0$ $\sum V = 0: V_x + 14,1 кН/м \cdot x – 14,1 кН = 0$ -> $V_x = 14,1кН – 14,1 кН/м \ cdot х$ 92}{2} = -1,76 кНм$ 4. Диаграммы изгибающего момента и силы сдвига Диаграммы могут быть построены с помощью инструмента, такого как Excel, с использованием приведенных выше формул или нарисованы вручную, если известны геометрические форма распределения. Диаграмма поперечной силы – консоль Диаграмма изгибающего момента – консольный 
Положим x = 0,5м и посмотрим, какие результаты мы получим для изгибающего момента: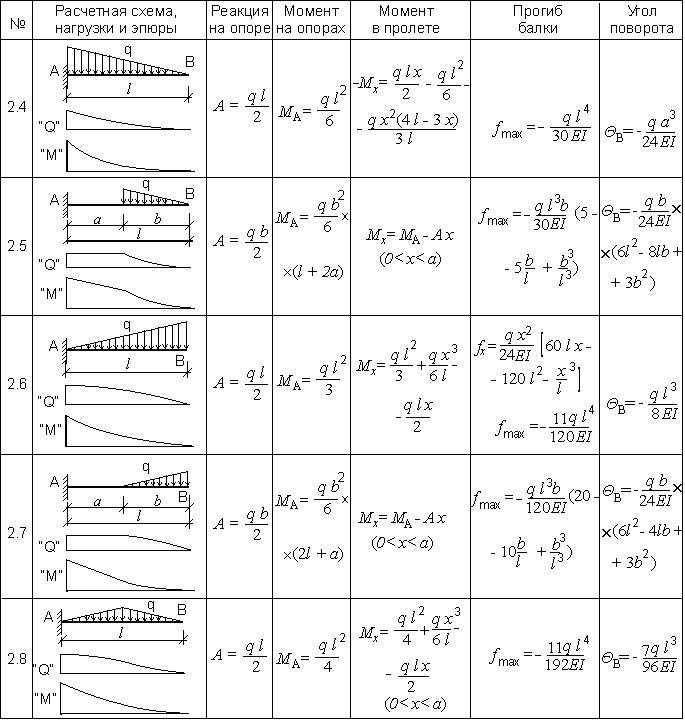
👨🏫 Изгибающий момент и поперечные силы от линейной нагрузки
