Основы расчета элементов конструкций, работающих на изгиб (часть 1). Прочность.

В строительстве под балкой принимают несущий элемент в конструкций зданий различного назначения (как промышленных, так и гражданских), который работает в основном, как правило, на изгиб. При этом балка воспринимает вертикальные нагрузки приходящие от покрытий, перекрытий, второстепенных балок и т.д. передает их на опоры (колонны, главные балки, стены). С практической точки зрения, использование балок имеет рациональный смысл для перекрытия пролетов примерно до 24 м. При расстояниях свыше 24 м использование балок не рационально с экономической точки зрения (расход металла на перекрытие по балкам становиться гораздо больше, чем, к примеру, перекрытия выполненного с помощью стальных ферм).

По материалу балки разделяются на изготовляемые из cтали, железобетона, древесины.

В свою очередь стальные балки разделяются на прокатные (изготовляются из прокатных профилей различного сортамента) и сварные. Балки из железобетона аналогично разделяются на монолитные (выполняемые непосредственно в условиях строительной площадки) и сборные (изготовляемые на заводах ЖБИ). Деревянные балки делятся по исполнению на балки из цельного бруса, клеёные балки, а также балки составного сечения.

При этом в балки могут разделяться в зависимости от назначения на прогоны (балка, опирающаяся непосредственно на опорные части здания — колонны, стены, пилоны), ригели (балка, соединяющая колонны и стойки и служит для опирания прогонов или плит) и перемычки (балка, используемая для перекрытия проемов для окон и дверей). По расчетной схеме балки разделяются на разрезные, неразрезные и консольные.

Рассмотрим работу балки в случае простого изгиба от действия равномерно распределенной нагрузки q. Данная схема работы балки наиболее характерна в строительной практике. В реальности, если балка просто опирается на опоры, то один конец балки является шарнирно-подвижным, а противоположный — шарнирно-неподвижным.

При этом в каждом сечении балки возникают, как поперечные силы Q, так и изгибающие моменты M. Значения M и Q можно определить по формулам, взятым из курса строительной механики.

При этом напряженное состояние поперечного изгиба можно характеризовать наличием нормальных σ и касательных напряжений τ в рассматриваемом сечении балки. Нормальные напряжения направлены перпендикулярно плоскости сечения балки, при этом характер изменения значения по высоте сечения балки носит линейный характер, и достигают максимальных растягивающих в самых нижних слоях, а максимальных сжимающих значений в самых верхних слоях. При этом абсолютные значения этих напряжений между собой равны.

В случае касательных напряжений τ, то они находиться в плоскости сечения и достигают максимума в уровне центрального слоя (или нейтральной оси). Зависимость распределения по сечению касательных напряжений — параболическая.

Если взглянуть на эпюру изгибающих моментов и поперечной силы в случае простого изгиба балки, то видно, что нормальные напряжения σ достигают максимума к середине пролета балки, уменьшаясь в обе стороны от середины и на опорах их значение равно нолю. Касательные напряжения τ в отличии от нормальных достигают максимума на опорах, а при приближении к центру пролета балка они становятся равными нолю.

Для упругих и однородных по сечению материалов зависимости нормальных напряжений от изгибающего момента в рассматриваемом поперечном сечении изгибаемого элемента можно получить по формулам позаимствованных из предмета сопротивления материалов

где М_x— изгибающий момент балки, определяемый по эпюре моментов в соответствующем сечении балки;

W_x – момент сопротивления относительно местной оси х, в общем случае (прямоугольные деревянные балки и т.д.) можно вычислить используя формулы представленные в справочниках по сопротивлению материалов; для стальных профильных балок — по сортаменту металлопроката.

Что же касается касательных напряжений, то их можно определить по формуле

,где Q_x— значение поперечной силы в сечении.

S_x — статический момент сечения, который определяется по табличным данным или формулам сопротивления материалов

I_x — момент инерции сечения, можно определить аналогично Sx и Wx по формулам или таблицам

b – ширина сечения балки

Из рассмотренного выше мы можем сделать вывод, что расчет балок

на прочность в общем случае состоит из проверки соблюдения двух условий.

Первое:

Нормальные напряжения при изгибе в сечении балки не должны превышать расчетных значений сопротивления материала на растяжение и на сжатие.

Второе:

Касательные напряжения, достигающие своих наибольших значений в уровне нейтрального слоя(центральной оси) также не должны превышать расчетных значений материала сдвигу.

При работе прямоугольных деревянных балок от действия, равномерно распределенной нагрузки касательные напряжения, как правило, не достигают опасных значений из-за сравнительной большой ширины балки, поскольку ширина балки b находиться в знаменателе в формуле определения касательных напряжений балки, следовательно, чем больше b, тем меньше τ.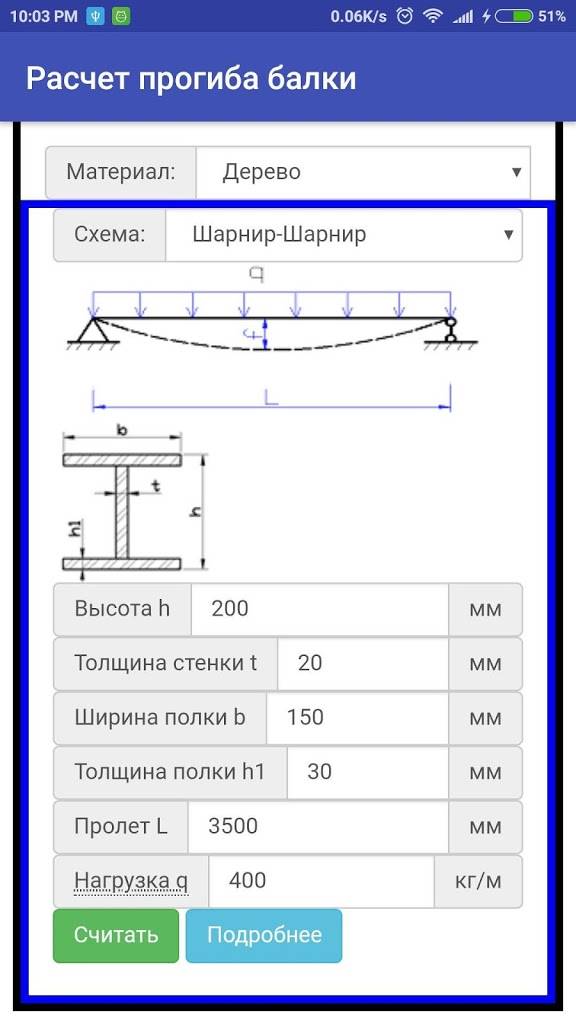 Необходимо отметить, что для стальных прокатных двутавровых балок заложены такие значение толщин стенок в сечениях, что при действии равномерно распределенной нагрузки даже с учетом совместного действия касательных и нормальных усилий в сечении не создается опасного напряженного состояния и в любом случае прочность будет обеспечена. Но что касается расчета прокатных стальных балок в случае, если на балку действуют сосредоточенные нагрузки, то расчет на действие касательных напряжений необходим.

Расчет балки на выносливость.

По выносливости грузоподъемность балок определяется в местах повышенной концентрации напряжений. Наиболее опасными и потому подлежащими проверке являются, как правило, места обрыва поясных листов.

Расчет на выносливость аналогичен расчету на прочность по нормальным напряжениям. Отличие состоит в том, что расчетное сопротивление металла в проверяемом сечении принимают с понижающим коэффициентом, а также учитывают снижение динамического воздействия подвижного состава в расчетах на выносливость.

Расчет ведется по формуле:

— переходный коэффициент;

— коэффициент понижения расчетного сопротивления при расчетах на выносливость;

— суммарная нормативная интенсивность постоянных нагрузок (без учета кэффициента надежности)

Классы балок при расчете на выносливость.

Таблица 1.7

Балка	Место-положение сечения	Ωk=Ωp, м2	θ	W0, см3	β	ξ	β/ξ	γв	kв, кН/м пути	kн, кН/м пути	1+μ	Кв
Продольная Б	В середине пролета	3,78	0,88	5694,86	1,3	1	1,3	0,867	526,47	23,35	1,76	12,807
Поперечная П	Сечение 2-2	10,18	0,89	9445,59	1,3	1	1,3	0,880	315,85	20,70	1,66	9,200

Продольная балка (в середине пролета):

Поперечная балка (сечение 2-2):

4. Расчет балок на прочность поясных заклепок.

   

Грузоподъемность балок по прочности прикрепления их поясов к стенке должна определяться в зонах действия наибольших сдвигающих усилий, величина которых в основном зависит от значений действующих на балку поперечных сил.

Грузоподъемность балок по прочности поясных заклепок определяется на участках пояса длиной 100 см.

Допускаемая временная нагрузка, кН/м пути:

а) при непосредственном опирании поперечин на верхний пояс балок:

— приведенная расчетная площадь поясных заклепок, см²:

; — приведенная расчетная площадь одной заклепки, см²;

— число заклепок на рассматриваемом участке пояса длиной 100 см;

— коэффициент, учитывающий собственный вес балок;

— статический момент площади поперечного сечения брутто пояса балки относительно ее нейтральной оси;

— параметр, зависящий отзначений и , учитывающий сосредоточенное давление от непосредственного опирания мостовых поперечин на верхний пояс балок.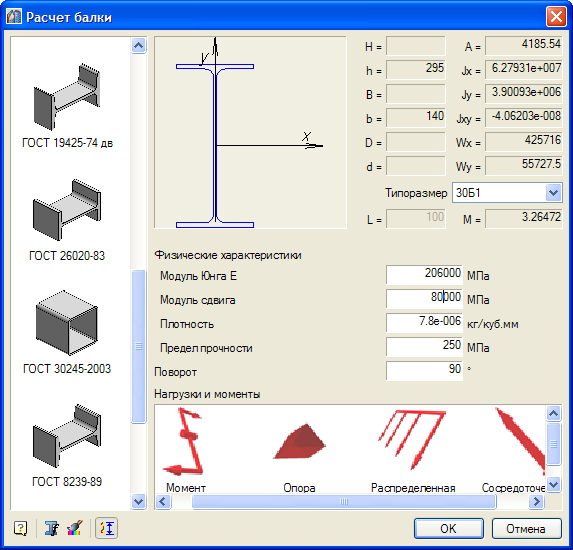

Мостовые поперечины непосредственно опираются на верхний пояс продольной балки

Классы балок при расчете на прочность поясных заклепок.

Таблица 1.8(а)

Балка	Место-положение сечения	nз	μ0, 1/см2	Fβ0, см2	nk	αp	S’бр, см3	Ωk, м2	Iбр, см4	Аз	kп, кН/м пути	kн, кН/м пути	1+μ	Кп
Продольная Б	На опоре	12,5	0,199	62,80	1,1445	1,1	2455,02	2,75	474310,34	1,785	986,37	23,35	1,76	23,994

б) если поперечины не непосредственно опираются на верхние пояса:

Мостовые поперечины не непосредственно опираются на верхний пояс поперечной балки

Расчетные модули > Балки > Общий анализ балок

 

Нужно больше? Задайте нам вопрос

 

Модуль «Общий анализ балки» предлагает функции анализа балки, но не включает никаких процессов проектирования.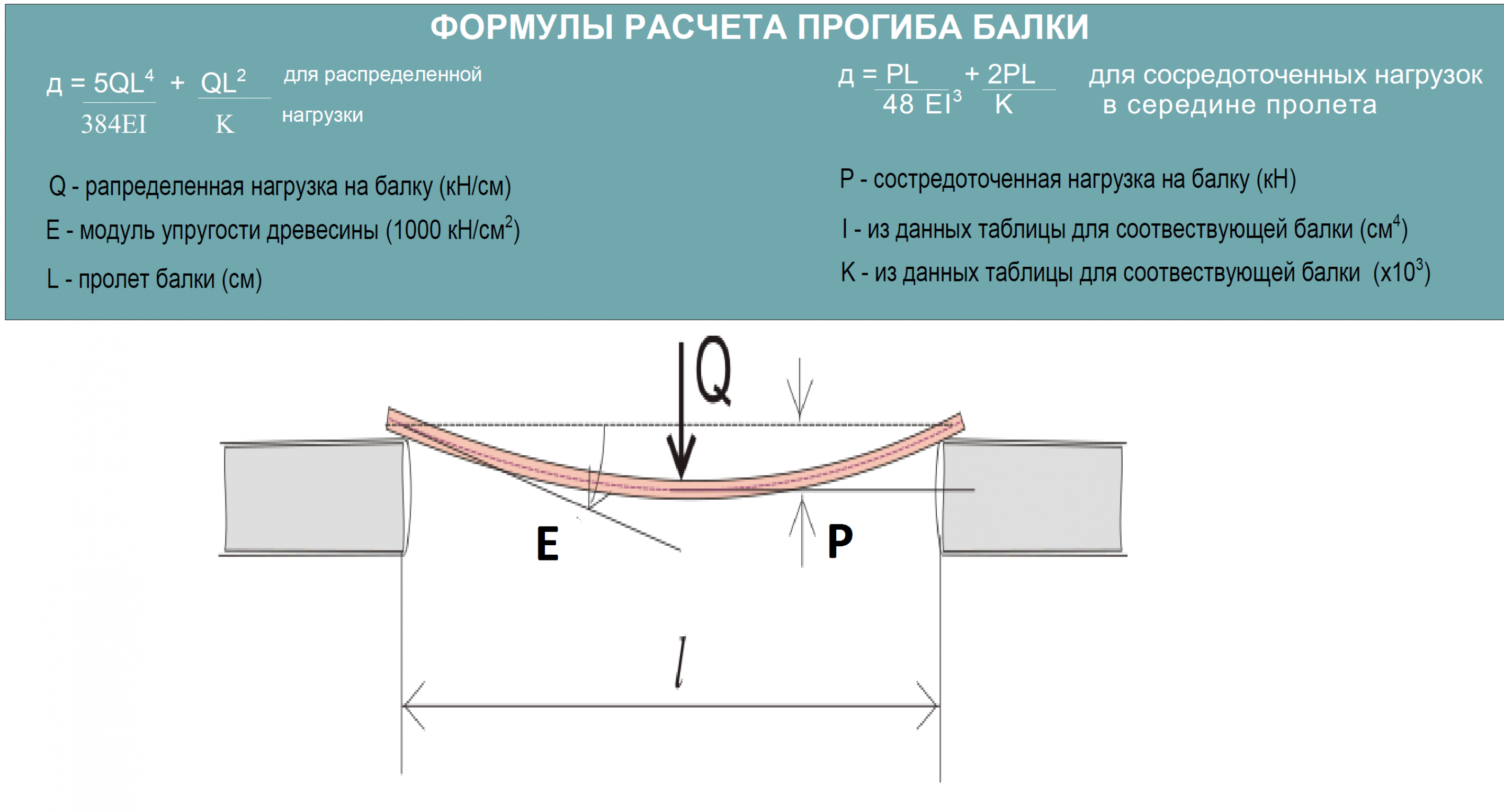 Таким образом, он может быть полезным инструментом в ситуациях, когда требуются только результаты анализа, такие как сдвиг, момент, реакции и прогибы.

 

Вкладка «Общие данные»:

 

Вкладка «Общие данные» позволяет задать условия пролета, длины пролета и условия поддержки практически так же, как эта информация предоставляется в других балочных модулях. Дополнительные пояснения см. в теме. В дополнение к этим фрагментам данных вкладка «Общие данные» также содержит поля ввода для модуля упругости при изгибе, а также площади поперечного сечения и момента инерции каждого пролета балки, как показано ниже:

 

 

Вкладка «Нагрузки на пролет»:

 

На вкладке «Нагрузки на пролет» можно указать нагрузки на один пролет за раз. Поведение инструментов на этой вкладке идентично инструментам, описанным для использования в других модулях балки. Дополнительные пояснения см. в теме.

 

 

Вкладка «Нагрузки на все пролеты»:

 

На вкладке «Нагрузки на все пролеты» можно указать нагрузки на все пролеты одновременно. Поведение инструментов на этой вкладке идентично инструментам, описанным для использования в других модулях балки. Дополнительные пояснения см. в теме.

 

 

Вкладка «Сочетания нагрузок»:

 

На вкладке «Сочетания нагрузок» представлены анализируемые сочетания нагрузок. Он также предлагает следующие возможности:

 

• Выбрать другой набор сочетаний нагрузок,

• Изменить значения, используемые в качестве коэффициентов нагрузки, и

• Включить и выключить определенные сочетания.

 

Дополнительные пояснения см. в разделе.

 

 

Модуль общего анализа балки предлагает параметры вывода, аналогичные параметрам вывода, предоставляемым другими модулями балки, за исключением того, что результаты расчета не предоставляются.

 

Нижняя половина экрана предназначена для отображения результатов. Вертикальная полоса вкладок в левой части экрана позволяет выбирать между Расчетами, Эскизом и Диаграммой, как описано ниже:

 

Расчеты:

 

Вкладка «Расчеты» содержит четыре подвкладки:

 

Сводные результаты: Отображает экстремальные моменты, максимальный сдвиг, экстремальные отклонения и экстремальные реакции.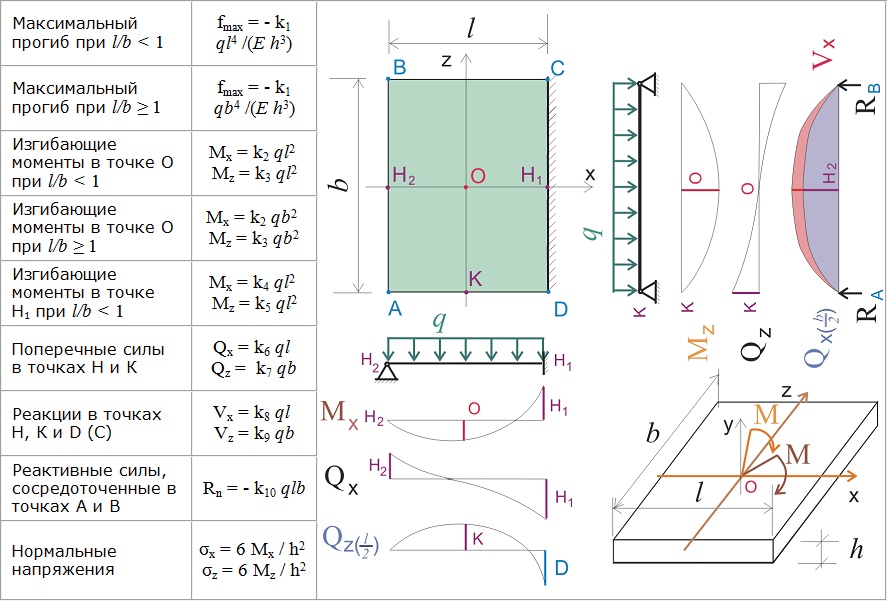

 

 

Максимальные комбинации: Отображает экстремальные моменты и сдвиги для каждого пролета для всех сочетаний нагрузок.

 

 

M-V-D: Резюме:  Отображает момент, сдвиг и прогиб с небольшим шагом вдоль всех пролетов. Момент и сдвиг отображаются для всех комбинаций нагрузок. Прогиб отображается только для комбинаций рабочих нагрузок.

 

 

 

Реакции опор:  Отображает реакции опор для всех опор, для всех сочетаний нагрузок.

 

 

Эскиз:

 

Отображает эскиз балки с указанием длины пролета, условий опоры и приложенных нагрузок.

 

 

Диаграмма:

 

Отображает графическое изображение балки с наложенными графиками момента, сдвига или прогиба для выбранного сочетания нагрузок или для огибающей всех сочетаний нагрузок с.

 

Как рассчитать данные луча, если вашего дела нет в таблице

Часто бывает так, что моя балка нагружена так, как не указано в таблице параметров. Итак, что мне делать?

Существует несколько подходов к расчету моментов балки когда вашего случая нагрузки нет в таблице:

• Рассчитайте нагрузку на балку с нуля
• Упрощение загрузки дела в таблицу
• Увеличьте нагрузку и используйте известный ящик
• Добавление нескольких дел из таблицы

Я объясню каждый в большая глубина.

Рассчитайте нагрузку на балку с нуля

Это, безусловно, самый сложный метод расчета моментов или прогиба на балке. Не изобретайте велосипед! Мы умные инженеры, давайте делать то, что делаем лучший: сделать предположения и выбрать один из других вариантов.

В некоторых случаях нам может понадобиться вывести собственные формулы. Наиболее заметным является случай, когда нас интересует отклонение, но наша балка имеет сужающееся поперечное сечение. Другой случай, когда у нас есть балка, прогибающаяся под собственным весом, но имеющая несколько поперечных сечений. В этих случаях нам нужно будет обратиться к уравнению отклонения балки:

Где M — момент, E — модуль Юнга, I — момент инерции площади, а v — вертикальное отклонение.

Итак… По возможности избегайте выбора этой опции. Только математика того не стоит.

Упростить загрузку до случая в таблице

Упрощение загрузки часто быстро обходиться. Когда я впервые Начав как инженер-конструктор, я измерял штифты с помощью распределенных нагрузок. вокруг цилиндров и отверстий. Это заняло гораздо больше времени для расчета и привести к головной боли. Несколько лет назад коллега бросил мне вызов. подход, и я рад, что он это сделал. Мы оба Решил несколько задач по-своему и по-своему. В любом случае мы пришли к одинаковым результатам. С тех пор я изменился, чтобы делать это гораздо более простой способ.

Итак, мое первое предложение — рассматривать точечные нагрузки как точечные нагрузки. Я пытался рассматривать их как распределенные нагрузки, потому что они действовали на несколько дюймов балки, а не только на точку.

Следующее мое предложение состоит в том, чтобы попытаться упростить постоянно распределенные нагрузки до точечных нагрузок, а параболические возрастающие нагрузки до линейно возрастающих нагрузок.

Много распределенных нагрузок увеличивайте, но не начинайте с нуля. В В этом случае разделите нагрузку на постоянное распределение и линейное или параболическая возрастающая нагрузка от нуля. величина постоянного распределения будет наименьшим значением переменное распределение. Затем вычтите это значение из распределения переменных.

Наконец, можете ли вы игнорировать или комбинировать определенные нагрузки? Часто, весом конструкции можно пренебречь. Или возможно, вес можно комбинировать с нагрузкой в ​​центре (или рядом с ним) луч.

Пилатес для улучшения подвижности позвоночника

Включите JavaScript

Пилатес для улучшения подвижности позвоночника

Увеличьте нагрузку и используйте известный футляр

Аналогично предыдущему Предположение, что чрезмерная нагрузка может дать более быстрые, но менее точные результаты.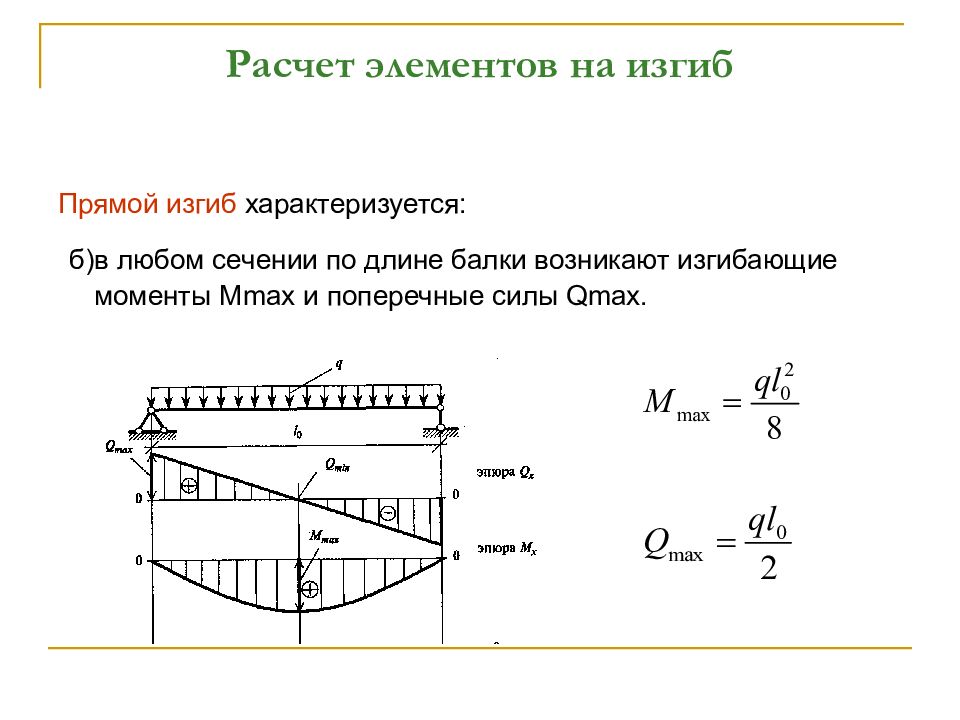 Часто я просто ищу быстрый путь / нет расчета на встрече и нужен грубый ответ быстро. Завышение нагрузки и приложение ее к известному (часто запоминается) случай нагрузки дает мне возможность дать один из трех ответов в течение нескольких минут: да, анализ не требуется или требуется дополнительный анализ. Как правило, я осторожен, когда даю ответ «Да». Чтобы это произошло, я обычно требуется расчетный коэффициент более 5: 1 для пластичного материала. «Нет» слетает с моих губ немного свободнее. и это зарезервировано для всего, что меньше, чем коэффициент проектирования 1: 1. Ответ «необходим дополнительный анализ» вещи между ними.

Чтобы быстро выполнить эти расчеты, я бы запомнил следующие формулы:

Консольная балка с точечной нагрузкой на конце: M = P * L

Консольная балка с распределенная нагрузка: M = w * L ² / 2 или M = P * L / 2

Балка с простой опорой с точечной нагрузкой: M = P * a * b / L

Неподвижная балка с точечной нагрузкой нагрузка в центре: M = P * L / 8

M равнодействующая момент, P — приложенная точечная нагрузка, w — распределенная нагрузка, L — балка длина, «а» — расстояние от одного конца до груза, а «b» — расстояние от нагрузки к другому концу.

Как уже упоминалось, этот метод даст вам быстрый ответ, но результаты не будут такими точными. Пожалуйста, используйте этот метод с осторожностью и всегда выполняйте более глубокий расчет, прежде чем приступить к проектированию.

Добавить несколько ящиков вместе

Итак, я сохранил лучшее альтернатива напоследок. Расчет балки можно сложить вместе с помощью простой алгебры.

Позвольте мне объяснить, а затем мы рассмотрим пример. первое, что я хочу сделать, это выбрать правильные конечные условия. Когда я прикладываю к своей балке несколько нагрузок, они все должны иметь одинаковые конечные условия. Есть шесть основных конечных условий, для которых вы найдете таблицы.

1. Фиксированный на одном конце, обычно называемый консольный
2. Фиксируется на одном конце и направляется на другом другой
3. Просто поддерживается с каждой стороны
4. Фиксированный на каждом конце
5. Фиксируется на одном конце и поддерживается на другой
6. Просто поддерживается с выступом

Следующим шагом является изоляция все загружения.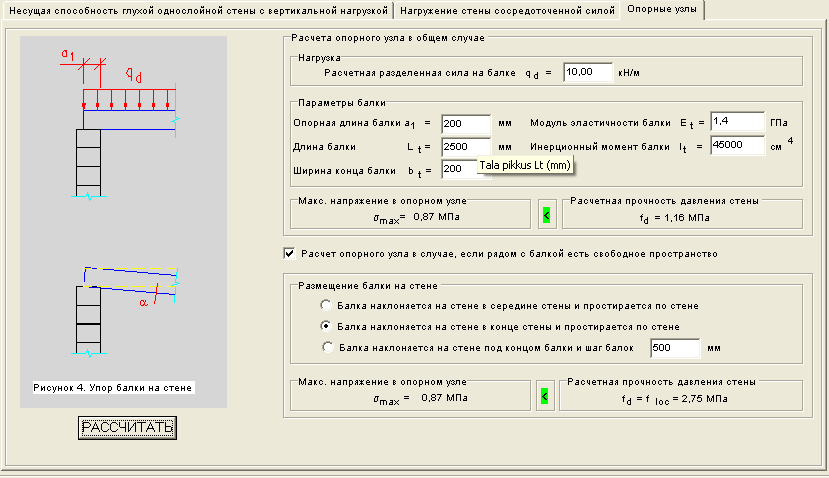 Это может означать все точечные нагрузки, распределенные нагрузки и моментные нагрузки. Для каждого из них должен быть свой вариант нагрузки.

Как только эта информация необходимо определить точки интереса. Для консольной балки это, скорее всего, на консольном конце. Однако там могут быть и другие точки интереса, если балка имеет сужающееся поперечное сечение. В зависимости от ваших нагрузок их может быть от 3 до 7. очки были вы хотите момент рассчитан. Обычно я обозначаю эти точки заглавными буквами и пропускаю I, L, M, O, P, Q и R, потому что они уже используются в расчетах или их легко спутать с цифрами.

Теперь самое сложное Шаг, вам нужно будет рассчитать сдвиг и момент в каждой из точек, которые вы выбраны для каждого загружения. Много столов иметь информацию на данный момент в ключевых точках, но вам нужно будет найти таблицу который имеет момент как функцию расстояния по длине. Например, моя таблица для фиксированной балки с точечная нагрузка со смещением не дает мне уравнения на данный момент на всем пути через. Это дает мне это для длина от левой опоры до груза, но не с другой стороны. Это может сильно затруднить поиск момент для всех случаев по всем точкам. я используйте числа для каждого загружения, начиная с 1.

В этот момент вы можете просто сложите все Моменты в каждой точке следующим образом:

M _A = M _A1 + M _A2 +…+ M _An . Очень просто.

Аналогично, поперечные силы так же складываем:

В _А = В _А1 + В _А2 +…+ В _Ан

И прогибы тоже!

Δ _A = Δ _A1 + Δ _A2 +…+ Δ _An

Как только вы получите все эти дела в точке А, переходим к точкам Б и С и…. Вы получаете дрейф. Прежде чем я перейду к примеру, обязательно следите за своими знаками. Вообще говоря, точка нагрузки считают положительными. Если у вас есть загрузка, отметьте это знаком минус (-)! Моментные нагрузки также могут быть сложными. Момент по часовой стрелке обычно положительный.

Одна банкнота отклонение: во многих случаях есть только прогиб для определенных случаев и для критических точек. Хотя вы можете добавлять отклонения вместе, это может не стоит тратить время на то, чтобы выяснить, каков прогиб по всему пролет балки.

В другой статье мы рассмотрели объединение связки нагрузок на траверсу светофора. Пожалуйста, обратитесь к этому как к примеру добавления нескольких разделов вместе. Я хочу сделать еще один пример с разными опорами.

Пример

В качестве примера мы иметь 100-дюймовую длинную балку, которая просто поддерживается на каждом конце. Мы поместим точечную нагрузку в 2000 фунтов на 65 дюймов, распределенная нагрузка 80 фунтов / дюйм от 25 до 45 дюймов и вес балки при 4 фунтах на дюйм.

При осмотре мы можем выберите несколько проблемных областей, которые мы выберем для расчета. Во-первых, каждая конечная точка должна быть посмотрел на. Для точечной нагрузки это будет на 65 дюймов. Распределение веса будет быть в центре, что составляет 50 дюймов.   сегментированная распределенная нагрузка немного сложнее. Если использовать постоянное сечение, мы знаем что отклонение будет самым высоким там, где момент самый высокий. Согласно нашей таблице, это место а+р ₁ /w и это значение мы рассчитаем чуть позже.

Итак, наши точки представляют интерес: A = 0 дюймов, B = a+R1/w, C = 50 дюймов, D = 65 дюймов и E = 100 дюймов. Мы рассчитаем момент и поперечную силу. Поскольку А и Е являются точками реакции, момент и прогиба по определению не существует, но мы рассчитаем сдвиг реакции.

Теперь приступим. Мы хотим разделить наши три случая. Они показаны вместе на виде сверху с отмеченными точками AE. Затем они разделяются на отдельные загружения. (Все изображения таблиц любезно предоставлены изданием Blodgett’s Design of Weldments, опубликованным Lincoln Electric. У вас должна быть копия. Посетите mentoredengineer.com/resources, чтобы купить и получить другие справочные материалы)

Вариант нагрузки 1

Это просто поддерживаемый вариант с нецентрированной нагрузка. Нагрузка составляет 2000 фунтов на 65 дюймов. Формула момента как функция x, Mx, дается только до тех пор, пока x не станет меньше a. Чтобы решить эту проблему, я перевернул свою ссылку и начал отсчитывать мой момент как функцию y, начиная справа, Мой. Уравнение моментов: M = П*а*у/л. Если я объявлю, что y = L-x, я можно подставить это в исходное уравнение и получить M = P*a*(L-x)/L. Это техника, которую можно использовать во многих случаев и должен быть в вашем поясе инженерных инструментов.

Следует также отметить что поперечные силы отрицательны с правой стороны. Это верно, но имейте в виду, что сила от реакции R2 направлена ​​вверх и возвращает поперечную силу к 0 фунтам. Не забудьте инвертировать эту силу, когда расчет реакций.

Теперь обратимся к MathCAD для расчета моментов и поперечных сил во всех пяти точках интереса. Вы можете видеть, что самый высокий момент находится в точке D, поэтому мы выбрали ее. Также обратите внимание, что величина поперечных сил в сумме составляет 2000 фунтов, а моменты на каждом конце равны 0 дюйм-фунтов. Это хорошие вещи, чтобы проверить для каждого случая.

Вариант нагрузки 2

Вариант нагрузки 2 распределенная нагрузка, вызванная весом балки. Его вклад будет минимальным. общий дизайн и именно поэтому этот компонент часто игнорируется. Самое интересное в этой загрузке напряжение сдвига всегда уменьшается. Это приводит к постоянной параболической форме кривой момента. Этот случай нагрузки очень легко рассчитать потому что это непрерывная функция.

Когда мы перейдем к MathCAD, мы увидим, что наш момент равен 0 дюйм-фунтов на концах, а поперечные силы равны нагрузке 4 фунта/дюйм * 100 дюймов. Самая высокая моментная нагрузка находится в центре, как мы и ожидали. было бы.

Вариант нагрузки 3

Вариант нагрузки 3 наиболее сложно, потому что есть три части кривой, которые необходимо проанализировать. Напряжение сдвига постоянно, когда x меньше чем «а» или больше, чем «с». Это линейно между «а» и «с» и линейно между ними двумя. При интегрировании, чтобы получить момент, наклон будет линейной до и после нагрузки и параболической для нагрузки.

Я хочу указать здесь что при уменьшении расстояния b графики и формулы представляют случай сосредоточенная точечная нагрузка. Часто, сегментированная распределенная нагрузка может быть аппроксимирована как точечная нагрузка, если b мало по сравнению с общей длиной. момент окажется немного выше. И наоборот, если у вас большая точечная нагрузка, вы можете распределить ее на уменьшить момент, индуцируемый балкой.

Именно в этом разделе что мы вычислим местоположение B, которое происходит, когда момент самый высокий. Это происходит при x = a +R ₁ /w или 38 in.

Еще раз MathCAD подтверждает, что момент и поперечные силы проверяются в конечных точках. Максимальный момент находится в точке B, как и предсказывает формула, и по определению сдвиг равен 0 фунтов. участок)

Собираем все вместе

Последним шагом является суммирование всех отдельных компонентов и определение максимальной нагрузки.