Расчет однопролетной балки переменного сечения по норме Еврокод 3
Конструктивная система и нагрузки
Сварной двутавр из стали марки С235 имеет следующие размеры в мм:
Высота = 500/300
Ширина = 200
Толщина стенки = 14
Толщина полки = 14
Толщина шва = 4
Pисунок 01 — Конструктивная система и нагрузки
Расчет по общему методу 6.3.4 EN 1993-1-1
Расчет балки выполняется в модуле RF-/STEEL EC3 как расчет блока стержней. Поскольку блоки стержней по умолчанию рассчитываются в модуле RF-/STEEL EC3 по общему методу, дальнейшие настройки не требуются. In Maske «1.7 Knotenlager» und dem damit verbundenen Ausschnittsfenster können die Randbedingungen des Stabsatzes sehr gut kontrolliert werden. Кроме того, здесь можно проверить ориентацию местной системы координат. Местную систему координат можно активировать, щелкнув соответствующую кнопку под изображением частичного вида.
Как видно из граничных условий узловых опор, в расчете по общему методу существуют степени свободы, которые характеризуют разрушение плоскости рамы. В данном примере узловые опоры определяются как боковые и торсионные заделки. Предустановленные опоры уже соответствуют данному типу опор, так что можно сразу начать расчет.
Pисунок 02 — Ввод узловых опор
Расчет по общей методике выполнен и дает результат 0,97. Критический коэффициент αcr, op равен 1,647.
Pисунок 03 — таблица результатов
Тип отказа можно проверить в отдельном окне частичного просмотра, которое можно открыть, щелкнув по кнопке [Формы колебаний] справа от максимального расчетного соотношения.
Pисунок 04 — Собственная форма
Pисунок 05 — Графическое отображение результатов
Расчет по методу второго порядка с помощью модуля RF-/STEEL Warping Torsion
Чтобы сравнить результаты расчета по общему методу с расчетом по методу второго порядка, необходимо продублировать расчетный случай, нажав на кнопку «Файл» → «Копировать случай».
Теперь новый расчетный случай можно скорректировать для расчета по методу второго порядка. Расчет по методу второго порядка с учетом депланации выполняется как расчет на эквивалентные напряжения и его можно выбрать в «Подробности» → «Кручение с депланацией».
Этот метод расчета доступен только для блоков стержней. Как и в первом расчетном случае, необходимо проверить и отрегулировать узловые опоры. Как видно в окне для ввода узловых опор, расширение модуля RF-/STEEL Warping Torsion учитывает не только четыре, а семь степеней свободы. В нашем примере важно обеспечить концы стержней в направлении X свободными опорами; в противном случае осевая сила не будет применена к компоненту.
Pисунок 06 — Ввод узловых опор
Для последующего расчета важно не только ввести узловые опоры, но и, в частности, задать несовершенство. Ее можно найти, например, в национальном приложении к норме EN 1993-1-1. В таблице NA.
2 представлена соответствующая информация для данного примера: e0/1 = 1/300 применяется для сварного двутавра с h/b> 2. Это значение необходимо удвоить, если коэффициент гибкости находится в диапазоне от 0,7 до 1,3. Коэффициент гибкости можно задать с помощью значения λcr, op в первом расчетном случае по общему методу. В нашем примере предварительно задано значение 1/300. Наконец, можно приступить к расчету.
Pисунок 07 — Определение несовершенства
Расчет выполнен, результат равен 0,90. Критическое значение потери устойчивости равно 1,651.
Pисунок 08 — таблица результатов
Pисунок 09 — Графическое отображение результатов
Расчет по методу второго порядка с применением модуля RF-/STEEL Warping Torsion и RF-/STEEL Plasticity
Для более эффективного расчета доступно расширение RF-/STEEL Plasticity дополнительного модуля RF-/STEEL EC3.
Он позволяет анализировать внутренние силы по методу второго порядка из расчета кручения с депланацией с помощью метода частичных внутренних сил по Киндману для расчета устойчивости блока стержней или по симплекс-методу для общих сечений.
После копирования второго расчетного случая, можно активировать пластический расчет в «Подробности» → «Пластичность». При копировании второго расчетного случая уже были адаптированы правильные узловые опоры. Однако необходимо проверить и исправить несовершенство. В таблице NA.2 указано значение 1/200 для пластического расчета сварного двутавра с h/b> 2.
Pисунок 10 — Определение несовершенства
Теперь можно приступить к расчету.
Pисунок 11 — таблица результатов
Pисунок 12 — Графическое отображение результатов
Заключение
Для конических конструктивных элементов в модуле RF-/STEEL EC3 доступны два метода расчета.
В дополнение к интегрированному общему методу по гл. 6.3.4 из EN 1993-1-1, можно выполнить расчет по методу второго порядка, включая учет коробления в расширении модуля RF-/STEEL Warping Torsion. Кроме того, расчет на кручение при депланации можно применить и к другим ситуациям сечений и нагрузок.
Для более эффективного расчета можно в дополнение к расчету на кручение с депланацией выполнить пластический расчет по методу частичных внутренних сил (PIFM) или по симплекс-методу в расширении модуля RF-/STEEL Plasticity.
Литература
| [1] | DIN EN 1993-1-1: 2010-12 с NA: 2015-08 |
Курс обучения «Расчёт балки и фермы»
2 день
Моделирование и анализ металлической стропильной фермы на статическую нагрузку
- Постановка задачи
- Формирование стержневой расчётной модели с использованием различных методов
- Анализ результатов расчёта задачи (мозаики перемещений узлов, эпюры/мозаики усилий в стержнях)
- Вычисление опорных и внутренних реакций (система «Нагрузка на фрагмент»).
Анализ результатов расчёта на устойчивость в постановке Л. Эйлера (система «Устойчивость») - Подготовка исходных данных для автоматизированного вычисления расчётных сочетаний усилий (РСУ)
- Описание исходных данных для подбора и проверки металлических сечений для элементов конструкции фермы
- Режим «Конструирование»: интерпретация и анализ результатов. Графический и табличный вывод
- Ответы на вопросы
Анализ результатов расчёта на устойчивость в постановке Л. Эйлера (система «Устойчивость»)Практическое задание №1
Моделирование стропильной конструкции большего пролёта, расчёт перемещений и усилий, анализ результатов
Практическое задание №2
Вычисление опорных реакций. Расчёт конструкции на устойчивость, анализ результатов
Практическое задание №3
Редактирование расчётной схемы стропильной фермы, конструирование, анализ результатов расчёта
Моделирование и анализ поперечной рамы каркаса промышленного здания
- Постановка задачи
- Формирование расчётной модели поперечной рамы каркаса: описание геометрии модели, жёсткостей её элементов и опорных закреплений, статических нагрузок и воздействий
- Анализ первых результатов расчёта задачи
- Уточнение расчётной модели рамы: описание особенностей внутренних связей и геометрии (шарнирных соединений, эксцентриситетов примыкания элементов)
- Формирование таблиц расчётных сочетаний (РСН и РСУ)
- Сравнительный анализ уточнённых результатов расчёта
- Ответы на вопросы
Практическое задание №4
Моделирование поперечной рамы каркаса, анализ результатов расчёта перемещений, усилий в элементах и реакций опор.
Практическое задание №5
Редактирование расчётной схемы поперечной рамы каркаса, анализ уточнённых результатов расчёта перемещений, усилий.
|
COSTRUC (Сталебетон) — пакет программ для расчета и проектирования сталебетонных и сборно-монолитных железобетонных конструкций. Программа COBEM (composite beams) Комбинированные балки по VTR и Eurocode 4 Программа позволяет произвести быстрый конструктивный расчет и оптимизацию балок. Полный объем проверок осуществляется по Eurocode 4. Расчет на противопожарную безопасность предусмотрен для всех систем комбинированных балок. Новые возможности данной версии:
Системы:
Сечения комбинированных балок:
Усилия в сечении:
Проверки в предельном состоянии несущей способности:
Проверки в предельном состоянии эксплуатационной пригодности:
Проверки в стадии монтажа:
Программа COBEM+ Поддерживаются все функции программы COBEM, а также следующие дополнительные функции:
Программа COSIB (composite single beams) Комбинированные однопролетные балки по Eurocode 4 Программа позволяет произвести быстрый конструктивный расчет и оптимизацию однопролетных балок. Новые возможности данной версии:
Системы:
Сечения комбинированных балок:
Нагрузки:
Усилия в сечениии:
Проверки:
Программа COCOL (composite columns) Комбинированные колонны по DIN 18806 и Eurocode 4 Программа позволяет произвести быстрый конструктивный расчет и оптимизацию комбинированных колонн различной формы. Проверки (эксплуатационная пригодность, несущая способность, надежность соединений) проводятся по DIN 18806 и Eurocode 4. Возможно проведение расчета на огнеупорность для всех систем. Системы:
Сечения комбинированных колонн:
Сечения стальных колонн:
Нагрузки:
Усилия в сечениии:
Проверки:
Программа COCOL+ Поддерживаются все функции программы COCOL, а также следующие дополнительные функции:
Программа COSLAB (composite slabs) Системы комбинированных перекрытий в соответствии с Eurocode 4 Программа позволяет произвести быстрый конструктивный расчет и оптимизацию комбинированных перекрытий. Системы:
Сечения:
Нагрузки:
Усилия в сечениии:
Проверки в предельном состоянии несущей способности:
Проверки в предельном состоянии эксплуатационной пригодности:
Программа COSECB (composite section beams) Сечения комбинированных балок по VTR и Eurocode 4 Программа позволяет определить все необходимые характеристики упругости сечения, а также несущую способность сечения (полностью пластичное и/или с ограничением деформации). С помощью программы COSECB можно рассчитывать сечения балок:
Сечения:
Проверки:
Программа COWOP (composite web openings) Проверка больших фрагментов стенок для комбинированных балок Программа выводит для сечений значения имеющейся несущей способности по моментам и поперечным силам. Новые возможности данной версии:
Сечения комбинированных балок:
Нагрузки:
Проверки:
|
As
Проверки (эксплуатационная пригодность, несущая способность, надежность соединений) проводятся по Eurocode 4 (включая нормы Германии, Австрии и Италии) с учетом несущей способности дюбелей. Возможно проведение расчета на огнеупорность для всех комбинированных однопролетных систем балок. Многократная генерация сечений и большое число проверок обеспечивают быстрый и надежный расчет.
as,quer)
Проверки (эксплуатационная пригодность, несущая способность, надежность соединений) проводятся по соответствующему допуску к эксплуатации и по Eurocode 4. Конструктивный расчет на огнестойкость проводится на основе технической экспертизы на огнестойкость (расчетный метод второго уровня). Благодаря многочисленным проверкам, реализованным в программе, достигается высокая точность расчета
На уровне сечения учитывается влияние ползучести и усадки, а также разрушения бетона для заданного временного периода напряжения. Предусмотрены проверки несущей способности сечения: упругая (соблюдение пластического растяжения), упруго-пластичная (соблюдение указанных ограничений по растяжению) или пластичная (использование предела текучести для всех частей сечения).
Если несущая способность заданного сечения недостаточна, то указывается основная причина отказа (например: локальный отказ на сдвиг болтов с головками), что позволяет пользователю, основываясь на результатах расчета, целенаправленно оптимизировать сечение. Программу COWOP можно приобрести как отдельный модуль. Но особый интерес представляет использование программы совместно с программой COBEM, предназначенной для конструктивного расчета комбинированных многопролетных балок. Данные по фрагментам стенки и нагружениям, уже рассчитанные в позиции COBEM, можно передать в COWOP и провести для них проверку без ввода дополнительных данных, просто нажав на кнопку. Однопролетная или многопролетная (неразрезная) балка (плита).
Что выбрать?В данной статье я буду говорить о балках. Но вся информация в ней точно так же касается и плит перекрытия, которые также бывают однопролетными и многопролетными (неразрезными).
Итак, есть балка, у которой несколько пролетов (например, на четыре колонны в ряд нужно опереть балку под перекрытие). Какую расчетную схему лучше выбрать? На чем остановиться: на обыкновенных однопролетных балках от колонны до колонны или же выбрать многопролетную – не зря же она так называется, а у нас как раз много пролетов и нужно перекрыть.
Для того, чтобы всегда делать правильный выбор, не обязательно каждый раз проводить расчет обоих балок и делать технико-экономическое сравнение. Нужно понять их особенности.
Однопролетная балка – это самый простой вариант. Она экономична в изготовлении, работает у нее только нижняя арматура (верхняя устанавливается конструктивно), рассчитать ее тоже проще простого.
В чем же ее недостатки? При увеличении размеров пролета (расстояния между опорами) однопролетная балка сдает позиции. Приходится сильно увеличивать сечение, вырастает арматура, а если пролет слишком уж большой, балка просто не проходит по расчету (обычно критическим становится расчет по второму предельному состоянию – либо прогиб больше нормы, либо трещины больше допустимого).
Многопролетная (неразрезная) балка – это вариант, который используется, если однопролетной балки не достаточно для того, чтобы перекрыть слишком большие пролеты или чтобы выдержать значительную нагрузку. Многопролетная балка – это и двухпролетная, и трехпролетная, ну и так далее. Много – значит больше одного.
В чем же многопролетная балка выигрывает по сравнению с однопролетной? Количество пролетов здесь играет не очень большую роль (но об этом мы еще поговорим), а вот основное влияние в том, что балка неразрезная. А значит, она не прерывается над колоннами.
Главное – не прерывается ее армирование. Правильно законструированная неразрезная балка может выдержать намного большую нагрузку и перекрыть намного больший пролет, чем однопролетная.
Рассмотрим, в чем разница в работе этих двух конструкций: однопролетной и многопролетной (неразрезной) балки. На рисунке ниже утрированно показаны деформации балок, опирающихся на колонны.
На верхней схеме каждый пролет перекрывает однопролетная балка. Опирание балок шарнирное (почему именно шарнирное, можно почитать здесь). При такой схеме балки спокойно изгибаются под весом нагрузки. Нижняя зона у них растянута (показано синим), именно у растянутой зоны устанавливается рабочая арматура, которая берет на себя все растягивающие усилия (бетон на растяжение практически не работает, сразу трещит). На опорах балки спокойно поворачиваются, этот поворот создает дополнительный прогиб плит.
На нижней схеме все три пролета перекрывает неразрезная балка. Ее работа сложнее, чем у однопролетной: под весом нагрузки в пролете балка прогибается вниз, но на опорах она выгибается в обратную сторону.
И это чередование изгибов, чередование растянутых зон (синяя внизу, красная вверху) играет нам на руку. Так как у плиты не могут быть растянуты сразу две стороны, растяжение верхней зоны над опорами (красное) уменьшает растяжение нижней зоны в пролете (синее).
Если сравнить длину растянутой зоны на схеме с однопролетными балками и на схеме с неразрезной балкой, у однопролетных длина растянутой зоны балки (синей) в каждом пролете больше (при одинаковых исходных условиях – величине пролетов, нагрузках, сечении балок). А раз длина растянутой зоны больше, то и изгибающий момент будет больше, и армирование нижней зоны в пролете больше, и прогиб больше, и трещины раскроются шире – так как все эти величины взаимосвязаны.
Получается, что за счет прогиба балки над опорой в обратную сторону, мы получаем существенное сокращение всех перечисленных выше составляющих. А значит, мы создаем более выносливую конструкцию, способную легче выдержать как больший пролет, так и большую нагрузку.
В чем тогда подвох? Ведь не бывает так, чтобы где-то уменьшилось и при этом нигде не увеличилось. В случае с неразрезной балкой, в виде компенсации мы получаем растяжение в верхней зоне балки над опорой. А это значит, что в этой зоне появляется рабочая арматура (часто она бывает даже больше пролетной). Это значит, что в этой зоне появляется риск возникновения трещин (нужно выполнять проверочный расчет по второй группе предельных состояний). В общем, даром изменение расчетной схемы балке не дается.
В каких случаях нужно применять неразрезные балки при многопролетной схеме?
- Если однопролетные балки не выдерживают нагрузку.
- Если расстояние между опорами для однопролетных балок слишком велико.
Почему в случае с небольшим расстоянием между опорами и небольших нагрузках на балку применять неразрезные балки не стоит? Просто потому, что это не экономично – вы будете вынуждены заложить в балку не только нижнюю рабочую арматуру на всю длину балки, но и дополнительно еще верхнюю рабочую (а рабочая всегда больше конструктивной).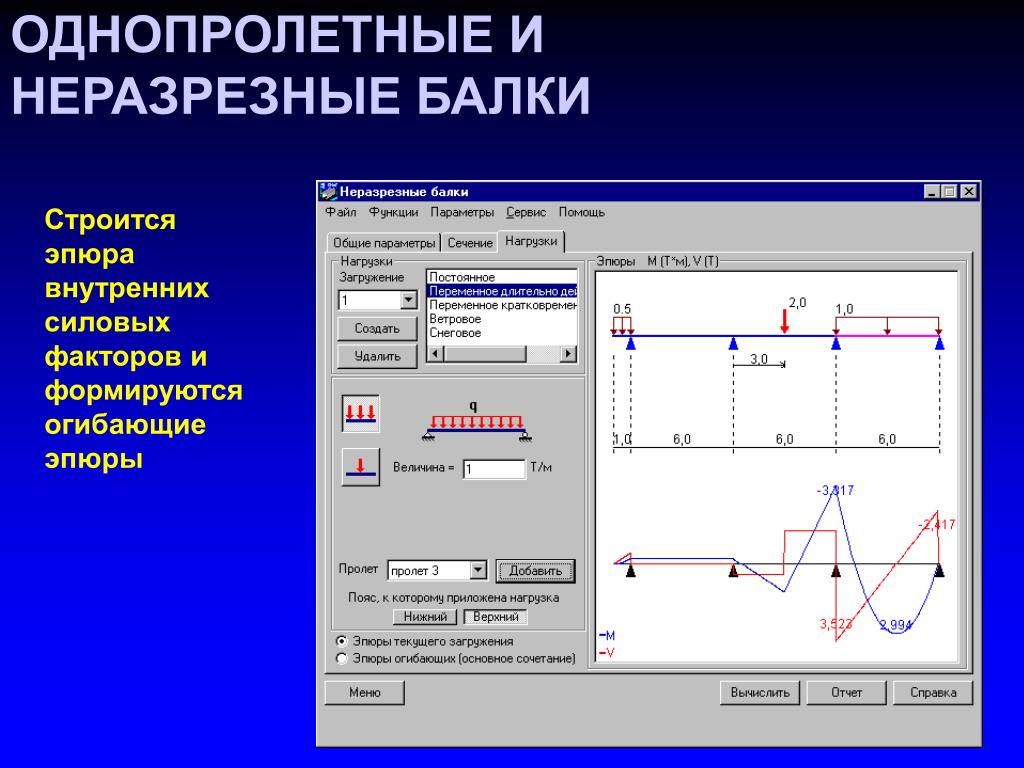
В сумме будет перерасход арматуры по сравнению с однопролетной рабочей схемой.
Если вы хотите узнать, что бывает с недоармированной неразрезной балкой, можете ознакомиться с этой статьей.
class=»eliadunit»>Пролетная балка — обзор
6 Теорема о трех моментах
Используя уравнение упругой кривой для однопролетной балки, разработанное в разделе 2, довольно легко вывести уравнение, связывающее друг с другом значения изгибающий момент на любых трех соседних опорах неразрезной балки. Это уравнение, известное как уравнение трех моментов, включает в себя для любой данной непрерывной балки одновременно только три неизвестные статические величины, и по этой причине оно может значительно упростить вычислительную процедуру при большом количестве опор. .Предположим, нам дана непрерывная балка с числом пролетов s > 1. В соответствии с практикой, использованной в предыдущих примерах, мы будем предполагать, что каждая промежуточная опора может оказывать только вертикальную (поперечную) реакцию.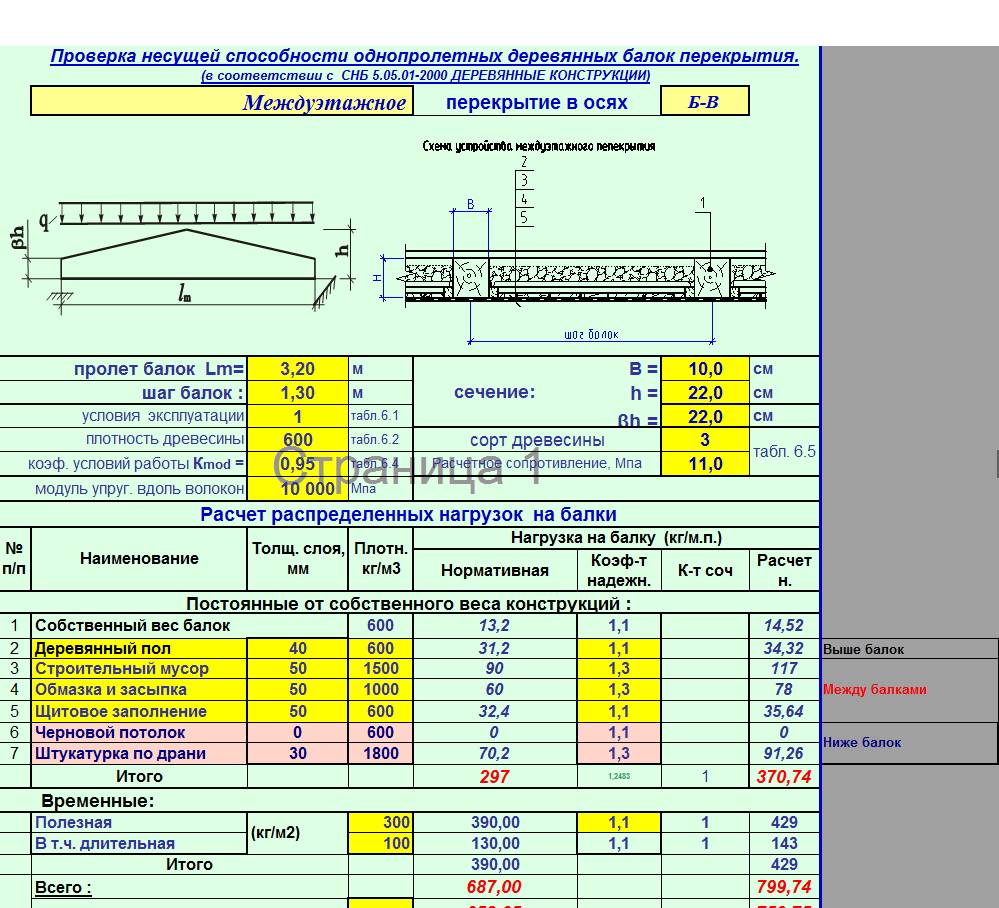
Пусть на рис. 24 представлен произвольный пролет (за исключением двух концевых пролетов), обозначенный как l r , вырезанный в поперечном направлении из вышеуказанной балки на опорах O r –1 и O r .Полученная таким образом однопролетная балка представляет собой простую балку. Пусть оси координат для него равны x r , O r –1 , y r –1 , как показано на рисунке. Нагрузка на эту новую простую балку такая же, как и до выделения пролета из неразрезной балки. Соответствующая функция нагрузки для этой нагрузки будет обозначена как S r (x) . В соответствии с статическими требованиями выбранная таким образом балка будет оставаться в равновесии, и ее кривая прогиба останется неизменной, если концевые секции балки нагружены: (а) равнодействующей всех внешних сил, действующих на неразрезную балку, и слева от соответствующего концевого сечения и (b) результирующий момент этих сил по отношению к данному концевому сечению.
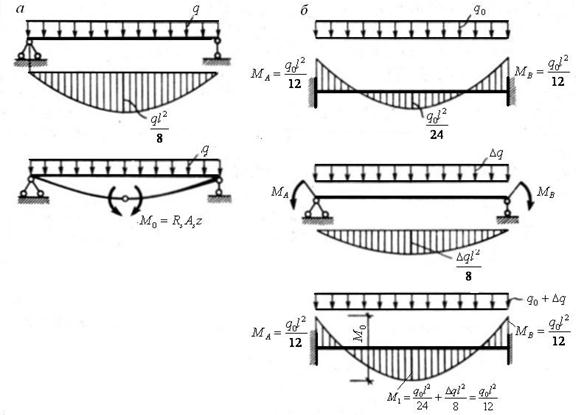Пусть результирующая сила и момент в левой концевой части обозначены как P r –1 и M r –1 соответственно, а на правом конце — P r и — M r . †
РИС. 24.
Кривая прогиба такой простой балки была определена в разделе 2 (случай 7) и дается формулой. (2.2.45) и, если учесть изменение обозначений, получим следующие соотношения для r -го пролета
(2.6.1) yr − 1 (xr) = yr − 1 ′ (0) xr − Mr − 1Bxr22 + Arxr36 + Sr (xr), y′r − 1 (0) = 16lr [lr2S ″ r (lr) −6Sr (lr ) + lr2B (2Mr − 1 + Mr)], Ar = −1lrS ″ r (lr) −1Blr (Mr − Mr − 1) ⋅
Следовательно, очевидно, что если для данного пролета непрерывной балки нагрузка на пролет, а также изгибающие моменты на опорах известны, кривая прогиба пролета полностью определена, и, следовательно, можно найти все другие соответствующие данные.
Наклон балки на левой опоре определяется вторым соотношением уравнения.
(2.6.1). Продифференцируя уравнение упругой кривой и положив x r = l r , получим наклон на правой опоре как
(2.6.2) y′r − 1 (lr) = 13lr [3lrS′r (lr) −lr2S ″ r (lr) −3Sr (lr)] −− 1B (Mr − 1lr6 + Mrlr3) ⋅
Применяя сейчас ур. (2.6.1) к пролету ( r + 1) уклон у левой опоры пролета ( r + 1) составляет
(2.6.3) y′r (0) = 16lr + 1 [lr + 12S ″ r + 1 (lr + 1) −6Sr + 1 (lr + 1)] ++ 1B (Mrlr + 13 + Mr + 1lr + 16),
и поскольку кривая прогиба непрерывна, наклон кривой также должен быть непрерывным в каждой точке балки, следовательно, на r -й опоре мы имеем
(2.6.4) y′r − 1 (lr) = y′r (0),
или по ур.(2.6.2) и (2.6.3) получаем
(2.6.5) Mr − 1lr + 2Mr (lr + lr + 1) + Mr + 1lr + 1 = −Blr [6Sr (lr) + 2lr2S ″ r (lr) −− 6lrS′r (lr)] — Blr + 1 [lr + 12S ″ r + 1 (lr + 1) −6Sr + 1 (lr + 1)] (r = 1,2,…, s) ⋅
Это уравнение трех моментов. Правая часть этого уравнения определяется функцией нагрузки S r (x) , жесткостью B и длиной пролетов l r и l ( r +1) .
† В классической форме уравнения трех моментов правая часть обычно несколько иная.Вместо приведенной здесь функции нагрузки S r (x) продукты Ω r a r и Ω ( r +1) · b ( r +1 , где Ω r обозначает площадь диаграммы изгибающего момента соответствующего пролета (рассматриваемой как свободно опертая балка и отделенная от остальных, т.е. без учета концевых моментов), а a r и b r обозначают горизонтальные расстояния центроидов диаграмм изгибающего момента от левой и правой опор соответственно.
В этих обозначениях классическая форма уравнения трех моментов:
(2.6.6) Mr − 1lr + 2Mr (lr + lr + 1) + Mr + 1lr + 1 = −6Ωrarlr − 6Ωr + 1br + 1lr + 1⋅
В этой форме уравнение трех моментов тесно связано с методом площади-момента, который широко используется при решении гиперстатических задач, а также с методом суперпозиции, в котором гиперстатические задачи с помощью некоторого упрощающего предположения, сводятся к статически детерминированным задачам, решение которых даст статически неопределимые величины.
Чтобы использовать ур. (2.6.6) сначала должна быть определена его правая часть, а это, в свою очередь, требует знания диаграмм изгибающих моментов в соответствующих пролетах r и ( r + 1), причем оба пролета должны быть рассматриваются как независимые простые балки, несущие только «свою» нагрузку. Этот последний этап может быть решен только с помощью уравнений статики; тем не менее, видно, что вся процедура довольно сложна.
Можно показать, что
(2.6.7) Ωr = 12 [2S ′ (lr) −lrS ″ (lr)], ar = 23 [3lrS ′ (lr) −lr2S ″ (lr) −3S (lr)] [2S ′ (lr) −lrS ″ ( lr)], br = 6S (lr) −lr2S ″ (lr) 3 [2S ′ (lr) −lrS ″ (lr)]
и, следовательно, проверил, что обе формы уравнения трех моментов (2.6.5) и (2.6.6) взаимно эквивалентны.
Из ур. Из (2.6.5) видно, что количество этих соотношений равно количеству промежуточных опор ( с) , а изгибающие моменты на опорах могут быть рассчитаны путем решения одновременных с уравнений.Что касается конечных моментов M 0 и M (l) , они должны задаваться граничными условиями.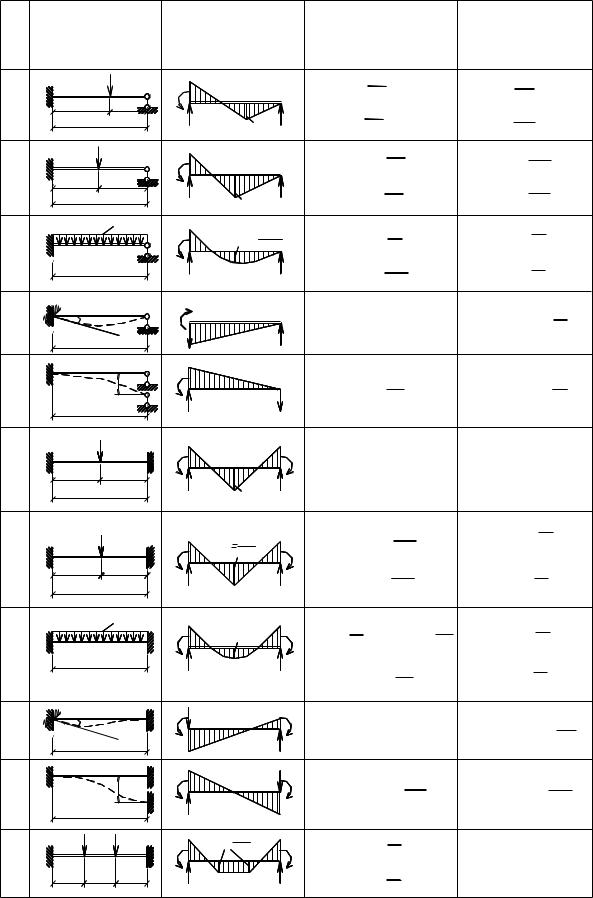
Если концы неразрезной балки свободно поддерживаются, тогда M 0 = M (l) = 0 и два экв. (2.6.5) сильно упростить. Если один или оба конца жестко встроены, то M 0 или / и M (l) будут найдены из условия, что на встроенных концах не происходит вращения. Следовательно, появятся одно или два дополнительных уравнения:
(2.6.8) 2M0l1 + M1l1 = −Bl1 [l12S ″ 1 (l1) −6S1 (l1)], Msls + 1 + 2M (l) ls + 1 = −Bls + 1 [6Ss + 1 (ls + 1) ++ 2ls + 12S ″ s + 1 (ls + 1) −6ls + 1S′s + 1 (ls + 1)] ⋅
Таким образом, в каждом случае у нас есть достаточное количество уравнений для определения неизвестных моментов на каждой опоре, если мы хотим решить проблему неразрезной балки с помощью теоремы о трех моментах. Можно заметить, что путем нахождения изгибающих моментов по всем опорам проблема непрерывной балки также практически решается для уравнения. (2.6.2) кривая упругости в каждом пролете полностью определена, что дает полную картину статического поведения балки.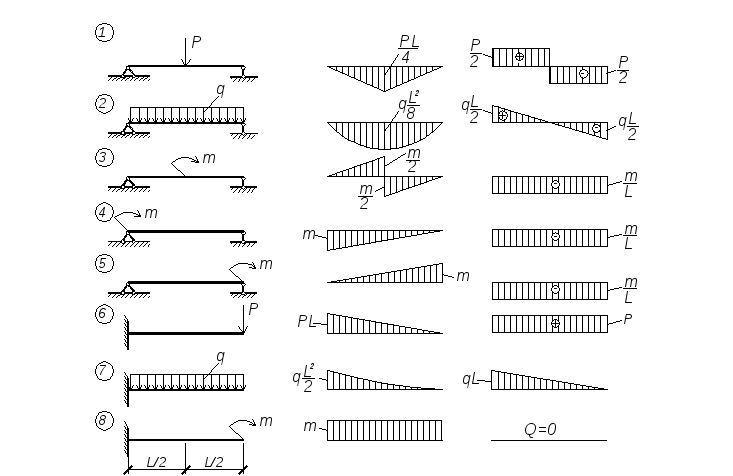
Изгибающие моменты в различных сечениях тогда определяются как
(2.6.9) Mr − 1 (xr) = Mr − 1 − xrlr [Mr − 1 − Mr − BS ″ r (lr)] — BS ″ r ( xr),
, а уравнение силы сдвига —
(2.6.10) Qr − 1 (xr) = 1lr [Mr − 1 − Mr − BS ″ r (lr) + BlrS ″ r (xr)] ⋅
Реакции на концевых опорах будут получены непосредственно из уравнения силы сдвига:
(2.6.11) R0 = Q0 (0) = 1l1 [M0 − M1 − BS ″ 1 (l1)],
(2.6.11) .12) R (l) = — Qs + 1 (ls + 1) = 1lS + 1 [M (l) −Ms + BS ″ s + 1 (ls + 1) −Bls + 1S ″ ′ s + 1 (ls +1)] ⋅
Что касается реакций на промежуточных опорах, они выражаются величиной скачков на диаграмме силы сдвига на каждой опоре; мы имеем, следовательно,
Rr = Qr (0) −Qr − 1 (lr)
и при подстановке соответствующих значений, найденных из ур.(2.6.10) это становится
(2.6.13) Rr = BlrS ″ r (lr) −BS ″ ′ r (lr) −Blr + 1S ″ r + 1 (lr + 1) ++ Mr − Mr − 1lr −Mr + 1 − Mrlr + 1⋅
(PDF) Оценка работы однопролетной балки в разрезе с трещинами
IOP Conf.
Серия: Материаловедение и инженерия 603 (2019) 032055
В Польше за последние 20 лет произошли большие и часто далеко идущие изменения в проектировании
строительных работ, включая изменения в нормативных положениях. Последняя поправка к правилам
, заключающаяся в окончательном введении в действие Еврокода 2, часть 1-1 [5] и замене им других противоречащих друг другу национальных стандартов
, произошла в 2010 году.Этот стандарт, во многих отношениях отличающийся более или менее
от стандарта PN-B-03264: 2002 [6], адаптирующего польские положения к действующим в то время нормативным актам Европейского Союза
, содержит положение, значительно ограничивающее возможности приложения
только к новым, спроектированным конструкциям. Кроме того, в пункте 1.1.2. использование гладких стержней было исключено
, что отражено в таблице C.1 приложения C. Свойства арматуры.Нижний предел
характеристического предела текучести fyk до 400 МПа не включает ранее широко использовавшуюся в Польше гладкую сталь
, а также некоторые виды ребристой стали.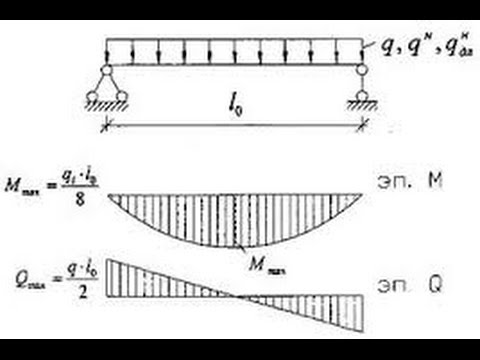
С другой стороны, в пункте 7.3.4.
вышеупомянутый стандарт имеет коэффициент k1, зависящий от арматуры, что позволяет использовать как ребристую, так и гладкую арматуру
. Это побудило авторов статьи выполнить расчеты предельного состояния трещинообразования
согласно PN-EN 1992-1-1: 2008 [5] для балки с гладкими стержнями и средней степенью армирования
, несмотря на ограничения стандарт обсуждался выше, обсуждая их, и
сравнивая результаты с экспериментальными результатами.Эти действия основаны на сходстве между процедурами
, содержащимися в PN-EN 1992-1-1: 2008 [5] и PN-B-03264: 2002 [6] на основе более ранней версии Еврокода
и разрешающей использование гладкой арматуры.
Указанные выше стандарты, которые для простоты будут называться PN-EN и PN-B,
, предоставляют следующие формулы для расчета ширины трещины:
PN-EN (1)
PN-B (2)
где:
wk — максимальная ширина трещины,
sr, не более — максимальный шаг трещин,
srm — средний шаг трещин,
— коэффициент, выражающий отношение расчетной ширины трещины к средней ширине,
см — средняя деформация в бетоне между трещины,
см — средняя деформация в арматуре между трещинами с учетом эффектов растяжения
жесткости.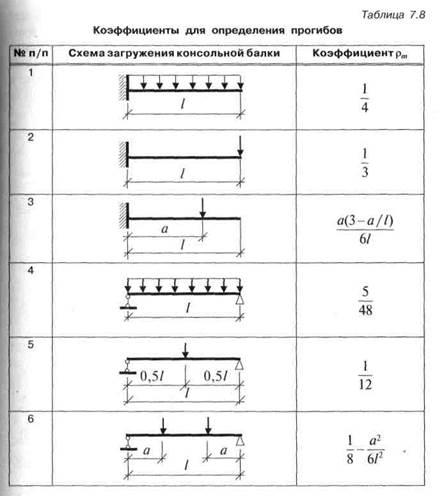
Принимая во внимание значимость коэффициента, утверждается, что в обоих случаях одним из факторов, учитываемых в учете
, является максимальное расстояние между трещинами. Кроме того, при выводе формул в [7] показано
, что деформация
см в формуле (2) представляет собой разность между средней деформацией арматуры и средней деформацией
бетона в участок между двумя трещинами. Как оказалось, в принципе обе формулы
одинаковы.
Расстояние между трещинами рассчитывается в PN-EN по одной из двух формул, выбранных в соответствии с расстоянием между стержнями
. В этой работе использовалась формула (7.11), а с PN-B формула (113):
PN-EN
(3)
PN-B
(4)
где:
c — крышка,
p, eff,
r — коэффициент эффективного армирования,
k1.
— коэффициент, учитывающий свойства связки,
k2 — коэффициент, учитывающий распределение деформации.
В обеих приведенных выше формулах расстояние между трещинами зависит от условий сцепления бетона с арматурной сталью
, а значение коэффициента k1 равно 0,8 для ребристых стержней и 1,6 для гладких стержней. Таблица
Пролет балки зависит от нескольких переменных: сорта и породы пиломатериалов, размера пиломатериалов и нагрузки, которую они несут.Меньшее количество стоек на верхних палубах обычно более желательно для пассажиров, и это заставляет использовать более крупные материалы для каркаса для более длинных пролетов. Максимальные значения пролета балки основаны на максимальной ожидаемой временной нагрузке, а также на других факторах. Строительные нормы для жилых настилов требуют только 40 фунтов на квадратный фут в некоторых областях, но проверьте свои местные требования, чтобы убедиться, что вы знаете какие-либо дополнительные местные правила. Кроме того, многие жители предпочитают опалубку настила, рассчитанную на более высокие нагрузки.
Чем длиннее балка, тем большую площадь настила поддерживает балка, и, следовательно, балка поддерживает большую площадь.
Таблица пролетов балок настила из пиломатериалов
Примечание. Приведенная ниже диаграмма диапазона представляет собой пример представления диаграмм диапазона. Поскольку строительный кодекс и пролеты пиломатериалов время от времени обновляются, вам всегда следует проверять актуальность используемой диаграммы пролетов. См. Соответствующий раздел кодов или NDS для подтверждения правильности используемой диаграммы диапазона.
Размерные пролеты балок настила из пиломатериалов, поддерживающие одиночный пролет балок с выступами или без них:
| Пролет балки | ||||||||
|---|---|---|---|---|---|---|---|---|
| Виды | Размер балки | 6 ‘ | 8 мин. | 10 ‘ | 12 ‘ | 14 ‘ | 16 ‘ | 18 ‘ |
| Сосна южная | 2-2×6 | 6′-8 « | 5′-8 « | 5′-1 « | 4′-7 « | 4′-3 « | 4′-0 « | 3′-9 « |
| 2-2×8 | 8′-6 « | 7′-4 « | 6′-6 « | 5′-11 « | 5′-6 « | 5′-1 « | 4′-9 « | |
| 2-2×10 | 10′-1 « | 8′-9 « | 7′-9 « | 7′-1 « | 6′-6 « | 6′-1 « | 5′-9 « | |
| 2-2×12 | 11′-11 « | 10′-4 « | 9′-2 « | 8′-4 « | 7′-9 « | 7′-3 « | 6′-9 « | |
| 3-2×6 | 7′-11 « | 7′-2 « | 6′-5 « | 5′-10 « | 5′-5 « | 5′-0 « | 4′-9 « | |
| 3-2X8 | 10′-7 « | 9′-3 « | 8′-3 « | 7′-6 « | 6′-11 « | 6′-5 « | 6′-1 « | |
| 3-2X10 | 12′-9 « | 11′-0 « | 9′-9 « | 8′-9 « | 8′-3 « | 7′-8 « | 7′-3 « | |
| 3-2X12 | 15′-0 « | 13′-0 « | 11′-7 « | 10′-6 « | 9′-9 « | 9′-1 « | 8′-7 « | |
Дугласская пихта-лиственница, Подол-Пихта, Ель-Сосна-Пихта, Редвуд, Кедр, Сосна Пондероза, Сосна красная | 3X6 ИЛИ 2-2X6 | 5′-2 « | 4′-5 « | 3′-11 « | 3′-7 « | 3′-3 « | 2′-10 « | 2′-6 « |
| 3X8 OR 2-2X8 | 6′-7 « | 5′-8 « | 5′-1 « | 4′-7 « | 4′-3 « | 3′-10 « | 3′-5 « | |
| 3X10 OR 2-2X10 | 8′-1 « | 7′-0 « | 6′-3 « | 5′-8 « | 5′-3 « | 4′-10 « | 4′-5 « | |
| 3X12 OR 2-2X12 | 9′-5 « | 8′-2 « | 7′-3 « | 6′-7 « | 6′-1 « | 5′-8 « | 5′-4 « | |
| 4X6 | 6′-2 « | 5′-3 « | 4′-8 « | 4-3 « | 3′-11 « | 3′-8 « | 3′-5 « | |
| 4X8 | 8′-2 « | 7′-0 « | 6′-3 « | 5′-8 « | 5′-3 « | 4′-11 « | 4′-7 « | |
| 4X10 | 9′-8 « | 8′-4 « | 7′-5 « | 6′-9 « | 6′-3 « | 5′-10 « | 5′-5 « | |
| 4X12 | 11′-2 « | 9′-8 « | 8′-7 « | 7′-10 « | 7′-3 « | 6′-9 « | 6′-4 « | |
| 3-2X6 | 7′-1 « | 6′-5 « | 5′-9 « | 5′-3 « | 4′-10 « | 4′-6 « | 4′-3 « | |
| 3-2X8 | 9′-5 « | 8′-3 « | 7′-4 « | 6′-8 « | 6′-2 « | 5′-9 « | 5′-5 « | |
| 3-2X10 | 11′-9 « | 10′-2 « | 9′-1 « | 8′-3 « | 7′-7 « | 7′-1 « | 6′-8 « | |
| 3-2X12 | 13′-8 « | 11′-10 « | 10′-6 « | 9′-7 « | 8′-10 « | 8′-3 « | 7′-10 « | |
Предполагается, что временная нагрузка 40 фунтов на квадратный фут, статическая нагрузка 10 фунтов на квадратный фут, предел прогиба простой пролетной балки L / 360, длина консоли L / 180 предел прогиба, No.
2 Степень напряжения и влажные условия эксплуатации.
РАСЧЕТ ФИКСИРОВАННЫХ КОНЕЧНЫХ МОМЕНТОВ ДЛЯ ОДНОПРОЛЕТНОЙ ФИКСИРОВАННОЙ БАЛКИ, ПОДВЕРЖЕННОЙ ТОЧЕЧНОЙ НАГРУЗКОЙ В ЕГО ЦЕНТРЕ
РАСЧЕТ ФИКСИРОВАННЫХ КОНЕЧНЫХ МОМЕНТОВ ДЛЯ ОДНОПРОЛЕТНОЙ ФИКСИРОВАННОЙ БАЛКИ, ПОДВЕРЖЕННОЙ ТОЧЕЧНОЙ НАГРУЗКОЙ В ЕГО ЦЕНТРЕ
админ 18.05.2020
Мохаммад Сохель Ахтар, инженер-строитель, Нью-Дели, Индия
«Почувствуйте структуру»
Здесь, в конце этой статьи, вы найдете приставку с расчетами для определения фиксированных конечных моментов для однопролетной фиксированной балки, которая подвергается точечной нагрузке в ее центре.
Для нахождения фиксированных конечных моментов использовался принцип суперпозиции и уравнения совместимости. Вы будете удивлены, насколько сложно было преобразовать неопределенный луч в несколько определенных лучей.
Все преобразованные определенные балки при добавлении представляют собой одну и ту же неопределенную балку, и расчет отклонения индивидуально для каждой преобразованной определенной балки и добавление их всех в указанном месте, чтобы можно было сформировать уравнение совместимости, поможет нам определить внутренние силы, такие как моменты и сдвиг.
Чтобы понять всю концепцию, просмотрите прилагаемый лист расчетов, и я на 100% уверен, что вы найдете его очень отличным от любых учебников. Кроме того, у вас может не быть той же процедуры в учебниках, поскольку большая часть учебников не так глубоко разбирается в более простом обнаружении фиксированных конечных моментов. Я шаг за шагом объяснил всю концепцию.
В таблице расчетов я не объяснил, как определять диаграмму BMD & M / EI, поскольку это не является предметом нашего анализа.Наша цель анализа — определить фиксированные конечные моменты. В любом случае, пожалуйста, посетите мои предыдущие блоги в категории расчета прогиба, в которых я подробно рассказывал о формировании диаграммы BMD & M / EI.
Люди боятся анализировать сложную неопределенную структуру, потому что считают ее сложной. Если здраво рассуждать, вы можете преобразовать любую неопределенную балку в более простые определенные балки, тогда я гарантирую, что ваша половина работы сделана и вы будете решать только простые уравнения.
Как инженер-строитель, мы не должны игнорировать анализ консольных балок, подвергающихся различным видам нагружения. Вы заметите, если вы сможете решить для консольных балок, то сможете и для каркасной конструкции. Во-первых, здание — это не что иное, как вертикальная консоль, и во время анализа любого каркаса мы должны обладать большим умением и умением преобразовывать кадры в вертикальные консоли и горизонтальные балки, чтобы их можно было преобразовать в определенные балки. После этого все остальное будет решением только алгебраических уравнений.
Аналогичным образом, для структурной динамики, вы имеете дело с дифференциальными уравнениями для облицовки второго порядка, и после получения отклика в любой момент времени в виде максимального смещения, скорости и ускорения для динамической нагрузки или начального смещения конструкции ваша работа становится простой.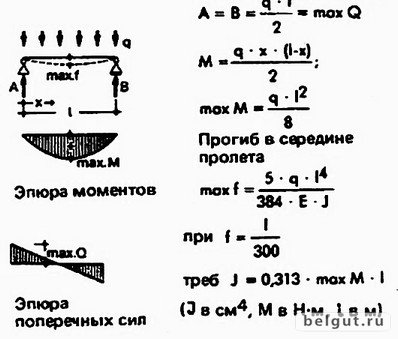
потому что после этого вы выполняете только статический анализ, и анализ вашей структуры становится статической проблемой.
Это серия 1 для расчета фиксированных концевых моментов для центральных точечных нагрузок, и я буду предлагать различные схемы нагружения в однопролетной неподвижной балке, чтобы узнать ее фиксированные концевые моменты.
Вам необходимо понимать концепцию фиксированных конечных моментов, потому что во время анализа балок и рам с использованием методов отклонения откоса и методов распределения моментов важно знать самый быстрый метод определения фиксированных конечных моментов.
Загрузите pdf для расчета фиксированных конечных моментов для центральной точечной нагрузки для однопролетной фиксированной балки
Спасибо
Mohammad Sohel Akhtar (инженер-строитель), Дели, Индия
Базовые значения для однопролетных балок
‘) var cartStepActive = true var buybox = document.
querySelector («[id-данных = id _» + отметка времени + «]»). parentNode ; []. slice.call (buybox.querySelectorAll («. покупка-опция»)). forEach (initCollapsibles) функция initCollapsibles (подписка, индекс) {
var toggle = subscription.querySelector («. цена-опции-покупки»)
subscription.classList.remove («расширенный»)
var form = subscription.querySelector («. Purchase-option-form»)
if (form && cartStepActive) {
var formAction = form.getAttribute («действие»)
form.setAttribute («действие», formAction.replace («/ checkout», «/ cart»))
document.querySelector («# сценариев электронной торговли»). addEventListener («загрузка», bindModal (форма, formAction, отметка времени, индекс), false)
}
var priceInfo = subscription.
querySelector («. price-info»)
var buyOption = toggle.parentElement if (переключить && форму && priceInfo) {
переключать.setAttribute («роль», «кнопка»)
toggle.setAttribute («tabindex», «0») toggle.addEventListener («клик», функция (событие) {
var extended = toggle.getAttribute («aria-extended») === «true» || ложный
toggle.setAttribute («расширенный ария»,! расширенный)
form.hidden = расширенный
если (! расширено) {
покупка вариант.classList.add («расширенный»)
} еще {
buyOption.classList.remove («расширенный»)
}
priceInfo.hidden = расширенный
}, ложный)
}
} function bindModal (form, formAction, timestamp, index) {
var weHasBrowserSupport = window.
fetch && Array.from return function () {
var Buybox = EcommScripts? EcommScripts.Ящик для покупок: null
var Modal = EcommScripts? EcommScripts.Modal: null
if (weHasBrowserSupport && Buybox && Modal) {
var modalID = «ecomm-modal_» + отметка времени + «_» + индекс
var modal = новый модальный (modalID)
modal.domEl.addEventListener («закрыть», закрыть)
function close () {
форма.querySelector («кнопка [тип = отправить]»). focus ()
} form.setAttribute (
«действие»,
formAction.replace («/ checkout», «/ cart? messageOnly = 1»)
)
form.
addEventListener (
«Отправить»,
Buybox.interceptFormSubmit (
Buybox.fetchFormAction (window.fetch),
Buybox.triggerModalAfterAddToCartSuccess (модальный),
console.log,
),
ложный
)
document.body.appendChild (modal.domEl)
}
}
} function initKeyControls () {
документ.addEventListener («нажатие клавиши», функция (событие) {
if (document.activeElement.classList.contains («покупка-опция-цена») && (event.code === «Space» || event.code === «Enter»)) {
if (document.activeElement) {
event.
preventDefault ()
document.activeElement.click ()
}
}
}, ложный)
} function initialStateOpen () {
var buyboxWidth = buybox.offsetWidth
; []. slice.call (buybox.querySelectorAll («. покупка-опция»)). forEach (function (option, index) {
var toggle = option.querySelector («. покупка-вариант-цена»)
var form = option.querySelector («. Purchase-option-form»)
var priceInfo = option.querySelector («. цена-информация»)
if (buyboxWidth> 480) {
toggle.click ()
} еще {
if (index === 0) {
переключать.нажмите ()
} еще {
toggle.
setAttribute («расширенная ария», «ложь»)
form.hidden = «скрытый»
priceInfo.hidden = «скрыто»
}
}
})
} initialStateOpen () если (window.buyboxInitialised) вернуть
window.buyboxInitialised = true initKeyControls ()
}) ()Балка с дискретной массой (M) и распределенной массой (m)
Габаритные размеры Материал Нагрузка
Утилизация Деформация (кратковременная нагрузка) Деформация (постоянная нагрузка) Собственная частота Стресс Мертвая нагрузка
Как пользоваться калькулятором
Калькулятор предназначен для плотников, которые хотят решать простые статические задачи.
Пожалуйста, используйте его с пониманием и не полагайтесь на результаты.
Используется Балкентеория Эйлера – Бернулли
для расчета внутренних сил. Характеристики материала и запас прочности древесины соответствуют стандарту DIN 1052: 2004-08.
На погрузочной площадке коэффициенты безопасности не применяются!
Размеры
- b : ширина профиля
- h : высота профиля
- l : длина балки
Материал
- Выберите свой материал.Все параметры рассчитываются согласно DIN 1052: 2004-08 \ для выбранной древесины, использования и продолжительности загрузки.
- Custom: Здесь вы можете использовать свои собственные параметры материала.
Нагрузка
- M : Дискретная масса в центре балки.
- м : Распределите массу (например, снеговую нагрузку). Обратите внимание, что m указано в [кг], а — не в [кг / мм]!
- Вес нетто : Калькулятор автоматически добавляет вес нетто балки.
Использование
- Изгиб : Отношение текущего напряжения изгиба к допустимому напряжению изгиба.
- Сдвиг : Отношение текущего напряжения сдвига к допустимому напряжению сдвига.
Деформация (кратковременная нагрузка)
- d : Прогиб балки без утечки. Деформацией сдвига пренебрегают.
Деформация (постоянная нагрузка)
- d : Прогиб балки с утечкой.Деформацией сдвига пренебрегают.
Собственная частота
- f : Самая низкая собственная частота изгиба из-за нагрузок M, m конечный вес нетто.
Напряжение
- Напряжение изгиба : Максимальное напряжение изгиба.
- Напряжение сдвига : максимальное напряжение сдвига.
Собственная нагрузка
- Собственная нагрузка : Статическая нагрузка на балку. Эта нагрузка включается в расчет прочности.
Изменения
28.12.2019
- Добавлены материалы
- Удалить кнопку «решить»
2020-05-22
2021-11-14
- Исправление ошибки в вычислении собственной частоты
Глубина луча для пролета 5 м, 6 м, 7 м, 8 м, 9 м и 10 м и формула
Глубина луча для пролета 5м, 6м, 7м, 8м, 9м и 10м и формула , привет, ребята, в этой статье мы знаем о расчете глубины луча | глубина балки на пролёт 5м | глубина балки на пролет 6м | глубина балки на пролёт 7м | глубина балки на пролёт 8м | глубина балки на пролёт 9м | глубина балки на пролет 10 м | формула глубины балки | отношение глубины балки к пролету | отношение глубины луча к ширине | Как рассчитать глубину и ширину балки?
Глубина балки для 5м 6м 7м 8м 9м и 10м пролет и формула Балка представляет собой изгибающийся структурный элемент из бетона , который передает вертикально всю статическую нагрузку, динамическую нагрузку плиты на колонну.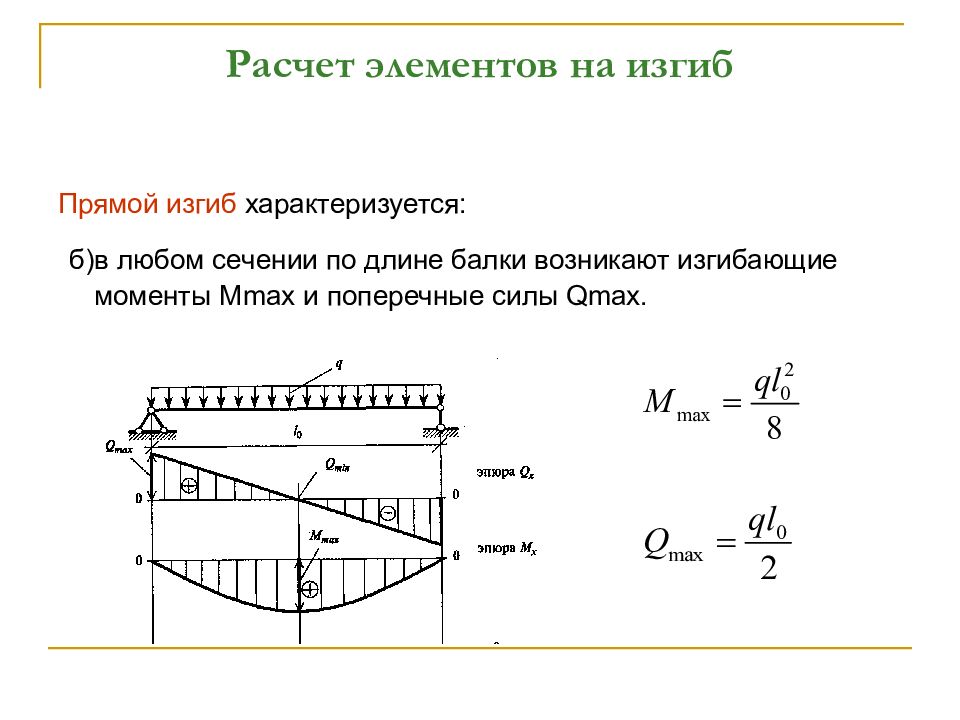
Горизонтальная нагрузка плиты напрямую передается на балку. Балка испытывает изгибающий момент и выдерживает нагрузку, приложенную к ней плитой. Максимальное количество арматуры предусмотрено в середине зоны растяжения и на стыке обоих концов балки с колонной зоны сжатия.
◆ Вы можете подписаться на меня на Facebook и подписаться на наш канал Youtube
Вам также следует посетить: —
1) что такое бетон, его виды и свойства
2) Расчет количества бетона для лестницы и его формула
Все мы знаем, что расчет размера балки необходим и незаменим при проектировании здания.В этом посте вы узнаете, как рассчитать глубину балки перед проектированием балки для планов проектирования двух-трехэтажных зданий или планов проектирования многоэтажных зданий.
Для проектирования балки глубина балки должна зависеть не только от пролета балки, но и от высоты колонны для конструкции, а также от статической и временной нагрузки здания, действующей на нее с коэффициентом гибкости.
Важно знать, как рассчитать размер балки по глубине, расчет нагрузки, марку бетона и марку стали.Вы можете спроектировать его с помощью формулы расчета балки и калькулятора расчета бетонной балки. Просто очистите концепцию один раз и начните с данного процесса.
Кроме того, вы можете легко создать расчет балки по формуле расчета бетонной балки, доступной на различных сайтах. Тем не менее, как инженер-строитель, вы должны знать формулу расчета балок и процедуру их расчета, а также иметь правильное понимание основных принципов физики и инженерной статики, поскольку они важны для проектирования и определения размеров балок.Инженер-строитель обладает полными знаниями и полностью оборудован для выбора материала, размера и формы, а также для проверки нагрузок, действующих на балку, расчета сил и напряжений в конструкции.
Как рассчитать глубину и ширину балки? Как рассчитать размер балки: — Балка бывает различных типов, например консольная балка, балка с несъемной опорой и неразрезная балка.
Расчет минимального размера балки RCC согласно IS 456 2000, отношение пролета к эффективной глубине балки составляет 7 для консольной балки, 20 для свободно опертой балки и 26 для неразрезной балки.
Стандартный размер бетонной балки должен быть не менее 9 ″ × 9 ″ (225 мм × 225 мм) с 4 шт. Толщиной 12 мм из стали Fe500 и бетоном марки m20 с хомутом [электронная почта защищена] ″ C / C.
1) Расчет глубины и ширины свободно опертой балки: —
Примечание согласно IS — 13920
A) отношение ширины к глубине должно быть более 0,3 (ширина / глубина> 0,3).
B) глубина балки не должна превышать 1/4 (1/4) свободного пролета.
Пролет балки в свету = 5 м = 5000 мм
Эффективная глубина = пролёт / базовое значение
Общая глубина = эффективная глубина + диаметр стержня / 2 + размер прозрачной крышки.
Ширина балки = Глубина / 1,5 (ширина балки не менее 200 мм).
Пролет свободно опертой балки = 5000 мм
Эффективная глубина балки d = 5000/20 = 250 мм
Общая глубина балки = эффективная глубина + диаметр стержня / 2 + размер прозрачной крышки.
Предположим, что размер прозрачной крышки = 25 мм
Диаметр стержня = 16 мм
Общая глубина D = 250 мм + 16/2 мм + 25 мм
Общая глубина D = 283 мм, Ее следует принять равной 300 мм.
Ширина балки = D / 1,5, 300 / 1,5 = 200 мм, поэтому ширина балки должна быть не менее 200 мм в случае блочной стены и 225 мм в случае кирпичной стены. Так что ширина балки принята как минимум 225мм.
Теперь проверьте это,
Ширина / глубина = 225/300 = 0,75> 0,3, это безопасно
Теперь мы можем проверить глубину балки = 1/4 × 5000 = 1250> 300, да, это безопасно.
Глубина и ширина балки с простой опорой: — балка с простой опорой, пролетом 5 м, толщиной 9 дюймов. Кирпичная стена, с помощью линейки для большого пальца, глубина балки должна составлять 300 мм, ширина — 225 мм, размер балки 9 ″ × 12 ″ (225 мм × 300 мм) с использованием 4-миллиметрового прутка из стали Fe500 толщиной не менее M20 и хомутов [электронная почта защищена] ″ C / C.
2) Расчет глубины и ширины консольной балки: —
Примечание согласно IS — 13920
A) отношение ширины к глубине должно быть более 0,3 (ширина / глубина> 0,3).
B) глубина балки не должна превышать 1/4 (1/4) свободного пролета.
Свободный пролет консольной балки = 2 м = 2000 мм
Эффективная глубина = пролет / базовое значение
Общая глубина = эффективная глубина + диаметр стержня / 2 + размер прозрачной крышки.
Ширина балки = Глубина / 1.5 (ширина балки не менее 200 мм).
Пролет консольной балки = 2000 мм
Эффективная глубина балки d = 2000/7 = 285 мм
Общая глубина балки = эффективная глубина + диаметр стержня / 2 + размер прозрачной крышки.
Предположим, что размер прозрачной крышки = 25 мм
Диаметр стержня = 16 мм
Общая глубина D = 285 мм + 16/2 мм + 25 мм
Общая глубина D = 318 мм. Ее следует принять как 325 мм.
Ширина балки = D / 1,5, 325 / 1,5 = 216 мм, поэтому ширина балки должна быть не менее 200 мм в случае блочной стены и 225 мм в случае кирпичной стены.
Так что ширина балки принята как минимум 225мм.
Теперь проверьте это,
Ширина / глубина = 225/325 = 0,69> 0,3, это безопасно
Теперь мы можем проверить глубину балки = 1/4 × 2000 = 500> 300, да, это безопасно.
Глубина и ширина консольной балки: — консольная балка с пролетом 2 м, толщиной 9 дюймов. Кирпичная стена, с помощью линейки для большого пальца, глубина балки должна быть 325 мм, ширина 225 мм, размер балки 9 дюймов × 13 дюймов (225 мм × 325 мм) с использованием 4nos прутка 16 мм из стали Fe500 с классом бетона не ниже M20 и хомуты [защита электронной почты] ″ C / C.
3) Расчет глубины и ширины неразрезной балки: —
Примечание согласно IS — 13920
A) отношение ширины к глубине должно быть более 0,3 (ширина / глубина> 0,3).
B) глубина балки не должна превышать 1/4 (1/4) свободного пролета.
Пролет сплошной балки = 5 м = 5000 мм
Эффективная глубина = пролёт / базовое значение
Общая глубина = эффективная глубина + диаметр стержня / 2 + размер прозрачной крышки.
Ширина балки = Глубина / 1.5 (ширина балки не менее 200 мм).
Пролет неразрезной балки = 5000 мм
Эффективная глубина балки d = 5000/26 = 192,3 мм
Общая глубина балки = эффективная глубина + диаметр стержня / 2 + размер прозрачной крышки.
Предположим, что размер прозрачной крышки = 25 мм
Диаметр стержня = 16 мм
Общая глубина D = 192 мм + 16/2 мм + 25 мм
Общая глубина D = 225 мм. Ее следует принять равной 225 мм.
Ширина балки = D / 1,5, 225 / 1,5 = 150 мм, поэтому ширина балки должна быть не менее 200 мм в случае блочной стены и 225 мм в случае кирпичной стены.Так что ширина балки принята как минимум 225мм.
Теперь проверьте это,
Ширина / глубина = 225/225 = 1> 0,3, это безопасно
Теперь мы можем проверить глубину балки = 1/4 × 5000 = 1250> 300, да, это безопасно.
Глубина и ширина неразрезной балки: — Сплошная балка с пролетом 5 м, кирпичная стена толщиной 9 дюймов, с помощью линейки для большого пальца, глубина балки должна составлять 225 мм и ширина 225 мм, размер балки 9 ″ × 9 ″ (225 мм × 225 мм) с использованием 4nos прутка 16 мм из стали Fe500 с классом бетона не ниже M20 и хомуты [защита электронной почты] ″ C / C.
Отношение глубины балки к ширине : — согласно IS — 13920
отношение ширины к глубине должно быть более 0,3 (ширина / глубина> 0,3).
Отношение глубины балки к пролету : — Расчет минимального размера балки RCC согласно IS 456 2000, для пролета консольной балки к эффективной глубине балки отношение 7, 20 для балки с простой опорой и 26 для неразрезной балки.
Формула глубины балки: — Балка бывает различных типов, например консольная балка, балка с простой опорой и неразрезная балка.Расчет минимального размера балки RCC в соответствии с IS 456 2000, формула глубины балки для консольной балки составляет L / 7 (отношение пролета к эффективной глубине балки равно 7), L / 20 для балки с простой опорой и L / 26 для неразрезной балки.
Глубина балки для пролета от 3 до 4 м: — в соответствии с общим правилом большого пальца для жилого дома с ж / б колонной, глубина балки для пролета от 3 до 4 м должна быть 9 ″ (225 мм), минимальный размер балки 9 ″ × 9 ″ (225 мм × 225 мм), с использованием 2 шт.
Размера арматуры T12 вверху и 2 шт. Размера арматуры T12 внизу Fe 500, используемого для бетона марки m20 с хомутами [защищено по электронной почте] ″ C / C с прозрачной крышкой 25 мм, в качестве конструкции конструкции, высота здания и приложенная к нему нагрузка.
Глубина балки для пролета 5 м: — в соответствии с общим правилом большого пальца для жилого дома, глубина балки для пролета 5 м должна составлять 300 мм, минимальный размер балки для пролета 5 м составляет 9 ″ × 12 ″ (225 мм × 300 мм), при этом глубина балки составляет 300 мм, ширина — 225 мм, с использованием 2 шт. размера арматуры T16 наверху и 2 шт. размера арматуры T16 снизу из Fe 500, используемого для бетона марки m20 с хомутами [электронная почта] ″ C / C с прозрачной крышкой 25 мм
по проекту конструкция, высота здания и приложенная к нему нагрузка.
Для данного пролета балки = 5 м = 5000 мм, глубина балки для балки с простой опорой составляет L / 20, эффективная глубина должна быть 5000/20 = 250 мм, общая глубина = 250 + 12/2 + 25 = 281 мм, следует принимать глубину как 300 мм, ширина = 300 / 1,5 = 200 мм, но, по крайней мере, ширина должна быть 225 мм, поэтому размер балки для пролета 5 м составляет 9 ″ × 12 ″ (225 мм × 300 мм), при этом глубина балки составляет 300 мм, а ширина — 225 мм, при использовании 2nos размера арматуры T16 вверху и 2nos размера арматуры T16 внизу Fe 500, используемого для бетона марки m20 со скобами [email protected] ″ C / C с прозрачной крышкой 25 мм.
Глубина балки для пролета 6 м: — в соответствии с общим правилом большого пальца для жилого дома, глубина балки для пролета 6 м должна составлять 350 мм, минимальный размер балки для пролета 6 м составляет 10 ″ × 14 ″ (250 мм × 350 мм), при этом глубина балки составляет 350 мм и ширина 250 мм, с использованием 2 шт. размера арматуры T16 наверху и 2 шт. размера арматуры T16 снизу из Fe 500, используемого для бетона марки m20 с хомутами [электронная почта] ″ C / C с прозрачной крышкой 25 мм
в соответствии с проектом конструкция, высота здания и приложенная к нему нагрузка.
Для данного пролета балки = 6 м = 6000 мм, глубина балки для балки с несущей балкой L / 20, эффективная глубина должна быть 6000/20 = 300 мм, общая глубина = 300 + 16/2 + 25 = 333 мм, следует принимать глубина равна 350 мм, ширина = 350 / 1,5 = 233 мм, что принимается за 10 ″ (250 мм), поэтому размер балки для пролета 6 м составляет 10 ″ × 14 ″ (250 мм × 350 мм), при этом глубина балки составляет 350 мм, а ширина — 250 мм.
, используя 2 шт. размера арматуры T16 сверху и 2 шт. размера арматуры T16 снизу из Fe 500, используемого для бетона марки m20 с хомутами [email protected] ″ C / C с прозрачной крышкой 25 мм.
Глубина балки для пролета 7 м: — в соответствии с общим правилом большого пальца для жилого дома с ж / б колонной, глубина балки для пролета 7 м должна составлять 400 мм, минимальный размер балки для пролета 7 м составляет 12 ″ × 16 ″ (300 мм × 400 мм), в котором глубина балки составляет 400 мм, а ширина — 300 мм, с использованием 2 шт. размера арматуры T16 вверху, 2 шт. размера арматуры T16 внизу и 2 шт. размера T12 в качестве коленчатого стержня из Fe 500, используемого для бетона марки m20 с хомутами [email protected] ″ C / C с прозрачной крышкой 25 мм как конструкция, высота здания и нагрузка на него.
Для данного пролета балки = 7 м = 7000 мм, глубина балки для балки с несущей балкой L / 20, эффективная глубина должна быть 7000/20 = 350 мм, общая глубина = 350 + 16/2 + 25 = 383 мм, следует принимать глубина равна 400 мм, ширина = 400 / 1,5 = 266 мм, что принимается как 12 ″ (300 мм), поэтому размер балки для пролета 7 м составляет 12 ″ × 16 ″ (300 мм × 400 мм), при этом глубина балки составляет 400 мм, а ширина — 300 мм.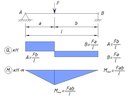
с использованием 2 шт. размера арматуры T16 вверху, 2 шт. размера арматуры T16 внизу и 2 шт. размера T12 в качестве кривошипа из Fe 500, используемого с бетоном марки m20 с хомутами [электронная почта] ″ C / C с прозрачной крышкой 25 мм.
Глубина балки для пролета 8 м: — в соответствии с общим правилом большого пальца для жилого дома с ж / б колонной, глубина балки для пролета 8 м должна составлять 450 мм, минимальный размер балки для пролета 8 м составляет 12 ″ × 18 ″ (300 мм × 450 мм), в котором глубина балки составляет 450 мм, ширина — 300 мм, с использованием 2 шт. размера арматуры T16 вверху, 2 шт. размера арматуры T16 внизу и 2 шт. размера T12 в качестве коленчатого стержня из Fe 500, используемого для бетона марки m20 с хомутами [email protected] ″ C / C с прозрачной крышкой 25 мм как конструкция, высота здания и нагрузка на него.
Для данного пролета балки = 8 м = 7000 мм, глубина балки для балки с опорой составляет L / 20, эффективная глубина должна быть 8000/20 = 400 мм, общая глубина = 400 + 16/2 + 25 = 433 мм, следует принимать глубина равна 450 мм, ширина = 450 / 1,5 = 300 мм, что принимается равным 12 ″ (300 мм), поэтому размер балки для пролета 8 м составляет 12 ″ × 18 ″ (300 мм × 450 мм), при этом глубина балки составляет 450 мм, а ширина — 300 мм.
с использованием 2 шт. размера арматуры T16 вверху, 2 шт. размера арматуры T16 внизу и 2 шт. T12 в качестве кривошипа из Fe 500, используемого с бетоном марки m20 с хомутами [email protected] ″ C / C с прозрачной крышкой 25 мм.
Глубина балки для пролета 9 м: — в соответствии с общим правилом большого пальца для жилого дома с ж / б колонной, глубина балки для пролета 9 м должна составлять 500 мм, минимальный размер балки для пролета 9 м составляет 12 ″ × 20 ″ (300 мм × 500 мм), в котором глубина балки составляет 500 мм, а ширина — 300 мм, с использованием 2 шт. размера арматуры T16 вверху, 2 шт. размера арматуры T16 внизу и 2 шт. размера T12 в качестве коленчатого стержня из Fe 500, используемого для бетона марки m20 с хомутами [email protected] ″ C / C с прозрачной крышкой 25 мм как конструкция, высота здания и нагрузка на него.
Для данного пролета балки = 9 м = 9000 мм, глубина балки для балки с опорой составляет L / 20, эффективная глубина должна быть 9000/20 = 450 мм, общая глубина = 450 + 16/2 + 25 = 483 мм, следует принимать глубина равна 500 мм, ширина = 500 / 1,5 = 333 мм, что равно 12 ″ (300 мм), поэтому размер балки для пролета 9 м составляет 12 ″ × 20 ″ (300 мм × 500 мм), при этом глубина балки составляет 500 мм, а ширина 300 мм, используя 2 шт.
Размера арматуры T16 вверху, 2 шт. Размера арматуры T16 внизу и 2 шт. Размера T12 в качестве кривошипа из Fe 500, используемого для бетона марки m20 с хомутами [электронная почта] ″ C / C с прозрачной крышкой 25 мм.
Глубина балки для пролета 10 м: — в соответствии с общим правилом большого пальца для жилого дома с ж / б колонной, глубина балки для пролета 10 м должна составлять 600 мм, минимальный размер балки для пролета 10 м составляет 12 ″ × 24 ″ (300 мм × 600 мм), в котором глубина балки составляет 600 мм, а ширина — 300 мм, с использованием 2 шт. размера арматуры T16 вверху, 2 шт. размера арматуры T16 внизу и 2 шт. размера T12 в качестве коленчатого стержня из Fe 500, используемого для бетона марки m20 с хомутами [email protected] ″ C / C с прозрачной крышкой 25 мм как конструкция, высота здания и нагрузка на него.
Для данного пролета балки = 10 м = 10000 мм, глубина балки для балки без опоры L / 20, эффективная глубина должна быть 10000/20 = 500 мм, общая глубина = 500 + 16/2 + 25 = 533 мм, следует принимать глубина равна 600 мм, ширина = 600 / 1,5 = 400 мм, что принимается равным 12 ″ (300 мм), поэтому размер балки для пролета 10 м составляет 12 ″ × 24 ″ (300 мм × 600 мм), при этом глубина балки составляет 600 мм, а ширина — 300 мм.