Расчет балки на прогиб
вернуться в раздел РАСЧЕТЫ КМ И КЖ
Здесь представлены формулы расчета для нахождения значений изгибающих моментов и прогибов для различных балок.
| Однопролетные балки на двух шарнирных опорах | ||
| 1 | Расчет балки на двух шарнирных опорах при одной сосредоточенной нагрузке | Смотреть расчет |
| 2 | Расчет балки на двух шарнирных опорах при двух сосредоточенных нагрузках | Смотреть расчет |
| 3 | Расчет балки на двух шарнирных опорах при одной равномерно-распределенной нагрузке | Смотреть расчет |
| 4 | Расчет балки на двух шарнирных опорах при одной неравномерно-распределенной нагрузке | Смотреть расчет |
| 5 | Расчет балки на двух шарнирных опорах при действии изгибающего момента | Смотреть расчет |
| Балки с жестким защемлением на двух опорах | ||
| 6 | Расчет балки с жестким защемлением на опорах при одной сосредоточенной нагрузке | Смотреть расчет |
| 7 | Расчет балки с жестким защемлением на опорах при двух сосредоточенных нагрузках | Смотреть расчет |
| 8 | Расчет балки с жестким защемлением на опорах при одной равномерно-распределенной нагрузке | Смотреть расчет |
| 9 | Расчет балки с жестким защемлением на опорах при одной неравномерно-распределенной нагрузке | Смотреть расчет |
| 10 | Расчет балки с жестким защемлением на опорах при действии изгибающего момента | Смотреть расчет |
| Балки с жестким защемлением на одной опоре (консольные) | ||
| 11 | Расчет однопролетной балки с жестким защемлением на одной опоре при одной сосредоточенной нагрузке | Смотреть расчет |
| 12 | Расчет однопролетной балки с жестким защемлением на одной опоре при одной равномерно-распределенной нагрузке | Смотреть расчет |
| 13 | Расчет однопролетной балки с жестким защемлением на одной опоре при одной неравномерно-распределенной нагрузке | Смотреть расчет |
| 14 | Расчет однопролетной балки с жестким защемлением на одной опоре при действии изгибающего момента | Смотреть расчет |
| Балки двухпролетные | ||
| 15 | Расчет двухпролетной с шарнирными опорами при одной сосредоточенной нагрузке | Смотреть |
| 16 | Расчет двухпролетной с шарнирными опорами при двух сосредоточенных нагрузках | |
| 17 | Расчет двухпролетной с шарнирными опорами при одной равномерно-распределенной нагрузке | Смотреть |
| 18 | Расчет двухпролетной с шарнирными опорами при одной неравномерно-распределенной нагрузке | Смотреть |
| 19 | Расчет двухпролетной с шарнирными опорами при одной неравномерно-распределенной нагрузке | Смотреть |
Расчет однопролетной балки | Статья в журнале «Молодой ученый»
Автор: Крячик Юлия Вячеславовна
Рубрика: Технические науки
Опубликовано в
Молодой учёный
№50 (184) декабрь 2017 г.
Дата публикации: 17.12.2017 2017-12-17
Статья просмотрена: 1419 раз
Скачать электронную версию
Скачать Часть 1 (pdf)
Библиографическое описание:Крячик, Ю. В. Расчет однопролетной балки / Ю. В. Крячик. — Текст : непосредственный // Молодой ученый. — 2017. — № 50 (184). — С. 59-65. — URL: https://moluch.ru/archive/184/47284/ (дата обращения: 05.03.2023).
В данной статье мы произведем расчет методом конечных элементов однопролетной балки с данными, которые мы зададим для примера. Балка разбивается на пять конечных элементов имеющих одинаковою длину и изгибную жесткость (EI). Для решения этой задачи нам необходимо:
1) Привести все исходные к системе СИ
2) Изобразить расчетную схему балки в соответствии с вариантами закрепления и обозначить на ней величины нагрузки и размеры;
3) Построить эпюры N(x), M(x) для всей конструкции в целом.
Рис. 1. Однопролетная балка
Исходные данные
длина балки | L, м | 8 | |
сила | F1, кН | 20 | |
F2, кН | 27 | ||
распределенная нагрузка | f, кН/м | 9,8 | |
модуль упругости | E, ГПа | 200 | |
момент инерции сечения | I, см4 | 9840 | |
Варианты закрепления концов балки (жесткости упругих опор и заделок) | |||
Ko_0 | ∞ | ||
Kz_0 | 0 | ||
Ko_L | ∞ | ||
Kz_L | 0 | ||
Используем матрицу индексов для формирования матрицы жесткости К.
Номер столбца, в котором находится j определяет левый индекс матрицы жесткости конечного элемента. Номер столбца, в котором находится индекс j определяет второй индекс матрицы жесткости конечного элемента.
Формируем вектор внешних воздействий Pall. Чтобы сформировать вектор эквивалентных нагрузок, берем конечный элемент стандартного вида и накладываем его на конечный элемент расчетной модели. Устанавливаем соответствие между параметрами конечного элемента стандартного вида и параметрами всей расчетной модели.
Из уравнения равновесия конечного элемента [k]{q}={r}+{p} выражаем вектор реактивных усилий {r} {r}= [k]{q}-{p}
Эпюра изгибающих моментов жестко заделанной балки
Эпюра перерезывающих сил жестко заделанной балки
В ходе выполнения данной задачи для расчетов и построения графиков мы использовали программное средство MathCAD.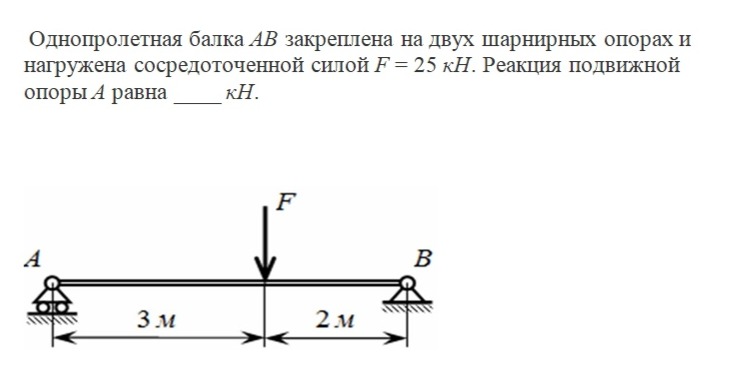 Рассчитав методом конечных элементов однопролетную балку, мы построили эпюры перерезывающих сил и изгибающих моментов для нее.
Рассчитав методом конечных элементов однопролетную балку, мы построили эпюры перерезывающих сил и изгибающих моментов для нее.
Основные термины (генерируются автоматически): конечный элемент, однопролетная балка, заделанная балка, номер столбца, расчетная модель, стандартный вид, формирование матрицы жесткости.
Похожие статьи
Алгоритмы
формирования матрицы жесткости треугольного…Разработаны алгоритмы получения матриц
(1). где – матрица жесткости, – векторы узловых сил и перемещений КЭ базового разбиения ДвКЭ, T – транспонирование.
где – матрица жесткости, – векторы узловых сил и перемещений КЭ базового разбиения ДвКЭ, T – транспонирование.
Рис. 3. Расчетная схема балки. Базовая дискретная модель балки состоит из изотропных однородных КЭ 1-го порядка формы куба со стороной .
Расчетное исследование влияния типа конечных элементов на…где: Ke — матрица жесткости элемента [4].
Похожие статьи. Сравнительный анализ на основе метода конечных элементов работы балок с гофрированной стенкой в условиях стесненного кручения.
Совершенствование методики
расчёта пологих железобетонных…Расчётный пролёт балки l0 принимаем равным. (1). где l — длина балки, м; l’ — величина заделки балки в кирпичную стену, м.
(1). где l — длина балки, м; l’ — величина заделки балки в кирпичную стену, м.
Расширенный порядок расчета усиления железобетонных элементов на основе деформационной
При расчёте плит в виде кольца матрица жёсткости элемента внутреннего круга основания может быть построена аналогично (12) и (13), если
Сравнительный анализ на основе метода конечных элементов работы балок с гофрированной стенкой в условиях стесненного кручения.
Алгоритм получения
матрицы жесткости четырехугольного…Ключевые слова: объемный конечный элемент, матрица жесткости, вектор узловых неизвестных.
Вектор-столбец внутренней точки конечного элемента определяется в матричном виде выражением.
Устойчивость железобетонного изгибаемого
элемента (балки) под…Железобетонная балка задана в виде двух КЭ—моделей
Расчет однопролетной балки. Ремонт наклонных плоскостей надрессорной балки вагонов. О дискретизации нормального сечения железобетонного элемента с неоднородными свойствами бетона при расчете по…
Ремонт наклонных плоскостей надрессорной
балки вагоновКлючевые слова: надрессорная балка, наклонные плоскости, износостойкая наплавка, сварка.
При плановых видах ремонта планки, ранее приваренные на наклонных плоскостях, удалить.
Расчет однопролетной балки.
Похожие статьи
Алгоритмы
формирования матрицы жесткости треугольного…Разработаны алгоритмы получения матриц жесткости треугольного конечного элемента в трех вариантах. Компоненты вектора узловых неизвестных принимаются в виде перемещений, а гидростатическое давление считается постоянным по площади четырехугольника…
Расчет балок с микронеоднородной структурой с применением…(1). где – матрица жесткости, – векторы узловых сил и перемещений КЭ базового разбиения ДвКЭ, T – транспонирование.
Рис. 3. Расчетная схема балки.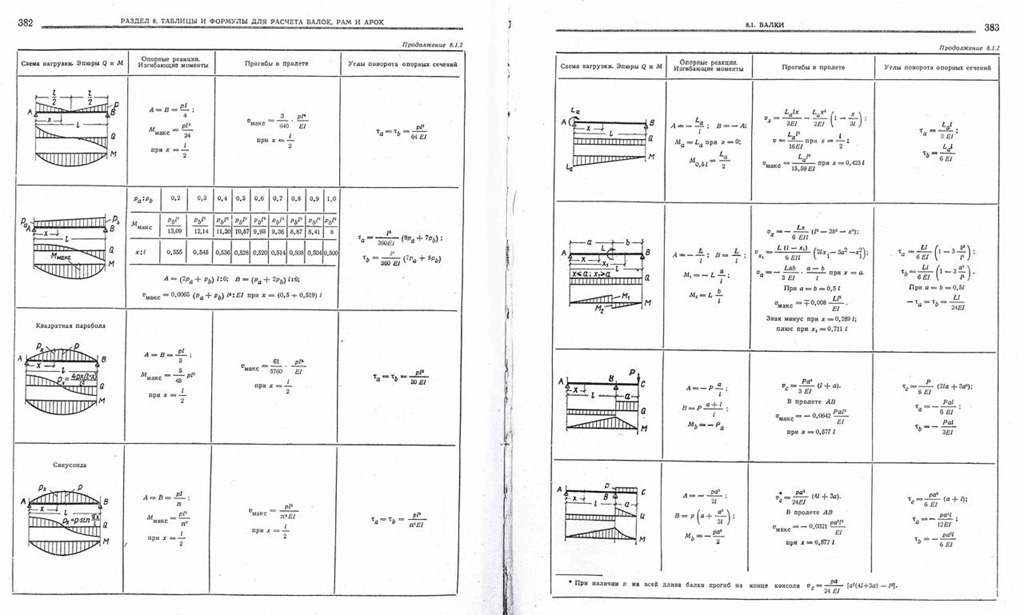 Базовая дискретная модель балки состоит из изотропных однородных КЭ 1-го порядка формы куба со стороной .
Базовая дискретная модель балки состоит из изотропных однородных КЭ 1-го порядка формы куба со стороной .
где: Ke — матрица жесткости элемента [4].
Похожие статьи. Сравнительный анализ на основе метода конечных элементов работы балок с гофрированной стенкой в условиях стесненного кручения.
Совершенствование методики
расчёта пологих железобетонных…Расчётный пролёт балки l0 принимаем равным. (1). где l — длина балки, м; l’ — величина заделки балки в кирпичную стену, м.
Расширенный порядок расчета усиления железобетонных элементов на основе деформационной модели.
При расчёте плит в виде кольца матрица жёсткости элемента внутреннего круга основания может быть построена аналогично (12) и (13), если
Сравнительный анализ на основе метода конечных элементов работы балок с гофрированной стенкой в условиях стесненного кручения.
Алгоритм получения
матрицы жесткости четырехугольного…Ключевые слова: объемный конечный элемент, матрица жесткости, вектор узловых неизвестных.
Вектор-столбец внутренней точки конечного элемента определяется в матричном виде выражением.
Устойчивость железобетонного изгибаемого
элемента (балки) под…Железобетонная балка задана в виде двух КЭ—моделей
Расчет однопролетной балки. Ремонт наклонных плоскостей надрессорной балки вагонов. О дискретизации нормального сечения железобетонного элемента с неоднородными свойствами бетона при расчете по…
Ремонт наклонных плоскостей надрессорной
балки вагоновКлючевые слова: надрессорная балка, наклонные плоскости, износостойкая наплавка, сварка.
При плановых видах ремонта планки, ранее приваренные на наклонных плоскостях, удалить.
Расчет однопролетной балки.
Без гарантии, используйте на свой страх и риск. Размеры Материал
Использование
How to use the calculator Калькулятор предназначен для технически заинтересованных людей, которые ищут простой и быстрый способ расчета несущей способности однопролетной балки. Вы должны знать:
Изменения28.12.2019
22.05.2020
14.11.2021
Анализ однопролетных балок
Обзор Эта программа обеспечивает анализ однопролетных балок с различными условиями нагрузки и опоры. Приведены максимальные моменты, сдвиги, реакции и прогибы. Основные возможности этой программы также содержатся в различных программах проектирования балок в подразделениях стали, бетона и древесины. Эта программа выполняет более подробный анализ и предлагает больше вариантов загрузки, чем большинство программ для проектирования.
Можно проанализировать однопролетную балку с опциональными консолями, а концевые опоры можно изменить, чтобы получить практически любую конфигурацию.
Допустимые нагрузки обширны. Можно ввести равномерную нагрузку, нагрузку частичной длины, трапециевидную, сосредоточенную и моментную нагрузку. Для неполной длины и трапециевидных нагрузок ввод очень прост, достаточно ввести начальную и конечную величины и местоположения. Программа использует местоположения, чтобы определить, как нагрузка прилагается к центральным и консольным пролетам.
ПРИМЕЧАНИЕ! Все места нагрузки указаны относительно ЛЕВОЙ опоры. Расстояния положительны по направлению к правой опоре и отрицательны по левой консоли. В программе также имеется раздел ЗАПРОС, позволяющий вам вводить места вдоль пролета, где вы хотели бы исследовать условия.
Допущения и ограничения
Пример Ввод данных для этого примера показан на снимках экрана, сопровождающих разделы «Вкладки ввода данных» и «Результаты и графики». Пример относится к двухконсольной балке с нагрузками, приложенными к центральному пролету и консоли. Поскольку эта программа не выполняет автоматических расчетов для нескольких местоположений динамической нагрузки, дается только один набор результатов. Вот базовый эскиз геометрии и нагрузки:
Вкладки ввода данных Этот набор вкладок содержит записи для всех входных данных в этом расчете. Пока вы вводите данные и переключаетесь между этими вкладками, вы можете просматривать желаемую результирующую информацию на вкладках в правой части экрана (расчетные значения, эскизы, диаграммы и т. д.). Перерасчет выполняется после изменения любых входных данных.
Вкладка «Общие»
Центральный пролет, левая консоль, правая консоль Введите длину пролета для центрального пролета и консолей. Если для конечной фиксации задано значение Фиксированная, любая запись длины консоли или нагрузок, выходящих за пределы фиксированной опоры, будет игнорироваться. Распределенные нагрузки, выходящие за пределы фиксированной опоры, будут просто усечены.
Конечная фиксация Эта запись позволяет указать комбинацию конечной фиксации балки. Порядок слов относится к левым и правым концам луча.
Инерция и модуль упругости Ввод обоих этих элементов необходим программе для расчета отклонений. Если одна или обе эти записи равны нулю, отклонения будут равны «0,0».
Вкладка «Равномерность» На этой вкладке представлены данные для приложения равномерных нагрузок по всей длине к центральному пролету и консолям. Положительные значения действуют вместе с силой тяжести и отклоняют балку вниз, что приводит к сжатию верхнего волокна.
Вкладка «Точка» На этой вкладке представлены записи, позволяющие ввести до 14 точечных нагрузок. «Местоположение» — это расстояние от левой опоры до места сосредоточения нагрузки.
Вкладка трапециевидной формы На этой вкладке можно указать до 8 равномерных нагрузок полной или частичной длины с различными начальными и конечными значениями. Величина «Левая/Начало» относится к левой стороне нагрузки. Величины могут быть положительными или отрицательными значениями на обоих концах или на каждом из них. «Местоположение» — это расстояние от левой опоры до местоположения начальной или конечной точки нагрузки. Если значение «Местоположение» отрицательное, то оно находится на левой консоли.
Вкладка «Момент» На этой вкладке представлены записи, так что вы можете ввести до 8 моментов. «Местоположение» — это расстояние от левой опоры до места сосредоточения нагрузки. Если значение «Местоположение» отрицательное, то оно находится на левой консоли. Если значение превышает длину центрального пролета, то оно находится на правой консоли. Случаи, когда вводятся отрицательные положения без левой консоли или с «фиксированной» левой опорой, игнорируются. Аналогичное поведение происходит для значений Location, которые длиннее, чем расстояние Center Span.
Вкладка «Запрос» Эта вкладка позволяет ввести конкретные положения на пролете балки и получить данные о моменте, сдвиге и прогибе. Точность этих значений составляет до ближайшей 1/500 диапазона.
Вкладки «Результаты и графики» На этом наборе вкладок представлены расчетные значения, полученные в результате ввода данных на «Вкладках ввода данных». Поскольку при каждом вводе данных выполняется перерасчет, информация на этих вкладках всегда отражает точные и текущие результаты, эскиз проблемы или диаграмму напряжения/прогиба.
Вкладка «Результаты» Эта вкладка содержит результирующие расчетные значения для анализа балки.
Максимальный момент и положение Максимальные моменты в местоположении показаны при его местоположении, измеренном от левой опоры. Максимальный положительный момент (сжатие в верхней части балки) между опорами. Сканируется вся длина балки, и если происходит сжатие опоры из-за кантилевера, это также будет учтено.
Моменты….Макс.+, Макс. -, Левая и правая концевые опоры Эти значения представляют собой максимальное и минимальное значения для центрального пролета и фактического момента на концевой опоре. M Сканируется вся длина балки, и если происходит сжатие опоры из-за кантилевера, это также будет включено.
Сдвиг Эти значения представляют собой максимальный сдвиг на каждой опоре.
Реакции Это расчетные вертикальные реакции на каждой опоре от заданных нагрузок.
Максимальные прогибы Когда и момент инерции, и модуль упругости отличны от нуля, в этой области отображаются прогибы балки для центрального и консольного пролетов (если применимо). Все 250 пролетных строений проверяются на максимальное отклонение, и задаются как положение, так и отклонение.
Вкладка «Эскиз» На этой вкладке представлен эскиз балки с показанными нагрузками и результирующими значениями. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
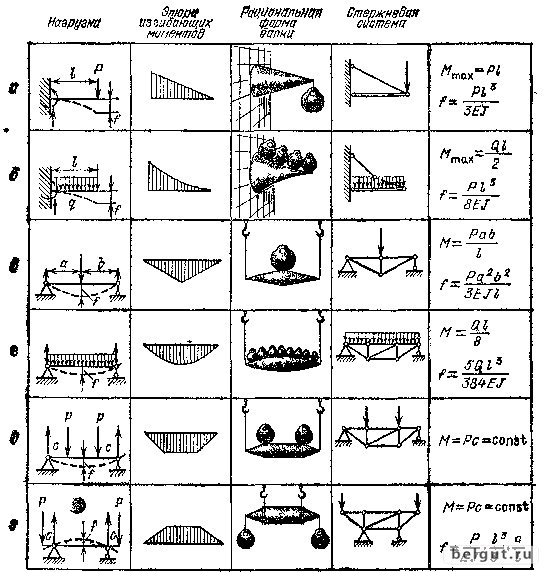
 0L, нейтральный AXIS :
0L, нейтральный AXIS : Пожалуйста, используйте его с проницательностью и не полагайтесь на результаты.
Пожалуйста, используйте его с проницательностью и не полагайтесь на результаты. 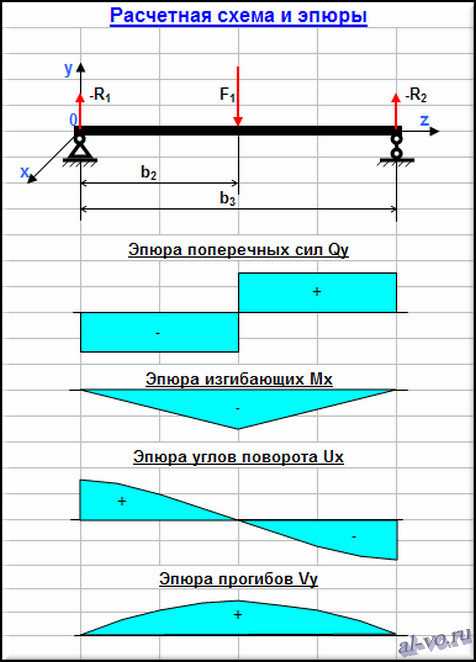

 ….простые опоры, консоли с подпиранием, фиксированные на обоих концах, чистые консоли или двойные консоли.
….простые опоры, консоли с подпиранием, фиксированные на обоих концах, чистые консоли или двойные консоли. Расчетные значения обычно находятся в пределах 1/5000 от фактического числа.
Расчетные значения обычно находятся в пределах 1/5000 от фактического числа. После каждого ввода данных вы можете просмотреть результаты на правом наборе вкладок.
После каждого ввода данных вы можете просмотреть результаты на правом наборе вкладок.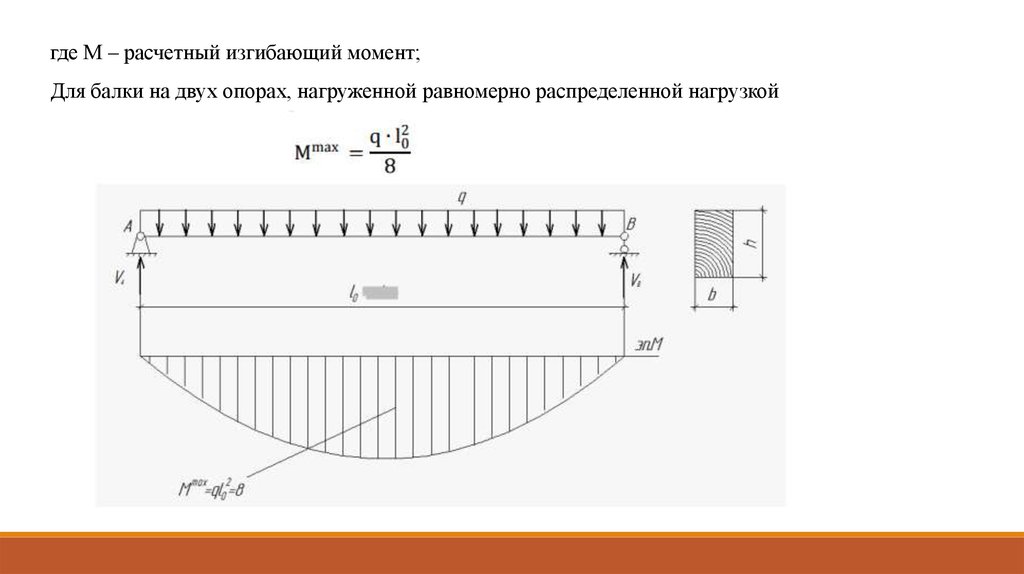 .. в основном консольный конец.
.. в основном консольный конец.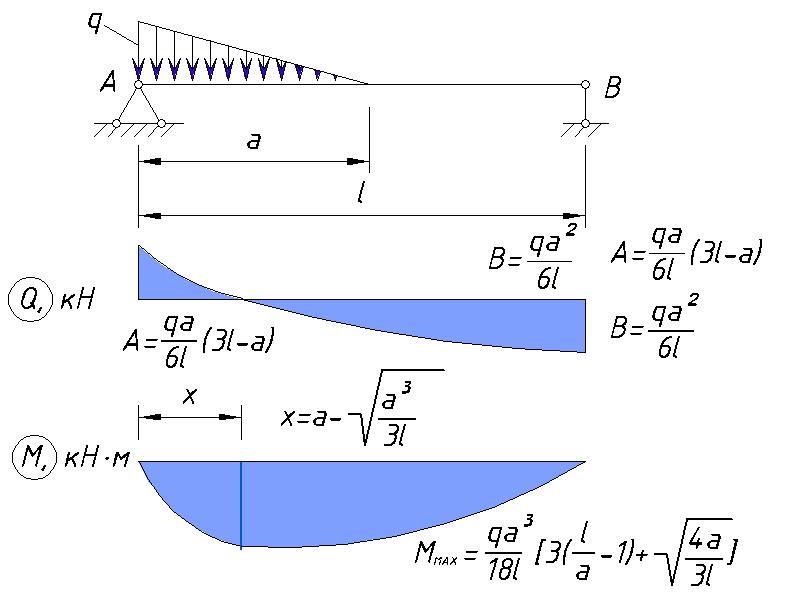 Если значение «Местоположение» отрицательное, то оно находится на левой консоли. Если значение превышает длину центрального пролета, то оно находится на правой консоли. Случаи, когда вводятся отрицательные положения без левой консоли или с «фиксированной» левой опорой, игнорируются. Аналогичное поведение происходит для значений Location, которые длиннее, чем расстояние Center Span. Положительные значения действуют вместе с силой тяжести и отклоняют балку вниз, что приводит к сжатию верхнего волокна.
Если значение «Местоположение» отрицательное, то оно находится на левой консоли. Если значение превышает длину центрального пролета, то оно находится на правой консоли. Случаи, когда вводятся отрицательные положения без левой консоли или с «фиксированной» левой опорой, игнорируются. Аналогичное поведение происходит для значений Location, которые длиннее, чем расстояние Center Span. Положительные значения действуют вместе с силой тяжести и отклоняют балку вниз, что приводит к сжатию верхнего волокна. Если значение превышает длину центрального пролета, то оно находится на правой консоли. Случаи, когда вводятся отрицательные положения без левой консоли или с «фиксированной» левой опорой, игнорируются. Аналогичное поведение происходит для значений Location, которые длиннее, чем расстояние Center Span. Положительные значения действуют вместе с силой тяжести и отклоняют балку вниз, что приводит к сжатию верхнего волокна.
Если значение превышает длину центрального пролета, то оно находится на правой консоли. Случаи, когда вводятся отрицательные положения без левой консоли или с «фиксированной» левой опорой, игнорируются. Аналогичное поведение происходит для значений Location, которые длиннее, чем расстояние Center Span. Положительные значения действуют вместе с силой тяжести и отклоняют балку вниз, что приводит к сжатию верхнего волокна. Положительные значения действуют вместе с силой тяжести и отклоняют балку вниз, что приводит к сжатию верхнего волокна.
Положительные значения действуют вместе с силой тяжести и отклоняют балку вниз, что приводит к сжатию верхнего волокна. Это максимальное значение абсолютного значения при неповрежденном вздохе. Фактические приращения длины пролета, используемые для определения точности, зависят от длины центрального пролета и длины консоли. Балка без консолей будет разделена на 500 приращений. Когда используются консоли, каждый пролет делится на часть 500 приращений в соответствии с его процентом от общей длины балки.
Это максимальное значение абсолютного значения при неповрежденном вздохе. Фактические приращения длины пролета, используемые для определения точности, зависят от длины центрального пролета и длины консоли. Балка без консолей будет разделена на 500 приращений. Когда используются консоли, каждый пролет делится на часть 500 приращений в соответствии с его процентом от общей длины балки. Это значение определяется путем проверки двух элементов:
Это значение определяется путем проверки двух элементов: