Калькулятор модуля сечения

Вычисление модуля сечения представляет собой интересный способ изучения реакции балки на напряжение при изгибе . С помощью этого инструмента вы сможете рассчитать модуль упругого и пластического сечения двутавровых сечений и многих других распространенных структурных форм.

Если вы не знаете, что такое модуль сопротивления, в следующей статье мы поговорим о нем, о разнице между эластичным и пластичным вариантом и формулах для его расчета. Продолжай читать!

Что такое модуль упругого сечения?

Чтобы узнать, откуда берется модуль сопротивления, вспомним широко известную формулу изгиба , используемую для определения максимального напряжения в балке, подвергаемой изгибу:

σmax=McI=MI/c\sigma_{max} = \frac {Mc}{I} = \frac{M}{I/c}σmax​=IMc​=I/cM​

, где:

• σmax\sigma_{max}σmax​ — максимальное нормальное напряжение в балке. Это напряжение возникает на расстоянии ссс от нейтральной оси.
• ccc — Наибольшее перпендикулярное расстояние от нейтральной оси до точки сечения;
• МММ — Изгибающий момент относительно нейтральной оси ; и
• III — момент инерции поперечного сечения балки относительно нейтральной оси .

Напомним, что это уравнение применимо только в том случае, если луч удовлетворяет следующим условиям:

• Это призматический луч (то есть в форме прямоугольной призмы).
• Он симметричен относительно оси, перпендикулярной нейтральной оси.
• Его материал однороден и ведет себя согласно закону Гука.

Например, мы можем использовать формулу изгиба для следующего случая:

Балка при изгибе.

Как и момент инерции площади, расстояние ccc зависит исключительно от геометрии сечения. Мы можем объединить III и ccc и создать новое геометрическое свойство, которое полностью объясняет влияние геометрии на нормальное напряжение. Это свойство известно как модуль упругого сечения или модуль упругого сечения :

S=IcS =\frac{I}{c}S=cI​

Благодаря этому новому свойству теперь мы можем рассчитать максимальное нормальное напряжение из-за изгиба, зная только MMM и SSS:

σmax=MS\sigma_{max} = \frac{M}{S}σmax​=SM​

Как и для момента инерции, мы можем определить модуль сечения для направлений x и y .

Выбор оси будет зависеть от направления вектора импульса. Например, если вектор момента действует в x-направлении (наиболее распространенная ситуация), мы выбираем модуль сечения в 0003 направление x .

Тем не менее, если мы столкнемся с ситуацией несимметричного изгиба (изгиб в различных направлениях или плоскостях), нам придется использовать методы, которые требуют модуль сечения в обоих направлениях. В последнем разделе этой статьи вы можете посмотреть таблицу с различными формулами модуля упругости и пластичности сечения для разных осей.

Что такое модуль пластического сечения?

Модуль пластического сечения имеет ту же функцию, что и его упругий аналог, но для ситуаций, в которых мы превзошли предел текучести материала и он больше не проявляет линейного упругого поведения. Модуль упругого сечения позволяет рассчитать пластический момент

сечения:

Mp=ZσYM_p = Z\sigma_YMp​=ZσY​

где:

• MpM_pMp​ — пластический момент;
• ZZZ — Модуль пластического сечения; и
• σY\sigma_YσY​ — Предел текучести материала балки.

Пластический момент относится к моменту, необходимому для того, чтобы вызвать пластическую деформацию по всем волокнам секции балки. Как известно, при изгибе нормальное напряжение больше в точках, наиболее удаленных от нейтральной оси, и, следовательно, в этих точках оно прежде всего достигнет предела текучести. Как только момент ( M ) равен пластическому моменту ( M _p ), предел текучести будет достигать всего сечения.

Объяснение концепции пластического момента.

С помощью предыдущего уравнения мы можем легко предсказать изгибающий момент, который вызовет пластическую деформацию

, зная только модуль пластического сечения и предел текучести.

Теперь, когда мы знаем понятия, давайте рассмотрим различные формулы для расчета модуля сечения.

Формулы для расчета момента сопротивления

В следующей таблице вы можете посмотреть формулы модуля упругости и пластичности, которые используются в этом калькуляторе модуля сечения.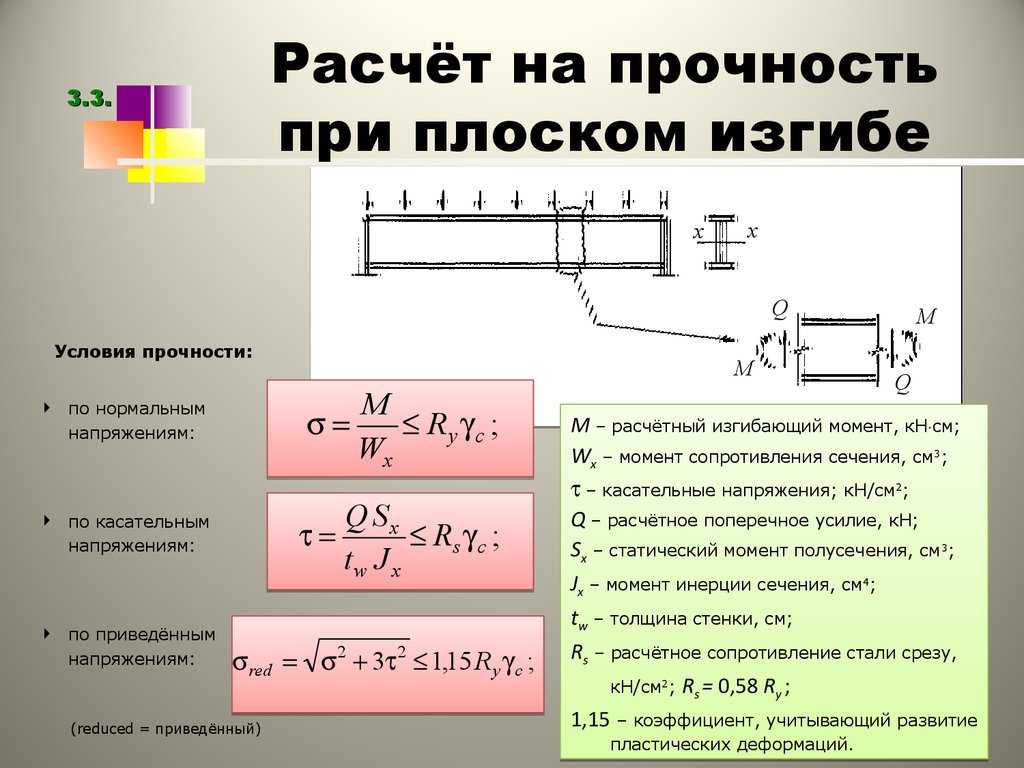 Прокрутите вбок, чтобы отобразить всю таблицу.

Форма		Модуль упругости сечения (S)	Модуль пластического сечения (Z)
Квадрат		yc=xc=a/2y_c = x_c = a/2 yc=xc=a/2 94)Ix​=Iy​=4π​(R4−Ri4​)
		Sx=Sy=IxycS_x = S_y =\frac{I_x}{y_c}Sx​=Sy​=yc​Ix​​

Калькулятор К-фактора: для идеальной гибки листового металла

К-фактор — это фундаментальное понятие в SolidWorks для проектирования листового металла, которое имеет решающее значение для освоения производства листового металла.

Сначала нужно понять К-фактор.

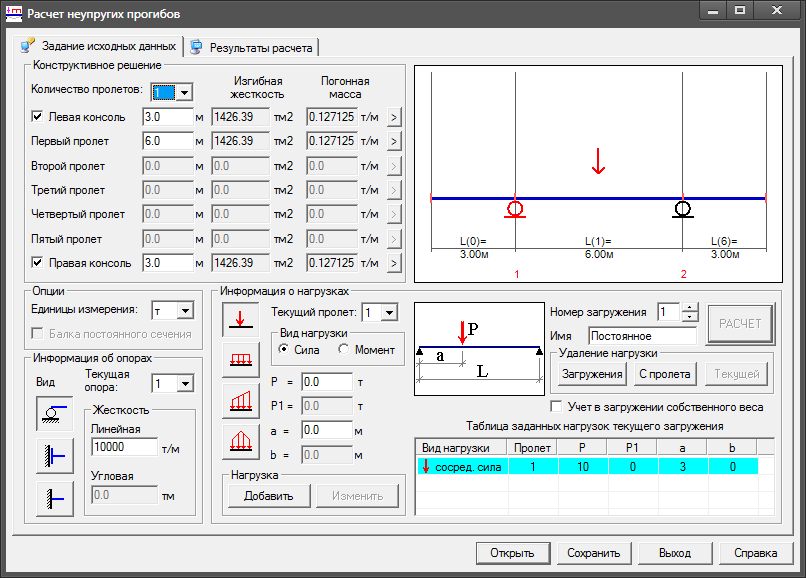
Что такое К-фактор?

Это отношение расстояния между нейтральным слоем и внутренней поверхностью изгиба к толщине листового металла.

Как показано на диаграмме ниже, K = t / T . Из определения К-фактора ясно, что это константа больше 0 и меньше 1.

Поскольку К-фактор связан с положением нейтрального слоя, что такое нейтральный слой?

Принцип работы гибки ш…

Включите JavaScript

Принцип работы гибки листового металла

В зоне деформации изгиба материал вблизи внутренней поверхности сжимается, и сжатие тем сильнее, чем ближе к нему находится на внутренней поверхности.

Точно так же материал вблизи внешней поверхности растягивается, и растяжение тем сильнее, чем ближе он находится к внешней поверхности.

Переход от сжатия к растяжению как переход от внутренней поверхности к внешней, при условии, что материал уложен тонкими слоями (большинство металлических материалов слоистыми), в середине материала должен быть слой, который не сжимается ни растянутый.

Мы называем этот слой нейтральным слоем.

Обычно нейтральный слой нельзя увидеть или потрогать, поскольку он находится внутри металла.

Его положение связано с неотъемлемыми свойствами материала, что означает, что К-фактор связан с материалом.

Исходя из определения нейтрального слоя, размер листа в развернутом виде равен ширине нейтрального слоя, как показано на рисунке выше.

Размер листа в развернутом виде = прямая А + прямая В + дуга С (длина нейтрального слоя в очаге деформации).

К-фактор также называется коэффициентом положения нейтрального слоя.

Для большинства материалов К-фактор представляет собой число, меньшее или равное 0,5 при проектировании и обработке листового металла.

Важность К-фактора при гибке листового металла

К-фактор является важным понятием в производстве листового металла, поскольку он определяет угол изгиба гибочной машины, а также влияет на форму и размер формируемого листового металла.

При изготовлении листового металла К-фактор представляет коэффициент регулирования упругости листового металла в процессе гибки.

Другими словами, контролируя величину К-фактора, можно контролировать степень деформации листового металла и добиваться точности обработки.

Факторы, влияющие на значения К-фактора

Перед расчетом К-фактора необходимо понять, какие факторы на него влияют. Вот несколько основных факторов:

1. Материал и твердость штамповки листового металла

Чем больше материал и твердость, тем больше давление в процессе гибки, и, следовательно, К-фактор также будет увеличиваться.

2. Толщина листового металла

Толщина листового металла напрямую влияет на величину К-фактора. K-фактор более толстого листового металла обычно меньше, чем у более тонкого листового металла.

3. Угол изгиба

Чем больше угол изгиба, тем больше К-фактор. Следовательно, угол изгиба следует учитывать при проектировании деталей из листового металла для его влияния на форму.

4. Гибочный инструмент

Различные гибочные инструменты могут по-разному влиять на К-фактор. Правильный выбор инструмента для гибки может уменьшить размер К-фактора.

Как рассчитать К-фактор?

Коэффициент k — ​​это независимая величина, которая описывает, как происходит изгибание листового металла в широком диапазоне ситуаций с геометрическими параметрами и как он разворачивается. Это также независимое значение, используемое для расчета допуска на изгиб (BA) в различных ситуациях, таких как толщина материала, радиус/угол изгиба.

Приведенные ниже рисунки помогут нам лучше понять подробное определение k-фактора.

В толщине деталей из листового металла имеется нейтральный слой или ось. Материал листового металла в нейтральном слое зоны изгиба не растягивается и не сжимается, и это единственное место в зоне изгиба, где он остается недеформированным. На диаграмме он представлен в виде пересечения розовой и синей областей.

В процессе изгиба розовая область сжимается, а синяя растягивается. Если нейтральный слой листового металла остается недеформированным, то длина дуги нейтрального слоя в области изгиба одинакова в его согнутом и сплющенном состояниях.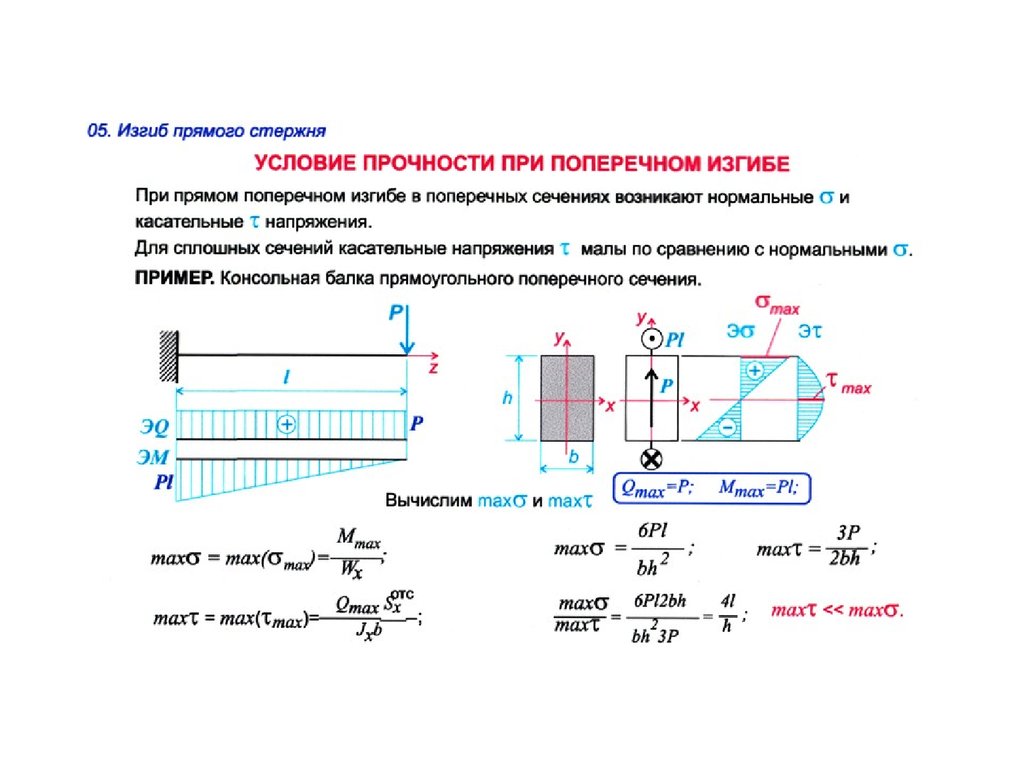

Следовательно, припуск на изгиб (BA) должен быть равен длине дуги нейтрального слоя в области изгиба детали из листового металла. Эта дуга представлена ​​на рисунке зеленым цветом.

Положение нейтрального слоя в листовом металле зависит от конкретных свойств материала, таких как пластичность.

Предположим, что расстояние между нейтральным слоем листового металла и поверхностью равно «t», то есть глубина от поверхности детали из листового металла до материала листового металла в направлении толщины равна t.

Таким образом, радиус дуги нейтрального слоя листового металла может быть выражен как (R+t).

Используя это выражение и угол изгиба, длину дуги нейтрального слоя (BA) можно выразить следующим образом:

BA = Pi*(R+T)*A/180

Для упрощения определения нейтрального слоя в листовом металле и с учетом применимости ко всем толщинам материала вводится понятие k-фактора. В частности, коэффициент k представляет собой отношение толщины положения нейтрального слоя к общей толщине детали из листового металла, то есть:

K = t/T

Следовательно, значение K всегда находится в диапазоне от 0 до 1. Если k-фактор равен 0,25, это означает, что нейтральный слой расположен на 25% толщины листового материала, и если он равен 0,5, то это означает, что нейтральный слой расположен в середине всей толщины и так далее.

Объединив два приведенных выше уравнения, мы можем получить следующее уравнение (8):

BA = Pi*(R+K*T)*A/180 (8)

Где некоторые значения, такие как A, R и T определяются реальной геометрической формой.

Формула расчета К-фактора

В соответствии с приведенным выше расчетом мы можем легко получить формулу для расчета К-фактора:

K=(BA*180/(Pi*A)-R)/T

• BA=припуск на изгиб
• R=внутренний радиус изгиба
• K=коэффициент k, который равен t/T
• T=толщина материала
• t=расстояние от внутренней поверхности до нейтральной оси
• A=угол изгиба (угол, на который изгибается материал)

Пример расчета:

На основании предоставленной информации:

Толщина листового металла T = 1 мм Угол изгиба A = 90° Радиус изгиба R = 1 мм Коэффициент допуска на изгиб BA = 2,1 мм

Формула для расчета коэффициента К:

K=(BA*180/(Pi*A)-R)/T

Подставляя данные значения в формулу, получаем:

K = (2,1 × 180/(3,14 × 90) – 1)/1

Упрощая это уравнение, получаем:

К ≈ 0,337

Следовательно, коэффициент К для данных параметров примерно равен 0,337.

Калькулятор К-фактора

Мы предлагаем два разных калькулятора для расчета значения К-фактора. Окончательные результаты могут немного отличаться, но они точно будут соответствовать вашим требованиям.

Калькулятор #1

Если известны допуск на изгиб и внутренний радиус изгиба, вы можете использовать следующий калькулятор для расчета коэффициента k, а также расстояния от внутренней поверхности до нейтральной оси.

Калькулятор #2

Если известны только внутренний радиус изгиба и толщина материала, можно использовать следующий калькулятор для расчета k-фактора.

Таблица коэффициентов К

Ниже приведены коэффициенты К для обычных металлических материалов.

• Мягкая медь или мягкая латунь: K=0,35
• Полужесткая медь или латунь, мягкая сталь, алюминий и т. д.: K=0,41
• Бронза, твердая бронза, холоднокатаная сталь, пружинная сталь и т. д.: K= 0,45

Таблица К-фактора

90 805 0,8 9080 5 1,5

Толщина (SPCC/SECC)	К-фактор (все углы, включая угол R)
0,615
1	0,45
1,2	0,35
0,348
2	0,455
3	0,349
4	0,296

Таблица уменьшения изгиба

90 114

Толщина (SPCC/SECC)	Вычет изгиба (только для 90 углов)
0,8	1
1	1,5
1,2	2
1. 5	2.5
2	3
3	5
4	7
5	10

В следующей таблице показаны допуски на изгиб, полученные определенным производителем, только для справки. 90 805 7,0

Толщина материала (T)	SPCC	Al	SUS	Медь
0,8	1,4	1,4	1,5	–
1,0	1,7	1,65	1,8	–
1,2	1,9	1,8	2,0	–
1,5 9013 4	2,5	2,4	2,6	–
2,0	3,5	3,2	3,6	37 (R3)
2,5	4,3	3,9	4,4	–
3,0	5,1	4,7	5,4	5 . 0 ( R3)
3,5	6,0	5,4	6,0
4,0	6,2	7,2	6,9 (R3)

Примечание: Допуск на изгиб для меди представляет собой коэффициент, когда внутренний угол изгиба равен R3. Если для гибки используется острый пуансон, величина припуска на изгиб должна соответствовать таковой для алюминиевого сплава или определяться пробным изгибом.

Закон изменения К-фактора и нейтрального слоя

1. Даже для одного и того же материала К-фактор при фактической обработке не является постоянным, и на его конкретное значение влияет технология обработки.

На стадии упругой деформации при изгибе листового металла нейтральная ось располагается посередине толщины листа.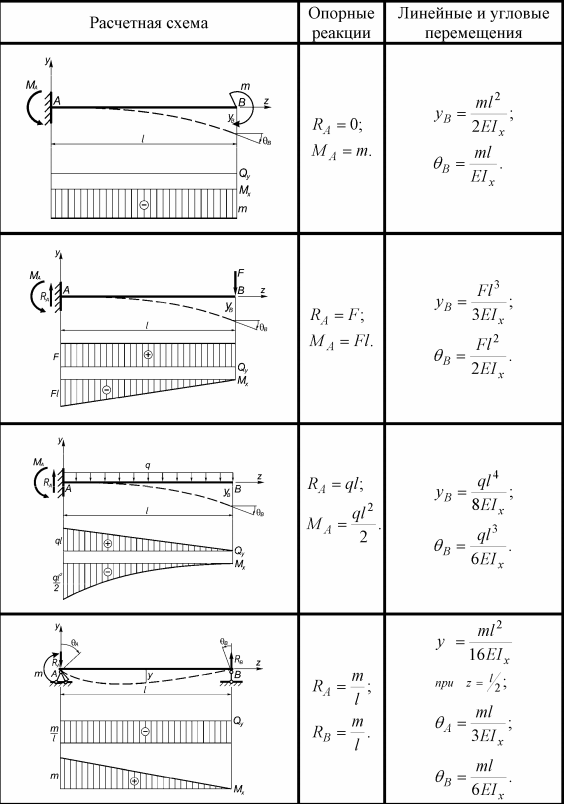

Однако по мере увеличения деформации изгиба штампованной заготовки материал подвергается преимущественно пластической деформации.

В это время пластическая деформация необратима, и нейтральный слой сместится на внутреннюю сторону изгиба при изменении состояния деформации.

Чем сильнее пластическая деформация материала, тем больше смещение нейтрального слоя внутрь изгиба.

Так как же отразить интенсивность пластической деформации при изгибе листа?

Мы можем использовать параметр R/T, чтобы отразить интенсивность деформации пластины. R представляет собой внутренний радиус изгиба, а T обозначает толщину пластины.

Меньшее отношение R/T указывает на более высокий уровень деформации пластины и большее смещение нейтрального слоя внутрь.

Данные в таблице ниже относятся к пластинам с прямоугольным поперечным сечением при определенных условиях обработки.

Как показано в таблице, коэффициент положения нейтрального слоя K увеличивается с увеличением R/T.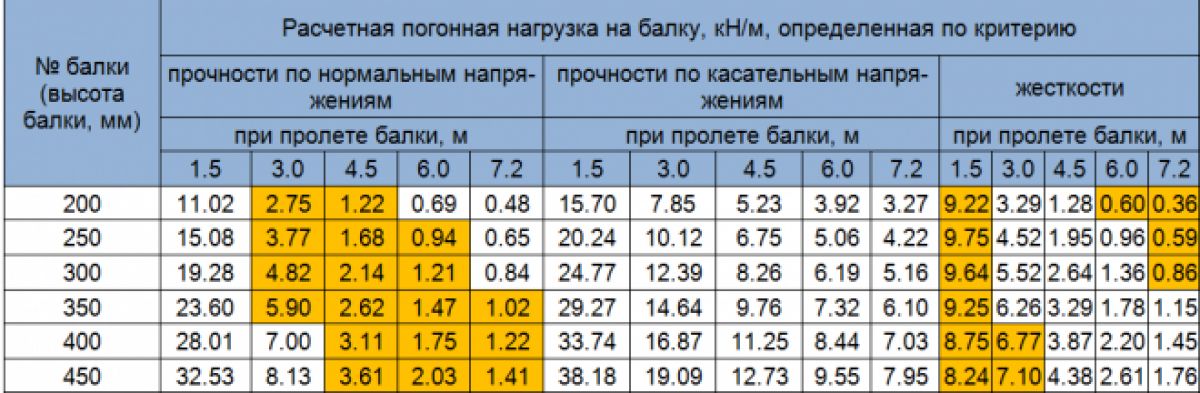

Свойства материала и методы гибки могут повлиять на положение нейтрального слоя.

90 127

Р/Т	К
0,1	0,21
0,2	0,22
0,3	0,23
0,4	0,24
0,5	0,25
0,6	0,26
0,7	0,27
0,8	0,3
1	0,31
1,2	0,33
1,5	0,36
2	0,37
2,5	0,4
3	0,42
5	0,46
75 9013 4	0,5

В это время радиус нейтрального слоя можно рассчитать по следующей формуле:

ρ = R + KT

Из них:

• ρ – радиус нейтрального слоя
• R – внутренний радиус изгиба
• K – коэффициент положения нейтрального слоя
• T – толщина материала

Проще С точки зрения, как только радиус нейтрального слоя определен, его длина развертывания может быть рассчитана на основе геометрии, а затем может быть рассчитана длина развертывания листа.

2. Вообще говоря, при одинаковых условиях гибки, чем мягче материал листового металла, тем ниже его значение K и тем больше смещение нейтрального слоя внутрь изгиба.

В Руководстве по машинному оборудованию есть три стандартных таблицы гибки, применимые к 90-градусной гибке.

Таблица коэффициента К для различных материалов

Таблица	Материал	Коэффициент К
# 1	Мягкая латунь, медь	0,35
# 2	Жесткий латунь, медь, мягкая сталь, алюминий	0,41
# 3	Твердая латунь, бронза, холоднокатаная сталь, пружинная сталь	0,45

3. Для изгибов с меньшим внутренним радиусом угол изгиба также может влиять на изменение коэффициента К.

Чем больше угол деформации изгиба, тем больше смещение нейтрального слоя к внутренней стороне изгиба.

Часто задаваемые вопросы о К-факторе

Зачем нужна калибровка К-фактора?

В процессе расчета гибки листового металла нам часто требуется калибровать k-фактор. Так зачем нам калибровать К-фактор?

В SolidWorks значение вычета для изгиба под углом, отличным от 90 градусов, вычисляется только путем ввода. Это может быть очень хлопотно.

Чтобы избежать вычисления значения вычета для изгиба под углом, отличным от 90 градусов, вместо этого используется k-фактор.

Однако как точно определить k-фактор для листового металла разной толщины? Это требует калибровки.

Вот анализ калибровки:

1. Первым шагом является определение значения вычета, необходимого для различных толщин листового металла на практике.
2. Второй шаг — калибровка коэффициента k в SolidWorks. При рисовании листового металла установите для внутреннего радиуса значение 0,1 для калибровки, поскольку разные внутренние радиусы имеют развертку с разным k-фактором. Обратите внимание, что для калибровки внутренний радиус должен быть установлен равным 0,1. Некоторые могут спросить, а что если после калибровки внутренний радиус не 0,1? В этом случае просто измените его на 0,1 для развертывания.
3. Третий этап — этап калибровки. В SolidWorks согните лист металла размером 10×10 мм и толщиной 1,5 мм под углом 9 мм.Угол 0 градусов с внутренним радиусом 0,1 и значением вычета 2,5 мм для получения длины развертывания 17,5 мм.
4. Четвертый шаг — изменить значение вычета на k-фактор. Начните с установки приблизительного значения, например, 0,3. Длина в развернутом виде не будет 17,5 мм. Затем попробуйте отрегулировать коэффициент k, пока длина разворачивания не станет 17,5 мм. Таким образом, k-фактор может быть откалиброван до 0,23, что даст длину развертывания 17,5 мм.
5. Повторите этот процесс, чтобы откалибровать различные значения и записать их в таблицу.

Как оптимизировать К-фактор при изготовлении листового металла?

Поняв, как рассчитать k-фактор и факторы, влияющие на него, нам нужно знать, как его оптимизировать. Вот несколько важных методов оптимизации:

Выбор подходящих материалов и твердости

Выбор подходящих материалов и твердости очень важен. Это может снизить давление в процессе гибки, тем самым уменьшая k-фактор.

Расчетная толщина листового металла разумная

При проектировании листового металла необходимо разумно учитывать толщину листового металла. Чем меньше толщина листового металла, тем меньше давление в процессе гибки, тем самым снижается k-фактор.

Контроль угла изгиба

При проектировании листового металла необходимо обратить внимание на контроль угла изгиба. Чем больше угол изгиба, тем больше коэффициент k, который может вызвать деформацию. Правильный выбор угла изгиба может уменьшить размер k-фактора.

Выберите подходящий инструмент для гибки

Выбор инструментов для гибки листового металла также очень важен. Выбор подходящего инструмента для гибки может уменьшить коэффициент k и, таким образом, уменьшить деформацию.

Почему К-фактор не может превышать 0,5?

Чтобы понять, почему К-фактор не может превышать 0,5, сначала нужно узнать, что такое К-фактор.

Чтобы разобраться с К-фактором, нужно понять, что такое нейтральный слой.

Вы понимаете, что при гибке детали из листового металла создается небольшая дуга, похожая на гибку вальцами, но с меньшим радиусом, чем при гибке листового металла.

Независимо от используемого метода невозможно добиться идеально прямого угла при изгибе и всегда будет небольшая дуга.

Если нижний радиус матрицы мал, радиус заготовки мал; если нижний радиус матрицы большой, радиус заготовки большой.

Затем переходим к нейтральному слою.

Как известно, детали из листового металла имеют толщину.

При изгибе его в дугу вы заметите, что размеры длины его внутренней поверхности уменьшаются, а размеры длины его внешней поверхности увеличиваются.

Отсюда берется припуск на изгиб.

Например, если вы согните угловую деталь с внешним диаметром 20 x 20, она всегда будет разворачиваться меньше, чем на 40, независимо от толщины пластины.

Это связано с тем, что после изгиба размеры его наружной поверхности увеличиваются.

Таким образом, если вы зададите размер в развернутом виде равным 40, размер в сложенном виде составит 20 с одной стороны и более 20 с другой.

Однако в большинстве случаев необходимо заранее знать размеры получаемого изгиба (дуги).

Но в большинстве случаев необходимо знать размеры полученного изгиба (дуги) для расчета его размеров в развернутом виде.

Издавна считалось, что какой бы толщины не был лист, как бы ни уменьшались внутренние размеры и как бы не увеличивались внешние размеры, размер среднего слоя листа не изменится.

Средний слой, который остается постоянным, называется нейтральным слоем.

В связи с растущим спросом на точность размеров продукта было обнаружено, что величина уменьшения внутри не обязательно соответствует степени расширения снаружи.

В частности, когда результирующая дуга небольшая (например, изгиб), она становится на 0,3 меньше внутри, но на 1,7 больше снаружи.

Становится очевидным, что слой (нейтральный слой), который остается постоянным по размеру, не обязательно располагается в середине толщины листа, а находится ближе к внутренней части.

Расстояние от внутренней части до нейтрального слоя, деленное на всю толщину листа, называется К-фактором.

Да, вы правы, максимальное расстояние от внутренней части нейтрального слоя до середины толщины пластины.

Таким образом, расстояние от внутренней части до середины, деленное на всю толщину листа, составляет 0,5, что дает К-фактор 0,5, что является максимальным значением, которое может быть достигнуто.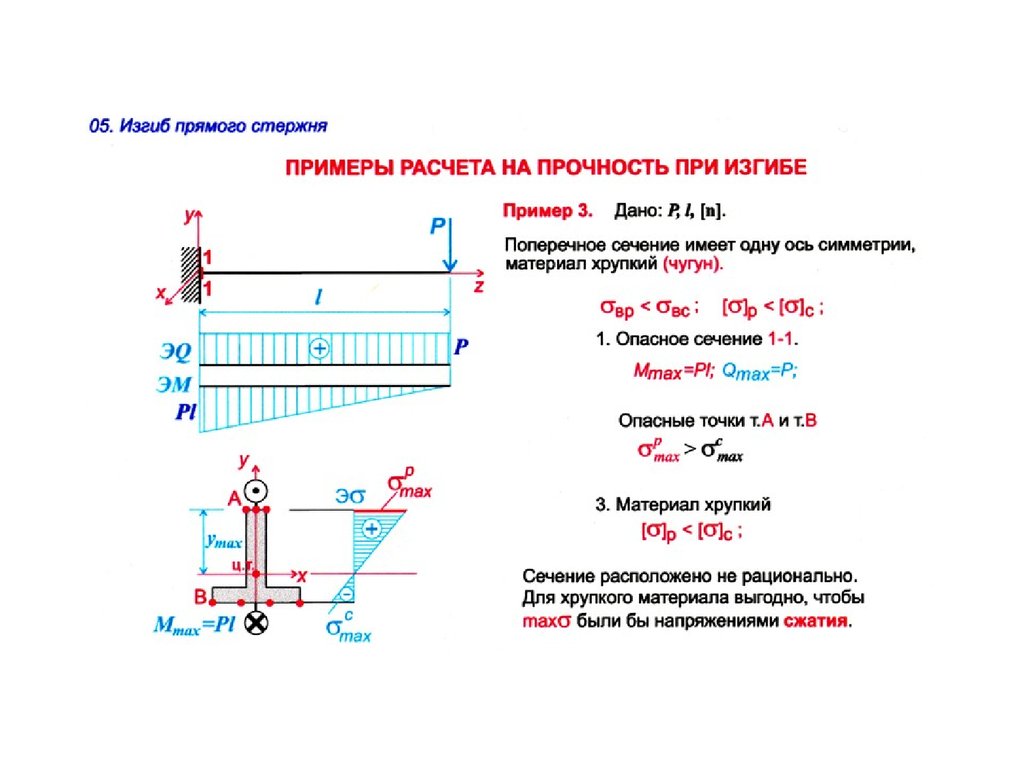

По этим причинам К-фактор для листового металла не должен превышать 0,5. Я надеюсь, что эта статья помогла прояснить ваше понимание.

Где взять К-фактор?

К-фактор можно получить у поставщиков материалов, экспериментальных или эмпирических данных, руководств или калькулятора, приведенного выше, для расчета.

Советы и рекомендации по расчету К-фактора

К-фактор различается для различных материалов и толщины листового металла. Во время фактического производственного процесса внешние факторы, такие как приспособления и сила гибки, используемые для гибки, могут вызвать несоответствие между размерами исходного материала и конечного продукта.

Таким образом, К-фактор необходимо скорректировать в соответствии с фактическими условиями обработки, чтобы получить эмпирическое значение, которое может точно предсказать результаты изготовления листового металла.

Применение калькулятора К-фактора

После многолетнего опыта в производстве листового металла допуски на изгиб для каждого типа листового металла были обобщены и усовершенствованы предшественниками.