Расчет балки
Подробный ход решения — расчет балки, построение эпюр
Заменим распределенную нагрузку равнодействующей
Q1 = 6·2 = 12кН
Составим уравнения равновесия для определения реакций опор
Σ MA = + P · 2 + M + Q1 · 3 — RE · 6= + 12 · 2 + 8 + 12 · 3 — RE · 6=0
Σ ME = — P · 4 + M — Q1 · 3 + RA · 6= — 12 · 4 + 8 — 12 · 3 + RA · 6=0
Из этих уравнений находим реакции опор
RA = 12.67кН.
RE = 11.33кН.
Записываем уравнения поперечных сил и изгибающих моментов на участках балки , используя метод сечений
На участке AB: (0 ≤ z1 ≤ 2 м )
Q(z1) = + RA = + 12.67 = 12.667 кН
M(z1) = + RA · z = + 12.67 · z
M(0) = 0 кНм
M(2) = 25.333 кНм
На участке BC: (2 ≤ z2 ≤ 4 м )
Q(z2) = + RA — P — q1·(z — 2) = + 12.67 — 12 — 6·(z — 2)
Q(2) = 0.667 кН
Q(4) = -11.333 кН
M(z2) = + RA · z — P·(z — 2) — q1·(z — 2)2/2 = + 12.67 · z — 12·(z — 2) — 6·(z — 2)2/2
M(2) = 25.333 кНм
M(4) = 14.667 кНм
Поскольку поперечная сила на участке пересекает ноль при z = 2.11 м, в этой точке будет экстремум на эпюре M
M(2.11) = 25.4 кНм
На участке CD: (4 ≤ z3 ≤ 5 м )
Q(z3) = + RA — P — Q1 = + 12.67 — 12 — 12 = -11.333 кН
M(z3) = + RA · z — P·(z — 2) — Q1·(z — 3) = + 12.67 · z — 12·(z — 2) — 12·(z — 3)
M(4) = 14.667 кНм
M(5) = 3.333 кНм
На участке DE: (5 ≤ z4 ≤ 6 м )
Q(z4) = + RA — P — Q1 = + 12.67 — 12 — 12 = -11.333 кН
M(z4) = + RA · z — P·(z — 2) + M — Q1·(z — 3) = + 12.
M(5) = 11.333 кНм
M(6) = 0 кНм
Максимальный момент в балке составляет Mmax = 25.4 кНм. По этому значению подбираем сечение балки.
Условие прочности при изгибе σ = Mmax / W ≤ [σ]
Отсюда, минимально необходимый момент сопротивления вычисляем по формуле Wmin=Mmax / [σ]
Меню сайтаРасчет геометрических характеристик сечений он-лайн NEW — считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления.
Расчет балок на прочность он-лайн — построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной
сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн. Расчет рам, ферм балок он-лайн NEW — эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы. Лекции — теория, практика, задачи… Примеры решения задач Справочная информация — ГОСТы, сортамент проката, свойства материалов и другое. Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое). Форум сопромата и механики Книги — разная литература по теме. Заказать задачу Друзья сайта (ссылки) WIKIbetta Разработчикам (сотрудничество) Веб-мастерам (партнёрка) О проекте, контакты Подпроекты |
Базовый курс лекций по сопромату, теория, практика, задачи. ::Оглавление:: 3. Изгиб. Определение напряжений. 3.5. Построение эпюр изгибающих моментов и поперечных сил. Рассмотрим пример построения эпюр поперечных сил Q и изгибающих моментов Mx. 1. Изображаем расчетную схему (рис. 3.9, а). 2. Определяем реакции опор. Первоначально выбираем произвольное направление реакций (рис. 3.9, а) Так как реакция RB с минусом, изменяем выбранное направление на противоположное (рис. 3.9, б), а про минус забываем. Проверка: RA — 2qa + RB — qa = qa — 2qa + 2qa — qa = 0. 3. Расчетная схема имеет три силовых участка. I участок АС: 0 1 В сечении возникают внутренние усилия: поперечная сила и изгибающий момент при z1 = 0 M II участок CB: 0 2 На этом участке при z2 = 0 Q = qa, Mx = -qa2; при z2 = 2 Q = -qa, Mx = qa2. На 2-м участке в уравнении моментов аргумент z2 имеет 2-ю степень, значит эпюра будет кривой второго порядка, т.е. параболой.
На этом участке поперечная сила меняет знак (в начале участка +qa, а в конце -qa), значет на эпюре Mx будет экстремум в точке, Q = 0.
Определяем координату сечения, в котором экстремальное значение Mx, приравнивая нулю выражение поперечной силы на этом участке. Определяем величину экстремального момента (с учетом знака): III учаток BD: 0 3 Здесь Q = qa = const; Mx = -qa*z3; при z3 = 0 Mx = 0; при z3 = a Mx = -qa2 .4. Строим эпюры Q и Mx (рис. 5. Проверка построения. ::Оглавление:: ПримерыПример 1. Расчет статически определимой балки, подбор сечения. Полезные ресурсы по теме «Изгиб»1. Он-лайн программа (версия 2004 года), которая выдаст расписанное решение любой балки. Пример результата. 2. Он-лайн программа (версия 2008 года), которая строит 4 вида эпюр и рассчитывает реакции для любых балок (даже для статически неопределимых). |
СообществоВходРешение задачРасчет редукторовДля Android (рекомендую)NEW Mobile Beam 2.0 Java 2 ME |
Сопромат расчет балки на прочность
Произвести полный расчет на прочность и проверить жесткость изгибаемой статически определимой двутавровой балки (рис. 1) при следующих данных: F=40кН, q=30 кН/м, a=0,8 м, l=4м, допустимые нормальные и касательные напряжения: [ σ ]=160 МПа и [ τ ]=100 МПа, допустимый прогиб балки [f]= l/400
Определение опорных реакций
Подробно, пример определения опорных реакций для балки рассмотрен здесь
А также в нашем видеоуроке:
Построение эпюр Q и М
По этим данным построены эпюры Q и М.
Подбор сечения двутавровой балки
Так как Мmах = 45 кНм, то
По сортаменту выбираем двутавр № 24, для которого Wx = 289 см 3 , Ix= 3460 см 4 , Smax = 163 см 3 , h = 24 см, bп = 11,5 см, t = 0,95 см, d = bc = 0,56 см, h = h-2t = 22,1 см.
Этот двутавр будет работать при максимальном нормальном напряжении в крайнем волокне опасного сечения.
Проверка сечения балки по касательным напряжениям
Так как Qmax = 68 кН, то
Построение эпюр нормальных σ и касательных τ напряжений в неблагоприятном сечении балки:
В отношении главных напряжений неблагоприятным является сечение над левой опорой, в котором:
Значение напряжений в различных точках по высоте двутавра сведены в таблицу 1
Проверка прочности балки по главным напряжениям
Наиболее опасной точкой в неблагоприятном сечении является точка 3. В этой точке σ 1=118 МПа и σ 3= -16 МПа. Проверяем прочность в этой точке по третьей гипотезе прочности согласно неравенству σ 1 — σ 3≤ [ σ ].
Так как 118 — ( -16) = 134 θ
откуда θ = -8,48∙10 -3 радиан.
Прогиб в пролете при z=l/2=4/2=2 м.
Аналогично определяется прогиб на конце консоли при z = l + a =4+0,8 = 4,8 м.
Расчет по допускаемым напряжениям на прочность при изгибе.
– при симметричном сечении
Проверка прочности по предельным состояниям.
– максимальный изгибающий момент от расчетных нагрузок.
n – коэффициент перегрузки.
– нормативная нагрузка.
Рр – расчетная нагрузка.
– коэффициент условия работы.
Если материал работает неодинаково на растяжение и сжатие, то прочность проверяется по формулам:
где Rp и Rсж – расчетное сопротивление на растяжение и сжатие
Расчет по несущей способности и учетом пластической деформации.

В предыдущих методах расчета прочность проверяется по максимальны напряжениям в верхних и нижних волокнах балки. При этом средние волокна оказываются недогруженными.
Оказывается, если нагрузку увеличивать дальше, то в крайних волокнах напряжение дойдет до предела текучести σт ( в пластичных материалах), и до предела прочности σnч ( в хрупких материалах). При дальнейшем увеличении нагрузки хрупкие материалы разрушатся, а в пластичных материалах напряжения в крайних волокнах далее не возрастают, а растут во внутренних волокнах. (см. рис.)
Несущая способность балки исчерпывается, когда по всему сечению напряжения достигнут σт.
W пл – пластический момент сопротивления
– статический момент растянутой и сжатой зон относительно нейтральной оси.
где – коэффициент надежности по материалу.
где R – расчетное сопротивление.
Для прямоугольного сечения:
W пл=bh 2 /4 – для прямоугольного сечения.
W =bh 2 /6 – обычный момент сопротивления.
Примечание: для прокатных профилей (швеллер и двутавр) пластический момент Wnл=(1.1÷1,17)×W
Касательные напряжения при изгибе балки прямоугольного сечения. Формула Журавcкого.
Так как момент в сечении 2 больше момента в сечении 1, то напряжение σ2>σ1=>N2>N1.
В этом случае элемент abcd должен переместиться влево. Этому перемещению препятствуют касательные напряжения τ на площадке cd.
– уравнение равновесия, после преобразования которого получается формула для определения τ: – Формула Журавского
где Q – поперечная сила,
Sотс – статический момент отсеченной части относительно нейтральной оси,
J-момент инерции всего сечения относительно нейтральной оси, b – ширина балки на уровне y.
Распределение касательных напряжений в балках прямоугольного, круглого и двутаврового сечений.
1. Прямоугольное сечение:
– формула для сечения на расстоянии у от нейтральной оси.
– формула для сечения на расстоянииу от нейтральной оси.
– формула для сечения под углом α.
3. Двутавровое сечение.
Для стенки двутавра
вычисляют по формуле:
Для полки: условно вертикальные касательные напряжения определяют по формуле:
В полках двутавров возникают касательные напряжения, направленные горизонтально:
На рисунке показан общий характер распределения τ в сечении двутавра.
Главные напряжения при изгибе. Проверка прочности балок.
Выделим из балки участок, на который действует максимально поперечная сила Qmax и изгибающий момент Mmax.
Наиболее опасными точками являются сечение A и точка Б.
Прочность проверяется по напряжениям в этих точках.
На практике обычно ограничиваются проверкой сечения A:
[σсж]
Если же балка короткая, то проверяют точку Б:
где Rсрез – расчетное сопротивление материала на срез.
В точке D на элемент действует нормальные и касательные напряжения, поэтому в некоторых случаях их совместное действие вызывает опасность для прочности. В этом случае элемент D проверяют на прочность используя главные напряжения.
В нашем случае: , следовательно:
Используя σ1 и σ2 по теории прочности проверяют элемент D.
По теории наибольших касательных напряжений имеем: σ 1 – σ2≤R
Примечание: точку D следует брать по длине балки там, где одновременно действуют большие M и Q.
По высоте балки выбираем такое место, где одновременно действуют значения σ и τ.
1. В балках прямоугольного и круглого сечения отсутствуют точки, в которых одновременно действуют большие σ и τ. Поэтому в таких балках проверка точки D не делается.
Поэтому в таких балках проверка точки D не делается.
2. В балках двутаврового сечения на границе пересечения полки со стенкой (т. А) одновременно действуют большие σ и τ. Поэтому они проверяются на прочность в этой точке.
В прокатных двутаврах и швеллерах в зоне пересечения полки со стенкой сделаны плавные переходы (закругления). Стенка и полка подобраны так, что точка A оказывается в благоприятных условиях работы и проверка прочности не требуется.
В составных (сварных) двутавровых балках проверка точки А необходима.
В качестве примера, возьмем металлическую балку на двух опорах. Запишем для нее формулу для вычисления прогиба, посчитаем его численное значение. И также в конце этой статьи дам ссылки на другие полезные статьи с примерами определения прогибов для различных расчетных схем.
Что такое прогиб балки?
Под действием внешней нагрузки, поперечные сечения балки перемещаются вертикально (вверх или вниз), эти перемещения называются прогибами. Сопромат позволяет нам определить прогиб балки, зная ее геометрические параметры: длину, размеры поперечного сечения. И также нужно знать материал, из которого изготовлена балка (модуль упругости).
Кстати! Помимо вертикальных перемещений, поперечные сечения балки, поворачиваются на определенный угол. И эти величины также можно определить методом начальных параметров.
ν-прогиб сечения C; θ-угол поворота сечения C.
Прогибы балки необходимо рассчитывать, при расчете на жесткость. Расчётные значения прогибов не должны превышать допустимых значений. Если расчетное значение меньше, чем допустимое, то считают, что условие жесткости элемента конструкции соблюдается. Если же нет, то принимаются меры по повышению жесткости. Например, задаются другим материалом, у которого модуль упругости БОЛЬШЕ. Либо же меняют геометрические параметры балки, чаще всего, поперечное сечение. Например, если балка двутаврового профиля №12, не подходит по жесткости, принимают двутавр №14 и делают перерасчет. Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.
Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.
Метод начальных параметров
Метод начальных параметров, является довольно универсальным и простым методом. Используя этот метод можно записывать формулу для вычисления прогиба и угла поворота любого сечения балки постоянной жесткости (с одинаковым поперечным сечением по длине.)
Под начальными параметрами понимаются уже известные перемещения:
- в опорах прогибы равны нулю;
- в жесткой заделке прогиб и угол поворота сечения равен нулю.
Расчет прогибов балки
Посмотрим, как пользоваться методом начальных параметров на примере простой балки, которая загружена всевозможными типами нагрузок, чтобы максимально охватить все тонкости этого метода:
Реакции опор
Для расчета нужно знать все внешние нагрузки, действующие на балку, в том числе и реакции, возникающие в опорах.
Система координат
Далее вводим систему координат, с началом в левой части балки (точка А):
Распределенная нагрузка
Метод начальных параметров, который будем использовать чуть позднее, работает только в том случае, когда распределенная нагрузка доходит до крайнего правого сечения, наиболее удаленного от начала системы координат. Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.
Если бы нагрузка была приложена вот таким способом:
То можно было бы сразу приступать к расчету перемещений. Нам же потребуется использовать один хитрый прием – ввести дополнительные нагрузки, одна из которых будет продолжать действующую нагрузку q, другая будет компенсировать это искусственное продолжение. Таким образом, получим эквивалентную расчетную схему, которую уже можно использовать в расчете методом начальных параметров:
Вот, собственно, и все подготовительные этапы, которые нужно сделать перед расчетом.
Приступим непосредственно к самому расчету прогиба балки. < 3 >>< 6 >]
< 3 >>< 6 >]
- Начало и конец распределенных нагрузок нужно умножать на дробь:
Формулы прогибов
С учетом всех вышеописанных правил запишем окончательное уравнение для сечения C:
В этом уравнении содержится 2 неизвестные величины – искомый прогиб сечения C и угол поворота сечения A.
Поэтому, чтобы найти прогиб, составим второе уравнение для сечения B, из которого можно определить угол поворота сечения A. Заодно закрепим пройденный материал:
Выражаем угол поворота:
Подставляем это значение в наше первое уравнение и находим искомое перемещение:
Вычисление прогиба
Значение получили в общем виде, так как изначально не задавались тем, какое поперечное сечение имеет рассчитываемая балка. Представим, что металлическая балка имеет двутавровое поперечное сечение №30. Тогда:
Таким образом, такая балка прогнется максимально на 2 см. Знак «минус» указывает на то, что сечение переместится вниз.
Расчет балки прокатного профиля и выбор ее номера по сортаменту.
Примеры решения задач по сопротивлению материалов
На этой странице приведен пример решения задачи по Сопромату, в которой необходимо произвести расчет горизонтальной балки, нагруженной поперечными силовыми факторами. По результатам расчетов внутренних силовых факторов осуществлен подбор размеров сечения балки из расчета на прочность.
Результаты расчетов балки оформлены эпюрами изгибающих моментов и поперечных сил.
Здесь можно скачать готовые варианты контрольных работ по сопромату (прикладной механике) для учащихся Алтайского Государственного технического университета.
Варианты контрольных работ можно скачать в формате Word для ознакомления с порядком решения заданий, или для распечатывания и защиты (при совпадении вариантов).
Расчет двутавровой балки
Условие задачи:
На горизонтально расположенную балку, закрепленную на двух шарнирных опорах, действуют активные нагрузки: изгибающий момент М, сосредоточенная сила F и распределенная нагрузка q (см. рис. 3).
рис. 3).
Материал стержня – сталь Ст.3.
Требуется:
Построить эпюры поперечных сил QY и изгибающих моментов МX и подобрать сечение балки из расчета на прочность.
Исходные данные:
Нагрузки:
- М = 6 кН×м;
- F = -7 кН;
- q = -8 кН/м;
- a = 2 м;
- Сечение балки: двутавр.
Координаты приложения нагрузок:
- ZM = 3а — координата приложения изгибающего момента;
- ZF = а — координата приложения сосредоточенной силы;
- начало распределенной нагрузки: Zq = 2а;
- конец распределенной нагрузки: Zq = 3а;
- ZB = 3а — координата опоры В.
Указания:
Шарнирно-неподвижную опору А располагать на левом конце балки, этот же конец балки принимаем за начало координат.
Шарнирно-неподвижную опору В и внешние нагрузки располагать на соответствующих участках, в соответствии с которыми разбиваем балку на силовые участки.
Силовым участком считать ту часть балки, в пределах которой законы измерения QY и MX остаются постоянными.
Решение:
1. Из условия равновесия балки определим неизвестные опорные реакции RА и RВ (см. рис. 3). Для этого составляем уравнения равновесия для изгибающих моментов сначала относительно опоры А, затем относительно опоры В.
При этом изгибающие моменты, направленные по часовой стрелке относительно опоры считаем отрицательными, против часовой стрелки – положительными.
∑МА = М — q×a×2,5а — F×а + RВ×3а = 0,
откуда находим реакцию RВ:
RВ = (qa×2,5а + F×а – М)/3а = (8×2×2,5×2 + 7×2 – 6)/3×2 =14,67 кН.
∑МВ = М + q×a×0,5а + F×2а – RА×3а = 0,
откуда находим реакцию RА:
RА = (М + qa×0,5а + F×2а)/3а = (6 + 8×2×0,5×2 + 7×2×2)/3×2 = 8,33 кН.
Произведем проверку правильности найденных значений опорных реакций, используя уравнение равновесия действующих на балку сил с учетом их направления:
∑FY = RА – F – q×a + RВ = 8,33 – 7 – 8×2 + 14,67 = 0.
Опорные реакции найдены правильно.
2. Составим уравнения внутренних усилий QY и MX для каждого силового участка балки.
2.1. Участок I: 0 ≤ Z1 ≤ 2 м.
- QY1 = RA ;
- MX1 = — RA×ZY.
На протяжении всего участка I внутренняя сила равна RA = 8,33 кН.
Изгибающий момент на этом силовом участке изменяется линейно, поэтому для построения эпюры достаточно рассчитать его значение в двух крайних сечениях участка:
- МX1=0 = 0;
- МX1=2 = -8,33×2 = -16,66 кН×м.
2.2. Участок II: 2 м ≤ Z2 ≤ 4 м.
- QY2 = RА – F = 8,33 – 7 = 1,33 кН;
- MX2 = — RА×(2м + Z2) + F×Z2.
Изгибающий момент на этом силовом участке тоже изменяется линейно:
- МX2=2 = -16,66 кН×м;
- МX2=4 = -8,33×(2+2) + 7×2 = -19,32 кН×м.
2.3. Участок III: 4 м ≤ Z3 < 6 м (кроме крайней точки В, где приложен момент М).
QY3 = RА – F — q×Z3;
MX3 = — RА×(4м + Z3) + F×(2м + Z3) + q×Z3×Z3/2).
В крайней точке В (Z3 = 2 м) алгебраическая сумма всех изгибающих моментов должна быть равна нулю:
MX3=6м = — RА×(4 м + Z3=2м) + F×(2м + Z3=2м) + q×Z3=2м × Z3=2м /2) + М =
= -8,33×6 +7×4 + 8×2×1 + 6 = 0.
Сила QY3 на силовом участке III изменяется линейно, поэтому для построения эпюры находим ее значение в крайних сечениях участка:
- QY Z3=0 = RА – F — q×Z3=0 = 8,33 — 7 = 1,33 кН;
- QY Z3=2 = RА + q×Z3=2 = 8,33 — 7 — 8×2 = -14,67 кН,
т. е. сила в крайней точке равна реакции опоры B, но направлена в противоположную сторону, что свидетельствует о правильности произведенных расчетов. Поскольку сила на силовом участке III поменяла знак, то изгибающий момент МX при QY = 0 имеет экстремальное значение. Найдем координату экстремальной точки Z3экст и величину экстремального изгибающего момента MXэкст.
QY = RА – F — q× Z3экст = 0 , откуда: Z3экст = (RА – F) / q = (8,33 – 7)/8 = 0,166 м.
Подставив полученное значение в уравнение изгибающего момента, получим:
MXэкст = — RА×(4м + Z3экст) + F×(2м + Z3экст) + q×Z3экст×Z3экст/2) =
= -8,33×4,166+7×2,166 + 8×0,1662/2 = -19,43 кН×м.
Изгибающий момент на силовом участке III изменяется по квадратичной зависимости, поэтому его эпюра имеет криволинейный вид. Для того, чтобы построить эпюру изгибающих моментов на этом участке необходимо вычислить значение моментов в нескольких промежуточных точках.
- MX3=0 = -8,33×4 +7×2 = -19,32 кН×м;
- MXэкст = -19,43 кН×м;
- MX3=0,5м = -8,33×4,5 +7×2,5 + 8×0,52/2 = -18,985 кН×м;
- MX3=1м = -8,33×5 +7×3 + 8×12/2 = -16,65 кН×м;
- MX3=1,5м = -8,33×5,5 +7×3,5 + 8×1,52/2 = 15,255 кН×м;
- MX3=2м = -6,0 кН×м.
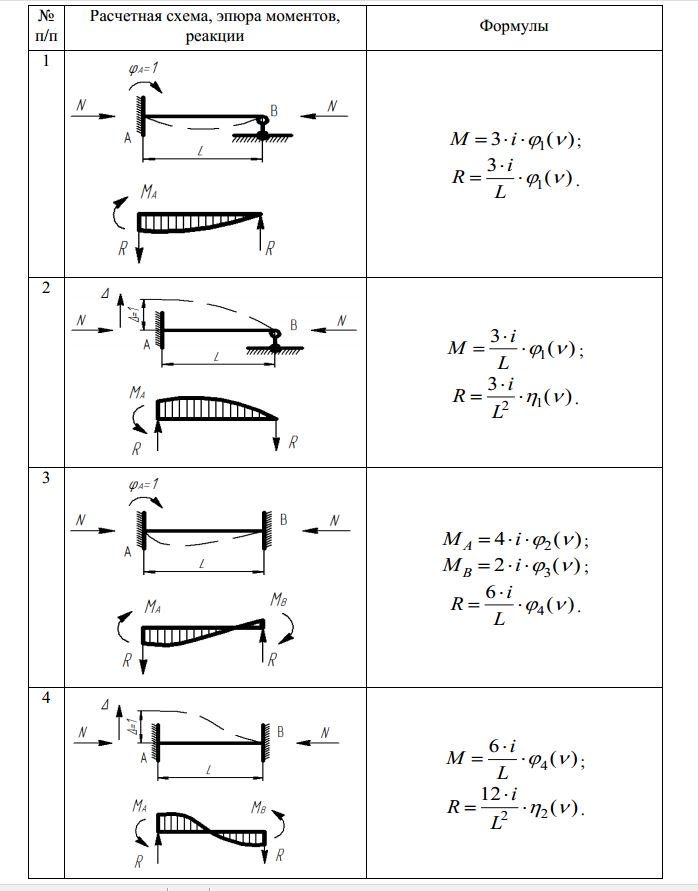
3. По результатам расчетов строим эпюры поперечных сил и изгибающих моментов (рис. 4 внизу страницы).
4. По эпюре МX определяем опасное сечение балки, где изгибающий момент имеет максимальное значение (по абсолютной величине):
MXmax = 19,43 кН×м.
Размер сечения (по условию варианта задания — № двутавра) вычисляем из условия прочности при изгибе по осевому моменту сопротивления сечения:
WX = MXmax/[σ] = 19,43×103/160×106 = 0,000121 м3 = 121 см3.
По таблице сортаментов выбираем двутавр №18, у которого момент сопротивления WX = 143 см3 (ближайший по сортаменту двутавр №16 имеет момент сопротивления сечения равный 109 см3, что недостаточно для выполнения условия прочности).
***
Расчет статически неопределимой балки
Сопротивление материалов
Главная страница
Дистанционное образование
Специальности
Учебные дисциплины
Олимпиады и тесты
Расчет металлической балки на прогиб: учимся составлять формулы
Приветствую тебя, читатель экспресс-курса — «сопромат для чайников» на сайте – SoproMats.ru. Меня зовут Константин Вавилов, я являюсь автором статей по сопромату и других материалов данного ресурса. В этой статье, будем рассматривать универсальную методику расчета прогибов балки — метод начальных параметров. Как и любая другая статья для чайников, на нашем проекте, этот материал будет изложен максимально просто, лаконично и без лишних заумных терминов.В качестве примера, возьмем металлическую балку на двух опорах. Запишем для нее формулу для вычисления прогиба, посчитаем его численное значение. И также в конце этой статьи дам ссылки на другие полезные статьи с примерами определения прогибов для различных расчетных схем.
Что такое прогиб балки?
Под действием внешней нагрузки, поперечные сечения балки перемещаются вертикально (вверх или вниз), эти перемещения называются прогибами. Сопромат позволяет нам определить прогиб балки, зная ее геометрические параметры: длину, размеры поперечного сечения. И также нужно знать материал, из которого изготовлена балка (модуль упругости).
Кстати! Помимо вертикальных перемещений, поперечные сечения балки, поворачиваются на определенный угол. И эти величины также можно определить методом начальных параметров.
ν-прогиб сечения C; θ-угол поворота сечения C.
Прогибы балки необходимо рассчитывать, при расчете на жесткость. Расчётные значения прогибов не должны превышать допустимых значений. Если расчетное значение меньше, чем допустимое, то считают, что условие жесткости элемента конструкции соблюдается. Если же нет, то принимаются меры по повышению жесткости. Например, задаются другим материалом, у которого модуль упругости БОЛЬШЕ. Либо же меняют геометрические параметры балки, чаще всего, поперечное сечение. Например, если балка двутаврового профиля №12, не подходит по жесткости, принимают двутавр №14 и делают перерасчет. Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.
Метод начальных параметров
Метод начальных параметров, является довольно универсальным и простым методом. Используя этот метод можно записывать формулу для вычисления прогиба и угла поворота любого сечения балки постоянной жесткости (с одинаковым поперечным сечением по длине.)
Под начальными параметрами понимаются уже известные перемещения:
- в опорах прогибы равны нулю;
- в жесткой заделке прогиб и угол поворота сечения равен нулю.
Расчет прогибов балки
Посмотрим, как пользоваться методом начальных параметров на примере простой балки, которая загружена всевозможными типами нагрузок, чтобы максимально охватить все тонкости этого метода:
Реакции опор
Для расчета нужно знать все внешние нагрузки, действующие на балку, в том числе и реакции, возникающие в опорах.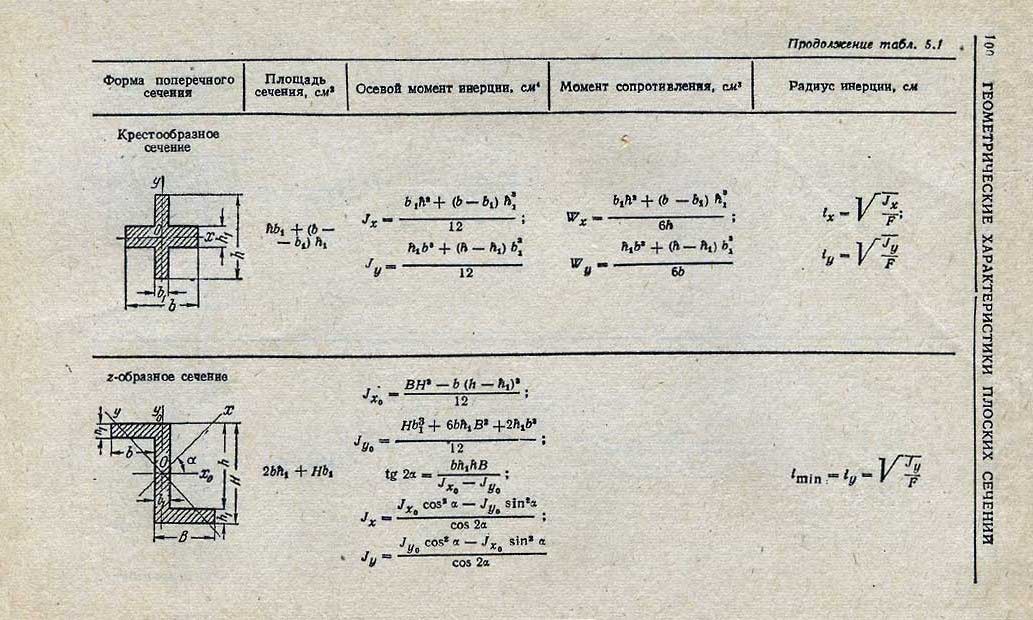
Система координат
Далее вводим систему координат, с началом в левой части балки (точка А):
Распределенная нагрузка
Метод начальных параметров, который будем использовать чуть позднее, работает только в том случае, когда распределенная нагрузка доходит до крайнего правого сечения, наиболее удаленного от начала системы координат. Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.
Если бы нагрузка была приложена вот таким способом:
То можно было бы сразу приступать к расчету перемещений. Нам же потребуется использовать один хитрый прием – ввести дополнительные нагрузки, одна из которых будет продолжать действующую нагрузку q, другая будет компенсировать это искусственное продолжение. Таким образом, получим эквивалентную расчетную схему, которую уже можно использовать в расчете методом начальных параметров:
Вот, собственно, и все подготовительные этапы, которые нужно сделать перед расчетом.
Приступим непосредственно к самому расчету прогиба балки. Рассмотрим наиболее интересное сечение в середине пролета, очевидно, что это сечение прогнется больше всех и при расчете на жесткость такой балки, рассчитывалось бы именно это сечение. Обзовем его буквой – C:
Относительно системы координат записываем граничные условия. Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:
\[ { V }_{ A }=0\quad при\quad x=0 \]
\[ { V }_{ B }=0\quad при\quad x=8м \]
Записываем уравнение метода начальных параметров для сечения C:
\[ E{ I }_{ z }{ V }_{ C }=… \]
Произведение жесткости балки EI и прогиба сечения C будет складываться из произведения EI и прогиба сечения в начале системы координат, то есть сечения A:
\[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+ … \]
Напомню, E – это модуль упругости первого рода, зависящий от материала из которого изготовлена балка, I – это момент инерции, который зависит от формы и размеров поперечного сечения балки. { 4 } } =-2см \]
{ 4 } } =-2см \]
На этом, пожалуй, закончу данный урок. Если у вас возникли какие-либо вопросы по представленным материалам, задавайте вопросы в комментариях к этой статье. А также рекомендую вам посмотреть другие примеры определение прогибов этим методом. Там вы найдете более сложные задачи, определение углов поворотов, примеры расчета консольных балок (с жесткой заделкой).Таким образом, такая балка прогнется максимально на 2 см. Знак «минус» указывает на то, что сечение переместится вниз.
Прямой поперечный изгиб (задачи по сопромату)
Пример решения задачи «прямой поперечный изгиб» №1
Условие примера задачи на прямой поперечный изгиб
Для консольной балки, нагруженной распределенной нагрузкой интенсивностью кН/м и сосредоточенным моментом кН·м (рис. 3.12), требуется: построить эпюры перерезывающих сил и изгибающих моментов , подобрать балку круглого поперечного сечения при допускаемом нормальном напряжении кН/см2 и проверить прочность балки по касательным напряжениям при допускаемом касательном напряжении кН/см2. Размеры балки м; м; м.
Расчетная схема для задачи на прямой поперечный изгиб
Рис. 3.12
Решение задачи «прямой поперечный изгиб»
Определяем опорные реакции
Горизонтальная реакция в заделке равна нулю, поскольку внешние нагрузки в направлении оси z на балку не действуют.
Выбираем направления остальных реактивных усилий, возникающих в заделке: вертикальную реакцию направим, например, вниз, а момент – по ходу часовой стрелки. Их значения определяем из уравнений статики:
.
Составляя эти уравнения, считаем момент положительным при вращении против хода часовой стрелки, а проекцию силы положительной, если ее направление совпадает с положительным направлением оси y.
Из первого уравнения находим момент в заделке :
кН·м.
Из второго уравнения – вертикальную реакцию :
кН.
Полученные нами положительные значения для момента и вертикальной реакции в заделке свидетельствуют о том, что мы угадали их направления.
Строим эпюры перерезывающих сил и изгибающих моментов
В соответствии с характером закрепления и нагружения балки, разбиваем ее длину на два участка. По границам каждого из этих участков наметим четыре поперечных сечения (см. рис. 3.12), в которых мы и будем методом сечений (РОЗУ) вычислять значения перерезывающих сил и изгибающих моментов.
Сечение 1. Отбросим мысленно правую часть балки. Заменим ее действие на оставшуюся левую часть перерезывающей силой и изгибающим моментом . Для удобства вычисления их значений закроем отброшенную нами правую часть балки листком бумаги, совмещая левый край листка с рассматриваемым сечением.
Напомним, что перерезывающая сила, возникающая в любом поперечном сечении, должна уравновесить все внешние силы (активные и реактивные), которые действуют на рассматриваемую (то есть видимую) нами часть балки. Поэтому перерезывающая сила должна быть равна алгебраической сумме всех сил, которые мы видим.
Приведем и правило знаков для перерезывающей силы: внешняя сила, действующая на рассматриваемую часть балки и стремящаяся «повернуть» эту часть относительно сечения по ходу часовой стрелки, вызывает в сечении положительную перерезывающую силу. Такая внешняя сила входит в алгебраическую сумму для определения со знаком «плюс».
В нашем случае мы видим только реакцию опоры , которая вращает видимую нами часть балки относительно первого сечения (относительно края листка бумаги) против хода часовой стрелки. Поэтому
кН.
Изгибающий момент в любом сечении должен уравновесить момент, создаваемый видимыми нами внешними усилиями, относительно рассматриваемого сечения. Следовательно, он равен алгебраической сумме моментов всех усилий, которые действуют на рассматриваемую нами часть балки, относительно рассматриваемого сечения (иными словами, относительно края листка бумаги). При этом внешняя нагрузка, изгибающая рассматриваемую часть балки выпуклостью вниз, вызывает в сечении положительный изгибающий момент. И момент, создаваемый такой нагрузкой, входит в алгебраическую сумму для определения со знаком «плюс».
И момент, создаваемый такой нагрузкой, входит в алгебраическую сумму для определения со знаком «плюс».
Мы видим два усилия: реакцию и момент в заделке . Однако у силы плечо относительно сечения 1 равно нулю. Поэтому
кН·м.
Знак «плюс» нами взят потому, что реактивный момент изгибает видимую нами часть балки выпуклостью вниз.
Напомним, что при определении знака изгибающего момента мы мысленно освобождаем видимую нами часть балки от всех фактических опорных закреплений и представляем ее как бы защемленной в рассматриваемом сечении (то есть левый край листка бумаги нами мысленно представляется жесткой заделкой).
Сечение 2. По-прежнему будем закрывать листком бумаги всю правую часть балки. Теперь, в отличие от первого сечения, у силы появилось плечо: м. Поэтому
кН; кН·м.
Сечение 3. Закрывая правую часть балки, найдем
кН;
кН·м.
Сечение 4. Закроем листком левую часть балки. Тогда
кН;
кН·м.
Сечение 5. По-прежнему закроем левую часть балки. Будем иметь
кН;
кН·м.
Сечение 6. Опять закроем левую часть балки. Получим
.
По найденным значениям строим эпюры перерезывающих сил (рис. 3.12, б) и изгибающих моментов (рис. 3.12, в).
Под незагруженными участками эпюра перерезывающих сил идет параллельно оси балки, а под распределенной нагрузкой q – по наклонной прямой вверх. Под опорной реакцией на эпюре имеется скачок вниз на величину этой реакции, то есть на 40 кН.
На эпюре изгибающих моментов мы видим излом под опорной реакцией . Угол излома направлен навстречу реакции опоры. Под распределенной нагрузкой q эпюра изменяется по квадратичной параболе, выпуклость которой направлена навстречу нагрузке. В сечении 6 на эпюре – экстремум, поскольку эпюра перерезывающей силы в этом месте проходит здесь через нулевое значение.
Определяем требуемый диаметр поперечного сечения балки
Условие прочности по нормальным напряжениям имеет вид:
,
где – момент сопротивления балки при изгибе. Для балки круглого поперечного сечения он равен:
Для балки круглого поперечного сечения он равен:
.
Наибольший по абсолютному значению изгибающий момент возникает в третьем сечении балки: кН·см.
Тогда требуемый диаметр балки определяется по формуле
см.
Принимаем мм. Тогда
кН/см2 кН/см2.
«Перенапряжение» составляет
,
что допускается.
Проверяем прочность балки по наибольшим касательным напряжениям
Наибольшие касательные напряжения, возникающие в поперечном сечении балки круглого сечения, вычисляются по формуле
,
где – площадь поперечного сечения.
Согласно эпюре , наибольшее по алгебраической величине значение перерезывающей силы равно кН. Тогда
кН/см2 кН/см2,
то есть условие прочности и по касательным напряжениям выполняется, причем, с большим запасом.
Пример решения задачи «прямой поперечный изгиб» №2
Условие примера задачи на прямой поперечный изгиб
Для шарнирно опертой балки, нагруженной распределенной нагрузкой интенсивностью кН/м, сосредоточенной силой кН и сосредоточенным моментом кН·м (рис. 3.13), требуется построить эпюры перерезывающих сил и изгибающих моментов и подобрать балку двутаврового поперечного сечения при допускаемом нормальном напряжении кН/см2 и допускаемом касательном напряжении кН/см2. Пролет балки м.
Пример задачи на прямой изгиб – расчетная схема
Решение примера задачи на прямой изгиб
Определяем опорные реакции
Для заданной шарнирно опертой балки необходимо найти три опорные реакции: , и . Поскольку на балку действуют только вертикальные нагрузки, перпендикулярные к ее оси, горизонтальная реакция неподвижной шарнирной опоры A равна нулю: .
Направления вертикальных реакций и выбираем произвольно. Направим, например, обе вертикальные реакции вверх. Для вычисления их значений составим два уравнения статики:
; .
Напомним, что равнодействующая погонной нагрузки , равномерно распределенной на участке длиной l, равна , то есть равна площади эпюры этой нагрузки и приложена она в центре тяжести этой эпюры, то есть посредине длины.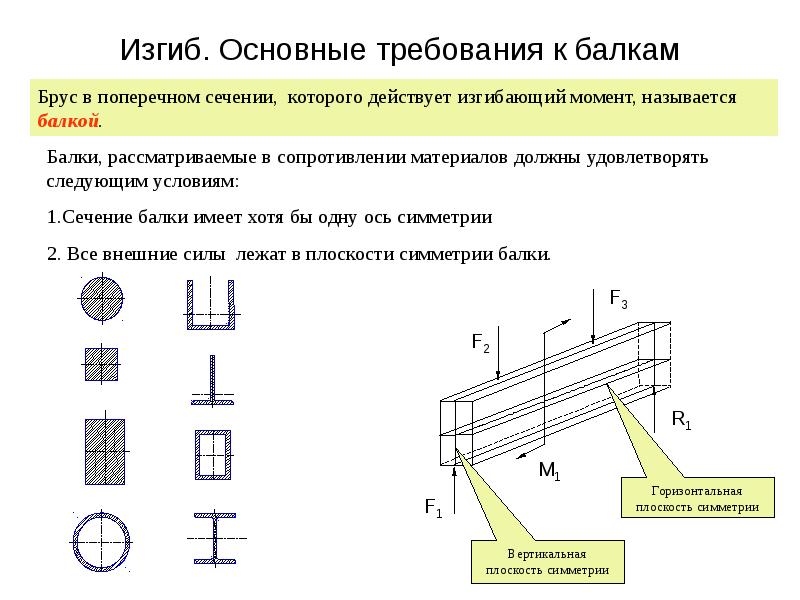
Тогда
кН;
;
кН.
Делаем проверку: .
Напомним, что силы, направление которых совпадает с положительным направлением оси y, проектируются (проецируются) на эту ось со знаком плюс:
,
то есть верно.
Строим эпюры перерезывающих сил и изгибающих моментов
Разбиваем длину балки на отдельные участки. Границами этих участков являются точки приложения сосредоточенных усилий (активных и/или реактивных), а также точки, соответствующие началу и окончанию действия распределенной нагрузки. Таких участков в нашей задаче получается три. По границам этих участков наметим шесть поперечных сечений, в которых мы и будем вычислять значения перерезывающих сил и изгибающих моментов (рис. 3.13, а).
Сечение 1. Отбросим мысленно правую часть балки. Для удобства вычисления перерезывающей силы и изгибающего момента , возникающих в этом сечении, закроем отброшенную нами часть балки листком бумаги, совмещая левый край листка бумаги с самим сечением.
Перерезывающая сила в сечении балки равна алгебраической сумме всех внешних сил (активных и реактивных), которые мы видим. В данном случае мы видим реакцию опоры и погонную нагрузку q, распределенную на бесконечно малой длине. Равнодействующая погонной нагрузки равна нулю. Поэтому
кН.
Знак «плюс» взят потому, что сила вращает видимую нами часть балки относительно первого сечения (края листка бумаги) по ходу часовой стрелки.
Изгибающий момент в сечении балки равен алгебраической сумме моментов всех усилий, которые мы видим, относительно рассматриваемого сечения (то есть относительно края листка бумаги). Мы видим реакцию опоры и погонную нагрузку q, распределенную на бесконечно малой длине. Однако у силы плечо равно нулю. Равнодействующая погонной нагрузки также равна нулю. Поэтому
.
Сечение 2. По-прежнему будем закрывать листком бумаги всю правую часть балки. Теперь мы видим реакцию и нагрузку q, действующую на участке длиной .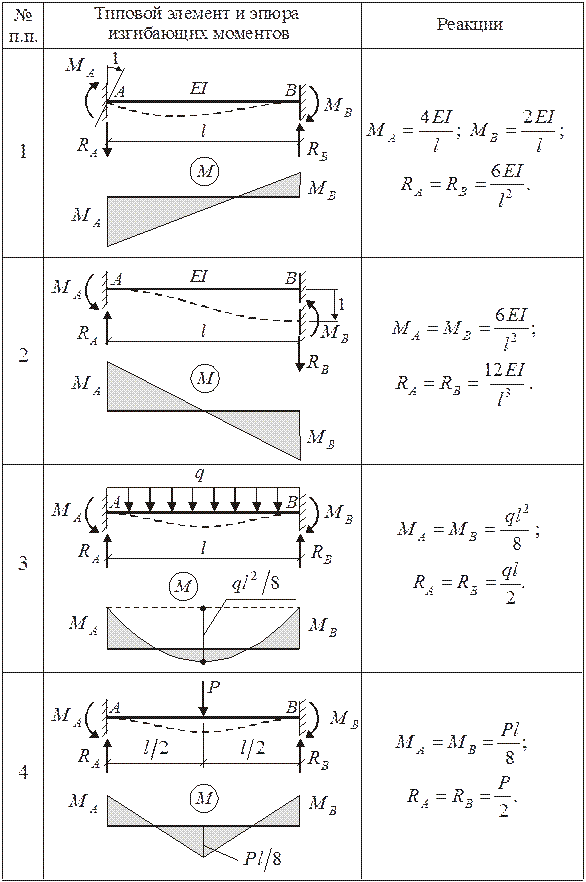 Равнодействующая погонной нагрузки равна . Она приложена посредине участка длиной . Поэтому
Равнодействующая погонной нагрузки равна . Она приложена посредине участка длиной . Поэтому
кН;
кН·м.
Напомним, что при определении знака изгибающего момента мы мысленно освобождаем видимую нами часть балки от всех фактических опорных закреплений и представляем ее как бы защемленной в рассматриваемом сечении (то есть левый край листка бумаги нами мысленно представляется жесткой заделкой).
Сечение 3. Закроем правую часть. Получим
кН;
кН·м.
Сечение 4. Закрываем листком правую часть балки. Тогда
кН;
кН·м.
Теперь, для контроля правильности вычислений, закроем листком бумаги левую часть балки. Мы видим сосредоточенную силу P, реакцию правой опоры и погонную нагрузку q, распределенную на бесконечно малой длине. Равнодействующая погонной нагрузки равна нулю. Поэтому
кН;
кН·м.
То есть все верно.
Сечение 5. По-прежнему закроем левую часть балки. Будем иметь
кН;
кН·м.
Сечение 6. Опять закроем левую часть балки. Получим
кН;
.
По найденным значениям строим эпюры перерезывающих сил (рис. 3.13, б) и изгибающих моментов (рис. 3.13, в).
Убеждаемся в том, что под незагруженным участком эпюра перерезывающих сил идет параллельно оси балки, а под распределенной нагрузкой q – по прямой, имеющей наклон вниз. На эпюре имеется три скачка: под реакцией – вверх на 37,5 кН, под реакцией – вверх на 132,5 кН и под силой P – вниз на 50 кН.
На эпюре изгибающих моментов мы видим изломы под сосредоточенной силой P и под опорными реакциями. Углы изломов направлены навстречу этим силам. Под распределенной нагрузкой интенсивностью q эпюра изменяется по квадратичной параболе, выпуклость которой направлена навстречу нагрузке. Под сосредоточенным моментом – скачок на 60 кН ·м, то есть на величину самого момента. В сечении 7 на эпюре – экстремум, поскольку эпюра перерезывающей силы для этого сечения проходит через нулевое значение (). Определим расстояние от сечения 7 до левой опоры.
Перерезывающая сила
.
Отсюда
м.
Экстремальное значение изгибающего момента в сечении 7 равно:
кН·м.
Определяем требуемый момент сопротивления балки из условия прочности по нормальным напряжениям
Согласно эпюре , максимальный по алгебраической величине изгибающий момент возникает в третьем поперечном сечении балки: кН·см. Тогда
см3.
По сортаменту (см. прил. 1, табл. П1.3) подбираем двутавр № 30а, имеющий см3.
Проверяем прочность балки по наибольшим касательным напряжениям
Наибольшие касательные напряжения, возникающие в поперечном сечении двутавровой балки, вычисляются по формуле
.
По сортаменту для выбранного нами двутавра определяем, что статический момент половины сечения относительно нейтральной оси см3, момент инерции относительно нейтральной оси см4, а толщина стенки см.
Согласно эпюре , наибольшее по алгебраической величине значение перерезывающей силы кН. Тогда
кН/см2 кН/см2,
то есть условие прочности по касательным напряжениям выполняется.
Варианты задач по теме «прямой поперечный изгиб» для самостоятельного решения
Условие задачи на прямой изгиб для самостоятельного решения
Для двух заданных схем балок (рис. 3.11) требуется:
1. построить эпюры перерезывающих сил и изгибающих моментов ;
2. подобрать из условия прочности по нормальным напряжениям ( кН/см2) балку круглого поперечного сечения для схемы a и балку двутаврового поперечного сечения для схемы б;
3. проверить прочность подобранных балок по касательным напряжениям (кН/см2).
Варианты расчетных схем
Рис. 3.11
Варианты исходных данных к задаче для самостоятельного решения «прямой поперечный изгиб»
Номер схемы (рис. 3.11) | l, м | M, кН·м | P, кН | q, кН/м | |||
1 | 3 | 0,2 | 0,6 | 0,2 | 8 | 5 | 10 |
2 | 4 | 0,3 | 0,5 | 0,3 | 7 | 6 | 11 |
3 | 5 | 0,4 | 0,4 | 0,3 | 6 | 7 | 12 |
4 | 6 | 0,5 | 0,3 | 0,2 | 5 | 8 | 13 |
5 | 3 | 0,6 | 0,7 | 0,2 | 4 | 9 | 14 |
6 | 4 | 0,7 | 0,5 | 0,3 | 8 | 10 | 9 |
7 | 5 | 0,8 | 0,4 | 0,6 | 7 | 5 | 10 |
8 | 6 | 0,2 | 0,6 | 0,3 | 6 | 6 | 11 |
9 | 3 | 0,3 | 0,5 | 0,4 | 5 | 7 | 12 |
0 | 4 | 0,4 | 0,4 | 0,2 | 4 | 8 | 8 |
Расчет балок переменного сечения (Лекция №30)
Подбор сечений балок равного сопротивления.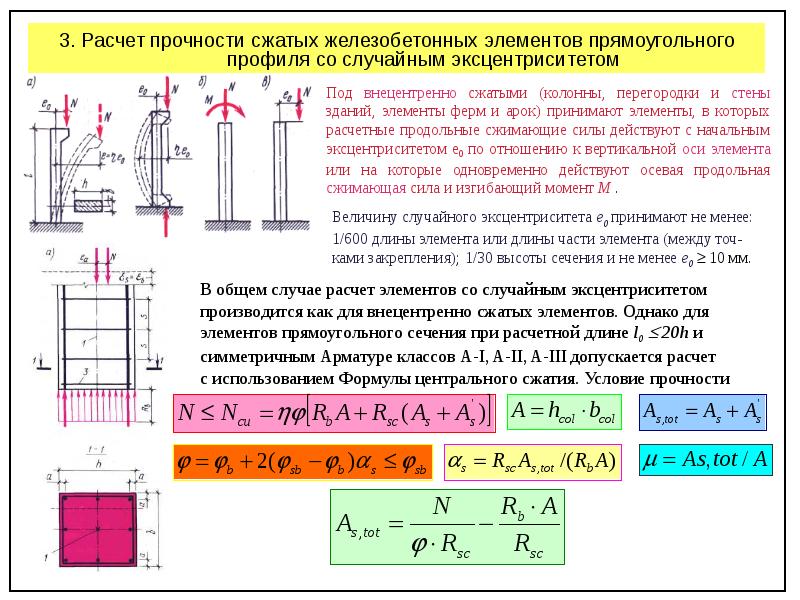
Все предыдущие расчеты относились к балкам постоянного сечения. На практике мы имеем часто дело с балками, поперечные размеры которых меняются по длине либо постепенно, либо резко.
Ниже рассмотрено несколько примеров подбора сечения и определения деформаций балок переменного профиля.
Так как изгибающие моменты обычно меняются по длине балки то, подбирая ее сечение по наибольшему изгибающему моменту, мы получаем излишний запас материала во всех сечениях балки, кроме того, которому соответствует . Для экономии материала, а также для увеличения в нужных случаях гибкости балок применяют балки равного сопротивления. Под этим названием подразумевают балки, у которых во всех сечениях наибольшее нормальное напряжение одинаково и должно быть равно допускаемому.
Условие, определяющее форму такой балки, имеет вид
и
Здесь М(х) и W(x) изгибающий момент и момент сопротивления в любом сечении балки; W(х) для каждого сечения балки должен меняться пропорционально изгибающему моменту.
Эти условия справедливы и для сечения с наибольшим изгибающим моментом; если обозначить момент сопротивления балки в сечении с наибольшим изгибающим моментом , то можно написать:
(1) |
Покажем ход вычислений на примере. Рассмотрим балку пролетом l, защемленную концом А и нагруженную на другом конце силой Р (Рис.1). Выберем сечение этой балки в виде прямоугольника; задачу о надлежащем изменении момента сопротивления можно решать, меняя высоту или ширину балки или тот и другой размер вместе.
Рис.1. Расчетная схема балки равного сопротивления
Пусть высота балки будет постоянной , а ширина переменной. Момент сопротивления в сечении на расстоянии х от свободного конца будет , а изгибающий момент ; момент сопротивления опорного сечения , a наибольший изгибающий момент в опорном сечении . В расчете имеют значения лишь абсолютные величины М(х) и
В расчете имеют значения лишь абсолютные величины М(х) и
По формуле (1) получаем:
откуда
т. е. ширина меняется по линейному закону в зависимости от х. При ширина равна .
Вид балки в фасаде и плане показан на Рис.1. Такое очертание балки получается, если учитывать ее прочность только по отношению к нормальным напряжениям; ширина в сечении В обращается в нуль.
Однако необходимо обеспечить прочность и по отношению к касательным напряжениям. Наименьшая ширина балки, требуемая этим условием, определится из уравнения
или, так как
Таким образом, исправленное очертание балки предопределяет минимальный размер ширины и утолщение свободного края консоли.
Определение деформаций балок переменного сечения.
При определении прогибов и углов поворота для балок с переменным сечением надлежит иметь в виду, что жесткость такой балки является функцией от х. Поэтому дифференциальное уравнение изогнутой оси принимает вид
где J(x) переменный момент инерции сечений балки.
До интегрирования этого уравнения можно выразить J(x) надлежащей подстановкой через J, т. е. через момент инерции того; сечения, где действует ; после этого вычисления производятся так же, как и.для балок постоянного сечения.
Покажем это на примере, разобранном выше. Определим прогиб балки равного сопротивления, защемленной одним концом, нагруженной на другом конце силой Р и имеющей постоянную высоту. Начало координат выберем на свободном конце балки.
Тогда
Дифференциальное уравнение принимает вид:
Интегрируем два раза:
Для определения постоянных интегрирования имеем условия: точке А при прогиб и угол поворота или
и
отсюда
и
Выражения для у и принимают вид;
Наибольший прогиб на свободном конце балки В получится при : он равен
Если бы мы всю балку сделали постоянного сечения с моментом инерции J, то наибольший прогиб был бы
т. е. в 1 раза меньше.
е. в 1 раза меньше.
Таким образом, балки переменного сечения обладают большей гибкостью по сравнению с балками постоянной жесткости при одинаковой с ними прочности. Именно поэтому, а не только ради экономии материала, они и применяются в таких конструкциях, как рессоры.
Дальше…
Напряжение и отклонение балки | MechaniCalc
ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.
Многие конструкции можно представить как прямую балку или как набор прямых балок. По этой причине анализ напряжений и прогибов в балке является важной и полезной темой.
В этом разделе рассматриваются поперечная сила и изгибающий момент в балках, диаграммы сдвига и момента, напряжения в балках и таблица общих формул прогиба балок.
Содержание
Сила сдвига и изгибающий момент
Чтобы найти поперечную силу и изгибающий момент по длине балки, сначала решите внешние реакции при граничных условиях. Например, консольная балка ниже имеет приложенную силу, показанную красным, а реакции показаны синим цветом при фиксированном граничном условии:
После того, как были решены внешние реакции, сделайте разрезы секций по длине балки и решите реакции на каждом разрезе секции.Пример разреза показан на рисунке ниже:
Когда балка разрезается по сечению, при вычислении реакций можно учитывать любую сторону балки. Выбранная сторона не влияет на результаты, поэтому выберите наиболее легкую. На рисунке выше выбрана сторона балки справа от разреза. Реакции на разрезе показаны синими стрелками.
Подписать Конвенцию
Знаки сдвига и момента важны.Знак определяется после того, как сделан разрез и решены реакции для части балки на одной стороне разреза. Сила сдвига в разрезе секции считается положительной, если она вызывает вращение выбранной секции балки по часовой стрелке, и считается отрицательной, если вызывает вращение против часовой стрелки. Изгибающий момент в разрезе секции считается положительным, если он сжимает верхнюю часть балки и удлиняет нижнюю часть балки (т.е. если он заставляет балку «улыбаться»).
Изгибающий момент в разрезе секции считается положительным, если он сжимает верхнюю часть балки и удлиняет нижнюю часть балки (т.е. если он заставляет балку «улыбаться»).
Исходя из этого соглашения о знаках, поперечная сила в разрезе секции на рисунке выше является положительной, поскольку она вызывает вращение выбранной секции по часовой стрелке.Момент отрицательный, так как он сжимает нижнюю часть балки и удлиняет ее верх (т. Е. Заставляет балку «хмуриться»).
Ознакомьтесь с нашим калькулятором балок, основанным на методике, описанной здесь.
- Расчет напряжений и прогибов в прямых балках
- Строит диаграммы сдвига и момента
- Может указывать любую конфигурацию ограничений, сосредоточенных сил и распределенных сил
Диаграммы сдвига и момента
Сдвиговый и изгибающий моменты балки обычно выражаются диаграммами.Диаграмма сдвига показывает сдвиг по длине балки, а диаграмма моментов показывает изгибающий момент по длине балки. Эти диаграммы обычно показаны сложенными друг на друга, и комбинация этих двух диаграмм представляет собой диаграмму момента сдвига. Диаграммы момента сдвига для некоторых общих конечных условий и конфигураций нагрузки показаны в таблицах прогиба балок в конце этой страницы. Пример диаграммы момента сдвига показан на следующем рисунке:
Общие правила построения диаграмм момента сдвига приведены в таблице ниже:
| Диаграмма сдвига | Схема моментов |
|---|---|
|
|
Напряжения изгиба в балках
Изгибающий момент M по длине балки можно определить по диаграмме моментов.Изгибающий момент в любом месте балки затем можно использовать для расчета изгибающего напряжения по поперечному сечению балки в этом месте. Изгибающий момент изменяется по высоте поперечного сечения в соответствии с формулой изгиба , приведенной ниже:
где M — изгибающий момент в интересующем месте по длине балки, I c — центроидный момент инерции поперечного сечения балки, а y — расстояние от нейтральной оси балки до интересующей точки по высоте. поперечного сечения.Отрицательный знак указывает, что положительный момент приведет к сжимающему напряжению выше нейтральной оси.
Напряжение изгиба равно нулю на нейтральной оси балки, которая совпадает с центром тяжести поперечного сечения балки. Напряжение изгиба линейно увеличивается от нейтральной оси до максимальных значений на крайних волокнах вверху и внизу балки.
Максимальное напряжение изгиба определяется как:
где c — центроидное расстояние поперечного сечения (расстояние от центроида до крайнего волокна).
Если балка асимметрична относительно нейтральной оси, так что расстояния от нейтральной оси до верха и низа балки не равны, максимальное напряжение будет возникать в самом дальнем от нейтральной оси месте. На рисунке ниже растягивающее напряжение в верхней части балки больше, чем сжимающее напряжение в нижней части.
Модуль упругости поперечного сечения объединяет центроидный момент инерции I c и центральное расстояние c:
Преимущество модуля сечения заключается в том, что он характеризует сопротивление сечения изгибу одним термином. Модуль упругости сечения можно подставить в формулу изгиба для расчета максимального напряжения изгиба в поперечном сечении:
Модуль упругости сечения можно подставить в формулу изгиба для расчета максимального напряжения изгиба в поперечном сечении:
Ознакомьтесь с нашим калькулятором балок, основанным на методике, описанной здесь.
- Расчет напряжений и прогибов в прямых балках
- Строит диаграммы сдвига и момента
- Может указывать любую конфигурацию ограничений, сосредоточенных сил и распределенных сил
Напряжения сдвига в балках
Сила сдвига V по длине балки может быть определена из диаграммы сдвига.Сила сдвига в любом месте вдоль балки затем может использоваться для расчета напряжения сдвига по поперечному сечению балки в этом месте. Среднее напряжение сдвига по поперечному сечению определяется как:
Напряжение сдвига меняется по высоте поперечного сечения, как показано на рисунке ниже:
Напряжение сдвига равно нулю на свободных поверхностях (вверху и внизу балки) и максимально в центре тяжести. Уравнение для касательного напряжения в любой точке, расположенной на расстоянии y 1 от центра тяжести поперечного сечения, определяется следующим образом:
где V — поперечная сила, действующая в месте поперечного сечения, I c — центроидный момент инерции поперечного сечения, а b — ширина поперечного сечения.Все эти термины являются константами. Член Q — это первый момент области, ограниченной интересующей точкой и крайним волокном поперечного сечения:
Напряжения сдвига для нескольких общих поперечных сечений обсуждаются в следующих разделах.
Напряжения сдвига в прямоугольном сечении
Распределение касательного напряжения по высоте прямоугольного поперечного сечения показано на рисунке ниже:
Первый момент площади в любой заданной точке y 1 по высоте поперечного сечения рассчитывается по формуле:
Максимальное значение Q приходится на нейтральную ось луча (где y 1 = 0):
Напряжение сдвига в любой заданной точке y 1 по высоте поперечного сечения рассчитывается по формуле:
где I c = b · h 3 /12 — центроидный момент инерции поперечного сечения.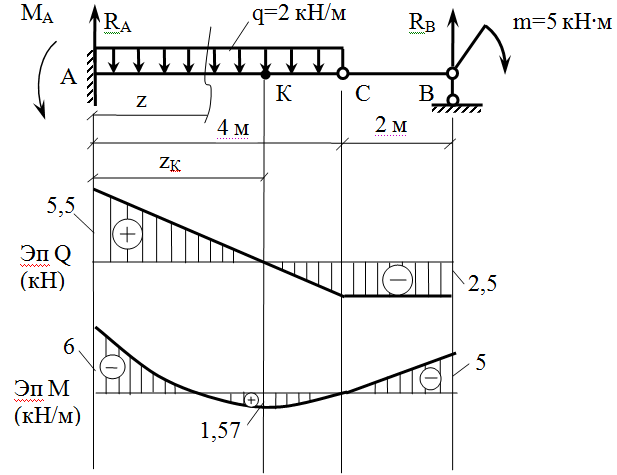 Максимальное напряжение сдвига возникает на нейтральной оси балки и рассчитывается по формуле:
Максимальное напряжение сдвига возникает на нейтральной оси балки и рассчитывается по формуле:
где A = b · h — площадь поперечного сечения.
Обратите внимание, что максимальное напряжение сдвига в поперечном сечении на 50% выше, чем среднее напряжение V / A.
Напряжения сдвига в круглых сечениях
Круглое поперечное сечение показано на рисунке ниже:
Уравнения для касательного напряжения в балке были получены с использованием предположения, что касательное напряжение по ширине балки является постоянным.Это предположение справедливо в центре тяжести кругового поперечного сечения, хотя нигде больше не действует. Следовательно, хотя распределение напряжения сдвига по высоте поперечного сечения не может быть легко определено, максимальное напряжение сдвига в сечении (возникающее в центре тяжести) все же может быть вычислено. Максимальное значение первого момента Q, возникающего в центроиде, определяется как:
Затем максимальное напряжение сдвига рассчитывается по формуле:
где b = 2r — диаметр (ширина) поперечного сечения, I c = πr 4 /4 — центроидный момент инерции, а A = πr 2 — площадь поперечного сечения.
Напряжения сдвига в круглых сечениях труб
Круглое поперечное сечение трубы показано на рисунке ниже:
Максимальное значение первого момента Q, возникающего в центроиде, определяется как:
Затем максимальное напряжение сдвига рассчитывается по формуле:
где b = 2 (r o — r i ) — эффективная ширина поперечного сечения, I c = π (r o 4 — r i 4 ) / 4 — центроидный момент инерции, а A = π (r o 2 — r i 2 ) — площадь поперечного сечения.
Напряжения сдвига в двутавровых балках
Распределение напряжения сдвига вдоль стенки двутавровой балки показано на рисунке ниже:
Уравнения для касательного напряжения в балке были получены с использованием предположения, что касательное напряжение по ширине балки является постоянным.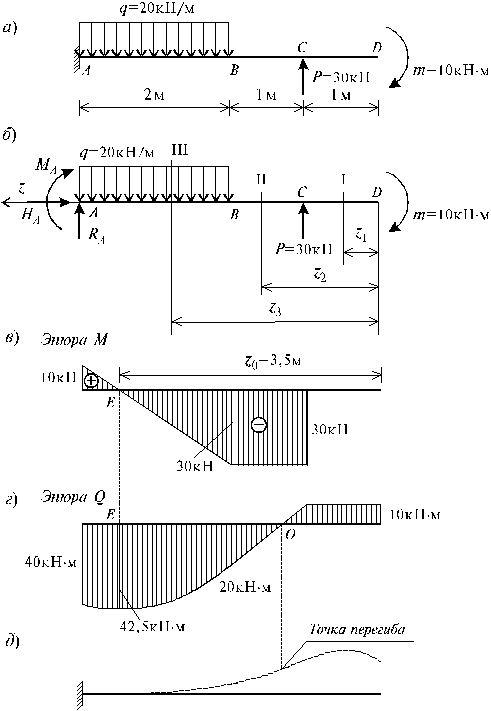 Это предположение справедливо для стенки двутавровой балки, но недопустимо для полок (особенно там, где стенка пересекает полки). Однако стенка двутавровой балки принимает на себя подавляющую часть силы сдвига (примерно 90% — 98%, согласно Гиру), и поэтому можно консервативно предположить, что стенка несет всю силу сдвига.
Это предположение справедливо для стенки двутавровой балки, но недопустимо для полок (особенно там, где стенка пересекает полки). Однако стенка двутавровой балки принимает на себя подавляющую часть силы сдвига (примерно 90% — 98%, согласно Гиру), и поэтому можно консервативно предположить, что стенка несет всю силу сдвига.
Первый момент площади перемычки двутавровой балки определяется как:
Напряжение сдвига вдоль стенки двутавровой балки определяется по формуле:
где t w — толщина стенки, а I c — центроидный момент инерции двутавровой балки:
Максимальное значение напряжения сдвига возникает на нейтральной оси (y 1 & равно; 0), а минимальное значение напряжения сдвига в полотне возникает на внешних волокнах полотна, где оно пересекает фланцы y 1 & equals; & pm; h w /2):
Ознакомьтесь с нашим калькулятором балок, основанным на методике, описанной здесь.
- Расчет напряжений и прогибов в прямых балках
- Строит диаграммы сдвига и момента
- Может указывать любую конфигурацию ограничений, сосредоточенных сил и распределенных сил
Таблицы прогиба балки
В таблицах ниже приведены уравнения прогиба, наклона, сдвига и момента вдоль прямых балок для различных конечных условий и нагрузок. Вы можете найти исчерпывающие таблицы в таких источниках, как Гир, Линдебург и Шигли.Однако приведенные ниже таблицы охватывают большинство распространенных случаев.
Консольные балки
Балки с простой опорой
Несъемные несущие балки
Подпишитесь, чтобы получать обновления о последних улучшениях:
Список литературы
- Будинас-Нисбетт, «Машиностроительный проект Шигли», 8-е изд.
- Гир, Джеймс М., «Механика материалов», 6-е изд.
- Линдебург, Майкл Р., «Справочное руководство по машиностроению для экзамена на физическую форму», 13-е изд.
- «Руководство по анализу напряжений», Лаборатория динамики полета ВВС, октябрь 1986 г.
Расчет напряжения изгиба секции балки
Как рассчитать напряжение изгиба в балках?В этом руководстве мы рассмотрим, как рассчитать изгибающее напряжение балки, используя формулу изгибающего напряжения, которая связывает распределение продольных напряжений в балке с внутренним изгибающим моментом, действующим на поперечное сечение балки.Мы предполагаем, что материал балки — линейно-упругий (т.е. применим закон Гука). Напряжение изгиба важно, и, поскольку изгиб балки часто является определяющим результатом при проектировании балки, это важно понимать.
1. Расчет напряжения изгиба вручнуюДавайте посмотрим на пример. Рассмотрим двутавровую балку, показанную ниже:
На некотором расстоянии по длине балки (ось x) она испытывает внутренний изгибающий момент (M), который обычно можно найти на диаграмме изгибающего момента.Общая формула для изгиба или нормального напряжения в сечении:
Для конкретного сечения балки очевидно, что напряжение изгиба будет максимальным на расстоянии от нейтральной оси (y). Таким образом, максимальное напряжение изгиба будет возникать либо в ВЕРХНЕ, либо в НИЖНЕЙ части секции балки, в зависимости от того, какое расстояние больше:
Давайте рассмотрим реальный пример нашей двутавровой балки, показанной выше. В нашем предыдущем уроке по моменту инерции мы уже обнаружили, что момент инерции относительно нейтральной оси равен I = 4.74 × 10 8 мм 4 . Кроме того, в руководстве по центроиду мы обнаружили, что центроид и, следовательно, расположение нейтральной оси находятся на расстоянии 216,29 мм от нижней части секции. Это показано ниже:
Очевидно, что очень часто требуется МАКСИМАЛЬНОЕ напряжение изгиба, которое испытывает секция. Например, предположим, что мы знаем из нашей диаграммы изгибающего момента, что балка испытывает максимальный изгибающий момент 50 кН-м или 50 000 Нм (преобразование единиц изгибающего момента).
Затем нам нужно определить, находится ли верх или низ секции дальше всего от нейтральной оси. Ясно, что нижняя часть секции находится дальше на расстояние c = 216,29 мм. Теперь у нас достаточно информации, чтобы найти максимальное напряжение, используя приведенную выше формулу напряжения изгиба:
Точно так же мы можем найти напряжение изгиба в верхней части секции, поскольку мы знаем, что оно составляет y = 159,71 мм от нейтральной оси (NA):
Последнее, о чем следует беспокоиться, это то, вызывает ли напряжение сжатие или растяжение волокон секции.Если балка прогибается в форме буквы «U», то верхние волокна испытывают сжатие (отрицательное напряжение), а нижние волокна — растяжение (положительное напряжение). Если балка провисает, как перевернутая буква «U», то все наоборот: нижние волокна сжимаются, а верхние — растянуты.
2. Расчет напряжения изгиба с использованием балки SkyCivКонечно, вам не нужно делать эти расчеты вручную, потому что вы можете использовать SkyCiv Beam — калькулятор напряжения изгиба, чтобы определить напряжение сдвига и изгиба в балке! Просто начните с моделирования балки с опорами и приложите нагрузки.Как только вы нажмете «Решить», программа покажет максимальные напряжения из этого калькулятора напряжения изгиба. На изображении ниже показан пример двутавровой балки, испытывающей напряжение изгиба:
Начните расчет напряжения изгиба с помощью SkyCiv Beam Calculator:Бесплатный калькулятор луча
Бесплатный калькулятор луча | Калькулятор изгибающего момента, поперечной силы и прогиба
Добро пожаловать в наш бесплатный онлайн-калькулятор диаграмм изгибающего момента и поперечной силы, который может генерировать диаграммы реакций, поперечных сил (SFD) и изгибающих моментов (BMD) консольной балки или просто поддерживаемой балки.Используйте этот калькулятор пролета балки, чтобы определить реакции на опоры, построить диаграмму сдвига и момента для балки и рассчитать прогиб стальной или деревянной балки. Бесплатный онлайн-калькулятор балки для создания реакций, расчета прогиба стальной или деревянной балки, построения диаграмм сдвига и момента балки. Это бесплатная версия нашего полного программного обеспечения SkyCiv Beam. Доступ к нему можно получить из любой из наших Платных учетных записей, которая также включает в себя полное программное обеспечение для структурного анализа.
Бесплатный онлайн-калькулятор балки для создания реакций, расчета прогиба стальной или деревянной балки, построения диаграмм сдвига и момента балки. Это бесплатная версия нашего полного программного обеспечения SkyCiv Beam. Доступ к нему можно получить из любой из наших Платных учетных записей, которая также включает в себя полное программное обеспечение для структурного анализа.
Используйте интерактивное окно выше, чтобы просмотреть и удалить длину балки, опоры и добавленные нагрузки. Любые внесенные изменения автоматически перерисовывают диаграмму свободного тела для любой балки с опорой или консольной балкой. Калькулятор реакции балки и расчет изгибающего момента запускаются после нажатия кнопки «Решить» и автоматически генерируют диаграммы сдвига и изгибающего момента. Вы также можете щелкнуть отдельные элементы этого калькулятора балки LVL, чтобы редактировать модель.
Калькулятор пролета балки легко рассчитает реакции на опорах.Он может рассчитывать реакции на опорах консольных или простых балок. Это включает в себя расчет реакций для консольной балки, которая имеет реакцию изгибающего момента, а также силы реакции x, y.
Вышеупомянутый калькулятор пролета стальной балки — это универсальный инструмент для проектирования конструкций, используемый для расчета изгибающего момента в алюминиевой, деревянной или стальной балке. Его также можно использовать в качестве калькулятора несущей способности балки, используя его в качестве калькулятора напряжения изгиба или напряжения сдвига. Он способен выдерживать до 2 различных сосредоточенных точечных нагрузок, 2 распределенных нагрузки и 2 момента.Распределенные нагрузки могут быть расположены так, чтобы они были равномерно распределенными нагрузками (UDL), треугольными распределенными нагрузками или трапециевидными распределенными нагрузками. Все нагрузки и моменты могут быть направленными как вверх, так и вниз по величине, что должно учитывать наиболее распространенные ситуации анализа балок. Расчет изгибающего момента и поперечной силы может занять до 10 секунд, и обратите внимание, что вы будете перенаправлены на новую страницу с реакциями, диаграммой поперечной силы и диаграммой изгибающего момента балки.
Расчет изгибающего момента и поперечной силы может занять до 10 секунд, и обратите внимание, что вы будете перенаправлены на новую страницу с реакциями, диаграммой поперечной силы и диаграммой изгибающего момента балки.
Одна из самых мощных функций — использование его в качестве калькулятора отклонения балки (или калькулятора смещения балки). Это можно использовать для наблюдения расчетного прогиба балки с опорой или консольной балки. Возможность добавлять формы сечения и материалы делает его полезным в качестве калькулятора деревянных балок или в качестве калькулятора стальных балок для проектирования балок lvl или i. На данный момент эта функция доступна в SkyCiv Beam, который имеет гораздо больше функций для проектирования деревянных, бетонных и стальных балок.
SkyCiv предлагает инженерам широкий спектр программного обеспечения для структурного анализа и проектирования облачных вычислений. Как постоянно развивающаяся технологическая компания, мы стремимся внедрять инновации и совершенствовать существующие рабочие процессы, чтобы сэкономить время инженеров в их рабочих процессах и проектах.
Сопротивление изгибу | Сталь | FIN EC
Сопротивление изгибу
класс = «h2″>Сопротивление изгибу рассчитывается для классов 1 и 2 по следующей формуле:
Где: | W pl, y , W pl, z |
|
f y | γ M0 |
|
Сопротивление изгибу для классов 3 и 4 рассчитывается в четырех точках поперечного сечения.Эти точки расположены в углах поперечного сечения.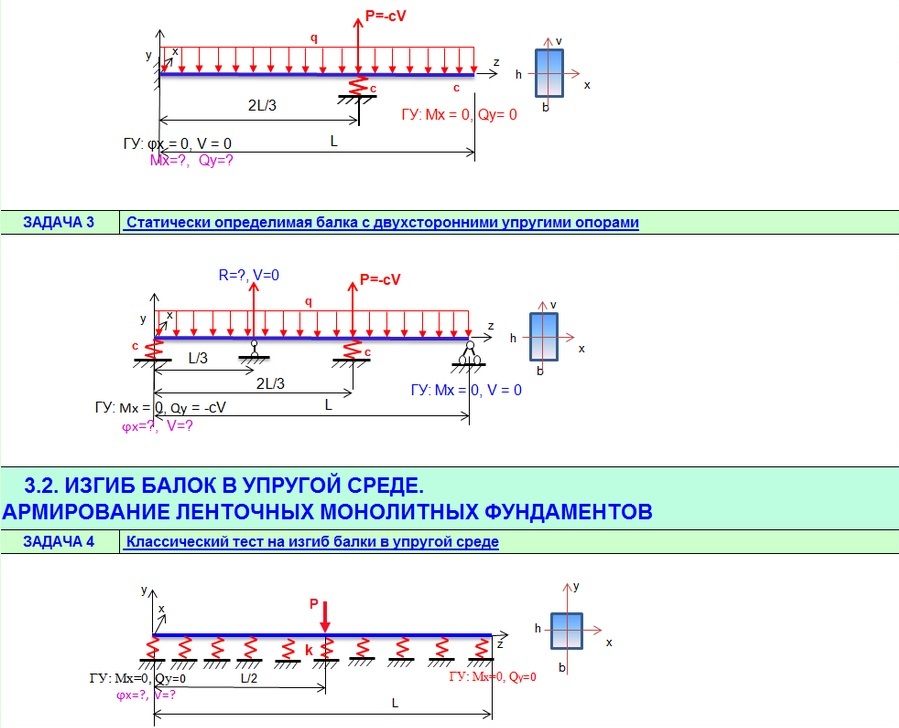
Где: | i W y , 90 i |
|
f y | ||
γ M0 |
|
Следующее выражение используется для класса 4
i W eff, y , 90 012 i W eff, z |
| |
f y | ||
γ M0 |
|
Рассчитано сопротивление изгибу перфорированного поперечного сечения для классов 1 и 2 по следующей формуле
Где: | W pl, y, osl , W pl, z, osl |
|
f u | ||
γ M2 |
| |
Где: | i W y, osl , 90 i osl |
|
f u | ||
γ M2 |
|
Следующее выражение используется для класса 4
Где: | i W y , eff, osl , i W z, eff, osl |
|
f u | ||
γ M2 | 0 Частичный коэффициент запаса прочности |
0 Минимальное из значений
M c, Rd, y и M c, Rd, y, osl или M c, R d, z и M c, Rd, z, osl используется при проверке.
Расчетное значение сопротивления уменьшено для « Высокий сдвиг, » (описан в главе « Низкий и высокий сдвиг, »).
Где находится: | i W pl, y, красный , i W pl, z, красный 9009 |
|
f y | ||
91 γ 90 M0 |
|
Уменьшенные модули пластического сечения рассчитываются как модули пластического сечения с уменьшенной прочностью в стенах, которые подвергаются « высокому сдвигу ».Уменьшение основано на коэффициентах ρ z и ρ y , которые рассчитываются в соответствии с главой « Низкий и высокий сдвиг ». Минимум значений M c, Rd, y и M c, Rd, y, красный или M c, Rd, z и M c, Rd, z, красный используется при поверке.
Сопротивление изгибу, включая эффект продольного изгиба при кручении
Ú Сопротивление изгибу определяется по формуле
Где: | χ |
|
M c, Rd, y , M c , Rd, z |
Понижающие коэффициенты для продольного изгиба при кручении χ LT, y и χ LT, z зависят от значения упругого критического момента для поперечного изгиба.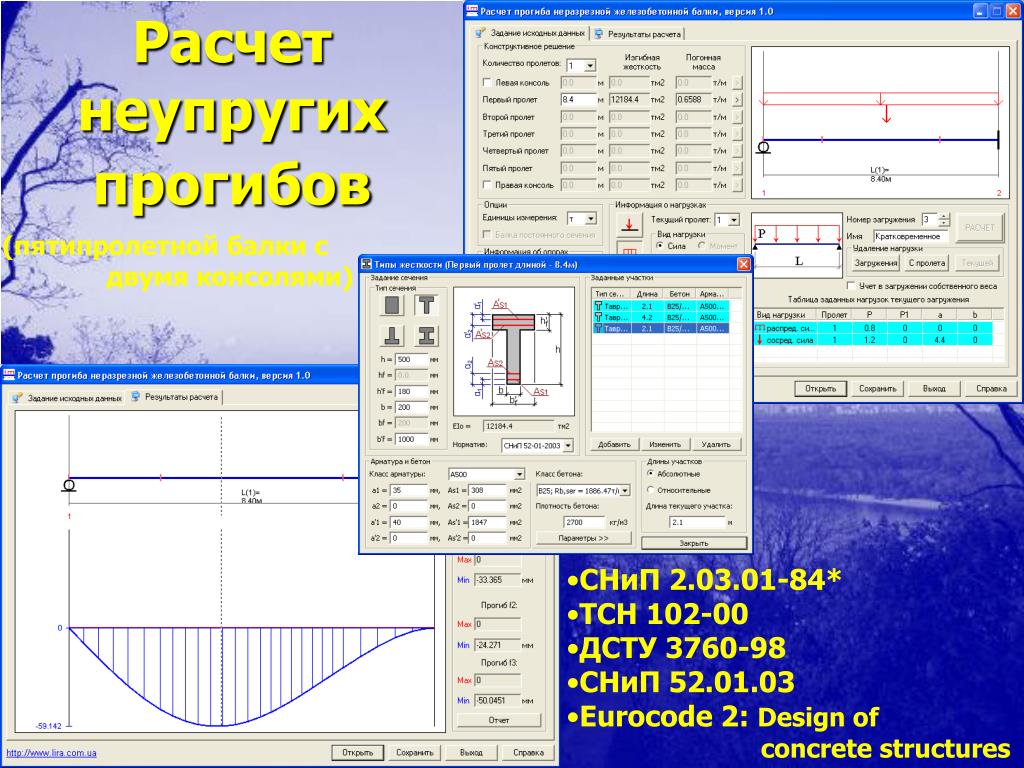 изгиб при кручении M cr , который рассчитывается согласно выражению
изгиб при кручении M cr , который рассчитывается согласно выражению
, где коэффициент μ cr 9 0091 — критический момент, определяемый следующими выражениями
Безразмерный коэффициент кручения k wt рассчитывается по формуле
ζ г — безразмерный параметр, учитывающий положение нагрузки относительно центра сдвига
ζ j — безразмерный параметр, учитывающий несимметричность поперечных сечений
Где это: | 11 9011 1 , C 2 , C 3 |
|
k z , k y , k w 903 79 |
| |
E |
| |
G 401 | I z , I y |
|
L |
| |
I ω |
| |
I t |
| |
z g , y g |
|
и z j и y j задаются выражениями
Где находится: | z s , y s |
|
Относительная гибкость рассчитывается с помощью критического момент M cr :
Где: | W y , W z |
|
Значение коэффициента несовершенства α LT устанавливается в соответствии с кривыми потери устойчивости a , b , c , d . Коэффициенты χ LT, y и χ LT, z задаются выражениями
Коэффициенты χ LT, y и χ LT, z задаются выражениями
, однако должно выполняться следующее условие:
, где
Влияние бокового продольного изгиба. не рассматривается для поперечных сечений, устойчивых к низкому короблению (например, RHS), и для случаев, когда изгибающий момент действует вокруг слабой оси поперечного сечения.
Балки — поддерживаются на обоих концах
Напряжение в изгибающейся балке можно выразить как
σ = y M / I (1)
, где
σ = напряжение (Па (Н / м) 2 ), Н / мм 2 , psi)
y = расстояние до точки от нейтральной оси (м, мм, дюйм)
M = изгибающий момент (Нм, фунт дюйм)
I = момент инерции (м 4 , мм 4 , в 4 )
Калькулятор ниже можно использовать для расчета максимального напряжения и прогиба балок с одной одиночной или равномерно распределенной нагрузкой.
Балка, поддерживаемая на обоих концах — равномерная непрерывная распределенная нагрузка
Момент в балке с равномерной нагрузкой, поддерживаемой на обоих концах в положении x, может быть выражен как
M x = qx (L — x) / 2 (2)
где
M x = момент в положении x (Нм, фунт дюйм)
x = расстояние от конца (м, мм, дюйм)
Максимум момент находится в центре балки на расстоянии L / 2 и может быть выражен как
M max = q L 2 /8 (2a)
где
M макс = максимальный момент ( Нм, фунт-дюйм)
q = равномерная нагрузка на единицу длины балки (Н / м, Н / мм, фунт / дюйм)
9142 2 L = длина балки (м, мм, дюйм)
Максимальное напряжение
Уравнения 1 и 2a могут быть объединены, чтобы выразить максимальное напряжение в балке с поддержанной равномерной нагрузкой на обоих концах на расстоянии L / 2 как
σ max = y max q L 2 / (8 I) (2b)
где
σ max = максимальное напряжение (Па (Н / м 2 ), Н / мм 2 , psi)
y max = расстояние до крайней точки от нейтральной оси (м, мм, дюйм)
- 1 Н / м 2 = 1×10 -6 Н / мм 2 = 1 Па = 1.
 4504×10 -4 фунтов на кв. Дюйм
4504×10 -4 фунтов на кв. Дюйм - 1 фунт / дюйм (фунт / дюйм 2 ) = 144 фунта на квадратный дюйм (фунт на / фут 2 ) = 6 894,8 Па (Н / м 2 ) = 6,895×10 — 3 Н / мм 2
Максимальный прогиб :
δ max = 5 q L 4 / (384 EI) (2c)
где
δ макс = максимальный прогиб (м, мм, дюйм)
E = Модуль упругости (Па (Н / м 2 ), Н / мм 2 , psi)
Прогиб в положении x:
δ x = qx ( L 3 — 2 L x 2 + x 3 ) / (24 EI) (2d)
Примечание! — прогиб часто является ограничивающим фактором при проектировании балки.Для некоторых применений балки должны быть прочнее, чем требуется при максимальных нагрузках, чтобы избежать недопустимого прогиба.
Силы, действующие на концы:
R 1 = R 2
= q L / 2 (2e)
где
R = сила реакции (Н, фунт)
Пример — балка с равномерной нагрузкой, метрические единицы
Балка UB 305 x 127 x 42 длиной 5000 мм несет равномерную нагрузку 6 Н / мм .Момент инерции балки составляет 8196 см 4 (81960000 мм 4 ) , а модуль упругости стали, используемой в балке, составляет 200 ГПа (200000 Н / мм 2 ) . Высота балки 300 мм (расстояние от крайней точки до нейтральной оси 150 мм ).
Максимальное напряжение в балке можно рассчитать
σ max = (150 мм) (6 Н / мм) (5000 мм) 2 / (8 (81960000 мм 4 ))
= 34.3 Н / мм 2
= 34,3 10 6 Н / м 2 (Па)
= 34,3 МПа
Максимальный прогиб балки можно рассчитать
δ макс = 5 (6 Н / мм) (5000 мм) 4 / (( 200000 Н / мм 2 ) ( 81960000 мм 4 ) 384)
= 2,98 мм
Расчет балки с равномерной нагрузкой — метрические единицы
- 1 мм 4 = 10 -4 см 4 = 10 -12 м 4
- 1 см 4 = 10 -8 м = 10 4 мм
- 1 дюйм 4 = 4.
 16×10 5 мм 4 = 41,6 см 4
16×10 5 мм 4 = 41,6 см 4 - 1 Н / мм 2 = 10 6 Н / м 2 (Па)
Расчет балки равномерной нагрузки — британские единицы
Пример — балка с равномерной нагрузкой, британские единицы
Максимальное напряжение в стальной широкополочной балке W 12 x 35 дюймов, 100 дюймов длиной , момент инерции 285 дюймов 4 , модуль упругости 200 psi
, при равномерной нагрузке 100 фунтов / дюйм можно рассчитать как
σ max = y max q L 2 / (8 I)
= (6.25 дюймов (100 фунтов / дюйм) (100 дюймов) 2 / (8 (285 дюймов 4 ))
= 2741 (фунт / дюйм 2 , psi)
Максимальное отклонение может можно рассчитать как
δ max = 5 q L 4 / (EI 384)
= 5 (100 фунтов / дюйм) (100 дюймов) 4 / ((2
00 фунтов / дюйм
2 ) (285 дюймов 4 ) 384)= 0,016 дюйма
Балка, поддерживаемая на обоих концах — нагрузка в центре
Максимальный момент в балке с центральной нагрузкой, поддерживаемой с обоих концов :
M max = FL / 4 (3a)
Максимальное напряжение
Максимальное напряжение в балке с одноцентровой нагрузкой, поддерживаемой на обоих концах:
σ max = y max FL / (4 I) (3b) 900 12
, где
F = нагрузка (Н, фунт)
Максимальный прогиб может быть выражен как
δ max = FL 3 / (48 EI) (3c)
Силы, действующие на концы:
R 1 = R 2
= F / 2 (3d)
Калькулятор балки с одним центром нагрузки — метрические единицы
Калькулятор балки с одним центром нагрузки — британская система мер Единицы
Пример — балка с одной центральной нагрузкой
Максимальное напряжение в стальной широкополочной балке «W 12 x 35», 100 дюймов длиной , момент инерции 285 дюймов 4 , модуль упругости 200 psi
, с центральной нагрузкой 10000 фунтов можно рассчитать как
σ max = y max FL / (4 I)
= (6. 25 дюймов) (10000 фунтов) (100 дюймов) / (4 (285 дюймов 4 ))
25 дюймов) (10000 фунтов) (100 дюймов) / (4 (285 дюймов 4 ))
= 5482 (фунт / дюйм 2 , psi)
Максимальный прогиб можно рассчитать как
δ макс = FL 3 / EI 48
= (10000 фунтов / дюйм) (100 дюймов) 3 / ((200 фунтов / дюйм
2 ) (285 дюймов 4 ) 48 )
= 0,025 дюйма
Некоторые типичные пределы отклонения по вертикали
- Общее отклонение: пролет / 250
- отклонение при динамической нагрузке: пролет / 360
- консоли: пролет / 180
- балки деревянных перекрытий для дома: пролет / 330 (макс. 14 мм)
- хрупкие элементы: пролет / 500
- подкрановые балки: пролет / 600
Балка, поддерживаемая на обоих концах — эксцентричная нагрузка
Максимальный момент в балке с одиночной эксцентричной нагрузкой в точке нагрузки:
M макс = F ab / L (4a)
Максимальное напряжение
Максимальное напряжение в балке с одноцентровой нагрузкой, поддерживаемой с обоих концов:
σ max = y max F ab / (LI) (4b)
Максимальный прогиб в точке нагрузки можно выразить как
δ F = F a 2 b 2 / (3 EIL) (4c)
Силы, действующие на концы:
R 1 = F b / L (4d)
R 2 = F a / L (4e)
Балка, поддерживаемая на обоих концах — две эксцентрические нагрузки
Максимальный момент (между нагрузками) в балке с двумя эксцентрическими нагрузками:
M max = F a (5a)
Максимальное напряжение
Максимальное напряжение в балке с двумя эксцентрическими нагрузками, поддерживаемыми на обоих концах:
σ max = y max F a / I (5b)
Максимум прогиб в точке нагрузки можно выразить как
δ F = F a (3L 2 — 4 a 2 ) / (24 EI) (5c)
Силы, действующие на концы:
R 1 = R 2
= F (5d)
Вставьте балки в свою модель Sketchup с помощью Engineering ToolBox Sketchup Extension
Балка поддерживается на обоих концах — трехточечная нагрузка
Максимальный момент (между нагрузками) в балке с тремя точечными нагрузками:
M max 90 091 = FL / 2 (6a)
Максимальное напряжение
Максимальное напряжение в балке с тремя точечными нагрузками, поддерживаемыми с обоих концов:
σ max = y max FL / (2 I) ( 6b)
Максимальный прогиб в центре балки можно выразить как
δ F = FL 3 / (20. 22 E I) (6c)
22 E I) (6c)
Силы, действующие на концы:
R 1 = R 2
= 1,5 F (6d)
I Расчет прочности на прочность балки
Калькулятор расчета прочности двутавровой балки для расчета нормальное напряжение, напряжение сдвига и напряжение фон Мизеса в критических точках данного сечение двутавра.
Поперечная нагрузка на двутавровую балку может привести к нормальным напряжениям и напряжениям сдвига. одновременно на любом поперечном сечении двутавра.Нормальное напряжение на данном поперечном сечении изменяется относительно расстояние y от нейтральной оси, и оно наибольшее в самой дальней точке от нервная ось. Нормальное напряжение также зависит от изгибающего момента в сечение и максимальное значение нормального напряжения в двутавровой балке возникает там, где изгибающий момент наибольший. Максимальное напряжение сдвига возникает на нейтральной оси двутавровой балки, где сила сдвига максимальна.
Примечание. Для получения дополнительной информации о см. разделы «Напряжения сдвига в тонкостенных элементах» и «Конструкция балок и валов на прочность »главы механики материалов .
Примечание: V и M — поперечная сила и изгибающий момент в сечении, как показано на фигура. Посетить » «Калькуляторы прогиба и напряжения несущей балки». Для расчета поперечной силы и изгибающего момента.
Примечание. Предполагается, что на несущую балку действует вертикальная сила сдвига в вертикальной плоскости симметрии.
| РЕЗУЛЬТАТЫ | ||
| Параметр | Стоимость | |
| Площадь поперечного сечения [A] | — | мм ^ 2 см ^ 2 дюйма ^ 2 фута ^ 2 |
| Первый момент площади для секции A [Q A ] | — | мм ^ 3 см ^ 3 дюйма ^ 3 фута ^ 3 |
| Первый момент площади для секции B [Q B ] | — | |
| Первый момент площади для секции D [Q D ] | — | |
| Второй момент площади [I zz ] | — | мм ^ 4 см ^ 4 дюйма ^ 4 фута ^ 4 |
| Расчет напряжений на участке A | МПапсикси | |
| Нормальное напряжение [σ x_A ] | — | |
| Напряжение сдвига [τ xy_A ] | — | |
| Напряжение по Мизесу при A [σ v_A ] | — | |
| Расчет напряжений на участке B | ||
| Нормальное напряжение при B [σ x_B ] | — | |
| Напряжение сдвига при B [τ xy_B ] | — | |
| Напряжение фон Мизеса при B [σ v_B ] | — | |
| Расчет напряжений на участке D | ||
| Нормальное напряжение при D [σ x_D ] | — | |
| Напряжение сдвига при D [τ xy_D ] | — | |
| Напряжение по Мизесу при D [σ v_D ] | — | |
Примечание: используйте точку «.»как десятичный разделитель.
Примечание. Напряжения являются положительными числами, и это величины напряжений в луч. Он не делает различий между растяжением и сжатием конструкции. луч.
Примечание. Эффекты концентраций напряжений не учитываются в расчетах.
Двутавровая балка: Двутавровая балка — разновидность балки. часто используется в фермах в зданиях.Двутавровая балка обычно изготавливается из конструкционные стали, подвергнутые горячей и холодной прокатке или сварке. Верхняя и нижняя пластины двутавровой балки называются полками, а вертикальная пластина, соединяющая полки, называется стенкой.
Нормальное напряжение: Напряжение действует перпендикулярно поверхности (поперечному сечению).
Второй момент области: способность поперечного сечения противостоять изгибу.
Напряжение сдвига: Напряжение, действующее параллельно поверхности (поперечному сечению), имеет режущий характер.
Напряжение: Среднее усилие на единицу площади, которое приводит к деформации материала.
Механика материалов: изгиб — нормальное напряжение »Механика тонких конструкций
Моменты области
Чтобы рассчитать напряжение (и, следовательно, деформацию), вызванное изгибом, нам нужно понять, где находится нейтральная ось балки и как рассчитать второй момент площади для данного поперечного сечения.
Начнем с представления произвольного поперечного сечения — чего-то не круглого, не прямоугольного и т. Д.
На изображении выше произвольная форма имеет область, обозначенную A . Мы можем посмотреть на небольшую дифференциальную область dA , которая существует на некотором расстоянии x и y от начала координат. Мы можем посмотреть на первый момент площади в каждом направлении по следующей формуле:
Первый момент площади — это интеграл длины по площади — это означает, что единицы длины будут кубическими [L 3 ].Это важно, потому что помогает нам определить центр тяжести объекта. Центроид определяется как «среднее положение области x (или y )». Математически это утверждение выглядит так:
Крайняя правая часть приведенных выше уравнений будет очень полезна в этом курсе — она позволяет нам разбить сложную форму на простые формы с известными площадями и известными положениями центроидов. В большинстве инженерных сооружений есть как минимум одна ось симметрии — и это позволяет нам значительно упростить поиск центроида. Центроид должен располагаться на оси симметрии . Например:
Для поперечного сечения слева мы знаем, что центроид должен лежать на оси симметрии, поэтому нам нужно только найти центроид по оси y . Поперечное сечение справа еще проще — поскольку центр тяжести должен совпадать с осями симметрии, он должен находиться в центре объекта.
Теперь, когда мы знаем, как найти центроид, мы можем обратить внимание на второй момент площади.Как вы могли вспомнить из предыдущего раздела, посвященного кручению, это определяется как:
И, наконец, иногда нам нужно определить второй момент площади относительно произвольной оси x или y — такой, которая не соответствует центроиду. В этом случае мы можем использовать теорему о параллельных осях для его вычисления. В этом случае мы используем второй момент площади относительно центроида плюс член, который включает расстояния между двумя осями.
Это уравнение называется теоремой о параллельной оси .Это будет очень полезно на протяжении всего курса. Как описано во вводном видео к этому разделу, вычислить второй момент площади для простой формы может быть несложно. Для более сложных форм нам нужно вычислить I , вычислив отдельные I для каждой простой формы и комбинируя их вместе с помощью теоремы о параллельных осях.
Диаграммы сдвига и момента
Поперечная нагрузка относится к силам, перпендикулярным длинной оси конструкции.Эти поперечные нагрузки будут вызывать изгибающий момент M , который вызывает нормальное напряжение , и силу сдвига V , которая вызывает напряжение сдвига . Эти силы могут и будут меняться по длине балки, и мы будем использовать диаграммы сдвига и момента (V-M-диаграмма) , чтобы извлечь наиболее подходящие значения. Построение этих диаграмм должно быть вам знакомо по статике , но мы рассмотрим их здесь. При исследовании поперечно нагруженной балки необходимо учитывать два важных момента:
- Как нагружается балка?
- точечная нагрузка, распределенная нагрузка (равномерная или переменная), комбинация нагрузок…
- Как поддерживается балка?
- просто поддерживаемые, консольные, нависающие, статически неопределимые…
Знание нагрузок и опор позволит вам нарисовать качественную диаграмму V-M , а затем статический анализ свободного тела поможет вам определить количественное описание кривых .Давайте начнем с того, что вспомним наши правила знаков .
Эти правила знаков должны быть вам знакомы. Если сдвиг вызывает вращение против часовой стрелки, он положительный. Если момент изгибает балку таким образом, что он изгибается в «улыбку» или U-образную форму, это положительно. Лучший способ вспомнить эти диаграммы — это проработать пример. Начните с этой консольной балки — отсюда вы можете переходить к более сложным нагрузкам.
Нормальное напряжение при изгибе
Во многом изгиб и кручение очень похожи.Изгиб получается парой или изгибающим моментом M , который применяется. Как и при кручении, при чистом изгибе в материале существует ось, на которой напряжение и деформация равны нулю. Это называется нейтральной осью . И, как и при кручении, напряжение перестает быть равномерным по поперечному сечению конструкции — оно меняется. Давайте начнем с рассмотрения того, как ось z изгибает конструкцию. В данном случае мы не будем ограничиваться круговыми сечениями — на рисунке ниже мы будем рассматривать призматическое сечение.
Прежде чем мы углубимся в математику, лежащую в основе изгиба, давайте попробуем разобраться в этом концептуально. Может быть, лучший способ увидеть, что происходит, — это наложить изогнутую балку поверх исходной прямой балки.
Теперь вы можете заметить, что нижняя поверхность балки стала длиннее, а нижняя поверхность балки стала короче. Кроме того, по центру балки длина вообще не изменилась — соответствует нейтральной оси. Чтобы повторить это на языке этого класса, мы можем сказать, что нижняя поверхность находится под напряжением, а верхняя поверхность находится под давлением.Что-то более тонкое, но все же можно наблюдать из наложенного выше изображения, это то, что смещение луча изменяется линейно сверху вниз, проходя через ноль на нейтральной оси. Помните, это именно то, что мы видели и с кручением — напряжение линейно изменялось от центра к центру. Мы можем посмотреть на это распределение напряжений в поперечном сечении балки более подробно:
Теперь мы можем найти математическую связь между приложенным моментом и напряжением в балке.Мы уже упоминали, что балка линейно деформируется от одного края к другому — это означает, что деформация в направлении x увеличивается линейно с расстоянием по оси y- (или по толщине балки). Таким образом, деформация будет максимальной при растяжении при y = -c (поскольку y = 0 находится на нейтральной оси, в данном случае в центре балки), и будет максимальной при сжатии при y = c. . Мы можем записать это математически так:
Теперь это говорит нам кое-что о деформации, что мы можем сказать о максимальных значениях напряжения? Что ж, давайте начнем с умножения обеих частей уравнения на E , модуль упругости Юнга.Теперь наше уравнение выглядит так:
Используя закон Гука, мы можем связать эти величины со скобками под ними с напряжением в направлении x и максимальным напряжением. Это дает нам это уравнение для напряжения в направлении x — :
Наш последний шаг в этом процессе — понять, как изгибающий момент соотносится с напряжением. Для этого напомним, что момент — это сила, умноженная на расстояние. Если мы можем представить себе, что смотрим только на очень маленький элемент в балке, дифференциальный элемент, то мы можем записать это математически как:
Поскольку в нашем уравнении есть дифференциалы, мы можем определить момент M , действующий по площади поперечного сечения балки, интегрировав обе части уравнения.И, если мы вспомним наше определение напряжения как силы, приходящейся на площадь, мы можем написать:
Последний член в последнем уравнении — интеграл от y в квадрате — представляет второй момент площади относительно оси z (из-за того, как мы определили наши координаты). В декартовых координатах этот второй момент площади обозначается I (помните, в цилиндрических координатах он обозначался как J ). Теперь мы можем, наконец, записать наше уравнение для максимального напряжения и, следовательно, напряжения в любой точке оси y , как:
Важно отметить, что индексы в этом уравнении и направление вдоль поперечного сечения (здесь оно измеряется вдоль y ) все будут меняться в зависимости от характера проблемы, т.е.е. направление момента — вокруг какой оси изгибается балка? Мы основали наши обозначения на показе изогнутой балки на первом изображении этого урока.
Помните, в начале раздела я упоминал, что изгиб и кручение на самом деле очень похожи? На самом деле мы очень явно видим это в последнем уравнении. В обоих случаях напряжение (нормальное для изгиба и сдвиг для кручения) равно пара / момент ( M для изгиба и T для кручения), умноженному на положение вдоль поперечного сечения. , , потому что напряжение неоднородно по поперечному сечению (с декартовыми координатами для изгиба и цилиндрическими координатами для кручения), все деленное на второй момент площади поперечного сечения.
СводкаВ этом уроке мы узнали о моментов области и диаграмм момента сдвига . Из первого момента площади поперечного сечения мы можем вычислить центроид . Мы узнали, как вычислить второй момент площади в декартовых и полярных координатах, и мы узнали, как теорема о параллельной оси позволяет нам вычислить второй момент площади относительно центроида объекта — это полезно для разделения сложного поперечного сечения на несколько простых форм и объединение их вместе.Мы пересмотрели концепцию диаграмм сдвига и момента из статики. Эти диаграммы будут важны для определения максимальной силы сдвига и изгибающего момента вдоль сложно нагруженной балки, что, в свою очередь, потребуется для расчета напряжений и прогнозирования разрушения.
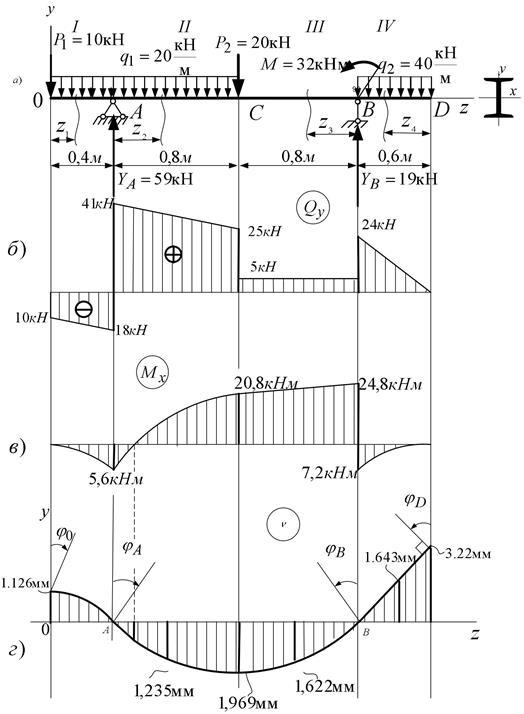 3.13, б и в).
3.13, б и в).  Наклон линии равен величине сдвига.
Наклон линии равен величине сдвига.