5.3. Расчет балок на прочность. Условие прочности при изгибе
Формула (5.13) решает вопрос о величине и распределении нормальных напряжений по сечению. Она выведена в предположении наличия чистого изгиба, когда сечения остаются плоскими.
Исследования показали, что когда поперечная сила не равна нулю, сечения не только поворачиваются, но и несколько искривляются под влиянием касательных напряжений. Однако это искривление для двух смежных сечений таково, что оно не меняет установленного выше закона распределения деформаций волокон, заключающихся между этими сечениями. Поэтому формула (5.13) может быть применена и в том случае, когда поперечная силане равна нулю.
Для проверки
прочности балки по нормальным напряжениям
необходимо найти наиболее напряженные
растянутые или сжатые волокна сечения.
Для этого необходимо применить формулу
(5.
. (5.14)
Обычно эту формулу преобразовывают, деля числитель и знаменатель на :
.
Величина
называется осевым моментом сопротивления
сечения и обозначается буквой.
Измеряется осевой момент сопротивления
единицами длины в третьей степени,
например (см3).
Физический смысл момента сопротивления
состоит в следующем: чем больше
,
тем больший изгибающий момент может
принять на себя балка, не подвергаясь
опасности разрушения. Таким образом,
величина момента сопротивления
характеризует влияние
формы и размеров поперечного сечения
балки на ее способность сопротивляться
внешним нагрузкам, не разрушаясь.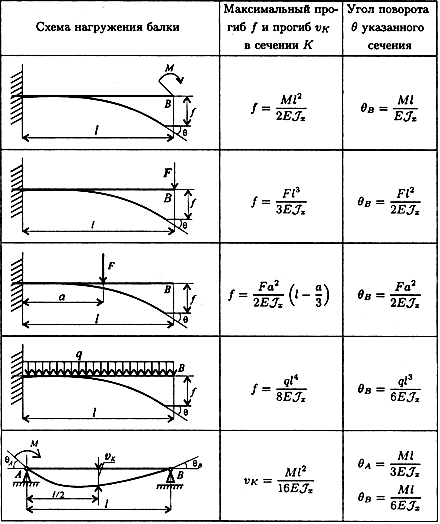
Максимальные напряжения, действующие в балке, могут быть найдены из выражения
. (5.15)
При симметричном относительно нейтральной линии сечении, например, прямоугольном, расстояния до крайних растянутых и сжатых волокон одинаковы и такое сечение имеет одно вполне определенное значение момента сопротивления относительно оси . Так, при высоте прямоугольника (Рис.5.7), равной
и .
Рис. 5.7
Если сечение несимметрично относительно нейтральной линии – тавр, мы получим два момента сопротивления: один для волокон А (Рис.5.7,б): и другой для волокон В:. Теперь в формулу (5.15) следует вводить: при вычислении напряжений в точке А и при вычислении напряжений в точке В.
Запишем условие
прочности при изгибе. Это условие
выражает ту мысль, что наибольшее
действительное напряжение должно быть
не больше допускаемого:
Это условие
выражает ту мысль, что наибольшее
действительное напряжение должно быть
не больше допускаемого:
(5.16)
Условие прочности (5.16) решает три задачи:
1. Задача проверочного расчета, заключающаяся в вычислении максимальных действительных напряжений в изгибаемой балке и сравнении этих напряжений с допускаемым. Если действительные напряжения не превышают допускаемой величины, считается, что прочность не нарушена и конструкцию можно эксплуатировать дальше.
2. Задача подбора величины допускаемой нагрузки. В результате решения этой задачи определяется допускаемое значение для расчетного изгибающего момента, а затем находятся допускаемые значения самих внешних нагрузок, функцией которых является расчетный изгибающий момент:
. (5.17)
3. Задача проектировочного расчета, заключающаяся в определении размеров поперечного сечения балки при известном расчетном изгибающем моменте и известном допускаемом напряжении:
. (5.18)
(5.18)
Здесь: требуемый момент сопротивления.
При расчете балок на прочность следует различать два случая. Первый случай, наиболее часто встречающийся при изгибе, когда материал одинаково сопротивляется растяжению и сжатию; в этом случае допускаемые напряжения для того и другого вида деформации равны между собой:
.
Тогда при симметричном сечении безразлично, проверять ли прочность растянутых или сжатых волокон, ибо для тех и других момент сопротивления и наибольшие действительные напряжения будут иметь одну и ту же величину. При несимметричном сечении в формулу (5.16) вместонадо подставить меньшее значение изи; оно будет относиться к наиболее удаленному волокну.
Второй случай имеет место, когда материал балки неодинаково сопротивляется растяжению и сжатию; тогда вместо одного условия прочности мы получаем два: одно -–для растянутых, другое – для сжатых волокон:
;
. (5.19)
(5.19)
В зависимости от того, чему лучше сопротивляется материал, что больше +или, приходится соответствующим образом конструировать сечение, выбирая его форму и размеры так, чтобыиудовлетворяли условию прочности.
Рассмотрим несколько примеров определения моментов сопротивления сечений и расчета балок на прочность.
Пример 5.2. У которой из фигур (Рис.5.8), имеющих одинаковую площадь, момент сопротивления относительно оси ,будет наибольшим? Определить наибольший момент сопротивления.
Рис.5.8
Решение:
В примере 4.8 были найдены моменты инерции каждого из сечений относительно центральной оси сечения .
Найдем моменты сопротивления:
для сечения круглой формы:
см3;
для сечения квадратной формы:
см3;
для сечения прямоугольной формы:
см3;
для сечения треугольной формы:
см3.
Таким образом, наибольший момент сопротивления оказался у сечения прямоугольной формы: см3.
Пример 5.3.На рисунке изображены поперечные сечения 4х балок (Рис.5.9), изготовленных из одинакового материала. Которая из балок является наиболее прочной?
Рис.5.9
Решение:
Наиболее прочной будет балка, у которой момент сопротивления относительно оси будет наибольший. Вычислим моменты сопротивлениядля каждого из сечений.
Квадратное сечение.
см3.
Прямоугольное сечение.
см3.
Круглое сечение.
см3;
Ромбовидное сечение. Рассматриваемое сечение получилось путем поворота горизонтальной оси квадратного сечения на 45 0. В результате момент инерции сечения относительно осине изменился и может быть вычислен как для квадратного сечения:
см4.
Осевой момент сопротивления найдем, разделив момент инерции на :
см3.
Таким образом, наибольший момент сопротивления оказался у круглого поперечного сечения: см3. Следовательно, балка с круглым поперечным сечением обладает наибольшей прочностью.
Пример 5.4.Как изменится прочность балки, если поперечное сечение будет переведено из положения “I” в положение “II” (Рис.5.10)?
Рис.5.10
Решение:
1. Вычислим осевой момент сопротивлениядля положения сеченияI :
см3.
2. Вычислим осевой момент сопротивлениядля положения сеченияII:
см3.
3. Найдем отношение осевых моментов инерции для положения сеченияI
и II:
Таким
образом, при переводе сечения из положения
I в положениеII
прочность балки уменьшается в 3
раза.
Напряжение при изгибе и расчет балок на прочность
При поперечном изгибе балки от произвольной внешней нагрузке в ее поперечных сечениях возникают перерезывающие силы и изгибающие моменты (рис. 8.20, а).
Рисунок 8.20 – Напряжения в поперечных сечениях балки при ее поперечном изгибе
К изгибающему моменту М в сечении х приводят нормальные напряжения , действующие перпендикулярно плоскости поперечного сечения (рис. 8.20, б). Перерезывающая сила является равнодействующей касательных напряжений , действующих в плоскости сечения.
Приведем формулы для вычисления этих напряжений, необходимых для проверки прочности балки.
Рассматривая деформацию волокна балки, проходящего через точку А сечения балки (см. рис. 8.20, б), можно получить формулу для нормальных напряжений :
где – изгибающий момент в сечении х по длине балки; – вертикальная координата т. А, отсчитываемая от нейтральной оси (н.о.) сечения, где определяется напряжение; – центральный осевой момент инерции сечения балки относительно центральной оси z (н.о.), проходящий через центр тяжести сечения.
А, отсчитываемая от нейтральной оси (н.о.) сечения, где определяется напряжение; – центральный осевой момент инерции сечения балки относительно центральной оси z (н.о.), проходящий через центр тяжести сечения.
Из формулы (8.11) следует, что нормальные напряжения распределяются по высоте сечения по линейному закону: для изогнутой при изгибе балки (см. рис. 8.20, а) верхние волокна балки сжимаются (такие напряжения принимаются со знаком «-»), а нижние – растягиваются (принимаются со знаком «+»). Поэтому, чтобы автоматически учесть знаки напряжений, изгибающего момента
График изменения нормальных напряжений по высоте изгибаемой балки (см. рис. 8.22, а) называется эпюрой (эп. ), показанной на рис. 8.21, а.
Эп. показывают в плоскости сечения балки (рис. 8.21, б, в), разворачивая действительную эпюру в объемном изображении по направлению к оси z на 90˚.
Рисунок 8.21 – Эпюры нормальных и касательных напряжений для балки прямоугольного сечения
Эпюры показываются знаками напряжений , откладывая положительные значения справа, а отрицательные – слева от вертикальной линии.
Из эпюры видно, что максимальные нормальные напряжения по модулю возникают в наиболее удаленных от н.о. точках сечения балки при .
Величина в формуле (8.11), зависящая только от размеров и формы поперечного сечения балки и называемая осевым моментом сопротивления сечения, рассчитывается по формуле
Следовательно, условие прочности на изгиб балок по нормальным напряжениям будет:
Для балок симметричного профиля относительно н.о. величина одинакова для кратных точек сечения.
Для балки несимметричного поперечного сечения, например, несимметричный двутавр (рис. 8.22, а) Эп. показанна на рис. 8.22, б.
Рисунок 8.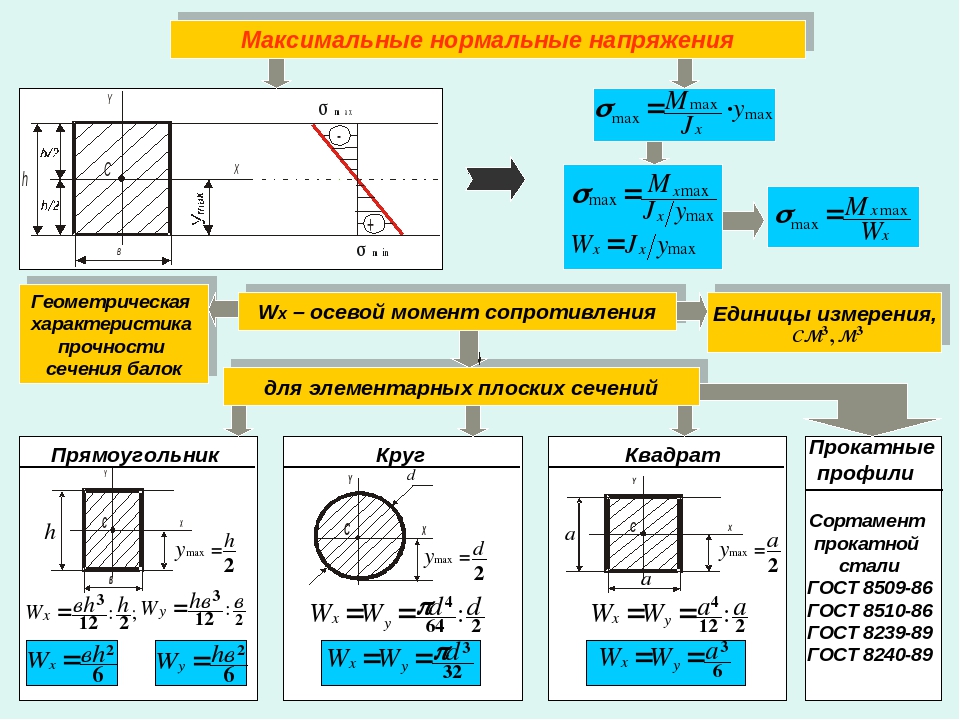 22 – Эпюры нормальных и касательных напряжений для несимметричного двутавра
22 – Эпюры нормальных и касательных напряжений для несимметричного двутавра
Для такой балки
где – минимальный момент сопротивления сечения, .
Для большинства балок в различных конструкциях нормальные напряжения являются наибольшими и по ним проверяется прочность таких элементов конструкций:
где – наибольший по модулю изгибающий момент в опасном сечении балки; – допускаемое нормальное напряжение, равное ( – коэффициент запаса прочности, – предел текучести материала).
Условие прочности (8.15) дает возможность решать такие три задачи: 1) определять напряжение, если известны изгибающий момент, действующий на балку, и момент сопротивления сечения; 2) определять допустимую нагрузку через изгибающий момент и момент сопротивления сечения; 3) определять момент сопротивления, а по нему и размеры сечения, если известны изгибающий момент и допускаемое напряжение.
Формула для касательных напряжений при поперечном изгибе балки была впервые получена Д. И. Журавским при рассмотрении условия равновесия отсеченного элемента балки и носит имя формулы Журавского:
И. Журавским при рассмотрении условия равновесия отсеченного элемента балки и носит имя формулы Журавского:
где – перерезывающая сила в сечении балки; – момент сопротивления части площади сечения балки по одну сторону от точки А (см. рис. 8,22, а), где рассчитывается величина ; – центральный момент инерции площади поперечного сечения балки, относительно горизонтальной оси z; – горизонтальный размер сечения балки, где вычисляется .
Распределение касательных напряжений по высоте сечения балки называется эпюрой (эп. и соответствует закону квадратичной параболы (см. рис. 8.22, в, г). Знаки напряжений на эп. не проставляются. Наибольшие касательные напряжения возникают в точке центра тяжести сечения балки, а в крайних точках по высоте сечения – .
Следует заметить, что для балок составного поперечного сечения (например, составной двутавр на рис. 8.22, а) в точках сопряжения стенки и полок значения будут двузначны, т. к. для стенки величина формуле (8.16) соответствует толщине стенки t, а для полок величина равна их ширине. Поэтому на эп. (см. рис. 8.22, в) величины касательных напряжений в полках значительно меньше величин , относящихся к одноименным точкам стенки. Этими небольшими напряжениями в полках пренебрегают и строят эпюру только для стенки (см. рис. 8.22, г).
к. для стенки величина формуле (8.16) соответствует толщине стенки t, а для полок величина равна их ширине. Поэтому на эп. (см. рис. 8.22, в) величины касательных напряжений в полках значительно меньше величин , относящихся к одноименным точкам стенки. Этими небольшими напряжениями в полках пренебрегают и строят эпюру только для стенки (см. рис. 8.22, г).
Для коротких и высоких балок величины касательных напряжений соизмеримы с величинами нормальных напряжений . Поэтому для таких балок, где существенную роль играет деформация сдвига, проверяется условие прочности по касательным напряжениям , где – допускаемое касательное напряжение, выбираемое из нормативных документов.
С проверками прочности балок связаны гипотезы прочности.
Для простейший напряженных состояний условия прочности состоят в сопоставлении максимальных напряжений с величинами допускаемых напряжений:
а) для одноосного растяжения-сжатия (рис.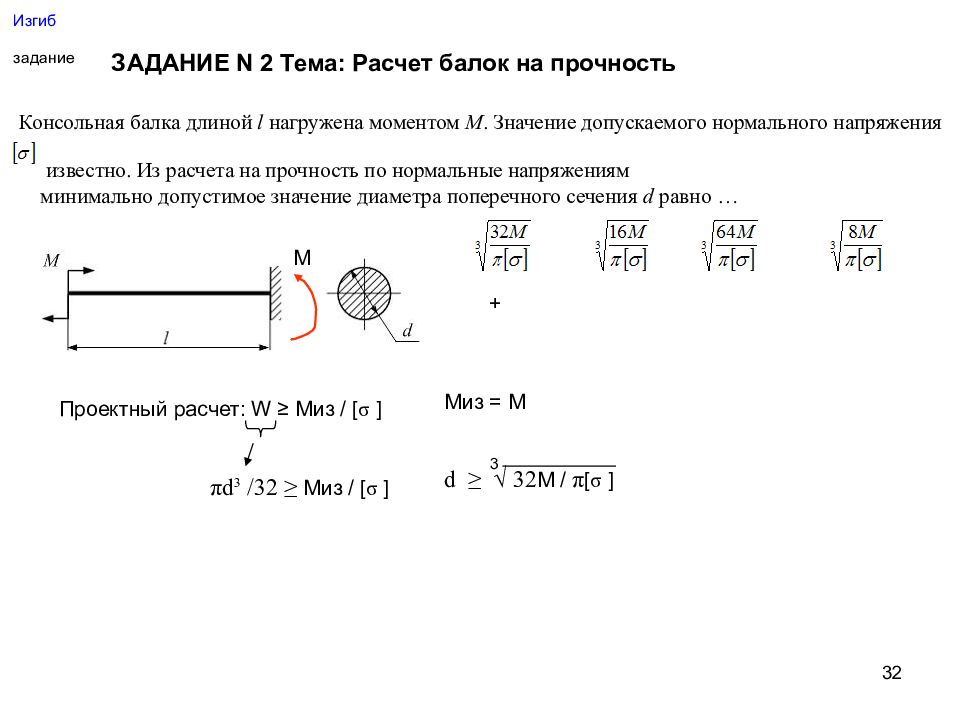 8.23, а)
8.23, а)
б) при сдвиге (срезе) на рис. 8.23, б
Рисунок 8.23 – Простейшие виды деформаций растяжения- сжатия(а), сдвига (б)
В то же время при поперечном изгибе балок в некоторых точках поперечных сечений возникают как нормальные, так и касательные напряжения. То есть напряженное состояние здесь будет двухосным (сложным). Поэтому вводятся так называемые гипотезы прочности, которые устанавливают признаки равнопрочности (эквивалентности) сложных напряженных состояний простейшим. Наиболее распространенными являются следующие гипотезы прочности:
а) гипотеза наибольших касательных напряжений (третья гипотеза прочности), согласно которой два напряженный состояния равнопрочны (простейшее и сложные), если максимальные касательные напряжения для них одинаковы. Проверка прочности проводится здесь по приведенным (эквивалентным) напряжениям:
где – приведенные напряжения; – напряжения в поперечном сечении балки, где действует наибольший изгибающий момент .
б) энергетическая теория, называемая четвертой гипотезой прочности, соответствует условию:
Условиями (8.17) и (8.28) можно установить наиболее напряженную точку по высоте сечения балки.
Так, для симметричной двутавровой балки (рис. 8.24) наиболее опасными точками по нормальным напряжениям будут т. 1, 5:
В этих точках нет касательных напряжений.
Опасной точкой по касательным напряжениям будет т. 3, где действуют максимальные касательные напряжения, а нормальные напряжения равны нулю:
Рисунок 8.24 – К проверке прочности двутавровой балки
Однако есть точки т.т. 2, 4, где существуют и нормальные, и касательные напряжения. Для них и осуществляется проверка по приведенным напряжениям, например, по формуле (8.17):
Здесь
где перерезывающая сила определяется в том сечении, в котором действует ; – статический момент полки относительно н. о.
о.
Узнать еще:
Балки Прочность при изгибе — Энциклопедия по машиностроению XXL
Все рассмотренные примеры расчета на прочность при изгибе относятся к тем случаям, когда опасной является одна из точек крайних волокон балки (рис. 249, б) и напряженное состояние в ней линейное (рис. 250, а). Как уже отмечалось, в подавляющем большинстве практически важных случаев этого расчета достаточно. [c.262]В проектировочном расчете бруса большой кривизны для определения размеров поперечного сечения можно воспользоваться условием прочности при изгибе балки с соответствуюш,ей формой поперечного сечения, а затем, несколько увеличив полученные размеры, проверить прочность бруса по условию (15.19). Если брус большой кривизны изготовлен из материала, имеющего различные допускаемые напряжения на растяжение и на сжатие (некоторые чугуны, пластмассы и т. п.), то условие прочности должно выполняться для крайних точек сечения как в растянутой, так и в сжатой областях. [c.439]
[c.439]
Величина называется осевым моментом сопротивления или моментом сопротивления при изгибе. Момент сопротивления является геометрической характеристикой поперечного сечения балки, определяющей ее прочность при изгибе. [c.152]
Если материал балки хрупкий, например закаленная сталь, чугун, текстолит и др., то расчет на прочность при изгибе проводят по напряжениям растяжения и сжатия. У хрупких материалов (см. 2.9) предел прочности при сжатии выше предела прочности при растяжении (Срс ир)- Следовательно, поперечным сечениям балок из хрупких материалов целесообразно придавать асимметричную форму относительно нейтральной оси (рис. 2.78) и располагать бал- [c.214]
Эта формула представляет собой условие прочности при изгибе ее называют также формулой проверочного расчета, так как в таком виде ею пользуются, когда величина изгибающего момента и размеры поперечного сечения балки известны. [c.289]
[c.289]
Занятия в аудитории по построению эпюр должны занять примерно 6 часов и завершиться проведением контрольной работы (желательно двухчасовой), в которой требуется построить эпюры для двухопорной и консольной (жестко защемленной одним концом) балок. Конечно, можно ограничиться одной задачей, дав контрольную работу на один час, но тогда следует в контрольную работу по расчетам на прочность при изгибе включить задачу, в которой придется построить эпюры для балки со всеми видами нагрузок и не менее чем с тремя участками нагружения. [c.127]
Большинство расчетов на прочность при изгибе относится к тем случаям, когда опасной является одна из точек крайних волокон балки. Напряженное состояние в этой точке линейное, и расчет производится по формуле (7.6). [c.204]
Расчетные уравнения прочности при изгибе аналогичны расчетным уравнениям, рассмотренным выше. Они дают возмол ность также решать три задачи 1) определять напряжение, если известны изгибающий момент, действующий на балку, и момент сопротивления сечения балки 2) определять изгибающий момент, действующий на балку, если известны допускаемое напряжение и момент сопротивления сечения, и 3) определять момент сопротивления, а по нему и размеры сечения, если известны изгибающий момент и допускаемое напряжение. [c.228]
Для того, чтобы произвести расчет балки на прочность при изгибе, необходимо знать наибольшие значения поперечной силы Qy и изгибающего момента и положение сечений, в которых они действуют. В связи с этим возникает необходимость определить закон изменения Qy и по длине балки. Для этой цели обычно строят эпюры поперечных сил и изгибающих моментов, которые представляют собой графическое изображение функций Qy и М . [c.122]
Геометрия образцов и методы испытаний. Для проведения сравнительных испытаний должна быть надежно измерена толщина материала. Предел прочности при сдвиге методом, показанным на рис. 21.9, обычно составляет 25 % предела прочности при изгибе по методу короткой балки . Оба метода допустимы. [c.343]
Для обеспечения прочности балки необходимо, чтобы максимальные нормальные напряжения в опасном сечении, т.е. в сечении, где изгибающий момент наибольший, не превосходили допускаемой величины. Условие прочности при изгибе по нормальным напряжениям для симметричных относительно нейтральной оси сечений имеет вид [c.115]
Прочность балки, работающей на изгиб, проверяется, как правило, по наибольшим нормальным напряжениям. Условие прочности при изгибе балки по нормальным напряжениям имеет вид [c.160]
Рассмотрим теперь расчет па прочность при изгибе балки, материал которой по-разному работает на растяжение и сжатие, т.е. когда [сг]р ф [сг]с. В этом случае условия прочности сводятся к следуюш им [c.215]
Так как волокна балки при изгибе работают на растяжение и на сжатие, то расчет на изгиб следует вести по допускаемому напряжению на растяжение или на сжатие (смотря по тому, какое из двух имеет меньшую величину). Поэтому условие прочности при изгибе имеет вид [c.151]
Итак, для расчета балки на прочность при изгибе по формулам (111) или (112) необходимо [c.152]
Так как осевой момент сопротивления является характеристикой прочности при изгибе, то из формулы (115) можно заключить, что размеры сторон прямоугольника в и к) по-разному влияют на прочность балки сторона, параллельная силовой линии, входит в выражение в квадрате и потому влияет на прочность значительно сильнее, чем сторона, перпендикулярная к силовой линии. [c.156]
Таким образом, балка такого профиля содержит дополнительный полуторный запас прочности при изгибе (если ее материал обладает площадкой текучести). [c.441]
Величина /л у = называется о с е в ы м м о м е н т о м сопротивления сечения и является геометрической характеристикой поперечного сечения балки, определяющей ее прочность при изгибе . [c.122]
Решение. Материал оси — сталь Ст5. Так как ось направляющего блока неподвижная и находится под действием постоянной нагрузки, рассчитаем ее на статическую прочность при изгибе. Рассчитываемую ось блока можно рассматривать как свободно лежащую двухопорную балку (рис. 16.7,6) с двумя сосредоточенными силами F со стороны подшипников. [c.284]
Уравнение прочности при изгибе имеет вид о=Мтах/№ материала балки. При этом [а]/[ар ] или [ст]=[ас ], где [ор ] — допускаемое напряжение на растяжение [ос ] — допускаемое напряжение на сжатие.. [c.290]
Однако, чтобы не страдала надежность расчетов, при допущении о равенстве модулей Юнга сжатой и растянутой зоны изгибаемой балки, следует вносить соответствующую корректуру в величину допустимого предела прочности при изгибе [ст] . [c.42]
Расчеты на прочность с учетом пластических деформаций будут рассмотрены в гл. 18. Здесь ограничимся лишь определением нормальных напряжений при изгибе балки прямоугольного поперечного сечения, материал которой не следует закону Гука на протяжении всего процесса нагружения, причем зависимости между напряжениями и деформациями различны при растяжении и сжатии. [c.326]
Для обеспечения прочности балки необходимо, чтобы наибольшие растягивающие и наибольшие сжимающие напряжения при изгибе в опасном сечении, т. е. в сечении, где М имеет наибольшее значение, не превосходили соответствующих допускаемых напряжений (рассматриваются только балки с постоянным по всей длине поперечным сечением). [c.151]
Какая геометрическая характеристика сечения влияет на прочность балки и какая — на жесткость балки при изгибе [c.273]
Условие прочности балки при изгибе заключается в том, что максимальное нормальное напряжение в опасном сечении не должно превышать допускаемое. [c.247]
Балки равного сопротивления изгибу. При изгибе балок постоянного сечения (за исключением случая чистого изгиба) все сечения, кроме опасного, имеют излишний запас прочности, что свидетельствует о нерациональном использовании материала. Наиболее рациональной будет такая форма балки, при которой напряжения во всех поперечных сечениях будут равны допускаемому. Такие балки называются балками равного сопротивления изгибу. [c.262]
Формула для определения напряжений (13.1.1) будет справедлива и для других балок, поэтому условие прочности при косом изгибе может быть записано для любой балки в следующем виде [c.224]
Таким образом, при поперечном изгибе балки материал ее находится в неоднородном плоском напряженном состоянии. Условие прочности должно быть записано для так называемой опасной точки балки, т. е. той точки, где материал находится в наиболее напряженном состоянии. Опасной будет одна из следующих трех точек а) точка, где нормальное напряжение достигает наибольшей величины б) точка, где касательное напряжение достигает наибольшей величины в) точка, где ант, хотя и не принимают наибольших значений, но в своей комбинации создают наиболее невыгодное сочетание, т. е. наибольшее эквивалентное напряжение по принятой для расчета теории прочности. При этом таких точек может оказаться несколько. [c.274]
Расчеты на прочность с учетом пластических деформаций будут рассмотрены в гл. 19. Здесь ограничимся лишь определением нормальных напряжений при изгибе балки прямоугольного поперечного сечения, материал которой не следует закону Гука на протяжении всего процесса нагружения, причем зависимости между напряжениями и деформациями различны при растяжении и сжатии. Рассмотрим также случай изгиба при различных модулях упругости для растяжения и сжатия. Опыты показывают, что и в указанных случаях гипотеза плоских сечений справедлива. [c.346]
Как производится расчет на прочность при прямом изгибе балки из пластичного материала, имеющей постоянное по всей длине поперечное сечение Напишите зависимости для всех трех видов расчета проверочного, проектного и для расчета на определение допускаемой нагрузки. [c.338]
Для определения пределов прочности при сдвиге слоистых материалов широко используется как изгиб коротких балок с отношением l/h 5, так и Испытание пластинок в шарнирном четырехзвеннике. Использование этих методов для испытаний пространственно-армированных материалов не дает положительных результатов. При испытании на изгиб коротких балок даже с отношением llh яг 3 не происходит их разрушения от сдвига. Изменение формы поперечного сечения балки с прямоугольника на двутавр не. дает положительных результатов. [c.46]
В ряде случаев элементы конструкций должны быть рассчитаны не только на прочность, но и на жесткость. Расчет на жесткость элемента конструкции, имеющего форму бруса, заключается в определении наибольших угловых и линейных перемещений его поперечных сечений при заданной нагрузке и сопоставлении их с допускаемыми, зависящими от назначения и условий эксплуатации данного элемента. Например, рассчитывая вал на жесткость при кручении, ограничивают углы поворота поперечных сечений вокруг его продольной оси, а при расчете балки на жесткость при изгибе ограничивают величину прогиба. Иными словами, -условие жесткости можно выразить неравенством 8 [б], где 8 — перемещение рассматриваемого сечения, возникающее под заданной нагрузкой, а [8] — величина допускаемых перемещений, назначаемая конструктором. [c.190]
Как определяют предел прочности деревянной балки при изгибе [c.143]
Средняя высота клина h определяется из условия прочности на изгиб. Клин рассматривается как балка, свободно лежащая на двух опорах и равномерно нагруженная распределенной нагрузкой (рис. 29.1, е). При расчете принимают равномерное распределение нагрузки, хотя оно и несколько отличается от действительного. [c.486]
Заключительный этап изучения расчетов на прочность при изгибе — это расчет чугунной балки (балки из материала, различно сопротивляющегося растяжению и сжатию). Здесь наиболее интересны (и в то же время, пожалуй, наиболее трудны для учащихся) задачи на балки с разнозначными эпюрами изгибающих моментов. В этих задачах приходится самостоятельно выбирать рациональное расположение сечения и вести проверку прочности для двух предположительно опасных сечений. Одну задачу такого типа следует решить в аудитории, скажем, на определение допускаемой нагрузки, а вторую (на определение требуемых размеров сечения при заданном соотнощении размеров элементов сечения) дать на дом, Это не исключает включения подобной задачи в домащнюю расчетно-графическую работу на изгиб. [c.133]
Условие прочности при изгибе балки по касэтельным напряжениям [c.160]
Подбор поперечного сечения балки. Опасным является сечение Е, где возникает наибольший по абсолютной величине Мпах 72,5 кН м. Двутавровое сечение балки подбираем из условия прочности при изгибе при расчетном сопротивлении материала Жи = 200-10 кН/м2 (сталь) [c.87]
Уяк было показано вышеЗ При изгибе величина нормальных напряжений зависит от величины изгибающего момента, а величина касательных напряжений — от величины поперечной силы. Изгибающий момент или поперечная сила в любом сечении балки могут быть определены рассмотренными вывде методами, с помощью эпюр, rit и расчетах на прочность большое значение имеет распределение нот1аЛ1 ных и касательных напряжений по сечению. [c.171]
Расчет на прочность при простом изгибе. Брус, работающий на изгиб, часто назывглот балкой. При поперечном изгибе балок сплошных поперечных сечении касательные напряжения не оказывают влияния на прочность. Поэтому, как и при чистом изгибе, прочность таких балок в условиях поперечного изгиба определяется максимальной величиной пормг1Льных напряжений. [c.209]
При расчете оси на прочность ее оассматпивают как балку на шарнирных опорах (рис. 3.97). После построения эпюры изгибаю-щих моментов определяют из условия прочности на изгиб требуе-аметр d сечения, в котором изгибающии момент максимален [c.411]
Так как прочность поперечного сечения балки при изгибе определяется величиной его момента сопротивления W, а вес балки пропорционален площади ее поперечного сечения F, то степень экономичности поперечного сечения балки можно оценивать отно-W [c.113]
Срезка некоторой части поперечного сечения балки приводит, конечно, к уменьшению его момента инерции. Однако если при этом существенно уменьшается и высота сечегшя, то момент сопротивления его (и прочность балки при изгибе) может не только [c.269]
Очевидно, что напряжения во всех остальных сечениях призматической балкп будут меньше допускаемого и только при чистом изгибе напряжения во всех сечениях призматической балки одинаковы. В последнем случае все сечения балки равноопасны. Таким образом, при изгибе балки постоянного сечения, исключая случай чистого изгиба, все сечения балки, кроме опасного, имеют, лишний запас прочности, что указывает йа нерациональное использование в них материала. [c.271]
Расчет стальной балки на прогиб
При расчете стальных балок по II-й ГПС (по прогибам) необходимо создавать раскрепления для прогибов:
Информация из справки LIRA SAPR (Справка\Пояснения Сталь\Проверки прогибов):
Проверка прогиба осуществляется сопоставлением реально определенного относительного прогиба (L/f) с максимально возможным для данного конструктивного элемента прогибом.
В данной версии проверка выполняется только для балок на основании состава загружений во всех сочетаниях. Учитываются коэффициенты надежности по нагрузке (заданные при формировании РСУ в среде ПК ЛИРА-САПР) и коэффициенты сочетания.
Перемещения, вызванные загружениями с долей длительности 0, в данном расчете не используются.
Прогибы находятся для каждого сечения на основании распределения MY1, MZ1, QY1, QZ1 по длине элемента. Соответственно, увеличение количества расчетных сечений способствует более точному определению прогибов (особенно, если воздействуют сосредоточенные силовые факторы).
В режиме локального расчета элемента (см. справочную систему СТК-САПР) имеется возможность расчета прогибов по огибающим эпюрам изгибающего момента в запас. Это может потребоваться, когда редактируются расчетные сочетания усилий (или нагрузок) и теряется связь с результатами расчета на ПК ЛИРА-САПР основной схемы.
Важно: Предусмотрена возможность определять не чистые перемещения (относительно локальных осей Y и Z в недеформированной схеме), а прогиб относительно двух выбранных условно неподвижных точек – точек раскрепления (в случае консоли, например, относительно одной точки).
Схема к определению прогибов балки с раскреплениями и без раскреплений
На приведенном фрагменте показан механизм определения прогибов (они обозначены как di и dk) в конструктивном элементе с наложенными раскреплениями на элементы.
Если раскрепления не наложены, то прогиб принимается равным полному расстоянию до оси X.
Важно: Если балка (ригель) разбита по длине промежуточными узлами, то для нее необходимо создать конструктивный элемент и раскрепления для проверки прогибов создавать как для конструктивного элемента (т.е. для балки как единого целого). В расчете стальных конструкций коэффициент расчетной длины (и для балок, и для колонн, и для ферм) применяется к длине конечного элемента (КЭ), если не задан конструктивный элемент (КоЭ). Если задан КоЭ, то коэффициент расчетной длины применяется к полной длине КоЭ.
Пример расчета однопролетной балки
Расчётная модель рамы с цельным ригелем и разбитым на отдельные элементы
Согласно нормативной документации прогиб определяется от действия нормативных нагрузок. Поскольку в LIRA SAPR все нагрузки прикладываются к узлам и элементам их расчётными значениями, при определении прогибов программа определяет нормативное значение нагрузок путём деления их на коэффициент надёжности.
Посмотреть какие приняты коэффициенты надёжности, а также ввести их вручную, если это необходимо, можно в окне параметров расчёта.
Окно параметров расчёта, вызываемое из окна задания параметров для стальных конструкций
Подробнее о корректировке коэффициентов надёжности для расчета прогибов вручную читайте в статье «Коэффициенты к временным нагрузкам при проверке прогиба»
Мозаика результатов проверки назначенных сечений по 2 предельному состоянию
Предельно допустимый L/200=6000/200=30мм
Без задания раскреплений (по абсолютному перемещению узлов балки):
((39,8мм/ к-т надежности по нагрузке)/ 30мм))*100%=((39,8/1,1)/30)*100%=120,6%
С заданием раскреплений (по относительному перемещению узлов балки за вычетом перемещений опорных узлов):
((39,8мм-9,14)/ к-т надежности по нагрузке)/30мм))*100%=(((39,8-9,14)/1,1)/30)*100%=92,9%
Ручной ввод расчётной длины балки для расчёта прогибов
В диалоговом окне задания характеристик расчёта стальной балки присутствует группа параметров Расчёт по прогибу.
Информация из справки ЛИРА САПР:
Расчет по прогибу – данные для расчета прогиба. Длина пролета авто – вычисляется по положению раскреплений. Длина пролета точно – длина пролета при расчете приравнивается этому числу.
Рассмотрим раму из предыдущего примера, только теперь раскрепления для прогибов назначим для всех конструкций, а расчётные длины будем для первого случая задавать автоматическим способом, а для второго ручным.
Расчётная модель с информацией о назначенных расчётных длинах балок
Результаты расчётов прогибов балок
Предельно допустимый прогиб при длине 6 м L/200=6000/200=30мм
Предельно допустимый прогиб при длине 4 м L/200=4000/200=20мм
Проценты использования по предельному прогибу
Длина балки 6 м:
((39,8мм-9,14)/ к-т надежности по нагрузке)/30мм))*100%=(((39,8-9,14)/1,1)/30)*100%=92,9%
((39,8мм-9,14)/ к-т надежности по нагрузке)/30мм))*100%=(((39,8-9,14)/1,1)/20)*100%=139,4%
Расчёт прогибов стрельчатой арки
Пример — рама переменного сечения (РПС) пролётом 18 м. Соединение полурам в коньке — шарнирное, опирание полурам на фундамент — шарнирное.
Расчётная модель рамы
При этом в параметрах «Дополнительные характеристики» необходимо указать вручную пролет, с которым программа будет сравнивать прогиб (автоматическое определение пролета возможно только для линейных балок, где все конечные элементы (КЭ) конструктивного элемента (КоЭ) лежат на одной оси):
Эпюра перемещений fz ригеля одной полурамы (вдоль местной оси Z1 стержня)
Мозаика перемещений узлов по Z и «Раскрепления для прогибов» (раскреплён только ригель №4)
Результаты определения прогибов в СТК-САПР:
Результаты определения прогибов ригелей №2 и №4
Предельно допустимый L/200=17664/200=88.32 мм
Без задания раскреплений (по абсолютному значению на эпюре прогибов fz):
96.7/17644=1/182 — совпадает с результатом расчёта элемента №2
С заданием раскреплений (по относительному значению на эпюре прогибов fz):
(96.7-(-6.46))/17644=1/171 — совпадает с результатом расчёта элемента №4
Без задания раскреплений (по абсолютному значению перемещений узлов):
99.8/17644=1/177 — не совпадает ни с чем
Вывод: Расчёт на прогибы выполняется в местной системе координат стержня. Прогиб стрельчатых и цилиндрических арок, а также любых криволинейных конструкций, нужно определять по перемещениям узлов в глобальной системе координат и вручную сравнивать с предельно допустимыми значениями.
Расчёт прогибов цилиндрической арки
Пример – цилиндрическая арка пролётом 18 м, стрелой подъёма f = 9 м. Соединение всех элементов между собой — жёсткое, опирание на фундамент — шарнирное.
Нагрузки на арку приложены их расчётными значениями. Значения нагрузок для определения прогибов принимаются согласно СП 20.13330.2016 Нагрузки и воздействия, таблица Д.1 Приложения Д. В данном примере арка является конструкцией покрытия, прогиб которой должен определяться от постоянных и длительных нагрузок (п.2 табл. Д.1). Для визуализации перемещений от нормативных значений нагрузок, необходимо создать особое РСН с нормативными длительными значениями нагрузок. Нагрузки в данном РСН нужно поделить на коэффициент надёжности, с учётом длительности. На конструкцию действуют два загружения:
Загружение 1 — постоянное, коэффициент надёжности 1.1;
Загружение 2 — кратковременное, коэффициент надёжности 1.2, доля длительности 0.35;
Вычислим коэффициенты для перехода к нормативным значениям
Загружение 1 Kn=1/1.1=0.91;
Загружение 2 Kn=1/1.2*0.35=0.292
Таблица РСН с сочетаниями расчётных и нормативных значений нагрузок с учётом длительности.
Мозаика перемещений узлов цилиндрической арки от РСН2
Предельно допустимый прогиб L/200=18000/200=90 мм
Фактический прогиб (по абсолютному значению перемещений узлов): 32.2/18000=1/559 – меньше предельно допустимого значения.
Примечание: если подобная конструкция стоит на своих опорах, то перемещения опорных точек (для получения относительных перемещений) удобно получить через «Мозаику относительных перемещений», указав реперный узел.
Мозаика перемещений узлов в глобальной СК (абсолютных)
Мозаика перемещений узлов в глобальной СК относительно реперного узла
Напряжения и расчеты на прочность при изгибе.
Сопротивление материалов
Напряжения при изгибе
Нормальные напряжения при чистом изгибе
Как было установлено ранее, в поперечных сечениях балки при чистом изгибе возникают только нормальные напряжения растяжения и сжатия. Вопрос о распределении этих напряжений по поперечному сечению решается путем рассмотрения деформаций волокон балки.
Рассмотрим участок балки, подверженный деформации чистого изгиба. Двумя поперечными сечениями АВ и СD выделим элемент балки бесконечно малой длины ds (рис 1). Радиус кривизны нейтрального слоя балки обозначим ρ.
Рассмотрим слой волокон mn, находящийся на расстоянии y от нейтрального слоя NN. Это волокно в результате деформации изгиба удлинилось на величину nn1. Ввиду малости расстояния ds заштрихованные треугольники будем считать прямолинейными; эти треугольники подобны (n1F || mE):
Δ OEF ~ Δ Fnn1.
Из подобия треугольников запишем равенство:
nn1 / ds = y / ρ.
Так как левая часть этого равенства есть относительное удлинение, т. е. nn1 / ds = ε, то y / ρ = ε.
Применив закон Гука при растяжении и сжатии σ = Еε, получим:
σ = Еy / ρ.
Из этой формулы видно, что нормальные напряжения при изгибе распределены по высоте сечения неравномерно: максимальные напряжения возникают в волокнах, наиболее удаленных от нейтральной оси. По ширине сечения нормальные напряжения не меняются.
Распределение нормальных напряжений изображено на рис. 2.
Полученная формула для определения нормальных напряжений неудобна, так как в нее входит радиус кривизны нейтрального слоя.
Для вывода формулы, связывающей нормальные напряжения с изгибающим моментом, применим метод сечений и рассмотрим равновесие части балки, изображенной на рис. 3.
В плоскости поперечного сечения выделим бесконечно малую площадку dA, в пределах которой будем считать нормальные напряжения σ постоянными; тогда нормальная сила dN, действующая на площадку dA, будет равна:
dN = σdA.
Составим уравнения равновесия:
1. Σ Z = 0; ∫dN = 0, или: ∫σ dA = ∫Еy / ρ dA = Е / ρ ∫y dA = 0.
(ρ для данного сечения, а также модуль упругости Е – величины постоянные, поэтому вынесены за знак интеграла). Поскольку ρ и Е не равны нулю, значит, ∫y dA = 0. Этот интеграл представляет собой статический момент площади сечения относительно оси x, т. е. нейтральной оси бруса (балки). Равенство нулю статического момента инерции означает, что при изгибе нейтральная ось проходит через центр тяжести площади поперечного сечения;
2. Σ Ми = 0; — m + ∫y dN = 0.
Так как при чистом изгибе изгибающий момент равен внешнему моменту Ми = m, то
Ми = ∫y dN = ∫y dA = ∫y Еy / ρ dA = Е / ρ ∫y2 dA,
откуда:
Ми = Е I / ρ,
где: I = ∫y2 dA – момент инерции поперечного сечения относительно нейтральной оси; ЕI – жесткость сечения при изгибе.
Так как при чистом изгибе балки постоянного сечения Ми = const, то:
ρ = EI / Ми = const.
Следовательно, изогнутая ось такой балки представляет собой дугу окружности. Выражение радиуса кривизны подставим в формулу для определения нормальных напряжений; тогда:
σ = Еy / ρ = Ey / EI / Ми = Ми y / I.
Максимальное значение нормальные напряжения будут иметь у волокон, наиболее удаленных от нейтральной оси:
σmax = Ми ymax / I = Ми / I / ymax = Ми / W,
где W = I / ymax – момент сопротивления изгибу (или осевой момент сопротивления).
Момент сопротивления изгибу есть отношение осевого момента инерции поперечного сечения относительно нейтральной оси к расстоянию от этой оси до наиболее удаленного волокна.
Единица момента сопротивления сечения изгибу [W] = м3.
Итак, наибольшие нормальные напряжения при чистом изгибе вычисляются по формуле
σmax = Ми / W.
Нетрудно заметить, что эта формула по своей структуре аналогична формулам для определения напряжений при растяжении, сжатии, сдвиге и кручении.
***
Касательные напряжения при изгибе
Очевидно, что при поперечном изгибе, вызванном приложением к балке поперечной силы, в сечениях балки должны возникнуть касательные напряжения.
Определением зависимости между внешними нагрузками, геометрическими и физическими параметрами балок и касательными напряжениями, возникающими в них, занимался русский мостостроитель Д. И. Журавский, который в 1855 году предложил следующую формулу:
τ = QS / (I d).
Эта формула называется формулой Журавского и читается так:
касательные напряжения в поперечном сечении балки равны произведению поперечной силы Q на статический момент S относительно центральной оси части сечения, лежащей выше рассматриваемого слоя волокон, деленному на момент инерции I всего сечения относительно нейтральной оси и на ширину b рассматриваемого слоя волокон.
По формуле Журавского можно вывести зависимости для определения касательных напряжений в балках, имеющих разную форму поперечного сечения (прямоугольную, круглую и т. п.).
Например, для балки круглого сечения формула Журавского в результате преобразований выглядит так:
τmax = 4Q / (3A) = 4τсред / 3,
где Q – поперечная сила, вызывающая изгиб, А – площадь сечения балки.
Большинство балок в конструкциях рассчитывается только по нормальным напряжениям, и только три вида балок проверяют по касательным напряжениям:
— деревянные балки, т. к. древесина плохо работает на скалывание;
— узкие балки (например, двутавровые), поскольку максимальные касательные напряжения обратно пропорциональны ширине нейтрального слоя;
— короткие балки, так как при относительно небольшом изгибающем моменте и нормальных напряжениях у таких балок могут возникать значительные поперечные силы и касательные напряжения.
Максимальное касательное напряжение в двутавровой балке определяется по формуле Журавского, при этом геометрические характеристики таких балок берутся из справочных таблиц .
***
Расчеты на прочность при изгибе
Условие на прочность при изгибе заключается в том, что максимальное нормальное напряжение в опасном сечении не должно превышать допускаемое.
Полагая, что гипотеза о не надавливании волокон справедлива не только при чистом, но и при поперечном изгибе, мы можем нормальные напряжения при поперечном изгибе определять по такой же формуле, что и при чистом изгибе, при этом расчетная формула выглядит так:
σmax = Миmax / W ≤ [σ]
и читается так: нормальное напряжение в опасном сечении, определенное по формуле σmax = Миmax / W ≤ [σ] не должно превышать допускаемое.
Допускаемое нормальное напряжение при изгибе выбирают таким же, как при растяжении и сжатии.
Максимальный изгибающий момент определяют по эпюре изгибающих моментов или расчетом.
Так как момент сопротивления изгибу W в расчетной формуле стоит в знаменателе, то чем больше W, тем меньшие напряжения возникают в сечении бруса.
Ниже приведены моменты сопротивления изгибу для наиболее часто встречающихся сечений:
1. Прямоугольное сечение размером b x h: Wпр = bh2 / 6.
2. Круглое сечение диаметром d: Wкруг = π d3 / 32 ≈ 0,1d3
3. Кольцо размером D x d: Wкольца = ≈ 0,1 (D4 – d4) / D; (момент сопротивления кольцевого сечения нельзя определять, как разность моментов сопротивления большого и малого кругов).
***
Материалы раздела «Изгиб»:
Деформации растяжения и сжатия
Главная страница
Дистанционное образование
Специальности
Учебные дисциплины
Олимпиады и тесты
10. Изгиб. Расчеты на прочность и жесткость при изгибе
10. Изгиб. Расчеты на прочность и жесткость при изгибе
10.1 Чистый изгиб
Расчетные формулы для определения нормальных напряжений при изгибе обычно выводят из рассмотрения плоского чистого изгиба, который является наиболее простым случаем изгиба (рис.10.1).
Рис. 10.1 Плоский чистый изгиб
Чистый изгиб – такой вид нагружения, при котором в поперечных сечениях бруса возникают только изгибающие моменты Мх, а Q=0.
Чистый изгиб характерен тем, что из шести компонентов внутренних усилий только изгибающий момент не равен 0, а поперечные и нормальные силы отсутствуют. Для тех участков стержня, где соблюдается это условие, изгибающий момент остается постоянным (М = const). Изгибающий момент численно равен сумме моментов всех внешних сил, действующих на отсеченную часть балки относительно оси Ох. Эпюра изгибающих моментов строится на сжатом волокне. При этом изгибающий момент в балках считается положительным, если сжаты верхние волокна, т. е. элемент изгибается выпуклостью вниз.
Рассмотрим три стороны задачи об изгибе:
1. Статическая сторона задачи:
Условия чистого изгиба могут возникать при различных внешних нагрузках. Характерный пример показан на рисунке (простейший двухопорный стержень, нагруженный силами Р) (рис. 10.2).
Рис. 10.2 Напряжения при чистом изгибе
Рассмотрим условие равновесия, связывающее напряжения и внутренние усилия в поперечном сечении балки (рис. 10.3), опуская индекс x y момента, получим
(1)
(2)
(3)
(4)
Рис. 10.3 Поперечное сечение балки
2. Геометрическая сторона задачи:
При изгибе под действием моментов М ось балки искривляется (установлено экспериментально).
Рис. 10.4 Сетка, предварительно нанесенная на балку
Наблюдая за деформацией сетки, предварительно нанесенной на балку (рис. 10.4), можно заметить, что продольные линии при чистом изгибе искривляются по дуге окружности, контуры поперечных сечений остаются плоскими кривыми, пересекая продольные линии под прямыми углами (рис. 10.5). Это говорит о том, что при чистом изгибе поперечные сечения остаются плоскими и, поворачиваясь, становятся нормальными к изогнутой оси балки.
Фактически это есть доказательство того, что все сечения однородной балки при чистом изгибе не искривляются, а лишь поворачиваются. Это утверждение, будучи точным, для чистого изгиба, в общем случае является приближенным и именуется гипотезой плоских сечений (Бернулли).
Рис. 10.5 Деформация участка балки при чистом изгибе
Поворот плоских поперечных сечений одного относительно другого является результатом образования деформаций при чистом изгибе.
В сжатой области (сверху) волокна укорачиваются, а в зоне растяжения удлиняются. Зона растяжения в сечении балки разделяются нейтральным слоем с радиусом кривизны ρ. Длина нейтрального слоя при изгибе остается неизменной.
Рассмотрим два смежных сечения a и b, расположенных между собой на расстоянии dz (рис. 10.6).
Предположим, что левая часть неподвижна, а правая поворачивается относительно левого участка.
Рис. 10.6 Поворот правого участка относительно левого
При чистом изгибе найдем из рассмотрения деформации участка балки длиной dz относительное удлинение некоторого волокна, находящегося на расстоянии у от нейтрального слоя
(5) —относительное удлинение участка
3. Физическая сторона задачи:
При чистом изгибе вводится предположение о ненадавливаемости продольных слоев (рис.10.7).
Рис. 10.7 Деформация участка балки длиной dz
t = 0 – касательное напряжение
s¹0 – нормальное напряжение
Так как t = 0, то это значит, что волокна балки находятся в линейно напряженном состоянии
(6) — применяем закон Гука
4. Объединяем три стороны задачи:
(5)®(6) Þ (7)
(7)®(2)Þ
— осевой момент инерции, зависит от формы, размеров.
(8), где Е∙Ix — жесткость сечения при изгибе
Изменяется s по высоте сечения по линейному закону:
Напряжения при изгибе:
(9) – нормальные напряжения при изгибе.
Рис. 10.8 Сечение не имеющее горизонтальной оси симметрии
Максимальное напряжение при изгибе возникает в точках, наиболее удаленных от нейтральной линии.
— осевой момент сопротивления сечения
(9)®(4)Þ
— статический момент инерции
Значит, ось х – центральная. Таким образом, центр инерции проходит через центр тяжести сечения.
— центробежный момент инерции
Через ось у проходит силовая плоскость, значит, оси x и у – главные центральные оси.
Мы получили условия существования прямого изгиба (когда деформирование бруса происходит в силовой плоскости).
Для сечений с двойной симметрией унижн=уверхн=уmax
, где
— условие прочности при изгибе.
Рис. 10.9 Эпюра нормальных напряжений и сечение с горизонтальной осью симметрии
Пример (Рис. 10.10)
Подобрать номер двутавра
Рис. 10.10 Расчетная схема
Дано:
P=40 кН
A=1 м
[s]=160 МПа
Решение:
Растяжение – сжатие:
Кручение:
Изгиб:
— условие «экономичности»
,
Строим эпюры Q и M (рис. 10.11)(эпюра М строится на сжатых волокнах)
Рис. 10.11 Построение эпюр Q и M
Для этого определяем реакции RA,RB, используя уравнения равновесия
,
,
,
,
Опасное сечение над опорой В
Двутавр №22,
Для №22 перегрузка
Пример (И-1)
Для балки (Рис. 10.12) из расчета на прочность по нормальным напряжениям подобрать сечение в двух вариантах а) двутавровое б) полый прямоугольник. Проверить прочность балки по касательным напряжениям для двух вариантов. Построить эпюру касательных напряжений для прямоугольного сечения. Определить вертикальное перемещение сечения С. сравнить вес балок с прямоугольным и двутавровым сечением.
Рис. 10.12 Прямоугольное полое сечение и расчетная схема
Рис.10.13 Построение эпюр Q и M
Дано:
Решение:
Y:
(у правой)
(MD правой)
На третьем участке определяем максимум для момента:
Находим величину момента сопротивления:
1)для двутавра
подбираем номер двутавра №22 Wx.22=232·10-6
Проверка: % (недонапряжение)
Подбираем номер двутавра №20а Wx.20а=203·10-6
Проверка: % (перенапряжение)
Т.к. на практике допускаются перенапряжения до 5 %,
то выбираем № 22
2)для специального сечения
м
Определим площадь этого сечения:
м2
Проверим прочность балки по касательным напряжениям для двух вариантов сечений:
1)для двутавра
м
м
Па (меньше τдоп)
Двутавр удовлетворяет требованиям прочности
2)для прямоугольника
τ1=0
Па
Па
Па
Па
Определим вертикальное перемещение в сечении с:
Па
Па
1-й участок
2-й участок
3-й участок
4-й участок
5-й участок
Определяем металлоемкость:
Таким образом, балка двутаврового сечения обладает меньшей металлоемкостью, чем балка в виде прямоугольника(рис.10.14 и рис.10.15).
Рис. 10.14 Эпюра касательных напряжений для прямоугольного сечения
Рис. 10.15 Двутаврное сечение балки
10.2 Поперечный изгиб
Поперечный изгиб – это такой вид нагружения, при котором в поперечных сечениях бруса возникают не только изгибающие моменты Мх, но и поперечные силы Qу. Эта сила представляет собой равнодействующую элементарных распределенных сил, лежащих в плоскости сечения. В этом случае в поперечных сечениях возникают не только нормальные, но и касательные напряжения.
Возникновение касательных напряжений τ сопровождается появлением угловых деформаций. Поэтому, кроме основных смещений, свойственных чистому изгибу, каждая элементарная площадка сечения dF получает еще некоторые дополнительные угловые смещения, обусловленные сдвигом (рис. 10.16).
Рис. 10.16 Искривление поперечных сечений
Касательные напряжения распределены по сечению неравномерно, поэтому неравномерно будут распределены и угловые смещения. Это значит, что при поперечном изгибе в отличие от чистого изгиба поперечные сечения не остаются плоскими.
Найдем закон изменения касательных напряжений tzy=t при поперечном изгибе.
Для этого сначала рассмотрим случаи поперечного изгиба
(рис. 10.17):
Рис. 10.17 Эпюры Q и M при поперечном изгибе
Вычислить касательные напряжения проще всего через парные им напряжения, возникающие в продольных сечениях стержня. Выделим из бруска элемент длиной dz (рис. 10.18).
Рис. 10.18 Распределение касательных напряжений элемента бруска
При поперечном изгибе моменты, возникающие в левом и правом сечениях элемента, не одинаковы и отличаются на dM. Продольным горизонтальным сечением, проведенным на расстоянии у от нейтрального слоя, разделим элемент на две части и рассмотрим условия равновесия верхней части. Равнодействующая нормальных сил в левом сечении в пределах заштрихованной площади (отсеченной части) равна
Полагая, что справедливо распределение в виде:
, получим
,
где через у обозначена текущая ордината площадки dF. Разность нормальных сил в правом и левом сечении должна уравновешиваться касательными силами, возникающими в продольном сечении элемента (рис. 10.19)
Рис. 10.19 Распределение касательных напряжений τ(у) на участке dz
Полученный интеграл представляет собой статистический момент относительно оси х части площади, расположенной выше продольного сечения. Обозначим этот статистический момент через , тогда
Учитывая, что
Полученная формула носит название формулы Журавского. Она позволяет вычислить касательные напряжения, возникающие в продольных сечениях стержня.
Полный расчет балки на прочность при поперечном изгибе:
и ,
где Iх – осевой момент инерции сечения относительно центральной оси х;
b(y) – ширина живого сечения на уровне у;
Sхотсеч – статический момент площади, отсеченной уровнем у.
Пример
Найти закон изменения касательного напряжения t(у) на уровне у (рис. 10.20).
Рис. 10.20 Расчетная схема
Закон изменения t представляет собой параболу.
Прямой поперечный изгиб стержня (Лекция №20)
При прямом поперечном изгибе в сечениях стержня возникает изгибающий момент Мхи поперечная сила Qy рис. 1), которые связаны с нормальными и касательными напряжениями
Рис.1. Связь усилий и напряжений
а) сосредоточенная сила, б) распределенная
Рис.2. Модели прямого поперечного изгиба:
Выведенная в случае чистого изгиба стержня формула для прямого поперечного изгиба, вообще говоря, неприменима, поскольку из-за сдвигов, вызываемых касательными напряжениями , происходит депланация поперечных сечении (отклонение от закона плоских сечений). Однако для балок с высотой сечения h<l/4 (рис. 2) погрешность невелика и ее применяют для определения нормальных напряжений поперечного изгиба как приближенную. При выводе условия прочности при чистом изгибе использовалась гипотеза об отсутствии поперечного взаимодействия продольных волокон. При поперечном изгибе наблюдаются отклонения от этой гипотезы:
а) в местах приложения сосредоточенных сил. Под сосредоточенной силой напряжения поперечного взаимодействия могут быть достаточно велики и во много раз превышать продольные напряжения , убывая при этом, в соответствии с принципом Сен-Венана, по мере удаления от точки приложения силы;
б) в местах приложения распределенных нагрузок. Так, в случае, приведенном на рис. 2, б, напряжения от давления на верхние волокна балки . Сравнивая их с продольными напряжениями , имеющими порядок
,
приходим к выводу, что напряжения при условии, что h2 <<l2, так как .
Получим формулу для касательных напряжений . Примем, методика расчета нормальных напряжений известна, что касательные напряжения равномерно распределены по ширине поперечного сечения (рис. 3). Эта предпосылка выполняется тем точнее, чем уже поперечное сечение стержня. Точное решение задачи для прямоугольного поперечного сечения показывает, что отклонение от равномерного распределения , зависит от отношения сторон b/h. При (b/h) =1,0 оно составляет 12,6%, при (b/h) =0,5 только 3,3%.
Рис.3. Расчетная модель поперечного прямого изгиба
Непосредственное определение напряжений затруднительно, поэтому находим равные им (вследствие закона парности) касательные напряжения , возникающие на продольной площадке с координатой у элемента длиной dz, вырезанного из балки, (рис. 3). Сам элемент показан на рис. 4. От этого элемента продольным сечением, отстоящим от нейтрального слоя на у, отсекаем верхнюю часть, заменяя действие отброшенной нижней части касательными напряжениями (индекс гу в дальнейшем опускаем), равнодействующая которых показана на рис. 5. Здесь, согласно второй предпосылке
Рис.4. Расчетный элемент бруса
Рис.5. Фрагмент расчетного элемента бруса
по ширине элемента b. Нормальные напряжения и , действующие на торцевых площадках элемента, также заменим их равнодействующими
,
.
Согласно первой предпосылке нормальные напряжения определяются уже известным способом, , где статический момент отсеченной части площади поперечного сечения относительно оси Ох.
Рассмотрим условие равновесия элемента (рис. 5) составив для него уравнение статики :
откуда после несложных преобразований, учитывая, что
получаем формулу для касательных напряжений при нормальном поперечном изгибе призматического стержня которая называется формулой Журавского.
Рис.6. Распределение касательных напряжений по контуру прямоугольного сечения
В этой формуле by ширина сечения в том месте, где определяются касательные напряжения, а статический момент, подставляемый в эту формулу, может быть вычислен как для верхней, так и для нижней части (статические моменты этих частей сечения относительно его центральной оси Ох отличаются только знаком, так как статическим момент всего сечения равен нулю).
В качестве примера применения формулы Журавского построим эпюру касательных напряжений для случая прямоугольного поперечного сечения балки (рис. 6.). Учитывая, что для этого сечения
получаем
где F=bhплощадь прямоугольника.
Как видно из формулы, касательные напряжения по высоте сечения меняются по закону квадратичеокой параболы, достигая максимума на нейтральной оси
Сделаем несколько замечаний, касающихся расчетов на прочность при прямом поперечном изгибе. В отличие от простых видов деформации, когда в поперечных сечениях стержня возникает лишь один силовой фактор, к которым относятся и изученные выше растяжение (сжатие) и чистый изгиб, прямой поперечный изгиб должен быть отнесен к сложным видам деформации. В поперечных сечениях стержня при поперечном изгибе возникают два силовых фактора: изгибающий момент Мх и поперечная сила Qy (рис. 7), напряженное состояние является упрощенным плоским, при котором в окрестности произвольно выбранных точек поперечного сечения действуют нормальные и касательные напряжения. Поэтому условие прочности для таких точек должно быть сформулировано на основе какого-либо уже известного критерия прочности.
Однако учитывая, что наибольшие нормальные напряжения возникают в крайних волокнах, где касательные напряжения отсутствуют (рис. 7), а наибольшие касательные напряжения во многих случаях имеют место в нейтральном слое, где нормальные напряжения равны нулю, условия прочности в этих случаях формулируются раздельно по нормальным и касательным напряжениям
Рис.7 Распределение нормальных и касательных напряжений по контуру сечения
Рис.8. К сравнительной оценке модулей напряжения
Покажем, что доминирующая роль в расчетах на прочность балки, подвергнутой поперечному изгибу, будет принадлежать расчету по нормальным напряжениям. Для этого оценим порядок max и max на примере консольной балки, показанной на рис. 8:
так как
Тогда
откуда max <<max, а поскольку то доминирующим в этом случае будет расчет по нормальным напряжениям и условие прочности, например, для балки из пластичного материала, работающей на прямой изгиб, как и в случае чистого изгиба будет иметь вид:
РАЦИОНАЛЬНЫЕ ФОРМЫ ПОПЕРЕЧНЫХ СЕЧЕНИЙ ПРИ ИЗГИБЕ
Наиболее рациональным следует признать сечение, обладающее минимальной площадью при заданной нагрузке (изгибающем моменте) на балку. В этом случае расход материала на изготовление балки, будет минимальным. Для получения балки минимальной материалоемкости нужно стремиться к тому, чтобы по возможности наибольший объем материала работал при напряжениях, равных допускаемым или близким к ним. Прежде всего рациональное сечение балки при изгибе должно удовлетворять условию равнопрочности растянутой и сжатой зон балки. Иными словами необходимо, чтобы наибольшие напряжения растяжения (max ) н наибольшие напряжения сжатия (max ) одновременно достигали допускаемых напряжений и .
Поэтому для балки из пластичного материала (одинаково работающего на растяжение и сжатие: ), условие равнопрочности выполняется для сечений, симметричных относительно нейтральной оси. К таким сечениям относится, например, прямоугольное сечение (рис. 9, а), при котором обеспечено условие равенства . Однако в этом случае материал, равномерно распределенный по высоте сечения, плохо используется в зоне нейтральной оси. Чтобы получить более рациональное сечение, необходимо возможно большую часть материала переместить в зоны, максимально удаленные от нейтральной оси. Таким образом, приходим к рациональному для пластичного материала сечению в форме симметричного двутавра (рис. 9, б), у которого возможно большая часть материала сосредоточена на полках (горизонтальных массивных листах), соединенных стенкой (вертикальным листом), толщина которой назначается из условий прочности стенки по касательным напряжениям, а также из соображений ее устойчивости. К двутаврому сечению близко по критерию рациональности так называемое коробчатое сечение (рис. 9, в).
Рис.9. Распределение нормальных напряжений в симметричных сечениях
Рассуждая аналогично, приходим к выводу, что для балок из хрупкого материала наиболее рациональным будет сечение в форме несимметричного двутавра, удовлетворяющего условию равнопрочности на растяжение и сжатие (рис. 10):
которое вытекает из требования
Рис.10. Распределение напряжений несимметричного профиля сечения балки.
а) двутавр, б ) швеллер, в) неравнобокий уголок, г) равнобокий уголок
Рис.11. Используемые профили сечений:
Идея рациональности поперечного сечения стержней при изгибе реализована в стандартных тонкостенных профилях, получаемых методами горячего прессования или прокатки из рядовых и легированных конструкционных высококачественных сталей, а также алюминия и алюминиевых сплавов, получивших широкое распространение в строительстве, машиностроении, авиационном машиностроении. Широко распространены показанные на рис. 11: адвутавр, б швеллер, в неравнобокий уголок, гравнобокий уголок. Реже встречаются тавр, таврошвеллер, зетовый профиль и др. Употребляются также холодногнутые замкнутые сварные профили (рис. 12).
Рис.12. Замкнутые сварные профили
Поскольку по соображениям технологии сортамент стандартных профилей по размерам ограничен (например, наибольший прокатный двутавр согласно ГОСТ 823972 имеет высоту 550 мм), то для больших пролетов приходится применять составные (сварные или клепаные) балки.
Дальше…Краткий справочник по анализу пучка (формула)
ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.
На этой странице представлена краткая справочная таблица формул для расчета напряжений и прогибов в балках.
Сила сдвига и изгибающий момент
Чтобы найти поперечную силу и изгибающий момент по длине балки, сначала решите внешние реакции при граничных условиях.Затем сделайте разрезы по длине балки и решите реакции на каждом разрезе, как показано ниже. Выбранная сторона разреза не повлияет на результаты.
Подписать Конвенцию
| Ножницы | Изгибающий момент |
|---|---|
| Положительный сдвиг вызывает вращение выбранной секции балки по часовой стрелке, отрицательный сдвиг вызывает вращение против часовой стрелки. | Положительный момент сжимает верхнюю часть балки и удлиняет нижнюю часть (т.е. это заставляет луч «улыбаться»). Отрицательный момент заставляет луч «хмуриться». |
Диаграммы сдвига и момента
Сдвиговый и изгибающий моменты балки обычно выражаются с помощью диаграмм сдвига и момента. Здесь показан пример диаграммы момента сдвига.
Общие правила построения диаграмм момента сдвига приведены в таблице ниже.
| Диаграмма сдвига | Схема моментов |
|---|---|
|
|
Напряжения изгиба в балках
Напряжение изгиба в балке равно нулю на нейтральной оси и линейно увеличивается с расстоянием от нейтральной оси в соответствии с формулой изгиба :
| Формула изгиба (напряжение изгиба в зависимости отрасстояние от нейтральной оси): | |
| Максимальное напряжение изгиба возникает в крайнем волокне: |
где M — момент в точке по длине балки, взятый из диаграммы моментов.
Напряжение изгиба в несимметричной балке:
Модуль упругости сечения , S характеризует сопротивление изгибу поперечного сечения одним термином:
Максимальное напряжение изгиба в балке:
Напряжения сдвига в балках
Максимальное напряжение сдвига для общих поперечных сечений:
Таблицы отклонения балки
Таблицы уравнений прогиба, наклона, сдвига и момента вдоль прямых балок для различных конечных условий и нагрузок можно найти на этой странице.
Ознакомьтесь с нашим калькулятором балок, основанным на методике, описанной здесь.
- Расчет напряжений и прогибов в прямых балках
- Строит диаграммы сдвига и момента
- Может указывать любую конфигурацию ограничений, сосредоточенных сил и распределенных сил
Список литературы
- Будинас-Нисбетт, «Машиностроительный проект Шигли», 8-е изд.
- Гир, Джеймс М., «Механика материалов», 6-е изд.
- Линдебург, Майкл Р., «Справочное руководство по машиностроению для экзамена на физическую форму», 13-е изд.
- «Руководство по анализу напряжений», Лаборатория динамики полета ВВС, октябрь 1986 г.
Прочность материалов | Механика материалов
ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения.Пожалуйста, включите JavaScript.
Сопротивление материалов , также известное как Механика материалов , ориентировано на анализ напряжений и прогибов в материалах под нагрузкой. Знание напряжений и прогибов позволяет безопасно проектировать конструкции, способные выдерживать предполагаемые нагрузки.
Напряжение и деформация
Когда к конструктивному элементу прикладывается сила, в этом элементе в результате силы возникают как напряжение, так и деформация.Напряжение — это сила, переносимая элементом на единицу площади, и типичными единицами измерения являются фунт-сила / дюйм 2 (фунт / кв. Дюйм) для стандартных единиц США и Н / м 2 (Па) для единиц СИ:
где F — приложенная сила, а A — площадь поперечного сечения, на которую действует сила. Приложенная сила вызовет деформацию конструктивного элемента на некоторую длину, пропорциональную его жесткости. Деформация — это отношение деформации к исходной длине детали:
где L — деформированная длина, L 0 — исходная недеформированная длина, а δ — деформация (разница между ними).
Существуют различные типы нагрузки, которые приводят к различным типам напряжений, как показано в таблице ниже:
| Тип нагрузки | Тип напряжения | Иллюстрация |
|---|---|---|
| Осевая сила |
| |
| Усилие сдвига | Поперечное напряжение сдвига | |
| Изгибающий момент | Напряжение изгиба | |
| Торсион | Торсионное напряжение |
Осевое напряжение и изгибающее напряжение являются формами нормального напряжения , σ, поскольку направление силы перпендикулярно области, противодействующей силе.Поперечное напряжение сдвига и напряжение скручивания являются формами напряжения сдвига , τ, поскольку направление силы параллельно области, противодействующей силе.
| Нормальное напряжение | |
|---|---|
| Осевое напряжение: | |
| Напряжение изгиба: | |
| Напряжение сдвига | |
|---|---|
| Поперечное напряжение: | |
| Торсионное напряжение: | |
В уравнениях для осевого напряжения и поперечного напряжения сдвига F — это сила, а A — площадь поперечного сечения элемента.В уравнении для изгибающего напряжения M — изгибающий момент, y — расстояние между центральной осью и внешней поверхностью, а I c — центроидный момент инерции поперечного сечения относительно соответствующей оси. В уравнении для напряжения скручивания T — это кручение, r — радиус и J — полярный момент инерции поперечного сечения.
В случае осевого напряжения на прямом участке напряжение распределяется равномерно по всей площади.В случае напряжения сдвига распределение максимально в центре поперечного сечения; однако среднее напряжение определяется как τ = F / A, и это среднее напряжение сдвига обычно используется при расчетах напряжений. Более подробное обсуждение можно найти в разделе о касательных напряжениях в балках. В случае напряжения изгиба и скручивания максимальное напряжение возникает на внешней поверхности. Более подробное обсуждение можно найти в разделе о напряжениях изгиба в балках.
Так же, как основными типами напряжения являются нормальное напряжение и напряжение сдвига, основными типами деформации являются нормальная деформация и деформация сдвига .В случае нормальной деформации деформация перпендикулярна области, на которую действует сила:
В случае деформации поперечного сдвига деформация параллельна области, на которую действует сила:
где γ — деформация сдвига (безразмерная) и & phiv; — деформированный угол в радианах.
В случае деформации кручения элемент поворачивается на угол & phiv; вокруг своей оси.Максимальная деформация сдвига возникает на внешней поверхности. В случае круглого стержня максимальная деформация сдвига определяется как:
где & phiv; — угол закручивания, r — радиус стержня, а L — длина.
Деформации сдвига пропорциональны внутренней части стержня и связаны с максимальной деформацией сдвига на поверхности следующим образом:
где ρ — радиальное расстояние от оси стержня.
Закон Гука
Напряжение пропорционально деформации в упругой области кривой напряжения-деформации материала (ниже предела пропорциональности, когда кривая является линейной).
Нормальное напряжение и деформация связаны между собой:
σ = E & varepsilon;
где E — модуль упругости материала, σ — нормальное напряжение, а & varepsilon; это нормальный штамм.
Напряжение сдвига и деформация связаны между собой:
τ = G γ
где G — модуль сдвига материала, τ — напряжение сдвига, а γ — деформация сдвига.Модуль упругости и модуль сдвига связаны соотношением:
где ν — коэффициент Пуассона.
Закон Гука аналогичен уравнению силы пружины F = k δ. По сути, все можно рассматривать как пружину. Закон Гука можно перестроить, чтобы получить деформацию (удлинение) в материале:
| Осевое удлинение (от нормального напряжения) | ||
| Угол кручения (от напряжения сдвига / скручивания) |
Энергия деформации
Когда к конструктивному элементу прикладывается сила, этот элемент деформируется и накапливает потенциальную энергию, как пружина.Энергия деформации (то есть количество потенциальной энергии, накопленной из-за деформации) равна работе, затраченной на деформацию элемента. Полная энергия деформации соответствует площади под кривой отклонения нагрузки и имеет единицы дюйм-фунт-сила в обычных единицах США и Н-м в единицах СИ. Энергия упругой деформации может быть восстановлена, поэтому, если деформация остается в пределах упругости, то вся энергия деформации может быть восстановлена.
Энергия деформации рассчитывается как:
| Общая форма: | U = Работа = ∫ F dL | (площадь под кривой нагрузки-прогиб) |
| В пределах предела упругости: | (площадь под кривой нагрузки-прогиб) | |
| (потенциальная энергия пружины) |
Обратите внимание, что есть два уравнения для энергии деформации в пределах упругости.Первое уравнение основано на площади под кривой прогиба нагрузки. Второе уравнение основано на уравнении для потенциальной энергии, запасенной в пружине. Оба уравнения дают один и тот же результат, просто они выводятся несколько по-разному.
Более подробную информацию об энергии деформации можно найти здесь.
Жесткость
Жесткость, обычно называемая жесткостью пружины, — это сила, необходимая для деформации элемента конструкции на единицу длины.Все конструкции можно рассматривать как совокупность пружин, а силы и деформации в конструкции связаны уравнением пружины:
F = k δ макс
где k — жесткость, F — приложенная сила, а max — максимальное отклонение при прогибе в элементе.
Если прогиб известен, то жесткость элемента можно найти, решив k = F / δ max . Однако максимальный прогиб обычно неизвестен, поэтому жесткость необходимо рассчитывать другими способами.Таблицы прогиба балки можно использовать в общих случаях. Два наиболее полезных уравнения жесткости, которые необходимо знать, — это уравнения для балки с приложенной осевой нагрузкой и для консольной балки с концевой нагрузкой. Обратите внимание, что жесткость зависит от модуля упругости материала E, геометрии детали и конфигурации нагрузки.
Торсионный эквивалент уравнения пружины:
Т = к & phiv;
Особый интерес представляет жесткость вала при скручивающей нагрузке:
| Жесткость [дюйм * фунт-сила / рад] | Максимальный прогиб [рад] | Иллюстрация | |
|---|---|---|---|
| Вал с крутильной нагрузкой: |
Конструкция с несколькими путями нагружения
Если в конструкции есть несколько путей загрузки (т.е. в конструкции есть несколько элементов, которые разделяют нагрузку), нагрузка будет выше в более жестких элементах. Чтобы определить нагрузку, которую несет любой отдельный элемент, сначала вычислите эквивалентную жесткость элементов на пути нагружения, рассматривая их как пружины. В зависимости от их конфигурации они будут рассматриваться как некоторая комбинация пружин, включенных последовательно, и пружин, включенных параллельно.
Если элементы на пути нагружения нельзя рассматривать исключительно как пружины, включенные последовательно или как пружины, включенные параллельно, а скорее представляют собой комбинацию пружин, включенных последовательно и параллельно, тогда проблему необходимо будет решать итеративно.Определите подгруппу элементов, которые находятся либо последовательно, либо параллельно, и используйте приведенные уравнения для расчета эквивалентной жесткости, силы и прогиба в подгруппе. Затем подгруппу можно рассматривать как одиночную пружину с рассчитанными жесткостью, силой и прогибом, а затем эту пружину можно рассматривать как часть другой подгруппы пружин. Продолжайте группировать участников и решать, пока не будет достигнут желаемый результат.
Концентрации напряжений
Можно подумать, что силы и напряжения протекают через материал, как показано на рисунке ниже.Когда геометрия материала изменяется, линии потока перемещаются ближе друг к другу или дальше друг от друга, чтобы приспособиться. Если в материале есть разрыв, такой как отверстие или выемка, напряжение должно течь вокруг неоднородности, и линии потока будут уплотняться вместе вблизи этого разрыва. Это внезапное уплотнение потоковых линий приводит к резкому скачку напряжения — это пиковое напряжение называется концентрацией напряжений . Элемент, вызывающий концентрацию напряжений, называется подъемником напряжений .
Концентрации напряжений учитываются с помощью коэффициента концентрации напряжений . Чтобы найти фактическое напряжение в вязкости несплошности, рассчитайте номинальное напряжение в этой области и затем увеличьте его с помощью соответствующего коэффициента концентрации напряжений:
σ макс = K σ ном
где σ max — фактическое (масштабированное) напряжение, σ nom — номинальное напряжение, а K — коэффициент концентрации напряжений.При расчете номинального напряжения используйте максимальное значение напряжения в этой области. Например, на рисунке выше должна использоваться наименьшая площадь у основания галтеля.
Многие справочные руководства содержат таблицы и кривые коэффициентов концентрации напряжений для различных геометрических форм. Двумя наиболее полными наборами факторов концентрации напряжения являются факторы концентрации напряжения Петерсона и формулы Рорка для напряжения и деформации. MechaniCalc также предоставляет набор интерактивных графиков для общих факторов концентрации стресса.
По мере того, как мы удаляемся от источника стресса, концентрация стресса рассеивается. Принцип Сен-Венана — это общее практическое правило, гласящее, что расстояние, на котором рассеивается концентрация напряжений, равно наибольшему размеру поперечного сечения, несущего нагрузку.
Расчет концентрации напряжений особенно важен, когда материалы очень хрупкие или когда существует только один путь нагрузки. В пластичных материалах местная податливость позволит перераспределить напряжения и снизит напряжение вокруг стояка.По этой причине коэффициенты концентрации напряжений обычно не применяются к элементам конструкции, изготовленным из пластичных материалов. Коэффициенты концентрации напряжений также обычно не применяются при наличии избыточного пути нагружения, и в этом случае податливость одного элемента позволит перераспределить силы на элементы на других путях нагружения. Примером этого является набор болтов. Если один болт начинает прогибаться, другие болты в шаблоне принимают на себя большую нагрузку.
Комбинированные напряжения
В любой точке нагруженного материала общее состояние напряжения можно описать тремя нормальными напряжениями (по одному в каждом направлении) и шестью напряжениями сдвига (по два в каждом направлении):
Индексы нормальных напряжений σ указывают направление нормальных напряжений.Индексы касательных напряжений τ состоят из двух компонент. Первый указывает направление нормали к поверхности, а второй указывает направление самого напряжения сдвига.
Обычно напряжения в одном направлении равны нулю, так что полное напряжение возникает в одной плоскости, как показано на рисунке ниже. Это называется напряжением в плоскости . Плоское напряжение возникает в тонких пластинах, но оно также возникает на поверхности любой нагруженной конструкции. Напряжения на поверхности обычно являются наиболее критическими напряжениями, поскольку напряжение изгиба и скручивания максимизируется на поверхности.
На рисунке выше σ x и σ y — нормальные напряжения, а τ — напряжение сдвига. Напряжения уравновешиваются, так что точка находится в статическом равновесии. Поскольку все касательные напряжения равны по величине, для простоты индексы опущены. (Обратите внимание, однако, что знак напряжений на грани x будет противоположен знаку напряжений на грани y .)
Правильные условные обозначения показаны на рисунке.Для нормального напряжения растягивающее напряжение положительное, а сжимающее — отрицательное. Для напряжения сдвига значение по часовой стрелке положительное, а против часовой стрелки — отрицательное.
Если напряжения из рисунка выше известны, можно найти нормальное напряжение и напряжение сдвига в плоскости, повернутой на некоторый угол θ относительно горизонтали, как показано на рисунке ниже. Уравнения преобразования ниже дают значения нормального напряжения и напряжения сдвига на этой повернутой плоскости.
| Нормальное напряжение: | |
| Напряжение сдвига: |
Обратите внимание, что на рисунке выше θ отсчитывается от оси x, а положительное значение θ — против часовой стрелки.
В любой точке материала можно найти углы плоскости, при которых нормальные напряжения и напряжения сдвига максимизируются и минимизируются.Максимальное и минимальное нормальные напряжения называются главными напряжениями . Максимальные и минимальные касательные напряжения называются экстремальными касательными напряжениями . Углы главных напряжений и крайних касательных напряжений находятся путем взятия производной каждого уравнения преобразования по θ и нахождения значения θ, при котором производная равна нулю.
| Углы главного напряжения: | |
| Углы предельного напряжения сдвига: |
Указанные выше углы можно подставить обратно в уравнения преобразования, чтобы найти значения главных напряжений и экстремальных касательных напряжений:
| Основные напряжения: | |
| Экстремальные напряжения сдвига: |
Углы, при которых возникают основные напряжения, составляют 90 ° друг от друга.Главные напряжения всегда сопровождаются нулевым напряжением сдвига. Углы возникновения экстремальных касательных напряжений составляют 45 ° от углов главных напряжений. Экстремальные напряжения сдвига сопровождаются двумя равными нормальными напряжениями (σ x & plus; σ y ) / 2.
Вот пара полезных отношений:
| σ 1 & plus; σ 2 = σ x & plus; σ y | Сумма нормальных напряжений постоянна. |
| Максимальное напряжение сдвига составляет половину разницы главных напряжений. |
Круг Мора
Круг Мора — это способ визуализировать состояние напряжения в точке нагруженного материала. Это дает интуитивное представление о уравнениях преобразования напряжений и показывает, как напряжения на элементе изменяются в зависимости от угла поворота θ. Из круга Мора также становится ясно, каковы основные напряжения, экстремальные напряжения сдвига и углы, под которыми возникают эти напряжения.Пример круга Мора показан на рисунке ниже:
Чтобы построить круг Мора, сначала найдите центр круга, взяв среднее значение нормальных напряжений:
Поместите точки на окружности, представляющие напряжения на гранях x и y элемента напряжения. Напряжения на грани x будут иметь координаты (σ x , −τ), а напряжения на грани y будут иметь координаты (σ y , τ).Поместите точки на окружности для главных напряжений. Максимальное главное напряжение будет иметь координаты (σ 1 , 0), а минимальное главное напряжение будет иметь координаты (σ 2 , 0). Поместите точки на окружности для экстремальных касательных напряжений. Максимальное экстремальное напряжение сдвига будет иметь координаты (σ c , τ 1 ), а минимальное экстремальное напряжение сдвига будет иметь координаты (σ c , τ 2 ).
Все точки будут лежать по периметру круга.Круг имеет радиус, равный величине предельных касательных напряжений:
Напряженное состояние на гранях x и y элемента напряжения представлено черной линией в круге Мора, соединяющим точки (σ x , −τ) и (σ y , τ). Эта линия в круге Мора соответствует невращающемуся элементу на рисунке ниже. Если эту линию повернуть на некоторый угол, то значения точек на конце повернутой линии дадут значения напряжения на гранях x и y повернутого элемента.Важно отметить, что 360 градусов круга Мора эквивалентны 180 градусам элемента напряжения. Например, точки для грани x и грани y расположены на 180 градусов друг от друга на круге Мора, но они всего на 90 градусов на элементе напряжения.
Чтобы получить более интуитивное представление о том, как круг Мора связывает напряжения на элементе напряжения и как состояние напряжения изменяется в зависимости от угла поворота, см. Прилагаемый калькулятор круга Мора.
Приложения
Есть много структурных компонентов, которые обычно подвергаются анализу напряжений. Подробности анализа этих компонентов приведены в других разделах:
Расчет допустимого напряжения
Знание напряжений и прогибов позволяет безопасно проектировать конструкции, способные выдерживать предполагаемые нагрузки. Всегда желательно, чтобы напряжения в конструкции оставались в пределах прочности конструкции.Предел текучести материала обычно выбирается как предел прочности, с которым сравниваются расчетные напряжения.
Коэффициент запаса прочности , FS, рассчитывается как:
где σ фактический — это расчетное напряжение в конструкции, а предел — это предел максимального напряжения, обычно прочность материала, например предел текучести (S ty ). Коэффициент запаса прочности показывает, насколько фактическое напряжение ниже предельного напряжения.Значение FS должно быть больше или равно 1, чтобы конструкция не вышла из строя, но инженеры почти всегда будут проектировать с некоторым требуемым коэффициентом безопасности, превышающим 1. Требуемый коэффициент безопасности будет варьироваться в зависимости от критичности конструкции (т. Е. последствия разрушения конструкции), а также условия нагружения (т. е. какие типы нагрузок применяются, насколько они предсказуемы и т. д.). Высокое значение FS приведет к очень безопасной конструкции, но если значение FS слишком велико, конструкция может стать настолько большой и тяжелой, что больше не сможет успешно выполнять свою функцию.Поэтому при выборе подходящего запаса прочности приходится идти на компромиссы. Типичные значения FS варьируются от 1,15 до 10.
Запас прочности рассчитывается как:
В приведенном выше уравнении любое значение выше нуля указывает на то, что фактическое напряжение ниже предельного напряжения. Хотя запасы прочности обычно указываются в виде десятичных значений, гораздо более интуитивно понятно думать о запасах в процентах. Например, если предельное напряжение конструкции равно 1.В 5 раз превышающее фактическое напряжение, запас прочности составляет 50% (MS = 0,5).
Когда сообщается о факторах безопасности и запасах прочности, иногда требуемый коэффициент безопасности будет «вплетаться» в сообщаемые факторы. Например, инженеры могут потребовать, чтобы конструкция поддерживала коэффициент безопасности не менее 2, так что FS req = 2. Чтобы обеспечить требуемый коэффициент безопасности, сообщаемые FS и MS рассчитываются как:
Обратите внимание, что при включении необходимого коэффициента безопасности, FS req , сообщаемые FS и MS фактически являются запасами по отношению к FS req , а не по напряжению.
Список литературы
- Будинас-Нисбетт, «Машиностроительный проект Шигли», 8-е издание
- Доулинг, Норман Э., «Механическое поведение материалов: инженерные методы для деформации, разрушения и усталости», 3-е издание
- Гир, Джеймс М., «Механика материалов», 6-е издание
- Линдебург, Майкл Р., «Справочное руководство по машиностроению для экзамена на физическую форму», 13-е издание
- Пилки, Уолтер Д.и Пилки, Дебора Ф., «Факторы концентрации стресса Петерсона», 3-е издание.
- «Формулы Рорка для стресса и деформации», 8-е издание
Как рассчитать прочность на изгиб
Обновлено 28 января 2020 г.
Ли Джонсон
Проверено: Lana Bandoim, B.S.
Определение силы, которую объект может выдержать до разрушения, может пригодиться во многих ситуациях, особенно для инженеров. Это должно быть определено на основе экспериментальных результатов, которые, по сути, включают в себя воздействие на материал возрастающей силы до тех пор, пока он не сломается или не изгибается навсегда.Но выполнение реальных расчетов для определения прочности материала на изгиб может показаться действительно сложной задачей. К счастью, если у вас есть нужная информация, вы можете легко выполнить расчет.
Определение прочности на изгиб
Прочность на изгиб (или модуль разрыва ) — это величина силы, которую объект может выдержать без разрушения или постоянной деформации. Если это сложно понять, подумайте о деревянной доске, поддерживаемой с двух концов.
Если вы хотите узнать, насколько прочна древесина, один из способов ее проверки — это надавить все сильнее и сильнее на центр доски, пока она не сломается. Максимальное толкающее усилие, которое древесина может выдержать до разрушения, — это ее прочность на изгиб. Если бы другой кусок дерева был сильнее, он выдержал бы большую силу, прежде чем сломался бы.
Прочность на изгиб действительно говорит вам о максимальной величине напряжения, которое может выдержать материал (так что вы также можете видеть ссылки на «напряжение изгиба»), и она указывается как сила (в ньютонах или фунтах-силах) на единицу площади (в метрах в квадрате или квадратном дюйме).
Испытания по трем или четырем точкам
Есть два метода испытания прочности на изгиб, но они очень похожи. Длинный прямоугольный образец материала опирается на его концы, поэтому посередине нет опоры, но концы прочные. Затем к средней секции прикладывается нагрузка или сила до тех пор, пока материал не разорвется.
Для трехточечного испытания на прочность на изгиб постоянно возрастающая нагрузка прикладывается к центру образца до тех пор, пока в материале не произойдет излом или остаточный изгиб.Машина для испытания на изгиб может прилагать увеличивающееся количество силы и точно записывать величину силы в точке разрушения.
Испытание на четырехточечный изгиб очень похоже, за исключением того, что нагрузка прикладывается одновременно в двух точках, опять же по направлению к центру образца. Легче всего рассчитать прочность на изгиб, когда одна нагрузка или сила прикладываются на одной трети расстояния между опорами, а вторая — на двух третях расстояния между ними. Таким образом, в этом примере к средней трети образца будут приложены силы с обеих сторон.
Расчет прочности на изгиб при трехточечном испытании
Для трехточечного испытания прочность на изгиб (с учетом символа σ ) можно рассчитать по следующей формуле:
Сначала это может показаться пугающим, но как только вы узнаете, что каждый символ означает, что это довольно простое уравнение.
F означает максимальное приложенное усилие, L — длина образца, w — ширина образца и d — глубина образца.Итак, чтобы рассчитать прочность на изгиб ( σ ), умножьте силу на длину образца, а затем умножьте это на три. Затем умножьте глубину образца на себя (то есть возведите его в квадрат), умножьте результат на ширину образца, а затем умножьте его на два. Наконец, разделите первый результат на второй.
В единицах СИ длина, ширина и глубина будут измеряться в метрах, а сила — в ньютонах, с результатом в паскалях (Па) или ньютонах на квадратный метр.В британских единицах измерения длина, ширина и глубина будут измеряться в дюймах, а сила — в фунтах-силах, а результат — в фунтах на квадратный дюйм.
Расчет прочности на изгиб при четырехточечном испытании
При четырехточечном испытании используются те же символы, что и при расчете трехточечного испытания. Но если предположить, что две нагрузки или силы приложены таким образом, что они разделяют образец на три части, это выглядит намного проще:
Обратите внимание, что это в точности то же самое, что формула напряжения изгиба для трехточечных испытаний, но без коэффициента 3/2.Просто умножьте прилагаемую силу на длину, а затем разделите полученное значение на ширину материала, умноженную на его глубину в квадрате.
Сила сдвига и изгибающий момент
Сдвиг Диаграммы силы и изгибающего момента для балки с простой опорой Под равномерной нагрузкой
После рассчитываются опорные реакции, поперечная сила и изгиб диаграммы моментов могут быть построены.
Сдвиг сила сила в балке, действующая перпендикулярно к его продольной оси (x). В целях проектирования балка способность противостоять силе сдвига важнее, чем его способность противостоять осевой силе. осевой сила сила в балке, действующей параллельно к продольной оси.
Следующие представляет собой чертеж свободно опертой балки длиной L под равномерная нагрузка, q:
Эта балка имеет следующие реакции поддержки:
где R l и R r — реакции на левом и правом концах балки соответственно.
Ножницы силы на концах балки равны вертикальным силам опорных реакций. Сила сдвига F (x) при любом другом точку x на балке можно найти с помощью следующего уравнения.
где x равно расстояние от левого конца балки.
Сила сдвига диаграммы — это просто графики поперечной силы (по оси ординат) от положения различных точек вдоль балки (на ось абсцисс).Таким образом, следующая обобщенная поперечная сила диаграмма для балки, показанной выше.
Гибка момент в любой точке балки равен в область под диаграммой поперечных сил до этой точки. (Примечание: для балок с простой опорой изгибающий момент на концы всегда будут равны нулю.)
Для расчета по изгибающему моменту балка должна быть разделена на две части:
| (а) | один от x = 0 до x = L / 2 и |
| б) | г. другие от x = L / 2 до x = L. |
Гибка момент M (x) в любой точке x вдоль балки можно найти, используя следующие уравнения:
Изгибающий момент диаграммы — это просто графики изгибающего момента (по оси y) от положения различных точек вдоль балки (на ось абсцисс). Таким образом, обобщенный изгибающий момент диаграмма для балки, показанной выше.
Мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}} *
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{добавить в коллекцию.description.length}} / 500 {{l10n_strings.TAGS}} {{$ item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}} {{$ select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.АВТОР}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$ select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Как рассчитать и нарисовать диаграммы сдвига и изгибающего момента: 13 шагов
Введение: Как рассчитать и нарисовать диаграммы сдвига и изгибающего момента
Эти инструкции помогут вам рассчитать и нарисовать диаграмму сдвига и изгибающего момента, а также нарисовать результирующий прогиб. Знание того, как рассчитывать и рисовать эти диаграммы, важно для любого инженера, который имеет дело с любым типом конструкции, потому что очень важно знать, где большие нагрузки и изгиб возникают на балке, чтобы вы могли убедиться, что ваша конструкция может удерживать нагрузка.Есть несколько разных способов найти свои диаграммы, но этот самый простой для разметки, объяснения и понимания. Когда вы впервые приступаете к построению диаграмм, на их расчеты и рисование может уйти некоторое время, но по мере того, как вы станете лучше, это время значительно сократится. С помощью этих инструкций и некоторой практики вы сможете быстро и легко вычислить и нарисовать эти типы задач.
Добавить TipAsk QuestionDownload
Шаг 1: Материалы
Чтобы аккуратно завершить диаграмму усилия сдвига и изгибающего момента, вам потребуются следующие материалы.
— Линейка или прямая кромка
— Карандаш
— Ластик
— Калькулятор
Добавить TipAsk QuestionDownload
Шаг 2: Шаг 1: Знание воздействия сил на балки
— Знание того, как разные силы влияют на балки, важно для расчета сдвиговые и изгибающие моменты.
— Точечная сила вызовет прямоугольный сдвиг и треугольный изгибающий момент.
— Прямоугольная распределенная нагрузка вызовет треугольный сдвиг и квадратичный изгибающий момент.
Добавить TipAsk QuestionDownload
Шаг 3: Шаг 2: Найдите реакции, используя уравнения моментов
— Остановитесь на некоторой точке, которая позволит вам найти одну из равнодействующих сил.
— Вам может потребоваться использовать два уравнения, чтобы найти две разные силы.
Добавить TipAsk QuestionDownload
Шаг 4: Шаг 3: Найдите реакции, используя сумму сил
— Найдите ваши оставшиеся равнодействующие силы, используя сумму сил в направлениях x и y.
Добавить TipAsk QuestionDownload
Шаг 5: Шаг 4: Анализ конструкции, чтобы увидеть, как силы влияют на сдвиг
— Только силы, перпендикулярные балке, вызывают сдвиг.
— Точечные силы создают прямоугольный сдвиг.
— Прямоугольные распределенные силы создают треугольный сдвиг.
Добавить TipAsk QuestionDownload
Шаг 6: Шаг 5: Нарисуйте диаграмму сдвига
— Используя рассчитанные силы и анализ, нарисуйте диаграмму сдвига.
Добавить TipAsk QuestionDownload
Шаг 7: Шаг 6: Определите, как диаграмма сдвига повлияет на диаграмму изгиба
— Прямоугольные области сдвига вызовут треугольный изгиб.
— Треугольные области сдвига вызывают квадратичный изгиб.
Добавить TipAsk QuestionDownload
Шаг 8: Шаг 7: Расчет площади под кривыми сдвига
— Для прямоугольных областей умножьте высоту на длину.
— Для треугольных областей умножьте высоту на длину и разделите на 2 (уравнение для площади треугольника).
Добавить TipAsk QuestionDownload
Шаг 9: Шаг 8: Нарисуйте диаграмму изгибающего момента
— Зная площадь под кривой и проведенный анализ, нарисуйте диаграмму изгибающего момента.
Добавить TipAsk QuestionDownload
Шаг 10: Шаг 9: Укажите кривизну на диаграмме изгибающего момента
— Рассмотрите физическую реакцию сил.
— Балка изгибается в направлении сдвига.
Добавить TipAsk QuestionDownload
Шаг 11: Шаг 10: Нарисуйте прогиб
— Зная свою кривизну, нарисуйте приблизительную диаграмму прогиба.
— Углы между балками должны быть сохранены.
Добавить TipAsk QuestionDownload
Шаг 12: Видео
— Вот видео о том, как выполнить примерные диаграммы сдвига и изгибающего момента вместе с перемещением.
Добавить TipAsk QuestionDownload
Шаг 13: Заключение
Поздравляем! Вы закончили расчет и построение диаграмм сдвига и изгибающих моментов, а также приблизительную диаграмму прогиба.Это поможет вам научиться лучше вычислять все типы этих задач, и вы, безусловно, будете впереди всех, когда в следующий раз вам понадобится знать, как это сделать.
Добавить Подсказка Задать вопросЗагрузить
1 человек сделал этот проект!
Вы сделали этот проект? Поделитесь с нами!
Я сделал это!Рекомендации
Теория простого изгиба
🕑 Время считывания: 1 минута
Когда балка подвергается воздействию системы нагружения или пары сил, действующих на плоскость, проходящую через ось, балка деформируется.Проще говоря, эта осевая деформация называется изгибом балки. Из-за силы сдвига и изгибающего момента балка деформируется. Эти нормальные напряжения из-за изгиба называются напряжениями изгиба.Рис. 1: Типы изгибающих напряжений в сечении балки
Допущения для расчета напряжения изгиба Эти напряжения, возникающие в материале из-за изгиба, можно рассчитать с использованием определенного допущения, они равны- Балка изначально прямая и имеет постоянное поперечное сечение.
- Балка изготовлена из однородного материала и имеет продольную плоскость симметрии.
- Результирующая приложенных нагрузок лежит в плоскости симметрии.
- Геометрия всего элемента такова, что изгиб, а не коробление, является основной причиной отказа.
- Предел упругости нигде не превышен, а «E» одинакова при растяжении и сжатии.
- Плоские сечения остаются плоскими до и после гибки.
ФИГ 2: Чистые напряжения изгиба — это те напряжения, которые возникают только из-за собственной нагрузки балки.
2. Простое напряжение изгиба Изгиб будет называться простым изгибом, если он происходит из-за самонагрузки балки и внешней нагрузки.Этот тип изгиба также известен как обычный изгиб, и при этом типе изгиба возникает как напряжение сдвига, так и нормальное напряжение в балке. Как показано ниже на рисунке.Рис. 3: Простое напряжение изгиба
Формула для напряжения изгиба Где, M = изгибающий момент I = момент инерции секции относительно оси изгиба. = напряжение волокна на расстоянии «y» от центральной / нейтральной оси. E = модуль Юнга материала балки. R = радиус кривизны изогнутой балки.Если y заменить на c, расстояние до самого удаленного элемента, тогда Где Z = модуль упругости сечения и определяется как, Z = I / c Типы деформации изгиба 1. Нормальные штаммы В результате изгиба где-то между верхом и низом балки остается поверхность, на которой продольные волокна не изменяются по длине. Эта поверхность называется нейтральной поверхностью балки, а ее пересечение с любой плоскостью поперечного сечения называется нейтральной осью поперечного сечения.Все продольные волокна, кроме волокон на нейтральной поверхности, либо удлиняются, либо укорачиваются, тем самым создавая продольные деформации. Где k = кривизна = 1 / R Это уравнение показывает, что продольные деформации пропорциональны кривизне и линейно зависят от расстояния y от нейтральной поверхности. Это уравнение выводится из геометрии деформированной балки и не зависит от свойств материала. Уравнение действительно независимо от диаграммы деформации материала. 2. Поперечная деформация Осевые деформации сопровождаются боковыми или поперечными деформациями из-за эффекта коэффициента Пуассона. Положительные деформации сопровождаются отрицательными поперечными деформациями. Где коэффициент Пуассона. В результате этих деформаций изменяется форма поперечного сечения. Например, давайте рассмотрим случай балки прямоугольного поперечного сечения, подвергнутой чистому изгибу, чтобы вызвать растяжение вверху и сжатие внизу. Стороны прямоугольного сечения наклоняются друг к другу.Верхняя поверхность приобретает седловидную форму. Если продольная кривизна в плоскости xy считается положительной, то поперечная кривизна в плоскости yz отрицательна. Все плоскости балки, которые изначально были параллельны нейтральной поверхности, развивают антипластическую кривизну. Применимость формулы изгиба Нормальные напряжения, определенные по формуле изгиба, относятся к чистому изгибу, что означает, что поперечные силы не действуют на поперечное сечение. В случае неравномерного изгиба наличие поперечных сил вызывает коробление или деформацию поперечного сечения, таким образом, сечение, которое было плоским до изгиба, больше не является плоским после изгиба.Деформация из-за сдвига значительно усложняет поведение балки, но более подробный анализ показывает, что нормальные напряжения, рассчитанные по формуле изгиба, не претерпевают значительных изменений из-за наличия касательных напряжений и связанного с ними коробления.