Построение эпюр в рамах

Рассмотрим подробно порядок построения эпюр внутренних силовых факторов в раме.

Задача
Построить эпюры внутренних продольных и поперечных усилий и изгибающих моментов для плоской П-образной рамы, нагруженной силой, моментом и распределенной нагрузкой:

Рис. 1

Решение

Рама состоит из трех частей (левая и правая вертикальные стойки соединенные горизонтальным ригелем), но при этом имеет четыре силовых участка – AC, CD, BE и DE, на каждом из которых нам потребуется определить величину и направление внутренних усилий.

Для заданной расчетной схемы рамы ранее мы уже определили опорные реакции.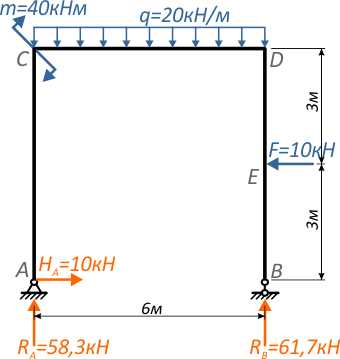

Рис. 2

Расчет значений

Обозначим силовые участки римскими цифрами.

Рис. 3

Для расчета значений, необходимых для построения эпюр, будем пользоваться методом сечений и соответствующими правилами знаков.

Начинаем с первого силового участка AC.

Мысленно рассекаем его в любом месте между крайними точками участка.

Рис. 4

Это сечение делит раму на две части:

1. нижнюю часть стойки до точки A
2. всю остальную часть, включая верхнюю от сечения часть левой стойки, ригель CD и правую стойку BD.

Можно рассмотреть любую из них, но для упрощения расчетов рекомендуется выбирать менее нагруженную часть конструкции.

Очевидно, что в данном случае проще рассматривать нижнюю часть стойки.

Расстояние от границы участка до сечения обозначим переменной y₁, возможные значения которой находятся в пределах от нуля до длины участка.

Рис. 5

Действие отброшенной части рамы заменим внутренними усилиями N_I, Q_I и M_I.

Рис. 6

Рассчитаем их:

В выражении для M_I переменная y₁ в первой степени, а значит, эпюра на этом участке будет изображаться прямой. Для ее построения необходимы значения в двух точках.
Рассчитаем их на границах участка, в точках A и C:

В записанных выражениях:
N_I – по правилу знаков для внутренних продольных сил – отрицательна, т.к. на участке имеет место сжатие;
Q_I – отрицательна, т.к. стремится повернуть рассматриваемую часть рамы против хода часовой стрелки;
Для изгибающих моментов M будем отмечать то, какие слои они стремятся сжать. В данном случае момент M_I сжимает правую сторону стойки.

Расчет значений внутренних силовых факторов для остальных участков рамы выполняется аналогично.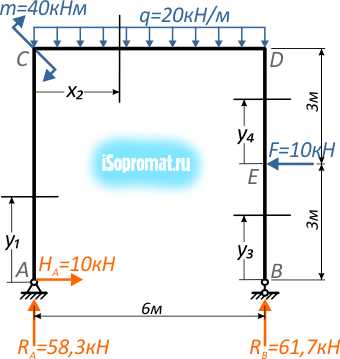

Рис. 7

На втором участке, проведя сечение (рис. 7), выберем для рассмотрения левую часть рамы (левая часть ригеля со стойкой AC).

Рис. 8

Продольную силу N_II здесь вызывает горизонтальная реакция H_A, которая сжимает ригель.
Поперечную силу Q_II в сечении дают реакция R_A и распределенная нагрузка q.
Изгибающий момент M_II создается всеми нагрузками расположенными слева от рассматриваемого сечения.
Опорные реакции R_A и H_A создают момент силы. Для момента создаваемого силой H_Aплечо одинаково для любого положения сечения, и равно длине стойки AC, для момента реакции R_A плечо переменное (y₂).
О том, как рассчитать момент, создаваемый распределенной нагрузкой q можно прочитать здесь.

Записываем выражения:

это уравнение прямой, поэтому рассчитаем значения на границах участка:

Сразу следует обратить внимание, что значения на границах участка имеют противоположные знаки, т.е. эпюра Q на данном участке пересекает базовую (нулевую) линию, следовательно, на эпюре моментов M_II в этом сечении будет экстремум (эпюры Q и M дифференциально зависимы).

Запишем выражение для изгибающих моментов:

получили уравнение параболы, для построения которой требуется минимум три точки.

Двумя из них будут граничные значения момента:

Третьей станет значение экстремума эпюры M на участке.

Рассчитаем его:
Выражение для Q_II приравниваем к нулю

откуда находим координату сечения рамы, где Q пересекает базовую линию.

подставляем ее в выражение для M_II и находим значение экстремума.

Для третьего участка рамы выбираем нижнюю часть (рис. 7):

Рис. 9

Записываем выражения:

Здесь имеется только продольная сжимающая сила.

На четвертом участке (рис. 7) тоже рассмотрим нижнюю часть стойки

Рис. 10

Граничные значения изгибающего момента

Расчет значений окончен, переходим к графическим построениям.

Построение эпюр

Для горизонтальных и вертикальных участков рамы положительные значения эпюр продольных N и поперечных сил Q будем откладывать соответственно вверх и вправо.
Как строить эпюры по рассчитанным значениям показано в следующем видео:

Эпюра внутренних продольных сил N:
Эпюра внутренних продольных сил N рамы

Рис. 11

Эпюра внутренних поперечных сил Q:
Эпюра внутренних поперечных сил Q рамы

Рис. 12

Эпюра изгибающих моментов M строится на сжатых волокнах рамы: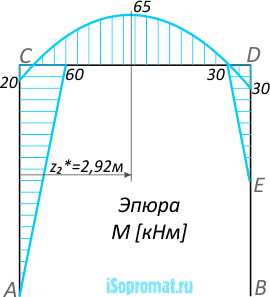
Эпюра внутренних изгибающих моментов M рамы

Рис. 13

Здесь следует обратить внимание на линию эпюры второго участка.
При расчете значений, граничные моменты получились отрицательными (-20 и -30кНм), т.е. они должны располагаться по одну сторону от базовой линии.
Экстремум момента положителен, следовательно, его следует откладывать по другую сторону базовой линии.

Эпюры внутренних силовых факторов для рамы построены.
Теперь необходимо выполнить их проверку.

Другие примеры решения задач >
Лекции по сопромату >

isopromat.ru

Расчет опорных реакций в рамах

Пример определения и проверки реакций в опорах П-образной плоской рамы нагруженной силой, моментом и распределенной нагрузкой.

Задача
Рассчитать опорные реакции в статически определимой раме

находящейся под действием системы нагрузок:

размер a=3м.

Решение

Расчет реакций

Перед началом решения задачи перенесем на расчетную схему числовые данные нагрузок и обозначим характерные точки (сечения) рамы буквами A, B, C, D и E.

Опорные реакции рамы будем определять из условия равновесия плоской системы сил.

В шарнирно-неподвижной опоре (т. A) могут возникать две составляющие реакции – горизонтальная H_A и вертикальная R_A, а в шарнирно-подвижной (т. B) только одна реакция – вертикальная R_B.

Зададим этим реакциям на данном этапе произвольное направление, например:

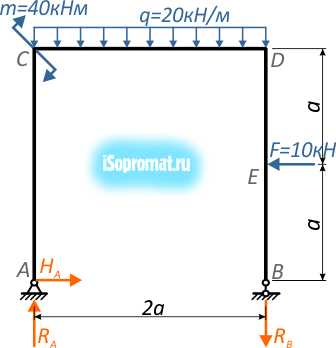
Для нахождения трех неизвестных усилий нам потребуется три уравнения статики: два уравнения суммы моментов относительно опорных точек и сумма проекций всех сил на горизонтальную ось X, которые должны равняться нулю.

Запишем их:

Из каждого уравнения выражаем и находим соответствующую величину опорной реакции:

Знак “-“ реакции R_B говорит о том, что произвольно выбранное направление оказалось неверным, и ее необходимо перенаправить в противоположную сторону, одновременно изменив знак на положительный.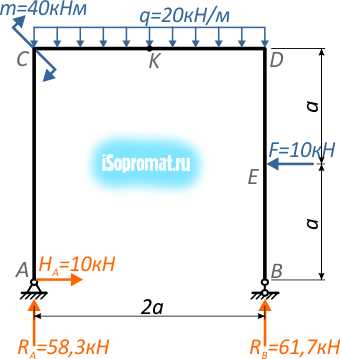

В задачах подобного рода после расчета реакций в опорах настоятельно рекомендуется выполнять проверку полученных значений, так как даже небольшая ошибка, в дальнейших расчетах может привести к неправильному результату.

Проверка реакций

Арифметическую проверку реакций выполним, записав сумму моментов относительно, например, середины ригеля CD (точки K):

Тождество выполняется, значит реакции определены верно.

После расчета и проверки опорных реакций можно приступать к построению эпюр внутренних силовых факторов в рамах.

Другие примеры решения задач >
Лекции по сопромату >

isopromat.ru

Расчет рамы по методу сил

 Расчет статически неопределимой рамы

ΣR=3+3=6, Ш=1

1)       Степень статической неопределимости n = R — Ш – 3 = 6 — 1 — 3 = 2.

2)       Выбор основной системы и эквивалентной системы.

Возможное количество ее вариантов бесконечно. Покажем только два из них. В первом варианте в качестве двух лишних неизвестных выберем внутренние усилия (

Q и N) в среднем сечении ригеля. Удалив внутренний шарнир, то есть то место, где и возникают эти усилия, получаем основную систему:

Соответствующая эквивалентная система показана рядом. Здесь введены стандартные обозначения неизвестных: Х₁вместо Q в шарнире и Х2 вместо N в шарнире.

Во втором варианте основной системы в качестве лишних неизвестных примем по одной реакции (реактивному моменту) в каждой из двух опор. Удалив соответствующие моментные  связи из жестких заделок, имеем:

3)       Составляем систему канонических уравнений при n=2:

  δ₁₁∙Х₁+ δ₁₂Х₂+ Δ_1F=0,

      δ₂₁

∙Х₁+ δ₂₂Х₂+ Δ_2F=0.

4)      Строим в основной системе три эпюры моментов:

от Х₁=1,  от Х2=1 и М_F от заданной нагрузки.

Все эпюры показаны на растянутых волокнах.

5)     Вычисляем коэффициенты уравнений:

6)    Решаем уравнения: 

откуда находим: Х₁=0, Х2=-17,5.

7)    Строим окончательную эпюру суммированием эпюр 

prosopromat.ru

6.5. Расчет рамы на прочность

В сечениях стержней плоской рамы возникают только три внутренних усилия: продольная сила N, поперечная сила Q, изгибающий момент М относительно оси, перпендикулярной плоскости изгиба (плоскости нагружения) рамы. Поэтому в плоских рамах строят три эпюры – N, Q и М.

Правила знаков для продольных и поперечных сил остаются такими же, как в балках. Правило знаков для изгибающего момента обычно не вводят, но ординаты эпюры М откладывают со стороны сжатых волокон, что позволяет судить по эпюре М о форме изгиба и действии изгибающих моментов.

В рамах следует проводить проверку статического равновесия узлов: сумма моментов, действующих во всех сечениях стержней, составляющих данный узел, равна нулю. Из условия равновесия узла следует правило: если узел соединяет два стержня, то при переходе через него момент не изменяется (или изменяется на величину внешнего сосредоточенного момента, приложенного к этому узлу).

Расчет рам на прочность обычно производится с учетом напряжений только от изгибающего момента .

Влияние продольной силы, как правило, несущественно. Оценить степень влияния напряжений от продольной силы можно, вычислив их по известной формуле и сравнив с напряжением от моментаМ|_max. При необходимости сечение рамы следует увеличить так, чтобы выполнялось условие прочности , гдеN берется в том же сечении, где действует М|_max.

Пример

Для заданной плоской рамы из условия прочности по нормальным напряжениям подобрать двутавровое сечение ([] = 160 МПа).

Решение

Вычертим в масштабе расчетную схему рамы с указанием численных значений заданных величин (рис. 6.7, а).

Запишем уравнения равновесия рамы и определим опорные реакции.

,

,

.

Указываем на расчетной схеме величину и фактическое направление всех реакций. При составлении уравнений реакцию R_В направили вверх. Так как реакция R_В получилась отрицательной, ее направление на расчетной схеме необходимо сменить на противоположное, т.е. вниз.

Выделим на расчетной схеме четыре участка. Запишем для каждого из них выражения внутренних усилий и найдем их значения на границах участков.

1.

2.

3.

4.

Строим эпюры N (рис. 6.7, б), Q (рис. 6.7, в), М (рис. 6.7, г). Положительные ординаты N и Q на ригеле откладываем вверх, на стойках – снаружи рамы. Эпюру М строим на сжатых волокнах.

Указание: расчетную схему рамы и эпюры N, Q, М разместить на одном листе.

Подбираем номер двутавра из условия прочности по нормальным напряжениям от максимального изгибающего момента.

|М|_max=300 кНм, . Назначаем двутавр № 55, у которогоW_х = 2035 см³, а площадь сечения А = 118 см².

Проверим прочность подобранного двутавра с учетом действия продольной силы в наиболее опасном сечении.

Ригель при z₂= 0, М = 300 кНм, N = 60 кН.

Как видим, нормальные напряжения от продольной силы составляют 3,47 % от напряжений, возникающих под действием изгибающего момента, и поэтому, как правило, могут не учитываться.

Контрольная работа № 5. Расчет балки на прочность по нормальным напряжениям

Для заданной балки из условия прочности по нормальным напряжениям определить размеры различных по форме поперечных сечений: двутавра, прямоугольника (с отношением сторон h/b = 2), квадрата, круга, кольца (при d/D = 0,7) и оценить их рациональность.

Схемы балок и численные данные выбираются в соответствии с шифром из рис. 6.8 и табл. 6.1.

Материал балки: сталь ст. 3 – [] = 160 МПа.

Таблица 6.1

Номер строки	Цифра шифра
	1-я	2-я	3-я	4-я	5-я	6-я
	схема	b, м	а, м	F, кН	q, кН/м	М, кНм
1	1	4,2	1,2	12	10	25
2	2	4,5	1,4	14	12	20
3	3	5,0	1,6	16	15	15
4	4	5,5	1,8	18	16	10
5	5	6,0	1,7	20	18	12
6	6	5,8	1,5	22	20	14
7	7	5,4	1,3	24	22	16
8	8	5,2	1,1	26	24	18
9	9	4,8	1,0	28	25	22
0	10	4,6	1,9	30	14	24

studfiles.net

Расчет статически неопределимой рамы (метод сил) с подбором сечения

Построить эпюры внутренних усилий М, Q, N и подобрать размеры поперечного сечения в виде двутавра из условия прочности по нормальным напряжениям для рамы, если дано F=80 кН, М=30кНм, q=60кН/м, h=2м, а=1,6м, EI_x=const, σ_adm=160МПа.

Итак, заданная система:

Найдем степень статической неопределимости системы:

n = R — Ш – 3 = 5 – 0 – 3 = 2,  где R – число всех неизвестных реакций,    Ш – число простых соединительных шарниров, в данной схеме их нет; 3 — количество уравнений статики.  Рама получилась дважды статически неопределима ( две «лишние» связи и требуется два дополнительных канонических уравнений метода сил).

Выбираем основную систему путем отбрасывания лишних связей: 

Зарисовываем эквивалентную систему: к основной системе прикладываем всю внешнюю нагрузку и вместо отброшенных связей неизвестные реакции Х₁, Х₂ .

Запишем систему канонических уравнений для выбранной эквивалентной системы:

Построим эпюру изгибающих моментов M_Fдля основной системы от действия заданных нагрузок, предварительно определив реакции и значения внутренних усилий в характерных сечениях. Определяем опорные реакции:

Так как Н_К и V_K получились со знаком минус, меняем их направление действия на схеме.

Определяем значения изгибающих моментов в характерных сечениях силовых участков.

Построим эпюру изгибающих моментов M_{F .}   Строим эпюру на сжатых волокнах.  

M_F

Проверка равновесия узлов:

Построим единичные эпюры изгибающих моментов  для основной системы от действия соответственно  

При действии    :

Сначала определим опорные реакции:

Определим изгибающие моменты на силовых участках:

Строим эпюру.

При действии     :

Опорные реакции:

Определим изгибающие моменты на силовых участках:

 

Строим эпюру.

Строим суммарную эпюру изгибающих моментов от действия единичных усилий:

 

 

Определим коэффициенты  канонических уравнений метода сил перемножением эпюр по формуле Симпсона

:

 

Итак, приступим к расчету:

 

 

Выполним проверку правильности вычисления единичных коэффициентов:

Проверка верна.

Определим грузовые коэффициенты:

Выполним проверку правильности вычисления грузовых коэффициентов:

Проверка верна.

Решаем систему канонических уравнений:

Построим эпюры изгибающих моментов для основной системы от действия  неизвестных усилий, для этого умножим единичные эпюры моментов на найденные значения X:   

Построим окончательную эпюру изгибающих моментов для заданной системы путём сложения составляющих 

Выполним деформационную проверку правильности построения эпюры М  — произведение окончательной и суммарной единичной эпюр должно быть равно нулю (разница не более 5%).

Проверка верна.

Построим эпюры поперечных и продольных сил, используя зависимость    , где      , и рассматривая уравнения равновесия для вырезанных узлов.

Поперечная сила на силовых участках:

Строим эпюру Q

Определяем продольную силу. Из рассмотрения равновесия узлов D и С  следует:

Строим эпюру N

Подбираем размеры поперечного сечения из условия прочности:

Согласно сортаменту прокатной стали выбираем двутавр  №27, у которого W_x= 371см³.

Перенапряжение составляет

Перенапряжение меньше 5% ,что допустимо.

 

prosopromat.ru

Сохранение и загрузка расчетов. Расчет рамы, фермы, балки он-лайн (на прочность)!! СОПРОМАТ, СТРОЙМЕХ (СТРОИТЕЛЬНАЯ МЕХАНИКА)

Это удобно Бывает так, что нужно кому-то в сети показать расчет (или схему). Достаточно передать ссылку на сохраненный расчет, чтобы другой человек увидел схему, а так же смог посмотреть результат расчета. Удобно. Не правда ли? Сохранение расчета Постройте схему. Нажмите «Сохранить расчет». При успешном сохранении построенной схемы Вы увидите сообщение. Убедитесь, посмотрите сохраненный расчет http://rama.sopromat.org/2009/?id=351 Загрузка расчета К сохраненной схеме можно перейти, например, по полученной при сохранении ссылки. (пример http://rama.sopromat.org/2009/?id=351) Или, зная номер сохраненного расчета, выполнить «Загрузку расчета».

Вход Новости сайта 01 июня 2010 г. Добавлена возможность экспорта результатов в формат DXF 18 марта 2010 г. Доработана Mini версия программы. 14 марта 2010 г. Добавлено немного пояснений при выводе хода решения методом конечных элементов (МКЭ). 11 марта 2010 г. По просьбам добавлен горизонтальный подвижный шарнир. 09 марта 2010 г. Теперь масштаб сохраняется! и при загрузке расчета показывает в том масштабе, в котором сохраняли. 05 февраля 2010 г. День Рождения проекта Рама.Сопромат.Орг

rama.sopromat.org

Решение задач про рамы — примеры

В данном разделе можно найти ссылки на задачи, связанные с расчетом рам. В этих задачах, часто, рассчитываются и строятся эпюры: продольных и поперечных сил, изгибающих моментов. Проводятся прочностные расчеты и расчеты на жесткость. В ходе прочностных расчетов уточняются размеры поперечных сечений, либо проверяется соблюдение условия прочности. Также эти задачи в этих задачах, нередко, определяется перемещения поперечных сечений.

Статически определимая рама

В этом разделе собраны задачи, про статически определимые рамы. В которых строятся эпюры, рассчитываются сечения, определяются перемещения.

Статически неопределимая рама

В этих задачах, расчет начинается с раскрытия статической неопределимости, которая при выполнении ручных расчетов раскрывается с помощью метода сил, либо метода перемещений. Часто, задачи данного типа решаются комбинированным методом. После раскрытия статической неопределимости, сценарий дальнейшего расчета может быть таким же как для статически определимой рамы.

sopromats.ru