Пример №11

Для статически неопределимой рамы (рис. 68, а) требуется:

1. построить эпюры внутренних усилий, используя метод сил;

2) выполнить деформационную проверку, приняв

Решение

Определим степень статической неопределимости. Рама имеет пять связей, в то время как три связи равновесие плоской системы обеспечивают три связи. Значит, рама дважды статически неопределима.

Образуем основную систему (рис. 68, б), которая является статически определимой и геометрически неизменяемой. Приложив к ней внешнюю нагрузку и неизвестные усилия в лишних связях Х₁, Х₂ получим эквивалентную систему (рис. 68, в).

Запишем канонические уравнения метода сил для дважды статически неопределимой системы:

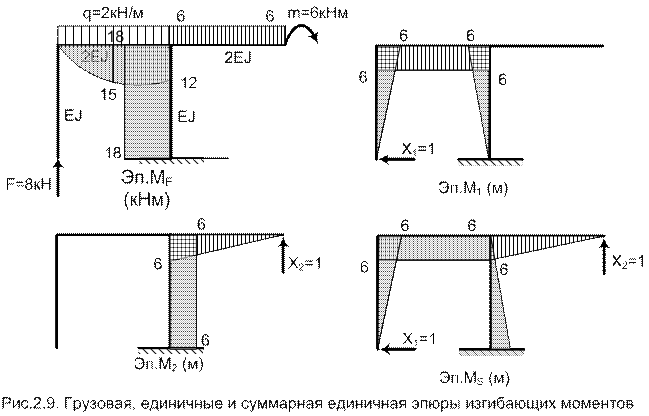
Построим эпюру изгибающих моментов в основной системе от внешних сил.

Участок 1

Участок 2

Участок 3

Рис. 68. Статически неопределимая рама: а – расчетная схема,

б – основная система, в – эквивалентная система

Рис. 69. Эпюра от внешних сил в основной системе

Построим эпюры изгибающих моментов и от единичных сил по направлению усилий,.

Рис. 70. Эпюра от силы X1=1 (б) в основной ситеме (а)

Участок 1

Участок 2

На участке 3

Рис. 71. Эпюра от силы X2=1 (б) в основной ситеме (а)

Участок 1

Участок 2

Участок 3

Запишем каноническое уравнение метода сил для системы дважды статические неопределимой.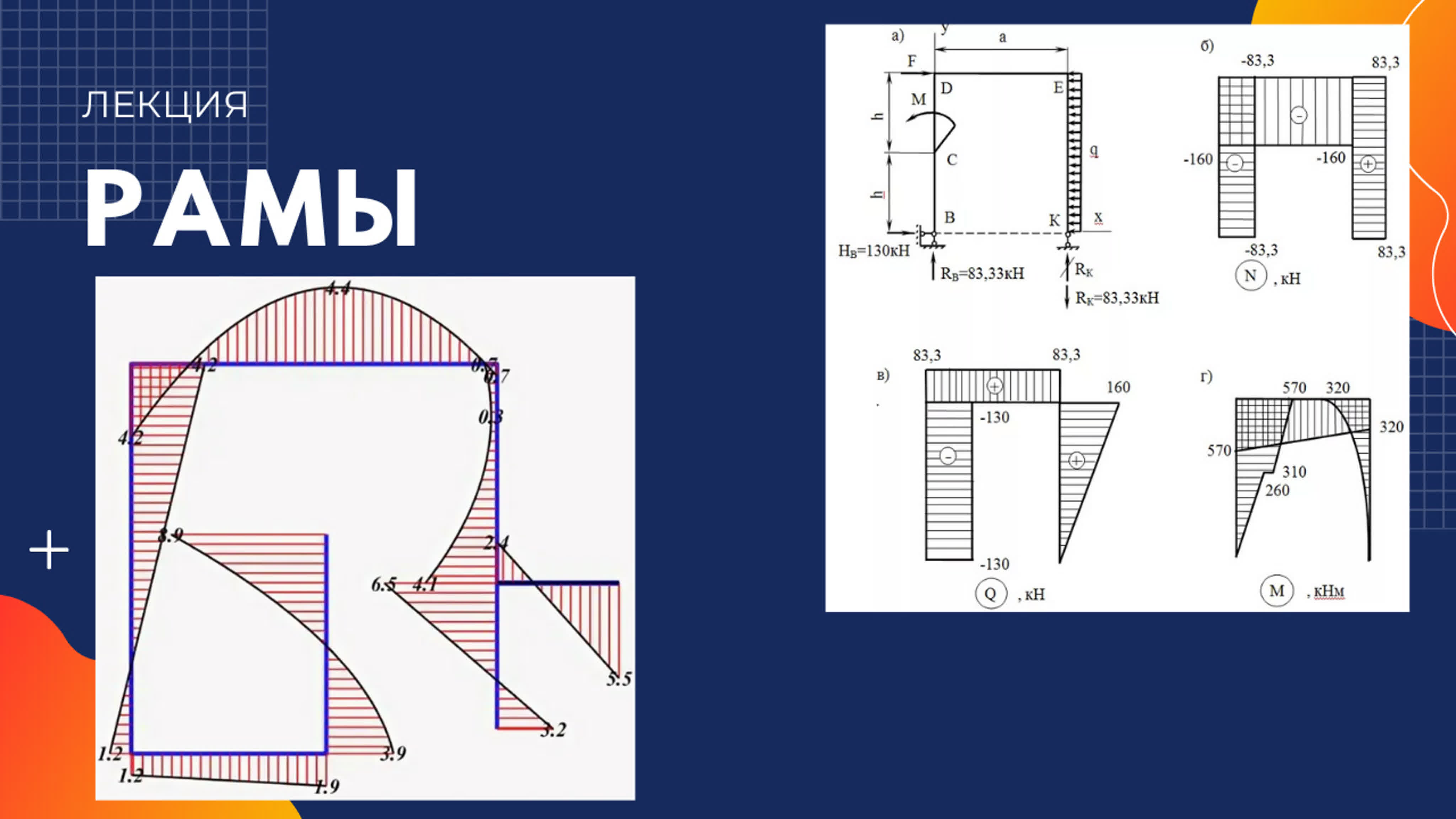

Определим коэффициенты канонических уравнений по правилу Верещагина:

;

;

;

;

.

Рис. 72. Суммарная единичная эпюра

Для проверки единичных коэффициентов построим суммарную единичную эпюру путем сложения ординат эпюрии «перемножим» ее саму на себя:

.

Полученный результат должен быть равен сумме «единичных» коэффициентов

.

;

.

Для проверки «грузовых» коэффициентов «перемножим» грузовую эпюру M_F и суммарную единичную эпюру :

.

Полученный результат должен быть равен сумме грузовых коэффициентов:

.

Имеем

.

Совпадение результатов говорит о правильности вычисления коэффициентов.

Подставим их значения в канонические уравнения и сократим на общий множитель:

_{Решив систему уравнений получим:}

X₁

=–3,98кН; X₂=2,14кН.

Знак «минус», свидетельствуют о том, что принятое направление Х₁ следует изменить на противоположное.

Строим эпюры внутренних усилий N, Q, M с учетом найденных значений Х₁ и Х₂, используя метод сечений.

Рис. 73. Эквивалентная система

Участок 1

Участок 2

Участок 3

Участок 4

Участок 5

Рис. 74. Эпюры внутренних усилий в раме: а – продольной силы;

б – поперечной силы; в – изгибающего момента

Произведем деформационную проверку. «Перемножим» эпюры M_z и . При этом результат должен быть близок к нулю (погрешность не должна превышать 5%).

погрешность

Для стойки указанного сечения, одинаково закрепленной в плоскостях xy и xz и сжатой центрально приложенной силой F, требуется подобрать размеры поперечного сечения, c учетом коэффициента продольного изгиба. Материал – сталь Ст.3.

Исходные данные: F =300 кН; l =2 м; R= 220 МПа.

Рис. 75. Центрально сжатый стержень: а– расчетная схема;

б– поперечное сечение

Решение

Для стойки, имеющей защемляющую и шарнирную опоры, коэффициент приведенной длины μ = 0,7. Определим геометрические характеристики сечения:

_{радиусы инерции сечения}

Гибкость стержня

.

Коэффициент продольного изгиба может принимать значения от нуля, до единицы. В первом приближении принимаем тогда:

По табл. (приложения 6) принимаем значение , которое существенно отличается от φ_1.

_{Во втором приближении коэффициент продольного изгиба приним}аем как среднее арифметическое:

По табл. (приложения 6) принимаем значение , которое отличается от_.

_{В третьем приближении коэффициент продольного изгиба приним}аем как среднее арифметическое:

По табл. (приложения 6) принимаем значение

Вычислим напряжения в третьем приближении:

_{Перенапряжение составляет}

_{Что в пределах допустимых 3%.}

_{Окончательно принимаем a=4 см.}

Сопромат. Раскрыть статическую неопределимость плоской рамы. Построить эпюры внутренних силовых факторов, дей

выполнено на сервисе Автор24

Студенческая работа на тему:

Сопромат. Раскрыть статическую неопределимость плоской рамы. Построить эпюры внутренних силовых факторов, дей

Как заказчик описал требования к работе:

Сопромат. Раскрыть статическую неопределимость плоской рамы. Построить эпюры внутренних силовых факторов, действующих в стержнях плоской рамы.

Стоимость
работы

20 ₽

Заказчик не использовал рассрочку

Гарантия сервиса
Автор24

20 дней

Заказчик принял работу без использования гарантии

Сопромат. Раскрыть статическую неопределимость плоской рамы. Построить эпюры внутренних силовых факторов, дей.jpg

Общая оценка

5

Положительно

Автор просто супер! Все понятно, доступно и вовремя. Всегда на связи, всегда поможет. Обращаюсь не в первый раз, очень довольна. Рекомендую!

Хочешь такую же работу?
Зарегистрироваться

Тебя также могут заинтересовать

по этому предмету по этому типу и предмету

Статически неопределимая балка

Решение задач

Сопротивление материалов

Стоимость:

150 ₽

Расчет статически определимой балки

Другое

Сопротивление материалов

Стоимость:

300 ₽

сопромат

Контрольная работа

Сопротивление материалов

Стоимость:

300 ₽

реферат на тему цементобетон

Реферат

Сопротивление материалов

Стоимость:

300 ₽

Определить положение центра тяжести составного сечения в соответствии с заданием

Решение задач

Сопротивление материалов

Стоимость:

150 ₽

Задача

Решение задач

Сопротивление материалов

Стоимость:

150 ₽

Нужна помощь на зачете, решить 2 задачи онлайн!

Помощь on-line

Сопротивление материалов

Стоимость:

700 ₽

Напряженное и деформированное состояние в точке,2 Сложное сопротивление,3 Устойчивость сжатых стержней

Решение задач

Сопротивление материалов

Стоимость:

150 ₽

Новое задание по сопротивлению материалов

Решение задач

Сопротивление материалов

Стоимость:

150 ₽

Определить прогиб в самой удалённой от заделки точке балки (на конце балки). Балка прямоугольник с соотношение

Решение задач

Сопротивление материалов

Стоимость:

150 ₽

Ргр сопромат

Контрольная работа

Сопротивление материалов

Стоимость:

300 ₽

Расчет геометрических характеристик сечений

Решение задач

Сопротивление материалов

Стоимость:

150 ₽

задача по сопротивлению материалов

Решение задач

Сопротивление материалов

Стоимость:

150 ₽

Новое задание по сопротивлению материалов

Решение задач

Сопротивление материалов

Стоимость:

150 ₽

Прочность стальных балок при изгибе

Решение задач

Сопротивление материалов

Стоимость:

150 ₽

Сжатие,растяжение

Решение задач

Сопротивление материалов

Стоимость:

150 ₽

задАчи по курсу: Введение в сопротивление материалов

Решение задач

Сопротивление материалов

Стоимость:

150 ₽

Сопротивление материалов

Решение задач

Сопротивление материалов

Стоимость:

150 ₽

11 задач по сопромату

Решение задач

Сопротивление материалов

Стоимость:

150 ₽

методы расчета элементов конструкции

Решение задач

Сопротивление материалов

Стоимость:

150 ₽

Сопротивление материалов

Решение задач

Сопротивление материалов

Стоимость:

150 ₽

Решение задач по сопромату

Решение задач

Сопротивление материалов

Стоимость:

150 ₽

Новое задание по сопротивлению материалов

Решение задач

Сопротивление материалов

Стоимость:

150 ₽

Анализ плоского напряженного сечения

Решение задач

Сопротивление материалов

Стоимость:

150 ₽

Читай полезные статьи в нашем

Закон Гука

Ученик Роберта Бойля и современник Ньютона известный английский естествоиспытатель Роберт Уайт Гук (Рис. 1) родился в небольшой деревушке Фрешуотер на острове Уайт в семье священника местной церкви в 1635г. Около 1660 года им была сформулирована закономерность «ut tensio sic vis», что в переводе с латыни означало «каково удлинение, такова сила». В печатных источниках это правило, носящее сегодня на…

подробнее

Зависимость сопротивления от материала

Мир, окружающий нас, материален, в том смысле, что объекты его наполняющие, состоят из материалов. Материалы могут быть природными или искусственными, но все они обладают некоторыми свойствами, среди которых особое место принадлежит способности противостоять механическим воздействиям.
Изучением способности материалов противодействовать воздействующим нагрузкам, занимается раздел механики твёрдого т…

подробнее

Измерение сопротивления материалов

Сопромат – наука в значительной мере экспериментальная. Начало её в таком качестве положил Леонардо да Винчи, одним из первых исследовавший прочность проволоки на разрыв при помощи созданной им экспериментальной установки. Схематически она выглядела так:

Рисунок 1. Экспериментальная установка Леонардо да Винчи. Автор24 — интернет-биржа студенческих работ
К проволочке подвешивалась пустая корзина, в…

подробнее

Что изучает наука сопротивление материалов?

Сопротивление материалов (Сопромат) является важной дисциплиной, которая изучается в высших учебных заведениях. Эта дисциплина учитывает величины и характеристики сил, воспринимаемые каждым элементом сооружения или оборудования, а также реальные условия эксплуатации.
Основной задачей, которая стоит перед сопротивлением материалов является обеспечение прочности, жесткости и устойчивости различных к…

подробнее

Закон Гука

Ученик Роберта Бойля и современник Ньютона известный английский естествоиспытатель Роберт Уайт Гук (Рис.1) родился в небольшой деревушке Фрешуотер на острове Уайт в семье священника местной церкви в 1635г. Около 1660 года им была сформулирована закономерность «ut tensio sic vis», что в переводе с латыни означало «каково удлинение, такова сила». В печатных источниках это правило, носящее сегодня на…

подробнее

Зависимость сопротивления от материала

Мир, окружающий нас, материален, в том смысле, что объекты его наполняющие, состоят из материалов. Материалы могут быть природными или искусственными, но все они обладают некоторыми свойствами, среди которых особое место принадлежит способности противостоять механическим воздействиям.
Изучением способности материалов противодействовать воздействующим нагрузкам, занимается раздел механики твёрдого т…

подробнее

Измерение сопротивления материалов

Сопромат – наука в значительной мере экспериментальная. Начало её в таком качестве положил Леонардо да Винчи, одним из первых исследовавший прочность проволоки на разрыв при помощи созданной им экспериментальной установки. Схематически она выглядела так:

Рисунок 1. Экспериментальная установка Леонардо да Винчи. Автор24 — интернет-биржа студенческих работ
К проволочке подвешивалась пустая корзина, в.