Расчет балки на прогиб — pouznaval.ru

Процесс проектирования современных строений и построек регулируется огромным количеством различных строительных норм и правил. В большинстве случаев нормы требуют обеспечения определенных характеристик, например, деформации или прогиба балок плит перекрытия под статической или динамической нагрузкой. Например, СНиП № 2.09.03-85 определяет для опор и эстакад прогиб балки не более чем в 1/150 длины пролета. Для чердачных перекрытий этот показатель составляет уже 1/200, а для межэтажных балок и того меньше – 1/250. Поэтому одним из обязательных этапов проектирования является выполнение расчета балки на прогиб.

Способы выполнить расчет и проверку на прогиб

Причина, по которой СНиПы устанавливают столь драконовские ограничения, проста и очевидна. Чем меньше деформация, тем больше запас прочности и гибкости конструкции. Для прогиба менее 0,5% несущий элемент, балка или плита все еще сохраняет упругие свойства, что гарантирует нормальное перераспределение усилий и сохранение целостности всей конструкции.

С увеличением прогиба каркас здания прогибается, сопротивляется, но стоит, с выходом за пределы допустимой величины происходит разрыв связей, и конструкция лавинообразно теряет жесткость и несущую способность.

Просчитать прогиб конструкции можно несколькими способами:

• Воспользоваться программным онлайн-калькулятором, в котором «зашиты» стандартные условия, и не более того;
• Использовать готовые справочные данные для различных типов и видов балок, для различных опор схем нагрузок. Нужно только правильно идентифицировать тип и размер балки и определить искомый прогиб;
• Посчитать допустимый прогиб руками и своей головой, большинство проектировщиков так и делают, в то время как контролирующие архитектурные и строительные инспекции предпочитают второй способ расчета.

К сведению! Чтобы реально представлять, почему так важно знать величину отклонения от первоначального положения, стоить понимать, что измерение величины прогиба является единственным доступным и достоверным способом определить состояние балки на практике.

Измерив, насколько просела балка потолочного перекрытия, можно с 99% уверенностью определить, находится ли конструкция в аварийном состоянии или нет.

Методика выполнения расчета на прогиб

Прежде чем приступать к расчету, нужно будет вспомнить некоторые зависимости из теории сопротивления материалов и составить расчетную схему. В зависимости от того, насколько правильно выполнена схема и учтены условия нагружения, будет зависеть точность и правильность расчета.

Используем простейшую модель нагруженной балки, изображенной на схеме. Простейшей аналогией балки может быть деревянная линейка, фото.

В нашем случае балка:

1. Имеет прямоугольное сечение S=b*h, длина опирающейся части составляет L;
2. Линейка нагружена силой Q, проходящей через центр тяжести изгибаемой плоскости, в результате чего концы поворачиваются на небольшой угол θ, с прогибом относительно начального горизонтального положения, равным f;
3. Концы балки опираются шарнирно и свободно на неподвижных опорах, соответственно, не возникает горизонтальной составляющей реакции, и концы линейки могут перемещаться в произвольном направлении.

Для определения деформации тела под нагрузкой используют формулу модуля упругости, который определяется по соотношению 

Е=R/Δ, где Е – справочная величина, R— усилие, Δ— величина деформации тела.

Вычисляем моменты инерции и сил

Для нашего случая зависимость будет выглядеть так: Δ = Q/(S·Е). Для распределенной вдоль балки нагрузки q формула будет выглядеть так: Δ = q·h/(S·Е).

Далее следует наиболее принципиальный момент. Приведенная схема Юнга показывает прогиб балки или деформацию линейки так, если бы ее раздавливали под мощным прессом. В нашем случае балку изгибают, а значит, на концах линейки, относительно центра тяжести, приложены два изгибающих момента с разным знаком. Эпюра нагружения такой балки приведена ниже.

Чтобы преобразовать зависимость Юнга для изгибающего момента, необходимо обе части равенства умножить на плечо L. Получаем

 Δ*L = Q·L/(b·h·Е).

Если представить, что одна из опор жестко закреплена, а на второй будет приложен эквивалентный уравновешивающий момент сил M_max = q*L*2/8, соответственно, величина деформации балки будет выражаться зависимостью Δх = M·х/((h/3)·b·(h/2)·Е). Величину b·h²/6 называют моментом инерции и обозначают W. В итоге получается Δх = M·х/(W·Е) основополагающая формула расчета балки на изгиб W=M/E через момент инерции и изгибающий момент.

Чтобы точно выполнить расчет прогиба, потребуется знать изгибающий момент и момент инерции. Величину первого можно посчитать, но конкретная формула для расчета балки на прогиб будет зависеть от условий контакта с опорами, на которых находится балка, и способа нагружения, соответственно для распределенной или концентрированной нагрузки. Изгибающий момент от распределенной нагрузки считается по формуле Mmax = q*L

2/8.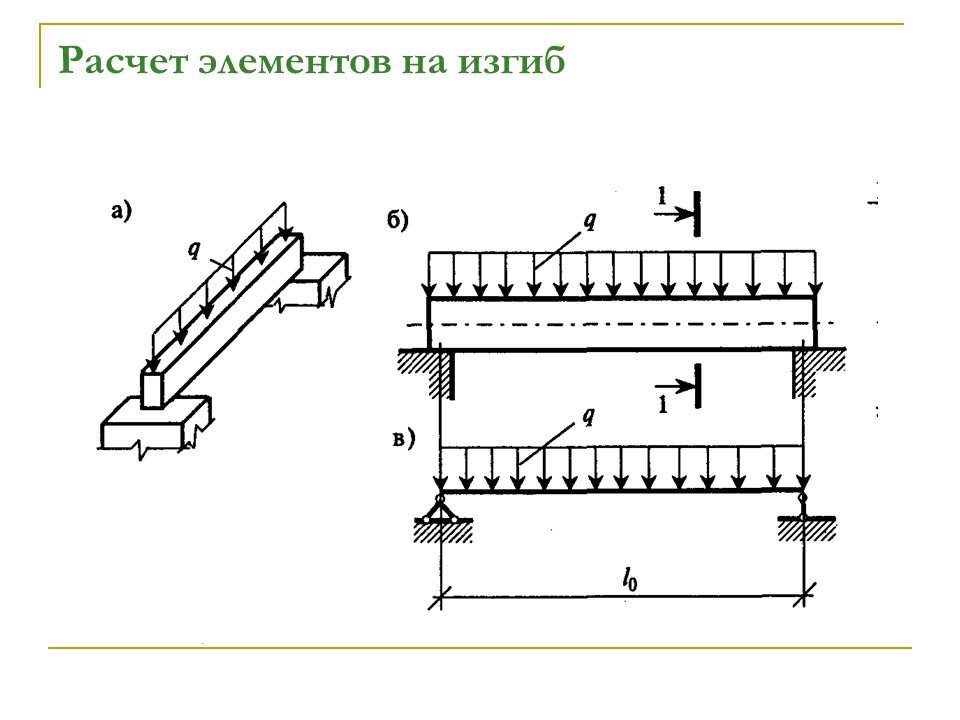 Приведенные формулы справедливы только для распределенной нагрузки. Для случая, когда давление на балку сконцентрировано в определенной точке и зачастую не совпадает с осью симметрии, формулу для расчета прогиба приходится выводить с помощью интегрального исчисления.

Момент инерции можно представить, как эквивалент сопротивления балки изгибающей нагрузке. Величину момента инерции для простой прямоугольной балки можно посчитать по несложной формуле W=b*h³/12, где b и h – размеры сечения балки.

Из формулы видно, что одна и та же линейка или доска прямоугольного сечения может иметь совершенно разный момент инерции и величину прогиба, если положить ее на опоры традиционным способом или поставить на ребро. Недаром практически все элементы стропильной системы крыши изготавливаются не из бруса 100х150, а из доски 50х150.

Реальные сечения строительных конструкций могут иметь самые разные профили, от квадрата, круга до сложных двутавровых или швеллерных форм. При этом определение момента инерции и величины прогиба вручную, «на бумажке», для таких случаев становится нетривиальной задачей для непрофессионального строителя.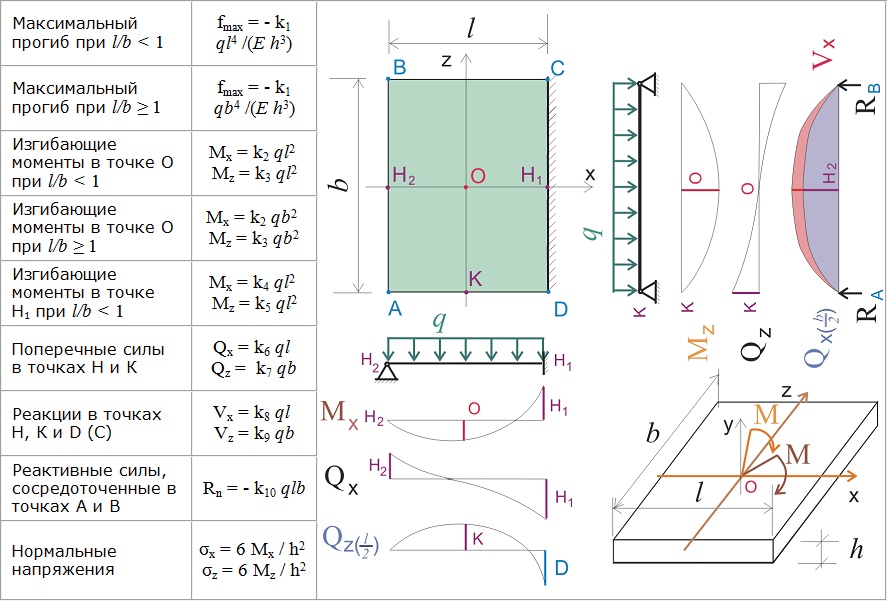

Формулы для практического использования

На практике чаще всего стоит обратная задача – определить запас прочности перекрытий или стен для конкретного случая по известной величине прогиба. В строительном деле очень сложно дать оценку запасу прочности иными, неразрушающими методами. Нередко по величине прогиба требуется выполнить расчет, оценить запас прочности здания и общее состояние несущих конструкций. Мало того, по выполненным измерениям определяют, является деформация допустимой, согласно расчету, или здание находится в аварийном состоянии.

Совет!

 В вопросе расчета предельного состояния балки по величине прогиба неоценимую услугу оказывают требования СНиПа. Устанавливая предел прогиба в относительной величине, например, 1/250, строительные нормы существенно облегчают определение аварийного состояния балки или плиты.

Например, если вы намерены покупать готовое здание, простоявшее достаточно долго на проблемном грунте, нелишним будет проверить состояние перекрытия по имеющемуся прогибу. Зная предельно допустимую норму прогиба и длину балки, можно безо всякого расчета оценить, насколько критическим является состояние строения.

Строительная инспекция при оценке прогиба и оценке несущей способности перекрытия идет более сложным путем:

• Первоначально измеряется геометрия плиты или балки, фиксируется величина прогиба;
• По измеренным параметрам определяется сортамент балки, далее по справочнику выбирается формула момента инерции;
• По прогибу и моменту инерции определяют момент силы, после чего, зная материал, можно выполнить расчет реальных напряжений в металлической, бетонной или деревянной балке.

Вопрос – почему так сложно, если прогиб можно получить, используя для расчета формулу для простой балки на шарнирных опорах f=5/24*R*L²/(E*h) под распределенным усилием. Достаточно знать длину пролета L, высоту профиля, расчетное сопротивление R и модуль упругости Е для конкретного материала перекрытия.

Ответ  прост — необходимо непросто рассчитать, но и сохранить на бумаге ход выполнения проверочного расчета, чтобы сделанные выводы о состоянии перекрытия можно было проверить и перепроверить по всем этапам проверки.

Совет! Используйте в своих расчетах существующие ведомственные сборники различных проектных организаций, в которых в сжатом виде сведены все необходимые формулы для определения и расчета предельного нагруженного состояния.

Заключение

Аналогичным образом поступает большинство разработчиков и проектантов серьезных построек. Программа – это хорошо, она помогает очень быстро выполнить расчет прогиба и основных параметров нагружения перекрытия, но важно также предоставить заказчику документальное подтверждение полученных результатов в виде конкретных последовательных расчетов на бумаге.

 

Балки допускаемый прогиб — Энциклопедия по машиностроению XXL

При малых деформациях величина второго слагаемого во много раз меньше первого. Действительно, при расчете обычных машиностроительных или строительных элементов нормы допускаемого прогиба составляют 1/100—1/1000 пролета в зависимости от условий работы балки, а получающиеся при этом углы поворота не превышают 1  [c. 272]

При малых деформациях величина второго слагаемого во много раз меньше первого. Действительно, при расчете обычных машиностроительных или строительных элементов нормы допускаемого прогиба составляют 1/100—1/1000 пролета в зависимости от условий работы балки, а получающиеся при этом углы поворота не превышают Г. Даже приняв больший предел для прогиба (/ = //100), наибольшую величину тангенса 0 получим следуюш,ей  [c.292]

Сечения изгибаемой балки перемещаются перпендикулярно к оси балки и поворачиваются вокруг своих нейтральных осей (рис. 103). Вероятны случаи, когда балка, удовлетворяя условию прочности, не обладает достаточной жесткостью, т. е. прогибы или углы поворота сечений недопустимо велики. Допускаемый прогиб балок, применяемых в строительных конструкциях и машиностроении, очень невелик обычно он назначается в долях  [c.115]

Это точное выражение радиуса кривизны можно заменить более простым, приближенны-м выражением, допускаемые прогибы при изгибе балок весьма невелики (составляют приблизительно одну тысячную долю длины балки) и упругая линия мало отличается от прямой.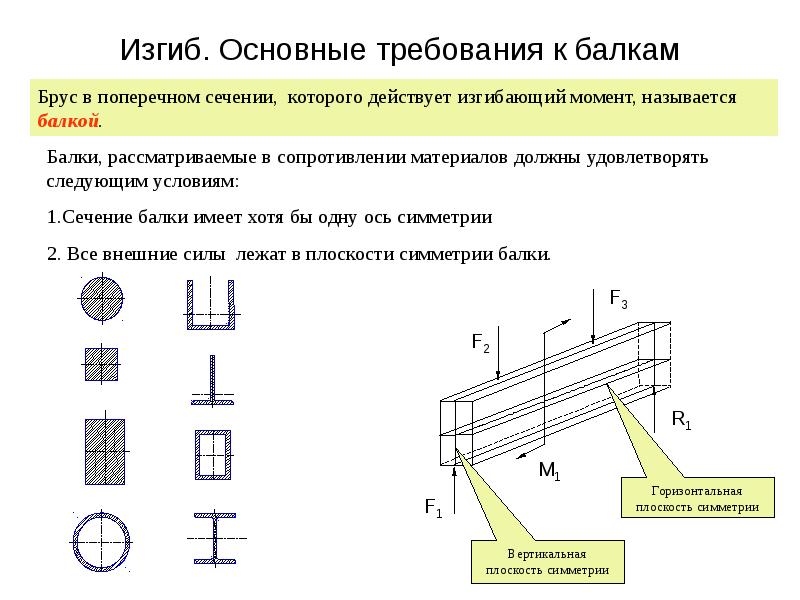 ВелИ чина dy/dx, представляющая собой tg9, т. е. тангенс угла, образованного касательной к упругой ЛИНИИ с положительным направлением оси х, настолько мала, что ее величина, будучи возведенной в квадрат, делается пренебрежимо малой  [c.249]

Пример 5.10. Дать анализ напряженно-деформированного состояния статически определимой балки (рисунок 5.7) и подобрать сечение двутавра из условий прочности и жесткости, если расчетное сопротивление R = 2 кН/см допускаемые прогибы в пролете [f np=inp /250 см, на консоли -[Л.= ,/125 см.  [c.282]

Консоль длиной 1 — 2м нагружена двумя равными силами Р = 10 кн ( 1 Т) так, что одна приложена в середине, а другая — на конце балки. Подобрать сечения двутавровой балки, если допускаемый прогиб [ ] =0,135 см.  [c.214]

Для балки (рис. 299) подобрать швеллерное сечение из расчета на прочность и жесткость, если Р = 10 кн ( 1 Г), д = 5кн/м ( 0,5 Т/м), допускаемое напряжение [[c. 214]

Подобрать двутавровое поперечное сечение стальной балки (рис. 2.207) из условий прочности и жесткости. Допускаемое напряжение [а] = 160 МН/м . Допускаемый прогиб [/] = //500.  [c.195]

Из условия жесткости стальной двутавровой балки (рис. 2.208) определить допустимую нагрузку Р. Допускаемый прогиб принять равным 1/800 пролета. Определить наибольшее нормальное напряжение в поперечном сечении балки при нагрузке, равной допускаемой.  [c.195]

Для деревянной балки (рис. 2.209) определить из условия жесткости допустимую интенсивность равномерно распределенной нагрузки. Допускаемый прогиб [/] = //250.  [c.196]

Подобрать из условия жесткости сечение стальной двутавровой балки (рис. 2.210). Допускаемый прогиб концов консолей [/] = 1 см.  [c.196]

Проверить жесткость деревянной балки (рис. 2.211), допускаемый прогиб для которой [/] = //200.  [c.196]

Проверить жесткость стальной двутавровой балки (рис. 2.216) с моментом инерции сечения = = 3800 см, если допускаемый прогиб для сечения С [/] = 1,2 см.-  [c.198]

Проверить стальную балку (рис. 2.299) по несущей способности, а также по второму предельному состоянию (на жесткость). Сосредоточенные нормативные нагрузки Р» состоят из 65% постоянной нагрузки и 35% временной. Принять =1,1 Пд= 1,3 т = 1. Расчетное сопротивление / = 210 МН/м . Наибольший допускаемый прогиб. [/] = //500.  [c.241]

Балки, удовлетворяя условию прочности, должны обладать достаточной жесткостью, т. е. прогибы и углы поворота сечений не должны превышать допускаемой величины. Допускаемый прогиб балок, применяемых в строительных конструкциях и машиностроении, очень невелик обычно он назначается в долях от пролета между опорами балки и составляет 1/200—1/1000 пролета  [c.111]

Во многих случаях принятые сечения балки, хотя и удовлетворяют требованию прочности, но балка недостаточно жестка, т. е. изогнутая ось имеет излишне большую кривизну, и прогибы их превышают допустимые пределы, установленные нормами проектирования. Поэтому, если задан допускаемый прогиб для балки, необходимое поперечное сечение подбирают из условия жесткости.  [c.146]

Поэтому балки перекрытий и других конструкций гражданских и промышленных зданий подбирают из условия жесткости, для чего обычно задается наибольший допускаемый прогиб. Техническими условиями и нормами проектирования для разных классов зданий и  [c.164]

При расчету на жесткость в формулу прогиба для заданной схемы балки и нагрузки подставляют значение. величины допускаемого прогиба и определяют величину требуемого момента инерции, по которому и принимают необходимое сечение балки. Для подбора стальных двутавровых и швеллерных балок пользуются сортаментами ГОСТов (8239—56 и 8240—56 ).  [c.165]

Кроме расчета плиты (панели) на прочность и прогиб производится расчет наружной обшивки на местный изгиб в пролете между продольными ребрами или поперечными. За расчетную схему принимается неразрезная балка. Проверяются нормальные напряжения и местный прогиб. Нормальные напряжения от местного изгиба могут суммироваться с нормальными напряжениями от общего изгиба. Допускаемые прогибы при местном изгибе принимаются не  [c.44]

При изгибе сечения балки перемещаются перпендикулярно к оси балки и поворачиваются вокруг своих нейтральных осей (рис. 152). Возможны случаи, когда балка, удовлетворяя условию прочности, не обладает достаточной жесткостью, т, е. прогибы или углы поворота сечений недопустимо велики. Допускаемый прогиб балок, применяемых в строительных конструкциях и машиностроении, очень невелик обычно он назначается в долях от пролета между опорами балки и составляет от 1/200 до 1/1000 пролета (в зависимости о-у назначения балки).  [c.246]

Определить допускаемый прогиб балки, показанной на рис. 125, если дано допускаемое напряжение [о]. Определить также прогиб для консоли, нагруженной на конце (рис. 122).  [c.137]

Подобрать сечение балки по условию жесткости, если допускаемый прогиб [/] = (1/200)/, а д =20 кН/м (рис. 66).  [c.86]

Проверить систему на резонанс, а также прочность и жесткость балки, если расчетное сопротивление Л = 210 МПа, допускаемый прогиб [/] = (1/400)/. Массой балки пренебречь.  [c.133]

Допускаемый прогиб [б] зависит от назначения и условий работы рассчитываемого элемента конструкции и колеблется в широких пределах. Например, для балок, валов или осей [б] выражают в долях пролета I (расстояния между опорами), т. е. принимают [б] = =11к, где к — положительное число. Например, для валов и шпинделей металлорежуш,их станков [б] = (0,005.. . 0,001) I, а для балок и перекрытий гражданских и промышленных зданий колеблется от //150 до 0,001 /. В частности, жесткость балки в примере 2.23 соответствует этому значению ее прогиб 5==ц, =0,001 /.  [c.228]

Определить диаметр деревянной балки круглого поперечного сечения, шарнирно опертой по концам и имеющей длину 3 м. На балку посредине ее пролета падает груз 160 кг, обладающий в начальный момент удара скоростью 50 см(сек. Допускаемое напряжение равно 80 кг1см наибольший допускаемый прогиб равен = 8-10 кг1см. Задачу решить, используя для вычисления динамического коэффициента точную и следующую приближенную формулу  [c.317]

Понятие жесткости усваивается учащимися труднее, чем прочности, поэтому, если даже этот материал не излагался, на следующем уроке при опросе надо уделить вопросу о жесткости и расчетах на жесткость особое внимание. Полагаем, что можно задавать учащимся, например, такие вопросрл Прогиб нагруженной балки составил 1/500 от длины ее пролета, а по нормам допускаемый прогиб 1/800 пролета. Что недостаточно прочность или жесткость балки  [c.52]

Подобрать номер стального швеллера, исходя из условий прочности и жесткости. Допускаемое напряжение [а] = 1600 кГ1см К Допускаемый прогиб [/] = //400. Сравнить веса балки, получаемые, из условий прочности и жесткости.  [c.124]

Однобалочные мосты (рис. 53, а) конструируют из двутавровых прокатных балок, размер которых (номер по стандарту) выбирают по условиям необлодимой жесткости (допускаемого прогиба) и из условий свободного прохода тележки или тельфера по нижним полкам балки. Горизонтальная жесткость моста до-Рис. 53 стигается установкой раскосов с од-  [c.578]

Проверить балку (рис. 300) на прочность и жесткость, если Р — Ъкн ( 0,5 Т), допускаемое напряжение [а ] = 160 Мн м ( 1бОО кПсм ) и допускаемый прогиб [у] = 5 мм.  [c.215]

Консоль из стального двутавра № 20 (рис. 2.300) нагружена сосредоточенной сплои Р», состоящей из 60% постоянной нагрузки и 40 о временной, и раыюмерно распределенной нагрузкой интенсивностью состоящей из 30% постоянной нагрузки и 70% временной. Коэффициенты перегрузки /г =1,1 Па = 1,4 коэффициент условий работы / = 0,9. Расчетное сопротивление р = 210 МН/м . Наибольший допускаемый прогиб свободного конца консоли [/ ] = //400. Проверить балку на несущую способность, а так ке по второму предельному состоянию (на жесткость).  [c.241]

Номер профиля ходового пути, обусловливающий толщину ездовой полки, определяют по максимальной расчетной нагрузке на каретку в зависимости от несущей способности ездовой полки пути. Следовательно, для каждого заданного профиля пути можно установить предельные нагрузки на каретку по прочности ездовой полки (см. ниже). При выбранном профиле расчет ходового пути сводится к определению максимального допускаемого расстояния между креплениями различных участков пути конвейера, т. е. свободного пролета балки пути. Пролет балки пути определяют из расчета на прочность от поперечного и местного изгиба, деформацию прогиба и устойчивость. При расчете на прочность следует учитывать, что при работе конвейера возможен значительный износ ездовых поверхностей путевой балки. Для надежной работы конвейера требуется повышенная жесткость ходового пути, особенно на участках, примыкающих к поворотным устройствам. Поэтому для балок из стали СтЗ рекомендуется принимать допускаемое напряжение на изгиб (поперечный и местный) Оп.д 1200 кгс/см , допускаемый прогиб fmax = 1/500 длины пролета коэффициент запаса по устойчивости % = 1,7 -h 2,0. Для стали 14Г2 можно принять Оп.д = 1400 к,гс/см .  [c. 101]

Пример 77. Подобрать сечение стальной двутавровой балки, нагружённой сплошной нагрузкой = 4 г/ж на полупролёте (фиг. 289), если допускаемое напряжение [а] = 1000 кг1см», а допускаемый прогиб не должен превышать  [c.365]

Балку траверсы проверяют на отсутствие трещин в сварных щвах и деформации. Дефекты сварных щвов восстанавливают заваркой. Допускаемый прогиб балки не более 1 мм на 1 м длины. При большей величине прогиба балку выправляют с предварительным подогревом. Без ремонта износ отверстия допускается до диаметра 70 мм, проушины балки траверсы — 71 мм. При большем износе отверстие вбсстанавливают наплавкой с последующей обработкой до номинального размера. Непараллельность оси проушины относительно оси захвата допускается не более Г мм на длине 1 м.  [c.210]

В ряде случаев в целях гарантии нормальной работы конструкции накладывают ограничения на максимальную величину прогиба i/max [i/] И мзксимальную величину угла поворота 0тахугол поворота соответственно.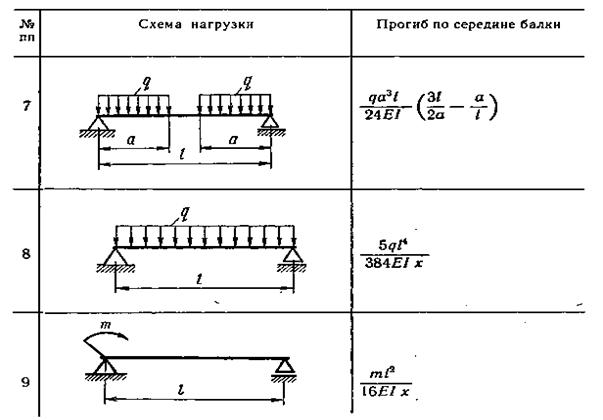 В машиностроении принято [у] = (1/1000 -г-1/300) I, где / — расстояние между опорами балки.  [c.178]

Ходовые пути крепят за хомуты к строительным элементам здания или поддерживающим конструкциям, как и грузонесущие конвейеры. Ходовой путь рассчитывают на поперечный изгиб, местный отгиб полок под катками тележек, на стесненное (изгибное) кручение от эксцентричного расположения катков тележек относительно вертикальной оси сечения профиля, проходящей через его центр изгиба, и на прогиб. Максимальное суммарное напряжение в балках для стали Ст. 3 не должно превышать 180 MhIm (1800 кПсм» ), допускаемый прогиб не более /400 пролета.  [c.268]

---

Расчет прогиба металлической балки. Методика расчета несущих конструкций из различных материалов

Деревянные балки перекрытий

Деревянные балки перекрытий часто являются наиболее экономичным вариантом. Деревянные балки легки в изготовлении и монтаже, имеют низкую теплопроводность по сравнению со стальными или железобетонными балками. Недостатки деревянных балок — более низкая механическая прочность, требующая больших сечений, низкая пожаростойкость и устойчивость к поражению микроорганизмами и термитами (если они водятся в вашей местности). Поэтому, деревянные балки перекрытий требуется тщательно обрабатывать антисептиками и антипиренами, например ХМ-11 или ХМББ производства фирмы Антисептик (С-Петербург).

Как расчитать необходимое сечение деревянной балки перекрытий?

Оптимальный пролет для деревянных балок — 2,5- 4 метра. Лучшее сечение для деревянной балки — прямоугольное с соотношением высоты к ширине 1,4:1. В стену балки заводят не менее чем на 12 см и гидроизолируют по кругу, кроме торца. Желательно закрепить балку анкером, заделанным в стену.

При выборе сечения балки перекрытия учитывают нагрузку собственного веса, которая для балок междуэтажных перекрытий, как правило стоставляет 190-220 кг/м2, и нагрузку временную (эксплуатационную), её значение принимают равной 200 кг/м2. Балки перекрытия укладывают по короткому сечению пролёта.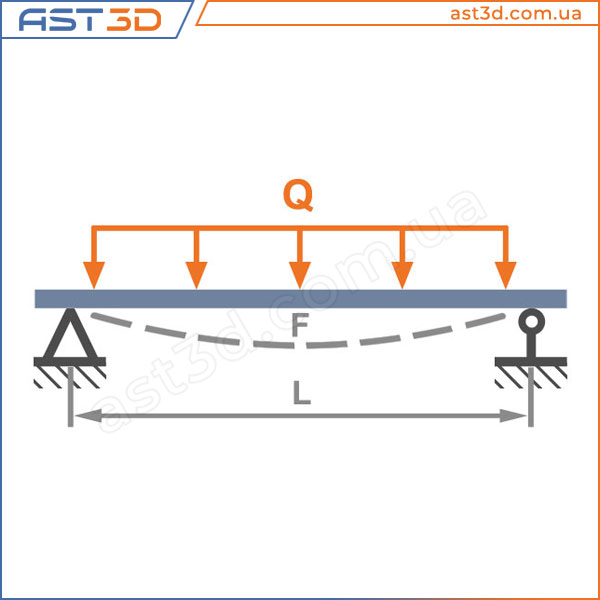 Шаг монтажа деревянных балок рекомендуется выбирать равным шагу установки стоек каркаса.

Для расчета минимального и оптимального сечения деревянной балки перекрытия можно воспользоваться он-лайн калькулятором Романова для деревянных балок перекрытий

Ниже приведены несколько таблиц, со значениями минимальных сечений деревянных балок для различных нагрузок и длинн пролетов:

Таблица сечений деревянных балок перекрытия в зависимости от пролёта и шага установки, при нагрузке 400кг/м2. — рекомендуется расчитывать именно на эту нагрузку

Если вы не используете утеплитель или не планируете нагружать перекрытия (например, перекрытие необитаемого чердака), то можно использовать таблицу для меньших значений нагрузок деревянных балок перекрытий:

Таблица минимальных сечений деревянных балок перекрытия в зависимости от пролёта и нагрузки, при нагрузках от 150 до 350 кг/м2.

Если вы используете вместо балок прямоугольного сечения круглы бревна, можно пользоваться следующей таблицей:

Минимальный допустимый диаметр круглых бревен, используемых в качестве балок междуэтажных перекрытий в зависимости от пролета при нагрузке 400 кг на 1 м2

Если вы хотите перекрыть большие прогоны, то рекомендуем воспользоваться опытом с сайта Околоток.

Стальные (металлические) двутавровые балки перекрытий

Двутавровая металлическая балка перекрытий обладает рядом неоспоримых преимуществ, только при одном недостатке — высокой стоимости. Металлической двутавровой балкой можно перекрыть большие пролеты со значительной нагрузкой, металлическая стальная балка негорюча и устойчива к биологическим воздействиям. Однако, металлическая балка может корродировать при отсутствии защитного покрытия и наличия в помещении агрессивных сред.

Для расчета параметров двутавровой металлической балки можно воспользоваться хорошей

В большинстве случаев в самодеятельном строительстве при расчетах в вышеуказанной программе или других ей подобных, следует считать, что металлическая балка имеет шарнирные опоры (то есть концы не фиксированы жестко — например, так как в каркасной стальной конструкции). Нагрузку на перекрытие со стальными двутавровыми металлическими балками с учетом собственного веса следует рассчитывать, как 350 (без стяжки) -500 (со стяжкой) кг/м2
Шаг между двутавровыми металлическими балками рекомендуется делать равным 1 метру. В случае экономии возможно увеличение шага между металлическими балками до 1200 мм.

Таблица для выбора номера двутавровой металлической балки при различном шаге и длине прогонов

Железобетонные балки перекрытий

При устройстве железобетонных балок нужно использовать следующие правила (по Владимиру Романову):

1. Высота железобетонной балки должна быть не менее 1/20 длины проема. Делим длину проема на 20 и получаем минимальную высоту балки. Например при проеме в 4 м высота балки должна быть не менее 0,2 м.
2. Ширину балки рассчитывают исходя из соотношения 5 к 7 (5 — ширина, 7 — высота).
3. Армировать балку следует минимум 4 прутками арматуры d12-14 (снизу можно толще) — по два сверху и снизу. Таблицы соотношения длины и массы арматуры различного сечения.
4. Бетонировать за один раз, без перерывов, чтобы ранее уложенная порция раствора не успела схватиться до укладки новой порции. С бетономешалкой бетонировать балки сподручнее, чем заказывать миксер. Миксер хорош для быстрой заливки больших объемов.

Вес строительной арматуры или сколько метров арматуры в тонне. Вес арматуры длиной 11,75 м. Вес арматуры диаметром от 5,5 до 32 мм.

Вес двутавра и количество метров в тонне двутавра

Балка — элемент в инженерии, представляющий собой стержень, который нагружают силы, действующие в направлении, перпендикулярном стержню. Деятельность инженеров зачастую включает в себя необходимость расчета прогиба балки под нагрузкой. Этой действие выполняется для того, чтобы ограничить максимальный прогиб балки.

Типы

На сегодняшний день в строительстве могут использоваться балки, изготовленные из разных материалов. Это может быть металл или дерево. Каждый конкретный случай подразумевает под собой разные балки. При этом расчет балок на прогиб может иметь некоторые отличия, которые возникают по принципу разницы в строении и используемых материалов.

Деревянные балки

Сегодняшнее индивидуальное строительство подразумевает под собой широкое применение балок, изготовленных из дерева. Практически каждое строение содержит в себе Балки из дерева могут использоваться как несущие элементы, их применяют при изготовлении полов, а также в качестве опор для перекрытий между этажами.

Ни для кого не секрет, что деревянная, так же как и стальная балка, имеет свойство прогибаться под воздействием нагрузочных сил. Стрелка прогиба зависит от того, какой материал используется, геометрических характеристик конструкции, в которой используется балка, и характера нагрузок.

Допустимый прогиб балки формируется из двух факторов:

• Соответствие прогиба и допустимых значений.
• Возможность эксплуатации здания с учетом прогиба.

Проводимые при строительстве расчеты на прочность и жесткость позволяют максимально эффективно оценить то, какие нагрузки сможет выдерживать здание в ходе эксплуатации. Также эти расчеты позволяют узнать, какой именно будет деформация элементов конструкции в каждом конкретном случае. Пожалуй, никто не будет спорить с тем, что подробные и максимально точные расчеты — это часть обязанностей инженеров-строителей, однако с использованием нескольких формул и навыка математических вычислений можно рассчитать все необходимые величины самостоятельно.

Для того чтобы произвести правильный расчет прогиба балки, нужно также брать во внимание тот факт, что в строительстве понятия жесткости и прочности являются неразрывными. Опираясь на данные расчета прочности, можно приступать к дальнейшим расчетам относительно жесткости. Стоит отметить, что расчет прогиба балки — один из незаменимых элементов расчета жесткости.

Обратите ваше внимание на то, что для проведения таких вычислений самостоятельно лучше всего использовать укрупненные расчеты, прибегая при этом к достаточно простым схемам. При этом также рекомендуется делать небольшой запас в большую сторону. Особенно если расчет касается несущих элементов.

Расчет балок на прогиб. Алгоритм работы

На самом деле алгоритм, по которому делается подобный расчет, достаточно прост. В качестве примера рассмотрим несколько упрощенную схему проведения расчета, при этом опустив некоторые специфические термины и формулы. Для того чтобы произвести расчет балок на прогиб, необходимо выполнить ряд действий в определенном порядке. Алгоритм проведения расчетов следующий:

• Составляется расчетная схема.
• Определяются геометрические характеристики балки.
• Вычисляется максимальную нагрузку на данный элемент.
• В случае возникновения необходимости проверяется прочность бруса по изгибающему моменту.
• Производится вычисление максимального прогиба.

Как видите, все действия достаточно просты и вполне выполнимы.

Составление расчетной схемы балки

Для того чтобы составить расчетную схему, не требуется больших знаний. Для этого достаточно знать размер и форму поперечного сечения элемента, пролет между опорами и способ опирания. Пролетом является расстояние между двумя опорами. К примеру, вы используете балки как опорные брусья перекрытия для несущих стен дома, между которыми 4 м, то величина пролета будет равна 4 м.

Вычисляя прогиб деревянной балки, их считают свободно опертыми элементами конструкции. В случае для расчета принимается схема с нагрузкой, которая распределена равномерно. Обозначается она символом q. Если же нагрузка несет сосредоточенный характер, то берется схема с сосредоточенной нагрузкой, обозначаемой F. Величина этой нагрузки равна весу, который будет оказывать давление на конструкцию.

Момент инерции

Геометрическая характеристика, которая получила название важна при проведении расчетов на прогиб балки. Формула позволяет вычислить эту величину, мы приведем ее немного ниже.

При вычислении момента инерции нужно обращать внимание на то, что размер этой характеристики зависит от того, какова ориентация элемента в пространстве. При этом наблюдается обратно пропорциональная зависимость между моментом инерции и величиной прогиба. Чем меньше значение момента инерции, тем больше будет значение прогиба и наоборот. Эту зависимость достаточно легко отследить на практике. Каждый человек знает, что доска, положенная на ребро, прогибается гораздо меньше, чем аналогичная доска, находящаяся в нормальном положении.

Подсчет момента инерции для балки с прямоугольным сечением производится по формуле:

J=b*h^3/12, где:

b — ширина сечения;

h — высота сечения балки.

Вычисления максимального уровня нагрузки

Определение максимальной нагрузки на элемент конструкции производится с учетом целого ряда факторов и показателей. Обычно при вычислении уровня нагрузки берут во внимание вес 1 погонного метра балки, вес 1 квадратного метра перекрытия, нагрузку на перекрытие временного характера и нагрузку от перегородок на 1 квадратный метр перекрытия. Также учитывается расстояние между балками, измеренное в метрах. Для примера вычисления максимальной нагрузки на деревянную балку примем усредненные значения, согласно которым вес перекрытия составляет 60 кг/м², временная нагрузка на перекрытие равна 250 кг/м², перегородки будут весить 75 кг/м². Вес самой балки очень просто вычислить, зная ее объем и плотность. Предположим, что используется деревянная балка сечением 0,15х0,2 м. В этом случае ее вес будет составлять 18 кг/пог.м. Также для примера примем расстояние между брусьями перекрытия равным 600 мм. В этом случае нужный нам коэффициент составит 0,6. 3/48*E*J, где:

F — сила давления на брус.

Также обращаем внимание на то, что значение модуля упругости, используемое в расчетах, может различаться для разных видов древесины. Влияние оказывают не только порода дерева, но и вид бруса. Поэтому цельная балка из дерева, клееный брус или оцилиндрованное бревно будут иметь разные модули упругости, а значит, и разные значения максимального прогиба.

Вы можете преследовать разные цели, совершая расчет балок на прогиб. Если вы хотите узнать пределы деформации элементов конструкции, то по завершении расчета стрелки прогиба вы можете остановиться. Если же ваша цель — установить уровень соответствия найденных показателей строительным нормам, то их нужно сравнить с данными, которые размещены в специальных документах нормативного характера.

Двутавровая балка

Обратите внимание на то, что балки из двутавра применяются несколько реже в силу их формы. Однако также не стоит забывать, что такой элемент конструкции выдерживает гораздо большие нагрузки, чем уголок или швеллер, альтернативой которых может стать двутавровая балка.

Расчет прогиба двутавровой балки стоит производить в том случае, если вы собираетесь использовать ее в качестве мощного элемента конструкции.

Также обращаем ваше внимание на то, что не для всех типов балок из двутавра можно производить расчет прогиба. В каких же случаях разрешено рассчитать прогиб Всего таких случаев 6, которые соответствуют шести типам двутавровых балок. Эти типы следующие:

• Балка однопролетного типа с равномерно распределенной нагрузкой.
• Консоль с жесткой заделкой на одном конце и равномерно распределенной нагрузкой.
• Балка из одного пролета с консолью с одной стороны, к которой прикладывается равномерно распределенная нагрузка.
• Однопролетная балка с шарнирным типом опирания с сосредоточенной силой.
• Однопролетная шарнирно опертая балка с двумя сосредоточенными силами.
• Консоль с жесткой заделкой и сосредоточенной силой.

Металлические балки

Расчет максимального прогиба одинаковый, будь это стальная балка или же элемент из другого материала.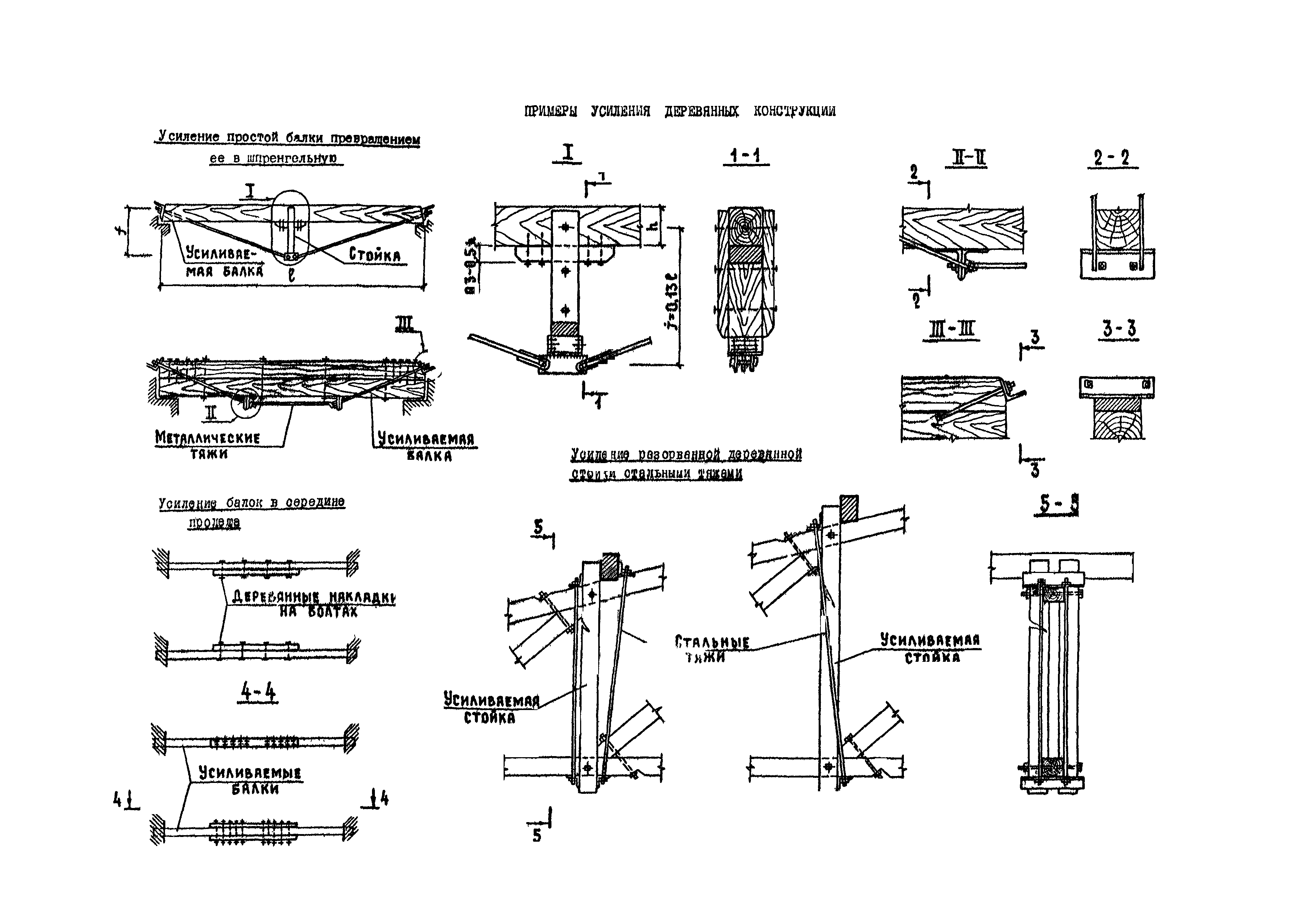 Главное — помнить о тех величинах, которые специфические и постоянные, как к примеру модуль упругости материала. При работе с металлическими балками, важно помнить, что они могут быть изготовлены из стали или же из двутавра.

Прогиб металлической балки, изготовленной из стали, вычисляется с учетом, что константа Е в данном случае составляет 2·105Мпа. Все остальные элементы, вроде момента инерции, вычисляются по алгоритмам, описанным выше.

Расчет максимального прогиба для балки с двумя опорами

В качестве примера рассмотрим схему, в которой балка находится на двух опорах, а к ней прикладывается сосредоточенная сила в произвольной точке. До момента прикладывания силы балка представляла собой прямую линию, однако под воздействием силы изменила свой вид и вследствие деформации стала кривой.

Предположим, что плоскость ХУ является плоскостью симметрии балки на двух опорах. Все нагрузки действуют на балку в этой плоскости. В этом случае фактом будет то, что кривая, полученная в результате действия силы, также будет находиться в этой плоскости. Данная кривая получила название упругой линии балки или же линии прогибов балки. Алгебраически решить упругую линию балки и рассчитать прогиб балки, формула которого будет постоянной для балок с двумя опорами, можно следующим образом.

Прогиб на расстоянии z от левой опоры балки при 0 ≤ z ≤ a

F(z)=(P*a 2 *b 2)/(6E*J*l)*(2*z/a+z/b-z 3 /a 2 *b)

Прогиб балки на двух опорах на расстоянии z от левой опоры при а ≤ z ≤l

f(z)=(-P*a 2 *b 2)/(6E*J*l)*(2*(l-z)/b+(l-z)/a-(l-z) 3 /a+b 2), где Р — прикладываемая сила, Е — модуль упругости материала, J — осевой момент инерции.

В случае балки с двумя опорами момент инерции вычисляется следующим образом:

J=b 1 h 1 3 /12, где b 1 и h 1 — значения ширины и высоты сечения используемой балки соответственно.

Заключение

В заключение можно сделать вывод о том, что самстоятельно вычислить величину максимального прогиба балки разных типов достаточно просто. Как было показано в этой статье, главное — знать некоторые характеристики, которые зависят от материала и его геометрических характеристик, а также провести вычисления по нескольким формулам, в которых каждый параметр имеет свое объяснение и не берется из ниоткуда.

И обрушения зданий необходимо выполнять расчет данных несущих конструкций. Балки изготавливаются из деревянного бруса, металлопроката и железобетона. Ниже приводятся простейшие методики расчетов и рекомендации по выбору балок из указанных материалов.

Расчет деревянных балок

Для расчета деревянных балок необходимо знать распределенную нагрузку на , длину балок и расстояние между ними. Балки укладываются параллельно короткой стороне здания, распределенная нагрузка выбирается равной 400 кг/кв. метр для межэтажных и 200 кг/кв. метр для чердачных перекрытий. Для примера рассчитаем балки для комнаты размерами 6х4,5 метра, при этом длина балки будет равна около пяти метров, но расчет ведется исходя из расстояния между стенами — 4,5 метра. Расстояние между балками выбираем равным 0,8 метра.

Рассчитываем максимальный изгибающий момент:

М = (q х hхl2) / 8 = 400 х 0,8 х 4,52 / 8 = 810 кгм = 81000 кгсм;

где q — распределенная нагрузка, h — расстояние между балками; l — длина пролета.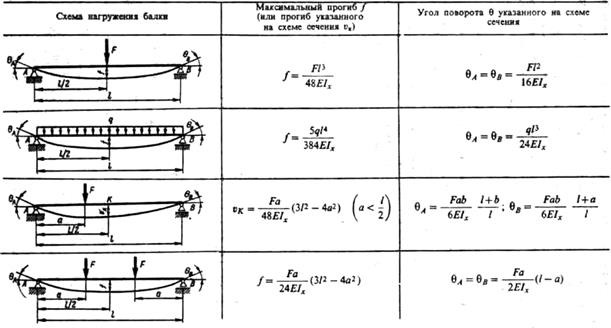

Требуемый момент сопротивления балки равен:

W = М / R = 81000 / 142,71 = 567,6 куб. см;

где R — расчетное сопротивление древесины, для сосны равное 14 МПа или 142,71 кгс/кв. см.

Задавая ширину сечения бруса (10 см) определяем высоту балки:

h = √(6W/b) = √(6 х 567,6/10)= 18,5 см;

где h — высота, b — ширина балки. Результаты расчетов показывают, что можно применить брус 10х20 см.

Оптимальное соотношение ширины и высоты балки равняется 1:1,4. Подставляя в формулы разные значения расстояний между балками и их ширины подсчитываем расход материалов и выбираем наиболее экономичный вариант при оптимальном сечении.

Для выбора деревянных балок можно воспользоваться онлайн калькулятором Романова или таблицами, в которых по результатам расчетов приведены наиболее типичные варианты. Подобные материалы можно легко найти в интернете.

Прогиб деревянной балки должен быть менее 1/250 ее длины, для нашего случая 450/250 = 1,8 см. Он рассчитывается по формуле:

f=(5ql4)/(384EI) = 5 х 400 х 4,5 х 4,5 х 4,5 х 4,5 / 384 х 109 х 6666.6667 х 10 — 8 = 3,2 см;

где E — модуль упругости, для древесины равный 109 кгс/м2; I — момент инерции, для балки прямоугольного сечения равный:

I = b x h4 / 12 = 10 х 203 / 12 = 6666.6667 см4.

В данном случае прогиб больше допустимого, поэтому следует выбрать брус большего сечения или уменьшить расстояние между балками и повторить расчеты.

Методика определения максимального изгибающего момента и момента сопротивления одинакова для балок из любого материала. Металлические балки чаще всего изготавливаются из двутавра. Величину допустимого момента сопротивления для выбранного профиля можно узнать в справочнике по металлопрокату или вычислить на онлайн калькуляторе по геометрическим размерам. Расчеты значительно облегчаются при использовании программ, имеющихся в интернете. В таблице указаны рекомендуемые номера двутавров при распределенной нагрузке 400 кгс/кв. м.

Расчет железобетонных балок

Заводские балки выбираются по допустимому моменту сопротивления, который указывается в документации. Выбор конструкции монолитных балок затруднен тем, что железобетон является материалом, состоящим из нескольких компонентов и предусмотреть влияние всех факторов на несущую способность балки довольно сложно. Методику расчетов смогут осилить лишь специалисты, изучившие сопромат и имеющие практический опыт.

• Бетон выдерживает значительные нагрузки на сжатие, а арматура — на растяжение, поэтому она устанавливается в растянутой зоне — нижней части балки.
• Высоту сечения балки выбирают большей 1/20 длины пролета, отношение высоты к ширине сечения — равным 7:5.
• Диаметр арматуры должен быть 12 мм и более, количество прутков — не менее 4, в нижней части сечения укладывается более толстая арматура (арматура в верхней части нужна, если балка изготавливается на почве и устанавливается на место подъемным краном).
• Бетонировка должна осуществляться в один прием, следующая порция бетона укладывается до схватывания предыдущей.
• Выбор балок упрощается при использовании программ, определяющих их сечение и количество арматуры.

Заключение

Приведенные формулы и рекомендации дают представление о методике расчетов и с большинстве случаев пригодны для выбора балок перекрытия. Более сложные методики учитывают все условия работы, при этом производится проверка на устойчивость к нагрузкам, действующим в разных направлениях.

При строительстве частных жилых домов, хозяйственных и других построек важно правильно рассчитывать параметры каждого элемента конструкции. Одним из ключевых элементов любой конструкции из дерева является перекрытие.

О материалах перекрытий

Правильно подобранный материал, выбор длины, сечения и схема установки определяет его долговечность и нагрузки, которые она способна выдержать. Выбор и расчет деревянных балок для перекрытия между этажами — это одни из самых важных решений в частном строительстве. Поскольку дерево экологически чистый материал и достаточно прочный.

Единственный предполагаемый минус древесины при сравнении с бетоном — это ее горючесть, показатель которой при необходимости можно снизить, если обработать дерево особыми составами.

Принято считать, что бетон огнеупорный, хотя это не совсем так: он трескается при температуре свыше 250 и осыпается при температуре 550 градусов, то есть полностью разрушается при пожаре. Поэтому хороший альтернативной бетону является именно дерево.

Но, чтобы рассчитать, сколько нужно древесины для постройки, чтобы не было ее переизбытка, чтобы при этом была обеспечена максимальная несущая способность этой деревянной балки, часто используют калькулятор автоматического расчета параметров перекрытия. Калькулятор на расчет балок перекрытия из дерева поможет быстро и достаточно точно определить показатели запаса прочности при использовании разных материалов и, соответственно, выбрать один из них. Лучшие материалы, параметры сечения, особенности конструкции, качественные балки перекрытия позволяют оптимально распределить нагрузку, не превышая при этом допустимой, а также кирпичные или сделанные из другого материала стены.

От чего зависит прочность перекрытия?

Основные параметры, которые влияют на качество перекрытия, зависят от свойств материала, технических параметров и условий эксплуатации.

Свойства древесных материалов:

• Вид дерева. Популярными породами для употребления в жилом строительстве считают сосну, ель, лиственницу. Иногда используют дуб, березу, осину, а также комбинированные материалы.
• Сорт. Определяют три сорта древесины, которые нумеруют 1 (самый лучший), 2 и 3. Сорт определяется предельным количеством сучков на древесине, изгиб балок, в том числе здоровых и прогнивших, количеством, глубиной и длиной трещин, другими пороками дерева. Детальные требования к древесине определяются стандартами, нормами, правилами (СНиП II-25-80, СП 64.13330.2011 и другими).

Каждый материал имеет свои характеристики прочности и прогиба, которые зависят от технических показателей, описанных ниже. Некоторые породы более легкие, другие — более стойкие к влаге.

Например, хвойные породы имеют лучшее сопротивление влаге. Первый сорт древесины отличается лучшим качеством, отсутствием изъянов, но он соответственно дороже.

Технические показатели:

• Тип балки. Определяют такие типы, как прямоугольный брус, круглые бревна, балки,. склеенные из досок или из шпона LVL.
• Длина пролета. Обычно балочный пролет для частных жилых домов составляет не более 6 метров. Важно помнить, что этот показатель отличается от длины самой балки, которая должна также захватывать опорные участки на стенах или других опорах.
• Высота и ширина балки. Для бруса, другой прямоугольной балки эти показатели могут быть одинаковыми или отличаться. Чем больше их высота, тем больше жесткость и меньше они прогибаются. В случае с бревнами в расчет берется диаметр или средний диаметр бревна. При выборе этих параметров учитывают также особенности и простоту изготовления, транспортировки, монтажа балок.
• Шаг балок. Это расстояние между двумя соседними балками в перекрытии. Чем ближе балки, тем выше их расход балок, прочность перекрытия, но уменьшается прогиб и максимальная нагрузка.
и сосредоточенная нагрузка, которые определяются стандартами и зависят от типа помещений, количества жильцов или работников, типа, количества мебели или оборудования в них и прочих особенностей их использования.
• Тип перекрытия. Имеются в виду междуэтажные перекрытия с повышенными требованиями относительного прогиба, который составляет 1/250; чердачные перекрытия, требования к которым ниже — 1/200; покрытия и настилы, относительный прогиб которых составляет 1/150.

Последние 3 пункта также определяются как условия эксплуатации деревянного перекрытия, которые зависят непосредственно от особенностей строительства.

Результат и пример расчета

Как работает калькулятор для расчета деревянных балок и как происходит расчет нагрузки — это главные вопросы, на которые следует здесь ответить.

2 главных показателя, определяющих качество перекрытия — это распределенная нагрузка на само перекрытие, а также сосредоточенная нагрузка на ригели, если они используются. Качество ригеля зависит также от способа его закрепления.

Онлайн-калькулятор автоматически показывает, насколько большим будет запас распределенной нагрузки и прогиба у перекрытие. Или же наоборот, укажет на перегрузку.

Пример расчета

Для примера использованы следующие входные параметры: сосновый брус, однопролетный для междуэтажного перекрытия, длина 6 метров, имеет квадратное сечение 120 на 120 миллиметров. Они будут расположены с шагом 40 сантиметров при нагрузке на балку, которая составляет 60 килограмм на квадратный метр.

Момент инерции сечения составит 1728 см⁴, а весят такие балки по 43 килограмма каждая.
В результате, расчетный прогиб такого перекрытия составит 23 миллиметра (или 1/261 относительного прогиба). Оно будет иметь запас по прогибу в 1,04 раза и при нагрузке 845 килограммов разрушиться.

Для соответствующего ригеля при сосредоточенной нагрузке в 90 кг расчетный прогиб составит 23 миллиметра, а запас по прогибу — 1,04 раза. Конструкция не выдержит нагрузки свыше 422 килограмм.
Следственно, эксперты-строители будут рекомендовать не использовать перекрытие между этажами с такими показателями, поскольку запас прогиба слишком мал.

Оптимальным считается показатель прогиба от 1,5 до 3 соответственно. Чем выше этот показатель, тем выше расход древесины, но чем ниже показатель запаса по прогибу, тем менее устойчивой получится постройка в целом и ее элементы в частности.

Польза калькулятора

С помощью калькулятора строитель может самостоятельно подобрать необходимые параметры, подбирая каждый из доступных или желательных вариантов и рассчитывая более выгодные материалы и тип балок.

Конструкторское бюро “Топинженер” — Прогиб предварительно напряженных балок

Прогиб предварительно напряженных балок

Прогибы предварительно напряженных, как и обычных железобетонных элементов при действии нормативных нагрузок, определенные с учетом (в необходимых случаях) длительного действия всей постоянной и части временной нагрузки, не должны превышать величин, указанных в действующих нормах.
Для предварительно напряженных железобетонных элементов и конструкций 3-й категории и для отдельных зон элементов и конструкций 2-й категории трещиностойкости ширина раскрытия нормальных и наклонных к оси элемента трещин должна быть не более:

а) для элементов, находящихся под давлением жидкости и работающих на центральное или внецентренное растяжение, если все сечение элемента растянуто — 0,1 мм;

б) для элементов, находящихся под давлением жидкости и работающих на изгиб и на внецентренное сжатие, а также на внецентренное растяжение, если часть сечения элемента сжата, а также для элементов, находящихся под давлением сыпучих материалов — 0,2 мм;

в) в остальных случаях — 0,3 мм.

Допускаемая ширина раскрытия трещин в железобетонных элементах, находящихся в условиях агрессивной среды, устанавливается по специальным нормативным документам для упругого тела с последующим сравнением полученных напряжений с расчетными сопротивлениями.

Прогиб предварительно напряженных балок

Приведенные результаты испытания подтвердили, что при длительном действии нагрузки прогиб предварительно напряженных балок, имеющих трещины в бетоне растянутой зоны, в зависимости от срока действия нагрузки увеличивается в 2-3 раза и более. Такое же увеличение прогиба наблюдается и в балках с ненапрягаемой арматурой. Однако абсолютная величина прироста прогиба предварительно напряженных балок существенно меньше, чем в балках с ненапрягаемой арматурой.

Таким образом, при длительном действии нагрузки предварительное напряжение оказало положительное влияние на уменьшение прогиба балок.

В рассмотренных исследованиях длительно действующей была внешняя нагрузка, от которой произошло увеличение прогиба балок и кривизны.

В тех случаях, когда основная внешняя нагрузка временная и действует непродолжительно, как, например, на подкрановых балках, пролетных строениях мостов малых пролетов и т. п., а собственный вес конструкции составляет небольшую долю от общей расчетной нагрузки, изменение прогиба и кривизны конструкции предопределяется усилием предварительного обжатия бетона. Для таких конструкций равнодействующая усилий напрягаемой арматуры является постоянно действующим фактором, вызывающим предварительное напряжение бетона. В период действия временно возникающей внешней на-грузки напряжения обжатия бетона снижаются, а после ее удаления бетон оказывается снова обжатым.

Экспериментальные исследования влияния технологических и конструкционных параметров на несущую способность металлических балок с гофрированной стенкой Текст научной статьи по специальности «Строительство и архитектура»

ПРОЕКТИРОВАНИЕ И КОНСТРУИРОВАНИЕ

СТРОИТЕЛЬНЫХ СИСТЕМ. ПРОБЛЕМЫ МЕХАНИКИ В СТРОИТЕЛЬСТВЕ

УДК 624.014

В.А. Зубков, А.О. Лукин

ФГБОУВПО «СГАСУ»

ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ ВЛИЯНИЯ ТЕХНОЛОГИЧЕСКИХ И КОНСТРУКЦИОННЫХ ПАРАМЕТРОВ НА НЕСУЩУЮ СПОСОБНОСТЬ МЕТАЛЛИЧЕСКИХ БАЛОК С ГОФРИРОВАННОЙ СТЕНКОЙ

Описаны методика, измерительная аппаратура, оборудование, а также результаты экспериментальных исследований балок с гофрированной стенкой синусоидального очертания. Исследовалось влияние параметров на несущую способность балок. Получены данные о критических нагрузках и видах предельного состояния при действии сосредоточенных сил с различной шириной участка передачи нагрузки. Произведена оценка несущей способности балок различной длины и высоты сечения при работе по однопролетной шарнирной схеме.

Ключевые слова: балки с гофрированной стенкой, эксперимент, потеря устойчивости, прогиб.

В современном строительстве все чаще в покрытии используются балки с гофрированной стенкой. При проектировании нагрузка на них может передаваться в виде сосредоточенных сил (прогоны) или равномерно распределяться по длине (монолитные железобетонные плиты или профилированный настил). Известно, что при равномерном распределении нагрузки по длине балки условия работы гофрированной стенки будут лучше, чем при наличии сосредоточенных сил. Это связано с возникновением значительных локальных напряжений в стенке под сосредоточенной силой и, как следствие, более ранней потерей местной устойчивости стенки. Изучению стальных балок с гофрированной стенкой посвящены работы Г.А. Ажермачева [1], С.Г. Барановской [2, 3], А.Н. Кретинина [4], М.В. Лазнюка [5], А.Н. Степаненко [6, 7], К.В. Чичулиной [8], H. Pasternak, G. Kubieniec [9], Gao J., Chen B.C. [10], но вопрос о несущей способности при действии сосредоточенных нагрузок остается не до конца изученным.

На кафедре металлических и деревянных конструкций Самарского государственного архитектурно-строительного университета были проведены экспериментальные исследования работы стальных балок с гофрированной стенкой при действии сосредоточенной статической нагрузки.

Целью исследования являлось экспериментальное изучение напряженно-деформированного состояния балок с гофрированной стенкой в зависимости от высоты ее сечения, пролета, а также ширины площадки передачи сосредоточенной нагрузки.

ВЕСТНИК ~

2/2013

Для проведения испытаний было отобрано шесть балок трех наиболее распространенных типов. Балки каждого типа имели двутавровое сварное сечение и отличались друг от друга величиной пролета и высотой стенки. Полки балок имели сечение 200*12 из стали С255 по ГОСТ 27772, а стенки были изготовлены из холоднокатаной листовой стали СтЗсп по ГОСТ 16523 толщиной 2,5 мм. Стенки имели в продольном направлении синусоидальный гофрированный профиль с длиной полуволны а = 77,5 мм и высотой гофра / = 20 мм (рис. 1).

1

х

■I-

I—■-.+.Ш-Н

Г

ь

Рис. 1. Параметры гофрированных балок

Прочностные и деформативные характеристики стали были определены путем испытания на растяжение образцов длиной 400 мм, сечением 30*2,5 мм (металл стенок) и 30*12 мм (металл полок). В ходе испытаний стандартных образцов установлено, что механические характеристики сталей соответствуют требованиям ГОСТ. Результаты испытаний приведены в табл. 1.

Табл. 1. Механические характеристики материалов

№ Наименование Сталь Размеры, мм Напряжение текучести с , МПа пг Предел прочности с, в7 МПа Относительная деформация е10, %

1 Стенка Холоднокатаная 400*30×2,5 235 373 30

2 Полка Горячекатаная 400*30*12 260 431 30

Для испытанных балок была принята следующая структура обозначения (табл. 2): БГС ЬХ,

где БГС — балка с гофрированной стенкой; Ь — пролет балки; X — ширина участка, через который передается сосредоточенная нагрузка, при X = 1 ширина участка принята 100 мм, т.е. равна ширине полки прогона, а при X = 2 ширина составляла 200 мм.

Табл. 2. Характеристики гофрированных балок

№ Шифр Пролет L, м Высота стенки балки h , мм w7 Ширина полок балки b , мм Толщина полок балки t мм Ширина участка на-гружения, мм

1 БГС 6.1 6 500 100

2 БГС 6.2 200

3 БГС 9.1 9 750 200 12 100

4 БГС 9.2 200

5 БГС 12.1 12 1250 100

6 БГС 12.2 200

Все балки испытывались как однопролетные свободно опертые конструкции с одной подвижной и другой неподвижной шарнирной опорой.ss

3000

P

а

3000

P

3000

9000

б

3000

P

3000

P

3000

P

3000

12000

в

Рис. 2. Схемы балок с гофрированной стенкой при испытании: а — БГС 6;

б — БГС 9; в — БГС 12

Сосредоточенную нагрузку создавали гидравлическими домкратами (рис. 3). Количество домкратов и насосных станций соответствовало количеству сил, которыми нагружали балку. Нагружение балок проводилось ступенями, с выдержкой во времени на каждой ступени в течение 10 мин. Величина ступеней для всех балок была принята одинаковой и равной Р = 10 кН.

При проведении испытаний контролировались следующие параметры: величины сосредоточенных сил; деформации краевых волокон металла в полках балки в середине пролета и в непосредственной близости от действия сосредоточенной нагрузки; относительная деформация металла в гофрах стенки под зоной приложения нагрузки; прогибы балки и осадка опор балки.

Величина приложенной нагрузки контролировалась манометрами, которые были градуированы совместно со всей гидравлической системой домкратов.

Деформацию металла в полках и стенках определяли методом электротензометрии. При этом были использованы тензометрические датчики с базой 20 мм, а в качестве вторичного прибора использовался тензометрический комплекс ТК 50, который позволял измерять деформацию металла с точностью до 10-6 единиц относительной деформации. Перед началом испытаний прибор ТК 50 совместно с датчиками был градуирован на тарировочной установке ТА-12.

Смещения сечений балок в пролете измерялись прогибомерами ПАО-6, а осадка опор — индикаторами часового типа ИЧ-10. Точность измерения перемещений составила 0,01 мм. Схема размещения приборов приведена на рис. 4.

Испытания прекращались после того, как приостанавливался прирост деформаций в полках или наблюдалось уменьшение ее величины.

Анализ данных с тензометрических датчиков показал, что наибольшее напряжение во всех балках возникает на участке гофров стенки под сосредоточенной силой на расстоянии 40.. .50 мм от верхней полки. Все участки стенки, в которых наблюдаются наибольшие напряжения, смещены с оси балки. В местах под сосредоточенными силами в стенке раньше всего наступает локальное предельное состояние, которое характеризуется достижением нормальных напряжений предела текучести.

1-1

Р

3

6

верхняя полка

— 13 — 16 —19

— 14 —17 —20

— 15 —18 —21

нижняя полка

22 25 28

— 23 —26 —29

— 24 —27 —30

Рис. 4. Схема датчиков для балок пролетом 9 м

При достижении нормальных локальных напряжений в гофрах стенки под сосредоточенной силой величин, соответствующих значениям расчетного сопротивления Л было установлено, что напряжения в полках балок находились в пределах (0,6…0,7)Лу (табл. 3).

Табл. 3. Сводная ведомость результатов для локального предельного состояния

№ Шифр балки Предельное состояние стенки Р, кН Напряжение в стенке под силой а, = а , loc.y т7 МПа Напряжение в полках а, МПа X7 Прогиб в середине пролета f мм Исчерпание несущей способности полок, %

1 БГС 6.1 90 165 15,4 68,8

2 БГС 6.2 92,3 150 15,05 62,5

3 БГС 9.1 80 235 135 18,2 56,3

4 БГС 9.2 109 229 25 95,4

5 БГС 12.1 84 169 24,5 70,4

6 БГС 12.2 97 164 26,4 68,3

Испытания показали, что при действии сосредоточенных сил исчерпание несущей способности гофрированных балок происходит за счет потери местной устойчивости гофра или достижения напряжений в полках предела текучести металла.

В балке БГС 6.1 напряжения в гофре стенки на участке приложения силы достигли предела текучести при Р = 90 кН (см. табл. 3), а потеря устойчивости гофра произошла при Р = 110 кН (рис. 5). Однако балка продолжала воспринимать нагрузку, максимальная нагрузка, созданная при испытании, равна 130 кН.

ВЕСТНИК

МГСУ.

2/2013

Рис. 5. Потеря устойчивости гофра стенки в балке БГС 6.1

В балке БГС 9.1 напряжения в гофре стенки на участке приложения силы достигли предела текучести при Р = 80 кН (см. табл. 3), а потеря устойчивости гофра произошла при Р = 120 кН. Максимальная нагрузка Р, которая была создана при испытании, равна 140 кН.

В балке БГС 6.2 общее предельное состояние наступило вследствие достижения напряжений в полках балок расчетного сопротивления (табл. 4).

Табл. 4. Сводная ведомость результатов для общего предельного состояния

№

Шифр балки

Предельное состояние стенки Р, кН

Напряжение в полках о, МПа

Прогиб в середине пролета

/, мм

Исчерпание

несущей способности полок, %

Примечание

БГС 6.1

130

239

24,48

99,6

Потеря уст. гофра Р = 110 кН

БГС 6.2

130

240

23,6

100

БГС 9.1

130

235,8

29,9

98,25

Потеря уст. гофра Р = 120 кН

БГС 9.2

120

240

28,5

100

Потеря уст. сжатой полки Р = 130кН

БГС 12.1

100

215,7

30,72

89,9

БГС 12.2

110

208,5

30,42

86,9

В балках БГС 12.1 и БГС 12.2 предельное состояние наступило из-за образования пластических шарниров в стенках балок под силами и возникших значительных остаточных деформаций. Максимальная нагрузка составила 100 и 110 кН соответственно (см. табл. 4). При этом напряжения в полках находились в пределах (0,87.. .0,9)К.

В ходе испытания было выявлено, что наступление предельного состояния всей гофрированной балки может быть связано с нарушением технологии изготовления. В балке БГС 9.2 пролетом 9 м результаты измерения геометри-

4

ческих характеристик показали, что продольная ось верхней полки смещена относительно продольной оси стенки на 8 мм. При нагрузке 75 кН верхний пояс балки начал изгибаться в горизонтальной плоскости на участке между приложениями сил и местами закрепления верхнего пояса в горизонтальной плоскости. Максимальная нагрузка Р, которая была создана при испытании, равна 130 кН. При максимальной нагрузке выгиб верхней полки в горизонтальной плоскости составил 25 мм, прогиб балки — 33,1 мм (рис. 6).

Рис. 6. Потеря общей устойчивости балки БГС 9.2

Смещение оси стенки с оси балки приводит к появлению эксцентриситета приложения силы, вследствие чего в сечениях гофрированной балки появляются напряжения от стесненного кручения, которые значительно влияют на напряженное состояние и могут привести к потере общей устойчивости.

В балках БГС 6.2, 9.2, 12.2 с шириной распределения сосредоточенной силы 200 мм местной потери устойчивости гофрированной стенки не наблюдалось. Очевидно, что при увеличении ширины участка распределения нагрузки локальные нормальные напряжения в гофрах стенки под сосредоточенной силой снижаются, а величина критической нагрузки увеличивается.

Для всех балок наблюдается практически линейная зависимость между величиной прогибов и уровнем нагрузки во всем диапазоне нагрузок. Нелинейная работа металла после наступления локального предельного состояния в стенке под сосредоточенной силой незначительно влияет на общие прогибы балки. Графики прогибов для балок с шириной распределения сосредоточенной нагрузки 100 мм приведены на рис. 7.

ВЕСТНИК

МГСХ-

2/2013

И

и

И

£ &

140 120 100 80 60 40 20 0

—

-Ф- БГС 6.1 БГС 9.1 БГС 12.1

0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34

Прогиб, мм

Рис. 7. График зависимости прогибов от нагрузки в середине пролета балок

Выводы. 1. Локальное предельное состояние в испытанных балках возникает вследствие достижения напряжения в гофрах стенки предела текучести металла. Напряжения в полках балок при локальном предельном состоянии балки не достигают расчетного сопротивления металла и находятся в пределах (0,6…0,7)-Л.

2. Общее предельное состояние в гофрированных балках при действии сосредоточенных сил возникает вследствие потери местной устойчивости гофра или достижения напряжениями в полках величины предела текучести металла.

3. Прогиб балок при достижении расчетного сопротивления металла в стенках находится в пределах 1/375.1/460 их длины, а при исчерпании несущей способности всей балки — 1/272.1/394. На всех ступенях загружения наблюдается практически линейная зависимость прогиб — нагрузка.

4. Отклонение продольной оси полок балок от продольной оси гофрированной стенки более чем на 3 мм ведет к снижению несущей способности балок и способствует потере общей устойчивости балки.

5. На величину локальных напряжений в гофрах стенки и величину критических нагрузок влияет ширина участка передачи сосредоточенной нагрузки на пояс.

Библиографический список

1. Ажермачев Г.А. Об устойчивости волнистой стенки при действии сосредоточенной нагрузки // Строительство и архитектура. 1963. № 3. С. 50—53.

2. Барановская С.Г. Прочность и устойчивость гофрированной стенки стальной двутавровой балки в зоне приложения сосредоточенных сил : автореф. дисс. … канд. техн. наук. Новосибирск, 1990. 18 с.

3. Местное напряженное состояние гофрированной стенки двутавровой балки при локальной нагрузке / В.В. Бирюлев, Г.М. Остриков, Ю.С. Максимов, С.Г. Барановская // Известия вузов. Строительство и архитектура. 1989. № 11. С. 13—15.

4. Крылов И.И., Кретинин А.Н. Эффективные балки из тонкостенных профилей // Известия вузов. Строительство. 2005. № 6. С. 11—14.

5. Лазнюк М.В. Балки з тонкою поперечно гофрованою стшкою при ди статичного навантаження : автореф. дисс. … канд. техн. наук. Киш, 2006. 19 с.

6. Степаненко А.Н. Исследование работы металлических балок с тонкими гофрированными стенками при статическом загружении : автореф. дисс. … канд. техн. наук. Свердловск, 1972. 20 с.

7. Степаненко А.Н. Испытание алюминиевых балок с гофрированной стенкой // Известия вузов. Строительство и архитектура. 1970. № 1. С. 31—35.

8. Шчуггн С.Ф., Чичулта К.В. Експериментальш дослвдження балок з профшьованою стшкою // Вюник ДНАБА. 2009. № 4(78). С. 161—165.

9. Pasternak H., Kubieniec G. Plate Girders with corrugated webs // Journal of Civil Engineering and Management. 2010. №16 (2). pp. 166—171.

10. Gao J., Chen B.C. Experimental research on beams with tubular chords and corrugated webs // Tubular Structures XII. Proceedings of Tubular Structures XII, Shanghai, China, 8—10 October 2008. pp. 563—570.

Поступила в редакцию в октябре 2012 г.

Об авторах: Зубков Владимир Александрович — кандидат технических наук, профессор кафедры металлических и деревянных конструкций, ФГБОУ ВПО «Самарский государственный архитектурно-строительный университет» (ФГБОУ ВПО «СГАСУ»), 443001, г. Самара, ул. Молодогвардейская, д. 194, 8 (846) 242-50-87;

Лукин Алексей Олегович — ассистент кафедры металлических и деревянных конструкций, ФГБОУ ВПО «Самарский государственный архитектурно-строительный университет» (ФГБОУ ВПО «СГАСУ»), 443001, г. Самара, ул. Молодогвардейская, д. 194, [email protected].

Для цитирования: Зубков В.А., Лукин А.О. Экспериментальные исследования влияния технологических и конструкционных параметров на несущую способность металлических балок с гофрированной стенкой // Вестник МГСУ 2013. № 2. С. 37—46.

V.A. Zubkov, A.O. Lukin

EXPERIMENTAL RESEARCH INTO THE INFLUENCE PRODUCED BY PROCESS-RELATED AND STRUCTURAL PARAMETERS ON THE BEARING CAPACITY OF METAL BEAMS WITH CORRUGATED WEBS

The article covers the experimental research into corrugated web beams exposed to the concentrated static load that has varied values of the width of load exposure. The authors describe the methodology of the experiment, instruments and machines involved in it, as well as the findings of the tests.

Six beams with sinusoidal webs were selected for testing purposes. The beams were 6, 9 and 12 m long, and their cross sections were 500, 750 and 1,250 mm long. All beams were tested as single-span simply supported structures with hinged rigidly or loosely fixed supports.

Beam tests have demonstrated that any failure to adhere to the beam manufacturing technology may seriously affect the load-bearing capacity of a beam. Any deviation of longitudinal axis flanges of beams from the longitudinal axis of a corrugated web in excess of 3 mm adversely affects the bearing capacity of beams and contributes to the overall beam stability loss.

The research findings have demonstrated that the limit state of tested beams arises due to the stress in the web corrugation.

Key words: corrugated web beams, experiment, buckling, deflection.

ВЕСТНИК ofon, ~

2/2013

References

1. Azhermachev G.A. Ob ustoychivosti volnistoy stenki pri deystvii sosredotochen-noy nagruzki [On Stability of a Wavy Wall Exposed to the Concentrated Load]. Izvestiya vuzov. Stroitel’stvo i arkhitektura [News of Higher Education Institutions. Construction and Architecture]. Novosibirsk, 1963, no. 3, pp. 50—53.

2. Baranovskaya S.G. Prochnost’ i ustoychivost’ gofrirovannoy stenki stal’noy dvutavro-voy balki v zone prilozheniya sosredotochennykh sil [Strength and Stability of the Corrugated Steel Web I-beam Exposed to Concentrated Forces]. Novosibirsk, 1990, 18 p.

3. Biryulev V.V., Ostrikov G.M., Maksimov Yu.S., Baranovskaya S.G. Mestnoe napry-azhennoe sostoyanie gofrirovannoy stenki dvutavrovoy balki pri lokal’noy nagruzke [Local Stress State of the Corrugated Web of I-beams Exposed to the Local Load]. Izvestiya vuzov. Stroitel’stvo i arkhitektura [News of Higher Education Institutions. Construction and Architecture]. Novosibirsk, 1989, no. 11, pp. 11—13.

4. Krylov I.I., Kretinin A.N. Effektivnye balki iz tonkostennykh profiley [Effective Thin-walled Beams]. Izvestiya vuzov. Stroitel’stvo. [News of Higher Education Institutions. Construction]. Novosibirsk, 2005, no. 6, pp. 11—14.

5. Laznyuk M.V. Balki z tonkoyu poperechno gofrovanoyu stinkoyu pri di’i statichnogo navantazhennya [Beams with a Thin Transversely Corrugated Web Exposed to the Static Load]. Kiev, 2006, 18 p.

6. Stepanenko A.N. Issledovanie raboty metallicheskikh balok s tonkimi gofrirovannymi stenkami pri staticheskom zagruzhenii [Research into Behaviour of Thin-walled Corrugated Web Metal Beams Exposed to Static Loading]. Sverdlovsk, 1972, 20 p.

7. Stepanenko A.N. Ispytanie alyuminievykh balok s gofrirovannoy stenkoy [Testing of Aluminum Beams with a Corrugated Web]. Izvestiya vuzov. Stroitel’stvo i arkhitektura [News of Higher Education Institutions. Construction and Architecture]. Novosibirsk, 1970, no. 1, pp. 31—35.

8. Pichugin S.F., Chichulina K.V. Eksperimental’ni doslidzhennya balok z profil’ovanoyu stinkoyu [Experimental Researches into Beams with Profiled Surfaces]. Visnik DNABA [Proceedings of Donbas National Academy of Civil Engineering and Architecture]. 2009, no. 4 (78), pp. 161—165.

9. Pasternak H., Kubieniec G. Plate Girders with Corrugated Webs. Journal of Civil Engineering and Management. 2010, no. 16 (2), pp. 166—171.

10. Gao J., Chen B.C. Experimental Research on Beams with Tubular Chords and Corrugated Webs. Tubular Structures XII. Proceedings of Tubular Structures XII. Shanghai, China, 8—10 October 2008, pp. 563—570.

About the authors: Zubkov Vladimir Aleksandrovich — Candidate of Technical Sciences, Professor, Department of Steel and Timber Structures, Samara State University of Architecture and Civil Engineering (SSUACE), 194 Molodogvardeyskaya st., Samara, 443001, Russian Federation;

Lukin Aleksey Olegovich — assistant lecturer, Department of Metal and Timber Structures, Samara State University of Architecture and Civil Engineering (SSUACE), 194 Molodogvardeyskaya st., Samara, 443001, Russian Federation; [email protected]; +7 (846) 332-14-65.

For citation: Zubkov V.A., Lukin A.O. Eksperimental’nye issledovaniya vliyaniya tekhno-logicheskikh i konstruktsionnykh parametrov na nesushchuyu sposobnost’ metallicheskikh balok s gofrirovannoy stenkoy [Experimental Research into the Influence Produced by Process-related and Structural Parameters on the Bearing Capacity of Metal Beams with Corrugated Webs]. Vestnik MGSU [Proceedings of Moscow State University of Civil Engineering]. 2013, no. 2, pp. 37—46.

Сверхнормативный прогиб деревянной подстропильной балки

Весьма часто к нам обращаются с подобной проблемой – возведена конструкция и после ее загружения образовался видимый, сверхнормативный прогиб. Допустимо ли это? Конечно же нет.

Сверхнормативный прогиб деревянной подстропильной балки

В действующих нормах указано, что к несущим конструкциям предъявляются два основных требования: конструкция должна быть прочной, то есть должна нести действующие на нее нагрузки и, она должна обладать необходимой жесткостью. Если, например, конструкция не обладает достаточной жесткостью, то она будет избыточно, сверхнормативно деформироваться. Жесткость конструкции зависит от многих факторов: сечения элементов конструкции, пролета конструкции (или ее расчетной длины) и значения действующих нагрузок. Определить соответствует ли конструкция требованиям жесткости возможно при помощи специального инженерного расчета, который называется проверка на обеспечение жесткости.

В этом фотоотчете рассмотрен случай сверхнормативного прогиба деревянной подстропильной балки, который был выявлен на стадии строительства двухэтажного жилого дома.

Общий вид навеса. Сверхнормативный прогиб главной балки навеса

Стропильные конструкции навеса

Стропильные ноги имеют чрезмерную подрезку в месте опирания на балку

Узел опирания деревянных балок на металлическую стойку

Опирание стропильных балок на пристенную балку

Непосредственно вблизи строящегося дома архитектором проекта была предусмотрена открытая летняя терраса под навесом. Стропильные конструкции навеса запроектированы деревянными.

С учетом постоянных и временных нагрузок (от веса снегового мешка вблизи стен дома) общая нагрузка на покрытие навеса составила 560 кгс/м². При обследовании поврежденной  конструкции и выполнения соответствующего расчета выявлено, что поперечное сечение балки недостаточно и жесткость подстропильной балки не обеспечена.

Решение задачи

После осмотра было принято решение выполнить усиление деформированной балки без демонтажа существующего кровельного покрытия навеса террасы. Перед усилением, для уменьшения деформации кровельного покрытия навеса, деревянная балка была выровнена посредством поддомкрачивания. Усиление было успешно реализовано путем подведения под деформированную балку  металлической дубль балки.

Общий расход стали на усиление деревянной подстропильной балки покрытия навеса составил 0,32 т.

Возникли вопросы? Есть похожие проблемы? Пишите в комментариях, постараюсь вам помочь.

В дальнейшем, также, вам могут пригодиться мои услуги по экспертизе и не только. Подробнее смотрите здесь.

ЭФФЕКТИВНОСТЬ УСИЛЕНИЯ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ СТАЛЬНЫМИ БАЛКАМИ

  Подведение стальных балок под железобетонные балки или плиты – довольно распространенный прием усиления. Основан он на принципе частичного разгружения – стальная балка является дополнительной (упругой) опорой и берет на себя часть полезной нагрузки. Однако эффективность такого усиления, как правило, невелика. Сечения стальных балок проектировщики зачастую подбирают простым суммированием несущих способностей усиливаемой и усиливающей балок: если существующая балка (плита) в состоянии воспринимать только часть расчетного изгибающего момента М, то сечение стальной балки подбирают из условия восприятия недостающей части.
Такой подход ошибочен по двум причинам. Во-первых, стальная балка включается в работу не с самого начала, а со времени приложения дополнительной нагрузки. Чем меньше разгружена железобетонная балка (плита), тем менее эффективно работает стальная балка. Во-вторых, доли совместно воспринимаемой нагрузки определяются не несущими способностями сечений, а совместными деформациями (прогибом f). Поэтому дополнительная нагрузка распределяется пропорционально жесткостям существующей и усиливающей конструкций.

Рис.1. Усиление подведением стальной балки: 1 — железобетонная балка, 2 — стальная балка.

  Поясним на примере (рис. 1). Железобетонная балка пролётом 6 метров имеет жесткость 81000 кНхм2 (при отсутствии трещин) и в состоянии воспринимать 80% расчетного изгибающего момента М = 290 кНхм. До начала усиления нагрузка на балку снижена наполовину, т.е. изгибающий момент в ней составляет 145 кНхм. Следовательно, из оставшейся половины изгибающего момента 30%М (ΔМb = 87 кНхм) должна воспринять железобетонная балка, а 20%M (Ms = 58 кНхм) — стальная. Поскольку прогибы балок одинаковы (fb = fs), пропорционально этим моментам должны быть и жесткости балок: ΔMb/Bb = Мs/Вs’ откуда Bs/Bb = 2/3, т. е. жесткость стальной балки Bs = 54000 кН хм2. Этой жесткости соответствует прокатный двутавр № 45, напряжения в котором при действии воспринимаемого им момента 58 кНхм составят 47 МПа, т. е. всего 1/5 расчетного сопротивления стали марки С235. Чем большая часть нагрузки снята с железобетонной балки до начала усиления, тем меньшее сечение потребуется для усиливающей балки и тем эффективнее она будет работать. Но даже при полном снятии нагрузки напряжения в последней (двутавр № 33а) составят всего 110 МПа.
Из приведенного примера видно, насколько неэффективно используется несущая способность усиливающей балки даже при самом раннем включении ее в работу. Правда, стальная балка будет нагружаться более интенсивно после образования трещин в железобетонной балке, когда жесткость последней заметно снижается. Однако строгий расчет их совместной работы затруднителен, а его результаты могут оказаться далекими от фактической работы.
  Чтобы повысить эффективность работы стальных усиливающих балок, нужно создать предварительное напряжение: усиливающую (стальную) балку частично нагрузить, а усиливаемую (железобетонную) частично разгрузить – еще до того, как будет приложена дополнительная внешняя нагрузка.
Выполнить предварительное напряжение можно разными способами. Один из них – оттянуть стальную балку книзу (прогнуть) с помощью подвешенных грузов, а в образовавшиеся между ней и железобетонной балкой зазоры вставить металлические распорки (пластины или пакеты из листов). После снятия грузов стальная балка стремится вернуться в исходное состояние (выпрямиться), но железобетонная этому препятствует. В результате, усиливающая балка нагружена силами, направленными сверху вниз, в усиливаемая – теми же силами, направленными снизу вверх (рис.2). Правда, при этом часть преднапряжения стальной балки теряется.

Рис.2. Предварительное напряжение усиливающей балки: 1 — железобетонная балка, 2 — стальная балка.

  Потери напряжений можно исключить, если подобную операцию осуществлять с помощью гидродомкратов, устанавливаемых на усиливающую балку, с контролем усилий в них по манометру. При таком способе происходит одновременный выгиб железобетонной балки и прогиб стальной. Более простой способ – использование вместо домкратов натяжных или упорных болтов, усилия в которых контролируются по величине взаимного смещения f (суммы выгиба и прогиба) железобетонной и стальной балок (рис. 3).

Рис.3. Усиление подведением домкратов: 1 — железобетонная балка, 2 — стальная балка, 3 — натяжные болты.

  Здесь не были упомянуты потери от обмятия контактных поверхностей, неизбежные при любом преднапряжении. При проектировании усиления их принимают обычно равными 20% начальной величины преднапряжения.  

Приведенный пример показывает, что усиление можно выполнять и без разгружения железобетонной конструкции, если создать в ней усилия обратного знака за счет предварительного напряжения усиливающей конструкции.
  После снятия подвешенного груза F стальная балка жесткостью Bs, получившая прогиб f (рис. 2, а), стремится выпрямиться, т.е. полностью утратить начальные напряжения, но железобетонная жесткостью Bb этому препятствует – она выгибается на величину fb в то время как прогиб стальной балки уменьшается до величины fs (рис. 2, б). Поскольку fs < f/ происходит частичная потеря напряжений, в результате чего железобетонная балка разгружается не всей силой F, а только ее частью ΔF. Эта же часть нагружает и усиливающую балку. Величина Доопределяется следующим образом. Если пренебречь потерями напряжений от обмятия контактных по-верхностей, то f = fb + fs. Тогда f = F(k/Bs), fb = ΔF(k/Bb), fs = ΔF(k/Bs), где k – условный коэффициент пропорциональности, зависящий от схемы приложения нагрузки (подвески грузов). Отсюда ΔF=FBb/(Bb+Bs). Следовательно, чем выше жесткость стальной балки по сравнению с железобетонной, тем меньше величина ΔF, тем больше потери напряжений.

Навигация по записям

(PDF) УЛУЧШЕННЫЙ МЕТОД ОЦЕНКИ ПРОГНОЗА В ПЕЧАТНЫХ СТАЛЬНЫХ двутавровых балках

УЛУЧШЕННЫЙ МЕТОД ОЦЕНКИ ПРОГНОСА В ПРЕДВАРИТЕЛЬНОМ

767

точно. Поскольку арматура не связана с элементом (или связана только в определенных точках

), максимальная прочность достигается в окончательной конструкции, что приводит к более высокому расходу стали для предварительного напряжения

. Обычно поперечное сечение не может быть использовано полностью. Поэтому требуется

большей глубины или дополнительного предварительного напряжения.

1.5 Применение техники предварительного напряжения стали

В зависимости от типа конструкции и ее будущих рабочих условий предварительное напряжение может составлять

, применяемое во время монтажа или на заводе-изготовителе. Предварительное напряжение может применяться в одно- или многоступенчатом режиме

. При использовании материала больший эффект можно получить при многоступенчатом предварительном напряжении

. Это предварительное напряжение возможно только при постоянной нагрузке. Последовательность шагов

, используемая для создания предварительного напряжения, зависит от типа конструкции или нагрузки, а

зависит от ее влияния на экономию, требуемую от предварительного напряжения.Предварительное напряжение

используется как при проектировании новых, так и существующих конструкций. Усиление существующей конструкции

предварительным напряжением приводит к увеличению ее несущей способности и жесткости с минимальным расходом дополнительного материала

. Учитывая его конструктивное использование, предварительное напряжение

было успешно применено при проектировании новых конструкций, таких как фермы, рамы, арки,

ферм, зданий, башен, мачт и мостов, а также для усиления старых мостов.

Ниже приведены некоторые из типичных применений технологии предварительно напряженной стали, в которой внешние арматуры

возможны, практичны и экономичны.

1. Фермы: Предварительно напряженные фермы используются в промышленных зданиях и на крышах котлов

.

2. Мосты: в последнее время было построено много больших металлических мостов с применением предварительного напряжения

(балки моста, предварительно напряженные арматурой)

3. Листовые конструкции и стеновые конструкции: они предварительно напряжены, так что они могут выдерживать сжатие

. эффективно загружать.

4. Мачты и башни: Предварительно напряженная сталь используется в мачтах и ​​башнях для увеличения жесткости конструкции

.

2. ОБЗОР ЛИТЕРАТУРЫ

Компания Coff [2] в США предложила мост с предварительно напряженной стальной пластинчатой ​​балкой пролетом 250 футов.

Финн и Нидхэм [4] выполнили обширную программу испытаний для предварительно напряженной стальной фермы

пролетом 90 футов. Петров [9, 10] исследовал параметры предварительно напряженных стальных балок для проектирования

с тросами по всей длине балки.Ferjencik [3], Tochacek и Amrhein

[14] описали прогресс в проектировании предварительно напряженной стали в Чехословакии. Исследования начались в

1960, и в результате этого исследования были приняты фактические проектные спецификации. Ferjencik

разработал каталог применений предварительного напряжения, включая его применение к фермам и фермам

. Точачек и Мехта [15] указали, что коэффициент запаса прочности для частей

предварительно напряженных стальных конструкций, подвергающихся как растяжению, так и сжатию, может быть уменьшен на

на 20% при расчетном рабочем напряжении.Беленя [1] провела испытания предварительно напряженной однородной балки

. Kalburgi [6] разработал уравнения для нахождения оптимального двутаврового сечения из предварительно напряженной стали

с безразмерными параметрами. Троицкий и др. [8] провели исследование предварительно напряженных стальных непрерывнопролетных балок

. Рассел и Сайдер [12] провели исследование предварительно напряженных стальных балок

для однопролетных мостов. Раман Сингх и др. [11] провели тематическое исследование

Упрощенная процедура определения максимального прогиба балки

• Член

  БЕСПЛАТНО

• Не член

  10 долларов.00

Ку, Бенджамин (1967). «Упрощенная процедура определения максимального прогиба балки», Engineering Journal , Американский институт стальных конструкций, Vol. 4. С. 123-125.

Максимальное отклонение балки играет важную роль в дискуссиях, касающихся проектирования конструкций.Строительные нормы и правила, такие как ACI-63 и Спецификация AISC, ограничивают прогиб, вызванный временной нагрузкой, до 1/360 пролета балки. Расчет конструкции балки для соответствия спецификациям обычно требует утомительных и длительных вычислений. В этой статье предлагается следующая упрощенная процедура: для любой балки с переменным моментом инерции, подверженной концевым моментам и боковым нагрузкам, сначала используйте матричное умножение, чтобы определить сегмент, на котором произойдет максимальное отклонение. Затем, используя граничные условия сегмента, повторите матричное умножение, чтобы получить максимальный прогиб.

• Опубликовано: 1967, 3 квартал

Калькулятор прогиба балки и напряжения

На этой странице можно найти прогиб, а также максимальное напряжение. свободно опертой балки, калькулятор всегда учитывает собственный вес балки. и добавляет его к указанным вами нагрузкам.Выбирайте из австралийских стальных профилей, УНИВЕРСАЛЬНЫХ БАЛКОВ, ПАРАЛЛЕЛЬНЫХ ФЛАНЦЕВЫХ КАНАЛОВ, УНИВЕРСАЛЬНЫХ СТОЛБОВ и Z / C PURLINS. Также можно обнаружить отклонение луча правой стороны. Тип материала ограничивается сталью (модуль упругости 210 000 МПа), деревом и алюминием. Все входные значения должны быть метрическими.

Прогиб балки и максимальное напряжение балки.

Прогиб от собственного веса:
Прогиб от нагрузки:
Прогиб от продолжительной нагрузки:

Полный прогиб:

Максимальное напряжение:

3.91 мм
32,01 мм
7,14 мм

43.06 мм

156,48 МПа

Для выбора нестандартных размеров ИСПОЛЬЗУЙТЕ ЗНАЧЕНИЯ НИЖЕ из раскрывающегося списка.
Оставьте значение толщины фланца (толщина стенки) пустым, чтобы указать твердое тело.
Единицы должны быть в мм.

Схема прогиба балки.

Ниже приведены неокругленные данные

Модуль упругости: 210000 (Н / мм ² )
Момент инерции: 271188 (мм ⁴ )
Расстояние по перпендикуляру от нейтральной оси: 38 (мм)
Вес материала.Усилие на мм: 0,0273436 (Н / мм)
Материал: сталь
Сечение: 76X38X1,6 RHS
Сила нагрузки: 700 Н
Непрерывная нагрузка Сила на мм: 0,05 Н / мм
Отклонение балки от собственного веса балки: 3,

16995894 мм
Отклонение балки от силы в центре балки: 32,009364557265 мм
Прогиб от постоянной нагрузки, поддерживаемой балкой: 7,1449474458181 мм
Полное отклонение этой балки с простой опорой : 43.061683702672 мм
Максимальное напряжение от центральной силы: 122.60867000015 МПа
Напряжение от собственного веса балки: 11,973437246486 МПа
Напряжение от продолжительной нагрузки: 21,894405357169 МПа
Максимальное напряжение в балке.

Лучшее руководство по минимизации отклонения луча — опытный инженер

Как инженер, во многих случаях проектирование балки только на основе напряжений недостаточно.Дорожки и настилы предназначены для отклонения, потому что человеческий разум ощущает движение, и если оно чрезмерное, и если движение слишком сильное, он приходит к выводу, что конструкция небезопасна.

Другой пример конструкции на отклонение — крыло самолета. У коммерческих самолетов крылья очень жесткие по сравнению с крыльями грузовых военных самолетов. Никто не хочет смотреть в окно и видеть, как крыло подпрыгивает от 10 до 15 футов вверх и вниз во время грозы. Можно сделать вывод, что в любой момент крылья могут сразу сломаться.

Чтобы уменьшить прогиб балки, рассмотрите следующие возможности:

• Уменьшить нагрузку / момент
• Уменьшить длину балки
• Изменить концевые опоры
• Добавить консольную секцию на конце (концах)
• Увеличить момент инерции площади
• Увеличьте модуль упругости
• Добавьте другие балки, чтобы разделить нагрузку

Расчет на прогиб, а не на то напряжение, которое иногда бывает необходимо.Эмпирические правила при проектировании отклоняющей балки:

• Прогиб при действующей и статической нагрузке не может превышать L / 240 и
• Прогиб при действующей нагрузке не может превышать L / 360

В этом вам поможет мой калькулятор балки Ultimate. Давайте посмотрим, как каждый из них изменит отклонение луча.

Уменьшите нагрузку / момент

Очевидно, что это самый простой способ уменьшить прогиб, но, скорее всего, маловероятный. Если я проектирую дорожку для одного человека, мне нелегко снизить свой вес (хотя мне действительно нужно сбросить несколько фунтов).Кроме того, существует множество стандартов, определяющих требуемые постоянные и статические нагрузки. Скорее всего, это не стартер.

Уменьшить длину балки

Этот вариант тоже довольно очевиден, но зачастую невозможен. Вероятно, вы уже оптимизировали это в своем дизайне. Если вы строите мост, вы хотите, чтобы сваи были на твердом основании, но если это невозможно, вы хотите, чтобы они были на мелководье.

Если вы можете перемещать опоры балки, подумайте о том, чтобы один или оба конца были консольными.Подробнее об этом чуть позже.

Возможно, переместите опоры ближе

Замените концевые опоры

Замена концевых опор позволит вам увеличить жесткость балки без изменения сечения балки. Вот иерархия опор с их относительной жесткостью к консольной балке.

1. Фиксируется на каждом конце (48x)
2. Фиксируется на одном конце, поддерживается на другом (23x)
3. Поддерживается на обоих концах (9,6x)
4. Фиксируется на одном конце, направляется на другом (3x)
5. Консольный на одном конце (1x)

В каждом случае вы можете видеть, что преимущество перехода на одну ступень вверх по иерархии опор делает ту же балку почти в три раза более жесткой.Если у вас консольная балка, добавление опоры под свободный конец изменит жесткость на неподвижную и поддерживаемую балку, увеличив жесткость в 23 раза!

Самая распространенная опора балки поддерживается с обеих сторон, также известная как простая опора. Эта балка уже достаточно жесткая и ее легко построить. Однако, если мы сделаем один пролет балки тремя опорами, мы фактически изменим центральную часть на почти неподвижную опору. Я говорю «почти зафиксировано», потому что опора все еще может вращаться в среднем положении.Однако эта опора все еще прикреплена к другим концам, поэтому она должна занять некоторое время у центральной опоры. Если эта максимальная нагрузка на балку симметрична относительно центральной опоры, мы можем предположить, что соединение зафиксировано в центре. Это сделает нашу балку в 2,4 раза жестче, чем была раньше. Это небольшое изменение, которое может похвастаться отличными результатами.

Балка с тремя опорами

Добавить консольную секцию на конце (-ях)

Это способ сохранить ту же общую длину балки при уменьшении расстояния между опорами.Из иерархии, перечисленной выше, балка с простой опорой в 9,6 раз жестче консольной балки, это означает, что я могу фактически консольно отвести балку с одного конца на 10,4% (1 / 9,6)

Добавление консоли к одному концу балки

Например, если бы у меня была 100-дюймовая балка с простой опорой, я мог бы переместить опору на одном конце примерно на 10% от общей длины. Это не только снижает прогиб на 31% (результаты зависят от используемых материалов и поперечного сечения), но также при использовании в настиле дает ощущение, будто настил выходит за пределы того места, где должен.Прекрасное чувство для владельца колоды.

При необходимости вы можете сделать это на обоих концах балки.

Увеличение момента инерции площади

Глядя на приведенную ниже формулу общей балки, мы видим, что если момент остается неизменным, то только момент инерции площади. I и модуль упругости E могут быть изменены для уменьшения прогиба v. В этом разделе мы обсудим момент инерции области.

Общий вид уравнения пучка.

Момент инерции площади полностью зависит от формы поперечного сечения.По мере увеличения поперечного сечения увеличивается момент инерции. Фактически, для прямоугольника, если вы удвоите высоту, вы в четыре раза увеличите момент инерции. Однако, если вы увеличите ширину вдвое, вы только удвоите момент инерции.

Что делать со следующими структурными формами

Круглые трубки или труба

При использовании круглой трубы или трубы самое простое решение — утолщить стену. Например, труба толщиной 1/4 дюйма становится толщиной 3/8 дюйма или труба сортамента 40 меняется на трубу сортамента 80.По мере утолщения стены вы увидите лишь умеренное увеличение жесткости. Этого может быть достаточно, но ваша секция становится тяжелее. В какой-то момент дополнительный вес может фактически увеличить прогиб.

Лучшее решение — увеличить внешний диаметр трубы или трубы и сохранить исходную толщину стенки. Если это невозможно, подумайте о переходе на квадратную трубку.

Квадратная трубка

Квадратная труба очень похожа на круглую трубу, но у нее есть то преимущество, что весь материал находится на внешнем крае, и она отлично подходит для изгиба как в горизонтальном, так и в вертикальном направлениях (при условии наличия горизонтальной балки).Имея это в виду, убедитесь, что плоская поверхность на трубке ориентирована с наибольшим моментом на трубке . В нагруженном состоянии трубка не такая прочная, как алмазная.

Неповоротная и повернутая квадратная труба

Уголки

Углы — плохие лучи. Если у вас возникли проблемы со слишком большим отклонением угла, подумайте о том, чтобы изменить его форму. Любая форма лучше. Просто сделай это. Вы меня поблагодарите.

Балки с широким фланцем

Широкополочные балки предлагают широкий выбор решений для вашего дизайна.4) Увеличение Вес по сравнению с
по сравнению с W16 x 31 W16 x 31 301 — — W16 x 45 586 1.46 W16 x 67 954 3,16 2,16

Из приведенной выше таблицы вы можете видеть, что переход от W16 x 31 к W16 x 45 удваивает жесткость, увеличивая вес только на 45%.Переход на W16 x 67 удваивает вес и втрое увеличивает жесткость.

Если ваша широкополочная балка воспринимает нагрузки на слабую ось, подумайте о том, чтобы загнать боковые стороны внутрь. Вообще говоря, пластины не нужно тщательно продумывать, чтобы оказывать большое влияние.

Увеличить модуль упругости

Увеличить модуль упругости в большинстве случаев сложно. Практически единственный способ увеличить это — сменить материал. Если вы уже используете сталь, вы находитесь на вершине пищевой цепочки; больше нет места для улучшения.

В области пластмасс и других металлов гораздо больше возможностей. Часто переход со стандартного пластика на армированный волокном пластик, стекловолокно или углеродное волокно является хорошим шагом.

Ниже приведен список обычных предметов и их модулей упругости, отсортированных от наивысшего к наименьшему. Если вам нужно минимизировать прогиб, выберите материал выше в этом списке.

4

Материал	Модуль упругости (тыс. Фунтов на кв. Дюйм)	Материал	Модуль упругости (тыс. Фунтов / кв. Монель	48000	Золото	10733
Инконель	31000	Алюминий	10008
Сталь	29000	Сталь				Сталь		Олово	6817
Никель	25000	Хром	5221
Армированный углеродным волокном Пластик	21756	Бериллий Медь	2611
Серый чугун	18855	Дерево (пихта Дугласа)	1885
Силикон
Серебристый никель	18500	Древесноволокнистая плита средней плотности — МДФ	580
Алюминиевая бронза	17405	Ацеталь	406			Медь
Фосфорная бронза	16824	ПВХ	348-595
Титановый сплав	16000	Нейлон 6-6	290-580
	116
Бронза	14504	LDPE	16 — 65

Добавить другие балки для распределения нагрузки

Добавление дополнительных балок для несения нагрузки может быть эффективным способом минимизировать прогиб. 2 или psf), W — ширина конструкции, а n — количество балок.

Центральная балка отвечает за 18 ″ ширины груза, а концы принимают только 9 ″ нагрузки. Вот почему добавление еще одного луча таким образом контрпродуктивно.

Теперь, чтобы каждая балка несла равную часть нагрузки, нам нужно переместить внешние балки так, чтобы расстояние от центра внешних балок до конца было половиной расстояния между балками. На рисунке ниже показано правильное соотношение.

Равно нагруженные балки

Это работает, потому что каждая секция балки отвечает за 6 дюймов нагрузки с каждой стороны.

В следующий раз, когда вы будете проезжать под бетонным мостом, посмотрите, как расположены балки.

Резюме

Есть много способов минимизировать прогиб балки. Рассмотрение нагрузок, опор, свойств сечения и материала позволит вам увидеть, какие варианты доступны для повышения жесткости вашей балки.

Связанные

% PDF-1.4 % 2195 0 объект > эндобдж xref 2195 505 0000000016 00000 н. 0000010456 00000 п. 0000037334 00000 п. 0000037567 00000 п. 0000043607 00000 п. 0000043661 00000 п. 0000043715 00000 п. 0000043769 00000 п. 0000043823 00000 п. 0000043877 00000 п. 0000043931 00000 п. 0000043985 00000 п. 0000044039 00000 п. 0000044093 00000 п. 0000044147 00000 п. 0000044201 00000 п. 0000044255 00000 п. 0000044309 00000 п. 0000044363 00000 п. 0000044417 00000 п. 0000044471 00000 п. 0000044525 00000 п. 0000044579 00000 п. 0000044633 00000 п. 0000044687 00000 п. 0000044741 00000 п. 0000044795 00000 п. 0000044849 00000 п. 0000044903 00000 п. 0000044957 00000 п. 0000045011 00000 п. 0000045065 00000 п. 0000045119 00000 п. 0000045173 00000 п. 0000045227 00000 п. 0000045281 00000 п. 0000045335 00000 п. 0000045389 00000 п. 0000045443 00000 п. 0000045497 00000 п. 0000045551 00000 п. 0000045605 00000 п. 0000045659 00000 п. 0000045713 00000 п. 0000045767 00000 п. 0000045821 00000 п. 0000045875 00000 п. 0000045929 00000 п. 0000045983 00000 п. 0000046037 00000 п. 0000046091 00000 п. 0000046145 00000 п. 0000046199 00000 п. 0000046253 00000 п. 0000046307 00000 п. 0000046361 00000 п. 0000046415 00000 н. 0000046469 00000 п. 0000046523 00000 п. 0000046577 00000 п. 0000046631 00000 н. 0000046685 00000 п. 0000046739 00000 п. 0000046793 00000 п. 0000046847 00000 п. 0000046901 00000 п. 0000046955 00000 п. 0000047009 00000 п. 0000047063 00000 п. 0000047117 00000 п. 0000047171 00000 п. 0000047225 00000 п. 0000047279 00000 н. 0000047333 00000 п. 0000047559 00000 п. 0000048133 00000 п. 0000048176 00000 п. 0000048230 00000 н. 0000048284 00000 п. 0000048338 00000 н. 0000048392 00000 н. 0000048446 00000 п. 0000048500 00000 н. 0000048554 00000 п. 0000048608 00000 п. 0000048662 00000 н. 0000048716 00000 п. 0000048770 00000 п. 0000048824 00000 н. 0000048878 00000 н. 0000048932 00000 н. 0000048986 00000 п. 0000049040 00000 н. 0000049094 00000 н. 0000049148 00000 п. 0000049202 00000 п. 0000049256 00000 п. 0000049310 00000 п. 0000049364 00000 п. 0000049418 00000 п. 0000049472 00000 п. 0000049526 00000 п. 0000049580 00000 п. 0000049634 00000 п. 0000049688 00000 п. 0000049742 00000 п. 0000049796 00000 п. 0000049850 00000 п. 0000049904 00000 н. 0000049958 00000 н. 0000050012 00000 п. 0000050035 00000 п. 0000050696 00000 п. 0000050719 00000 п. 0000051229 00000 п. 0000051252 00000 п. 0000051771 00000 п. 0000051794 00000 п. 0000052237 00000 п. 0000052260 00000 п. 0000052701 00000 п. 0000052724 00000 п. 0000053211 00000 п. 0000053234 00000 п. 0000053721 00000 п. 0000053935 00000 п. 0000054150 00000 п. 0000054416 00000 п. 0000054636 00000 п. 0000054855 00000 п. 0000055085 00000 п. 0000055302 00000 п. 0000055520 00000 п. 0000055712 00000 п. 0000055928 00000 п. 0000056185 00000 п. 0000056396 00000 п. 0000056592 00000 п. 0000056854 00000 п. 0000057107 00000 п. 0000057366 00000 п. 0000057598 00000 п. 0000057829 00000 п. 0000058072 00000 п. 0000058304 00000 п. 0000058538 00000 п. 0000058771 00000 п. 0000058993 00000 п. 0000059223 00000 п. 0000059448 00000 н. 0000059672 00000 п. 0000059894 00000 п. 0000060132 00000 п. 0000060361 00000 п. 0000060589 00000 п. 0000060816 00000 п. 0000061001 00000 п. 0000061250 00000 п. 0000061435 00000 п. 0000061616 00000 п. 0000061801 00000 п. 0000061992 00000 п. 0000062173 00000 п. 0000062366 00000 п. 0000062557 00000 п. 0000062748 00000 н. 0000137253 00000 н. 0000137434 00000 н. 0000137615 00000 н. 0000137796 00000 н. 0000137989 00000 н. 0000138173 00000 н. 0000138364 00000 н. 0000138555 00000 н. 0000138745 00000 н. 0000138940 00000 н. 0000139130 00000 н. 0000139323 00000 н. 0000139514 00000 н. 0000139699 00000 н. 0000139890 00000 н. 0000140075 00000 н. 0000140260 00000 н. 0000140445 00000 н. 0000140630 00000 н. 0000140815 00000 н. 0000140996 00000 н. 0000141222 00000 н. 0000141458 00000 н. 0000141696 00000 н. 0000141941 00000 н. 0000142168 00000 п. 0000142399 00000 н. 0000142631 00000 н. 0000142874 00000 н. 0000143102 00000 п. 0000143331 00000 н. 0000143577 00000 н. 0000143810 00000 н. 0000144059 00000 н. 0000144293 00000 н. 0000144532 00000 н. 0000144772 00000 н. 0000145018 00000 н. 0000145260 00000 н. 0000145497 00000 н. 0000145734 00000 н. 0000145973 00000 н. 0000146205 00000 н. 0000146442 00000 н. 0000146679 00000 п. 0000146929 00000 н. 0000147167 00000 н. 0000147406 00000 н. 0000147647 00000 н. 0000147889 00000 н. 0000148128 00000 н. 0000148367 00000 н. 0000148623 00000 н. 0000148859 00000 н. 0000149094 00000 н. 0000149330 00000 н. 0000149564 00000 н. 0000149823 00000 п. 0000150070 00000 н. 0000150306 00000 н. 0000150542 00000 н. 0000150779 00000 н. 0000151017 00000 н. 0000151253 00000 н. 0000151503 00000 н. 0000151737 00000 н. 0000151919 00000 н. 0000152103 00000 н. 0000152287 00000 н. 0000152469 00000 н. 0000152653 00000 н. 0000152835 00000 н. 0000153020 00000 н. 0000153202 00000 н. 0000153384 00000 н. 0000153568 00000 н. 0000153750 00000 н. 0000153942 00000 н. 0000154133 00000 н. 0000154324 00000 н. 0000154516 00000 н. 0000154707 00000 н. 0000154892 00000 н. 0000155073 00000 н. 0000155255 00000 н. 0000155446 00000 н. 0000155637 00000 н. 0000155822 00000 н. 0000156054 00000 н. 0000156285 00000 н. 0000156509 00000 н. 0000156731 00000 н. 0000156961 00000 н. 0000157188 ​​00000 н. 0000157423 00000 н. 0000157654 00000 н. 0000157882 00000 н. 0000158110 00000 н. 0000158329 00000 н. 0000158532 00000 н. 0000158746 00000 н. 0000158940 00000 н. 0000159125 00000 н. 0000159314 00000 н. 0000159530 00000 н. 0000159749 00000 н. 0000159964 00000 н. 0000160182 00000 п. 0000160400 00000 н. 0000160612 00000 н. 0000160845 00000 н. 0000161027 00000 н. 0000161269 00000 н. 0000161453 00000 н. 0000161637 00000 н. 0000161878 00000 н. 0000162120 00000 н. 0000162363 00000 н. 0000162620 00000 н. 0000162802 00000 н. 0000162986 00000 н. 0000163230 00000 н. 0000163489 00000 н. 0000163732 00000 н. 0000163990 00000 н. 0000164233 00000 н. 0000164426 00000 н. 0000164668 00000 н. 0000164910 00000 н. 0000165094 00000 н. 0000165336 00000 н. 0000165521 00000 н. 0000165703 00000 н. 0000165946 00000 н. 0000166128 00000 н. 0000166319 00000 н. 0000166512 00000 н. 0000166694 00000 н. 0000166886 00000 н. 0000167129 00000 н. 0000167373 00000 н. 0000167566 00000 н. 0000167809 00000 н. 0000168001 00000 н. 0000168183 00000 п. 0000168365 00000 н. 0000168550 00000 н. 0000168741 00000 н. 0000168985 00000 н. 0000169177 00000 н. 0000169421 00000 н. 0000169614 00000 н. 0000169870 00000 н. 0000170132 00000 н. 0000170324 00000 н. 0000170516 00000 н. 0000170712 00000 н. 0000170905 00000 н. 0000171087 00000 н. 0000171331 00000 н. 0000171569 00000 н. 0000171807 00000 н. 0000172065 00000 н. 0000172308 00000 н. 0000172545 00000 н. 0000172785 00000 н. 0000173039 00000 н. 0000173283 00000 н. 0000173525 00000 н. 0000173761 00000 н. 0000173997 00000 н. 0000174232 00000 н. 0000174475 00000 н. 0000174717 00000 н. 0000174954 00000 н. 0000175204 00000 н. 0000175441 00000 н. 0000175683 00000 н. 0000175921 00000 н. 0000176161 00000 н. 0000176405 00000 н. 0000176647 00000 н. 0000176840 00000 н. 0000177078 00000 н. 0000177319 00000 н. 0000177501 00000 н. 0000177756 00000 н. 0000177779 00000 н. 0000178177 00000 н. 0000178358 00000 н. 0000178587 00000 н. 0000178843 00000 н. 0000179029 00000 н. 0000179282 00000 н. 0000179470 00000 н. 0000179714 00000 н. 0000179952 00000 н. 0000180032 00000 н. 0000180318 00000 н. 0000207216 00000 н. 0000207457 00000 н. 0000210136 00000 п. 0000210395 00000 н. 0000210579 00000 н. 0000210856 00000 н. 0000211112 00000 н. 0000211353 00000 п. 0000211615 00000 н. 0000211820 00000 н. 0000212070 00000 н. 0000212314 00000 н. 0000212534 00000 н. 0000212814 00000 н. 0000213061 00000 н. 0000213281 00000 н. 0000213489 00000 н. 0000213691 00000 п. 0000213884 00000 н. 0000214116 00000 п. 0000214408 00000 н. 0000214670 00000 н. 0000214920 00000 н. 0000215167 00000 н. 0000215390 00000 н. 0000215619 00000 н. 0000215923 00000 н. 0000216176 00000 н. 0000216417 00000 н. 0000216679 00000 н. 0000216980 00000 н. 0000217230 00000 н. 0000217489 00000 н. 0000217733 00000 н. 0000217995 00000 н. 0000218257 00000 н. 0000218489 00000 н. 0000218760 00000 н. 0000219031 00000 н. 0000219302 00000 н. 0000219567 00000 н. 0000219805 00000 н. 0000220112 00000 н. 0000220359 00000 н. 0000220603 00000 н. 0000220853 00000 н. 0000221094 00000 н. 0000221368 00000 н. 0000221609 00000 н. 0000221859 00000 н. 0000222109 00000 н. 0000222351 00000 п. 0000222595 00000 н. 0000222839 00000 н. 0000223092 00000 н. 0000223336 00000 н. 0000223589 00000 н. 0000223830 00000 н. 0000224074 00000 н. 0000224363 00000 п. 0000224633 00000 н. 0000224904 00000 н. 0000225169 00000 н. 0000225440 00000 н. 0000225702 00000 н. 0000225964 00000 н. 0000226226 00000 н. 0000226530 00000 н. 0000226786 00000 н. 0000227057 00000 н. 0000227319 00000 н. 0000227575 00000 н. 0000227825 00000 н. 0000228081 00000 н. 0000228343 00000 н. 0000228599 00000 н. 0000228864 00000 н. 0000229159 00000 н. 0000229421 00000 н. 0000229689 00000 н. 0000229966 00000 н. 0000230204 00000 н. 0000230481 00000 н. 0000230764 00000 н. 0000230996 00000 н. 0000231312 00000 н. 0000231535 00000 н. 0000231809 00000 н. 0000232080 00000 н. 0000232390 00000 н. 0000232661 00000 н. 0000232926 00000 н. 0000233218 00000 н. 0000233537 00000 н. 0000233808 00000 н. 0000234079 00000 п. 0000234344 00000 п. 0000234531 00000 н. 0000234719 00000 п. 0000234906 00000 н. 0000235093 00000 н. 0000235280 00000 п. 0000235467 00000 н. 0000235651 00000 п. 0000235838 00000 н. 0000236025 00000 н. 0000236212 00000 н. 0000236400 00000 н. 0000236584 00000 н. 0000236772 00000 н. 0000236957 00000 н. 0000237145 00000 н. 0000237333 00000 п. 0000237521 00000 п 0000237712 00000 н. 0000237897 00000 п. 0000238081 00000 н. 0000238272 00000 н. 0000238457 00000 н. 0000238641 00000 н. 0000238825 00000 н. 0000239009 00000 н. 0000239193 00000 н. 0000239377 00000 н. 0000239564 00000 н. 0000239752 00000 н. 0000239937 00000 н. 0000240124 00000 н. 0000240309 00000 н. 0000240496 00000 п. 0000240683 00000 п. 0000240870 00000 н. 0000241057 00000 н. 0000241241 00000 н. 0000241429 00000 н. 0000241617 00000 н. 0000241808 00000 н. 0000241999 00000 н. 0000010653 00000 п. 0000037309 00000 п. трейлер ] >> startxref 0 %% EOF 2196 0 объект > эндобдж 2698 0 объект > поток H [T HEiGQQAEQPʹ 첍 5he)%) t2.Vik3h [3evf {}} 3 | Ͽ

RAM SS — Прогиб и развал стальной балки — RAM | STAAD Wiki — RAM | STAAD

	Применимо к
	Продукты:	RAM структурная система; RAM Сталь
	Версия (и):	Любая
	Площадь:	Дизайн
	Автор оригинала:	Группа технической поддержки Bentley

Критерии — Критерии прогиба и Критерии — Критерии прогиба вместе определяют, будут ли балки изгибаться при проектировании программы.Подробную информацию о том, как именно это делается, см. В руководстве по стальной балке Ram, раздел 10.13. Ниже приведен пример наиболее распространенного случая: без опор, композитная конструкция .

В этом примере используются критерии развала и прогиба по умолчанию:

Это означает, что балки будут изгибаться тогда и только тогда, когда прогиб, вызванный 80% приложенной статической нагрузки конструкции, превышает 0,25 дюйма.

Рассматриваемая балка представляет собой 20-футовую балку, а CDL опирается на собственный вес балки и настила.Учитывая, что 100% этой нагрузки действует на предварительно составную балку без опор, прогиб составляет 1,061 дюйма вниз в середине пролета. Отклонение из-за 80% CDL, следовательно, составляет 0,8 * 1,061 = 0,85 дюйма. Таким образом, программа имеет наклон 0,75 дюйма, что в 3 раза больше увеличения развала 0,25 дюйма.

Прогиб под действием динамической нагрузки рассчитывается с использованием свойств композита (Ieff) и, следовательно, представляет собой меньший общий прогиб, даже если приложенные нагрузки могут быть больше, чем CDL. Эта динамическая нагрузка уже может быть уменьшена, если площадь притока балки достаточно велика. Временные нагрузки конструкции используются только при предварительном контроле прочности балки, а не при первоначальной проверке прогиба.

Значение Post Composite также основано на эффективной инерции составной балки. Рассматриваемая пост-композитная нагрузка — это любая статическая нагрузка выше и выше CDL плюс динамическая нагрузка. Это часто называют наложенной нагрузкой.

Таким образом, общая чистая нагрузка может быть рассчитана по формуле:

Чистый общий прогиб = Начальное отклонение + Вылет из композитного материала - изгиб

В приведенном выше случае это

0.759 = 1,061 + 0,448 - 0,75

Также стоит отметить, что начальный прогиб в этом случае достаточно велик, чтобы превзойти обычные пределы прогиба L / 240 для статических нагрузок, но это нормально, потому что не имеет ограничения на начальные прогибы (с использованием наших критериев прогиба по умолчанию). Пока пределы прогиба под действием динамической нагрузки и пределов общего прогиба нетто в норме, предупреждение не выводится.

Также стоит отметить, что даже при изгибе эта балка теоретически отклоняется на 1.061 «- 075» = 0,311 дюйма во время строительства. Программа не увеличивает статическую нагрузку на конструкцию, чтобы учесть дополнительный бетонный слой, который может образоваться из такого пунда . Приложенные нагрузки следует увеличивать вручную, если это вызывает беспокойство.

Нет, балка Ram Steel проверяет только местный прогиб балок, а не совокупный прогиб балок плюс прогиб опор.

The Criteria — Camber определяет, нужно ли изгибать композитные балки или несоставные балки для всей модели.В случаях, когда вам не нужен изгиб на определенных балках, рассмотрите возможность добавления специальных критериев прогиба с начальным пределом прогиба, равным или меньшим минимального развала, и назначьте эти критерии прогиба рассматриваемой балке:

Все переносимые статические и динамические нагрузки, действующие на композитные балки, являются частью конструкции после композитных материалов. Для передаточных колонн это обычно имеет смысл, поскольку составная балка нижнего уровня должна быть упрочнена к моменту загрузки верхнего уровня.Для подвесных колонн это не так однозначно, но передающая нагрузка по-прежнему учитывается только в пост-композитном дизайне в Ram Steel.

Передаточные нагрузки не включают собственный вес колонны, поскольку расчет колонны обычно выполняется после расчета балки. Рекомендуется точечная нагрузка для расчетного собственного веса колонны.

В случае, когда составная балка спроектирована без составной части (т. Е. С 0 шпильками), проверки прогиба выполняются с использованием критериев несоставного прогиба.Подробнее о причинах, по которым композитные балки проектируются без шпилек, см. В FAQ по стальным балкам Ram.

RAMSS Beams [FAQ]

Технические примечания и часто задаваемые вопросы по продукту

Технические примечания и часто задаваемые вопросы о конструкционных продуктах

Отклонение — Designing Buildings Wiki

Прогиб — с инженерной точки зрения — это степень, в которой элемент конструкции меняет форму при приложении нагрузки. Изменение может быть расстоянием или углом и может быть видимым или невидимым, в зависимости от интенсивности нагрузки, формы компонента и материала, из которого он изготовлен.

Прогиб является решающим фактором при проектировании конструкции, и невнимание к нему может иметь катастрофические последствия.

Различные типы нагрузки могут вызывать отклонения . К ним относятся точечные нагрузки, равномерно распределенные нагрузки, ветровые нагрузки, поперечные нагрузки, а также давление на грунт и землетрясения, и это лишь некоторые из них. Когда нагрузка вызывает слишком большой прогиб , компонент может выйти из строя.

Компоненты и конструкции, которые подвергаются отклонению на , включают балки, колонны, перекрытия, стены, настилы мостов, стены туннелей, плотины и так далее.Мост Золотые Ворота Сан-Франциско может раскачиваться на 4 метра при сильном ветре.

Неструктурные компоненты также могут отклоняться, например панели облицовки здания могут отклоняться внутрь под воздействием сильной ветровой нагрузки.

Учитывая возможность разрушения конструкции, строительные нормы и правила обычно определяют, каким должен быть максимально допустимый прогиб на для обеспечения безопасности пользователей здания и общей структурной целостности. Для балки это обычно выражается как часть пролета, например, отклонение балки не должно превышать 1/360 части пролета; Итак, если пролет составляет 5 м, отклонение не должно быть больше 13.9мм. Обычно это измеряется в средней точке луча.

Конструктивный элемент будет меньше прогибаться под нагрузкой, если его жесткость или жесткость увеличится. Обычно этого можно добиться, усилив его секцию или увеличив ее размер; последнее также может увеличить его стоимость.

Также следует учитывать сам материал. Например, поскольку алюминий примерно в три раза гибче, чем сталь, он часто рассчитан на прогиб , а не на прочность.Напротив, стекло относительно негибкое: даже небольшие отклонения на в стальной раме могут привести к разрушению стекла.