Виды деревянных балок перекрытия — расчет балки на изгиб, прочность и нагрузку

10.07.2018 2674

Стены и перекрытия – основные элементы любого строительства.

Назначение перекрытия – разделять этажи в доме, а также нести и распределять нагрузку от расположенных вверху составляющих – стен, крыши, коммуникаций, мебели, деталей интерьера.

Можно выделить несколько видов перекрытия: металлическое, железобетонное и деревянное.

Более подробно остановимся на деревянных перекрытиях, поскольку именно они получили наибольшее распространение в частном строительстве.

Деревянное балочное перекрытие обладает преимуществами и недостатками

Плюсы:
красивый внешний вид;
малый вес дерева;
ремонтопригодность;
высокая скорость монтажа.

Минусы:
-без специальной защитной пропитки горючи;
-низкая прочность по сравнению с железобетонными или металлическими балками;
-подвержены воздействию влаги, грибка и живых организмов;
-могут деформироваться от перепадов температур

Материал для деревянных балок перекрытия должен обладать определенными свойствами и соответствовать требованиям:

*прочность. Материал перекрытия должен выдерживать возможные нагрузки. Следует учитывать воздействие как *постоянных нагрузок, так и переменных;
*жесткость. Означает способность материала сопротивляться изгибу;
*звуко- и теплоизоляция;
*пожарная безопасность.

Типы и виды деревянных перекрытий — классификация
1. По назначению

Подвальное и цокольное перекрытие по деревянным балкам
Основное требование к такому перекрытию – высокая прочность. Поскольку в данном случае, балки будут служить основой для перекрытия пола и соответственно, должны выдерживать значительную нагрузку.

Совет. Если под первым этажом будет располагаться гараж или большой подвал лучше делать деревянное перекрытие по металлическим балкам. Поскольку деревянные подвержены гниению и не всегда могут выдержать значительную нагрузку. Или же уменьшить расстояние между балками.

Чердачное перекрытие по деревянным балкам
Принцип конструктивного устройства может быть независимым или являться продолжением крыши, т. е. частью стропильной системы. Первый вариант более рационален, т.к. является ремонтопригодным, плюс, обеспечивает лучшую звукоизоляцию.

Междуэтажное перекрытие по деревянным балкам
Конструктивная особенность заключается в эффекте два в одном – балки перекрытия между этажами с одной стороны являются лагами для пола, а с другой, опорами для потолка. Пространство между ними заполняется тепло- и звукоизоляционными материалами, с обязательным использованием пароизоляции. Пирог снизу обшивается гипсокартоном, а сверху застилается половой доской.

2. По виду

Деревянные балки перекрытия также различаются между собой, и каждый вид имеет свои преимущества.
*Цельные (цельномассивные) деревянные балки перекрытия

Для их изготовления применяется массив дерева твердых пород хвойных или лиственных деревьев.

*Межэтажные перекрытия по деревянным балкам, могут быть выполнены цельными только при незначительной длине пролета (до 5 метров).

*Клееные деревянные балки перекрытия
Снимают ограничение по длине, поскольку данная технология изготовления позволяет реализовать балки перекрытия большой длины.

За счет повышенной прочности деревянные клееные балки применяются в тех случаях, когда требуется выдержать повышенную нагрузку на перекрытие.

Сечение деревянных балок перекрытия
Как показывает практика, сечение балок деревянного перекрытия оказывает существенное влияние на способность балки выдерживать несущую нагрузку. Поэтому, необходимо предварительно выполнить расчет сечения деревянных балок перекрытия.

Деревянные балки перекрытия прямоугольного или квадратного сечения
В деревянных домах в качестве межэтажных балок в декоративных целях может использоваться бревно.

Деревянные балки перекрытия круглого сечения (или овального)
Как правило используются для устройства чердачных перекрытий. Круглая балка отличаются высокой устойчивостью на изгиб (зависит от диаметра).

Максимальная длина деревянной балки перекрытия из оцилиндрованного бревна составляет 7, 5 м.п.

Деревянные двутавровые балки перекрытия
Могут быть изготовлены из массива дерева, или в сочетании ОСБ и фанеры. Активно используются в каркасном строительстве.

Деревянные двутавровые балки перекрытия
Преимущества деревянных двутавровых балок:
точные размеры;
возможность использования на длинных пролетах;
исключена возможность деформирования;
малый вес;
уменьшение мостиков холода;

возможность закрепить коммуникации;
возможность монтажа своими руками без привлечения специальной техники;
широкая сфера применения.
Недостатки:
-высокая стоимость;
-неудобны для утепления плитами.

Правильный подбор сечения деревянной балки должен быть включен в расчетный план, в противном случае, конструкция перекрытия окажется недостаточно или избыточно жесткой (лишняя статья расходов).

Расчет деревянного перекрытия
Расстояние между деревянными балками перекрытия определяется:

Во-первых, предполагаемыми нагрузками.
Нагрузка, в свою очередь может быть постоянной – вес перекрытия, вес перегородок между комнатами или вес стропильной системы.

А также переменной – она принимается равной 150 кг/м. кв. (Согласно СНиП 2.01.07-85 «Нагрузки и воздействия»). К переменным нагрузкам относят вес мебели, оборудования, находящихся в доме людей.

Совет. Поскольку учесть все возможные нагрузки затруднительно, следует проектировать перекрытие с запасом прочности. Профессионалы рекомендуют добавлять 30-40 %.
Во-вторых, жесткостью или нормативной величиной прогиба.
Для каждого вида материала ГОСТом устанавливаются свои пределы жесткости. Но формула для расчета одинакова – отношение абсолютной величины прогиба к длине балки. Значение жесткости для чердачных перекрытий не должно превышать 1/200, для междуэтажных 1/250.

На величину прогиба оказывает влияние и порода древесины, из которой изготовлена балка.

Расчет перекрытия по деревянным балкам
Предположим, что расстояние между деревянными балками составляет 1 м.п. Общая длина балки 4 м.п. А предполагаемая нагрузка составит 400 кг/м.кв.

Значит, наибольшая величина прогиба будет наблюдаться при нагрузке

Мmax = (q х l в кв.

) / 8 = 400х4 в кв./8 = 800 кг•м.кв.

Рассчитаем момент сопротивления древесины на прогиб по формуле:

Wтреб = Мmax / R. Для сосны этот показатель составит 800 / 142,71 = 0,56057 куб. м

R — сопротивление древесины, приведенное в СНиП II-25-80 (СП 64.13330.2011) «Деревянные конструкции» введенные в эксплуатацию в 2011 г.

В таблице приведено сопротивление лиственницы.

Если используется не сосна, тогда значение следует скорректировать на переходящий коэффициент (приведен в СНиП II-25-80 (СП 64.13330.2011)).

Пример расчета балки показал, что сопротивление балки на прогиб может уменьшиться вдвое. Следовательно, нужно изменить ее сечение.

Расчёт деревянных балок перекрытия можно выполнить с применением выше приведенной формулы. Но можно использовать специально разработанный калькулятор расчета деревянных балок перекрытия. Он позволит учесть все моменты, не утруждая себя поиском данных и расчетом.

В-третьих, параметрами балки.
Длина деревянных балок перекрытия цельных может составлять не более 5 метров для междуэтажных перекрытий.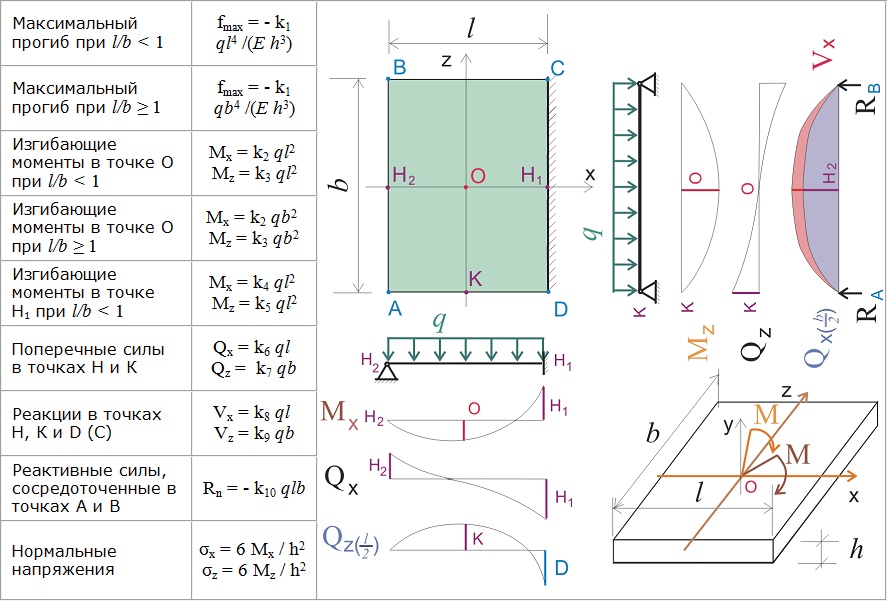

Для чердачных перекрытий длина пролета может составлять 6 м.п.

Таблица деревянных балок перекрытия содержит данные для расчета подходящей высоты балок.

Толщина деревянных балок перекрытия рассчитывается исходя из предпосылки, что толщина балки должно быть не меньше 1/25 ее длины.

Например, балка длиной 5 м.п. должна иметь ширину 20 см. Если выдержать такой размер сложно, можно достичь нужной ширины путем набора более узких балок.

Следует знать:
Если балки сложить рядом они выдержат нагрузку в два раза больше, а если сложить друг на друга — выдержат нагрузку в четыре раза больше.
Используя график, представленный на рисунке можно определить возможные параметры балки и нагрузку, которую она в силах вынести. Учтите, что данные графика пригодны для расчета однопролетной балки. Т.е. для того случая, когда балка лежит на двух опорах. Измеряя один из параметров можно получить желаемый результат. Обычно в качестве изменяемого параметра выступает шаг балок деревянного перекрытия.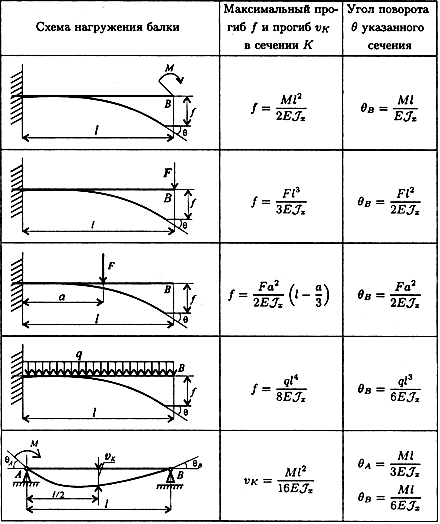

расчетов станет составление чертежа, который будет служить наглядным пособием при работе.

Чтобы качественно и надежно осуществить своими руками перекрытие по деревянным балкам, чертеж должен содержать все расчетные данные.

БАЛКИ, балок, Виды, деревянных, изгиб, нагрузку, перекрытия, прочность, расчет

виды нагрузок, выбор правильного сечения балки, примеры и возможные ошибки

Наиболее ответственной конструкцией при проектировании и строительстве деревянного дома является перекрытие, которое опирается на стены, локальные вертикальные опоры и работает на изгиб в пределах одного этажа.

Расчёт деревянного перекрытия сводится к определению габаритов поперечного сечения балок, поверх которых устраивается конструкция пола вышележащего этажа, и шага между ними.

После определения данных геометрических параметров проводится проверка прочности по двум группам предельных состояний.

Содержание

• 1 Виды нагрузок
• 2 Требования к ним
• 3 Пример сбора нагрузок
• 4 Высчитываем на прочность
• 5 Как рассчитать на прогиб?
• 6 Возможные ошибки при вычислении
• 7 Полезное видео
• 8 Заключение

Виды нагрузок

Деревянные перекрытия, как и любые другие пролётные конструкции, воспринимают полезные нагрузки, вызывающие внутренние усилия в горизонтальных несущих элементах.

Все загружения, прикладываемые к данным конструктивным элементам, делятся на следующие виды:

1. Постоянные нагрузки, которые прикладываются единожды и не изменяются на протяжении всего срока эксплуатации объекта. В деревянных конструкциях постоянные нагрузки разделяются наследующие подвиды:
   • Собственный вес несущих балок.
   • Масса вышележащей конструкции пола, полученная методом послойного суммирования каждого элемента пирога.
   • Вес вышележащих перегородок и других ограждающих конструкций, при условии, что вертикальные оси данных элементов смещены относительно несущих опор перекрытия.
2. Временные нагрузки, прикладываемые на перекрытие в процессе эксплуатации.

   При определении этого загружения учитывается масса предметов мебели, а также людей, эксплуатирующих здание.

   Нагрузка принимается из нормативных значений СНиП, как равномерно распределённая по площади каждой функциональной зоны.

3. Особые штамповые, линейные или точечные нагрузки – прикладываются локально в местах, где необходимо усиленное перекрытие. Например, вес ванны с водой в санузле.

Все указанные нагрузки суммируются и прикладываются к несущим балкам в виде равномерно распределённого по её длине загружения, что и служит основанием для расчёта прочности.

Требования к ним

Все деревянные конструкции классифицируются по свойствам породы древесины, из которой они выполнены. Так как каждый материал имеет разные показатели плотности, массы, природной прочности волокон в радиальном или тангенциальном направлении, то и прочностные характеристики у них сильно рознятся:

1. Лиственница – твёрдая хвойная порода:
   • сжатие – 64,5 МПа;
   • растяжение – 125,0 МПа;
   • скалывание – 9.4 – 9,9 МПа;
   • изгиб – 111,5 МПа.
2. Дуб – твёрдая лиственная порода:
   • сжатие – 57,5 МПа;
   • растяжение – 128,8 МПа;
   • скалывание – 10.2 – 12,2 МПа;
   • изгиб – 107,5 МПа.
3. Сосна – мягкая хвойная порода:
   • сжатие – 48,5 МПа;
   • растяжение – 103,5 МПа;
   • скалывание – 7. 3 – 7,5 МПа;
   • изгиб – 79,3 МПа.
4. Берёза – мягкая лиственная порода:
   • сжатие – 57,5 МПа;
   • растяжение – 128,8 МПа;
   • скалывание – 10.2 – 12,2 МПа;
   • изгиб – 107,5 МПа.
5. Клеёный брус из сосны – составная конструкция повышенной прочности:
   • сжатие – 53,5 МПа;
   • растяжение – 118,6 МПа;
   • скалывание – 14.9 МПа;
   • изгиб – 101,5 МПа.

В данном списке 1 МПа = 1 Н/мм².

Имея под рукой данные табличные показатели прочности древесины разных сортов, можно без труда проверить корректность подбора сечения балки или шага элементов в перекрытии.

Пример сбора нагрузок

Если необходимо собрать постоянные и эксплуатационные нагрузки на несущие балки перекрытия, нужно знать все геометрические характеристики помещения, материал полов, функциональное назначение здания и породу древесины несущего элемента.

Например, требуется рассчитать нагрузки на сосновые балки перекрытия стандартного деревянного дома с габаритами 6 x 6 м, сечение балки – брус 200 x 100 мм, шаг 900 мм. Алгоритм данного действия выглядит следующим образом:

• Собственный вес каждой балки (m1) составит V (объём конструкции, или произведение всех 3 её линейных габаритов) x r (плотность сосны). То есть, m1 = 0,2 м x 0,1 м x 6 м x 500 кг/м³ = 60 кг, или 10 кг на 1 м. п.
• Вес пирога пола – сосновые половые доски толщиной 50 мм. Чтобы собрать нагрузку на одну балку, необходимо выделить её грузовую площадь. Она равняется половине пролёта между несущими элементами, отложенного от оси конструкции в каждую сторону, и помноженного на длину балки.

  Расстояние между брусьями – 90 см = 0,9 м, следовательно, грузовая площадь S1 = (0,45 + 0,45) x 6 = 5,4 м². Таким образом, масса пола m2 = S1 x t (толщина пола) x r = 5,4 м² x 0,05 м x 500 кг/м³ = 135 кг, или 22,5 кг на 1 м. п.

• Нормативная равномерно распределённая эксплуатационная нагрузка для жилых зданий составляет m3 = 150 кг/м2. То есть, данная нагрузка на балку составит F1 = m3 x S1 = 150 кг/м² x 5,4 м² = 810 кг, или 135 кг на 1 м. п.
• Суммарная нагрузка, приходящаяся на 1 балку перекрытия, определяется как F = m1 + m2 + F1 = 60 кг + 135 кг + 810 кг = 1005 кг, или 167,5 кг на 1 м. п.

Учитывая, что любая конструкция должны быть подобрана с небольшим запасом прочности, СНиП требует преобразования нормативной величины в расчётную.

Так, по табличным значениям можно определить, что коэффициент запаса по нагрузке от собственного веса конструкций составляет gn = 1.1, а для временного загружения – 1,4. То есть, конечное значение составит q = (m1 + m2) x 1,1 + F1 x 1,4 = (60 кг + 135 кг) x 1,1 + 810 кг x 1,4 = 1348,5 кг, или 224,75 кг на 1 м. п. (2,2475 Н/мм²).

Высчитываем на прочность

После сбора нагрузок на балки перекрытия, необходимо проверить правильность выбранного сечения материала. Для этого потребуется провести несложный расчёт в соответствии со следующим алгоритмом:

Основная формула проверки прочности подобранного сечения по предельному состоянию 1 группы регламентируется СП 64. 13330.2017 «Деревянные конструкции» и выглядит как:

M / Wрасч < RИ, где:

• M – значение изгибающего момента от приложенной расчётной нагрузки.
• Wрасч – предел прочности заданного сечения, при достижении которого наступит разрушение конструкции.
• RИ – расчётное сопротивление древесины на изгиб.

Изгибающий момент М в стандартной балке, шарнирно опёртой по двум концам, вычисляется из элементарной формулы сопромата:

M = ql2 / 8, где:

q – суммарная расчётная нагрузка на элемент.

В данном примере составляет 224,75 кг/м, а l – пролёт, который перекрывает балка – 6 м.

M = 224,75 кг/м x 62 / 8 = 1011,375 кг*м, или 10113750 Н*мм.

Расчётное сопротивление древесины RИ представляет собой произведение нормативного показателя данной величины, приведённой выше, с учётом ряда коэффициентов надёжности.

RИ = Rn x MДЛ x MВ x MТ x MСС, где:

• MДЛ = 0,6 – коэффициент, учитывающий работу конструкции.
• MВ = 0,9 – характеризует естественную среду эксплуатации.
• MТ = 0,85 – показатель комнатной температуры.
• MСС = 0,9 – коэффициент, учитывающий срок службы сооружения не менее 75 лет.

Следовательно, при Rn для сосны 79,3 МПа (Н/мм²),

RИ = 79,3 x 0,6 x 0,9 x 0.86 x 0,9 = 32,76 Н/мм².

Из формулы условия прочности M / Wрасч < RИ, при известных значениях М и RИ, легко вывести Wрасч = M / RИ, то есть

Wрасч = 10113750 Н*мм / 32,76 Н/мм² = 308723 мм³.

Далее, исходя из известных параметров поперечного сечения деревянной балки b и h, которые оставляют 100 мм и 200 мм, соответственно, можно найти величину момента сопротивления фактического сечения по формуле: W = bh3/6 = 100 x 2002 / 6 = 666667 мм³.

При сравнении этих двух величин, видно, что показатель фактического момента сопротивления сечения почти в 2 раза превышает минимально допустимый параметр, и балка выдержит все приложенные к ней нагрузки, с учётом понижающих коэффициентов.

Если расчётный показатель оказался меньше, необходимо назначить новые габариты сечения и повторно проверить их с учётом приведённых выше формул.

Видео о расчете сечения балок деревянного перекрытия:

Как рассчитать на прогиб?

Если балки перекрытия удовлетворяют критериям прочности, это ещё не значит, что конструкцию можно эксплуатировать. Помимо 1 существует также 2 группа предельных состояний, и перекрытие должно удовлетворять требованиям допустимых деформаций под действием нагрузки, с учётом внутреннего сопротивления несущих элементов. Данный расчёт на прогиб выполняется следующим образом:

В соответствии с таблицей СП 20.13330.2016 «Нагрузки и воздействия», предельно допустимый по эстетико-психологическим соображениям прогиб fult балки при пролёте l = 6 м должен составлять не более fult = 1/200, или 6000 мм / 200 = 30 мм.

Фактическая деформация изгибаемого деревянного элемента определяется по формуле:

f = 5ql4/384ЕI, где:

• Е – модуль упругости древесины, который определяется из табличных значений и составляет 12600 МПа (Н/мм2).
• I – момент инерции, зависящий от геометрии сечения.

I для прямоугольно балки составляет bh4/12 = 100 x 2003 / 12 = 66666667 мм⁴.

Таким образом, расчётный прогиб составит:

f = (5 x 2,2475 x 60004) / (384 x 12600 x 66666667) = 45,15 мм.

Расчёт показал, что балка заданного сечения не удовлетворяет условию предельно допустимой деформации, и габариты придётся увеличить.

Принимая в расчёт новое сечение 150 x 250 мм, расчёт проводится заново:

I = 150 x 2503 / 12 = 195312500 мм⁴.

f = (5 x 2,2475 x 60004) / (384 x 12600 x 195312500) = 15,41 мм.

Из полученного расчёта видно, что прямоугольная балка из сосны с габаритами поперечного сечения 150 x 250 мм полностью удовлетворяет условиям предельного прогиба. Повторный расчёт прочности не имеет смысла, так как с увеличением размеров сечений растёт коэффициент надёжности.

Возможные ошибки при вычислении

Инженеры, не имеющие достаточного опыта в расчёте деревянных конструкций, нередко допускают грубые ошибки, а именно:

• Неверное соотношение единиц измерения влечёт за собой значительные отклонения от верного результата расчёта.
• Пренебрежения расчётом по 2 группе предельных состояний может вызвать слишком сильный прогиб уже смонтированной конструкции.
• Неверный сбор нагрузок окажется далёк от истинного показателя.
• Пренебрежение коэффициентами запаса прочности могут также повлечь за собой ошибочный результат.

Результатом подобных ошибок могут стать непредвиденные прогибы или разрушение конструктивного элемента. В таких случаях владелец объекта недвижимости будет вынужден проводить дорогостоящее усиление перекрытий, а, при самом неблагоприятном исходе событий, могут пострадать люди.

Полезное видео

В данном видео полный расчет деревянного перекрытия:

Заключение

Перед выполнением рабочего проекта, необходимо провести детальный расчёт по 2 группам предельных состояний для конструктивных элементов здания. Он состоит из назначения оптимального сечения балок перекрытия, сбора нагрузок на конструктивный элемент и проверки выбранных параметров на прочность и деформации.

Изгиб при сдвиге в калькуляторах деревянных балок

Древесина, благодаря своим уникальным анизотропным свойствам, имеет модуль сдвига, который обычно намного ниже ее модуля упругости по сравнению с другими материалами, такими как сталь. Таким образом, сдвиговые прогибы могут оказывать существенное влияние на общий прогиб балки. Чтобы приспособиться к этому, мы даем вам возможность учитывать приблизительную деформацию при сдвиге в наших канадских и американских калькуляторах деревянных балок. Эта статья предназначена для краткого описания теории, лежащей в основе нашего приближения. 94} = q(x) — \frac{EI}{\kappa AG}$ 

В то время как некоторым понравится прогулка по переулку памяти из университета, эти дифференциальные уравнения трудно решить и трудно применять на практике. К счастью, в большинстве случаев сдвиговая составляющая прогиба считается незначительной и поэтому игнорируется. Однако, когда это необходимо учитывать, имеется относительно мало ресурсов на деформации сдвига в балках именно потому, что обычно ими можно пренебречь. Однако есть четыре формулы, которые регулярно появляются в литературе*: 92/2\каппа АГ$ Консольная балка под точечной нагрузкой $P$ $\Delta_s = PL/ \каппа AG$

* См. Формулы Рорка для напряжения и деформации, или Расчет сварных конструкций Омер В. Блоджетт

Обсудим каждый параметр отдельно. Но сначала, глядя на приведенные выше формулы, можно заметить закономерность — все эти формулы включают уравнение для пикового момента на соответствующих им пролетах. Например, свободно опертая балка под точечной нагрузкой имеет максимальный момент как $M = PL/4$, что мы можем ясно видеть в формуле прогиба при сдвиге. Таким образом, мы можем сказать, что для этих четырех конкретных случаев прогиб при сдвиге точно равен $M_s / \kappa AG$, где $M_s$ — пиковый рабочий момент в пролете.

Таким образом, в этих случаях у нас остается следующая формула для прогиба при сдвиге: $M_s / \kappa AG$. Параметр $\kappa$ относится к своего рода коэффициенту формы, учитывающему распределение касательных напряжений по поперечным сечениям. Для прямоугольных сечений этот коэффициент в точности равен $\kappa = 5/6$. Это зависит от других форм сечения, но, поскольку в настоящее время мы рассматриваем только прямоугольные сечения, мы остановимся здесь. Далее у нас есть площадь $A$. Это просто общая площадь поперечного сечения $b \times d$.

Наконец, у нас есть модуль сдвига $G$. В то время как для большинства металлов это можно легко определить с помощью формул, для дерева у нас нет такой роскоши! Вместо этого модуль сдвига обычно определяют путем испытаний. Часто встречающееся приближение состоит в том, чтобы просто взять $G = E/16$, где E — модуль упругости. Это то, что мы делаем в ClearCalcs. Обратите внимание, что это соотношение на самом деле значительно различается между различными видами и продуктами — порядка +/- 50%.

наиболее значимое предположение , который мы делаем в ClearCalcs, заключается в том, что мы также предполагаем, что эта формула является разумным приближением для отклонения при сдвиге в каждой балке. Как правило, это дает очень близкие результаты к теоретическим результатам, однако может быть некоторый небольшой неконсерватизм, который, скорее всего, будет наблюдаться в многопролетных и/или статически неопределимых балках.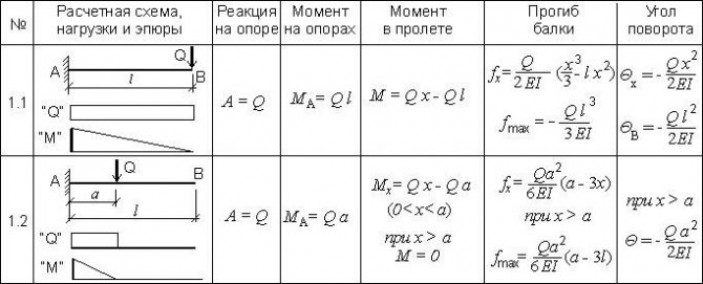 В основном это происходит из-за того, что жесткость балки на сдвиг также влияет на то, как нагрузки распределяются по опорам. Принимая во внимание, что прогиб при сдвиге является небольшой составляющей полного прогиба, а сама жесткость при сдвиге является важным приближением, мы считаем, что наш метод расчета прогиба при сдвиге дает результаты, подходящие для проектирования. Если требуются чрезвычайно высокоточные результаты, этот метод может оказаться неадекватным.

AWC также предлагает альтернативный метод в своем Руководство по инженерным деревянным конструкциям для оценки прогиба при сдвиге деревянных балок, где прогиб при сдвиге напрямую связан с эквивалентным прогибом в равномерно нагруженной балке. Однако мы обнаружили, что это приближение имеет тенденцию значительно отличаться от значений, предсказанных теорией — например, оно завышает сдвиговое отклонение кантилевера более чем на 200%.

«Кажущийся» модуль упругости?

Несмотря на то, что в Канаде стандарты и спецификации производителей в США не так распространены, они иногда ссылаются на «кажущийся» модуль упругости, особенно в клееных балках и конструкционных композитах, таких как LVL. Цель этого состоит в том, чтобы избежать выполнения расчетов прогиба при сдвиге, просто уменьшив модуль упругости, используемый при расчетах прогиба при изгибе. Обычно это принимается за уменьшение эластичности на 5%, что после округления обычно приводит к уменьшению «истинного» модуля упругости на 100 000 фунтов на квадратный дюйм. В APA есть подробная статья об идее кажущегося модуля упругости здесь: https://www.apawood.org/publication-search?q=tt-082&tid=1

Деревянные двутавровые балки

Деревянные двутавровые балки особенно подвержены деформациям при сдвиге, и это всегда следует учитывать. Поскольку они не имеют прямоугольного сечения и однородного материала, производители обычно напрямую указывают значение жесткости на сдвиг, определенное в ходе испытаний, как правило, в форме $K = 8\kappa AG/$, где конечное значение $\kappa AG$ определяется непосредственно из испытаний (т. е. коэффициент формы, площадь и модуль сдвига не нужно рассчитывать отдельно). Коэффициент 8 присутствует в уравнении, так как большинство балок используются только при равномерных нагрузках, что упрощает расчет прогиба при сдвиге. Однако принципы остаются прежними.

Обратите внимание, что прогиб при сдвиге применяется к сечениям двутавровой балки в Калькуляторе деревянных балок AU, но не выполняется для других деревянных сечений AU.

В техническом бюллетене APA по двутавровым балкам с рабочими характеристиками указано значение жесткости на сдвиг K, которое следует использовать для двутавровых балок.

Проектирование деревянных балок — Structville

Проектирование изгибаемых элементов, таких как деревянные балки, в основном включает рассмотрение последствий таких воздействий, как изгиб, отклонение, вибрация, боковое изгибание, сдвиг и опора. Процесс проектирования таких конструкций описан в Еврокоде 5 (EN 1995-1-1:2004), и в этой статье показан пример конструкции.

Пример конструкции

Балка из пиломатериалов глубиной 75 мм на 200 мм в жилом доме выдерживает характерную нагрузку, показанную выше. Балка имеет пролет в свету 2,75 м, опорная длина ограничена 100 мм на каждом конце, относится к классу прочности C24 в соответствии с BS EN 338:2003 и работает в условиях класса эксплуатации 2. Балка в поперечном направлении удерживается от бокового изгиба по всей ее длине.

Учитывая это;

Г _{к . удл}  = 1 . 3 кН/м (характеристика равномерно распределенного постоянного действия)
Q _{k . удл} = 1 . 5 кН/м (характеристика равномерно распределенного среднесрочного действия)
G _{k . р} = 1 . 00 кН характеристическая точечная нагрузка в середине пролета

1. Геометрические характеристики балки
Ширина балки b = 75 мм
Глубина балки h = 200 мм
Пролет балки в свету, l _{c 9009 0} = 2750 мм
Длина подшипника b _l  = 100 мм
Расчетный пролет балки l = ( l _c + l _b ) = 2750 + 100 = 2850 = 2,85 м
Секция модуль пучка о у – y ось, W _y = bh ² /6 = (75 × 200 ² )/6 = 5 × 10 90 165 5 мм ³

2.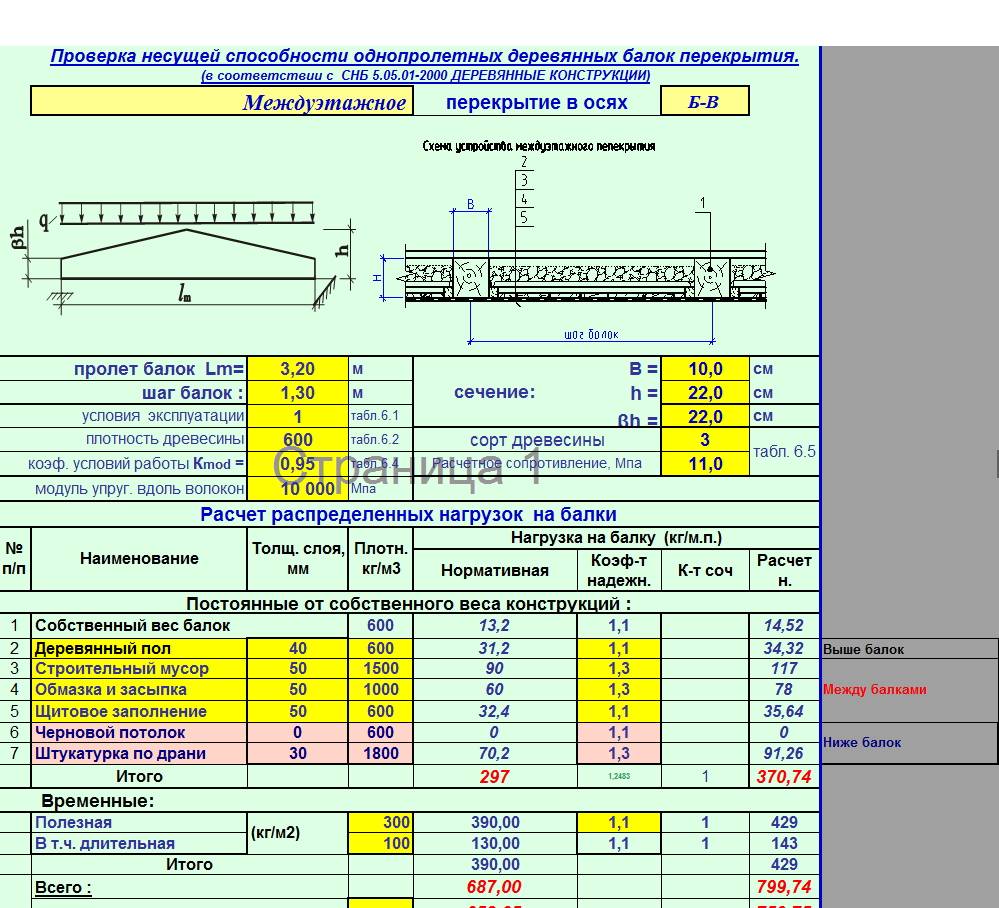 Древесина свойства
Класс прочности C24 (BS EN 338:2003, Таблица 1 ):
Характеристическая прочность на изгиб,   f _{m . k} = 24 Н/мм ²
Характеристическая прочность на сдвиг, f _{v . к} = 2 . 5 Н/мм ²
Нормативная прочность на смятие, f _{c , 90 , 90 090 к} = 2 . 5 Н/мм ²
Пятый процентильный модуль упругости параллельно волокнам, E _{0 . 05} = 7 . 4 кН/мм ²
Средний модуль упругости параллельно волокнам, E _{0 , среднее} = 11 кН/мм ²
Средний модуль сдвига, G _{0 , означает} = 0 . 69 кН/мм ²
Средняя плотность бруса, ρ _м = 420 кг/м ³

3. Коэффициенты запаса прочности
(UKNA по BS EN 1990:2002, Таблица NA.A1.2(B) )) для ULS
Постоянные действия, γ _{Г. УЛС} = 1 . 35
Переменные действия, γ _{Q. ULS} = 1 . 5

(UKNA to BS EN 1990:2002, Table NA.A1.1 – Категория A)
Коэффициент для квазипостоянного значения переменного воздействия, ψ ₂ = 0 . 3

(UKNA to EC5, Table NA.3 )
Коэффициент материала для массивной древесины на ULS, γ _M = 1 . 3

4. Действия

(i) ULS
(a) Характеристический собственный вес балки, G _k,swt 900 55
Г _{к , swt} = b · h · g · ρ _m = (0,075 × 0,2 × 9,81 × 420)/1000 = 0 . 062 кН/м
Расчетное воздействие от собственного веса балки, F _{d , SWT}
F _{d , SWT} = γ 9008 9 Г. _УЛС · Г _{к . СВТ} = 1,35 × 0,062 = 0 . 0837 кН/м

(б) Характеристика постоянного действия от точечной нагрузки, G _k,p
G _k 900 89 , _стр = 1 . 00 кН
Расчетное постоянное воздействие от точечной нагрузки, F _{d . p}
F _{d , p} = γ _G. 9 0043 _УЛС · G _{к . p} = 1,35 × 1,0 = 1 . 35 кН

(c) Характеристика постоянного действия от UDL, G _k,udl
Г _{к , удл} = 1 . 3 кН/м
Расчетное воздействие из-за постоянного действия UDL, F _{d , p ,} 9 0089 удл
Ф _{д , р , удл} = γ _{Г. УЛС} · Г _{к . udl}   =1,35 x 1,3 = 1,755 кН/м

(г) Характеристика среднесрочного действия за счет UDL, Q _k,udl 900 77 К _{к , удл} = 1 . 5 кН/м
Расчетное воздействие за счет переменного действия UDL, F _{d , q , удл}
Ф _{д , q , удл} = γ _Q. 900 89 ULS · Q _{k .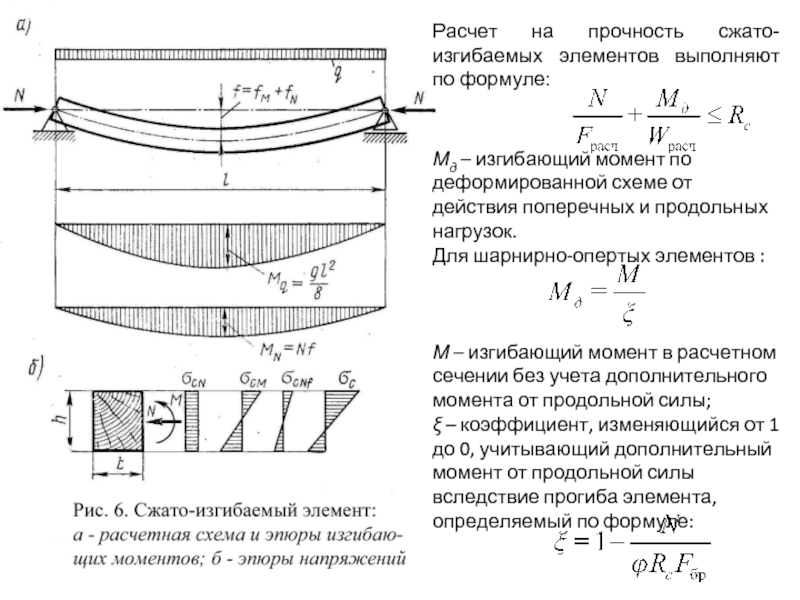 udl} = 1,5 × 1,5 = 2,25 кН/м

Итого UDL @ ULS = 0 . 0837 + 1,755 + 2,25 = 4,1 кН/м
Общее сосредоточенное действие при ULS = 1,35 кН

5. Поправочные коэффициенты
Коэффициент для средней продолжительности нагрузки и класса эксплуатации 2, k _{мод . со средним = 0 . 8 (EC5, Таблица 3.1)
Коэффициент размера для глубины более 150 мм, k h = 1 . 0 (EC5, уравнение (3.1) )
Поперечная устойчивость балки: k крит = 1 (EC5, 6.3.3 ))
Коэффициент несущей способности k c,90 90 090 = (принимается как 1.0) (EC5, пункт 6.1.5(2))
Коэффициент деформации для класса эксплуатации 2, k по умолчанию = 0 . 8 (EC5, Таблица 3.2 )
Коэффициент распределения нагрузки, k sys не имеет значения k sys = 1,0}

9005 4 (6) Прочность на изгиб
Расчетный изгибающий момент;

M _d = ql ² /8 + PL/4 = (4,1 × 2,85 ² )/8 + (1,35 × 2,85)/4 = 4,162 + 0,96 = 5,122 кНм

Расчетное напряжение изгиба , σ _{м , 9г} = (5,122 × 10 ⁶ )/( 5 × 10 ⁵ ) = 10,244 Н/мм ²

Расчетная прочность на изгиб, f _{m ,y, d} = ( k 900 43 _{мод средний} · к _{система} · к _ч · ф _{м . k} )/ γ _M = (0,8 × 1,0 × 1,0 × 24)/1,3 = 14 . 77 Н/мм ²

σ _{m ,y, d} < f _{м ,y, d}   Разрез в порядке на изгиб

(7) Прочность на сдвиг
Расчетное усилие сдвига V _d = ql/2 + P/2 = (4,1 × 2,85)/2 + (1,35/2) = 6,52 кН

Расчетное напряжение сдвига, τ _{v . d} (EC5, уравнение (6.60) )
τ _{v . d} = 1,5 В _d /bh _ef = (1,5 × 6,52 × 1000)/(75 × 200) = 0,652 Н/мм ²

Расчетная прочность на сдвиг, f _{v , d} = ( к _{мод . мед} · к _сис · ф _{в . k} )/ γ _M = (0,8 × 1,0 × 2,5)/1,3 = 1,54 Н/мм ²

τ 900 43 _{v . d} < f _{v , d}   Секция в порядке при сдвиге

(8) Несущая способность
Расчетная несущая сила будет равна расчетной поперечной силе в балке, В _d

Расчетное напряжение смятия, σ _{c , 90 , д}   = В _д /б · л _b = (6,52 × 1000)/(75 × 100) = 0,833 Н/мм ²

Расчетная несущая способность, (EC5, уравнение (6.3) ))

900 42 ф _{в . 90 . d} = ( k _{mod . med} · k _{sys 9009 0 · к с 90 · ф с . 90 . k )/ γ M = (0,8 × 1,0 × 2,5)/1,3 = 1,54 Н/мм ²}

σ _{c , 90 , d}   < f _{c . 90 . d}   Секция в порядке по опоре

(9) Прогиб

Мгновенный прогиб из-за постоянных воздействий

u _{инст,точка,G} = (1/4) × [1/ (11 × 75 × 200 ³ )] × 2850 ³ × [1 + 1,2 × (11/0 . 69) × (200/2850) ² ] = 0,959 мм

U _{инст,удл,Г} = (5/32) × [(1,3 × 10 ^-3 + 0,062 × 10 ^-3 )/(11 × 75 × 200 ^{G = и _{инст, точка,G} + U _inst,udl,G = 0,959 + 2,287 = 3,246 мм}

Мгновенное отклонение из-за переменного действия

U _inst,Q = (5/32) × [(1,5 × 10 ^-3 )/(11 × 75 × 200 ³ )] × 2850 ⁴ × [1 + 0,96 × (11/0 .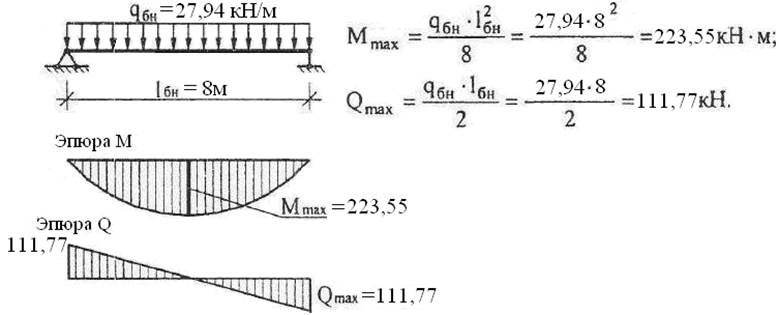 69) × (200/2850) ² ] = 2,519 мм

Суммарный постоянный и переменный мгновенный прогиб = u _inst = u _inst,G + u _inst,Q = 3,246 + 2,519 = 5,765 мм

Еврокод 5 предел прогиба (таблица 7.2, EC5) w _инст = l /300 = 2850/300 = 9,5 мм (u _инст < w _inst Мгновенное отклонение в порядке)

Окончательное отклонение
Окончательное отклонение из-за постоянных воздействий u _fin,G = u _inst,G (1 + k 900 89 по определению ) (уравнение 2.3, EC5 )
u _fin,G = 3,246  (1 + 0,8) = 5,843 мм

Конечный прогиб от переменных и квазипостоянных воздействий,  u _fin,Q = u _inst,Q (1 + 9 0042 ψ ₂ k _{по умолч.} ) (уравнение 2.4, EC5)
u _fin,Q = u _inst,Q (1 + ψ ₂ k _def ) = 2,519 (1 + 0,3 × 0,8 ) = 3,12 мм

Окончательный прогиб из-за постоянного действия
u _net,fin = u _fin,G + u _fin,Q = 5,843 + 3,12 = 8,963 мм

Предел прогиба w _net,fin = л /150 = 2850/150 = 19 мм

Прогиб балки удовлетворительный

Чтобы загрузить эту проектную статью в формате PDF, нажмите ЗДЕСЬ.