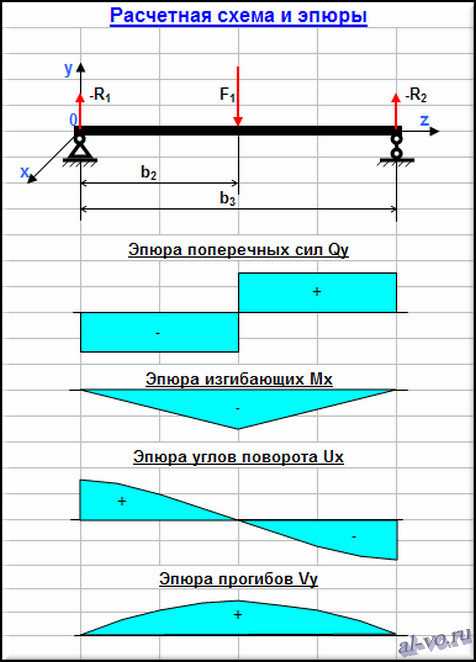
Как рассчитать прогиб балки при строительстве дома

Содержание:

1. Какие бывают балки

2. Как добиться максимальной прочности конструкции

3. Заключение

Расчет балки на прочность и прогиб осуществляется по отношению к любым конструкциям для проверки надежности. В процессе эксплуатации, на нее воздействуют внутренние и внешние факторы, природные явления, из-за чего она может деформироваться. Строители сравнивают этот элемент конструкции со стержнем, закрепляющимся на опорах.

От величины опор, зависит сложность проведения самостоятельных расчетов. Чтобы рассчитать основную нагрузку, нужно сложить силы, которые направлены к сечению перпендикулярно. Расчет максимального прогиба балки позволит узнать степень наивысшей деформации.

Какие бывают балки

Неважно, какая конструкция предусмотрена проектом, балка должна быть выполнена исключительно из надежного, прочного стройматериала.

Они имеют отличия по величине параметров: сечение, длина, форма. Зачастую, для их создания используются пиломатериалы или металл. 

Определение изгиба балки осуществляется исходя из вида стройматериала. Большая роль отводится структуре и однородности конструкции

Для выбора подходящего подрядчика, который досконально разбирается в вопросах строительных норм и правил малоэтажного домостроения воспользуйтесь поиском в каталоге Building Companion. В профиле каждой компании указана необходимая информация, портфолио, отзывы, можно разместить запрос на оценку стоимости услуги.

Найти компанию по генподряду и стройнадзору »

Из дерева

Такие конструкции применяются при сооружении домов с одним этажом. Деревянный брус подойдет для создания потолков, а также полов. Для выполнения расчета нагрузки балки на прогиб, нужно учесть ряд величин:

• Материал. У каждого пиломатериала уникальный прочностные характеристики, параметры гибкости и твердости.
• Геометрия (речь идет о форме, а также сечении).
• Степень допустимых нагрузок (давление на стройматериал).

На степень изгиба влияет не только реальное давление, но и любые возможные воздействия.

Из металла

Они более сложны ввиду своего сечения и состава. Стальные конструкции производятся путем выливания разных металлов. Выполняя вычисления, нужно учесть показатель жесткости, прочности соединения.

Соединение металлоконструкций между собой осуществляется с помощью разных технологий:

• Склепывание.
• Сваривание.
• Резьбовые соединители.

Балки с высокой прочностью применяются при сооружении многоэтажных домов. Нагрузки в них равномерным образом распределяются по всей длине.

Для выбора подходящего эксперта для документального сопровождения строительства дома рекомендуем воспользоваться поиском компаний в каталоге Building Companion. В профиле каждого подрядчика указана необходимая информация, портфолио, отзывы, можно разместить запрос на оценку стоимости услуги.

Найти эксперта по документальному сопровождению »

Как добиться максимальной прочности конструкции

С учетом норм, у балок, которые применяются на эстакаде, изгиб не должен превышать 1 сантиметра при длине конструкции в 1,5 метра. Для конструкций с другой длиной, этот показатель будет отличаться. Например, в случае с индивидуальными домами, чердачные балки длиной в 2 метра могут иметь прогиб до 1 сантиметра, в многоэтажных постройках, тот же 1 сантиметр будет справедливым для изделий длиной в 2,5 метра.

Для обеспечения надежности и прочности строения, расчет балки на прогиб выполняется на этапе создания проекта строения. От того, насколько сильной будет устойчивость бруса, зависит прочность постройки. Вес от потолка будет распределяться равномерным образом, к тому же будет сохраняться устойчивость сооружения. Из-за сильного прогиба бруса, о надежности потолочной конструкции говорить не приходится. В какой-то момент соединения разорвутся и строение начнет разрушаться.

Исходя из вида балки на прогиб, вычисления осуществляются разными способами:

• Использование онлайн-калькуляторов. Инструмент работает на основе программы, в которую нужно внести стандартные данные.
• Справочники информации. Воспользовавшись справочной информацией, можно сравнить параметры для самостоятельного расчета.
• Формула. С помощью формулы можно выполнить самостоятельные расчеты с максимальной точностью результатов.

В помещениях, эксплуатируемых много лет, определить степень его аварийности можно лишь после расчетов, определения, насколько проседают балки.

Полное вычисление балки на жесткость

Для решения задачи, используется формула:

• М – максимально возможный момент, возникающий в конструкции.
• Wn,min — сопротивление сечения.
• Ry — сопротивление стали в момент изгиба. Величина зависит от вида металла.
  
• γc — коэффициент рабочих условий.

Расчеты не представляют большой сложности, поэтому, реализовать их смогут даже строители без опыта. Но чтобы точно определить максимальный прогиб, составляется расчетная схема объекта, рассчитываются размеры балки с учетом сечения, вычисляется максимально возможная нагрузка, воздействующая на конструкцию. При вычислении двухопорных балок, одна из них является жесткой, а другая шарнирной.

Заключение

Перед тем началом строительных работ, любой проектировщик с большим опытом занимается расчетом изгиба балки. Так как от точности этих манипуляций зависит прочность будущей постройки, советуем поручить работы профессионалам. Безусловно, расчеты можно выполнить, воспользовавшись онлайн-калькулятором, но последствия от ошибок могут быть довольно печальными. Желательно, чтобы любые операции, связанные с величинами и показателями, выполнялись последовательно, руками специалиста, на бумаге.

В статье использованы фотографии с сайта

http://s-stroit.ru

.

Метод начальных параметров

В этой статье будут рассмотрены основные нюансы расчета прогибов, методом начальных параметров, на примере консольной балки. А также рассмотрим пример, где с помощью универсального уравнения, определим прогиб балки и угол поворота.

Теория по методу начальных параметров

Возьмем консольную балку, нагруженную сосредоточенной силой, моментом, а также распределенной нагрузкой. Таким образом, зададимся такой расчетной схемой, где присутствуют все виды нагрузок, тем самым охватим всю теоретическую часть по максимуму.

Обозначим опорные реакции в жесткой заделке, возникающие под действием внешней нагрузки:

Выбор базы и системы координат

Для балки выберем базу с левой стороны, от которой будем отсчитывать расстояния до приложения сил, моментов, начала и конца распределенной нагрузки.

Базу обозначим буквой O и проведем через нее систему координат:

Базу традиционно выбирают с левого краю балки, но можно выбрать ее и справа. Тогда в уравнении будут противоположные знаки, это может пригодиться в некоторых случаях — упростит немного решение. Понимание, когда принимать базу слева или справа, придет с опытом использования метода начальных параметров (МНП).

Универсальное уравнение МНП

После введения базы, системы координат и обозначения расстояний а, б, в, г записываем универсальное уравнение МНП, с помощью которого, будем рассчитывать прогиб балки (вертикальное перемещение сечения K, находящегося на свободном торце балки):

Теперь поговорим об этой формуле, проанализируем, так сказать:

• E – модуль упругости;
• I – момент инерции;
• V_K – прогиб сечения K;
• V_O – прогиб сечения O;
• θ_O – угол поворота сечения О.

Не буду приводить вывод этой формулы, не хочу отпугивать читателей, продвинутые студенты могут ознакомиться с выводом самостоятельно в учебнике по сопромату.

Я только расскажу об основных закономерностях этого уравнения и как записать его для любой балки постоянного сечения.

Итак, изучаем эту формулу слева направо. В левой части уравнения обознается искомый прогиб, в нашем случае V_K, который дополнительно умножается на жесткость балки — EI:

В уравнении всегда учитывается прогиб сечения балки, совпадающего с нашей базой EIV_O:

Также всегда учитывается угол поворота сечения, которое совпадает с выбранной базой. Причем произведение EIθ_O всегда умножается на расстояние от базы до сечения, прогиб которого рассчитывается, в нашем примере — это расстояние г.

Следующие компоненты этого уравнения учитывают всю нагрузку, которая находится слева от рассматриваемого сечения. В скобках расстояния от базы до сечения отнимаются расстояния от базы до соответствующей силы или момента, начала или конца распределенной нагрузки.

Скобка, в случае с сосредоточенными силами, возводится в 3 степень и делится на 6. Если сила смотрит вверх, то считаем ее положительной, если вниз, то в уравнении она записывается с минусом:

В случае с моментами скобка возводится во 2 степень и делится на 2. Знак у момента будет положительный, когда он направлен по часовой стрелке и отрицательным, соответственно, если против часовой стрелки:

Учет распределенной нагрузки

Теперь поговорим о распределенной нагрузке. Как уже говорилось, в уравнении метода начальных параметров должно учитываться начало и конец распределенной нагрузки. Но так как, конец распределенной нагрузки совпадает с сечением, прогиб которого мы хотим вычислить, в этом случае, в уравнении учитывается только ее начало.

Причем важно, даже если бы в этом сечении была сила или момент, их бы также не учитывали. Нас интересует все, что находится слева от рассматриваемого сечения.

Для распределенной нагрузки скобка возводится в 4 степень и делится на 24. А правило знаков такое же, как и для сосредоточенных сил.

Граничные условия

Чтобы решить уравнение, нам понадобятся еще кое-какие данные. С первого взгляда в уравнении у нас наблюдается три неизвестных: V_K, V_O и θ_O. Но кое-что мы можем почерпнуть из самой схемы. Мы знаем, в жесткой заделке не может быть никаких прогибов, и никаких поворотов, то есть V_O = 0 и θ_O = 0, это и есть так называемые начальные параметры или их еще называют граничными условиями. Теперь, если бы у нас была реальная задача, мы бы подставили все численные данные и нашли перемещение сечения K.

Если бы балка была закреплена с помощью шарнирно-подвижной и неподвижной опоры, тогда мы бы приняли прогибы в опорах равными нулю, но угол поворота в опорах был уже отличен от нуля. Более подробно об этом рассказано в другой моей статье, посвященной методу начальных параметров на примере балки на двух опорах.

Чуть не забыл про еще одну величину, которую часто требуется определять методом начальных параметров. Как известно, при изгибе, поперечные сечения балок, помимо того, что перемещаются вертикально (прогибаются) так еще и поворачиваются на какой-то угол. Углы поворота и прогибы поперечных сечений связаны дифференциальной зависимостью.
Если продифференцировать уравнение, которое мы получили для прогиба поперечного сечения K, то получим уравнение угла поворота этого сечения:

Пример расчета прогиба балки

Для закрепления пройденного материала предлагаю рассмотреть пример с заданными численными значениями всех параметров балки и нагрузок.

Условие задачи

Возьмем также консольную балку, которая жестко закреплена с правого торца. Будем считать, что балка изготовлена из стали (модуль упругости E = 2·10⁵ МПа), в сечении у нее двутавр №16 (момент инерции по сортаменту I = 873 см⁴). Рассчитывать будем прогиб свободного торца, находящегося слева.

Подготовительный этап

Проводим подготовительные действия, перед расчетом прогиба: помечаем базу O, с левого торца балки проводим координатные оси и показываем реакции, возникающие в заделке, под действием заданной нагрузки:

В методе начальных параметров есть еще одна особенность, которая касается распределенной нагрузки. Если на балку действует распределенная нагрузка, то ее конец, обязательно должен находиться на краю балки (в точке наиболее удаленной от заданной базы). Только в таком случае рассматриваемый метод будет работать.

В нашем примере, нагрузка, как видно, начинается на расстоянии 2 м от базы и заканчивается на 4 м. В таком случае нагрузка продлевается до конца балки, а искусственное продление компенсируется дополнительной, противоположно направленной нагрузкой. Тем самым в расчете прогибов будет уже учитываться 2 распределенные нагрузки:

Расчет прогиба

Записываем граничные условия для заданной расчетной схемы:

V_A = 0 при x = 6м

θ_A = 0 при x = 6м

Напомню, что нас, в этом примере интересует прогиб сечения O (V_O). Для его нахождения составим уравнение, для сечения A, в которое будет входить искомая величина:

В полученном уравнении у нас содержится две неизвестные величины: искомый прогиб V_O и угол поворота этого сечения — θ_O:

Но чтобы решить поставленную задачу, составим дополнительное уравнение, но только теперь, не прогибов, а углов поворотов, для сечения A:

Из второго уравнения найдем угол поворота:

После чего рассчитываем искомый прогиб:

Таким образом, свободный торец такой балки, прогнется практически на 6 см. Данную задачу, можно решить несколько проще, если ввести базу с правого торца. В таком случае для решения потребовалось бы лишь одно уравнение, однако, оно было бы немного объемнее, т.к. включало реакции в заделке.

Калькуляторы прогиба балки

— EngineerExcel

Расчет прогиба балки применим к нескольким сценариям проектирования конструкций. Например, расчет отклонения консольной балки может определить силы, действующие на крыло самолета.

Калькуляторы прогиба балки

Самый простой способ определить прогиб балки под действием силы или момента — использовать калькулятор и параметры балочной системы. В зависимости от балочной системы, консольной, просто поддерживаемой или неподвижно-фиксированной, были оценены различные случаи, чтобы получить уравнение для расчета отклонения балки как функции расстояния вдоль балки.

Калькуляторы прогиба консольной балки

Существует пять общих случаев для учета прогиба консольной балки.

Консольная балка с конечным усилием

Первый – это прогиб под действием силы на свободном конце балки, как показано ниже:

Прогиб балки можно рассчитать с помощью следующего уравнения:

где:

• F сила, приложенная к концу балки (Н)
• х — позиция вдоль балки, где оценивается прогиб (м)
• E — модуль Юнга материала балки (Па)
• I – момент инерции площади (м4)
• L общая длина балки (м)

Консольная балка с нагрузкой в ​​любой точке

Второе отклонение консольной балки — это отклонение из-за силы, приложенной в какой-либо точке, отличной от конца, как показано ниже:

Прогиб балки можно рассчитать с помощью следующих уравнений:

где a — расстояние от поддерживаемого конца до места действия силы (м).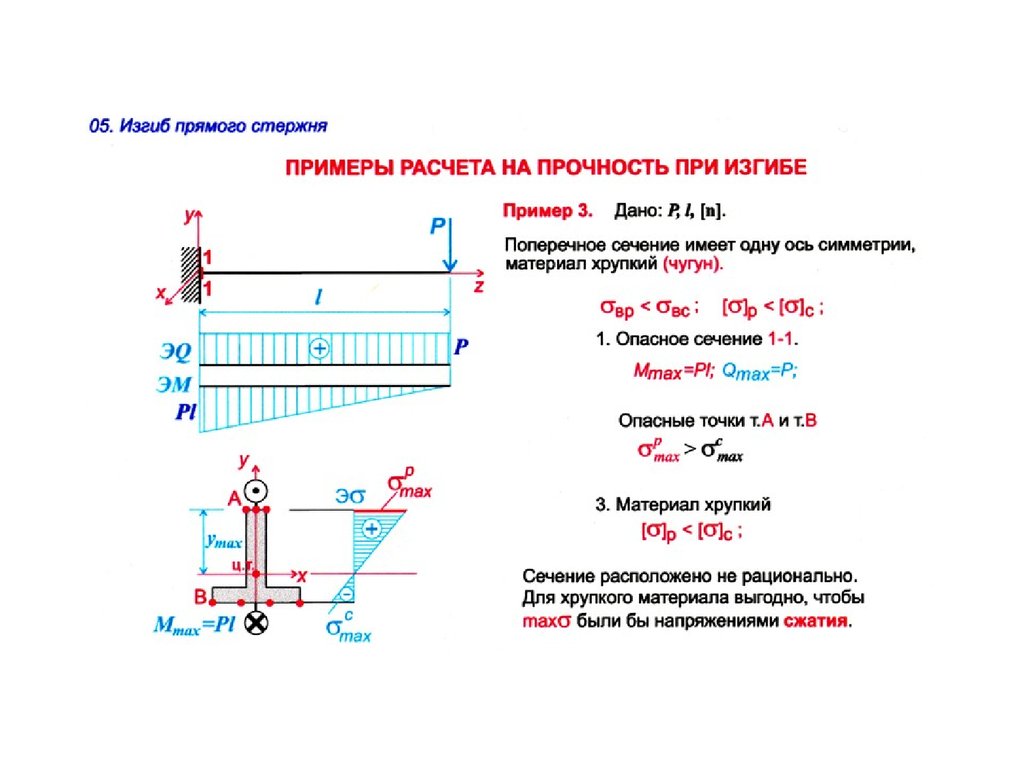

Консольная балка с равномерно распределенной нагрузкой

Третье отклонение консольной балки представляет собой отклонение из-за силы, приложенной равномерно по длине балки, как показано ниже:

Прогиб балки можно рассчитать с помощью следующего уравнения:

где w равномерная нагрузка (Н/м).

Консольная балка с треугольной распределенной нагрузкой

Четвертый прогиб консольной балки представляет собой прогиб из-за треугольной распределенной силы, приложенной по длине балки, как показано ниже:

Прогиб балки можно рассчитать с помощью следующего уравнения :

где w ₁ максимальное значение силы (Н).

Консольная балка с конечным моментом

Конечным прогибом консольной балки является прогиб из-за момента на свободном конце балки, как показано ниже:

Прогиб балки можно рассчитать с помощью следующего уравнения:

где M ₀ — момент, приложенный к свободному концу (Н∙м).

Калькуляторы прогиба свободно опертой балки

Просто опертая балка с нагрузкой в ​​любой точке

Существует семь общих случаев для рассмотрения прогиба свободно опертой балки. Первый – это отклонение из-за промежуточной силы, как показано ниже:

Отклонение балки можно рассчитать с помощью следующего уравнения:

, где a и b — расстояния по обе стороны от приложенной силы (м).

Свободно опертая балка с нагрузкой в ​​середине пролета

Второй прогиб свободно опертой балки — это прогиб из-за силы, приложенной к центру балки, как показано ниже:

Прогиб балки можно рассчитать с помощью Следующее уравнение:

Свободно опертая балка с равномерно распределенной нагрузкой

Третье отклонение свободно опертой балки — это отклонение из-за равномерно распределенной силы, как показано ниже:

Прогиб балки можно рассчитать с помощью следующего уравнения:

Свободно опертая балка с моментом на каждом конце

Четвертый прогиб свободно опертой балки — это прогиб из-за моментов на обеих опорах, как показано ниже:

прогиб можно рассчитать по следующему уравнению:

Свободно опертая балка с моментом на одном конце

Пятый прогиб свободно опертой балки — это прогиб из-за момента на одной опоре, как показано ниже:

Прогиб балки можно рассчитать по следующему уравнению:

Свободно опертая балка с моментом в центре

Окончательный прогиб свободно опертой балки — это прогиб из-за момента в центре балки, как показано ниже :

Прогиб балки можно рассчитать по следующему уравнению:

Калькуляторы прогиба фиксированной-фиксированной балки

Фиксированная-фиксированная балка с нагрузкой в ​​середине пролета отклонение луча.

Первый — это отклонение из-за силы в центре, как показано ниже:

Прогиб балки можно рассчитать с помощью следующего уравнения:

Неподвижно-неподвижная балка с равномерно распределенной нагрузкой

Другое фиксированно-неподвижное отклонение балки представляет собой отклонение из-за равномерно распределенной силы, как показано ниже:

Прогиб балки можно рассчитать с помощью следующего уравнения:

Дифференциальный расчет прогиба балки

Другой метод расчета прогиба балки включает использование дифференциального уравнения кривой прогиба для оценки поведения балки при изгибе. Здесь представлен обзор этого метода, однако конкретные детали выходят за рамки этого введения.

В этом методе используется общее уравнение, и его можно применять к любой комбинации сил и моментов, действующих в любой точке балки. Используемое уравнение:

где:

• v — прогиб балки (м)
• d ² v/dx ² — вторая производная прогиба относительно положения вдоль балки
• M — изгибающий момент вдоль балки в зависимости от положения (Н∙м)

Изгибающий момент в каждом сечении балки рассчитывается как функция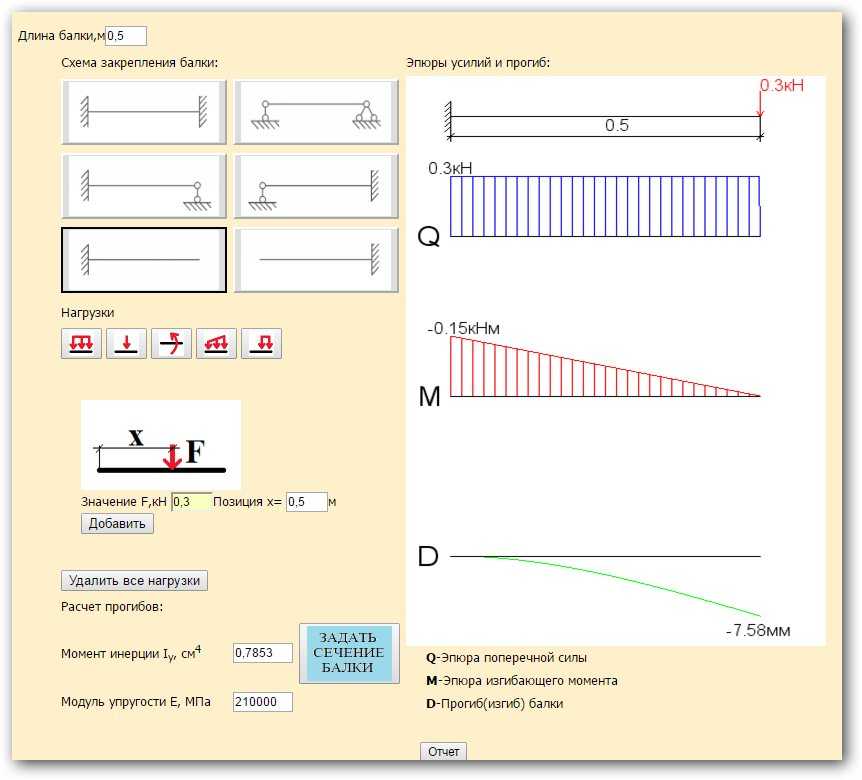

x . Затем каждая функция дважды интегрируется для решения EIv . Системные ограничения используются для создания системы уравнений, решение которой позволяет определить константы интегрирования. Наконец, отдельные уравнения могут быть использованы для определения отклонения v как функции x .

Применение прогиба балки

Путем расчета прогиба балки под действием силы или момента можно выбрать подходящий материал для конкретного применения. Форма балки будет определять момент инерции ее поперечного сечения. Используя это с модулем Юнга материала и требованиями к изгибу, балочную систему можно оптимизировать.

Таблицы отклонения балки | MechaniCalc

ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.

---

В таблицах ниже приведены уравнения для прогиба, наклона, сдвига и момента вдоль прямых балок для различных условий на концах и нагрузок. Вы можете найти исчерпывающие таблицы в таких справочниках, как Gere, Lindeburg и Shigley. Однако приведенные ниже таблицы охватывают большинство распространенных случаев.

Для получения информации об отклонении балки см. наш справочник по напряжениям и отклонениям в балках.

Консольные балки

Консоль, торцевая нагрузка		@ х = L @ х = L В = +F М = ​​-F (L — х) M макс = −ФЗ @ х = 0
Консоль, промежуточная нагрузка		(0 ≤ х ≤ а) (а ≤ х ≤ L) @ х = L (0 ≤ х ≤ а) (а ≤ х ≤ L) В = +F (0 ≤ х ≤ а) В = 0 (а ≤ х ≤ L) М = ​​-F (а — х) (0 ≤ х ≤ а) М = ​​0 (а ≤ х ≤ L)
Консоль, равномерно распределенная нагрузка		@ х = L @ х = L В = +w (L − x) В макс. = +wL @ х = 0 М = ​​-w (L — x) 2 / 2 M макс. = −wL 2 / 2 @ х = 0
Консоль, треугольная распределенная нагрузка		@ х = L @ х = L В макс. = +w 1 л / 2 @ х = 0 М макс. = −w 1 L 2 / 6 @ х = 0
Консоль, Конечный момент		@ х = L @ х = L М = ​​-М 0

Просто поддерживаемые балки

Просто поддерживаемые, промежуточная нагрузка		(0 ≤ х ≤ а) Для a ≥ b: @ (0 ≤ х ≤ а) @ х = 0 @ х = L В 1 = +Fb / L (0 ≤ х ≤ а) В 2 = −Fa / L (а ≤ х ≤ L) M max = +Fab / L @ х = а
Простая опора, центральная нагрузка		(0 ≤ х ≤ L/2) @ х = L/2 (0 ≤ х ≤ L/2) @ х = 0 @ х = L В 1 = +F / 2 (0 ≤ х ≤ L/2) В 2 = −F / 2 (L/2 ≤ x ≤ L) M макс. = FL / 4 @ х = L/2
Просто поддерживаемый, 2 нагрузки на равном расстоянии от опор		(0 ≤ х ≤ а) ( а ≤ х ≤ L — а ) @ х = L/2 (0 ≤ х ≤ а) ( а ≤ х ≤ L — а ) @ х = 0 @ х = L В 1 = +F (0 ≤ х ≤ а) В 2 = −F ( L — а ≤ x ≤ L ) M макс. = Fa ( а ≤ х ≤ L — а )
Простая опора, равномерная распределенная нагрузка		@ х = L/2 @ х = 0 @ х = L В = w (L/2 − x) В 1 = +wL / 2 @ х = 0 В 2 = −wL / 2 @ х = L M макс. = ширина 2 / 8 @ х = L/2
Простая опора, момент на каждой опоре		@ х = L/2 @ х = 0 @ х = L М = ​​М 0
Простая опора, момент в одну опору		@ x = L (1 − √3/3) @ х = 0 @ х = L В = −М 0 / л М макс. = М 0 @ х = 0
Простая опора, центральный момент		(0 ≤ х ≤ L/2) (0 ≤ х ≤ L/2) @ х = 0 @ х = L В = +M 0 / Л М = ​​М 0 х/л (0 ≤ х ≤ L/2) М макс. = М 0 / 2 @ х = L/2

Фиксированные-Фиксированные балки

Фиксированные-Фиксированные, центральная нагрузка		(0 ≤ х ≤ L/2) @ х = L/2 В 1 = +F / 2 (0 ≤ х ≤ L/2) В 2 = −F / 2 (L/2 ≤ x ≤ L) М = ​​F (4x — L) / 8 (0 ≤ х ≤ L/2) М 1 = М 3 = −FL / 8 @ х = 0 и х = L M 2 = +FL / 8 @ х = L/2
Фиксированная-фиксированная, равномерная распределенная нагрузка		@ х = L/2 В = w (L/2 − x) В 1 = +wL / 2 @ х = 0 В 2 = −wL / 2 @ х = L М = ​​w (6Lx — 6x 2 — L 2 ) / 12 M 1 = M 3 = −wL 2 / 12 @ х = 0 и х = L М 2 = ШЛ 2 / 24 @ х = L/2

---

Ознакомьтесь с нашим калькулятором луча, основанным на методологии, описанной здесь.