Прогиб балки: Расчет балки на прогиб и прочность

Прогиб балки | Полный обзор и важные отношения —

Содержание: Отклонение луча
  • Определение кривой прогиба
  • Определение угла отклонения
  • Определение отклонения
  • Граничные условия прогиба балки
  • Взаимосвязь между силами нагрузки, поперечной силой, изгибающим моментом, наклоном и прогибом
  • Уравнения и соотношения изгиба балки
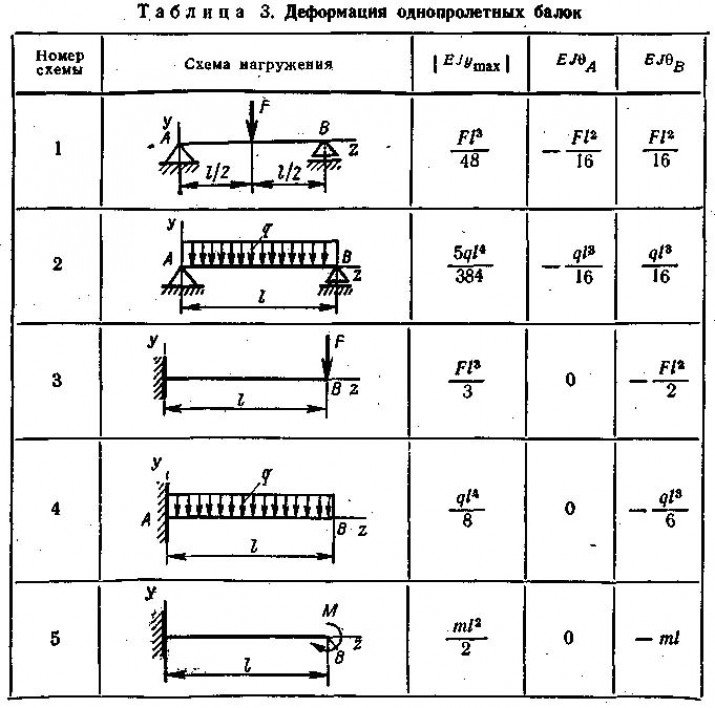
  • Таблица прогиба балки и формулы для стандартных случаев нагружения
  • Отклонение и наклон балки с примерами Случай I: выступающая балка
  • Случай II: определение максимального прогиба балки без опоры с точечной нагрузкой в ​​центре.
  • Случай III: определение максимального прогиба балки с простой опорой при сосредоточенной точечной нагрузке на расстоянии «а» от опоры А.
  • Метод двойной интеграции
  • Процедура метода двойного интегрирования
  • Метод двойного интегрирования для нахождения прогиба балки на примере консольная балка с равномерно распределенной нагрузкой
  • Метод двойного интегрирования для треугольной нагрузки

In инженерия, отклонение — степень смещения элемента конструкции под действием нагрузки (из-за его деформации). Это может относиться к углу или расстоянию. Расстояние прогиба элемента под нагрузкой можно рассчитать путем интегрирования функции, которая математически описывает наклон отклоненной формы элемента под этой нагрузкой. Существуют стандартные формулы для прогиба общих конфигураций балок и загружений в отдельных местах. В противном случае используются такие методы, как виртуальная работа, прямая интеграция, метод Кастильяно, метод Маколея или метод прямой жесткости.

Кривая отклонения

Когда балки нагружены поперечными или продольными нагрузками, начальная прямая продольная ось деформируется в кривую, известную как упругая кривая балки или кривая прогиба. Кривая прогиба — это деформированная ось выбранной балки.

Угол отклонения

Наклон можно определить как угол между продольной осью балки и касательной, построенной к кривой деформации балки в любом желаемом месте. Это угол поворота нейтральной оси луча. Измеряется в радианах.

прогиб

Отклонение — это поступление или смещение любой точки на оси балки, измеренное в направлении y от начальной прямой продольной оси до точки на кривой прогиба балки. Измеряется в миллиметрах. Прогиб представляет собой отклонение прямой продольной оси из-за поперечной нагрузки. Напротив, изгиб балки представляет собой отклонение начальной прямой продольной оси из-за осевой сжимающей нагрузки. Обычно он представлен как ‘у»

Если балка изгибается по дуге окружности, это называется изгибом по окружности; в противном случае это называется некруглым изгибом. Предположим, что на призматическую балку действует переменный изгибающий момент. В этом случае это приводит к изгибу некруглого типа, а если он подвергается постоянному изгибающему моменту, приводит к круговому изгибу балки.

Граничные условия прогиба балки
  1. y равен нулю на опоре штифта или ролика.
  2. y равен нулю на встроенной или консольной опоре.
  3. Предположим, что изгибающий момент и жесткость на изгиб являются разрывными функциями x. В этом случае невозможно написать одно дифференциальное уравнение для всей балки; уравнения кривой для двух соседних сегментов должны удовлетворять данным двум условиям на стыке сегментов:
  • 1. 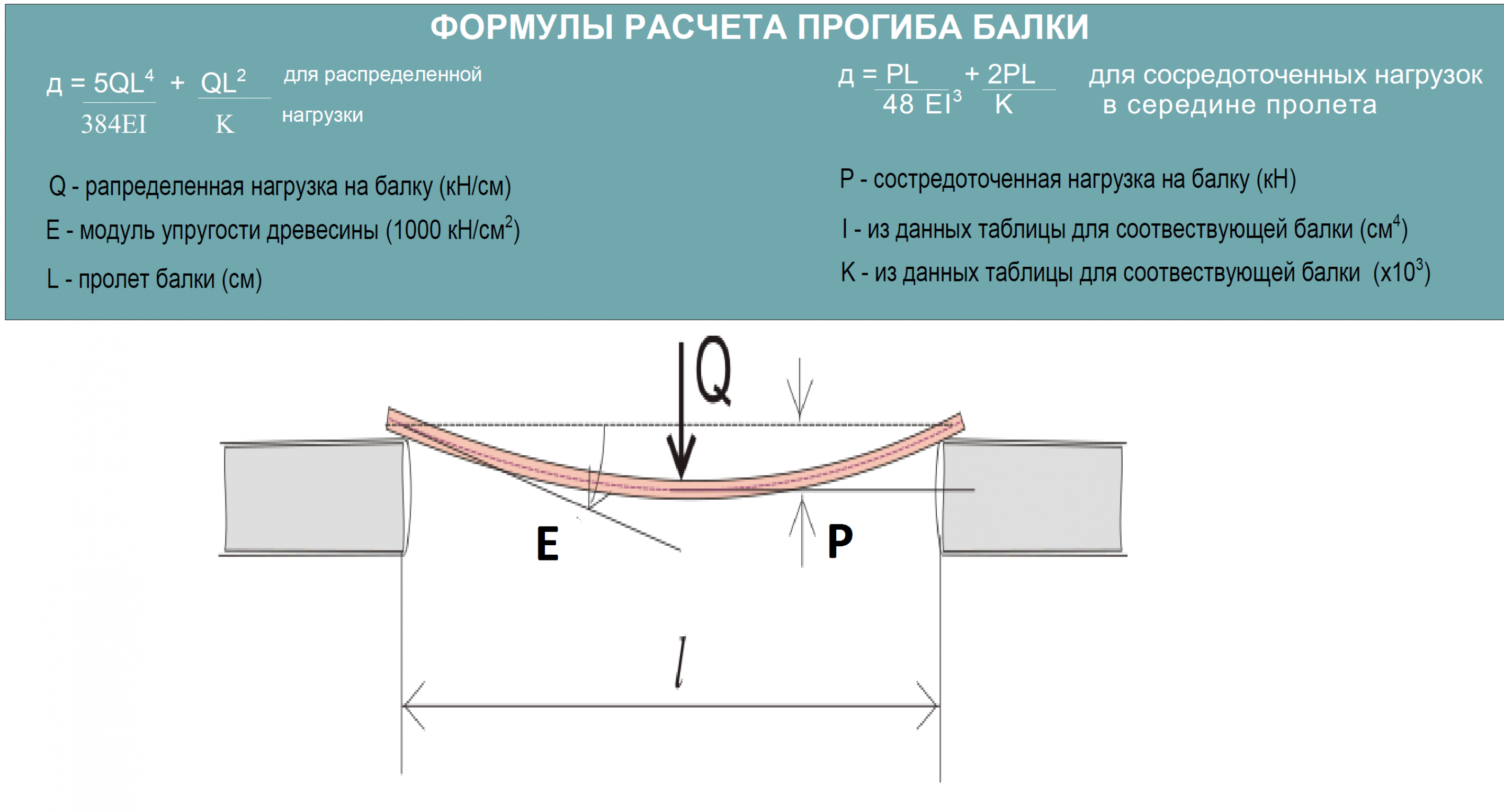4}

    Таблица прогиба балки и формулы для стандартных случаев нагружения:
    • Максимальный наклон и прогиб консольной балки происходит на свободном конце балки, в то время как на зажатом конце консольной балки не наблюдается наклона или прогиба.
    •  Для балки без опоры с симметричными условиями нагружения максимальный прогиб может быть найден в середине пролета. Максимальный уклон наблюдается у опор балки. Максимальный прогиб возникает при нулевом уклоне.
    https://www.pinterest.it/pin/711076228644344940/Наклон и прогиб для балки с простой опорой при различных условиях нагрузки

    Прогиб и наклон балки с примерами

    Случай I: Свисающая балка

    Рассмотрим выступающую стальную балку, несущую сосредоточенную нагрузку P = 50 кН на конце C.

    Для выступающей балки: (a) определить наклон и максимальное отклонение, (b) оценить наклон на расстоянии 7 м от точки A и максимальное отклонение по заданным данным. {- 3} \; m = -8.93 \; мм

    Метод двойной интеграции

    Если жесткость на изгиб EI постоянна, а момент является функцией расстояния x, интегрирование EI (d2 y) / (dx2 ) = M даст наклон

    EI \ frac {dy} {dx} = \ int M dx + C_1
    EIy = \ int \ int Mdxdx + C_1x + C_2

    где С1 и C2 являются константами. Они определяются с помощью граничных условий или других условий на балке. Вышеприведенное уравнение дает отклонение y как функцию от x; это называется уравнением кривой упругости или деформации.

    Вышеупомянутый метод анализа прогиба и наклона балки известен как метод двойного интегрирования для расчета прогибов балки. Если изгибающий момент и жесткость на изгиб являются непрерывными функциями x, одно дифференциальное уравнение может быть записано для всей балки. Для статически определенной балки существует две опорные реакции; каждая из них накладывает определенный набор ограничений на наклон упругой кривой. Эти ограничения называются граничными условиями и используются для определения двух постоянных интегрирования.

    Граничные условия метода двойного интегрирования
    1. y равен нулю на опоре штифта или ролика.
    2. y равен нулю на встроенной или консольной опоре.
    3. Предположим, что изгибающий момент и жесткость на изгиб являются разрывными функциями x. В этом случае невозможно написать одно дифференциальное уравнение для всей балки; уравнения кривой для двух соседних сегментов должны удовлетворять данным двум условиям на стыке сегментов:
    • 1. y для левой части должен быть равен y для правой части.
    • 2. Уклон левого участка должен быть равен уклону правого участка.

    Процедура метода двойного интегрирования
    • Нарисуйте упругую кривую балки и примите во внимание все необходимые граничные условия, такие как y равен нулю на опоре пальца или ролика и y равен нулю на встроенной или консольной опоре.
    • Определите изгибающий момент M на произвольном расстоянии x от опоры методом сечений. Используйте соответствующие правила изгибающего момента при нахождении момента М. для разрывного момента, уравнения кривой для двух соседних сегментов должны удовлетворять данным двум условиям на стыке между сегментами: 1. y для левой части должно быть равно y для правой секции. 2. Уклон левого участка должен быть равен уклону правого участка.
    • Проинтегрируйте уравнение дважды, чтобы получить наклон и прогиб, и не забудьте найти постоянное интегрирование для каждого сечения с использованием граничных условий.

    Примеры метода двойного интегрирования для определения прогиба балки

    Рассмотрим консольную балку длиной L, показанную на рисунке ниже, с равномерно распределенной нагрузкой. В консольной балке один конец зафиксирован, а другой конец может свободно двигаться. Мы выведем уравнение для наклона и изгибающего момента для этой балки, используя метод двойного интегрирования. 4}{120}

    у = -0.01758 \; м

    Чтобы узнать о прочности материала (нажмите здесь.)и метод площади момента Открыть.

    4.3 Определение прогиба балки

    Прогиб клеефанерной балки определяем согласно п.4.33 по формуле 50 [1].

    Прогиб балки без учета деформаций сдвига:

    здесь

    По табл.3 прил.4 [1] определяем:

    Полный прогиб балки

    Относительный прогиб балки

    где — предельный прогиб определенный методом линейной интерполяции по табл.19 [2].

    Коэффициент собственного веса клеефанерной балки:

    4 Двускатная клеедощатая армированная балка

    4.1 Сбор нагрузок

    Нагрузка, передаваемая на балку от панелей покрытия (см. табл. 1):

    нормативная ;

    расчетная .

    Определяем собственный вес балки в зависимости от нормативного веса кровли и снега:

    где — коэффициент собственного веса для однопролетных дощатоклееных балок прямоугольного сечения.

    Расчетная нагрузка от балки

    Отношение нормативного собственного веса покрытия к весу снегового покрова:

    В соответствии с п. 5.7 [2] принимаем коэффициент надежности по снеговой нагрузке .

    Расчетная снеговая нагрузка на 1м2 покрытия:

    .

    Нормативная нагрузка на 1м.п. балки:

    постоянная

    где — шаг балок

    временная

    суммарная

    Расчетная нагрузка на 1м.п. балки:

    постоянная

    временная

    суммарная

    Рис.

    6 Расчетная схема клеедощатой армированной балки

    4.2 Определение размеров балки

    Пролет балки , уклон верхнего пояса балки равен .

    Для изготовления балки используется древесина сосны 2-го сорта. Для армирования балки используется арматура периодического профиля класса S400 по СТБ 1704-2006.

    Для изготовления балки используем доски шириной 150мм и толщиной 40мм. После фрезерования толщина досок составит 40-7=33мм. Ширина балки после фрезерования заготовочных блоков по пласти будет 150-10=140мм. Высоту балки в середине пролета определяем из условия .

    С учетом принятой толщины досок после фрезерования высоту сечения балки принимаем . Армирование балки принимаем одиночное в растянутой зоне с .

    Рис.7 Геометрическая схема балки

    Высота балки на опоре

    Расчетный пролет балки .

    Расстояние от опоры балки до расчетного сечения:

    .

    Высота балки в расчетном сечении:

    .

    4.3 Геометрические характеристики приведенного сечения

    Площадь приведенного сечения

    здесь — коэффициент приведения стальной арматуры к древесине.

    Определяем расстояние до центра тяжести приведенного сечения:

    Приведенный к древесине момент инерции армированной балки:

    Приведенный к древесине момент сопротивления сечения:

    Рис.8 Поперечное сечение армированной балки в расчетном сечении

    4.4 Проверка прочности балки в расчетном сечении

    Расчетное сопротивление древесины сосны 2 сорта изгибу с введением коэффициентов и :

    Определяем изгибающие моменты и поперечное усилие в балке:

    момент в расчетном сечении

    максимальный момент в середине пролета балки

    поперечное усилие на опоре балки

    Нормальные напряжения в расчетном сечении

    следовательно, прочность балки на изгиб обеспечена.

    Вычисляем площадь арматуры .

    Принимаем два стержня S400 , площадью .

    О пределяем геометрические характеристики сечения на опоре балки

    ;

    ;

    ;

    Рис.9 Поперечное сечение армированной балки на опоре

    Касательные напряжения на опоре:

    Определяем геометрические характеристики сечения в середине балки:

    ;

    Проверяем принятое сечение на устойчивость плоской формы деформирования.

    Балка из плоскости изгиба закреплена распорками с шагом 3м связанными со связевыми фермами.

    Определяем необходимые коэффициенты:

    принимаем

    По табл. 2 прил. 4 [1] определяем коэффициент

    где

    Проверяем устойчивость плоской формы деформирования по формуле:

    Рис.10 Поперечное сечение армированной балки в середине пролета

    При ширине площадки опирания определяем требуемую длину площадки из условия смятия древесины:

    Прогиб балки — Гражданское строительство

    class=»eliadunit»>

    Во многих случаях конструкции конструкций и машин элементы должны сопротивляться силе, приложенной сбоку или поперек их осей. Такие элементы называются балочными. Основными элементами, поддерживающими перекрытия зданий, являются балки, подобно тому, как ось автомобиля является балкой. Многие валы действуют одновременно и как торсионы, и как балки. Пока можно сказать, что балка является неотъемлемой частью конструкции.

    Прогиб балки

    Прогиб балки означает состояние деформации балки от ее первоначальной формы под действием силы, нагрузки или веса.

    Одним из наиболее важных применений прогиба балки является получение уравнений, с помощью которых мы можем определить точные значения прогибов балки во многих практических случаях. Прогибы также используются при расчете статически неопределимых балок.

    Методы определения прогиба балки

    Существует несколько методов определения прогиба балки. Принцип один и тот же, но отличается техникой и непосредственной целью.

    • Метод прямого интегрирования
    • Метод момента площади
    • Метод сопряженных пучков
    • Метод суперпозиции

    Метод прямого интегрирования

    Прогибы балок от изгиба определяются по деформации, происходящей вдоль пролета. Это основано на гипотезе, что при изгибе плоские сечения балки остаются ровными. Пока будем считать, что изгиб происходит только около одной из главных осей поперечного сечения. Краевой вид нейтральной поверхности отклоненной балки называется упругой кривой балки. Дифференциальное уравнение кривой упругости балки: 9{4}} = \текст{q}\влево(х\вправо)\]

    Здесь q(x) — функция нагрузки. Выбор уравнения, которое мы будем использовать для определения v, зависит от того, насколько легко можно сформулировать выражение для момента, сдвига или нагрузки.

    Некоторые граничные условия:

    1. Зажимная или фиксированная опора:
    2. Роликовая или штифтовая опора:
      В данном случае. конец может свободно вращаться, поэтому момент равен нулю.
    3. Свободный конец:
    4. Управляемая поддержка:
    class=»eliadunit»>

    Проблемы с отклонением при разделении балок в целях моделирования. Сравнение прогибов разделенных и неразделенных балок

    1. Домашняя страница
    2. Tekla Structural Designer
    3. Проблемы прогиба при разделении балок в целях моделирования. Сравнение прогибов разъемных и нераздельных балок

    Tekla Structural Designer

    Не зависит от версии

    Tekla Structural Designer

    отклонение

    Разделенная балка

    Раздельная балка

    Моделирование

    Среда

    Не зависит от среды

    В В этой статье мы рассмотрим проблемы отклонения, когда балки разделены для целей моделирования, путем сравнение отклонений между разделенными и неразделенными балками.

    Подход к моделированию

    Две балки смоделированы по-разному.

    1. Верхняя балка, физическая балка с пролетом 18 м — опоры на концах, как и ожидалось.
    2. Нижняя балка, разделенная на три балки (каждая балка соединена с полностью фиксированной опорой, чтобы действовать как моментное соединение между балками). Обратите внимание, что это также имеет значение для проектирования, поскольку отдельные балки проверяются на LTB и т. д., а эффективные длины и профили моментов будут отличаться.

    Изображение


    Просмотр решателя

    Просмотрев представление «Сцена решения»

    Синие кружки обозначают опорные места для размещенных балок.

    Другие узлы — это узлы pdelta в середине пролета в центре каждого луча (необходимы для отображения форм колебаний и т. д.) К обоим результатам глобального отклонения

     

    Image


    применяется одна и та же нагрузка UDL.

    Программное обеспечение в представлении 3D-результатов покажет глобальные отклонения в узловых точках, где встречаются опоры/балки/раскосы/узлы. Следовательно, вы видите результаты в местах, выделенных синим цветом, отмеченных выше.

     

    Изображение


    Результаты локального отклонения. (Щелкните правой кнопкой мыши по балке > Открыть представление анализа нагрузки)

    Просмотр локальных прогибов отдельных стержней показывает локальные результаты для отдельных стержней

    Опорные концы балок считаются имеющими нулевое смещение, поскольку вы смотрите на локальное смещение между опорными точками.

    Это означает, что одинарная балка с пролетом 18 м покажет ожидаемые результаты.

      

    Изображение

    Однако лучи, разделенные на отдельные лучи, не будут такими, как ожидает Инженер.

    1-й луч (Л>П)

      

    Изображение

    2-й луч (Л>П)

      

    Изображение

    3-й луч (Л>П) 90 003

      

    Изображение


    Важен метод моделирования

    Из вышеизложенного ясно, что вы должны моделировать балки как физические балки с фактической требуемой полной длиной пролета, где это возможно.

    Если вы создаете модель как отдельные балки, то вы должны игнорировать проверки местных прогибов, выполняемые программой, и проверять локальные прогибы вручную вне программы. Вы можете взять глобальные значения отклонения из представления 3D-результатов, чтобы выполнить простую проверку предела.

    Местные прогибы могут быть четко получены из представления Анализ нагрузки от одиночной балки пролета 18 м, а результаты получены в любом месте по ее длине с помощью красного ползунка и просмотра результатов в окне свойств.

      

    Изображение

    Однако из представления 3D-результатов можно получить результаты только в узловых точках, как было указано выше.

    Если вы хотите получить глобальные 3D-результаты в «других» позициях, необходимо создать узел.

    Вы можете создать раскос, элемент анализа или что-то подобное, чтобы соединиться с элементом для создания узла. Вы также можете предоставить номинальную консоль или колонну, что-то для создания узла.