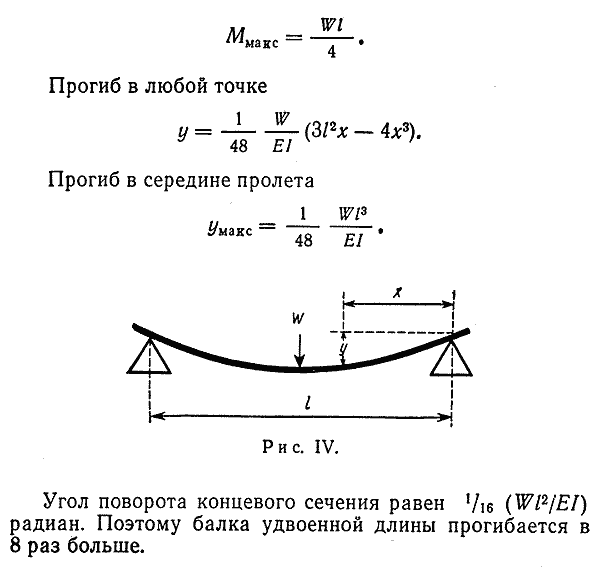
2.4.1. Приближенная формула определения прогиба балки при продольно-поперечном изгибе

Упругую линию балки, подверженную одновременному действию продольной и поперечной нагрузки, представим приближенно в виде синусоиды:

а — максимальный прогиб,

n — число полуволн упругой линии балки,

l — длина балки.

Подставим это выражение в дифференциальное уравнение продольно-поперечного изгиба балки:

Интегрируя уравнение, получаем:

Заметим, что:

, а для поперечного изгиба:

, где

y_п(x) — прогиб балки только от поперечных нагрузок.

С учетом приведенных соотношений дифференциальное уравнение продольно‑поперечного изгиба балки принимает вид:

, откуда

Введем обозначение:

, тогда:

Пример 6.3

Балка, лежащая на двух шарнирных опорах, одна из которых подвижная, а другая неподвижная, сжимается силой S, приложенной с эксцентриситетом е (рис.

6.9). Изгибная жесткость балки EI_z. Определить прогиб в середине балки.

Решение.

1. Определим энергетическим методом прогиб балки в середине пролета при действии только поперечной нагрузки. Для этого рассмотрим нагружение балки изгибающим моментом Se, который возникает в результате действия продольной силы S, приложенной с эксцентриситетом e (рис. 6.10а). Построим эпюру изгибающих моментов (рис. 6.10б).

Рисунок 6.10

Приложим в середине пролета единичное усилие (рис. 6.10в) и построим эпюру изгибающих моментов от единичной нагрузки (рис. 6.10г).

Перемножим полученные эпюры по правилу Верещагина, получим значение прогиба в середине пролета от действия поперечной нагрузки y_п(l/2):

2. Определим критическую нагрузку по формуле Эйлера при n = 1.

3. Прогиб в середине балки при одновременном действии продольной и поперечной нагрузок.

2.4.2. Дифференциальное уравнение изгибающих моментов при продольно‑поперечном изгибе балки

Как показано выше, изгибающий момент в продольном сечении балки при продольно-поперечном изгибе:

М_пп(х) = М_п(х) – S y(x)

Дифференцируя это выражение дважды и перенося слагаемое с y_пп(х) в левую часть, получим:

(1)

Учтем, что уравнение упругой линии при продольно‑поперечном изгибе:

,

а также, что для поперечного изгиба выполняются дифференциальные зависимости:

, тогда уравнение (1) принимает вид:

, где

Полученное уравнение является дифференциальным уравнением для изгибающих моментов при продольно‑поперечном изгибе. Интегрируя уравнение, получим распределение изгибающих моментов непосредственно, минуя вычисление прогибов.

2.5. Энергетический метод определения критической нагрузки

Суть метода заключается в составлении баланса потенциальной энергии и работы внешней нагрузки для криволинейной формы равновесия стержня.

Рассмотрим гибкий стержень, который нагружен осевой силой Р_кр и выведен поперечной силой из прямолинейного состояния (рис. 6.11). Если после снятия поперечной силы стержень сохранит устойчивую форму, то будем считать, что осевая нагрузка равна критической величине Р_кр.

Рисунок 6.11

Для деформированного состояния составим баланс энергии:

U = A, где:

U — потенциальная энергия стержня;

А — работа внешней нагрузки Р_кр.

Работа внешней нагрузки:

A=P_кр×Δ, где: (1)

Из рассмотрения рисунка можно видеть, что:

, откуда

Следовательно:

Выражение (1) для работы внешней нагрузки примет вид:

Потенциальная энергия стержня при его изгибе:

Уравнение баланса энергии принимает вид:

Учитывая, что при изгибе , окончательно получим, что критическая нагрузка равна:

(2)

Пример 6. 4

Определить критическую нагрузку для шарнирно закрепленного гибкого стержня длиной l.

Решение.

Зададимся уравнением упругой линии деформированного стержня в виде синусоиды:

Вычислим производные:

Подставим выражения производных в соотношение для определения критической нагрузки (2):

Полученная формула совпадает с формулой Эйлера.

Рассчет прогиба концевых балок мостового крана, способы и формулы

Рассчет прогиба концевых балок мостового крана, способы и формулы

Балка – элемент, представляющий жёсткий стержень, который нагружается вертикально действующими силами. Главный пролет крановых металлоконструкций имеет вид моста – конструктивного элемента, служащим для передвижения грузоподъемной тележки. В данном материале вы узнаете, как рассчитать прогиб концевых балок мостового крана.

Что такое прогиб? Это смещение поперечного сечения балки в вертикальном положении под воздействием оказываемой нагрузки. Узнать данную величину можно из следующих характеристик: длины и размеров поперечника балочной металлоконструкции.

Помимо перемещений в вертикальной плоскости, возможен поворот балки относительно начальной плоскости. Данная величина рассчитывается с помощью метода начальных параметров.

Вычисление пролетного прогиба проводится при оценке двутавра на жесткость. На основании полученных значений подбирается оптимальный размер сечения несущего моста кран-балки.

В настоящий момент выполнить расчетные вычисления прогиба можно несколькими способами:

• Воспользовавшись готовыми онлайн-калькуляторами (в том числе и на нашем сайте).
• Используя справочные материалы, определить искомое значение для данного типа и размера балок.
• Рассчитать величину прогиба с помощью формул.

Наиболее удобным и практичным способом определения прогиба считается метод начальных параметров, благодаря которому можно записать формулу вычисления искомого значения.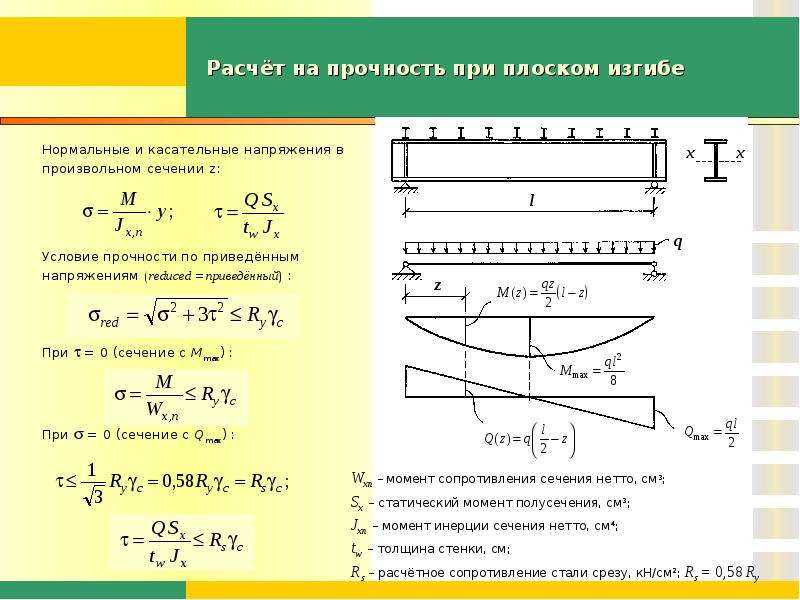

Под начальными параметрами понимают:

• Прогибы на опорных подкрановых узлах равны 0.
• В жёстких заделках искомые значения также равняются 0.

Для проведения расчета требуется знать все внешние нагрузки, оказываемые на главный пролет, и реакции опор. Задаются уравнения равновесия и система координат, на основании которой находятся недостающие значения. При необходимости для удобства подсчета вводятся дополнительные нагрузки. Общая жесткость балки складывается из жёсткости отдельных опор конструкции.

Для получения решения необходимо иметь следующие значения:

• Момент инерции.
• Геометрические характеристики.
• Вычисление максимальной нагрузки.

Подробно вычислительные работы для определения балочного прогиба изучаются в дисциплине «Сопротивление материалов».

Вернуться к списку статей

Наши услуги

Подкрановые пути

Модернизация и реконструкция крана

Радиоуправление краном

Ремонт кранового оборудования

Монтаж кранового оборудования

Техническое обслуживание грузоподъемных кранов

Обследование грузоподъемных кранов

Ремонт крановых колес

Мехобработка деталей

Наши товары

Крановое оборудование

Кран мостовой

Литейные производства

Изготовление металлоконструкций

Оборудование для аэропортов

Сергеев Евгений Иванович

Коммерческий директор ООО Машиностроительно-Литейное Объединение Буревестник

О компании

Мы рады приветствовать вас на интерактивной площадке нашего завода и благодарны за внимание к нашему предприятию и его деятельности в бизнесе.

Наш завод производит широкий ассортимент машиностроительной и металлургической продукции для различных отраслей отечественной экономики и многих зарубежных стран.

Высокий технический уровень, качество и надежность изделий с маркой нашего предприятия получили широкую известность и признание, создали заводу высокий авторитет в промышленном мире.

Читать подробнее о компании

Формула отклонения луча

| Напряжения и прогибы балок

Прогиб – это степень, в которой конкретный элемент конструкции может сместиться под действием значительной нагрузки. Его можно назвать углом или расстоянием. Расстояние отклонения стержня под нагрузкой напрямую связано с наклоном изогнутой формы стержня под этой нагрузкой. Его можно рассчитать путем интегрирования функции, описывающей наклон стержня под этой нагрузкой.

Балка — это длинная часть тела, способная удерживать нагрузку за счет сопротивления изгибу. Отклонение балки в определенном направлении при приложении к ней силы называется отклонением балки.

В зависимости от типа отклонения существует множество формул отклонения балки, приведенных ниже,

w = равномерная нагрузка (единицы силы/длины)

В = сдвиг

I = момент инерции

E = модуль упругости

d = отклонение

М = момент

  ШПИЛЬНАЯ БАЛКА С РАВНОМЕРНОЙ НАГРУЗКОЙ

В = w (L/2 – x)

М = wx/2 (L – x)

δ = wx/24EI (L ³ – 2 Lx ² + х ³ )

НЕПОДВИЖНАЯ БАЛКА С РАВНОМЕРНОЙ НАГРУЗКОЙ

В = Вт (L/2 – x)

M = Ш/12 (6Lx – L ² – 6x ² )

δ = wx ² /24EI (L – x) ²

БАЛКА НА ШТИФТАХ С РАВНОМЕРНОЙ НАГРУЗКОЙ

В = w(3L/8 – х)

М = ш х (3L/8 – х/2)

δ = wx/48EI (L ³ – 3Lx ² + 2x ³ )

СВОБОДНАЯ БАЛКА С РАВНОМЕРНОЙ НАГРУЗКОЙ

В = – wx

М = – wx ² /2

δ = с 24EI (x ⁴ – 4L ³ x + 3L ⁴ )

ШПИЛЬНАЯ БАЛКА С ТОЧЕЧНОЙ НАГРУЗКОЙ

В = Pb/L – P (x-a) ⁰

M = Pbx/L – P (x-a) ¹

δ = P/6EI [bx3/L – abx/L (2L – a) – (x – a) ³ ]

НЕПОДВИЖНАЯ БАЛКА С ТОЧЕЧНОЙ НАГРУЗКОЙ

В = Pb ² /L ³ (Л + 2а) – Р(х – а) ⁰

M = −Pab ² /L ² + Pb ² x/L3 (L + 2a) – P (x – a) ¹

δ = P/6EI [b ² x ³ /L ³ (L + 2a) – 3ab2x2/L2 – (x – a) ³ ]

БАЛКА НА ШТИФТАХ С ТОЧЕЧНОЙ НАГРУЗКОЙ

V = Pb ² /2L ³ (2L + a) – P(x – a) ⁰

M = Pb ² x/2L ³ (2L + a) – P (x – a) ¹

δ = P/6EI[b ² x ³ /2L ³ (2L + a) – 3ab ² x/2L – (x – a) ³ ]

СВОБОДНАЯ БАЛКА С ТОЧЕЧНОЙ НАГРУЗКОЙ

В = -Р(х – а) ⁰

М = -Р(х – а) ¹

δ = P/6EI [3b ² x – 2L ³ – a ³ – (x – a) ³ ]

Пример 1

Шарнирно-штифтовая балка длиной 50 см находится под равномерным грузом в 60 г, где х равен 5 см. Определить сдвиг.

Решение:

Данные параметры

Длина L = 50 см

Равномерная загрузка w = 60 г

Рабочий объем x = 5 см

Сдвиг определяется как V = w (L/2 – x)

= 0,06 кг (0,5/2 м – 0,05 м)

= 0,06 кг (0,25 – 0,05) м

= 0,012 кгм.

Вопрос 2: n неподвижно-неподвижная балка длиной 30 см подвергается равномерной нагрузке в 200 г при x = 20 см. Определите момент.

Решение:

Данные параметры

Длина L = 30 см,

Равномерная загрузка w = 200 г,

Рабочий объем x = 20 см

Момент

В = −wx ² /2

= −0,2 кг×0,2 ² / 2

= 0,004 кг м ² .

Формула прогиба балок с диаграммами для всех условий.

15.05.2021 19. 07.2020 от Вики

, когда есть вертикальное смещение в любой точке нагруженной балки, говорят, что оно равно прогиб балок . Максимальный прогиб балок происходит там, где уклон равен нулю.

Наклон луча определяется как угол между отклоненным лучом и фактическим лучом в той же точке.

Общие и стандартные уравнения для отклонения балок приведены ниже:

, где,
M = изгиб,
E = Модуль Youn .

Продукт E.I известен как жесткость на изгиб .

Существует много типов балок, и для этих различных типов балок или случаев формула не будет одинаковой. Он должен быть изменен в зависимости от случая или типа луча. Теперь давайте рассмотрим следующие случаи.

1. Свободно опертая балка с центральной точечной нагрузкой:

Свободно опертая балка AB длиной l несет точечную нагрузку в центре балки в точке C. Отражение в точке C будет:

2. Проще говоря, нагрузка с эксцентрической точкой:

Проще говоря внецентренная точечная нагрузка в точке C , как показано на рис. Прогиб балки задается следующим образом:

Так как b > a , то максимальное отклонение происходит в CB и на расстоянии от B is given by :

and maximum deflection is given by :

3. Simply Supported Beam With Uniformly Distributed Load :

A simply supported beam AB при равномерно распределенной нагрузке w /единица длины показана на рисунке ,

Максимальный прогиб происходит в средней точке C и определяется как:

4. Свободно поддерживаемая балка с плавно изменяющейся нагрузкой:

Свободно поддерживаемая балка из AB длиной l , несущая плавно изменяющуюся нагрузку от нуля на B до w/единицы длины на 8 A 8 , показано на рисунке ниже,

Максимальное отклонение балки происходит, когда x = 0,519 l и его значение определяется как:

Консольная балка AB длиной l , несущая точечную нагрузку на свободном конце, показана на рис. Прогиб в любом сечении х на расстоянии х от свободного конца определяется как:

Максимальный прогиб происходит на свободном конце (когда х = 0, ) и его значение определяется как

6. Консольная балка с равномерно распределенной нагрузкой:

Консольная балка AB длиной l , несущая равномерно распределенную нагрузку на единицу длины, представлена ​​на рис. Прогиб в любом сечении х на расстоянии х от В определяется выражением

Максимальное отклонение происходит на свободном конце (когда x = 0), и его значение дается

Когда кантилевер частично загружен, как показано на рис., то отклонение в точке C (на расстоянии от неподвижного конца) определяется как: 7. Консольная балка с постепенно меняющейся нагрузкой0255 B на единицу длины A показан на рис.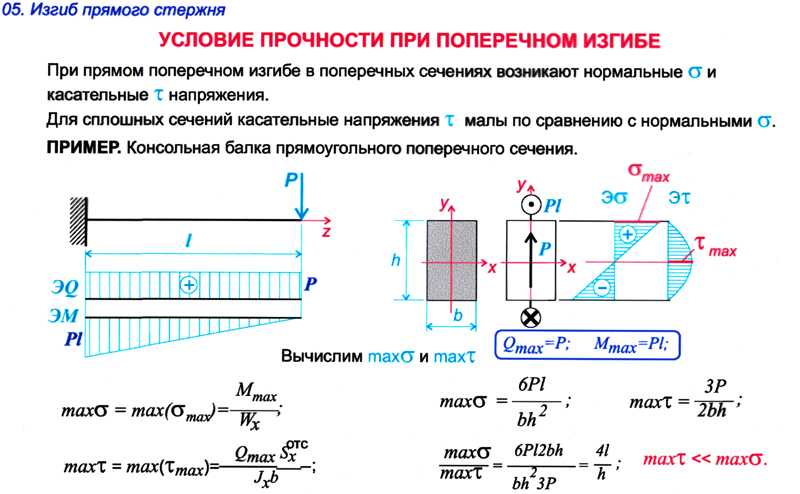 Прогиб в любом сечении X на расстоянии x от B определяется как

Максимальный прогиб происходит на свободном конце (при x = 0) и его значение определяется как

8 Фиксированная балка, несущая центральную точечную нагрузку:

Фиксированная балка AB длиной l , несущая точечную нагрузку в центре балки C , как показано на рис. Максимальное отклонение балки происходит при C , и его значение определяется как

9. Фиксированная балка, несущая внецентренную нагрузку:

нагрузка на C как показано на рис. Прогиб в любом сечении х на расстоянии х от А определяется как

Максимальное расстояние возникает, когда,

Следовательно Максимальное отклонение луча,

и отклонение под нагрузкой при C ,

10.