Продольные силы и их эпюры: Эпюра внутренних продольных сил

Содержание

5.4.9 Построение эпюры продольных сил в заданной раме

Эпюра продольных (нормальных) сил может быть построена способом вырезания узлов по эпюре поперечных сил. Первым вырезают узел, в котором действует не более двух неизвестных усилий.

К вырезанным узлам прикладывают действующие внешние сосредоточенные силы и поперечные силы, взятые со своим знаком из эпюры . Как видно из рис. 5.12, е, положительные поперечные силы вращают элемент вокруг узла по часовой стрелке, а отрицательные — против. Неизвестные продольные силы принимаем положительными при растяжении и направляем их от сечения.

Составим уравнения равновесия для сил, приложенных к двум узлам, показанным на рис. 5.12, е.

Узел 1.

Здесь ,

, т.к. левая и правая опоры шарнирно подвижные (аналогично происходит с подвижной заделкой и свободным концом без продольной силы).

Узел 2.

Проверка: т.к. усилия и действуют в одном и том же стержне, то они должны быть одинаковыми:

погрешность составляет .

Полученные ординаты откладываем перпендикулярно осям соответствующих элементов рамы, ставим знаки. Эпюра изображена на рис. 5.12, в.

5.4.10 Статическая проверка эпюр усилий

Для выполнения статической проверки изобразим раму с заданными нагрузками (см. рис. 5. 12, г). Опорные реакции берем из эпюр и со своими знаками: положительная поворачивает элемент рамы относительно узла по ходу часовой стрелки, отрицательная — против; положительная продольная сила направляется от опоры, отрицательная — к опоре.

Составим суммы проекций всех сил на горизонтальную и вертикальную оси, а также сумму их моментов относительно правой опоры с учетом того, что

(погрешность 0,04%).

Ошибки малы, следовательно, задача решена с достаточной точностью. Наглядное представление об «игре сил» в элементах рамы дает рис. 5.13, где отдельно показаны усилия, приложенные к торцевым сечениям стержней и к узлам. Такое представление позволяет легко убедиться в выполнении условий равновесия отдельных узлов и стержней, а также рамы в целом.

Рис. 5.13

5.4.11 Подбор двутаврового поперечного сечения стержней рамы

Подбор двутаврового поперечного сечения рамы производится из условия прочности на изгиб (предположим, что опорные стержни не теряют устойчивость). Тогда при максимальном изгибающем моменте и допускаемом напряжении , имеем

Выберем для всех стержней рамы симметричное сечение из четырех двутавров № 50 по ГОСТ 8239-89. Максимальный момент сопротивления одного двутавра ; рабочее напряжение

. Условие прочности выполнено.

5.5. Пример II

Рассмотрим симметричную раму, схема которой приведена на рис. 5.14.

Определение числа неизвестных:

Рис. 5.14

5.5.1 Выбор основной системы и лишних неизвестных

На рис. 15.5 приведены три варианта основных систем, полученных с учетом симметрии заданной конструкции, показаны соответствующие лишние неизвестные и построены единичные эпюры , и , а также грузовые эпюры для каждого из вариантов.

Для дальнейшего рассмотрения выбран второй вариант, основной системы (трехшарнирная рама) хотя более экономичным является первый вариант (легче строить и перемножать эпюры). Особенностью этой основной системы является то, что для определения реакций недостаточно трех уравнений равновесия рамы в целом. Дополнительное условие равновесия получается из рассмотрения равновесия отдельно левой и правой отсеченных частей рамы с учетом того, что момент в среднем шарнире

С известен (равен нулю, если в сечении С не приложены сосредоточенные моменты).

Рассмотрим подробнее построение грузовой эпюры для основной системы по выбранному варианту (рис. 5.16). Рама состоит из восьми участков. Так же, как в предыдущем примере, начало каждого участка отмечено на рис. 5.16 цифрой.

Определим опорные реакции из уравнений статики:

а)

б)

Рис. 5.15

в)

г)

Проверка.

Рис. 5.16

Определение внутренних усилий (значения реакций см. выше).

Участок1.

Участок 2. Так как консоль не загружена, то

Участок 3. .

в середине

Участок 4.

Участок 5.

В середине участка

Участок 6.

Участок 7. (т.к. консоль не загружена).

Участок 8.

По этим результатам построена эпюра (см. рис. 5.15, схема 2.5).

Сопромат. Эпюра продольных сил. И напряжений

В прошлой части мы говорили о том, что если мы мысленно разрежем деталь, исходя из сил приложенных к сечению сможем вычислить с какой силой деталь сопротивляется внешним воздействиям. Но любая конструкция – это не одно сечение, а сумма их бесконечного количества. Мы можем мысленно разделить деталь на бесконечно малые участки, для каждого из которых мы можем выяснить силу сопротивления материала. Однако бесконечный набор уравнений неудобно анализировать. Зато можно совместить значения в каждой конкретной точке и получить график, на котором будут видны значения сил сопротивления материала в каждой точке детали. Название используемое для такого графика: эпюра продольных сил. Или поперечных. И сегодня мы научимся их строить.

Эпюра продольных сил и напряжений при воздействии на образец только сил.

Загадка: брусок в две стороны тянут с силой в 1 Н. Какая сила сопротивления должна возникнуть в бруске, чтобы противодействовать внешнему воздействию?

Подсказка: одной стороной брусок закреплён к стене и его тянут с силой 1 Н. Изменилось ли сопротивление материала по сравнению с тем случаем, когда его тянули в разные стороны?

Ответ: и в том и в друг случае сила сопротивления материала была равна 1 Н, так как действие равно противодействию.

Если условный брусок жестко закреплён к стене в невесомом пространстве (т.е. считаем его вес равным нулю), и с одной из сторон его пытаются растянуть (или сжать, не принципиально) с некоторой силой, каждое сечение будет противодействовать деформации ровно с такой же силой.

Соответственно, эпюра продольных сил N по стержню (или, как правильно говорить в сопромате, эпюра) будет выглядеть вот так:

Однако, это ничего нам не говорит о напряжениях возникающих в теле. Для того нам необходимо разделить продольные силы на площадь сечения F и мы получим напряжения, которые возникают в каждой из точек сечения.

Эпюра нормальных напряжений по виду похожа на эпюру продольных сил. Однако «высоту» необходимо будет разделить на площадь поперечного сечения

Аналогичная ситуация справедлива и для поперечных сил. Возьмем брусок. Жестко закрепим его к стене и надавим на него с другого конца:

Тогда в каждом сечении бруска будет возникать сила противодействия равная силе, которую мы приложили.

Эпюра поперечных сил в сечении же будет выглядеть вот так:

При этом рассчитать касательные напряжения уже сложнее. Самый простой пример: распределение нагрузки по невесомому прямоугольному сечению. Тогда касательные напряжения будут равны в каждой точке сечения поперечной силе разделенной на его ширину. В более сложных случаях (в том числе при расчете массивного стержня) для того, чтобы вычислить касательные напряжения, необходимо будет учитывать геометрические характеристики сечения.

Равномерно распределенные нагрузки

Рассмотренный выше пример может показаться нереалистичным: что это за материал, на который не действуют силы гравитации? Ведь расчёт конструкций тем и сложен, что конструкции должны выдерживать некоторый вес и сами каким-то весом обладают.

Дело в том, что вес по материалу распределен равномерно. Т.е. мы не можем просто приложить в центр масс силу тяжести конструкции. Каждое сечение обладает своим весом, а сумма веса всех сечений и даёт в общий вес конструкции.

В таком случае нам гораздо проще разделить вес на длину конструкции и получить нагрузку на единицу длины конструкции.

Логично предположить, что тогда на каждое следующее сечение будет действовать нагрузка большая, нежели на предыдущее. Для поперечных нагрузок (т.е. когда балка закреплена одним концом горизонтально и на неё действует равномерно распределенная сила тяжести) это проще визуализировать:

Для продольных нагрузок равномерно-распределенную нагрузку визуализировать не удастся, однако принцип будет абсолютно таким-же:

Эпюра продольной силы и нормального напряжения под равномерно распределенной нагрузкой

На то сечение, которое мы закрепили на потолке, как не сложно догадаться, действует вся сила тяжести бруска.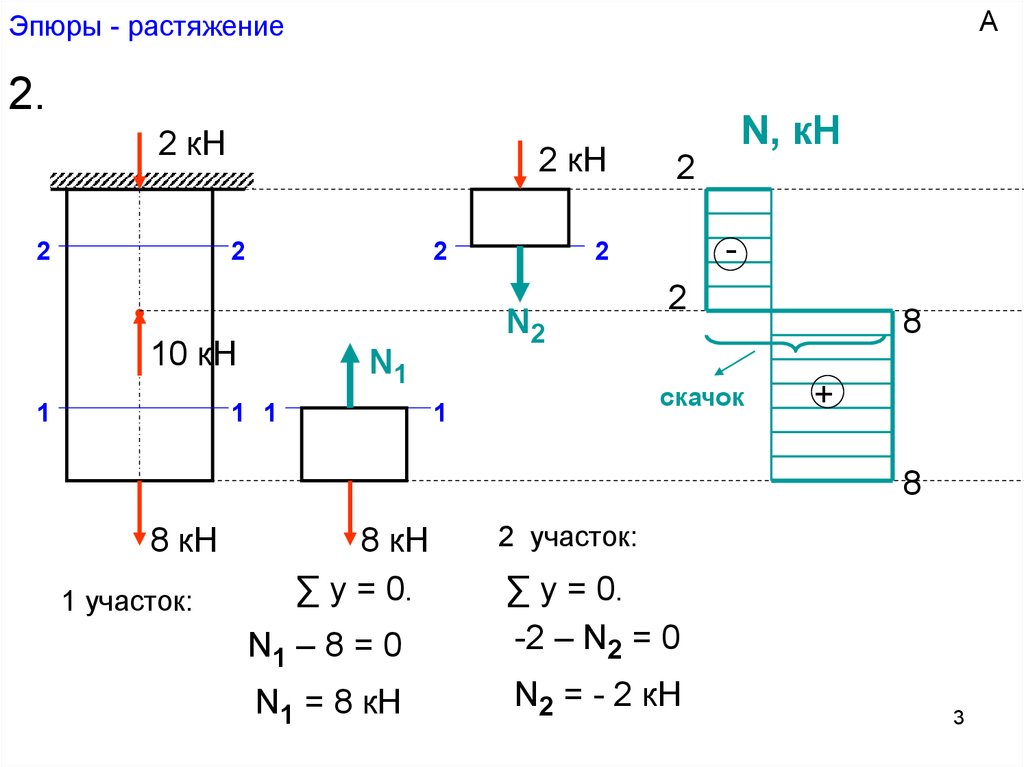 В формуле сила тяжести найдена как произведение площади F на длину стержня l и силу тяжести p(плотность материала) × g(ускорение свободного падения). Интуитивно понятно, что на каждое сечение ниже будет воздействовать вес стержня снизу. Самый простой способ: это вычесть из общего веса стержня вес стержня сверху. Для этого достаточно проинтегрировать удельный вес по расстоянию (dx) до нужного нам сечения.

N_x=Fρgl-∫ρgdx

В данном случае (стержень имеет одинаковые диаметр и плотность) на всей длине, достаточно перемножить dx на Fp.

N_x=Fρgl-∫ρgdx=Fρgl-Fρgx

Т.е. что мы можем заметить: нагрузка – это производная от эпюры продольных (или поперечных) сил. И наоборот, напряжение – первообразная от нагрузки. Это основное, что вы должны понять начиная изучать сопромат.

Эпюра продольных сил в сложных случаях

Существуют ситуации при которых нагрузка распределяется неравномерно. В таком случае нам необходимо знать закон распределения (т.е. формулу, согласно которой по длине распределена нагрузка). Нагрузка на сечение в точке x0+dx будет равна интегралу f(x) по dx. Т.е. необходимо будет найти интеграл от функции определенный от начала конструкции до необходимой нам точки (визуализирую на поперечных нагрузках, так как на продольных продемонстрировать распределенную нагрузку не получится):

Q_y=∫f(x)q_ydx

Если нам необходимо вычислить нагрузку на конструкцию при наличии и распределенной нагрузки и приложенных сил, достаточно просто сложить два этих графика вместе:

Брусок закреплен вертикально, крепится за “потолок”. Он имеет определенный вес, который можно получить перемножив плотность материала ρ, ускорение свободного падения g, площадь сечения F и длину стержня l. К его середине вертикально вниз приложена сила в 2P₁.

X₀-gρFl-2P₁=0

Соответственно, суммарно на “начало” стержня воздействует сумма приложенных сил и веса бруска:

X₀=gρFl+2P₁

Соответственно до середины бруска на каждую единицу длины напряжение ослабевает на вес отсеченного сверху бруска:

X_1(-)=X₀-gρFdX

В середине бруска внутреннее усилие ослабевает на 2P_1:

X₁₍₊₎=X₀-gρFdX-2P₁

Примечание: X_1(-) Продольная сила в точке перед местом приложения силы в точке X₁, X₁₍₊₎ продольная сила после приложения силы в точке X₁. Т.е. геометрически точка X_1(-) находится на пренебрежительно малую величину раньше приложенной силы.

После этого усилия в стержне продолжают ослабевать на размер веса отсеченного бруска:

X₂=X₁₍₊₎-gρFdX

Аналогично считаются и поперечные силы.

В следующих сериях…

Теперь мы умеем считать и визуализировать продольные и поперечные силы и нормальные и касательные напряжения. Однако это ничего не говорит о том, насколько деформируется материал, разрушится или сохранит свою прочность под нагрузкой. Об этом мы поговорим в следующей статье.

Над статьей работали:

Автор: К.А. Овчинников
Редактор: Д.А. Сабуров
Эксперты: Д.А. Сабуров, М.О. Ершов

Условия использования: свободное некоммерческое использование при условии указания автора и ссылки на первоисточник (статьи на действующем сайте интернет-журнала «Стройка Века»).

Для коммерческого использования — обращаться на почту:
buildxxvek@gmail. com

Лекции по сопротивлению материалов в СПбПУ им. Петра Великого
Лекции по сопротивлению материалов в БГТУ «ВОЕНМЕХ» им. Устинова

5 319

Что такое бесплатные диаграммы тела?

Одно из самых полезных вспомогательных средств для решения задачи статики — свободное тело диаграмма (ФБД). Диаграмма свободного тела представляет собой графическую, дематериализованную, символическую представление тела (структуры, элемента или сегмента элемента) в котором все соединительные «кусочки» были удалены. FBD – это удобный метод моделирования конструкции, структурного элемента или сегмента что находится под контролем. Это способ концептуализации структуры, и его составные элементы, чтобы можно было инициализировать анализ.

Все физические атрибуты структуры удалены. Это не завершается случайным образом, а скорее особым методом. Тело или его часть, изображается одной простой линией. Каждое соединение представлено исключительно соединением с различными свойствами или заменяется набором сил и моменты, которые будут представлять действие в этой связи. Внутренний силы, которые были бы обнаружены в узле (соединении или соединении), могут быть заменены репрезентативными внешними силами, где эта «часть» соединяется соединится с другим членом FBD. Все нагрузки представлены как силовые системы.

Изображение справа является ссылкой на фильм, иллюстрирующий путь в которой разрешена каждая из нагрузок на конструкцию (в данном случае на скамейку). Он также иллюстрирует, как каждая физическая нагрузка, воздействующая на должна быть представлена структура. Это означает, что все нагрузки заменены по векторам. Даже опоры заменены одиночными векторами.

Обратите внимание, как человек, банки и верхняя полка дематериализуются и заменяются по векторам. FBD в конце фильма не завершен. Чего не хватает?
Включено все, что нужно для решения силовой системы. на ФБД. Диаграммы свободного тела могут показаться ненужными в относительно простые текущие приложения, но по мере того, как проблемы становятся более сложными, их полезность возрастает.

Ниже приведен процесс определения реакции на стенке для консольная балка. Сначала рисуется FBD балки. Далее разрезаем балку освободиться от стены и заменить стену силами, которые поддерживали балка у стены, прежде чем она была срезана. Эти силы неизвестны, но это единственные силы, которые могут удерживать балку в равновесии. Они есть идентичны внутренним силам в балке в этой точке до того, как она была резать. Внутренние силы в балке перед ее отрывом от опоры также определяются, когда силы, которые будут удерживать или помещать FBD в находятся равновесия.

Неподвижная опора будет сопротивляться перемещению во всех направлениях и вращение (момент). FBD должен показывать все эти направления. Принципы равновесия всегда можно использовать для решения FBD. В приведенном выше FBD Sum Fy = 2K и Sum Fx = 0.

Силы 2K (нагрузка и вертикальная сила реакции) вызывают пару 10 вращений против часовой стрелки. K-FT, которому должен сопротивляться момент на конце отрезанного участка 10 K-FT, действующий по часовой стрелке.

Это иллюстрация трех различных структурных систем, которые одна нагрузка в 100 фунтов и одна нагрузка в 150 фунтов, действующие на них точно в тот же пункт. Они также поддерживаются роликовой опорой слева и закрепленная поддержка справа. Каждый из них может быть структурой любого типа. из материала…..дерево, сталь, бамбук или, возможно, бумага.

Это свободная диаграмма этих трех систем, которая была нарисована представлять систему сил. Обратите внимание, как вся внутренняя структура были удалены из этого представления. Внутреннее устройство не вопрос для определения опорных реакций! И, если опора и геометрия нагрузки одинакова, внешние реакции всегда будут оставаться прежним.

Уличный фонарь Умбрии
Это уличный фонарь, обычно встречающийся в Умбрии, Италия. Это выглядит как и многие лампы, найденные во всем мире. Три фотографии иллюстрируют, как диаграмма свободного тела для этой структуры должна быть задумана. Первый шаг должен дематериализовать лампу. Определите центр тела и нарисуйте это как прямая. Единственным идентифицируемым весом является лампа, так что это рисуется как вектор, как указано. Следующим шагом является определение того, что требуется на другом конце лампы для поддержания равновесия; что нужно чтобы лампа не улетела в космос? Эти силы (включая момент) нарисованы, как указано. Чего не хватает на этой иллюстрации? Должны быть включены величины момента и силы с левой стороны. на полной диаграмме свободного тела.

Веронская колонна
Существует множество ситуаций, в которых точные условия не могут быть определены на первый взгляд. Материальность и относительность жесткость элементов, которые поддерживаются/соединяются, дает подсказки что касается фактического поведения.

Это тонкая кирпичная колонна, поддерживающая деревянный навес старого замка. в Вероне, Италия. Как этот элемент соединен со стеной внизу?

Скорее всего, такое поведение можно было бы смоделировать как простое соединение. Кладка будет очень сложно передавать моменты, так как он не может развиваться требуемая растягивающая половина пары. Миномет тоже скорее всего поддаваться, если боковая нагрузка значительной силы должна была быть приложена. Однако, можно утверждать, что колонна может и, безусловно, сопротивляется небольшому величина боковой нагрузки. И, благодаря силе тяжести, тянущей каждый кирпичик внизу может быть возможность того, что база начнет сопротивляться умеренному момент до тех пор, пока сила растяжения не превышает силы сжатия за счет собственного веса конструкции. Итак, где это оставляет FBD? В руках дизайнера сделать выбор типа модели, которая он/она желает…. Какая правильная модель? Это зависит.

Портовый кран
Столкнувшись с проблемой, которая кажется сложной, первое, что нужно сделать делать это УПРОЩАТЬ!!! Определите узнаваемые части. Ищите значительные изменения структурной морфологии. Переверните изображение вверх ногами, если нужно для того, чтобы попытаться дематериализовать проблему.

В этом случае кран должен быть разделен как минимум на две узнаваемые части. Он имеет ферменную верхнюю конструкцию (А) и жесткую рамную нижнюю конструкцию (В). Мы можем разделить структуры на эти две части, потому что мы также можем распознавать что верхняя часть должна иметь возможность вращаться, в то время как нижняя часть остается «стабильно» или, по крайней мере, остается на месте. Два значительных можно определить веса или силы, действующие на деталь А; вес поднятый груз и большой бетонный блок уравновешивают его. Обратите внимание на родственника величины векторов сил. Если фактическая величина сил неизвестна, это один из способов представления этих величин.

Обратите также внимание на то, что некоторые части реальной конструкции крана в верхней части были оставлены без внимания. Есть ряд машин, которые занимают платформу над круговой поворотной дорожкой.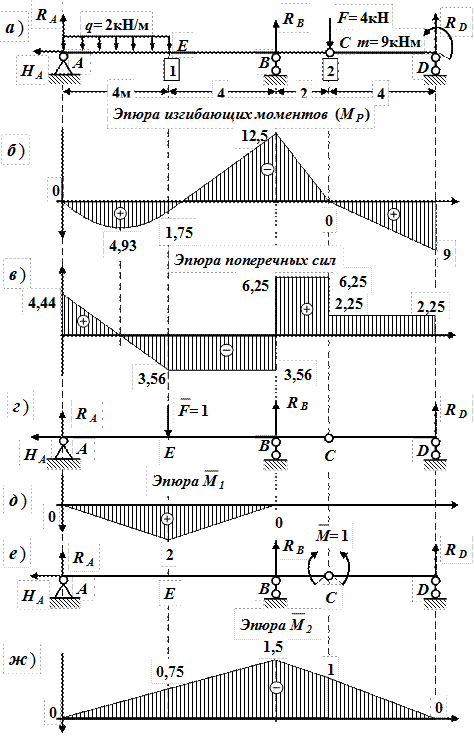 Это не совсем беспокойство в этом анализе, если они не являются постоянными И не имеют значительного веса. Если они НЕ учитываются, то их расположение по центру всего крана добавляет стабильности всей системе. Таким образом, более мелкие предметы, которые могут или могут отсутствовать, обычно ими пренебрегают.

Часть B состоит из массивной жесткой рамы из толстолистовой стали. Кажется, что ноги внизу каждого «нога», обеспечивающая «опору». Диаграмма свободного тела проходит через центр тяжести тела. раздел. Бывают случаи, когда положение центра тяжести фактически неизвестно. Когда это случае, то необходимо сделать «наилучшее предположение» относительно его местоположения. Как только это будет завершено, его можно будет протестировать как к его «правильности» по логике получившейся диаграммы. Бывают случаи, когда диаграмма свободного тела не кажется представлять что-либо близкое к построенной форме.

Обратите внимание, что «действие» на этом, нижнем кадре, состоит как из Force и Момент. Что создало эти две отдельные силы? Почему есть и момент, и вертикальная нагрузка? Почему не только вертикальная нагрузка? или только мгновение? Чтобы проанализировать эту часть фрейма, мы должны рассмотреть ВСЕ действия, которые исходят «сверху». По сути, это момент, вызванный тенденцией подъемного крана к опрокидыванию. НО, вертикальная нагрузка перемещаемая бита ДОЛЖНА также в какой-то момент упасть на землю. Он делает это через рамку. Попробуйте проанализировать кадр с помощью предполагаемые значения.

Какое влияние это оказывает на общую грузоподъемность крана? Как этот кран может выйти из строя? Какой элемент может выйти из строя первый?

Реакции Балки

Горизонтальной Компоненты реакции

An пример

Другое пример

Вопросы для размышления

Как будет завершена FBD для анкерных блоков для Frei Otto’s конструкция палатки?

Домашнее задание

Дополнительное чтение

Сьюард, Дерек. Понимание структур. Macmillan Press (Лондон). 1994. стр. 18 — 24.

Бесплатные диаграммы тел: типы, диаграммы и примеры

В физике мы имеем дело с гравитацией, нормальными силами, трением, сопротивлением и этот список можно продолжить. Иногда мы даже имеем дело со всеми этими силами одновременно. Как мы можем отслеживать все эти разные части? Диаграммы свободного тела — это один из инструментов, который физики используют для понимания всех этих различных, а иногда и противоположных сил, чтобы понять, как будет реагировать система.

Значение диаграмм свободного тела

Диаграмма свободного тела позволяет отслеживать все силы, действующие на объект.

Диаграмма свободного тела — это тип векторной диаграммы, отображающий объект и силы, действующие на него.

Чтобы нарисовать диаграмму свободного тела, нарисуйте стрелки, идущие от центра масс тела, чтобы показать действующие на него силы. Размер стрелки говорит нам о величине, а направление, в котором указывает стрелка, является направлением нашей силы. Это может показать нам, если наши силы неуравновешены, так что наша система ускоряется, или у нас есть статическая проблема, где у нас есть результирующая сила, равная нулю. Такая диаграмма является незаменимым инструментом для решения многих типов физических задач. Обратите внимание, что когда мы изначально рисуем нашу диаграмму, мы можем не знать величины сил. Обычно оценки достаточно, чтобы отслеживать, какие силы действуют на наш объект. В ходе численного решения значений мы можем обнаружить, что наши начальные величины силы были не совсем правильными. Объект, на который действуют силы, обычно изображают точкой или упрощенным рисунком объекта. Все остальное убрано, чтобы было понятно, какой объект нас интересует.

Типы сил, обычно отображаемые на диаграмме свободного тела

Некоторые из наиболее распространенных сил, наблюдаемых на диаграмме свободного тела, — это сила тяжести, которая притягивает объект к Земле, и нормальная сила, которая толкает объект вдали от точки соприкосновения. Трение и сопротивление работают против направления движения, замедляя движущийся объект. Сила натяжения работает, чтобы тянуть объекты. Центростремительная сила не дает объекту улететь во вращательном движении и всегда направлена к центру круга вращения.

Важно понимать, какие силы следует отображать, а какие нет. Единственные силы, показанные на диаграмме свободного тела, — это силы, действующие на объект. Любые силы, приложенные к нашему объекту, не должны отображаться. Например, если мы рассматриваем коробку, стоящую на полу, мы должны учитывать нормальную силу пола, давит на нашу коробку, но не нормальную силу, которую наша коробка давит на пол.

Пример внешних сил на диаграмме свободного тела, StudySmarter Originals

Здесь сила тяжести задается как \(F_\text{g}\), нормальная сила на первом изображении, \(F_\text{g}\), является нормальной силой пола, действующей на коробка. Это правильный способ отображения диаграммы свободного тела. Второе изображение слева показывает \(F_{\text{N}_1}\), нормальную силу пола, действующую на коробку. Он также неверно показывает \(F_{\text{N}_2}\), нормальную силу коробки, действующую на пол. Это неверно: мы никогда не должны показывать силы, действующие на наш объект, а только силы, действующие на наш объект.

Ваша диаграмма свободного тела должна включать только один объект. Если вы хотите включить больше, вы должны нарисовать отдельную диаграмму. Вот почему он называется «свободным»: мы смотрим на один изолированный объект.

Уравнения диаграммы свободного тела

Основная предпосылка диаграммы свободного тела состоит в том, чтобы квалифицировать все силы. Это предполагает, что мы используем второй закон Ньютона,

\[F_\text{net}=ma.\]

Это хорошее место для начала, но есть некоторые тонкости, которые нам нужно учитывать. Например, равна ли результирующая сила, действующая на наш объект, нулю? Если это так, то наши силы должны быть уравновешены, а если нет, то наши векторы сил не должны взаимно уравновешиваться. Рассмотрение формул — хороший способ начать решение проблемы, но не забывайте также учитывать лежащую в основе физику, описываемую формулами.

Примеры диаграмм свободного тела

Теперь, когда мы немного больше понимаем, что такое диаграмма свободного тела, давайте взглянем на несколько примеров.

Сложенные блоки

Распространенным примером, показывающим несколько более сложное использование нормальных сил, является стопка блоков.

Рассмотрим случай с тремя уложенными друг на друга бетонными блоками. Нарисуйте диаграммы свободного тела для каждого блока.

Сложенные блоки для задачи диаграммы свободного тела, StudySmarter Originals

Помните, что нам нужно нарисовать диаграмму свободного тела для каждого блока отдельно. Верхний блок \(A\) самый простой, поэтому мы начнем с него. Все, что у нас есть, действующая на этот блок, — это сила тяжести, которую мы назовем \(F_\text{g}\), и нормальная сила, приложенная блоком \(B\) к блоку \(A\). Мы назовем это \(F_{\text{N}_{BA}}\).

Диаграмма свободного тела блока \(A\), StudySmarter Originals

Обратите внимание, что это статическая система, поэтому сумма сил, действующих на каждый блок, должна быть равна нулю, как и результирующая сила, действующая на систему. В этом случае нормальная сила должна компенсировать силу тяжести.

Далее смотрим на блок \(B\). Это немного сложнее. Во-первых, у нас есть сила тяжести \(F_\text{g}\), которая сильнее, потому что блок \(B\) больше. У нас также есть две нормальные силы. Нормальная сила от блока \(A\), давит на блок \(B\), обозначенная \(F_{\text{N}_{AB}}\), и нормальная сила от блока \(C\), толкающего вверх по блоку \(B\), обозначенному \(F_{\text{N}_{CB}}\).

Диаграмма свободного тела блока \(B\), StudySmarter Originals

Наконец, у нас есть блок \(C\). Это похоже на блок \(B\), но единственная трудность состоит в том, чтобы удерживать нормальные силы прямыми и убедиться, что величины всех наших сил имеют смысл. Как обычно, у нас есть сила тяжести, \(F_\text{g}\). Наши нормальные силы — это нормальная сила от \(B\), давящая вниз на \(C\), \(F_{\text{N}_{BC}}\), и нормальная сила земли, давящая на \ (C\), который мы обозначаем как \(F_\text{N}\).

Диаграмма свободного тела блока \(C\), StudySmarter Originals

Блоки, соединенные шкивом

Шкивы перенаправляют силы, что делает их несколько более интересным случаем, чем стандартная диаграмма свободного тела.

Нарисуйте схему свободного тела для каждого блока, соединенного шкивом. Обратите внимание, что блоки сделаны из одного и того же материала.

Грузы на шкиве — StudySmarter Originals

Когда мы рисуем нашу диаграмму свободного тела, мы помним, что сила натяжения везде одинакова в системе шкивов. Итак, у нас есть схема ниже.

Диаграмма свободного тела блока \(A\) в системе шкивов , Шпилька ySmarter Originals

Здесь \(F_{\text{g}_A}\) — наша сила тяжести, а \(F_ \text{T}\) — это наше напряжение. Аналогично имеем следующее.

Диаграмма свободного тела блока B в системе шкивов , Шпилька ySmarter Originals

Здесь снова \(F_{\text{g}_A}\) — наша сила тяжести, а \(F_\text{T }\) это наше напряжение.

Трение на диаграмме свободного тела

Мы также можем изучить, как будут выглядеть силы трения на диаграмме свободного тела.

Рассмотрим блок, скользящий по пандусу с коэффициентом кинетического трения \(\mu_\text{k}\). Нарисуйте диаграмму свободного тела для блока.

Задача установки блока на пандусе, StudySmarter Originals

Силы, с которыми мы имеем дело, — это нормальная сила, гравитация и трение. Гравитация направлена вниз, нормальная сила перпендикулярна рампе, а трение действует против нашего направления движения.

Схема свободного тела блока на рампе с трением, StudySmarter Originals

Чтобы разбить их на составляющие, мы можем, однако, разделить нормальную силу и силу трения; есть трюк, чтобы сделать нашу жизнь немного проще. Если мы повернем наши координатные оси, чтобы выровнять их с нормальной силой, нам нужно только разделить гравитацию на ее составляющие.

Диаграмма свободного тела с повернутыми осями, StudySmarter Originals

Теперь мы повернем всю систему, чтобы нам было легче ее увидеть. Мы ничего не меняем на диаграммах ниже, мы просто меняем нашу перспективу так, чтобы \(y\) снова указывало вверх.

Вращение системы для возврата \(y\) вверх, StudySmarter Originals

Наконец, мы можем разделить нашу силу гравитации, и мы закончили.

Диаграмма свободного тела с повернутыми осями и разделением всех сил на их компоненты, StudySmarter Originals

Хотя это и не является строго необходимым, обычно бывает полезно разложить силы на их компоненты \(x\) и \(y\). Проблемы часто требуют рассмотрения компонентов сил, а не только самих сил.

Диаграмма свободного тела с центростремительной силой

В нашем последнем примере мы рассмотрим, как нарисовать диаграмму свободного тела, когда у нас есть равномерное круговое движение.

Рассмотрим мяч, прикрепленный к веревке на шесте, который вращается вокруг него, совершая равномерное круговое движение. Нарисуйте диаграмму свободного тела для мяча.

Мяч, прикрепленный веревкой к шесту и совершающий равномерное круговое движение, StudySmarter Originals

Обратите внимание, что на мяч действуют только две силы: сила натяжения \(F_\text{T}\) и сила гравитация, \(F_\text{g}\), поэтому наша диаграмма свободного тела относительно проста.

Диаграмма свободного тела для мяча, соединенного с шестом веревкой, StudySmarter Originals

Итак, при чем тут центростремительная сила? В этом случае центростремительная сила является чистой силой, действующей на наш объект. Мы можем увидеть, какова чистая сила, если мы разобьем наши силы на их компоненты \(x\) и \(y\). Гравитация уже действует только в направлении \(y\), поэтому нам просто нужно снять напряжение.

Диаграмма свободного тела с разделением натяжения на компоненты, StudySmarter Originals

Мяч не движется вверх и вниз, поэтому наши силы в направлении \(y\) уравновешиваются. Теперь легко видеть, что наша центростремительная сила есть сила натяжения в направлении \(х\). Обратите внимание, что когда мяч вращается, эта сила всегда будет указывать на центр круга вращения. Это подтверждает, что это наша центростремительная сила.

Диаграммы свободного тела — ключевые выводы

Диаграммы свободного тела ясно и кратко показывают все силы, действующие на объект.