Прочность тел зависит от: ПРОЧНОСТЬ • Большая российская энциклопедия

Содержание

Прочность | это… Что такое Прочность?

Прочность

твёрдых тел, в широком смысле — свойство твёрдых тел сопротивляться разрушению (разделению на части), а также необратимому изменению формы (пластической деформации) под действием внешних нагрузок. В узком смысле — сопротивление разрушению.

В зависимости от материала, вида напряжённого состояния (растяжение, сжатие, изгиб и др.) и условий эксплуатации (температура, время действия нагрузки и др.) в технике приняты различные меры П. (предел текучести, временное сопротивление, предел усталости и др.). Разрушение твёрдого тела — сложный процесс, зависящий от перечисленных и многих др. факторов, поэтому технические меры П. — условные величины и не могут считаться исчерпывающими характеристиками.

Физическая природа прочности. П. твёрдых тел обусловлена в конечном счёте силами взаимодействия между атомами и ионами, составляющими тело.

Эти силы зависят главным образом от взаимного расположения атомов. Например, сила взаимодействия двух соседних атомов (если пренебречь влиянием окружающих атомов) зависит лишь от расстояний между ними (рис. 1). При равновесном расстоянии r_o Прочность 10 нм эта сила равна нулю. При меньших расстояниях сила положительна и атомы отталкиваются, при больших — притягиваются. На критическом расстоянии r_k сила притяжения по абсолютной величине максимальна и равна F_т. Например, если при растяжении цилиндрического стержня с поперечным сечением S_o действующая сила Р, направленная вдоль его оси, такова, что приходящаяся на данную пару атомов внешняя сила превосходит максимальную силу притяжения F_т, то последние беспрепятственно удаляются друг от друга. Однако, чтобы тело разрушилось вдоль некоторой поверхности, необходимо, чтобы все пары атомов, расположенные по обе стороны от рассматриваемой поверхности, испытывали силу, превосходящую
F_т. Напряжение, отвечающее силе F_т, называется теоретической прочностью на разрыв σ_τ (σ_τ ≈ 0,1 Е, где Е — модуль Юнга). Но на опыте наблюдается разрушение при нагрузке Р*, которой соответствует напряжение σ = P*/S, в 100—1000 раз меньшее σ_τ. Расхождение теоретической П. с действительной объясняется неоднородностями структуры тела (границы зёрен в поликристаллическом материале, посторонние включения и др.), из-за которых нагрузка Р распределяется неравномерно по сечению тела.

Механизм разрушения. Зарождению микротрещин при напряжении ниже σ_τ способствуют термической Флуктуации. Если на участке поверхности S малых размеров (но значительно превышающем сечение одного атома) локальное напряжение окажется больше σ

τ, вдоль этой площадки произойдёт разрыв. Края разрыва разойдутся на расстояние, большее r_k, на котором межатомные силы уже малы, и образуется трещина (рис. 2). Локальные напряжения особенно велики у края образовавшейся трещины, где происходит Концентрация напряжений, причём они тем больше, чем больше её размер. Если этот размер больше некоторого критического r_c, на атомы у края трещины действует напряжение, превосходящее σ_т, и трещина растет дальше по всему сечению тела с большой скоростью — наступает разрушение. r_c определяется из условия, что освободившаяся при росте трещины упругая энергия материала покрывает затраты энергии на образование новой поверхности трещины:
r_c≈ Еγ / σ² (где γ — энергия единицы поверхности материала). Прежде чем возрастающее внешнее усилие достигнет необходимой для разрушения величины, отдельные группы атомов, особенно входящие в состав дефектов в кристаллах, обычно испытывают перестройки, при которых локальные напряжения уменьшаются («релаксируют»). В результате происходит необратимое изменение формы тела — пластическая деформация; ей также способствуют термической флуктуации.

Разрушению всегда предшествует большая или меньшая пластическая деформация. Поэтому при оценке r_c в энергию γ должна быть включена работа пластической деформации γ^Р, которая обычно на несколько порядков больше истинной поверхностной энергии γ. Если пластическая деформация велика не только вблизи поверхности разрушения, но и в объёме тела, то разрушение вязкое. Разрушение без заметных следов пластической деформации называется хрупким. Характер разрушения проявляется в структуре поверхности излома, изучаемой фрактографией (См. Фрактография) . В кристаллических телах хрупкому разрушению отвечает скол по кристаллографическим плоскостям спайности, вязкому — слияние микропустот (на фрактограммах выявляются в виде чашечек) и скольжение. При низкой температуре разрушение преимущественно хрупкое, при высокой — вязкое. температура перехода от вязкого к хрупкому разрушению называется критической температурой хладноломкости.

Поскольку разрушение есть процесс зарождения и роста трещин, оно характеризуется скоростью или временем τ от момента приложения нагрузки до момента разрыва, т. е. долговечностью материала. Исследования многих кристаллических и аморфных тел показали, что в широком интервале температур

Т (по абсолютной шкале) и напряжений σ, приложенных к образцу, долговечность τ при растяжении определяется соотношением

где τ₀ — приблизительно равно периоду тепловых колебаний атомов в твёрдом теле (10^-12сек), энергия U₀ близка к энергии сублимации (См. Сублимация) материала, активационный объём V составляет обычно несколько тысяч атомных объёмов и зависит от структуры материала, сформировавшейся в процессе предварительной термической и механической обработки и во время нагружения, k = 1,38 ․10^-16эрг/град — постоянная Больцмана. При низких температурах долговечность очень резко падает с ростом напряжения, так что при любых важных для практики значениях τ существует почти постоянное предельное значение напряжения σ₀, выше которого образец разрушается практически мгновенно, а ниже — живёт неограниченно долго.

Это значение σ₀ можно считать пределом прочности (см. табл.).

Некоторые значения прочности на растяжение, σ₀ в кгс/мм² (1 кгс/мм²= 10 Мн/м²)

———————————————————————————————————————————————-

| Материалы | σ₀ | σ₀/Е |

|———————————————————————————————————————————————|

| Графит (нитевидный кристалл) | 2400 | 0,024

| Сапфир (нитевидный кристалл) | 1500 | 0,028 |

| Железо (нитевидный кристалл) | 1300 | 0,044 |

| Тянутая проволока из высокоуглеродистой стали | 420 | 0,02 |

| Тянутая проволока из вольфрама | 380 | 0,009 |

| Стекловолокно | 360 | 0,035 |

| Мягкая сталь | 60

| 0,003 |

| Нейлон | 50 | |

———————————————————————————————————————————————-

Время τ затрачивается на ожидание термофлуктуационного зарождения микротрещин и на их рост до критического размера r_c.Когда к образцу прикладывают напряжение σ, он деформируется сначала упруго, затем пластически, причём около структурных неоднородностей, имевшихся в исходном состоянии или возникших при пластической деформации, возникают большие локальные напряжения (в кристаллах в голове заторможенных сдвигов — скоплений дислокаций (См. Дислокации)). В этих местах зарождаются микротрещины. Их концентрация может быть очень большой (например, в некоторых ориентированных полимерах до 10

15 трещин в 1 см³). Однако при этом их размеры, определяемые масштабом структурных неоднородностей, значительно меньше r_c. Трещины не растут, и тело не разрушается, пока случайно, например благодаря последовательному слиянию близко расположенных соседних микротрещин, одна из них не дорастет до критического размера. Поэтому при создании прочных материалов следует заботиться не столько о том, чтобы трещины не зарождались, сколько о том, чтобы они не росли.

Случайное распределение структурных неоднородностей по объёму образца, по размерам и по степени прочности и случайный характер термических флуктуаций приводят к разбросу значений долговечности (а также предела П.

σ₀) при испытаниях одинаковых образцов при заданных значениях σ и Т. Вероятность встретить в образце «слабое» место тем больше, чем больше его объём. Поэтому П. (разрушающее напряжение) малых образцов (например, тонких нитей) выше, чем больших из того же материала (т. н. масштабный эффект). Участки с повышенным напряжением, где легче зарождаются микротрещины, встречаются чаще у поверхности (выступы, царапины). Поэтому полировка поверхности и защитные покрытия повышают П. Напротив, в агрессивных средах П. понижена.

Меры повышения прочности. При создании высокопрочных материалов стремятся в первую очередь повысить сопротивление пластической деформации. В кристаллических телах это достигается либо за счёт снижения плотности дефектов (П. нитевидных кристаллов, лишённых подвижных дислокаций, достигает теоретической), либо за счёт предельно большой плотности дислокаций в мелкодисперсном материале. Второе требование — большое сопротивление разрушению — сводится к выбору материала с высокой теоретической П. σ_т = 0,1 Е. Создать материалы с модулем Юнга Е, превышающим максимальные встречающиеся в природе значения, можно искусственно, путем применения высоких давлений; однако в этом направлении делаются лишь первые шаги. Большие значения σ_т затрудняют зарождение микротрещин. Чтобы предотвратить их рост, материал должен быть достаточно пластичным. Тогда у вершины трещины необходимые для её роста высокие напряжения рассасываются за счёт пластической деформации. Сочетание высокой П. и пластичности достигается в сплавах термомеханической обработкой, в композитах — подбором материала волокон и матрицы, объёмной доли и размера волокон. Трещина, возникшая в прочной (обычно хрупкой) фазе сплава или в волокне композита, останавливается у границы с пластичной матрицей. Поэтому важной характеристикой высокопрочных материалов является сопротивление распространению трещины, или вязкость разрушения. При механическом измельчении материалов требуется пониженная П.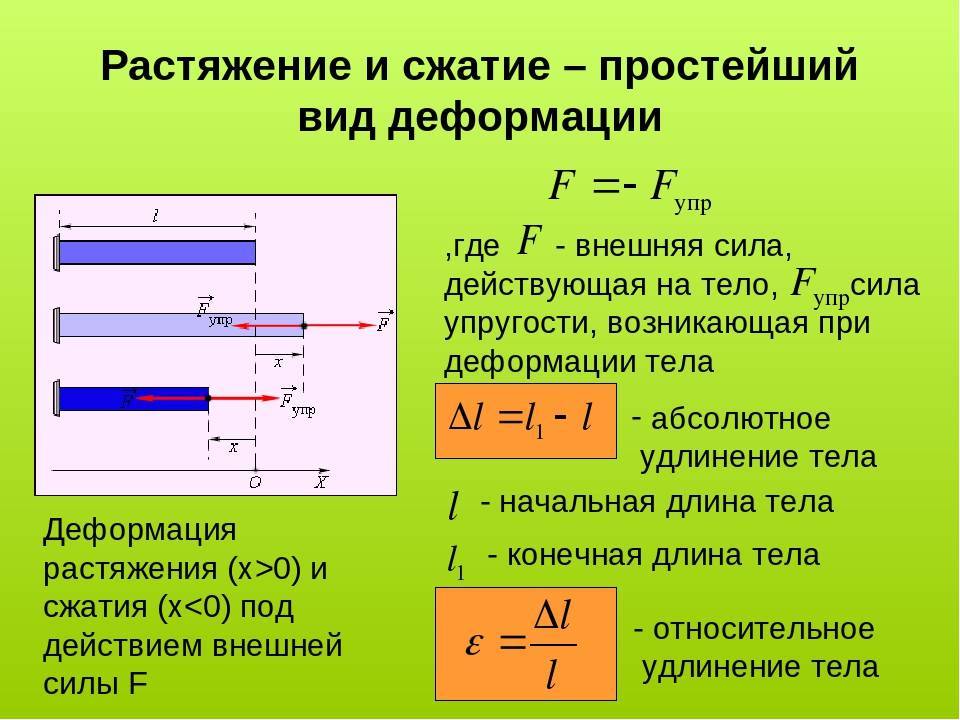 Она достигается воздействием поверхностно-активных сред (органические вещества, вода).

Лит.: Разрушение, пер. с англ., под ред. А. Ю. Ишлинского, т. 1, М., 1973; Работнов Ю. Н., Сопротивление материалов, М., 1962; Гуль В. Е., Структура и прочность полимеров, 2 изд., М., 1971; Механические свойства новых материалов, пер. с англ., под ред. Г. И. Баренблатта, М., 1966; Инденбом В. Л., Орлов А. Н., Проблема разрушения в физике прочности, «Проблемы прочности», 1970, № 12, с. 3; Регель В. Р., Слуцкер А. И., Томашевский Э. Е., Кинетическая природа прочности твердых тел, М., 1974.

А. Н. Орлов.

Рис. 1. Зависимость силы взаимодействия двух атомов от расстояния между ними.

Рис. 2. Трещина Гриффита. Стрелки указывают направление растяжения; заштрихована область, в которой сняты напряжения.

Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.

Игры ⚽ Нужен реферат?

Синонимы

безошибочность, безубыточность, безызносность, беспроигрышность, вибропрочность, дебелость, добротность, долговечность, долговременность, достоверность, живучесть, исправность, капитальность, крепкость, крепость, механопрочность, надежность, незыблемость, ненарушимость, неопровержимость, непоколебимость, неразрушаемость, неразрушимость, неразрывность, нерасторжимость, нерушимость, несокрушимость, несомненность, неуязвимость, носкость, обеспеченность, основательность, постоянность, солидность, стабильность, стойкость, твердость, убедительность, устойчивость, фундаментальность, электропрочность

Прочности предел
Прошивка

Полезное

2.

2. Теоретическая и реальная прочность твердых тел

Способность твердого тела оказывать сопротивление разрушению от внешнего воздействия (механического, теплового и др.) называется его прочностью. При разрушении рвутся связи между частицами кристаллической структуры без изменения агрегатного состояния вещества.

Под теоретической прочностью понимается прочность твердого тела, имеющего идеальную кристаллическую структуру.

2 3 . Теория прочности

Испытания прочности материалов твердых тел проводятся обычно в стандартных условиях. В конкретных случаях расчета на прочность напряженноесостояние твердого тела может быть самым различным. Существующие теории прочности позволяют с некоторыми допущениями вести прочностные расчеты, опираясь на показатели прочности или пластичности, полученные при

стандартных испытаниях, не прибегая к специальным испытаниям в сложном напряженном состоянии.

Современные теории прочности создавались главным образом для конструкционных материалов, а поэтому в качестве предельного состояния принимается достижение предела текучести твердого тела и лишь для хрупких тел — предела прочности.

2.4. Энергетическая теория прочности

Энергетическая теория прочности основана на предположении, что разрушение или достижение пластического состояния наступает тогда, когда удельная энергия формоизменения достигает предельного значения.

Классические теории прочности применимы только для изотропных материалов с одинаковым сопротивлением разрушению или пределом текучести при одноосных испытаниях на растяжение или сжатие. Горные породы не являются

таковыми. Однако, однозначность характеристик предельного состояния, получаемая при использовании этих теорий, очень удобна при анализе напряженного состояния в твердых телах. Последнее и определило использованиетретьей и четвертой теорий прочности в механике горных пород для качественного анализа.

Теория прочности Мора.

В отличие от классических, эта теория учитывает как разные значения сопротивлений разрушению при одноосном растяжении

и сжатии, так и очевидный факт, что разрушение или состояние пластичности зависит от нормальных напряжений. Эта теория прочности широко применяется в горном деле и строительстве. Характеристикой твердого тела, согласно теории прочности Мора, является зависимость предельное значение касательных напряжений от среднего напряжения.

Глава З.НЕКОТОРЫЕ ОСОБЕННОСТИ ДЕФОРМИРОВАНИЯ ПОРОД

3.1. Упругий гистерезис и упругое последействие

Для упругих твердых тел закон Гука выполняется лишь приближенно. В частности, модуль деформации при нагружении несколько меньше, чем при разгрузке, что в случае быстрой разгрузки обусловливает появление остаточной деформации

Это явление называется упругим гистерезисом. Однако с течением

времени остаточная деформация исчезает и твердое тело восстанавливает свои размеры. Это явление называется упругим последействием.

Явление упругого последействия и упругого гистерезиса легко объясняются с точки зрения дефектов кристаллической структуры. Напряжения в твердом теле вызывают направленное движение дислокаций и их перераспределение в соответствии с принципом получения наименьшей упругой энергии деформирования.

При быстром снятии нагрузки обратное перераспределение

дислокаций идет с быстро уменьшающимся градиентом напряжений и отстает во времени от разгрузки. Последнее проявляется как появление остаточных внутренних напряжений, а следовательно, и остаточной деформации (упругий гистерезис). С течением времени вследствие энергии внутренних напряжений

происходит перераспределений дислокаций, внутренние напряжения уменьшаются, уменьшается и остаточная деформация (упругое последействие).

Явления упругого гистерезиса и упругого последействия показывают на наличие зависимости деформации от времени, т.е. на проявление вязкостных свойств твердых тел. В этом случае модель твердого тела можно представить как комбинацию идеально упругого (тела Гука) и вязкого тел.

Инерция и масса

Первый закон движения Ньютона гласит, что «Объект в состоянии покоя остается в покое, а объект в движении остается в движении с той же скоростью и в том же направлении, если на него не действует неуравновешенная сила».

Объекты склонны «продолжать делать то, что они делают». На самом деле это естественная тенденция объектов сопротивляться изменениям в их состоянии движения. Эта тенденция сопротивляться изменениям в их состоянии движения описывается как инерция .

Инерция: сопротивление объекта изменению его состояния движения.

Представление Ньютона об инерции находилось в прямом противоречии с более популярными представлениями о движении. До Ньютона господствовала мысль, что это естественная склонность объектов останавливаться. Считалось, что движущиеся объекты в конце концов перестанут двигаться; сила была необходима, чтобы держать объект в движении. Но если его предоставить самому себе, движущийся объект в конце концов остановится, а покоящийся объект останется в покое; таким образом, идея, господствовавшая в мышлении людей почти за 2000 лет до Ньютона, заключалась в том, что естественной тенденцией всех объектов является принятие положения покоя.

Галилей и концепция инерции

Галилей, выдающийся ученый XVII века, разработал концепцию инерции. Галилей полагал, что движущиеся объекты в конце концов останавливаются из-за силы, называемой трением. В экспериментах с использованием пары наклонных плоскостей, обращенных друг к другу, Галилей заметил, что мяч будет катиться по одной плоскости и подниматься по противоположной плоскости примерно на одинаковую высоту. Если бы использовались более гладкие плоскости, мяч катился бы по противоположной плоскости еще ближе к исходной высоте. Галилей рассудил, что любая разница между начальной и конечной высотой связана с наличием трения. Галилей постулировал, что если бы трение можно было полностью устранить, то мяч достиг бы точно такой же высоты.

Далее Галилей заметил, что независимо от угла, под которым были ориентированы плоскости, конечная высота почти всегда равнялась начальной высоте. Если бы наклон противоположного склона был уменьшен, то мяч откатился бы на большее расстояние, чтобы достичь первоначальной высоты.

Рассуждения Галилея продолжились: если противоположный наклон поднять почти под углом 0 градусов, то мяч будет катиться почти вечно, пытаясь достичь первоначальной высоты. А если бы противоположный наклон был даже вовсе не наклонен (то есть если бы он был ориентирован по горизонтали), то… движущийся предмет продолжал бы двигаться… .

Смотри! В этом видео объясняется еще один мысленный эксперимент Галилея с использованием реального эксперимента, проведенного с современным оборудованием.

Силы не заставляют объекты двигаться

Исаак Ньютон основывался на размышлениях Галилея о движении. Первый закон движения Ньютона гласит, что сила равна , а не , необходимой для удержания объекта в движении. Сдвиньте книгу по столу и наблюдайте, как она скользит в исходное положение. Книга, движущаяся по столешнице, не останавливается из-за отсутствие силы; скорее это присутствие силы — эта сила является силой трения — которая приводит книгу в состояние покоя. В отсутствие силы трения книга продолжала бы двигаться с той же скоростью и направлением — вечно! (Или, по крайней мере, до конца столешницы.) Не требуется силы, чтобы удерживать движущуюся книгу в движении. На самом деле это сила, которая останавливает книгу.

Масса как мера количества инерции

Все объекты сопротивляются изменениям в состоянии их движения. У всех объектов есть эта тенденция — у них есть инерция. Но имеют ли одни объекты большую склонность сопротивляться изменениям, чем другие? Абсолютно да! Тенденция объекта сопротивляться изменениям в его состоянии движения зависит от массы. Масса есть та величина, которая зависит исключительно от инерции объекта. Чем больше инерция у объекта, тем больше у него масса. Более массивный объект имеет большую тенденцию сопротивляться изменениям в своем состоянии движения.

Предположим, что на столе для лекций по физике покоятся два, казалось бы, одинаковых кирпича. Тем не менее, один кирпич состоит из раствора, а другой кирпич состоит из пенополистирола. Не поднимая кирпичи, как вы могли бы сказать, какой кирпич был кирпичом из пенопласта ? Вы можете одинаково толкнуть кирпичи, чтобы изменить их состояние движения. Кирпич с наименьшим сопротивлением — это кирпич с наименьшей инерцией — и, следовательно, кирпич с наименьшей массой (т.0054 Пенополистироловый кирпич ).

Обычная физическая демонстрация основана на следующем принципе: чем массивнее объект, тем больше этот объект сопротивляется изменениям в состоянии своего движения. Демонстрация проходит следующим образом: на голову учителя кладут несколько массивных книг. На книги кладут деревянную доску и молотком вбивают в нее гвоздь. Из-за большой массы книг сила удара молота достаточно сопротивляется (инерция). Об этом свидетельствует тот факт, что учитель не чувствует удара молотка. (Конечно, эта история может объяснить многие наблюдения, которые вы ранее делали относительно своего «странного учителя физики».) Обычный вариант этой демонстрации включает разбивание кирпича о руку учителя быстрым ударом молотка. Массивные кирпичи противостоят силе и рука не поранится. (ВНИМАНИЕ: не пытайтесь проводить эти демонстрации дома

Смотри! Преподаватель физики объясняет свойство инерции, используя демонстрацию физики phun.

Проверьте свое понимание

1. Представьте себе место в космосе вдали от всех гравитационных и фрикционных влияний. Предположим, вы посещаете это место (только предположим) и бросаете камень. Рок будет

а. постепенно останавливаться.
б. продолжать движение в том же направлении с постоянной скоростью.

2. Объект массой 2 кг движется горизонтально со скоростью 4 м/с. Какая результирующая сила требуется, чтобы тело двигалось с этой скоростью и в этом направлении?

3. Мак и Тош спорят в столовой. Мак говорит, что если он бросит желе с большей скоростью, у него будет большая инерция. Тош утверждает, что инерция зависит не от скорости, а от массы. С кем ты согласен? Объяснить, почему.

4. Предположим, вы находитесь в космосе в невесомой среде , потребуется ли сила, чтобы привести объект в движение?

5. Фред большую часть воскресенья после обеда отдыхает на диване, смотрит профессиональные футбольные матчи и поглощает большое количество еды. Какое влияние (если таковое имеется) оказывает эта практика на его инерцию? Объяснять.

6. Бена Туклоуза преследует по лесу лось, которого он пытался сфотографировать. Огромная масса бычьего лося чрезвычайно устрашает. Тем не менее, если Бен сделает зигзагообразный рисунок через лес, он сможет использовать большую массу лося в своих интересах. Объясните это с точки зрения инерции и первого закона движения Ньютона.

7. Два кирпича лежат на краю лабораторного стола. Ширли Шешорт встает на цыпочки и замечает два кирпича. У нее появляется сильное желание узнать, какой из двух кирпичей самый массивный. Поскольку у Ширли проблемы с вертикальным положением, она не может дотянуться достаточно высоко и поднять кирпичи; однако она может дотянуться достаточно высоко, чтобы толкнуть кирпичи. Обсудите, как процесс толкания кирпичей позволит Ширли определить, какой из двух кирпичей самый массивный. Какую разницу заметит Ширли и как это наблюдение может привести к необходимому заключению?

Следующий раздел:

Перейти к следующему уроку:

Трение | Блог Гэри Гарбера

Трение вообще является очень сложной темой, если рассматривать причины трения на микроскопическом уровне. Я представлю здесь несколько макроскопических обобщений, применимых в большинстве случаев.

В общем случае величина силы трения зависит от шероховатости материала. Чем грубее или неровнее материал, тем больше будет трение.

Величина силы трения также зависит от Нормальной силы. Мы обычно думаем о нормальной силе как о противоположности веса. Если бы это было так, то мы могли бы нарисовать диаграмму свободного тела, как эта.

Итак, у нас есть сила тяжести направленная вниз, нормальная сила направленная вверх, приложенный «толчок» вправо и трение влево. Обратите внимание, что сила трения параллельна двум поверхностям. По мере увеличения силы нормальной силы (которой является сила между «скользящими» поверхностями) сила или величина трения также увеличивается.

Последовательно можно сказать, что трение параллельно поверхностям, а нормальная сила перпендикулярна. В приведенном выше случае трение горизонтальное.

Однако с тем же успехом мы могли бы иметь трение по вертикали или под углом. Представьте себе человека, который сжимает кусок мыла. Или ребенок, скользящий по шесту на детской площадке. В обоих этих случаях нормальная сила возникает НЕ из-за силы тяжести, а из-за сдавливания предметов чьими-то руками. Нормальная сила перпендикулярна полюсу, а сила трения параллельна поверхности полюса.

Аналогично, на наклонной плоскости нормальная сила по-прежнему перпендикулярна поверхности, а трение параллельно. В этом случае нормальная сила является только составляющей веса.

Когда у нас есть объект, который скользит по поверхности, мы называем силу сопротивления либо трением скольжения , либо кинетическим трением . Уравнение, описывающее величину этой силы трения, имеет вид

F _f = μ _k F _N

, где F _N — величина нормальной силы, а μ — коэффициент трения. μ описывает неровность или шероховатость поверхности. μ _k обычно представляет собой число от 0 до 1 и не имеет размеров. Это имеет смысл, если вы посмотрите, что обе части этого уравнения имеют Силу, выраженную в Ньютонах. k рядом с коэффициентом для кинетики.

При трении скольжения вы можете представить себе микроскопические «выпуклости» в материале, вызывающие сопротивление (что затушевывает правду об электростатических силах). Однако другой формой часто обсуждаемого трения является статическое трение . Когда вы пытаетесь толкнуть объект, он будет сопротивляться вам не только из-за собственной инерции, но и из-за статического трения между объектом и поверхностью, на которой он покоится. В этом случае вы можете думать о микроскопических выпуклостях как о застегивающихся вместе, как липучка.

Важно отметить, что статическое трение создается только в ответ на приложенную силу, аналогично тому, как нормальная сила создается только в ответ на приложенную силу. Из-за этого, имея дело с трением покоя, наше уравнение фактически имеет неравенство.

F _f ≤ μ _с F _N

Если приложенная сила превышает мкФ _Н,, то сила трения покоя преодолевается и объекты начинают скользить . s для статического в µ _s

Кроме того, в большинстве случаев коэффициент трения скольжения будет меньше коэффициента статического трения.

μ _k < μ _s

Одним из важных соображений относительно статического трения является то, как работает колесо. Когда колесо катит по земле, это , а не скольжение. Таким образом, катящаяся шина фактически использует статическое трение, чтобы продолжать движение. Когда ваша машина скользит или колеса заблокированы, тогда ваши шины скользят по земле, что очень опасно. Опять же, мы обязаны Угу, пещерному человеку, за это великое осознание.

Одно интересное заблуждение состоит в том, что величина трения зависит от скорости. Как только объект скользит, величина трения имеет тенденцию быть постоянной. Конечно, при трении выделяется тепло, и это может изменить свойства вещества.

Другой тип трения связан с гидродинамикой. В повседневной жизни вы можете думать об этом как о сопротивлении воздуха, но оно не ограничивается воздухом. К текучим средам относятся как жидкости, так и газы. Величина сопротивления жидкости зависит от скорости объектов, формы объекта и вязкости жидкости.

Пример:

Предположим, что через прилавок скользят словари весом 8,2 килограммы. Если коэффициент трения скольжения между книгой и прилавком равен 0,2, то какова сила трения книги?

м = 8,20 кг

μ _k = 0,200

F _f = ???