Сборник с примерами решения задач по сопротивлению материалов
- формат pdf
- размер 935.44 КБ
- добавлен 06 февраля 2009 г.
В сборнике представлены 6 примеров решения задач на темы:
— Растяжение и сжатие;
— Плоский поперечный изгиб;
— Сложное сопротивление бруса;
— Устойчивость центрально сжатых стержней.
Читать онлайн
Смотрите также
- формат djvu
- размер 1.64 МБ
- добавлен 27 марта 2011 г.
Л.: Ленинградский механический ин-т, 1981. — 89 с. В настоящий сборник включен ряд задач, предложенных на пяти городских олимпиадах (они помечены звездочками). Кроме того, сюда вошли, ранее встречавшиеся в литературе, приведенной в сборнике, а также задачи специально составленные для него. Большинство задач сопровождается кратким, но вполне достаточным для понимания решением, для остальных приведены указания и ответы. Указанные решения соответств…
— 89 с. В настоящий сборник включен ряд задач, предложенных на пяти городских олимпиадах (они помечены звездочками). Кроме того, сюда вошли, ранее встречавшиеся в литературе, приведенной в сборнике, а также задачи специально составленные для него. Большинство задач сопровождается кратким, но вполне достаточным для понимания решением, для остальных приведены указания и ответы. Указанные решения соответств…
- формат djvu
- размер 1.49 МБ
- добавлен 29 марта 2011 г.
Горький: Горьковский политехн. ин-т, 1986. – 104 с. В работе обобщается двадцатипятилетний опыт организации и проведения предметных олимпиад по сопротивлению материалов в Горьковском политехническом институте. Содержится около 250 оригинальных задач по сопротивлению материалов и строительной механике машин, описывается методика их решения. Работа рассчитана на студентов, участвующих в олимпиадах, и преподавателей, занимающихся руководством научно.
- формат djvu
- размер 5.17 МБ
- добавлен 22 ноября 2008 г.
Изд.2 М.: ФИЗМАТЛИТ, 2003. 632 с. Сборник соответствует стандартной программе полного курса, а его первые главы — программам различных сокращенных курсов сопротивления материалов. Каждый раздел предваряется кратким изложением теоретического материала; при этом общие положения вынесены в приложения. Теоретические части разделов заканчиваются резюме, в которых изложены алгоритмы решения соответствующих задач, и типовыми примерами. Задачи для самос…
- формат djv
- размер 6.34 МБ
- добавлен 22 ноября 2008 г.
М.: Высшая школа, 1970. — 544 с. Руководство к решению задач по сопротивлению материалов. Разобраны примеры решения задач на изгиб балок, тонкостенных сосудов, устойчивость стержней.
- формат pdf
- размер 25.53 МБ
- добавлен 01 марта 2010 г.
Авт:/Б. А. Антуфьев, А. Г. Горшков, О. В. Егорова, В. Н. Зайцев, А. Б. Костриченко, Д. И. Макаревский, Л. Н. Рабинский, А. В. Сибиряков, Д. В. Тарлаковский; Под ред. академика А. Ю. Ишлинского. — М.: Изд-во МАИ, 2001. — 544 с: ил. Сборник соответствует стандартной программе полного курса, а его первые главы — программам различных сокращенных курсов сопротивления материалов. Каждый раздел предваряется кратким изложением теоретического материала….
- формат djvu
- размер 1.14 МБ
- добавлен 22 апреля 2010 г.
Чебоксары, Чувашский университет. 2000. -56 с. Приведены краткие теоретические сведения с примерами решения задач по основным темам курса «Сопротивление материалов» и контрольные задания. Для студентов электротехнического и химического факультетов, изучающих курс «Прикладная механика».
Для студентов электротехнического и химического факультетов, изучающих курс «Прикладная механика».
- формат pdf
- размер 7.28 МБ
- добавлен 12 февраля 2009 г.
Сборник задач по сопротивлению материалов, для студентов технических университетов.
- формат djvu
- размер 619.13 КБ
- добавлен 13 мая 2010 г.
Центр тестирования МО РФ, 2002, 84 с. Учебно-методическое пособие для студентов и преподавателей технических вузов. В сборнике представлены тесты по сопротивлению материалов, составленные на основе «Государственного образовательного стандарта высшего профессионального образования». Сборник содержит 10 вариантов тестов. Сборник предназначен для дифференциации уровня подготовки студентов по отдельным разделам дисциплины (текущий контроль) и по всей. ..
..
- формат pdf
- размер 815.93 КБ
- добавлен 06 февраля 2009 г.
В сборнике представлены примеры решения задач для студентов большинства Российских вузов по темам: — Растяжение и сжатие: статически определимые системы статически неопределимые системы; — Кручение круглого бруса; — Изгиб плоских балок; — Геометрические характеристики плоских сечений; — Устойчивость сжатых стержней.
- формат pdf
- размер 852.48 КБ
- добавлен 25 октября 2008 г.
ГОСТы, СНиПы, формулы, эпюры и прочее. Все, что может пригодиться при решении задач по сопротивлению материалов
Меню сайта
Расчет геометрических характеристик сечений он-лайн NEW — считает любые сечения (сложные).
Расчет балок на прочность он-лайн — построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной
сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн. Расчет рам, ферм балок он-лайн NEW — эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы. Лекции — теория, практика, задачи… Примеры решения задач Справочная информация — ГОСТы, сортамент проката, свойства материалов и другое. Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое). Форум сопромата и механики
Книги — разная литература по теме. Заказать задачу Друзья сайта (ссылки) WIKIbetta Разработчикам (сотрудничество) Веб-мастерам (партнёрка) О проекте, контакты Подпроекты |
Пример №1. Расчет статически определимой балки, подбор сечения.Необходимо определить минимальный диаметр круглого сечения d балки в точке С. Посмотреть решение… Пример №2. Расчет статически неопределимой рамы методом перемещений.Необходимо построить эпюры внутренних силовых факторов, а так же найти реакции. Посмотреть решение… Пример №3. Расчет геометрических характеристик сечения.Необходимо рассчитать все основные геометрические характеристики сечения. Посмотреть решение… |
СообществоПоиск людей ВходРешение задач
Заказать задачу Расчет редукторов
Расчет редуктора он-лайн Для Android (рекомендую)NEWMobile Beam 2.0 Java 2 ME |
Тепловое расширение – Дополнение по сопротивлению материалов для энергетики
Основной корпус
Тепловое расширение
Цели обученияВ конце этого раздела вы должны уметь вычислять задачи, связанные с
- Неограниченным тепловым расширением
- Ограниченное тепловое расширение
Все материалы, подверженные изменению температуры, будут расширяться или сжиматься пропорционально их длине и перепаду температур.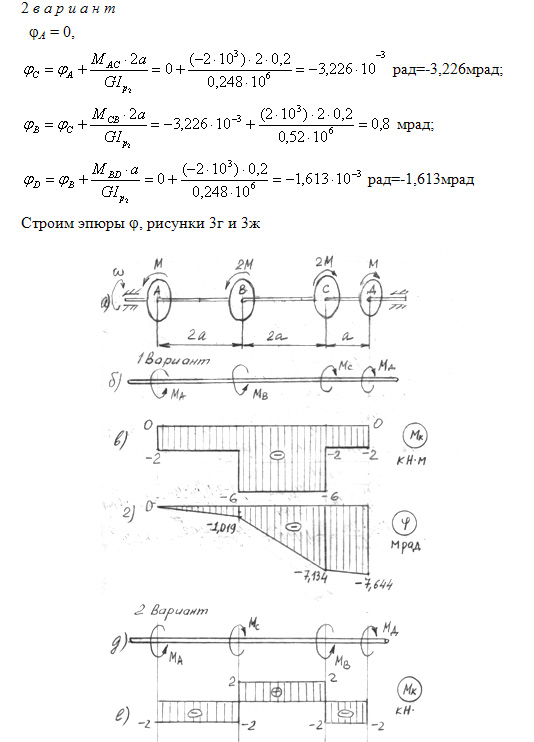 Некоторые материалы будут расширяться или сжиматься больше, чем другие; качественное свойство, показывающее, насколько они будут расширяться, известно как коэффициент линейного теплового расширения ( α ), измеряется в м/(м ºC) или (дюйм/дюйм ºF). Также можно использовать такие единицы, как 1/ºC или 1/ºF.
Некоторые материалы будут расширяться или сжиматься больше, чем другие; качественное свойство, показывающее, насколько они будут расширяться, известно как коэффициент линейного теплового расширения ( α ), измеряется в м/(м ºC) или (дюйм/дюйм ºF). Также можно использовать такие единицы, как 1/ºC или 1/ºF.
Изменение длины из-за теплового расширения рассчитывается с помощью:
, где δ — изменение длины, L — первоначальная длина (убедитесь, что обе они указаны в одних и тех же единицах измерения), а ΔT — разница температур.
Например, если сталь имеет коэффициент теплового расширения 11,7×10 -6 1/°C, это означает, что стержень длиной 1 м при повышении температуры на 1°C расширится на 11,7×10 -6 м, или 0,0117 мм. Это может показаться незначительной величиной, но если принять во внимание паровую трубу длиной 50 м, установленную при 12ºC и работающую при 212ºC (давление насыщения 2000 кПа), тепловое расширение будет эквивалентно 11,7 см или эквивалентной деформации 0,002. Это очень важно для проектировщиков трубопроводов, поскольку они должны учитывать это расширение или учитывать его при расчетах напряжения.
Это очень важно для проектировщиков трубопроводов, поскольку они должны учитывать это расширение или учитывать его при расчетах напряжения.
Объемное тепловое расширение твердых тел (изотропных материалов) рассчитывается аналогичным образом с использованием (3×α) в качестве коэффициента расширения. При расчете объемного расширения жидкостей коэффициент объемного расширения равен β с типичными значениями, указанными в The Engineering Toolbox.
Расширение трубопроводов
Как правило, трубопроводы имеют относительно большую длину и могут подвергаться значительному повышению температуры между монтажной и рабочей температурами. В результате могут возникнуть высокие напряжения теплового расширения, если опоры спроектированы неправильно. Кроме того, расширение трубы увеличивает нагрузку на патрубки машин и сосудов.
Холодная пружина трубы Существует множество статей и дискуссий по этой теме в группах проектирования трубопроводов, легко доступных через поиск в Интернете с использованием ключевых слов «труба холодная пружина» или «труба холодная протяжка»; это также рассматривается в ASME B31. 3.
3.
«Холодная пружина трубы» определяется как процесс преднамеренной деформации (обычно осуществляемой путем обрезки коротких или длинных участков трубы между двумя анкерами) трубы во время сборки для получения желаемого начального смещения и напряжения. Он также определяется как преднамеренное напряжение и упругая деформация трубопроводной системы во время цикла монтажа, чтобы позволить системе достичь более благоприятных реакций и напряжений в рабочем состоянии». [1]
Инженерам по эксплуатации рекомендуется ознакомиться с этой практикой, поскольку ее можно использовать в паровых трубах. Бывали случаи, когда наемные подрядчики при разборке паропроводов жаловались на то, что трубопроводы не подогнаны должным образом; трубы отскакивали назад при откручивании. Избегайте дорогостоящего ремонта и ненужных переделок, зная эту процедуру и зная свою установку.
Термические напряжения в композитных стержнях
«Композитная трубка состоит из двух различных сплавов, металлургически связанных друг с другом для достижения хороших свойств теплопередачи. Один сплав используется для защиты от коррозии, а другой часто используется в качестве одобренного материала для сосудов высокого давления.
Один сплав используется для защиты от коррозии, а другой часто используется в качестве одобренного материала для сосудов высокого давления.
Типичными областями применения композитных труб являются паровые котлы с агрессивными условиями, например:
- Котлы-утилизаторы черного щелока (BLRB)
- Охладители синтетического газа
- Котлы-утилизаторы
- Котлы-утилизаторы
Композитные трубы (композитные трубы) подходят для применений, когда условия снаружи и внутри трубы требуют свойств материала, которые не могут быть выполнены только одним материалом». [2]
Хотя студенты, изучающие энергетику, могут не увидеть непосредственного применения этих принципов, следующие типы задач являются частью их учебной программы 2 nd и 1 st .
Корпус А
На следующей диаграмме представлен типичный сценарий ограниченного теплового расширения с составными стержнями:
Учитывая все свойства и размеры материалов, цель состоит в том, чтобы рассчитать напряжение в каждом сечении при повышении температуры на заданное значение ΔT.
Когда стержни нагреты, каждый из них будет стремиться к расширению, эквивалентному их неограниченному ΔL. Учитывая, что расширение ограничено, каждый стержень будет подвергаться сжатию, что, в свою очередь, порождает сжимающие напряжения. Сумма двух соответствующих (пока еще воображаемых) деформаций сжатия будет равна сумме легко поддающихся количественному определению неограниченных тепловых расширений. Кроме того, учитывая, что силы, прилагаемые к каждому стержню, одинаковы (статическая/сбалансированная система), эту силу сжатия можно легко рассчитать. Учет площадей поперечного сечения каждого стержня приводит к нахождению напряжения, возникающего в каждом материале.
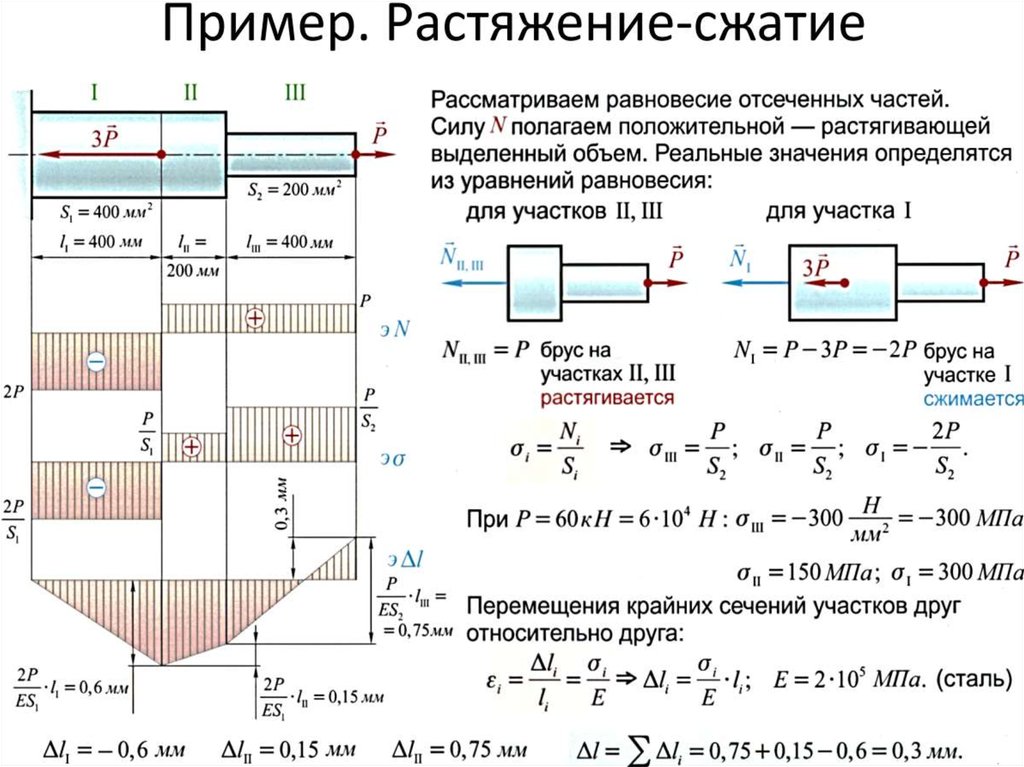
Чемодан Б
Во втором сценарии стержень закреплен с обоих концов внутри трубки из другого материала. При нагревании один материал расширялся бы больше, чем другой. Нижний расширяющийся материал будет вытягиваться наружу с натяжением вторым, который пытается расшириться больше. В свою очередь, материал, который свободно расширяется больше, втягивается (сжимается) материалом, расширяющимся меньше. Для пояснения см. следующий рисунок.
Для пояснения см. следующий рисунок.
Целью этого упражнения является определение напряжений, возникающих в каждом материале. Подход к решению этой задачи следующий.
- При нагревании латунная трубка натягивается стальным стержнем, создавая в трубке напряжение сжатия. Ограниченная деформация латунной трубы будет ( dL b – Y ), где Y – фактическая комбинированная деформация композитного стержня.
- Точно так же стальной стержень вытягивается латунной трубкой, создавая растягивающее напряжение. Фактическая (ограниченная) деформация стального стержня составляет ( Y-dL s ).
- Обратите внимание, что в приведенном выше dL указано свободное тепловое расширение каждого материала.
- Из диаграммы (dL b – Y) + (Y – dL s ) = dL b – dL s
- Подставьте в вышеприведенное dL=α×L×ΔT для каждого материала, разделите уравнение на L = исходная длина и найдите:
- ε латунь + ε сталь = (α латунь – α сталь ) × ΔT
- Подставьте E = σ / ε в вышеприведенное для каждого материала, и полученное уравнение представляет соотношение между напряжением в каждом материале, функцией только известных свойств упругого/термического расширения и разностью температур.

- (σ brass / E brass ) + (σ steel / E steel ) = (α brass – α steel ) × ΔT (eqn. B1)
- Второе уравнение основано на наблюдении, что внешнее тяговое усилие латуни равно внутреннему тяговому усилию стали. Это можно выразить как:
- σ Латунь × A Brass = σ Стальная × A Стальная (уравнение B2)
- Решите уравнение B2 для σ латуни и подставьте в уравнение B1. Решите уравнение B1 для α сталь и ваш окончательный результат зависит только от свойств материалов, поперечных сечений и разницы температур.
- Как только ответ σ сталь найден, вернитесь к уравнению B2 и найдите σ латунь .
- Это может показаться сложной задачей по математике/алгебре, и так оно и есть; однако это классическая задача со стандартным решением, что означает, что каждый вопрос будет решаться с использованием одного и того же подхода.
Проблема 1: Жаротрубный котел работает на бункерном мазуте. Резервуар-накопитель имеет открытую конструкцию, диаметр 2 м и высоту 3 м. Масло доливается при температуре окружающей среды 10ºC. Во время запуска температура резко повышается до 35ºC. На сколько сантиметров ниже верхней части бака вы можете заполнить бак, чтобы максимизировать объем масла и избежать утечки? Коэффициент линейного расширения материала резервуара составляет 12×10 -6 /ºC, а коэффициент объемного расширения масла составляет 9.×10 -4 /ºC.
Проблема 2: Во время установки болт корпуса турбины нагревается до 250ºC, а гайка затягивается так, чтобы не возникало напряжения (от руки). При остывании до рабочей температуры 50ºC болт надежно фиксирует узел. Определить растягивающее напряжение и деформацию болта, а также силу, воспринимаемую болтом. Эффективная длина болта 300 мм, диаметр 50 мм и болт E = 200 ГПа.
Определить растягивающее напряжение и деформацию болта, а также силу, воспринимаемую болтом. Эффективная длина болта 300 мм, диаметр 50 мм и болт E = 200 ГПа.
Задача 3: Новый надземный трубопровод будет транспортировать сырую нефть из Северной Альберты на юг. Для компенсации теплового расширения каждый прямой участок трубопровода будет оснащен гофрированными компенсаторами, допускающими осевое расширение на 23 мм и осевое сжатие на 18 мм (рисунок). Трубопровод будет проложен в начале лета, когда температура окружающего воздуха, по консервативным оценкам, может составлять 23ºC. Труба DN 600 Sch 40 и материал из углеродистой стали.
Определите максимальную длину прямой трубы между двумя опорными точками (в м) для экстремальных температур Альберты, предполагая, что из-за лесных пожаров температура металла трубы может достигать 100ºC. Для указанной длины трубы какое максимальное напряжение возникнет в материале, если тепловое расширение будет ограничено?
Задача 4: Прямая паровая труба диаметром 8 дюймов сортамента 40 установлена между двумя фиксированными анкерными опорами без учета расширения. Если сжимающее напряжение в трубе должно быть ограничено до 50,7 тысяч фунтов на квадратный дюйм при эксплуатации при температуре 430ºF, определите начальное растягивающее напряжение, которое должно быть приложено во время установки при температуре 60ºF. Какая эквивалентная растягивающая сила требуется для этой установки с холодными пружинами?
Если сжимающее напряжение в трубе должно быть ограничено до 50,7 тысяч фунтов на квадратный дюйм при эксплуатации при температуре 430ºF, определите начальное растягивающее напряжение, которое должно быть приложено во время установки при температуре 60ºF. Какая эквивалентная растягивающая сила требуется для этой установки с холодными пружинами?
Задача 5: Одноходовой двухтрубный теплообменник изготовлен из медных трубок номинальной толщины 1″ ASTM B88 типа K для внутренней трубы и стальных трубок номинального размера 2″ со средней толщиной стенки для внешней оболочки. Длина теплообменника 24″. Теплообменник собирается без напряжения при 20ºC, но в процессе эксплуатации температура стенок труб достигает 120ºC. Определите напряжения, создаваемые тепловым расширением как в стальных, так и в медных трубах. Использование:
- α сталь = 6,5×10 -6 дюйм/дюймºF; E сталь = 30×10 6 psi; данные о размерах из The Engineering Toolbox Steel Tubes
- α медь = 9,4×10 -6 дюйм/дюймºF; E медь = 17×10 6 psi; данные о размерах из Приложения D5 или медных трубок The Engineering Toolbox
Проблема 6: Порекомендуйте одно улучшение в этой главе.
Типы решений — различные типы, гомогенные и гетерогенные решения с видео
Определение решения
Решение определяется как
гомогенная смесь, которая в основном состоит из двух компонентов, а именно растворенного вещества и растворителя.
Например, соль и сахар — хорошая иллюстрация решения. Решение можно разделить на несколько компонентов.
Подробнее ⇒ Смесь гомогенная
Содержание
- Различные типы растворов
- Рекомендуемые видео
- Смеси
- Гомогенные и гетерогенные растворы
- Часто задаваемые вопросы – Часто задаваемые вопросы
На основании физического состояния растворители и растворенные вещества можно разделить на твердые, жидкие и газообразные растворы.
В твердых растворах растворенное вещество и растворитель находятся в твердом состоянии. Например, керамика и полимерные смеси. В жидких растворах твердое тело, газ или жидкость смешиваются в жидком состоянии. Газообразные растворы обычно представляют собой гомогенные смеси газов, таких как воздух. В зависимости от количества растворов и растворенных веществ его можно разделить на разбавленные и концентрированные растворы.
В жидких растворах твердое тело, газ или жидкость смешиваются в жидком состоянии. Газообразные растворы обычно представляют собой гомогенные смеси газов, таких как воздух. В зависимости от количества растворов и растворенных веществ его можно разделить на разбавленные и концентрированные растворы.
Различные типы растворов
В зависимости от степени растворения растворенного вещества в растворителе растворы можно разделить на перенасыщенные, ненасыщенные и насыщенные.
- A перенасыщенный раствор содержит большое количество растворенного вещества при температуре, при которой оно будет восстановлено, в результате чего лишнее растворенное вещество будет быстро кристаллизоваться.
- Ненасыщенный раствор — это раствор, в котором растворитель способен растворить любое большее количество растворенного вещества при данной температуре.
- Насыщенный раствор можно определить как раствор, в котором растворитель не способен растворять больше растворенного вещества при данной температуре.

Растворы бывают двух видов, в зависимости от того, является растворителем вода или нет.
- Водный раствор – Когда растворенное вещество растворяется в воде, раствор называется водным раствором. Например, соль в воде, сахар в воде и сульфат меди в воде.
- Неводный раствор – Когда растворенное вещество растворяется в растворителе, отличном от воды, это называется неводным раствором. Например, йод в четыреххлористом углероде, сера в сероуглероде, фосфор в этиловом спирте.
Растворы состоят из двух компонентов: растворителя и растворенного вещества. Другая классификация раствора зависит от количества растворенного вещества, добавленного к растворителю.
- A разбавленный раствор содержит небольшое количество растворенного вещества в большом количестве растворителя.
- Концентрированный раствор содержит большое количество растворенного вещества, растворенного в небольшом количестве растворителя.

Рекомендуемые видео
Смеси
Смесь состоит из двух или более веществ, но они не связаны химически. Напротив, соединение содержит различные элементы, которые связаны друг с другом. Например, рассмотрим смесь солей, то есть когда соль растворяется в воде, это смесь, но в идеале соли состоят из двух компонентов, а именно натрия и хлора.
Здесь натрий и хлор связаны друг с другом электростатической силой притяжения с образованием хлорида натрия, хотя в смеси нет химической связи между водой и солью. Следовательно, материя может быть классифицирована как смеси, соединения и элементы. Далее смеси можно классифицировать как гомогенные и гетерогенные смеси.
Подробнее ⇒ Смеси
Гомогенные и гетерогенные растворы
Гомогенные растворы — это растворы с однородным составом и свойствами по всему раствору. Например, чашка кофе, духи, сироп от кашля, раствор соли или сахара в воде и т. д.
Гетерогенные растворы — это растворы с неоднородным составом и свойствами по всему объему раствора. Раствор масла и воды, воды и мелового порошка и раствор воды и песка и др.
Раствор масла и воды, воды и мелового порошка и раствор воды и песка и др.
Примеры
Газированные напитки, смеси соленой воды или воды с сахаром и фруктовые соки являются некоторыми примерами растворов. Некоторые растворы носят гетерогенный характер и называются суспензиями.
Такие взвешенные частицы хорошо видны в растворе. Следовательно, при прохождении света через такие растворы он рассеивается в разные стороны. Лекарственные сиропы являются одним из лучших примеров этого.
Часто задаваемые вопросы – Часто задаваемые вопросы
Какое верное решение?
Истинный раствор представляет собой гомогенную комбинацию двух или более компонентов, погруженных в растворитель с размером частиц менее 10-9 мкм или 1 нм. Пример: Основной раствор сахара в воде. При использовании фильтровальной бумаги, часто незаметной невооруженным глазом, частицы невозможно отделить от реальных растворов.
Какой раствор уксуса?
Уксус, который может содержать ароматизаторы, представляет собой водный раствор уксусной кислоты и следовых химических веществ.
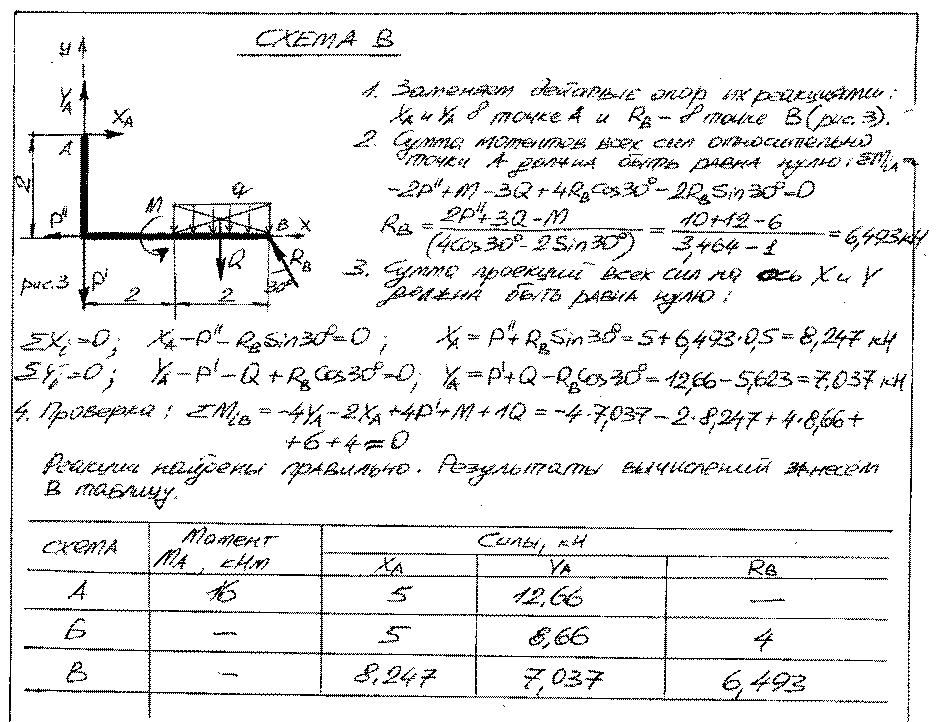 Определяет: площадь сечения, моменты инерции, моменты сопротивления.
Определяет: площадь сечения, моменты инерции, моменты сопротивления.

