Атаров М.М., Насонкин Ю.Д. Примеры решения задач по сопротивлению материалов
- Файлы
- Академическая и специальная литература
- Механика
- Сопротивление материалов
- Задачники и решебники по сопротивлению материалов
Сопротивление материалов
- формат djvu
- размер 3.
 56 МБ
56 МБ - добавлен 14 марта 2010 г.
Учебное пособие. Часть I
М.: МИСИ, 1990. -136 с.
В пособии рассмотрены задачи по определению напряженного и
деформированного состояний стержней и балок при растяжении-сжатии,
изгибе и кручении. Большое внимание уделено вопросам расчетов на
прочность по методу предельных состояний.
Пособие предназначено для студентов строительных специальностей
вузов, в первую очередь 29 . 03 , 29.04 и 39.12, изучающих курс
сопротивления материалов и теории упругости, пластичности и
ползучести в полном объеме.
Смотрите также
- формат pdf
- размер 1.1 МБ
- добавлен 15 апреля 2010 г.
Примеры решения задач к выполнению расчетно-проектировочных работ по сопротивлению материалов. Часть 1. Пример 1.1 Эпюры внутренних сил при центральном растяжении-сжатии. Пример 1.2 Построение эпюры крутящих моментов. Пример 1.3 Эпюры внутренних усилий при изгибе консольной балки. Пример 1.4 Эпюры при изгибе двухопорной балки. Пример 1.5 Эпюры при изгибе балки с подвесным пролетом. Пример 1.6 Растяжение с учетом собственного веса стержня. Пример…
Часть 1. Пример 1.1 Эпюры внутренних сил при центральном растяжении-сжатии. Пример 1.2 Построение эпюры крутящих моментов. Пример 1.3 Эпюры внутренних усилий при изгибе консольной балки. Пример 1.4 Эпюры при изгибе двухопорной балки. Пример 1.5 Эпюры при изгибе балки с подвесным пролетом. Пример 1.6 Растяжение с учетом собственного веса стержня. Пример…
- формат pdf
- размер 23.19 МБ
- добавлен 07 июля 2010 г.
Учебное пособие. – Барнаул: Изд-во АлтГТУ, 2010. – 124 с. В учебном пособии изложен лекционный материал по курсу сопротивления материалов, приведены примеры решения задач по основным видам расчетов.
- формат djvu
- размер 1.49 МБ
- добавлен 29 марта 2011 г.
Горький: Горьковский политехн. ин-т, 1986. – 104 с. В работе обобщается двадцатипятилетний опыт организации и проведения предметных олимпиад по сопротивлению материалов в Горьковском политехническом институте. Содержится около 250 оригинальных задач по сопротивлению материалов и строительной механике машин, описывается методика их решения. Работа рассчитана на студентов, участвующих в олимпиадах, и преподавателей, занимающихся руководством научно…
ин-т, 1986. – 104 с. В работе обобщается двадцатипятилетний опыт организации и проведения предметных олимпиад по сопротивлению материалов в Горьковском политехническом институте. Содержится около 250 оригинальных задач по сопротивлению материалов и строительной механике машин, описывается методика их решения. Работа рассчитана на студентов, участвующих в олимпиадах, и преподавателей, занимающихся руководством научно…
- формат djv
- размер 6.34 МБ
- добавлен 22 ноября 2008 г.
М.: Высшая школа, 1970. — 544 с. Руководство к решению задач по сопротивлению материалов. Разобраны примеры решения задач на изгиб балок, тонкостенных сосудов, устойчивость стержней.
- формат pdf
- размер 1.04 МБ
- добавлен 04 сентября 2009 г.
Учебное пособие для студентов всех механических специальностей очной и заочной форм обучения. Краматорск: ДГМА, 2005г. -168с. В учебном пособии даны основные сведения по сопротивлению материалов, которые читают студентам Донбасской государственной машиностроительной академии всех механических специальностей по первой части курса сопротивление материалов (по программе, рассчитанной на два семестра). Даны примеры расчета основных типов задач и рек…
Краматорск: ДГМА, 2005г. -168с. В учебном пособии даны основные сведения по сопротивлению материалов, которые читают студентам Донбасской государственной машиностроительной академии всех механических специальностей по первой части курса сопротивление материалов (по программе, рассчитанной на два семестра). Даны примеры расчета основных типов задач и рек…
- формат pdf
- размер 7.28 МБ
- добавлен 12 февраля 2009 г.
Сборник задач по сопротивлению материалов, для студентов технических университетов.
- формат djvu
- размер 5.5 МБ
- добавлен 26 апреля 2009 г.
«Высшая школа», 1967. 482c. Издание второе. Учебное пособие содержит краткое изложение основных положений курса «Сопротивление материалов», методические указания, примеры решения типовых задач.
- формат pdf
- размер 815.93 КБ
- добавлен 06 февраля 2009 г.
В сборнике представлены примеры решения задач для студентов большинства Российских вузов по темам: — Растяжение и сжатие: статически определимые системы статически неопределимые системы; — Кручение круглого бруса; — Изгиб плоских балок; — Геометрические характеристики плоских сечений; — Устойчивость сжатых стержней.
- формат pdf
- размер 852.48 КБ
- добавлен 25 октября 2008 г.
ГОСТы, СНиПы, формулы, эпюры и прочее. Все, что может пригодиться при решении задач по сопротивлению материалов
Практикум
- формат pdf
- размер 396.
 25 КБ
25 КБ - добавлен 26 марта 2011 г.
Улан-Удэ: Издательство ВСГТУ, 2006. — 60 с. Методические указания к выполнению расчетно-проектировочных работ по сопротивлению материалов для студентов инженерно-строительных специальностей очной и заочной форм обучения содержат примеры решений 12 типовых задач.
Подробные решения задач по теоретической механике с ответами
Здесь собраны основные примеры задач с решениями по теоретической механике. Рядом с условием задачи приводится ссылка на страницу с ее подробным решением и ответом. Задачи охватывают следующие разделы технической и теоретической механики: статика, кинематика, динамика материальной точки и системы тел.
Здесь приводятся условия задач по теоретической механике, имеющие подробные решения с ответами. Задачи сгруппированы по основным разделам теоретической механики: статика, кинематика и динамика. Чтобы посмотреть решение, нажмите на соответствующую ссылку в конце условия.
Чтобы посмотреть решение, нажмите на соответствующую ссылку в конце условия.
Статика
Условия задач
Найти графическим способом реакции опор балки AB, на которую действует сила P, приложенная в точке C.
Дано: P = 55 kH, AB = 10 м, AC = 7 м, BC = 3 м.
Решение
Найти реакции опор для того способа закрепления, при котором момент MA в опоре A имеет наименьшее значение.
Решение
Найти реакции опор балки.
Решение
Найти реакции опор составной конструкции.
Решение
Определить реакции стержней, поддерживающих тонкую однородную прямоугольную плиту в трехмерном пространстве.
Решение
Кинематика
Кинематика материальной точки
Определение скорости и ускорения точки по заданным уравнениям ее движения
Дано: Уравнения движения точки: x = 12 sin(πt/6), см; y = 6 cos2(πt/6), см.
Установить вид ее траектории и для момента времени t = 1 с найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Решение задачи
Поступательное и вращательное движение твердого тела
Дано:
t = 2 с; r1 = 2 см, R1 = 4 см; r2 = 6 см, R2 = 8 см; r3 = 12 см, R3 = 16 см; s5 = t3 – 6t (см).
Определить в момент времени t = 2 скорости точек A, C; угловое ускорение колеса 3; ускорение точки B и ускорение рейки 4.
Решение
Кинематический анализ плоского механизма
Дано:
R1, R2, L, AB, ω1.
Найти: ω2.
Решение с помощью
теоремы о проекциях скоростей
Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна E. Стержни соединены с помощью цилиндрических шарниров. Точка D расположена в середине стержня AB.
Дано: ω1, ε1.
Найти: скорости VA, VB, VD и VE; угловые скорости ω2, ω3 и ω4; ускорение aB; угловое ускорение εAB звена AB; положения мгновенных центров скоростей P2 и P3 звеньев 2 и 3 механизма.
Решение
Определение абсолютной скорости и абсолютного ускорения точки
Прямоугольная пластина вращается вокруг неподвижной оси по закону φ = 6t 2 – 3t 3 . Положительное направление отсчета угла φ показано на рисунках дуговой стрелкой. Ось вращения OO 1 лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой BD движется точка M . Задан закон ее относительного движения, т. е. зависимость s = AM = 40(t – 2t 3) – 40 (s — в сантиметрах, t — в секундах). Расстояние b = 20 см. На рисунке точка M показана в положении, при котором s = AM > 0 (при s < 0 точка M находится по другую сторону от точки A).
Найти абсолютную скорость и абсолютное ускорение точки M в момент времени t 1 = 1 с.
Решение задачи
Динамика
Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил
Рисунок к условию задачи.

Груз S, рассматриваемый как материальная точка массы m = 5кг, движется по шероховатой поверхности от точки A до точки B, в которой отрывается от поверхности и продолжает движение в воздухе до падения на наклонную поверхность в точке C. Движение происходит в плоскости рисунка.
В точке A, груз имел скорость vA = 1 м/с. Скорость в точке B: vB = 4 м/с. Участок AB представляет собой плоскую поверхность с углом наклона α = 30° к горизонту. На участке AB, кроме силы тяжести и силы трения, на груз действует постоянная сила Q = 10 Н, направленная под углом φ = 45° к поверхности. Коэффициент трения f = 0,1.
На участке BC, груз движется под действием только силы тяжести. Сопротивлением воздуха пренебречь. Поверхность, на которую падает груз, является плоской с углом наклона β = 15° к горизонту (см. рисунок). Точка D расположена ниже точки B на расстояние |BD| = h = 1 м.
Найти: Время движения tAB на участке AB; длину этого участка; время падения tBC от точки B к точке C; расстояние |DC|; уравнение траектории BC.
Решение задачи
Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием переменных сил
Рисунок к условию задачи.
Груз D массой m, получив в точке A начальную скорость V0, движется в изогнутой трубе ABC, расположенной в вертикальной плоскости. На участке AB, длина которого l, на груз действует постоянная сила T(ее направление показано на рисунке) и сила R сопротивления среды (модуль этой силы R = μV2, вектор R направлен противоположно скорости V груза).
Груз, закончив движение на участке AB, в точке B трубы, не изменяя значения модуля своей скорости, переходит на участок BC. На участке BC на груз действует переменная сила F, проекция Fx которой на ось x задана.
Считая груз материальной точкой, найти закон его движения на участке BC, т.е. x = f(t), где x = BD. Трением груза о трубу пренебречь.
Решение задачи
Теорема о движении центра масс системы
Найти перемещение плиты и реакцию направляющих.
Механическая система состоит из грузов D1, D2 и прямоугольной вертикальной плиты, движущейся вдоль горизонтальных направляющих. В момент времени t0=0, когда система находилась в покое, под действием внутренних сил грузы начинают двигаться по желобам, представляющим собой окружности.
Считая грузы материальными точками, и пренебрегая всеми сопротивлениями, определить закон движения плиты x3=f3(t) и полной нормальной реакции направляющих N=f(t).
Решение
В кривошипно-шатунном механизме кривошип OA и шатун AB представляют собой однородные стержни массой m1 и длиной l. Ползун B массой m2 движется в вертикальных направляющих. Определить вертикальную составляющую реакции шарнира O в функции угла φ, если кривошип вращается с постоянной угловой скоростью ω. Трением в направляющих ползуна пренебречь.
Решение
Теорема об изменении количества движения системы
Условие задачи. Плита 1 с движущимся грузом D.
Плита 1 с движущимся грузом D. Механическая система состоит из прямоугольной вертикальной плиты 1, движущейся вдоль горизонтальных направляющих, и груза D. В момент времени t0=0, когда скорость плиты u0, груз под действием внутренних сил начинает двигаться по прямолинейному желобу плиты. При этом расстояние s=AD изменяется по закону s=0,6 cos(πt2/4).
Считая груз материальной точкой, и пренебрегая всеми сопротивлениями, определить скорость плиты u1 в момент времени t1.
Решение
Теорема об изменении кинетического момента системы
Условие задачи. Найти угловую скорость плиты 1 с движущимся грузом 2. Однородная круглая радиуса R = 1,2 м горизонтальная платформа массой m1 = 24 кг вращается с угловой скоростью ω0 = 10 с-1 вокруг вертикальной оси z, отстоящей от центра масс C платформы на расстоянии OC = b = R/2.
В момент времени t0 = 0 с по желобу платформы, под действием внутренних сил, начинает двигаться груз D массой m2 = 10 кг по закону s = AD = 0,6t3, где s выражено в метрах, t – в секундах. Одновременно на платформу действует пара сил с моментом M = 2 + 3t2 (в ньютон-метрах).
Одновременно на платформу действует пара сил с моментом M = 2 + 3t2 (в ньютон-метрах).
Определить зависимость угловой скорости платформы как функцию времени.
Решение
Через блок перекинут канат; за точку A каната ухватился человек, к точке B подвязан груз одинаковой массы с человеком. Что произойдет с грузом, если человек станет подниматься по канату со скоростью v относительно каната? Масса блока в четыре раза меньше массы человека, и равномерно распределена по его ободу. Решение
Теорема об изменении кинетической энергии механической системы
Рисунок к условию задачи. Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3, блока 4 и подвижного блока 5. Заданы радиусы ступеней и радиусы инерции шкива 3 и блока 4. Блок 5 считать сплошным однородным цилиндром. Коэффициент трения груза 2 о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3. Участки нитей параллельны соответствующим плоскостям. К подвижному блоку 5 прикреплена пружина с коэффициентом жесткости с.
Участки нитей параллельны соответствующим плоскостям. К подвижному блоку 5 прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя. Деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент M сил сопротивления (от трения в подшипниках).
Заданы массы тел m1, m2, m3 , m4, m5, коэффициент жесткости пружины c, зависимость силы от перемещения F = f(s), величина момента M.
Определить значение центра масс тела 5 VC5 в тот момент времени, когда перемещение s груза 1 станет равным s1 = 0,2 м.
Решение задачи
Применение общего уравнения динамики к исследованию движения механической системы
Механическая система Механическая система состоит из однородных ступенчатых шкивов 1 и 2, обмотанных нитями, грузов 3-6, прикрепленных к этим нитям, и невесомого блока.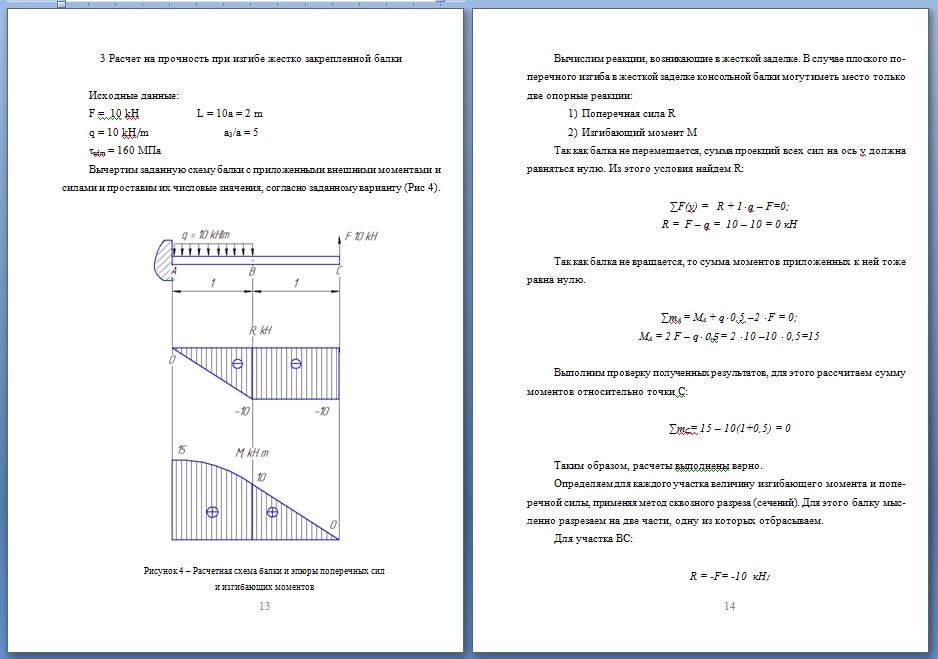 Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом M = 10 Н·м, приложенной к шкиву 1. Заданы радиусы ступеней шкивов, их радиусы инерции относительно осей вращения, а также веса шкивов и грузов. Грузы, веса которых равны нулю, на чертеже не изображать.
Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом M = 10 Н·м, приложенной к шкиву 1. Заданы радиусы ступеней шкивов, их радиусы инерции относительно осей вращения, а также веса шкивов и грузов. Грузы, веса которых равны нулю, на чертеже не изображать.
Пренебрегая трением, определить ускорение груза 5.
Решение
Применение принципа Даламбера к определению реакций опор вращающегося тела
Рисунок к условию задачи.Вертикальный вал AK, вращающийся равномерно с угловой скоростью ω = 10 с-1, закреплен подпятником в точке A и цилиндрическим подшипником в точке K.
К валу жестко прикреплены невесомый стержень 1 длиной l1 = 0,3 м, на свободном конце которого расположен груз массой m1 = 4 кг, и однородный стержень 2 длиной l2 = 0,6 м, имеющий массу m2 = 8 кг. Оба стержня лежат в одной вертикальной плоскости. Точки прикрепления стержней к валу, а также углы α и β заданы. Размеры AB=BD=DE=EK=b, где b = 0,4 м. Груз принять за материальную точку.
Точки прикрепления стержней к валу, а также углы α и β заданы. Размеры AB=BD=DE=EK=b, где b = 0,4 м. Груз принять за материальную точку.
Пренебрегая массой вала, определить реакции подпятника и подшипника.
Решение
Решение главы 05 — напряжения в балке
Решение главы 05 — напряжения в балке — сопротивление материалов по ЗингеруРеклама
Реклама
Реклама
Реклама
1 из 69
Верхний обрезанный слайд
Скачать для чтения офлайн
Машиностроение
Решения — Прочность материалов по Зингеру — Глава -05 — напряжения в балке.
Объявление
Объявление
Решение главы 05 — напряжения в балке — Сопротивление материалов по Зингеру
- Напряжения в балках
Силы и пары, действующие на балку, вызывают изгиб (изгибные напряжения) и сдвиг.
напряжения в любом поперечном сечении балки и прогиб перпендикулярно
продольная ось балки.
 Если к концам балки приложены пары и нет
на него действуют силы, изгиб называется чистым изгибом. Если силы производят изгиб,
изгиб называется обычным изгибом.
ПРЕДПОЛОЖЕНИЯ
При использовании следующих формул для изгибающих и касательных напряжений предполагается, что
плоское сечение балки по нормали к ее продольной оси до нагружения остается плоским
после приложения сил и пар, и что балка изначально прямая
и однородного поперечного сечения и что модули упругости при растяжении и
сжатия равны.
Формула изгиба
Напряжения, вызванные изгибающим моментом, известны как изгибные или изгибающие напряжения.
Предположим, что балка нагружена, как показано на рисунке.
Рассмотрим волокно на расстоянии y от нейтральной оси из-за кривизны луча,
под действием изгибающего момента волокно растягивается на величину cd. Поскольку
кривизна луча очень мала, bcd и Oba считаются подобными треугольниками.
Натяжение этого волокна равно
По закону Гука ε = σ/E, тогда
что означает, что напряжение пропорционально расстоянию y от нейтральной оси.
Если к концам балки приложены пары и нет
на него действуют силы, изгиб называется чистым изгибом. Если силы производят изгиб,
изгиб называется обычным изгибом.
ПРЕДПОЛОЖЕНИЯ
При использовании следующих формул для изгибающих и касательных напряжений предполагается, что
плоское сечение балки по нормали к ее продольной оси до нагружения остается плоским
после приложения сил и пар, и что балка изначально прямая
и однородного поперечного сечения и что модули упругости при растяжении и
сжатия равны.
Формула изгиба
Напряжения, вызванные изгибающим моментом, известны как изгибные или изгибающие напряжения.
Предположим, что балка нагружена, как показано на рисунке.
Рассмотрим волокно на расстоянии y от нейтральной оси из-за кривизны луча,
под действием изгибающего момента волокно растягивается на величину cd. Поскольку
кривизна луча очень мала, bcd и Oba считаются подобными треугольниками.
Натяжение этого волокна равно
По закону Гука ε = σ/E, тогда
что означает, что напряжение пропорционально расстоянию y от нейтральной оси.
- Учитывая дифференциальную площадь dA на расстоянии y от N.A., сила, действующая на площадь Равнодействующая всех элементарных моментов относительно Н.А. должна быть равна изгибающему момент на секции. но потом подставляя ρ = Ey / fb затем и Напряжение изгиба из-за кривизны балок равно
- Кривизна балки:
где ρ — радиус кривизны балки в мм (дюймах), M — изгибающий момент в
Н·мм (фунт·дюйм), fb — изгибающее напряжение в МПа (psi), I — центральный момент инерции
в мм4
(in4
), а c — расстояние от нейтральной оси до самого дальнего волокна в мм.
(в).
МОДУЛЬ СЕЧЕНИЯ
В формуле
отношение I/c называется модулем сопротивления сечения и обычно обозначается S с единицами измерения в мм3.
(в3
). Тогда максимальное напряжение изгиба можно записать как
Эта форма удобна тем, что значения S имеются в справочниках для широкого
ряд стандартных конструктивных форм.
Решенные проблемы в формуле изгиба
Проблема 503
Консольная балка шириной 50 мм, высотой 150 мм и длиной 6 м несет нагрузку,
изменяется равномерно от нуля на свободном конце до 1000 Н/м у стенки.
 (а) Вычислите
величина и местонахождение максимального изгибающего напряжения. (b) Определите тип и
величина напряжения в волокне в 20 мм от вершины балки на сечении 2 м
со свободного конца.
(а) Вычислите
величина и местонахождение максимального изгибающего напряжения. (b) Определите тип и
величина напряжения в волокне в 20 мм от вершины балки на сечении 2 м
со свободного конца. - Решение 503
- Проблема 504 Свободно поддерживаемая балка шириной 2 дюйма, высотой 4 дюйма и длиной 12 футов подвергается воздействию сосредоточенная нагрузка 2000 фунтов в точке на расстоянии 3 фута от одной из опор. Обозначить максимальное напряжение волокна и напряжение в волокне, расположенном на расстоянии 0,5 дюйма от вершины балки в середине. Решение 504
- Проблема 505
Ленточная пила из высокопрочной стали шириной 20 мм и толщиной 0,80 мм наезжает на шкивы 600
мм в диаметре. Какое максимальное изгибное напряжение развивается? Какой минимальный диаметр
шкивы можно использовать без превышения напряжения изгиба 400 МПа? Предположим, что Е = 200.
ГПа.
Решение 505
Задача 506
Плоский стальной стержень шириной 1 дюйм, толщиной ¼ дюйма и длиной 40 дюймов сгибают попарно.
 применяется на концах так, чтобы отклонение средней точки составляло 1,0 дюйм. Вычислить напряжение в
планка и величина пар. Используйте Е = 29× 106
фунтов на квадратный дюйм
Решение 506
применяется на концах так, чтобы отклонение средней точки составляло 1,0 дюйм. Вычислить напряжение в
планка и величина пар. Используйте Е = 29× 106
фунтов на квадратный дюйм
Решение 506 - Проблема 507 При лабораторных испытаниях балки, нагруженной концевыми парами, волокна в слое AB на рис. 507 увеличиваются на 60 × 10–3. мм, тогда как при CD уменьшаются на 100 × 10–3 мм на колеи 200 мм. Используя E = 70 ГПа, определите изгибное напряжение в верхней и нижние волокна. Решение 507
- Проблема 508 Определить минимальную высоту h балки, показанной на рис. П-508, если изгибное напряжение не должно превышать 20 МПа.
- Решение 508
Задача 509Секция, используемая в самолетах, состоит из труб, соединенных тонкими перемычками, как показано на рис.
Рис. П-509. Каждая трубка имеет площадь поперечного сечения 0,20 дюйма2. Если среднее напряжение в
трубы не должно превышать 10 тысяч фунтов на квадратный дюйм, определите общую равномерно распределенную нагрузку, которая может быть
поддерживается простым пролетом длиной 12 футов.
 Эффектом паутины пренебречь.
Эффектом паутины пренебречь. - Решение 509 Проблема 510 В качестве свободно опертой балки длиной 3 м используется стержень диаметром 50 мм. Обозначить наибольшая равномерно распределенная нагрузка, которая может быть приложена к правым двум третям балки, если изгибное напряжение ограничено 50 МПа.
- Решение 510 Задача 511 Свободно опертая прямоугольная балка шириной 2 дюйма и глубиной 4 дюйма несет равномерно распределенная нагрузка 80 фунтов/фут по всей длине. Какова максимальная длина балка, если изгибное напряжение ограничено до 3000 фунтов на квадратный дюйм? Решение 511
- Проблема 512
Круглый стержень диаметром 1 дюйм, показанный на рис. P-512, согнут в полукруг с
средний радиус 2 фута. Если P = 400 фунтов и F = 200 фунтов, рассчитайте максимальное напряжение изгиба
развиты в разделе а-а. Деформацией стержня пренебречь.
Решение 512
Задача 513
Прямоугольная стальная балка шириной 2 дюйма и глубиной 3 дюйма нагружена, как показано на рис. P-513.
Определить величину и местонахождение максимального напряжения изгиба.

- Решение 513
- Проблема 514 Прямоугольная рама, показанная на рис. П-514, несет равномерно распределенную нагрузку эквивалентно 200 Н на каждый метр горизонтальной проекции рамы; то есть общая нагрузка 1000 Н. Рассчитайте максимальное изгибающее напряжение в сечении а-а, если поперечное сечение составляет 50 мм кв. Решение 514
- Проблема 515 Повторить проб. 524, чтобы найти максимальное изгибающее напряжение в сечении b-b. Решение 515 Задача 516 Деревянная балка AB шириной 6 дюймов, глубиной 10 дюймов и длиной 10 футов поддерживается растяжкой. АС в положении, показанном на рис. П-516. Балка несет нагрузку, в том числе и собственную вес, 500 фунтов на каждый фут его длины. Рассчитайте максимальное изгибающее напряжение при середина луча.
- Решение 516
Задача 517
Прямоугольный стальной стержень шириной 15 мм, высотой 30 мм и длиной 6 м свободно поддерживается.
на его концах. Если плотность стали 7850 кг/м3
, определить максимальный изгиб
напряжение, вызванное весом стержня.
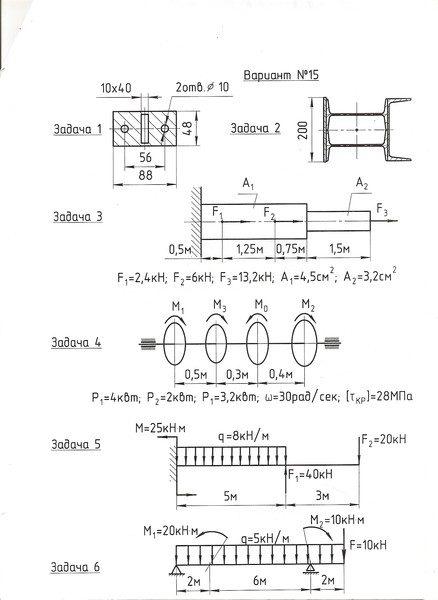 Решение 517
Решение 517 - Проблема 518 Консольная балка длиной 4 м состоит из двух швеллеров С200×28, склепанных между собой назад. Какой равномерно распределенный груз можно нести, кроме веса балки, не превышающей напряжения изгиба 120 МПа, если (а) стенки вертикальны и б) перемычки горизонтальны? Обратитесь к Приложению B учебника для свойств канала. Решение 518
- Проблема 519 30-футовая балка, свободно поддерживаемая на расстоянии 6 футов от любого конца, несет равномерно распределенную нагрузка интенсивности wo по всей его длине. Балка изготовлена сваркой двух S18×70 (см. приложение B к учебнику) секций вдоль их фланцев, чтобы образовать секцию, показанную на рис. Рис. П-519. Рассчитайте максимальное значение wo, если напряжение изгиба ограничено 20 тысячами фунтов на квадратный дюйм. Не забудьте указать вес балки. Решение 519
- Проблема 520
Балка сечением S310×74 (см. приложение Б учебника) используется как просто
опорная балка длиной 6 м. Найдите максимальную равномерно распределенную нагрузку, которую можно
применяется по всей длине балки, в дополнение к весу балки, если
изгибное напряжение не должно превышать 120 МПа.
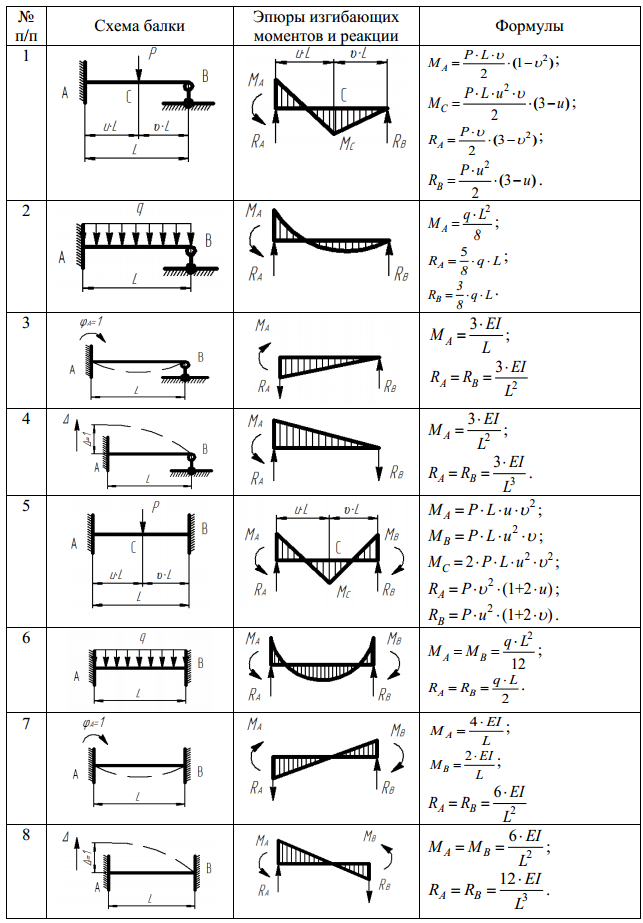 Решение 520
Решение 520 - Проблема 521 Балка, изготовленная из двух швеллеров C10 × 30, скрепленных вплотную друг к другу, просто опирается на заканчивается. Балка поддерживает центральную сосредоточенную нагрузку в 12 тысяч фунтов и равномерно распределенная нагрузка 1200 фунтов/фут, включая вес балки. Вычислить максимум длина балки, если изгибное напряжение не должно превышать 20 тысяч фунтов на квадратный дюйм. Решение 521
- Проблема 522 Коробчатая балка состоит из четырех досок размером 2 дюйма на 8 дюймов, надежно закрепленных шипами. вместе, чтобы сформировать сечение, показанное на рис. P-522. Покажите, что ИНА = 981,3 дюйма4 . Если wo = 300 фунт/фут, найти P, чтобы вызвать максимальное напряжение изгиба 1400 фунтов на квадратный дюйм. Решение 522 Задача 523 Решить задачу. 522, если wo = 600 фунтов/фут.
- Решение 523
- Проблема 524
Балка с сечением S380 × 74 несет общую равномерно распределенную нагрузку 3 Вт.
и сосредоточенная нагрузка W, как показано на рис.
 П-524. Определить W, если
изгибное напряжение ограничено 120 МПа.
Решение 524
П-524. Определить W, если
изгибное напряжение ограничено 120 МПа.
Решение 524 - Проблема 525 Квадратная деревянная балка, используемая в качестве железнодорожной шпалы, опирается на равномерно распределенную нагрузки и несет две равномерно распределенные нагрузки, каждая из которых в сумме составляет 48 кН, как показано на рис. P- 525. Определить размер сечения, если максимальное напряжение ограничено 8 МПа. Решение 525 Задача 526 Деревянная балка шириной 6 дюймов и глубиной 12 дюймов нагружена, как показано на рис. P-526. Если максимум изгибное напряжение составляет 1200 фунтов на квадратный дюйм, найдите максимальные значения wo и P, которые могут быть применены одновременно?
- Решение 526
- Проблема 527 В Проб. 526, если нагрузка на свес составляет 600 фунтов/фут, а длина свеса x футов, найдите максимальные значения P и x, которые можно использовать одновременно. Решение 527
- Экономические отделы
Из формулы изгиба fb = My / I видно, что напряжение изгиба в
нейтральная ось, где y = 0, равна нулю и линейно возрастает наружу.
 Это означает, что для
прямоугольное или круглое сечение большая часть поперечного сечения ближе к середине
участок недонагружен.
Для стальных балок или композитных балок вместо прямоугольной формы
площадь может быть организована таким образом, чтобы дать больше площади на внешнем волокне и сохранить
такая же общая глубина и экономия большого веса.
При использовании широкой полки или двутаврового сечения для длинных балок сжатые полки
имеют тенденцию к горизонтальному изгибу в стороны. Это коробление представляет собой эффект колонны, который может быть
предотвращается за счет обеспечения боковой поддержки, такой как система пола, так что полная допустимая
напряжения могут быть использованы, в противном случае напряжение должно быть уменьшено. Снижение стрессов
для этих балок будет обсуждаться стальная конструкция. При выборе конструктивного элемента
используется как балка, момент сопротивления должен быть равен или больше приложенного
изгибающий момент. Примечание: ( fb )max = M/S.
Приведенное выше уравнение показывает, что требуемый модуль поперечного сечения балки должен быть
равным или превышающим отношение изгибающего момента к максимально допустимому напряжению.
Это означает, что для
прямоугольное или круглое сечение большая часть поперечного сечения ближе к середине
участок недонагружен.
Для стальных балок или композитных балок вместо прямоугольной формы
площадь может быть организована таким образом, чтобы дать больше площади на внешнем волокне и сохранить
такая же общая глубина и экономия большого веса.
При использовании широкой полки или двутаврового сечения для длинных балок сжатые полки
имеют тенденцию к горизонтальному изгибу в стороны. Это коробление представляет собой эффект колонны, который может быть
предотвращается за счет обеспечения боковой поддержки, такой как система пола, так что полная допустимая
напряжения могут быть использованы, в противном случае напряжение должно быть уменьшено. Снижение стрессов
для этих балок будет обсуждаться стальная конструкция. При выборе конструктивного элемента
используется как балка, момент сопротивления должен быть равен или больше приложенного
изгибающий момент. Примечание: ( fb )max = M/S.
Приведенное выше уравнение показывает, что требуемый модуль поперечного сечения балки должен быть
равным или превышающим отношение изгибающего момента к максимально допустимому напряжению. А
проверка, включающая вес выбранной балки, необходима для завершения
расчет. При проверке момент сопротивления балки должен быть равен или больше
сумма момента динамической нагрузки, вызванного приложенными нагрузками, и момента постоянной нагрузки
из-за собственного веса балки.
Разделив обе части вышеприведенного уравнения на ( fb )max, получим проверочное уравнение
Предположим, что балки в следующих задачах надлежащим образом закреплены на боковых опорах.
отклонение. Не забудьте указать вес самой балки.
А
проверка, включающая вес выбранной балки, необходима для завершения
расчет. При проверке момент сопротивления балки должен быть равен или больше
сумма момента динамической нагрузки, вызванного приложенными нагрузками, и момента постоянной нагрузки
из-за собственного веса балки.
Разделив обе части вышеприведенного уравнения на ( fb )max, получим проверочное уравнение
Предположим, что балки в следующих задачах надлежащим образом закреплены на боковых опорах.
отклонение. Не забудьте указать вес самой балки. - Решенные задачи в экономических разделах Задача 529 Свободно опертая на концах балка длиной 10 м несет равномерно распределенную нагрузку 16 кН/м по всей длине. Какой самый легкий луч W-образной формы, который не превышает изгибное напряжение 120 МПа? Каково фактическое максимальное напряжение в выбранной балке? Решение 529
- Проблема 530 Повторить проб. 529, если распределенная нагрузка 12 кН/м и длина балки 8 м. Решение 530
- Проблема 531
15-футовая балка, свободно опертая на концах, несет сосредоточенную нагрузку 9000 фунтов в
середина пролета Выберите самую легкую S-образную секцию, которую можно использовать при допустимом напряжении
18 фунтов на квадратный дюйм.
 Каково фактическое максимальное напряжение в выбранной балке?
Решение 531
Каково фактическое максимальное напряжение в выбранной балке?
Решение 531 - Проблема 532 Балка, свободно опертая на концах пролета 25 футов, несет равномерно распределенную нагрузку. 1000 фунтов/фут по всей длине. Выберите самую легкую секцию S, которую можно использовать, если допустимое напряжение составляет 20 тысяч фунтов на квадратный дюйм. Каково фактическое максимальное напряжение в выбранной балке? Решение 532
- Проблема 533 Балка, просто поддерживаемая на пролете 36 футов, несет равномерно распределенную нагрузку 2000 фунт/фут в середине 18 футов. Используя допустимое напряжение 20 тысяч фунтов на квадратный дюйм, определите самую легкую подходящая W-образная балка. Каково фактическое максимальное напряжение в выбранной балке? Решение 533
- Проблема 534 Повторить проб. 533, если равномерно распределенная нагрузка изменена на 5000 фунтов/фут. Решение 534
- Проблема 535
Свободно поддерживаемая балка длиной 24 фута несет равномерно распределенную нагрузку в 2000 фунтов/фут.
 по всей длине и сосредоточенной нагрузке 12 тысяч фунтов на расстоянии 8 футов от левого конца. Если
допустимое напряжение составляет 18 тысяч фунтов на квадратный дюйм, выберите самую легкую подходящую W-образную форму. Что на самом деле
максимальное напряжение в выбранной балке?
Решение 535
по всей длине и сосредоточенной нагрузке 12 тысяч фунтов на расстоянии 8 футов от левого конца. Если
допустимое напряжение составляет 18 тысяч фунтов на квадратный дюйм, выберите самую легкую подходящую W-образную форму. Что на самом деле
максимальное напряжение в выбранной балке?
Решение 535 - Проблема 536 Свободно опертая балка длиной 10 м несет равномерно распределенную нагрузку 20 кН/м. по всей длине и сосредоточенной нагрузкой 40 кН в середине пролета. Если допустимый напряжение 120 МПа, определите самую легкую W-образную балку, которую можно использовать. Решение 536
- Каркас пола
В каркасе пола черный пол поддерживается световыми балками, называемыми балками пола или просто
балки, которые, в свою очередь, поддерживаются более тяжелыми балками, называемыми балками, затем балки проходят через
загрузить в столбцы. Обычно балка действует как свободно опертая балка, несущая равномерную нагрузку.
величины p на площади sL,
где
p = нагрузка на пол на единицу площади
L = длина (или пролет) балки
s = расстояние между центрами балок и
wo = sp = интенсивность распределенной нагрузки на балку.

- Решенные проблемы в каркасе пола Задача 538 Балки перекрытий шириной 50 мм и высотой 200 мм, свободно опертые на пролете 4 м, несут пол с нагрузкой 5 кН/м2 . Вычислите расстояние между центральными линиями балок, чтобы разработать напряжение изгиба 8 МПа. Какую безопасную нагрузку на пол можно нести на расстоянии между осями 0,40 м? Решение 538
- Проблема 539
Бревна размером 12 дюймов на 12 дюймов, расположенные на расстоянии 3 фута друг от друга по центрам, вбиваются в
заземляются и действуют как консольные балки для поддержки шпунтовой сваи перемычки. Что
максимальная безопасная высота воды за плотиной, если вес воды = 62,5 фунта/фут3
и (фб
)макс = 1200 фунтов на квадратный дюйм?
Решение 539
Задача 540
Бревна шириной 8 дюймов, глубиной 12 дюймов и длиной 15 футов, поддерживаемые сверху и
дно, поддержите плотину, сдерживающую воду глубиной 9 футов. Вода весит 62,5 фунта/фут3
. (а)
Вычислите расстояние между центральными линиями бревен, чтобы получить fb = 1000 фунтов на квадратный дюйм.
 (б) Будет ли это
расстояние будет безопасным, если максимальное fb, ( fb )max = 1600 фунтов на квадратный дюйм, и вода достигает своего
максимальная глубина 15 футов?
(б) Будет ли это
расстояние будет безопасным, если максимальное fb, ( fb )max = 1600 фунтов на квадратный дюйм, и вода достигает своего
максимальная глубина 15 футов? - Решение 540
- Проблема 541 Балки перекрытий длиной 18 футов в здании просто поддерживаются на концах и несут нагрузку. нагрузка на пол 0,6 фунта/дюйм2 . Если балки имеют сечение W10 × 30, определите осевую линию расстояние с использованием допустимого изгибающего напряжения 18 тысяч фунтов на квадратный дюйм. Решение 541
- Проблема 542 Выберите самые легкие секции W-образной формы, которые можно использовать для балок и ферм в Иллюстративная задача 537 учебника, если допустимое изгибающее напряжение равно 120 МПа. Пренебрегать веса членов. Решение 542
- Проблема 543
Часть плана этажа здания показана на рис. P-543. Общая загрузка
(включая динамические и стационарные нагрузки) в каждом отсеке, как показано на рисунке. Выберите самый легкий подходящий W, если
допустимое изгибное напряжение 120 МПа.
 Решение 543
Решение 543 - Несимметричные балки
Изгибное напряжение изменяется прямолинейно с расстоянием от нейтральной оси. Таким образом, для
симметричное сечение, такое как широкий фланец, сжимающие и растягивающие напряжения будут
одинаковый. Это будет желательно, если материал одинаково прочен как на растяжение, так и на
сжатие. Однако есть материалы, такие как чугун, которые прочны в
сжатие, чем растяжение. Поэтому желательно использовать балку с несимметричным
поперечное сечение, дающее большую площадь в сжимаемой части, что делает волокно более прочным
находится на большем расстоянии от нейтральной оси, чем более слабое волокно. Что-нибудь из этого
разделы показаны ниже.
Соотношение этих секций таково, что отношение расстояния нейтральной
оси от крайних волокон при растяжении и при сжатии такое же, как отношение
допустимые напряжения растяжения и сжатия. Таким образом, допустимые напряжения равны
достигли одновременно.
В этом разделе будут использоваться следующие обозначения:
fbt = напряжение изгиба волокна при растяжении
fbc = напряжение изгиба волокна при сжатии
NA = нейтральная ось
yt = расстояние натянутого волокна от N.
 A.
yc = расстояние волокна при сжатии от N.A.
Mr = момент сопротивления
Mc = момент сопротивления при сжатии
Mt = момент сопротивления растяжению
A.
yc = расстояние волокна при сжатии от N.A.
Mr = момент сопротивления
Mc = момент сопротивления при сжатии
Mt = момент сопротивления растяжению - Решенные проблемы в несимметричных балках Задача 548 Перевернутое тавровое сечение свободно опертой балки длиной 4 м имеет свойства, показанные на рис. Р-548. Балка несет равномерно распределенную нагрузку интенсивностью wo по всей своей длине. длина. Определить wo, если fbt ≤ 40 МПа и fbc ≤ 80 МПа. Решение 548
- Проблема 549 Балка с поперечным сечением, показанным на рис. П-549, нагружена таким образом, что максимальные моменты составляют +1,0P фунт-фут и -1,5P фунт-фут, где P — приложенная нагрузка в фунтов стерлингов. Определите максимальное безопасное значение P, если рабочие напряжения составляют 4 тыс.фунтов на кв. дюйм в растяжение и 10 ksi при сжатии. Решение 549
- Проблема 550 Решить проблему. 549, если максимальные моменты составляют +2,5P фунт·фут и -5,0P фунт·фут. Решение 550
- Проблема 551
Найти максимальные растягивающие и сжимающие изгибные напряжения консольной балки.
 показано на рис. П-551.
Решение 551
показано на рис. П-551.
Решение 551 - Проблема 552 Консольная балка несет силу и пару, показанные на рис. П-552. Обозначить максимальные растягивающие и сжимающие напряжения изгиба, развиваемые в балке. Решение 552
- Проблема 553 Определить максимальные напряжения растяжения и сжатия при изгибе, возникающие в пучка, как показано на рис. P-553. Решение 553
- Проблема 554 Определить максимальные растягивающие и сжимающие напряжения, возникающие в нависающая балка показана на рис. П-554. Поперечное сечение представляет собой перевернутую букву Т с заданные свойства. Решение 554
- Проблема 555 Балка несет сосредоточенную нагрузку W и общую равномерно распределенную нагрузку 4W как показано на рис. П-555. Какое безопасное значение W можно применить, если fbc ≤ 100 МПа и fbt ≤ 60 МПа? Можно ли приложить большую нагрузку, если секция перевернута? Объяснять.
- Решение 555
- Проблема 556
Т-образная балка поддерживает три сосредоточенные нагрузки, показанные на рис.
 P-556. Докажите, что НС
находится на 3,5 дюйма выше дна и что INA = 97,0 дюйма4
. Затем используйте эти значения для определения
максимальное значение P, чтобы fbt ≤ 4 тыс.фунтов/кв.дюйм и fbc ≤ 10 тыс.фунтов/кв.дюйм.
Решение 556
P-556. Докажите, что НС
находится на 3,5 дюйма выше дна и что INA = 97,0 дюйма4
. Затем используйте эти значения для определения
максимальное значение P, чтобы fbt ≤ 4 тыс.фунтов/кв.дюйм и fbc ≤ 10 тыс.фунтов/кв.дюйм.
Решение 556 - Проблема 557 Чугунная балка длиной 10 м, опирающаяся на рис. П-557, несет равномерно распределенная нагрузка интенсивностью wo (включая собственный вес). Допустимые напряжения fbt ≤ 20 МПа и fbc ≤ 80 МПа. Определите максимальное безопасное значение wo, если x = 1,0 м. Решение 557
- Проблема 558 В Проб. 557, найдите значения x и wo, чтобы wo было максимальным. Решение 558
Реклама
5.2 Метод соединений – инженерная механика: статика
Глава 5: Фермы
Метод соединений представляет собой форму анализа частиц. После определения сил реакции вы решаете неизвестные силы в каждом соединении, пока не найдете значение каждого элемента. Вы начинаете со своей модели:
Преобразование ограничений в силы реакции с соответствующими метками:
Теперь найдите силы реакции (R ax R ay R e ), рассматривая только внешние силы, используя уравнения равновесия для твердого тела:
$$\сумма F_x=0\\\сумма F_y=0\\\сумма M=0$$
Предполагая, что длина каждого элемента равна L:
$$\sum F_x=R_{ax} = 0, \\\underline{R_{ax} = 0}$$
$$\sum F_y=R_{ay}+R_e – F_g – F_f= 0, \\R_{ay} +R_e = 150 фунтов$$
$$\sum M_a= -L*F_g – 2L * F_f+3L*R_e = 0\\R_e = \frac{100L + 100L}{3L}\\\underline{R_e =66,7 фунта} $$
$$ R_{ay} = 150 фунтов – 66,7 фунтов\\ \underline{ R_{ay}= 83,3 фунтов }$$
Затем выберите соединение, в котором есть 2 или меньше неизвестных значений, таких как a или e. Это потому, что у вас есть только 2 уравнения для поиска неизвестных: [латекс]\сумма F_x=0 \текст{, } \сумма F_y=0[/латекс]. В следующей таблице показано количество известных и неизвестных сил в каждом суставе.
Это потому, что у вас есть только 2 уравнения для поиска неизвестных: [латекс]\сумма F_x=0 \текст{, } \сумма F_y=0[/латекс]. В следующей таблице показано количество известных и неизвестных сил в каждом суставе.
| Соединение: | и | б | с | д | и | ф | г | ||||||||||||||||||||||||||||||
| Известные силы: | 2 | 0 | 0 | 0 | 1 | 1 | 1 | ||||||||||||||||||||||||||||||
| Неизвестные силы: | 2 9\circ) = – (-96,2 \text{ фунт}) * (0,5) \\ \underline{F_{ag} = + 48,1 \text{ фунт}} \text{(натяжение)}$$ Затем перейдите к суставу b, потому что теперь у вас есть только 2 неизвестных в суставе b (F bc и F bg ). Продолжайте анализировать соединения, пока не рассчитаете нагрузку на все элементы:
И все! Если вы не указываете сжатие или растяжение, вы должны использовать положительные и отрицательные значения для обозначения растяжения и сжатия соответственно.
Вот второе объяснение, как решать методом соединений: Метод соединений — это процесс, используемый для расчета неизвестных сил, действующих на элементы фермы . Процесс, используемый в методе соединений, описан ниже:
Источник: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap.psu.edu/websites/5_structures/5-4_method_of_joints/methodofjoints.html
Дополнительные примеры с веб-страницы Engineering Mechanics: Пример 1:Найдите силу, действующую на каждый элемент ферменного моста, показанного ниже. Не забудьте указать, находится ли каждый элемент в растяжении или сжатии.
Решение: Источник: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap.psu.edu/websites/5_structures/5-4_method_of_joints/pdf/MethodOfJoints_WorkedExample1. |
 56 МБ
56 МБ э.
э.  Этот метод сосредоточен на стыках или точках соединения между элементами, и обычно это самый быстрый и простой способ решения всех неизвестных сил в конструкции фермы.
Этот метод сосредоточен на стыках или точках соединения между элементами, и обычно это самый быстрый и простой способ решения всех неизвестных сил в конструкции фермы.
 $$\sum\vec F=0\\\sum F_x=0\ :\сумма F_y=0$$
$$\sum\vec F=0\\\sum F_x=0\ :\сумма F_y=0$$